1976年唐山大地震发生后, 地震工作者一直关注晋冀蒙交界区地震活动, 并相继开展了多方面的研究工作^[1-3]。国内外许多震例表明，在地震孕育发生的过程中会观测到明显的断层形变前兆异常^[4]。虽然多种观测手段已应用于垂直形变监测^[5-6]，但历年的水准复测资料仍有不可替代的学术价值和应用价值^[7-9]。

目前基于水准复测数据的研究方法是对资料中连续观测点的数据进行处理分析，但随着时间的增加，多种原因导致水准点资料丢失，影响数据的连续性及利用率。鉴于此，本文提出多项式加权内插模型，以距离及断层信息确权，利用相邻复测年份的垂直形变量对研究区数据进行内插，提高水准数据的连续性及利用率，并以内插点的垂直形变量、形变速率及形变加速率构建状态向量，再利用卡尔曼滤波模型进行处理，以对研究区的垂直形变特征进行分析。

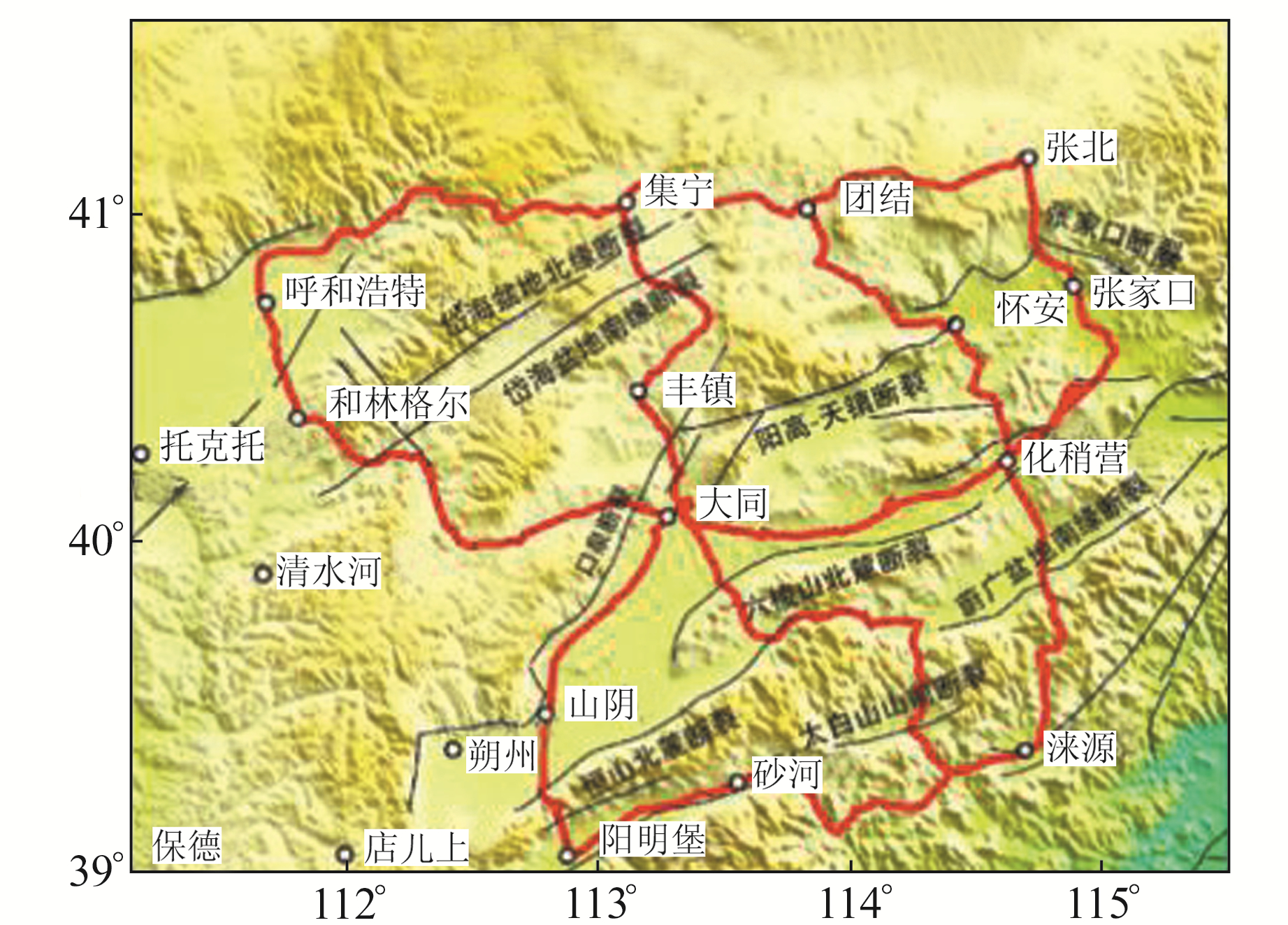
1 实验区域水准监测情况

中国地震局第一监测中心1980年对水准路线进行改造后，多次对晋冀蒙地区进行水准复测, 水准数据的复测最短时间间隔为3 a，而每年的监测任务都在3个月内完成。因此，本文利用静态平差的方式，以大同基岩点为基准点，进行复测年份水准网的平差计算。2018年完成晋冀蒙交界区最新一期水准复测工作，包括20条一等水准观测路线，总长度约1 980.7 km。复测路线如图 1所示。

为更好地利用2018年的水准复测数据，对研究区内历年的水准复测资料进行平差处理后，选择同名水准点进行统计，如表 1所示。

通过表 1可以看出，相邻复测年份水准点的重复率较高，基本都在40%左右，但由于受城市发展等因素的影响，时间间隔越久，水准点被破坏的越多，导致不同复测年份间水准点的重复率越低，在一定程度上影响数据的连续性。1984年与2018年水准点的重复率仅为13.07%，不仅难以准确计算观测区域的垂直形变特征，且被破坏点的前期观测数据也无法使用，降低了利用率。因此，本文构建多项式加权内插模型对相邻水准复测年份的垂直形变量结果进行内插，比对研究区内内插点垂直形变量的变化特征，以提高水准复测数据的利用率和连续性。

2 数据处理模型构建

当研究区内的数据量无法满足分析需求时，需要通过内插的方式进行补充。一般的内插手段有距离内插、线性内插等，但在大范围的水准数据分析中，这些内插手段效果不佳，因为地壳的垂直形变特征随着所处地块的不同，变化量也不同。因此，本文通过构建多项式加权内插模型完成晋冀蒙交界区的数据内插，并利用卡尔曼滤波模型对内插结果进行处理及分析。

2.1 多项式加权内插模型

以相邻复测年份求解的垂直形变量为准，以距离及断层位置确权，对内插点的形变量进行求解。假设待求内插点为i，选取内插点一定距离范围内的n个水准数据构建点集p，则内插点垂直形变量的求解公式为：

$ \left\{ \begin{array}{l} {h_i} = \sum\limits_{j = 1}^{j = n} {{h_{{p_j}}}} \cdot {\theta _j}\\ {\theta _j} = \frac{{{\vartheta _{{j_{{\rm{dis}}}}}} \cdot \vartheta _{{j_{{\rm{dc}}}}}^t}}{{\sum\limits_{j = 1}^{j = n} {{\vartheta _{{j_{{\rm{dis}}}}}}} \cdot \vartheta _{{j_{{\rm{dc}}}}}^t}}\\ {\vartheta _{{j_{{\rm{dis}}}}}} = \frac{{\sum\limits_{j = 1}^{j = n} {{{{\mathop{\rm dis}\nolimits} }_{ij}}} }}{{\sum\limits_{j = 1}^{j = n} {\frac{{\sum\limits_{j = 1}^{j = n} {\rm{d}} {\rm{i}}{{\rm{s}}_{ij}}}}{{{\rm{di}}{{\rm{s}}_{ij}}}}} }} \end{array} \right. $

(1)

式中，h_i为内插点i的垂直形变量；h_pj为点集p中第j个水准观测点的垂直形变量；θ_j为该点的权重，由距离$ {\vartheta _{{j_{{\rm{dis}}}}}}$及断层信息$ {\vartheta _{{j_{{\rm{dc}}}}}^t}$确定；$ {\vartheta _{{j_{{\rm{dc}}}}}^t}$取决于内插点及观测点与断层的位置关系，当内插点与观测点处于断层同侧时，$ {\vartheta _{{j_{{\rm{dc}}}}}}$取值为1，否则为K；t为内插点与观测点之间的断层个数。

K值的不同会导致内插精度的不同，本文利用2015~2018年晋冀蒙交界区数据进行内插，选择10%的观测数据进行精度评定。对于不同的K值，内插精度以中误差进行评定，计算结果如表 2(单位mm)所示。

通过比较，K值取0.3时内插效果最好。

2.2 精度评定

为了验证该模型的精度，以2015~2018年水准复测数据计算得到的垂直形变量中90%的数据作为实验数据，对晋冀蒙交界区垂直形变特征进行内插，以剩余的10%数据作为验证数据，对比反向距离内插法、线性内插法及多项式加权内插法的精度，结果如表 3(单位mm)所示。

从计算结果可以看出，线性内插法在大范围观测区域内进行水准内插时精度较低，内插结果与验证数据的最大差值为49.911 3 mm，中误差为26.105 1 mm。

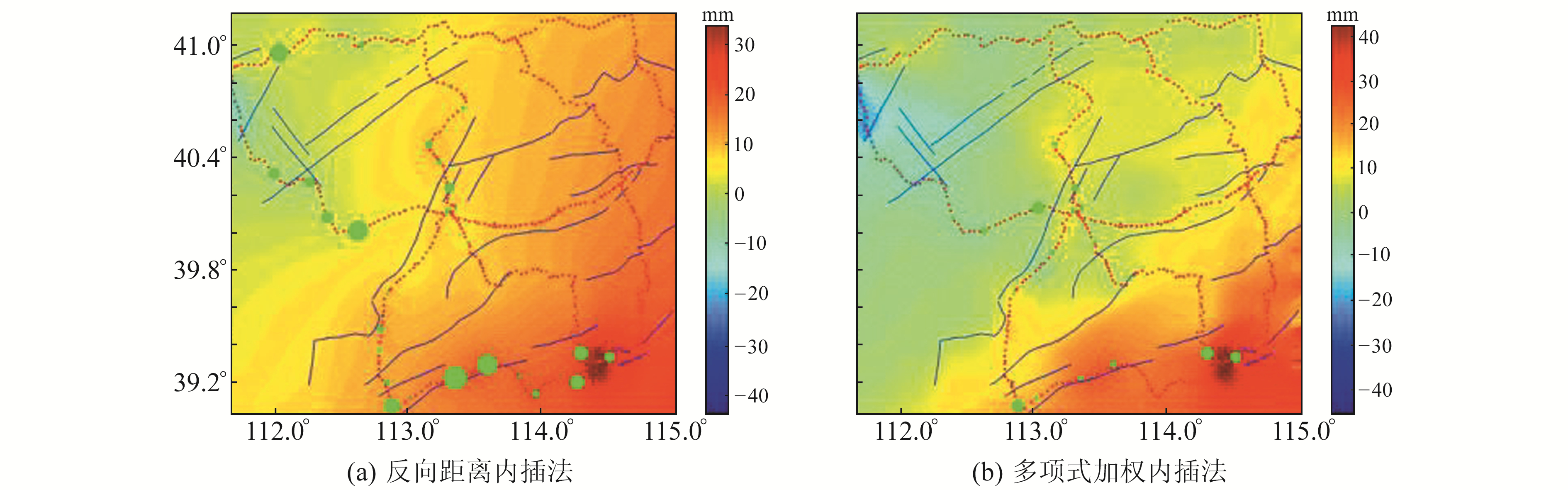
反向距离内插法是以一定范围内观测点距离的倒数作为权，对内插点的垂直形变量进行求解。本文反向距离内插法及多项式加权内插法结果差值的空间分布及大小如图 2所示，图中红色圆球为水准观测点，蓝色线条为研究区内的断层，底图为内插结果，绿色圆球为内插数据与验证数据的差值，其大小表示差值的大小。图 2(a)仅以距离作为确权的参数，垂直形变特征内插结果存在一定的误差，且大部分围绕在断层附近；图 2(b)以距离和断层信息确权，构建多项式加权内插模型，很大程度上提高了内插的精度，能够更加真实地反映研究区内的垂直形变特征。因此，本文利用多项式内插模型对研究区进行处理。

2.3 卡尔曼滤波处理

利用多项式加权内插模型对相邻水准复测年份的垂直形变量进行内插。假设地面点i在k时刻的垂直形变量为$ {{\mathit{\boldsymbol{\xi }}_i}(k)}$, 垂直形变速率为${{\mathit{\boldsymbol{\lambda }}_i}(k)} $，垂直形变加速率为$ {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}(k)}$，则：

$ {{\mathit{\boldsymbol{\xi }}_i}(k) = {\mathit{\boldsymbol{\lambda }}_i}(k)} $

(2)

$ {{{\mathit{\boldsymbol{\dot \lambda }}}_i}(k) = {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}(k)} $

(3)

内插点的状态向量可以描述为垂直形变信息、瞬时速率及瞬时加速率的函数，记为：

$ {f\left( {{\mathit{\boldsymbol{\xi }}_i}(k), {\mathit{\boldsymbol{\lambda }}_i}(k), {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}k} \right)} $

(4)

令i点的状态向量为$ {\mathit{\boldsymbol{X}}_i}(k)$，所有内插点的状态向量记为X(k)，测区范围内的状态模型可以表示为：

$ {\mathit{\boldsymbol{X}}_i}(k) = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\xi }}_i}(k)}\\ {{\mathit{\boldsymbol{\lambda }}_i}(k)}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}(k)} \end{array}} \right], \mathit{\boldsymbol{X}}(t) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_1}(k)}\\ {{\mathit{\boldsymbol{X}}_2}(k)}\\ \vdots \\ {{\mathit{\boldsymbol{X}}_n}(k)} \end{array}} \right] $

(5)

则k时刻的状态方程与观测方程为：

$ \left\{\begin{array}{l} \overline{\boldsymbol{X}}_{k+1}=\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k+1, k} \boldsymbol{X}_{k}+\boldsymbol{\omega}_{k}=\left[\begin{array}{ccc} \boldsymbol{I} & t & \frac{1}{2} t^{2} \\ 0 & \boldsymbol{I} & t \\ 0 & 0 & \boldsymbol{I} \end{array}\right] \boldsymbol{X}_{k}+\boldsymbol{\omega}_{k} \\ \boldsymbol{L}_{k+1}=\boldsymbol{B}_{k+1} \boldsymbol{X}_{k+1}+\boldsymbol{\Delta}_{k+1} \end{array}\right. $

(6)

式中，$\boldsymbol{X}_{k} $为k时刻的状态向量，$ \overline{\boldsymbol{X}}_{k+1}$为k+1时刻的预测状态向量，$ \boldsymbol{\omega}_{k}$为随机干扰，$ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k+1, k}$为状态转换参数，$ \boldsymbol{L}_{k+1}$为k+1时刻的观测值，$\boldsymbol{B}_{k+1} $为k+1时刻的已知系数矩阵，$ \boldsymbol{\Delta}_{k+1}$为k+1时刻的观测误差。

通过上式完成预测后，需要对卡尔曼增益矩阵$\boldsymbol{J}_{k+1} $及误差协方差矩阵$ \overline{\boldsymbol{D}}_{X}(k+1, k)$进行求解，进一步修正状态向量预测值$ \overline{\boldsymbol{X}}_{k+1}$：

$ \left\{\begin{array}{l} \overline{\boldsymbol{D}}_{X}(k+1, k)=\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k+1, k} \boldsymbol{D}_{X}(k) \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k+1, k}^{\mathrm{T}} \\ \boldsymbol{J}_{k+1}=\boldsymbol{D}_{X}(k+1, k) \boldsymbol{B}_{k+1}^{\mathrm{T}}+ \\ {\left[\boldsymbol{B}_{k+1} \boldsymbol{D}_{X}(k+1, k) \boldsymbol{B}_{k+1}^{\mathrm{T}}+\boldsymbol{D}_{\Delta}(k+1)\right]^{-1}} \end{array}\right. $

(7)

更新后的状态向量及协方差矩阵为：

$ \left\{\begin{array}{l} \boldsymbol{X}_{k+1}=\overline{\boldsymbol{X}}_{k+1}+\boldsymbol{J}_{k+1}\left[\boldsymbol{L}_{k+1}-\boldsymbol{B}_{k+1} \overline{\boldsymbol{X}}_{k+1}\right] \\ \boldsymbol{D}_{X}(k+1)=\left[\boldsymbol{I}-\boldsymbol{J}_{k+1} \boldsymbol{B}_{k+1}\right] \overline{\boldsymbol{D}}_{X}(k+1, k) \end{array}\right. $

(8)

通过上述方程实现研究区范围内内插点的滤波，对垂直形变量、形变速率及加速率进行求解。

3 实验分析

收集整理1984年以来晋冀蒙交界地区的水准复测数据，主要包括1984年、1987年、2002年、2006年、2015年及2018年共6期数据。对历年水准复测数据进行平差处理，以相邻年份同名水准点的垂直形变量为基准对相邻年份的研究区进行内插，并以内插点的垂直形变量、垂直形变速率及垂直形变加速率组成的状态向量构建卡尔曼滤波模型，对研究区数据进行滤波处理，并进行实验分析。

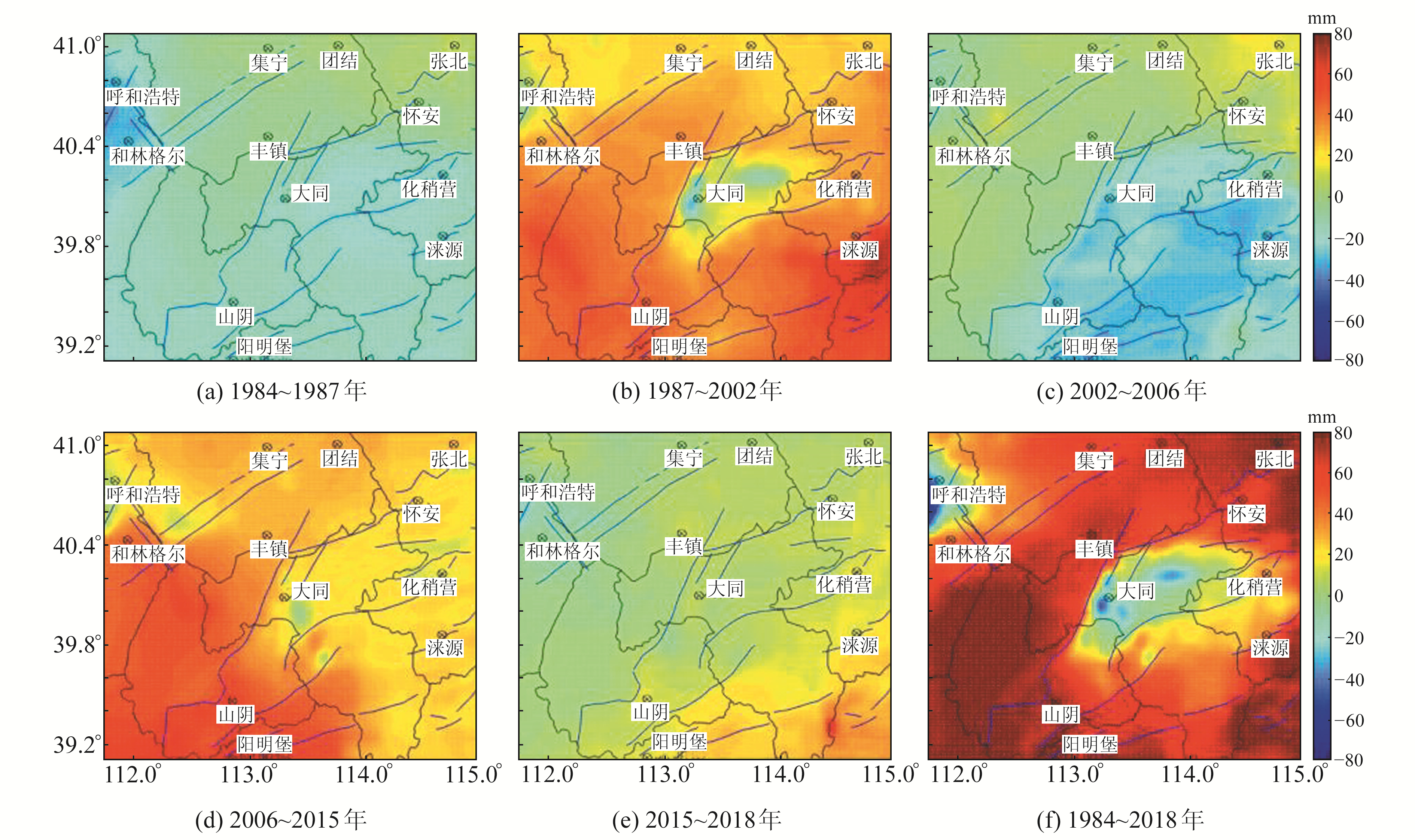
计算1984~1987年、1987~2002年、2002~2006年、2006~2015年和2015~2018年共5期垂直形变结果及1984~2018年整体形变结果。从图 3(a)可以看到，研究区在1984~1987年期间的差异沉降作用不是很明显，仅在呼和浩特盆地出现明显的差异沉降，另外沿着口泉断裂和阳高-天镇断裂出现幅度约10 mm/a的差异沉降变化，而六棱山北缘断裂两侧则未出现明显的差异变化。1987~2002年期间，研究区发生1989年大同6.0级地震，而图 3(b)也显示出明显的盆山差异活动，代表了研究区震间的垂直形变量。从2002~2006年数据结果(图 3(c))来看，研究区仍以继承性活动为主，盆地沉降，山区隆升。至2006~2015年期间(图 3(d))，研究区内继承性差异升降变化逐渐减弱，总体显示西南部隆升增强，可能与青藏高原块体对鄂尔多斯地块的推挤作用有关^[10]，也可能与2008年四川汶川8.0级地震有直接关系^[11]。2015~2018年的结果(图 3(e))显示，除蔚县盆地和五台山北麓断裂附近出现差异升降变化外，研究区范围内并未出现明显的差异升降变化。从连续多期数据来看，研究区差异升降运动逐渐减弱，转为以受青藏高原块体挤压运动为主，总体呈隆升状态，盆地与山区的差异升降运动不显著(这可能与数据分布有关)，断层可能存在闭锁状态，具有潜在的地震危险性，应注意拉张或者沉降区的出现。

另外，研究区1984~2018年的年均垂直形变量结果显示，大同盆地出现明显的沉降形变，且有2个沉降中心，第1个沉降中心位于大同市区，第2个沉降中心位于阳高县和阳原县之间。从沉降中心的位置来看，控制大同盆地升降运动的主要断裂为口泉断裂，其深度及规模远大于阳高-天镇断裂和六棱山北缘断裂，但由于沉降作用的持续进行，口泉断裂可能并未闭锁，因此其地震危险性可能并不是很强, 1989年的大同地震印证了这一可能性。该地震发生在六棱山北缘断裂(桑干河断裂)上，但震前该断裂附近并未出现明显的差异升降变化，可能存在一定程度的闭锁。因此，可能存在这样一种发震模式，即盆地西边界持续出现沉降，当盆地东边界无法“支撑”盆地内“块体”重量时，“块体”突然下落，从而发生地震。

综上所述，应注意研究区内新的沉降区或者差异升降运动的出现，其可能成为潜在的地震危险区，可配合跨断层水准资料的持续跟踪分析开展地震预测预报。

4 结语

本文提出多项式加权内插模型，针对水准复测结果，以距离及断层信息确权，对研究区内的垂直形变量进行处理，提高了水准复测数据的连续性和利用率。利用卡尔曼滤波模型对内插结果进行滤波，分析1984年以来晋冀蒙交界地区的垂直形变变化特征，发现与前人的研究结果相同，证明本文方法具有可行性，对地震研究有一定的参考意义。

虽然本文数据时间跨度相对较大，但水准复测期数仍有限，利用滤波结果进行预测时会存在偏差。后期会针对复测结果继续跟进，丰富数据量，实现对该区未来一段时间内垂直形变特征的预测。