国内外研究人员基于总体最小二乘(total least squares,TLS)算法开展的研究取得了丰硕成果[1-3],Neitzel[4]提出基于高斯-赫尔默特模型通过最小二乘法迭代收敛求解总体最小二乘解;Mercan等[5]利用四元数表示三维旋转矩阵,求得更加符合实际的加权总体最小二乘解。但以上研究中坐标转换的方法均没有考虑观测值含有粗差的情况,在空间坐标转换中普遍采用了基于选权迭代法的抗差估计算法。常见的等价权函数有Danish法[6]、IGGⅠ方案、IGGⅢ方案等,都是根据残差重新定权来降低粗差的影响。但是,一个全面的抗差方案应当包括观测空间和结构空间抗差[7],以上函数在使用加权总体最小二乘处理观测值含有粗差问题时有着共同的缺陷,即由于模型所采用的权因子函数是基于未调整的残差塑造的,理论上存在缺陷,导致结构空间不能抵抗粗差。本文基于加权对称相似变换方法[5],结合三段Danish法[6],采用一种中位数法求解具有抗差性的单位权中误差,进一步求得标准化残差,构造权因子函数,从而增强结构空间抵抗粗差的能力;并根据协因数传播定律推导残差协因数阵的表现形式,给出相应算法的迭代步骤,进行稳健加权对称相似变换。
1 基于四元数的加权对称相似变换(WSSTUQ)三维坐标转换的高斯-赫尔默特模型可以表示为[5]:
| $ \left[ {\begin{array}{*{20}{l}} {X + {e_X}}\\ {Y + {e_Y}}\\ {Z + {e_Z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{T_X}}\\ {{T_Y}}\\ {{T_Z}} \end{array}} \right] + k\mathit{\boldsymbol{R}}\left[ {\begin{array}{*{20}{l}} {x + {e_x}}\\ {y + {e_y}}\\ {z + {e_z}} \end{array}} \right] $ | (1) |
式中,y1=[X Y Z]T为目标坐标系下的观测向量,e1=[eX eY eZ]T为y1中所包含的随机误差;y2=[x y z]T为源坐标系下的观测向量,e2=[ex ey ez]T为y2中所包含的随机误差;TX、TY、TZ为坐标平移参数,k为旋转尺度,R为旋转矩阵。
设由随机误差向量e1、e2和未知参数ξ组成的观测方程为:
| $ \psi ({\mathit{\boldsymbol{e}}_{{1}}},{\mathit{\boldsymbol{e}}_{{2}}},\mathit{\boldsymbol{\xi }}) = h\left( {{\mathit{\boldsymbol{y}}_{{1}}} + {\mathit{\boldsymbol{e}}_{{1}}},{\mathit{\boldsymbol{y}}_{{2}}} + {\mathit{\boldsymbol{e}}_{{2}}},\mathit{\boldsymbol{\xi }}} \right) = 0 $ | (2) |
令随机误差向量和未知参数的近似值分别为e10、e20和ξ0,则式(1)线性化为:
| $ \begin{array}{l} f({\mathit{\boldsymbol{e}}_{{1}}},{\mathit{\boldsymbol{e}}_{{2}}},\mathit{\boldsymbol{\xi }}) \approx {\mathit{\boldsymbol{B}}_{{{{1}}_{{0}}}}}({\mathit{\boldsymbol{e}}_{{1}}} - \mathit{\boldsymbol{e}}_{{1}}^{{0}}) + {\mathit{\boldsymbol{B}}_{{{{2}}_{{0}}}}}({\mathit{\boldsymbol{e}}_{{2}}} - \mathit{\boldsymbol{e}}_{{2}}^{{0}}) + \\ \mathit{\boldsymbol{A}}(\mathit{\boldsymbol{\xi }} - {\mathit{\boldsymbol{\xi }}^{{0}}}) + \psi (\mathit{\boldsymbol{e}}_{{1}}^{{0}},\mathit{\boldsymbol{e}}_{{2}}^{{0}},{\mathit{\boldsymbol{\xi }}^{{0}}}) = {{0}} \end{array} $ | (3) |
式中,
总体最小二乘的目标函数为:
| $ \mathit{\Phi} = \mathit{\boldsymbol{e}}_{{1}}^{\rm{T}}\mathit{\boldsymbol{Q}}_{{1}}^{ - {\rm{1}}}{\mathit{\boldsymbol{e}}_{{1}}} + \mathit{\boldsymbol{e}}_{{2}}^{\rm{T}}\mathit{\boldsymbol{Q}}_{{2}}^{ - {\rm{1}}}{\mathit{\boldsymbol{e}}_{{2}}} = \min $ | (4) |
利用拉格朗日乘数λ重新构造目标函数为:
| $ \begin{array}{l} \mathit{\Phi} ({\mathit{\boldsymbol{e}}_{{1}}},{\mathit{\boldsymbol{e}}_{{2}}},\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\lambda }}) = \mathit{\boldsymbol{e}}_{{1}}^{\rm{T}}\mathit{\boldsymbol{Q}}_{{1}}^{ - {{1}}}{\mathit{\boldsymbol{e}}_{{1}}} + \mathit{\boldsymbol{e}}_{{2}}^{\rm{T}}\mathit{\boldsymbol{Q}}_{{2}}^{ - {{1}}}{\mathit{\boldsymbol{e}}_{{2}}} - \\ \;\;\;\;\;\;\;\;\;\;2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\psi ({\mathit{\boldsymbol{e}}_{{1}}},{\mathit{\boldsymbol{e}}_{{2}}},\mathit{\boldsymbol{\xi }}) = \min \end{array} $ | (5) |
要使Φ(e1, e2, ξ, λ)最小,则Φ(e1, e2, ξ, λ)关于e1、e2和ξ的偏导数应等于零,即:
| $ {\left. {\frac{{\partial \mathit{\Phi} }}{{2\partial {\mathit{\boldsymbol{e}}_{{1}}}}}} \right|_{{{{e}}_{{1}}}{{,}}{{{e}}_{{2}}}{{, {{ ξ}} , {{ λ}} }}}} = \mathit{\boldsymbol{Q}}_{{1}}^{ - {\rm{1}}}{\mathit{\boldsymbol{e}}_{{1}}} - \mathit{\boldsymbol{B}}_{{{{1}}_{{0}}}}^{\rm{T}}\mathit{\boldsymbol{\lambda }} = {{0}} $ | (6) |
| $ {\left. {\frac{{\partial \mathit{\Phi} }}{{2\partial {\mathit{\boldsymbol{e}}_{{2}}}}}} \right|_{{{{e}}_{{1}}}{{,}}{{{e}}_{{2}}}{{, {{ ξ}} , {{ λ}} }}}} = \mathit{\boldsymbol{Q}}_{{2}}^{ - {\rm{1}}}{\mathit{\boldsymbol{e}}_{{2}}} - \mathit{\boldsymbol{B}}_{{{{2}}_{{0}}}}^{\rm{T}}\mathit{\boldsymbol{\lambda }} = {{0}} $ | (7) |
| $ {\left. {\frac{{\partial \mathit{\Phi} }}{{2\partial \mathit{\boldsymbol{\xi }}}}} \right|_{{{{e}}_{{1}}}{{,}}{{{e}}_{{2}}}{{, {{ ξ}} , {{ λ}} }}}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }} = {{0}} $ | (8) |
| $ {\left. {\frac{{\partial \mathit{\Phi} }}{{2\partial \mathit{\boldsymbol{\lambda }}}}} \right|_{{{{e}}_{{1}}}{{,}}{{{e}}_{{2}}}{{, {{ ξ}} , {{ λ}} }}}} = \psi ({\mathit{\boldsymbol{e}}_{{1}}},{\mathit{\boldsymbol{e}}_{{2}}},\mathit{\boldsymbol{\zeta }}) = {{0}} $ | (9) |
整理可得:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_{{1}}} + {\mathit{\boldsymbol{B}}_{{{{2}}_{{0}}}}}{\mathit{\boldsymbol{Q}}_{{2}}}\mathit{\boldsymbol{B}}_{{{{2}}_{{0}}}}^{\rm{T}}}&\mathit{\boldsymbol{A}}\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}}&{{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat \lambda }}}^{{1}}}}\\ {{{\mathit{\boldsymbol{\hat \xi }}}^{{1}}} - {\mathit{\boldsymbol{\xi }}^{{0}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{w}}\\ {{0}} \end{array}} \right] = {{0}} $ | (10) |
求解式(10),可得未知参数
| $ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat e}}}_{{1}}}}\\ {{{\mathit{\boldsymbol{\hat e}}}_{{2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_{{1}}}}\\ {{\mathit{\boldsymbol{Q}}_{{2}}}\mathit{\boldsymbol{B}}_{{{{2}}_{{0}}}}^{{\rm T}}} \end{array}} \right]{\mathit{\boldsymbol{\hat \lambda }}^{{1}}} $ | (11) |
相应的单位权方差为:
| $ \sigma _0^2 = \frac{{\mathit{\boldsymbol{e}}_{{1}}^{\rm{T}}\mathit{\boldsymbol{Q}}_{{1}}^{ - {\rm{1}}}{\mathit{\boldsymbol{e}}_{{1}}} + \mathit{\boldsymbol{e}}_{{2}}^{\rm{T}}\mathit{\boldsymbol{Q}}_{{2}}^{ - {\rm{1}}}{\mathit{\boldsymbol{e}}_{{2}}}}}{{3m - 7}} $ | (12) |
式中,m为坐标点个数。根据式(10)~式(12)进行迭代计算,每次迭代更新
本文使用2个标量来评估方法的性能,即偏差和均方根误差:
| $ {\rm{bias}}{}_{{ {{ ξ}} }} = \sum\nolimits\limits_{i = 1}^n {({\mathit{\boldsymbol{\xi }}_{{i}}} - {\mathit{\boldsymbol{\xi }}_{{\rm{tv}}}})} /n $ | (13) |
| $ {\rm{RMSE}} = \sqrt {\sum\nolimits\limits_{i = 1}^n {{{({\mathit{\boldsymbol{\xi }}_{{i}}} - {\mathit{\boldsymbol{\xi }}_{{\rm{tv}}}})}^2}/n} } $ | (14) |
式中,n为模拟实验次数,ξi为第i次实验求得的参数,ξtv为参数真值。
2 基于四元数的加权对称相似变换稳健估计 2.1 稳健加权对称相似变换(RWSST)基于本文方法的稳健估计,关键技术是推导预测残差的协因数阵并构造所需的检验量。由式(6)~式(8)及式(10)可得,WSSTUQ方法在第(i+1)次迭代的预测残差向量Ve为:
| $ {\mathit{\boldsymbol{V}}_{{e}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat e}}_{{1}}^{{\rm{(}}i + {\rm{1)}}}}\\ {\mathit{\boldsymbol{\hat e}}_{{2}}^{{\rm{(}}i + {\rm{1)}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}\\ \mathit{\boldsymbol{N}} \end{array}} \right]\mathit{\boldsymbol{R}} $ | (15) |
式中,M=-Q1Qc(i)-1,N=-Q2BT(i)20Qc(i)-1,R=L-A(i) 1(i+1),Qc(i) =Q1+B(i)20Q2BT(i)20,L=y1-kRy2-[TX TY TZ]T。
根据协因数传播率[8]可得残差协因数阵为:
| $ {\mathit{\boldsymbol{Q}}_{{{{V}}_{{e}}}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{Q}}_{{R}}}{\mathit{\boldsymbol{M}}^{\rm{T}}}}&{\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{Q}}_{{R}}}{\mathit{\boldsymbol{N}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{Q}}_{{R}}}{\mathit{\boldsymbol{M}}^{\rm{T}}}}&{\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{Q}}_{{R}}}{\mathit{\boldsymbol{N}}^{\rm{T}}}} \end{array}} \right] $ | (16) |
根据式(15)得:
R=L-A(i) 1(i+1)=L-A(i)((AT)(i)(Qc(i))-1 (A(i)))-1(AT)(i)(Qc(i))-1L= (I-A(i)((AT)(i) (Qc(i))-1(A(i)))-1(AT)(i)(Qc(i))-1)L=(I-F(i))L式中,F=A(i)((AT)(i)(Qc(i))-1(A(i)))-1(AT)(i) (Qc(i))-1。
R的协因数阵为:
| $ {\mathit{\boldsymbol{Q}}_{{R}}} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{F}}^{(i)}}} \right){\mathit{\boldsymbol{Q}}_{{L}}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{F}}^{(i)}}} \right)^{\rm{T}}} $ | (17) |
又因为
| $ \begin{array}{l} \mathit{\boldsymbol{L}} = {\mathit{\boldsymbol{y}}_{{1}}} - {\left[ {\begin{array}{*{20}{c}} {{T_X}}&{{T_Y}}&{{T_Z}} \end{array}} \right]^{\rm{T}}} - k\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{y}}_{{2}}} = \\ \;\;\;\;\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{{3}}}}&{ - k\mathit{\boldsymbol{R}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_{{1}}}}\\ {{\mathit{\boldsymbol{y}}_{{2}}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{T_X}}\\ {{T_Y}}\\ {{T_Z}} \end{array}} \right] \end{array} $ | (18) |
式中,I3为大小为3的单位阵。则L的协因数阵为:
| $ {\mathit{\boldsymbol{Q}}_{{L}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{{3}}}}&{ - k\mathit{\boldsymbol{R}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_{{1}}}}&{{0}}\\ {{0}}&{{\mathit{\boldsymbol{Q}}_{{2}}}} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{{3}}}}&{ - k\mathit{\boldsymbol{R}}} \end{array}} \right]^{\rm{T}}} $ | (19) |
基于上述公式,对式(15)中的预测残差进行标准化:
| $ {{{\bar v}}_{{{eg}}}} = \frac{{{{{v}}_{{{eg}}}}}}{{{\sigma _0}\sqrt {{{{Q}}_{{{{v}}_{{{eg}}}}}}} }} $ | (20) |
式中,veg为第g个预测残差,Qveg为veg的协因数,σ0为单位权中误差。
采用由中位函数法计算的σ0代入标准化残差模型构建检验量,计算公式为[9-10]:
| $ {\sigma _0} = 1.483\;\mathop {\rm med}\limits_{g = 1}^n \left( {\left| {\frac{{{v_{eg}}}}{{\sqrt {{Q_{{v_{eg}}}}} }}} \right|} \right) $ | (21) |
采用稳健估计理论的选权迭代法,选取Danish权因子函数进行标准化残差稳健估计,第g个权因子为:
| $ {r_{gg}} = \left\{ {\begin{array}{*{20}{l}} {1.0,\left| {{{\bar v}_{eg}}} \right| < {k_0}}\\ {\exp \left( {1 - {{\left( {\frac{{{{\bar v}_{eg}}}}{{{k_1}}}} \right)}^2}} \right),{k_0} \le \left| {{{\bar v}_{eg}}} \right| < {k_1}}\\ {{{10}^{ - 10}},\left| {{{\bar v}_{eg}}} \right| \ge {k_1}} \end{array}} \right. $ | (22) |
式中,k0=1.5, k1=3.0。
综合式(1)~式(11),取P作为等价权矩阵。当进行不等精度独立观测时,根据以下公式求解对角线矩阵P的第g个等价权元素:
| $ {\bar p_g} = {p_g}{r_{gg}} $ | (23) |
当进行不等精度相关观测时,非对角矩阵P的第g行第l列的等价权元素可根据双因子函数模型求解:
| ${\bar p_{gl}} = {p_{gl}}\sqrt {{r_{gg}}{r_{ll}}} $ | (24) |
式中,rgg和rll形式相同。
2.2 稳健加权对称相似变换(RWSST)迭代过程本文将中位函数法与Danish权函数相结合,提出稳健加权对称相似变换(RWSST)的迭代求解方法。具体求解步骤如下:
1) 给定七参数初值ξ0,一般取k=1,其余为0;给定观测向量误差初值e10、e20,一般取误差初值为0,输入观测值权阵P;
2) 将输入初值代入式(6)~式(9),计算矩阵B1、B2、A;
3) 通过式(10)求解转换参数改正数dξ(i+1),通过式(11)求解预测残差Ve(i+1);
4) 将QR=(I-F(i))QL(I-F(i))T代入式(16),求解预测残差协因数阵Q(i+1)Ve;
5) 如果
6) 将获得的残差Ve及残差协因数阵QVe代入式(21),求解抗差性的单位权中误差σ0,然后将σ0代入式(20)构造标准化残差veg,最后通过veg构造权因子函数rgg;
7) 通过式(23)或式(24)计算pg或pgl,组建等价权矩阵p,得到观测值的新权值;
8) 重复步骤1)~5),最终得到七参数估值及观测值残差;
9) 由式(12)进行精度评定,输出σ02。
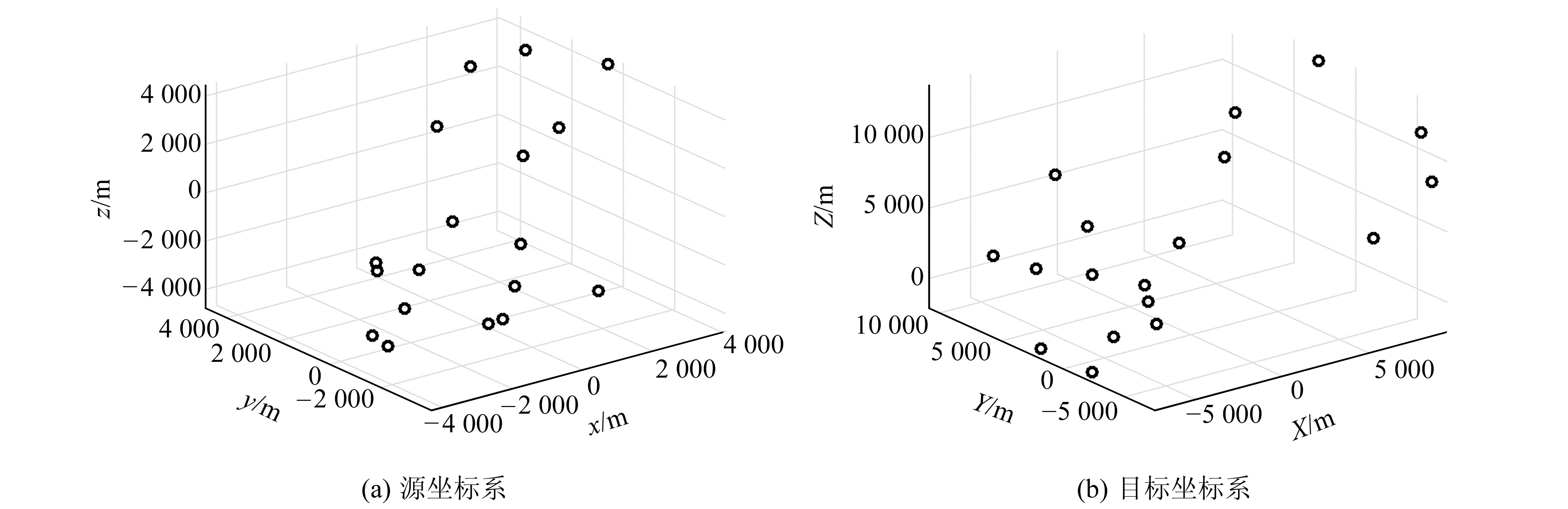
3 模拟算例本文仿真大旋转角坐标转换的实验数据,产生18个在源坐标系和目标坐标系下公共点的真实坐标(图 1)。源坐标系下的公共点坐标取值范围均在-4 000~4 000之间,且18个点位分布均匀;目标坐标系下的公共点真实坐标是由对应的源坐标系坐标与坐标转换参数转换而来。设定的坐标转换七参数为:平移参数(TX, TY, TZ)=(1 000 m, 2 000 m, 5 000 m),缩放因子k=2,旋转参数(θ, φ, ψ)=(57.3°, 65.95°, 98.25°)。然后,采用正态分布函数对公共点在源坐标系和目标坐标系下的坐标真值加入不等精度的随机误差,即生成一组仿真观测值,相应坐标系下的权值Px、Py、Pz、PX、PY、PZ在1~10之间随机产生,且单位权方差σ02在0~0.017 m2间随机产生,生成符合正态分布的随机误差,进而获得18个点位在两套坐标系下的仿真坐标,仿真数据为500组。
|
图 1 坐标分布 Fig. 1 Distribution of coordinates |
为研究多粗差点对本文方法的影响,对生成的每组仿真数据添加粗差,粗差大小为中误差的5~20倍,通过实验验证粗差点个数分别为1、2、3、4、5、6时的6种情形。
按照§2,使用4种方案(方案1:观测值仅含有随机误差时采用加权对称相似变换;方案2:观测值既含有随机误差又含有粗差时采用加权对称相似变换;方案3:观测值既含有随机误差又含有粗差时采用基于IGG的加权对称相似变换;方案4:观测值既含有随机误差又含有粗差时采用稳健加权对称相似变换)进行参数估计。而权函数的选取,在测量实践中认为IGG权函数更优[9],故采用IGG方法与本文方法进行对比。
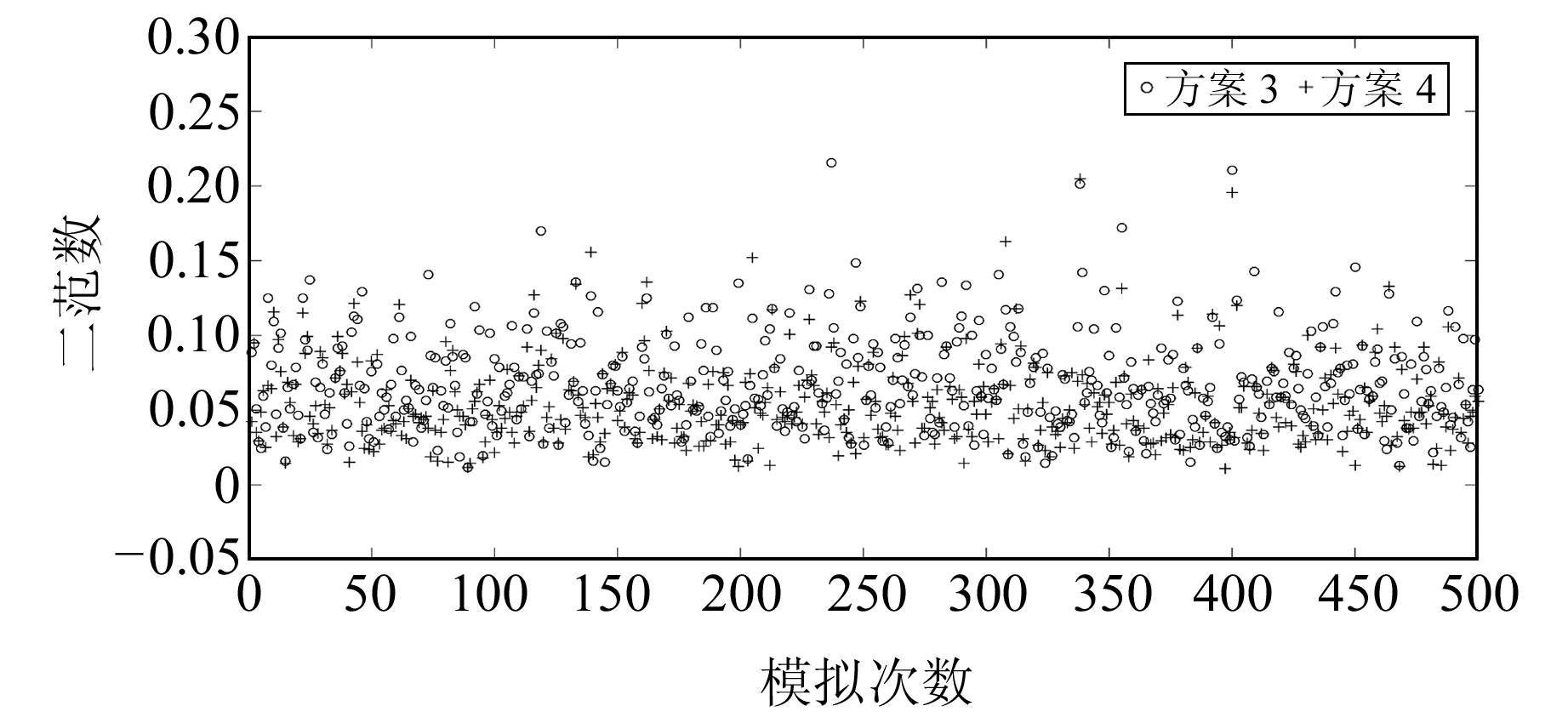
不同粗差点下各方案所求参数估值的均方根误差如表 1~6所示,6个粗差点下方案3和方案4参数偏差的二范数如图 2所示。
|
图 2 含有6个粗差点条件下采用方案3和方案4所得参数偏差二范数对比 Fig. 2 The norm comparison of two parameter deviation when schemes 3 and 4 contains six gross errors |
|
|
表 1 4种方案在1个粗差点条件下的均方根误差对比 Tab. 1 The RMSE comparison of the four schemes when there is one gross error |
|
|
表 2 4种方案在2个粗差点条件下的均方根误差对比 Tab. 2 The RMSE comparison of the four schemes when there are two gross errors |
|
|
表 3 4种方案在3个粗差点条件下的的均方根误差对比 Tab. 3 The RMSE comparison of the four schemes when there are three gross errors |
|
|
表 4 4种方案在4个粗差点条件下的均方根误差对比 Tab. 4 The RMSE comparison of the four schemes when there are four gross errors |
|
|
表 5 4种方案在5个粗差点条件下的均方根误差对比 Tab. 5 The RMSE comparison of the four schemes when there are five gross errors |
|
|
表 6 4种方案在6个粗差点条件下的均方根误差对比 Tab. 6 The RMSE comparison of the four schemes when there are six gross errors |
1) 当观测值只含有随机误差时方案1的结果最优;当观测值同时含有少量粗差时,方案2所得参数估值偏离真值;随着所含粗差点个数的增加,方案2所求参数估值偏离真值的速度加快,其结果严重偏离真值。这是因为方案2只能处理观测值含有随机误差的情况,无法顾及含有粗差的情况,不具备抵抗粗差的能力。
2) 表 1~3显示,当粗差点个数在1~3范围内时,方案3的IGG方法与方案4的稳健加权对称相似变换算法求解的转换参数均方根误差与方案1均方根误差相差甚微,即3个平移参数均方根误差差值均在5 mm以内,尺度比例因子均方根误差差值在10-7量级左右,由于3个欧拉角参数均方根误差差值变动较小,此处不作比较。因此,在含有较少粗差的情况下,方案4优于方案3,虽不明显但仍能证明方案4算法更合理,所求参数的解更精确可靠。
3) 表 4~6显示,当含有4~6个粗差点时,方案4所得七参数的均方根误差明显低于方案3,且在含有6个粗差点时,方案3七参数偏差的二范数明显比方案4的大,方案4七参数偏差的二范数分布更集中。随着粗差点个数的增多,方案3与方案4的七参数均方根误差增大速度加快,二者抵抗粗差的能力明显减弱,但方案4所得的各参数均方根误差仍小于方案3,且方案4所得的七参数均方根误差变化不明显,因此方案4明显优于方案3。
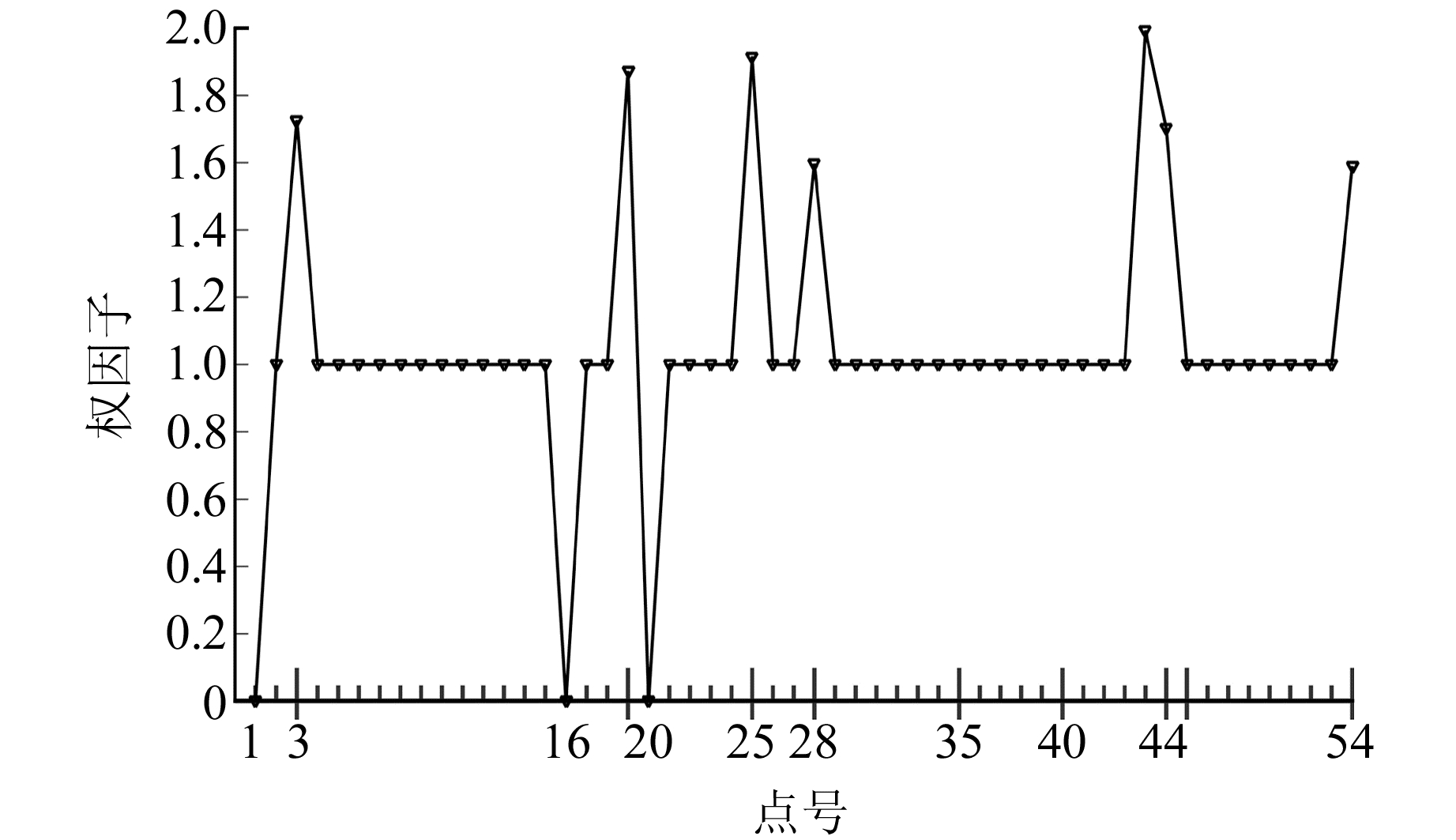
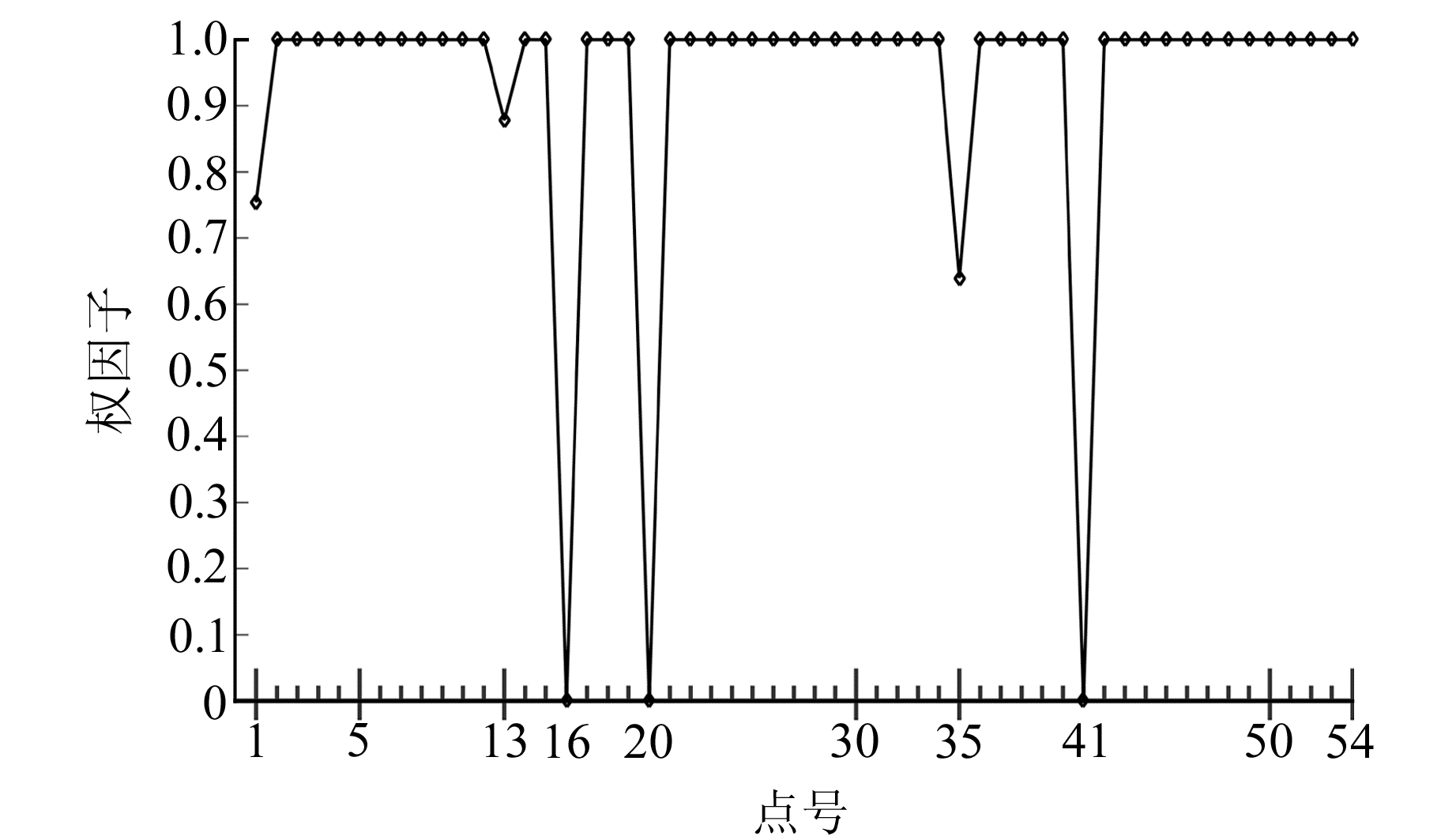
为进一步验证稳健加权对称相似变换(RWSST)对粗差的抵抗能力,求出迭代后的权因子,并作出各点的权因子图。设各点为等精度独立观测,将18个目标坐标系下的坐标(X, Y, Z)看作54个点号,并进行实验。实验1:在第1、第16、第20号点加入粗差,使用本文方法进行选权迭代,结果见图 3;实验2:在第1、第16、第20、第35、第41号点加入粗差,分别使用IGG方法和本文方法进行选权迭代,结果见图 4和5。
|
图 3 当目标坐标系下第1、第16、第20号点含有粗差时采用稳健加权对称相似变换迭代后的权因子 Fig. 3 The weight factor after iteration of the RWSST method while 1 st, 16 th and 20 th points in target system include the gross errors |
|
图 4 当目标坐标系下第1、第16、第20、第35、第41号点含有粗差时采用IGG方法迭代后的权因子 Fig. 4 The weight factor after iteration of IGG method while 1 st, 16 th, 20 th, 35 th and 41 th points in target system include the gross errors |
|
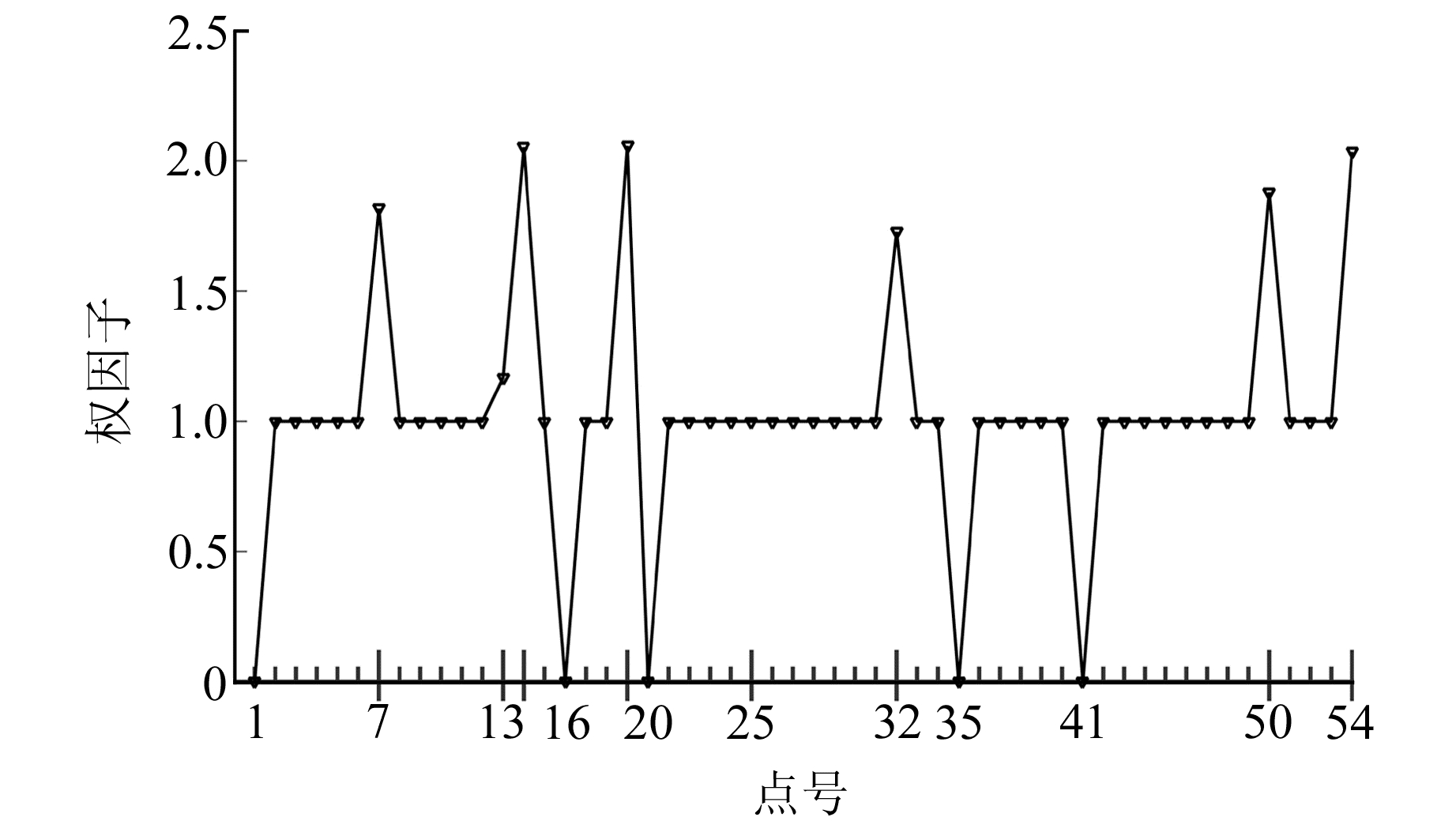
图 5 当目标坐标系下第1、第16、第20、第35、第41号点含有粗差时采用稳健加权总体最小二乘方法迭代后的权因子 Fig. 5 The weight factor after iteration of the RWSST method while 1 st, 16 th, 20 th, 35 th and 41 th points in target system include the gross errors |
由图 3可知,存在粗差的1号、16号和20号点迭代后的权因子均为0,说明本文方法能够较好地抵抗观测值中存在的粗差。
由图 4和5可知,针对于第1、第16、第20、第35、第41号点加入粗差的情况,基于IGG方法在第1、第21、第35号点迭代后的权因子小于1,第16、第20号、第41号点迭代后的权因子为0;本文方法中含有粗差的第1、第16、第20、第35、第41号点迭代后权因子均为0。通过对IGG方法和本文方法迭代后的权因子进行比较发现,稳健加权对称相似变换方法探测出可能存在粗差的数据更多,给出的权因子更合理。
4 实例采用文献[5]中真实数据进行计算,坐标点数据见表 7~8。在Solitude点的目标坐标和源坐标中分别加入粗差(5σx,5σy,5σz)和(-5σX,-5σY,-5σZ),设计4种方案进行计算(方案1:未加入粗差时使用加权对称相似变换算法(WSST-0);方案2:在Solitude点加入粗差时使用加权对称相似变换算法(WSST-1);方案3:在Solitude点加入粗差时使用基于IGG的加权对称相似变换算法(IGG-WSST);方案4:在Solitude点加入粗差时使用本文提出的稳健加权对称相似变换算法(RWSST)),计算结果见表 9~10。
|
|
表 7 源坐标系 Tab. 7 Original coordinate system |
|
|
表 8 目标坐标系 Tab. 8 Target coordinate system |
|
|
表 9 三维坐标转换七参数估值 Tab. 9 Seven-parameter estimation of three-dimensional coordinate transformation |
|
|
表 10 选权迭代后的权值 Tab. 10 Weight after selecting weight iteration |
从表 9可以看出,在1个对应点含有粗差时RWSST方法获得的七参数最接近不含粗差时使用WSST获得的七参数,理论上具有最优解。表 10进一步展示了IGG方法和本文方法在粗差点的权值情况,可以看出,在含有粗差的Solitude点上,IGG方法的权值稍有下降,说明IGG方法怀疑该点有粗差,但未将其淘汰,只是对其降低权值然后继续使用。反观本文的RWSST方法,含有粗差的Solitude点的权值直接降为0,说明本文方法能准确探测到该粗差点的位置,并将其剔除,不再使用含有粗差的观测点。
5 结语实验结果表明,当观测值仅含有随机误差时,方案1的结果最优;当观测值含有随机误差和1~3个粗差点时,使用本文稳健加权对称相似变换算法和IGG方法均能得出高精度的坐标转换参数,且二者差异甚微。随着粗差点的增加,IGG方法所求得的七参数均方根误差增大速度加快,所得参数解严重偏离真值,抗差能力严重减弱;而稳健加权对称相似变换算法所求得的均方根误差增大速度相对较慢,所得均方根误差较小,所得参数解较稳定,抗差能力明显较强。
| [1] |
王乐洋, 余航. 总体最小二乘方法的适用性研究[J]. 大地测量与地球动力学, 2014, 34(3): 121-124 (Wang Leyang, Yu Hang. Study on Applicability of Total Least Squares Method in Surveying Adjustment[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 121-124)
(  0) 0) |
| [2] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014(6): 575-581)
(  0) 0) |
| [3] |
Xu P L, Liu J N. Variance Components in Errors-in-Variables Models: Estimability, Stability and Bias Analysis[J]. Journal of Geodesy, 2014, 88(8): 719-734 DOI:10.1007/s00190-014-0717-9
(  0) 0) |
| [4] |
Neitzel F. Generalization of Total Least-Squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762 DOI:10.1007/s00190-010-0408-0
(  0) 0) |
| [5] |
Mercan H, Akyilmaz O, Aydin C. Solution of the Weighted Symmetric Similarity Transformations Based on Quaternions[J]. Journal of Geodesy, 2018, 92(10): 1113-1130 DOI:10.1007/s00190-017-1104-0
(  0) 0) |
| [6] |
王新洲. 高等测量平差[M]. 北京: 测绘出版社, 2006 (Wang Xinzhou. Higher Surveying Adjustment[M]. Beijing: Surveying and Mapping Press, 2006)
(  0) 0) |
| [7] |
周江文, 黄幼才, 杨元喜, 等. 抗差最小二乘法[M]. 武汉: 华中理工大学出版社, 1997 (Zhou Jiangwen, Huang Youcai, Yang Yuanxi, et al. Robustified Least Squares Approaches[M]. Wuhan: Huazhong University of Science and Engineering Press, 1997)
(  0) 0) |
| [8] |
王乐洋, 鲁铁定. 总体最小二乘平差法的误差传播定律[J]. 大地测量与地球动力学, 2014, 34(2): 55-59 (Wang Leyang, Lu Tieding. Propagation Law of Errors in Total Least Squares Adjustment[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 55-59)
(  0) 0) |
| [9] |
Yang Y, Song L, Xu T H. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6): 353-358
(  0) 0) |
| [10] |
刘超, 王彬, 赵兴旺, 等. 三维坐标转换的高斯-赫尔默特模型及其抗差解法[J]. 武汉大学学报:信息科学版, 2018, 43(9): 1320-1327 (Liu Chao, Wang Bin, Zhao Xingwang, et al. Three-Dimensional Coordinate Transformation Model and Its Robust Estimation Method Under Gauss-Helmert Model[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1320-1327)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

