2. 西安科技大学测绘科学与技术学院, 西安市雁塔中路58号, 710054;
3. 中国水利水电第十二工程局有限公司, 杭州市环城北路141号, 310004
大气加权平均温度是地基GNSS探测水汽的关键参量,其误差会进一步影响到GNSS水汽探测的精度和可靠性[1-3]。已有诸多学者开展了大气加权平均温度建模的研究[4-10],但大部分模型在建模时并未考虑Tm的垂直改正信息,并且由于大多数GNSS跟踪站并未配备并址的气象传感器,这些依赖实测气象数据的模型在地基GNSS实时水汽获取中难以应用。本文根据前人的建模思路[1-3],利用2012~2017年Kings Park(45004)站的探空资料,构建2种香港地区顾及高度改正的加权平均温度模型,并采用2018年探空廓线资料对模型在香港地区的精度和适用性进行评估,分析模型精度随季节变化的规律。
1 数据源与加权平均温度确定无线电探空可以提供高垂直分辨率的大气廓线资料,包括绝对温度、气压、露点温度、相对湿度、位势高度、风向及风速等,其时间分辨率为12 h。本文选用怀俄明州立大学(http://weather.uwyo.edu/upperair/sounding.html)提供的2012~2017年香港Kings Park站探空资料,构建香港地区顾及高度改正的加权平均温度模型,并利用2018年的数据对所构建模型的精度和地区适用性进行评估,再与Bevis公式及GPT2w经验模型进行对比分析。Kings Parks站的探空资料在对流层底部较为丰富,且整体质量较高,因而可以确定精确的加权平均温度,具体公式为[11]:
| $ {T_m} = \frac{{\int {\frac{e}{T}{\rm{d}}z} }}{{\int {\frac{e}{{{T^2}}}{\rm{d}}z} }} \approx \frac{{\sum\nolimits\limits_{i = 1}^N {\frac{{{e_i}}}{{{T_i}}}\Delta {h_i}} }}{{\sum\nolimits\limits_{i = 1}^N {\frac{{{e_i}}}{{T_i^2}}\Delta {h_i}} }} $ | (1) |
式中,e和T分别为测站上空大气水汽分压和绝对温度,Δh为相邻气压层的高差,i表示第i层。其中,水汽压可以采用如下公式计算[12]:
| $ e = 6.112\exp \left[ {\frac{{17.67(T - 273.15)}}{{T - 29.65}}} \right]\frac{{{R_H}}}{{100}} $ | (2) |
式中,RH为相对湿度。
2 顾及高度改正的Tm模型 2.1 香港地区Tm的垂直梯度GNSS测站高度与模型参考高度的差异会影响Tm的精度,进而影响地基GNSS水汽获取的精度,因此精确的高度改正是Tm建模需要考虑的因素之一。Zhang等[3]采用ERA-Interim大气再分析资料基于最小二乘方法确定了中国区域Tm的垂直递减率,发现其与高度呈线性关系。为了探索香港地区Tm与测站高度的关系,本文根据Zhang等[3]的方法,利用Kings Park站2012~2017年探空数据,计算每个历元下的Tm高度递减率,结果见图 1。

|
图 1 Tm垂直递减率的时间序列和功率谱 Fig. 1 Time series and power spectrum of the vertical lapse rate in Tm |
由图 1可知,香港地区Tm垂直递减率不仅与高程呈线性关系,还具有明显的年变化周期:从夏季到冬季,香港地区Tm垂直递减率从-6.2 K/km变化为-1.2 K/km。由此可见,忽略垂直改正信息将会在确定测站Tm时引入系统误差,影响地基GNSS反演的可降水量精度,这在地形高度起伏较大的地区尤其明显。因此,本文采用线性和余弦函数结合方式对Tm的垂直递减率进行拟合,以获取精确的Tm垂直改正信息。
2.2 模型构建本文建立香港地区顾及高度改正的加权平均温度(依赖气象参数的和不依赖气象参数的)模型拟采用如下公式:
| $ \begin{array}{c} T_m^{{\rm{gnss}}} = T_m^{{\rm{ref}}} + \gamma ({h_{{\rm{gnss}}}} - {h_{{\rm{ref}}}})\\ = T_m^{{\rm{ref}}} + ({\gamma _1} + {\gamma _2}\cos (2\pi \frac{{{\rm{doy}}}}{{365.25}}) + \\ {\gamma _3}\sin (2\pi \frac{{{\rm{doy}}}}{{365.25}}))({h_{{\rm{gnss}}}} - {h_{{\rm{ref}}}}) \end{array} $ | (3) |
式中,Tmgnss和Tmref分别为GNSS测站高度和模型参考高度的Tm值; γ为Tm的垂直递减率,可以分解为平均项γ1和年变化项,其中γ2和γ3为垂直递减率年周期系数。
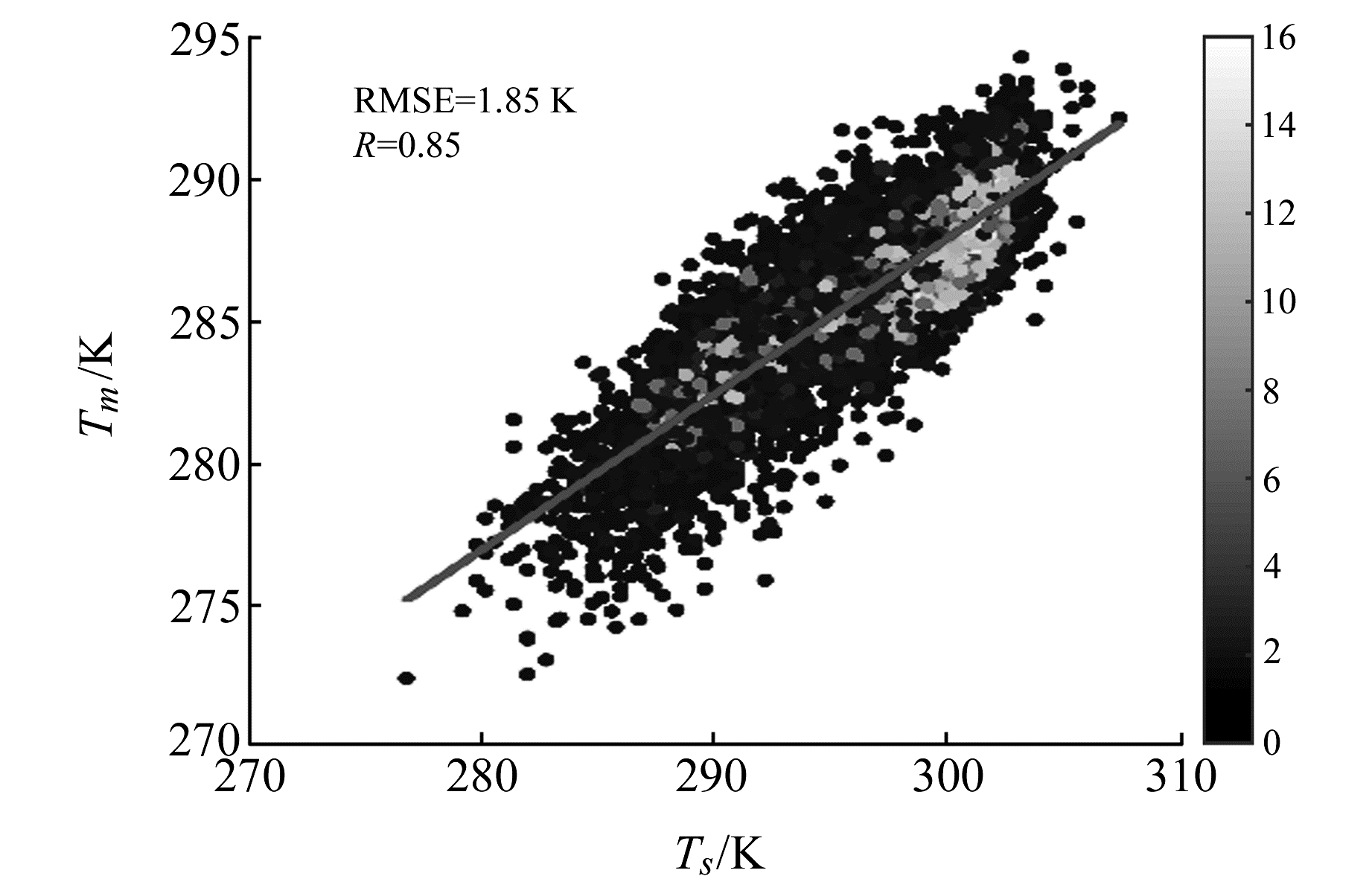
根据式(1)可知,加权平均温度定义为水汽压和绝对温度在天顶方向的积分,因此,Tmref可表示为与地表气象参数相关的函数。根据Kings Park站2012~2017年的探空资料分析Tmref与地面温度的关系,图 2和3分别为该站Tm与实测地表温度Ts的散点图和时间序列。由图 2可知,Tmref与地表实测温度Ts呈现较好的正相关性,相关系数为0.85。Zhang等[3]和Yao等[8]发现,Tm-Ts线性关系的残差序列存在明显的季节性,为此采用如下公式对Tmref进行拟合,建立香港地区依赖地表实测温度的Tm模型Tm_hk1:
|
图 2 Tm与地表温度的散点图 Fig. 2 Scatter of Tm and surface temperature |

|
图 3 Tm和Ts的时间序列 Fig. 3 Time series of Tm and Ts at reference height |
| $ \begin{array}{c} T_m^{{\rm{ref}}} = {\alpha _1} + {\alpha _2}T_s^{{\rm{ref}}} + {\alpha _3}\cos (2\pi \frac{{{\rm{doy}}}}{{365.25}}) + \\ {\alpha _4}\sin (2\pi \frac{{{\rm{doy}}}}{{365.25}}) + {\alpha _5}\cos (4\pi \frac{{{\rm{doy}}}}{{365.25}}) + \\ {\alpha _6}\sin (4\pi \frac{{{\rm{doy}}}}{{365.25}}) \end{array} $ | (4) |
式中,Tsref为参考高度的温度,α1为参考高度h0的Tm年均值,α2为与温度相关的系数,α3、α4及α5、α6为依赖气象参数模型在参考高度的季节项系数。公式的系数均采用2012~2017年的探空数据基于迭代最小二乘参数估计确定。
Ts at reference height GNSS跟踪站主要用于定位、导航、授时及地球物理研究等,大多数没有配备共址的气象传感器,导致依赖气象参数的Tm模型很难应用于实时或近实时地基GNSS水汽的探测。因此,本文同时建立香港地区不依赖气象参数的Tm模型,以更好地服务于该地区暴雨、强对流等极端天气的水汽监测。图 3为参考高度Tm和Ts的时间序列,可以看出,Tm具有明显的季节性周期。因此,这里采用Yao等[2]的建模思路来拟合Tmref,建立不依赖气象参数的模型Tm_hk2。拟合公式如下:
| $ \begin{array}{c} T_m^{{\rm{ref}}} = {\beta _1} + {\beta _{\rm{2}}}\cos (2\pi \frac{{{\rm{doy}}}}{{365.25}}) + \\ {\beta _{\rm{3}}}\sin (2\pi \frac{{{\rm{doy}}}}{{365.25}}) + {\beta _4}\cos (4\pi \frac{{{\rm{doy}}}}{{365.25}}) + \\ {\beta _5}\sin (4\pi \frac{{{\rm{doy}}}}{{365.25}}) \end{array} $ | (5) |
式中,β1为不依赖气象参数的模型在参考高度h0的Tm年均值; β2、β3及β4、β5为不依赖气象参数的模型在参考高度h0的季节项系数。公式的系数均采用2012~2017年的探空数据基于迭代最小二乘参数估计确定。香港地区2种加权平均温度模型的系数见表 1。
|
|
表 1 Tm_hk1和Tm_hk2模型的系数 Tab. 1 Coefficients of Tm_hk1 and Tm_hk2 models |
以由2018年Kings Park站探空数据基于离散积分公式确定的Tm为参考,讨论Bevis公式、GPT2w模型和所建立的Tm模型(Tm_hk1、Tm_hk2)在香港地区的精度和适用性,并分析模型精度随季节变化的规律。
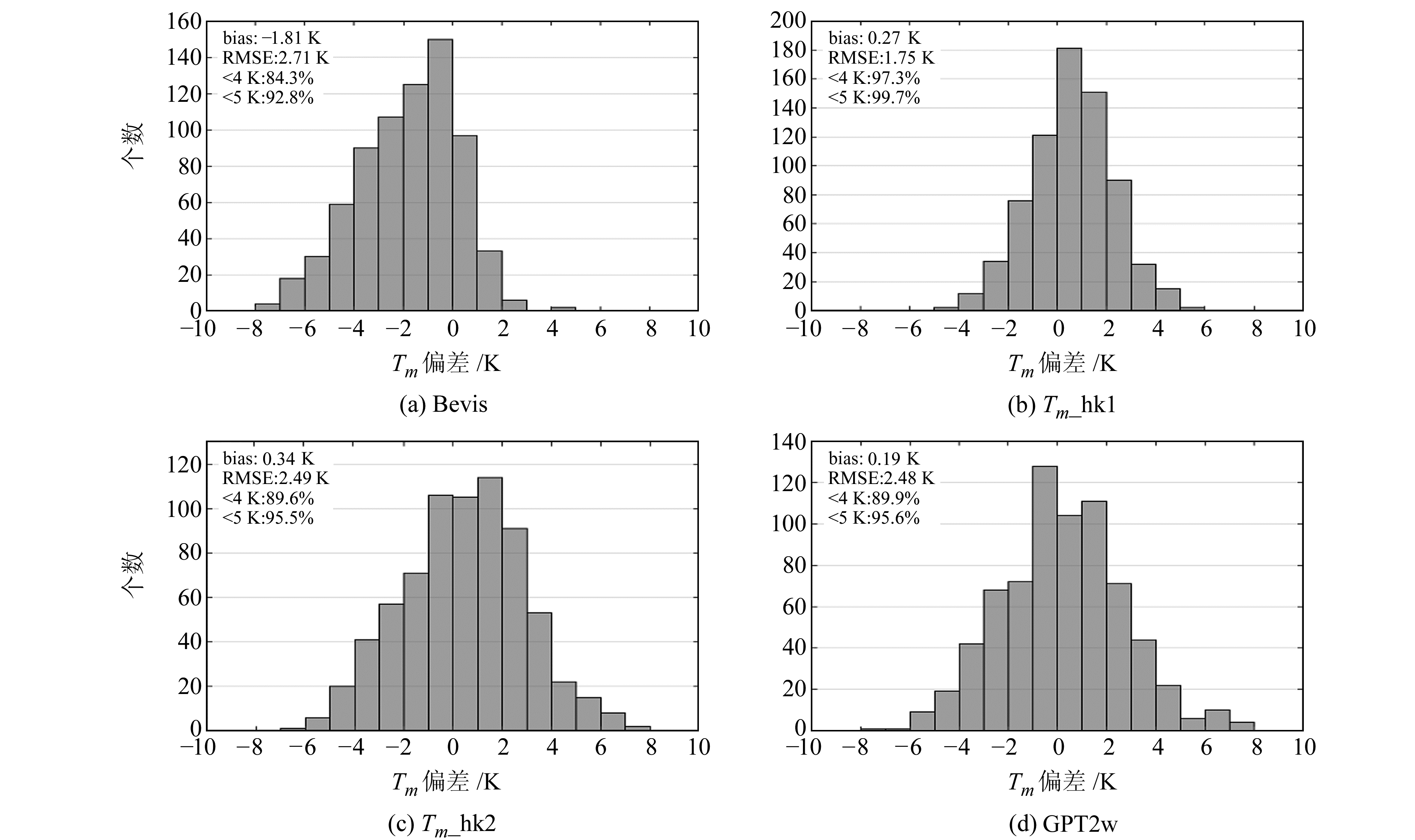
图 4为4种Tm模型的估值与探空积分参考值的偏差分布。由图可知,Bevis公式在香港地区具有较大的系统负偏差(-1.8 K)和均方根误差(2.7 K),表明Bevis公式低估了香港地区的加权平均温度; 依赖气象参数的本地模型Tm_hk1具有较高的精度,年均偏差优于0.3 K,均方根误差优于1.8 K; 与Bevis公式和不依赖气象参数的GPT2w模型相比,Tm_hk1模型的精度分别提升了35.4%和29.7%;不依赖气象参数的本地模型Tm_hk2与GPT2w模型精度相当,年均方根误差优于2.5 K。从Tm模型估值误差占比来看,Tm_hk1模型估值误差几乎全都小于5 K(占99.7%),与Bevis公式、GPT2w模型和Tm_hk2模型相比,误差小于4 K所占比例分别提升了13%、7.4%和7.7%。因此总体来看,依赖气象参数的Tm_hk1模型在香港地区具有较高的精度和适用性。
|
图 4 4种Tm模型值偏差分布直方图 Fig. 4 Histogram of biases of Tm values for the four Tm models |
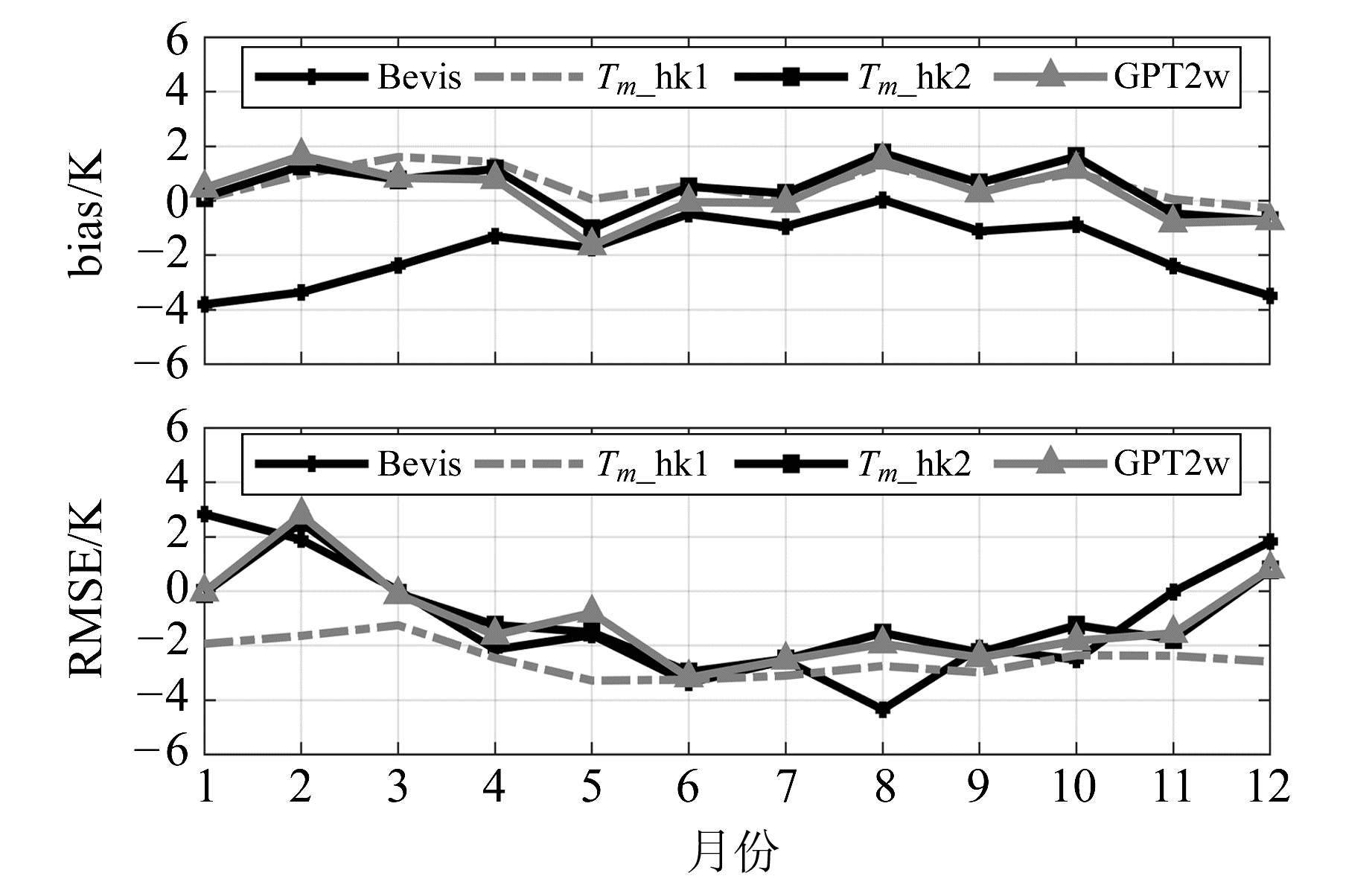
为评估4种Tm模型在不同季节的精度和适用性,将香港Kings Park站2018年探空数据按月进行分类,计算并统计各月Tm模型估值和探空积分值的月平均偏差及均方根误差。由图 5和表 2可知,在香港地区,Bevis公式、Tm_hk2模型和GPT2w模型的精度具有明显的季节性变化且变化趋势较为一致,总体为夏季模型精度较高(RMSE为1.3~2.2 K),冬季模型精度较低(RMSE为3.0~4.4 K); 由模型在各个季节的精度来看,Tm_hk1模型的精度要优于其他3个模型,其在不同季节均具有较高的精度和适用性,且各月模型精度十分接近(RMSE为1.4~2.4 K),模型估值的平均偏差基本优于1.0 K。可以发现,在各个季节,Bevis公式的月平均偏差最大,除了8月份外,其他月份Bevis公式均呈现明显的负偏差,这是因为基于北美探空资料回归分析确定的Bevis公式无法精确表征香港地区(靠近赤道)Tm的时空分布。
|
图 5 4种模型Tm值的月平均偏差和均方根误差 Fig. 5 Monthly biases and RMS errors of Tm values for the four models |
|
|
表 2 4种Tm模型在不同季节的精度统计 Tab. 2 Statistics of precision of the four Tm models during seasons |
高精度、可靠的大气加权平均温度Tm是地基GNSS水汽遥感的关键参数。本文选用2012~2017年Kings Park站探空资料,基于迭代最小二乘方法构建2种香港地区顾及高度改正的Tm模型——依赖气象参数的Tm_hk1模型和不依赖气象参数的Tm_hk2模型。此外,利用2018年探空资料对Bevis公式、GPT2w模型和本文构建的模型在香港地区的精度和适用性进行评估。结果表明,在香港地区,依赖气象参数的本地模型Tm_hk1具有较高的精度,年均偏差优于0.3 K,均方根误差优于1.8 K; 与Bevis公式和GPT2w模型相比,Tm_hk1模型的精度分别提升了35.4%和29.7%。不依赖气象参数的Tm_hk2模型与GPT2w模型精度相当,年均方根误差均优于2.5 K; 基于北美气象资料建立的Bevis公式精度最差(RMS:2.7 K),且具有较大的负偏差(bias为-1.8 K)。从季节性变化分析可知,Bevis公式、Tm_hk2模型和GPT2w模型精度均具有明显的季节性变化,总体为夏季精度较高(RMSE为1.3~2.2 K),冬季精度较低(RMSE为3.0~4.4 K)。Tm_hk1模型在不同季节均具有较高的精度和适用性,且各月Tm_hk1模型的精度十分接近(RMSE为1.4~2.4 K),模型估值的平均偏差基本优于1.0 K。综合来看,本文建立的2种顾及高度改正的Tm模型(Tm_hk1和Tm_hk2)在香港地区都具有较高的精度和适用性,对该地区地基GNSS实时水汽探测和强降雨等极端天气监测等研究具有重要意义。
| [1] |
Yao Y B, Zhang B, Xu C Q, et al. Improved One/Multi-Parameter Models that Consider Seasonal and Geographic Variations for Estimating Weighted Mean Temperature in Ground-Based GPS Meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282 DOI:10.1007/s00190-013-0684-6
(  0) 0) |
| [2] |
Yao Y B, Xu C Q, Zhang B, et al. GTm-Ⅲ: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal International, 2014, 197(1): 202-212 DOI:10.1093/gji/ggu008
(  0) 0) |
| [3] |
Zhang H X, Yuan Y B, Li W, et al. GPS PPP-Derived Precipitable Water Vapor Retrieval Based on Tm/Ps from Multiple Sources of Meteorological Data Sets in China[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(8): 4165-4183 DOI:10.1002/2016JD026000
(  0) 0) |
| [4] |
Ross R J, Rosenfeld S. Estimating Mean Weighted Temperature of the Atmosphere for Global Positioning System Applications[J]. Journal of Geophysical Research: Atmospheres, 1997, 102(D18): 21719-21730 DOI:10.1029/97JD01808
(  0) 0) |
| [5] |
李建国, 毛节泰, 李成才, 等. 使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析[J]. 气象学报, 1999, 57(3): 283-292 (Li Jianguo, Mao Jietai, Li Chengcai, et al. The Approach to Remote Sensing of Water Vapor Based on GPS and Linear Regression Tm in Eastern Region of China[J]. Acta Meteorological Sinica, 1999, 57(3): 283-292)
(  0) 0) |
| [6] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报:信息科学版, 2011, 36(4): 412-416 (Wang Xiaoying, Dai Zaiqiang, Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-416)
(  0) 0) |
| [7] |
王皓, 赵兴旺. 香港地区大气加权平均温度建模与研究[J]. 全球定位系统, 2019, 44(1): 119-124 (Wang Hao, Zhao Xingwang. Modeling and Research on Weighted Average Atmospheric Temperature in Hong Kong[J]. GNSS World of China, 2019, 44(1): 119-124)
(  0) 0) |
| [8] |
Yao Y B, Zhu S, Yue S Q. A Globally Applicable, Season-Specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. Journal of Geodesy, 2012, 86(12): 1125-1135 DOI:10.1007/s00190-012-0568-1
(  0) 0) |
| [9] |
朱爽. 北京地区地基GPS加权平均温度计算本地化模型研究[J]. 测绘工程, 2014, 23(4): 28-32 (Zhu Shuang. Research of Local Model of Weighted Mean Temperature of Ground-Based GPS in Beijing[J]. Engineering of Surveying and Mapping, 2014, 23(4): 28-32)
(  0) 0) |
| [10] |
臧建飞, 彭秀英, 胡卓, 等. 顾及周期性误差修正的加权平均温度模型构建[J]. 测绘科学, 2019, 44(8): 149-160 (Zang Jianfei, Peng Xiuying, Hu Zhuo, et al. Building of Three Improved Weighted Mean Temperature Model Considering the Periodic Error Correction[J]. Science of Surveying and Mapping, 2019, 44(8): 149-160)
(  0) 0) |
| [11] |
Davis J L, Herring T A, Shapiro I I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Science, 1985, 20(6): 1593-1607 DOI:10.1029/RS020i006p01593
(  0) 0) |
| [12] |
Wang X M, Zhang K F, Wu S Q, et al. Water Vapor-Weighted Mean Temperature and Its Impact on the Determination of Precipitable Water Vapor and Its Linear Trend[J]. Journal of Geophysical Research: Atmospheres, 2016, 121(2): 833-852 DOI:10.1002/2015JD024181
(  0) 0) |
2. College of Geomatics, Xi'an University of Science and Technology, 58 Mid-Yanta Road, Xi'an 710054, China;
3. Sinohydro Bureau 12 Co Ltd, 141 North-Huancheng Road, Hangzhou 310004, China
 2020, Vol. 40
2020, Vol. 40


