精密单点定位(PPP)是一种通过精密星历、精密钟差产品及各种误差模型改正进而获取高精度位置信息的定位模式[1-2],因具有作业模式灵活、成本低、精度高等优点被广泛应用[3-4]。随着全球卫星导航系统的发展,多系统组合精密单点定位成为研究热点,由于各导航系统的时间基准存在差异,在多系统组合导航中需要考虑系统间偏差(inter-system bias, ISB)的影响。许多学者已对ISB的来源、特性和模型进行了研究[5-10],但系统分析ISB处理方法间差异的研究较少,特别是其对非组合PPP的影响。本文基于GPS/BDS/Galileo非组合模型,分别将ISB作为常量模型、白噪声模型及随机游走模型进行处理,采用多天MGEX测站数据进行静态和仿动态解算,分析不同模型下ISB日跳变特性,并评估收敛时间和定位精度。
1 非组合精密单点定位及参数处理策略 1.1 GPS/BDS/Galileo非组合精密单点定位模型非组合PPP以载波相位和伪距观测值作为原始观测值,将电离层作为参数进行估计,GPS/BDS/Galileo非组合精密单点定位观测方程为:
| $ \left\{ \begin{array}{l} P_{1,r}^{{\rm G},j} = \rho _r^{{\rm G},j} + c\delta \tilde t_r^{\rm G} - c\tilde \delta {t^{{\rm G},j}} + M_r^{{\rm G},j}{T_{{\rm trop}}} + \tilde I_{1,r}^{{\rm G},j} + \varepsilon (P_{1,r}^{{\rm G},j})\\ P_{2,r}^{{\rm G},j} = \rho _r^{{\rm G},j} + c\tilde \delta t_r^{\rm G} - c\tilde \delta {t^{{\rm G},j}} + M_r^{{\rm G},j}{T_{{\rm trop}}} + {\gamma _G}\tilde I_{1,r}^{{\rm G},j} + \varepsilon (P_{,r}^{{\rm G},j})\\ L_{1,r}^{{\rm G},j} = \rho _r^{{\rm G},j} + c\tilde \delta t_r^{\rm G} - c\tilde \delta {t^{{\rm G},j}} + M_r^{{\rm G},j}{T_{{\rm trop}}} - \tilde I_{1,r}^{{\rm G},j} + \lambda _1^{\rm G}\tilde N_1^{\rm G} + \varepsilon (L_{1,r}^{{\rm G},j})\\ L_{2,r}^{{\rm G},j} = \rho _r^{{\rm G},j} + c\tilde \delta t_r^{\rm G} - c\tilde \delta {t^{{\rm G},j}} + M_r^{{\rm G},j}{T_{{\rm trop}}} - {\gamma _G}\tilde I_{1,r}^{{\rm G},j} + \lambda _2^{\rm G}\tilde N_2^{\rm G} + \varepsilon (L_{2,r}^{{\rm G},j})\\ P_{1,r}^{{\rm C},j} = \rho _r^{{\rm C},j} + c\tilde \delta t_r^{\rm G} + {\rm ISB}_r^{\rm C} - c\tilde \delta {t^{{\rm C},j}} + M_r^{{\rm C},j}{T_{{\rm trop}}} + \tilde I_{1,r}^{{\rm C},j} + \varepsilon (P_{1,r}^{{\rm C},j})\\ P_{2,r}^{{\rm C},j} = \rho _r^{{\rm C},j} + c\tilde \delta t_r^{\rm G} + {\rm ISB}_r^{\rm C} - c\tilde \delta {t^{{\rm C},j}} + M_r^{{\rm C},j}{T_{{\rm trop}}} + {\gamma _C}\tilde I_{1,r}^{{\rm C},j} + \varepsilon (P_{2,r}^{{\rm C},j})\\ L_{1,r}^{{\rm C},j} = \rho _r^{{\rm C},j} + c\tilde \delta t_r^{\rm G} + {\rm ISB}_r^{\rm C} - c\tilde \delta {t^{{\rm C},j}} + M_r^{{\rm C},j}{T_{{\rm trop}}} - \tilde I_{1,r}^{{\rm C},j} + \lambda _1^{\rm C}\tilde N_1^{\rm C} + \varepsilon (L_{1,r}^{{\rm C},j})\\ L_{2,r}^{{\rm C},j} = \rho _r^{{\rm C},j} + c\tilde \delta t_r^{\rm G} + {\rm ISB}_r^{\rm C} - c\tilde \delta {t^{{\rm C},j}} + M_r^{{\rm C},j}{T_{{\rm trop}}} - {\gamma _C}\tilde I_{1,r}^{{\rm C},j} + \lambda _2^{\rm C}\tilde N_2^{\rm C} + \varepsilon (L_{2,r}^{{\rm C},j})\\ P_{1,r}^{{\rm E},j} = \rho _r^{{\rm E},j} + c\tilde \delta t_r^{\rm G} + {\rm ISB}_r^{\rm E} - c\tilde \delta {t^{{\rm E},j}} + T_{{\rm trop}}^{{\rm E},j} + \tilde I_{1,r}^{{\rm E},j} + \varepsilon (P_{1,r}^{{\rm E},j})\\ P_{2,r}^{{\rm E},j} = \rho _r^{{\rm E},j} + c\tilde \delta t_r^{\rm G} + {\rm ISB}_r^{\rm E} - c\tilde \delta {t^{{\rm E},j}} + M_r^{{\rm E},j}{T_{{\rm trop}}} + {\gamma _C}\tilde I_{1,r}^{{\rm E},j} + \varepsilon (P_{2,r}^{{\rm E},j})\\ L_{1,r}^{{\rm E},j} = \rho _r^{{\rm E},j} + c\tilde \delta t_r^{\rm G} + {\rm ISB}_r^{\rm E} - c\tilde \delta {t^{{\rm E},j}} + M_r^{{\rm E},j}{T_{{\rm trop}}} - \tilde I_{1,r}^{{\rm E},j} + \lambda _1^{\rm E}\tilde N_1^{\rm E} + \varepsilon (L_{1,r}^{{\rm E},j})\\ L_{2,r}^{{\rm E},j} = \rho _r^{{\rm E},j} + c\tilde \delta t_r^{\rm G} + {\rm ISB}_r^{\rm E} - c\tilde \delta {t^{{\rm E},j}} + M_r^{{\rm E},j}{T_{{\rm trop}}} - {\gamma _E}\tilde I_{1,r}^{{\rm E},j} + \lambda _2^{\rm E}\tilde N_2^{\rm E} + \varepsilon (L_{2,r}^{{\rm E},j}) \end{array} \right. $ | (1) |
式中,P与L分别为伪距和载波相位观测值,G为GPS系统,C为BDS系统,E为Galileo系统,ρ为测站与卫星间几何距离,c为光速,δ
| $ \left\{ \begin{array}{l} \tilde \delta t_r^S = \delta t_r^S + d_{{\rm IF},r}^s\\ \tilde \delta {t^{S,j}} = \delta {t^{S,j}} + d_{{\rm IF}}^{S,j}\\ {\rm ISB}_r^S = {\rm d}t_r^S - {\rm d}t_r^{\rm G} + d_{{\rm IF}}^S - d_{{\rm IF}}^{\rm G}\\ {\gamma _i}\tilde I_{i,r}^{S,j} = {\gamma _i}I_{i,r}^{S,j} + d_{{\rm IF}}^{s,j} - d_i^{s,j} - \\ \;\;\;\;(d_{{\rm IF},r}^s - d_{i,r}^s)\\ \lambda _i^s\tilde N_i^S = \lambda _i^sN_{i,r}^{s,j} + 2(d_{{\rm IF}}^{s,j} - d_{{\rm IF},r}^s) + \\ \;\;\;\;\;(d_{i,r}^s - d_i^{s,j}) + (b_{i,r}^s - b_j^{s,j}) \end{array} \right. $ | (2) |
式中,i为频点,dis, j与di, rs分别为卫星端和接收机端的伪距硬件延迟,bjs, j与bi, rs分别为卫星端和接收机端的相位硬件延迟。假设同时观测到M颗卫星,则未知参数向量X为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{X}} = [x,y,z,{\rm MT},c{\rm d}{t_r},({\rm ISB}_r^S),(\tilde I_{r,1}^{S,j}),\\ \;(\tilde N_{r,1}^{S,j}),(\tilde N_{r,2}^{S,j})]\\ ({\rm ISB}_r^S) = [{\rm ISB}_r^{\rm E},{\rm ISB}_r^{\rm C}]\\ (\tilde I_{r,1}^{S,j}) = [\tilde I_{r,1}^{{\rm G},1} \cdots \tilde I_{r,1}^{{\rm G},{N_{\rm G}}},\tilde I_{r,1}^{{\rm C},1} \cdots \tilde I_{r,1}^{{\rm C},{N_{\rm C}}},\\ \;\;\tilde I_{r,1}^{{\rm E},1} \cdots \tilde I_{r,1}^{{\rm E},{N_{\rm E}}}]\\ (\tilde N_{r,1}^{S,j}) = [\tilde N_{r,1}^{{\rm G},1} \cdots \tilde N_{r,1}^{{\rm G},{N_{\rm G}}},\tilde N_{r,1}^{{\rm C},1} \cdots \tilde N_{r,1}^{{\rm C},{N_{\rm C}}},\\ \;\;\;\tilde N_{r,1}^{1,{N_{\rm E}}} \cdots \tilde N_{r,1}^{{\rm E},{N_{\rm E}}}] \end{array} \right. $ | (3) |
式中,NG、NC、NE分别为GPS、BDS、Galileo系统的观测卫星数量。
1.2 ISB模型处理策略根据式(1)将ISB参数分别作为常量模型、白噪声模型和随机游走模型进行处理,具体处理策略为:
1) 将ISB作为常量模型时可不考虑ISB随时间变化的部分,即σK2=0(记为PPP-CV模型),具体表达示为:
| $ {\rm{ISB}}_r^{\rm{S}}K{\rm{ = ISB}}_r^{\rm{S}}K - 1\;\sigma _K^2 = 0 $ | (4) |
式中,σK2为ISB的过程噪声,S为卫星导航系统,ISBrS(K)为第K个历元的ISB估计值。
2) 将ISB作为随机游走模型时,传递上一历元Kalman滤波解ISBrS(K-1),并考虑ISB随时间变化的部分ωK,该部分服从高斯正态分布。本文将σ2设置为0.01 m2(记为PPP-RW模型),具体表达示为:
| $ {\rm{ISB}}_r^{\rm{S}}(K){\rm{ = ISB}}_r^{\rm{S}}(K - 1) + {\omega _K},{\omega _k} \sim N(0,{\sigma ^2}) $ | (5) |
3) 将ISB作为白噪声模型进行处理时,认为相邻历元间ISB相互独立,在进行Kalman滤波时对ISB过程噪声赋予较大方差。本文将σ2设置为109 m2(记为PPP-WN模型),具体表达示为:
| $ {\rm{ISB}}_r^S \sim N(0,{\sigma ^2}) $ | (6) |
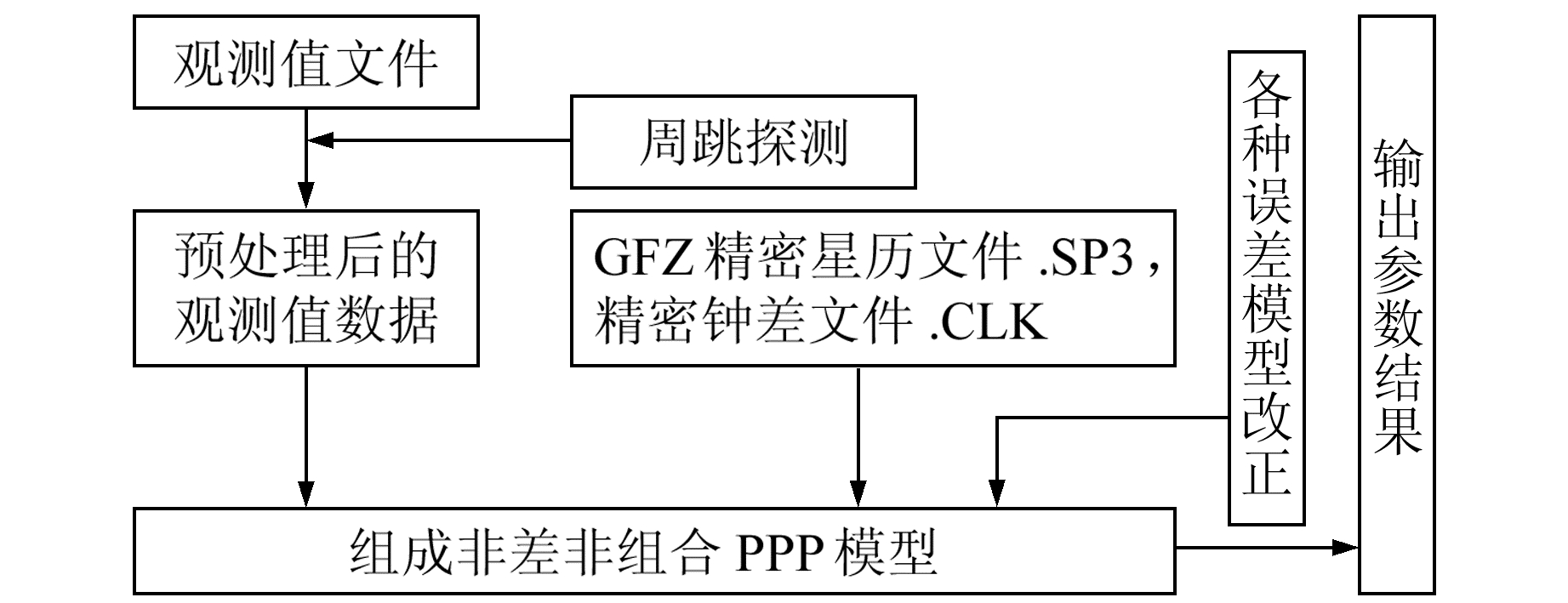
选取MGEX中可同时跟踪GPS、BDS、Galileo系统的ABMF、TLSE、DYNG、HKWS、PNGM、DARW、KARR等7个测站,测站主要分布在中低纬度地区。首先对数据进行预处理,剔除质量较差的观测数据,具体流程见图 1。本次实验选取GFZ提供的5 min间隔精密星历和30 s间隔精密钟差,电离层选取IGS发布的全球电离层格网产品(GIM),天线相位文件选择igs14.atx,具体参数处理策略见表 1。
|
图 1 数据处理流程 Fig. 1 Flow chart of data processing |
|
|
表 1 参数策略表 Tab. 1 Strategy of parameters |
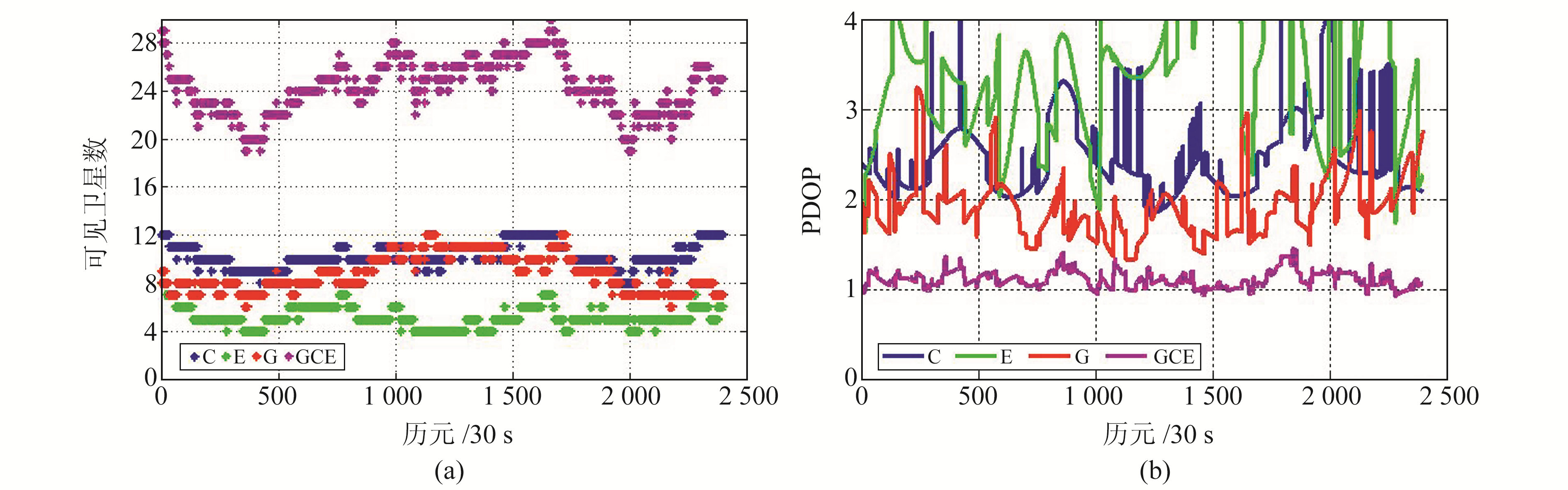
为验证解算ISB的可靠性,首先对多系统非组合PPP模型定位精度进行分析。以HKWS测站为例,图 2为单系统与组合系统的卫星可见数及其PDOP值。从图 2(a)可以看出,观测Galileo系统的卫星数最少,组合系统的卫星数最多,且明显多于单系统。图 2(b)中组合系统的PDOP值最小,且相对稳定。分析表明,组合导航系统能够改善空间几何结构,增强观测方程的稳定性,从而增加PPP解算的稳定性和可靠性。
|
图 2 HKWS测站卫星可见数与PDOP值 Fig. 2 Number of visible satellites and PDOP of HKWS station |
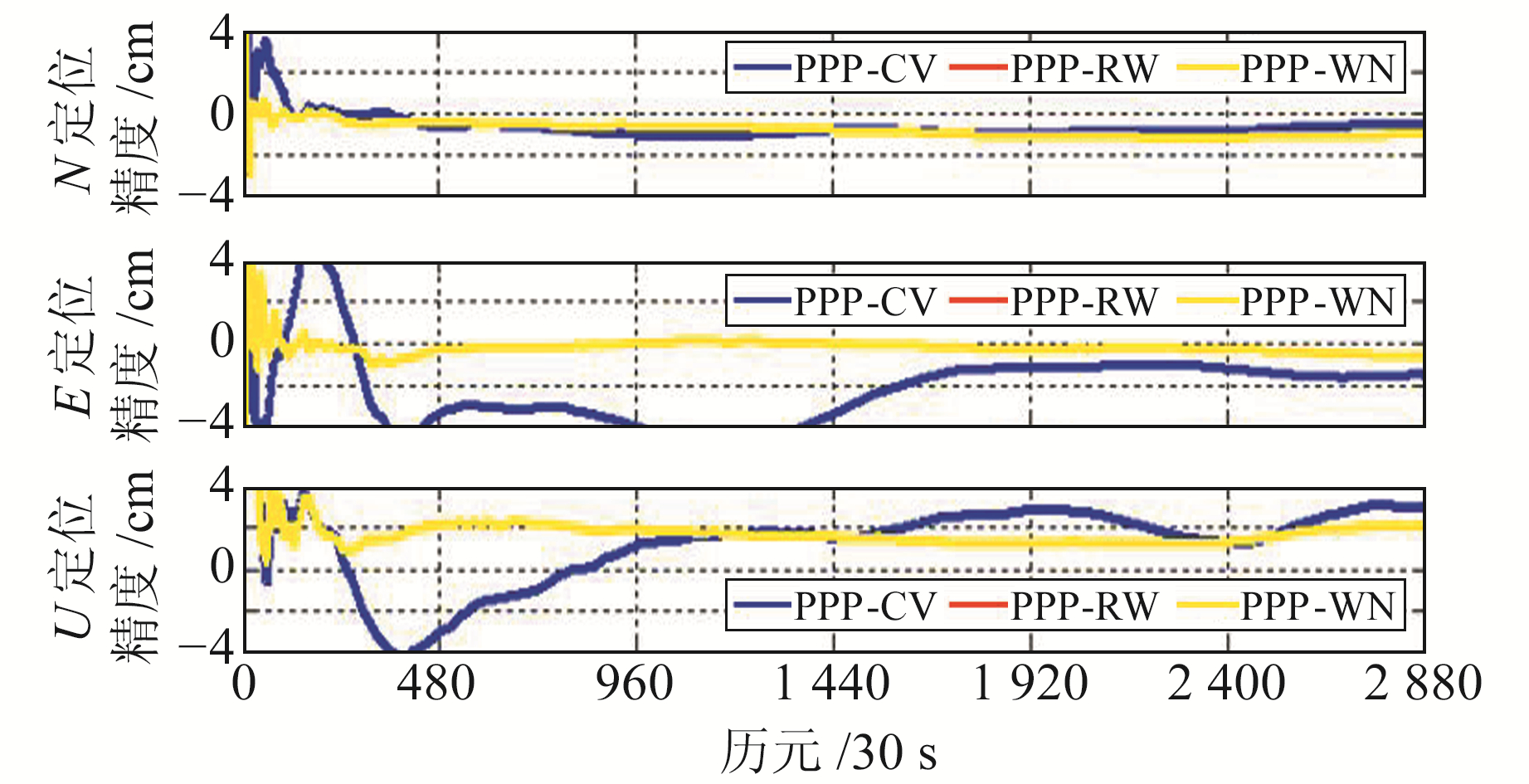
图 3为HKWS测站在3种ISB模型下的单天静态定位精度。从图中可以看出,PPP-RW模型与PPP-WN模型的精度基本一致,在3个方向上均优于PPP-CV模型,且在N、E方向上可收敛到mm级定位精度,在U方向上可收敛到cm级定位精度;PPP-CV模型在N方向上可收敛到mm级定位精度,在E、U方向上可收敛到cm级定位精度。上述分析表明,估计的ISB具有可靠性。
|
图 3 3种ISB模型静态PPP误差 Fig. 3 Static PPP errors of three different ISB models |
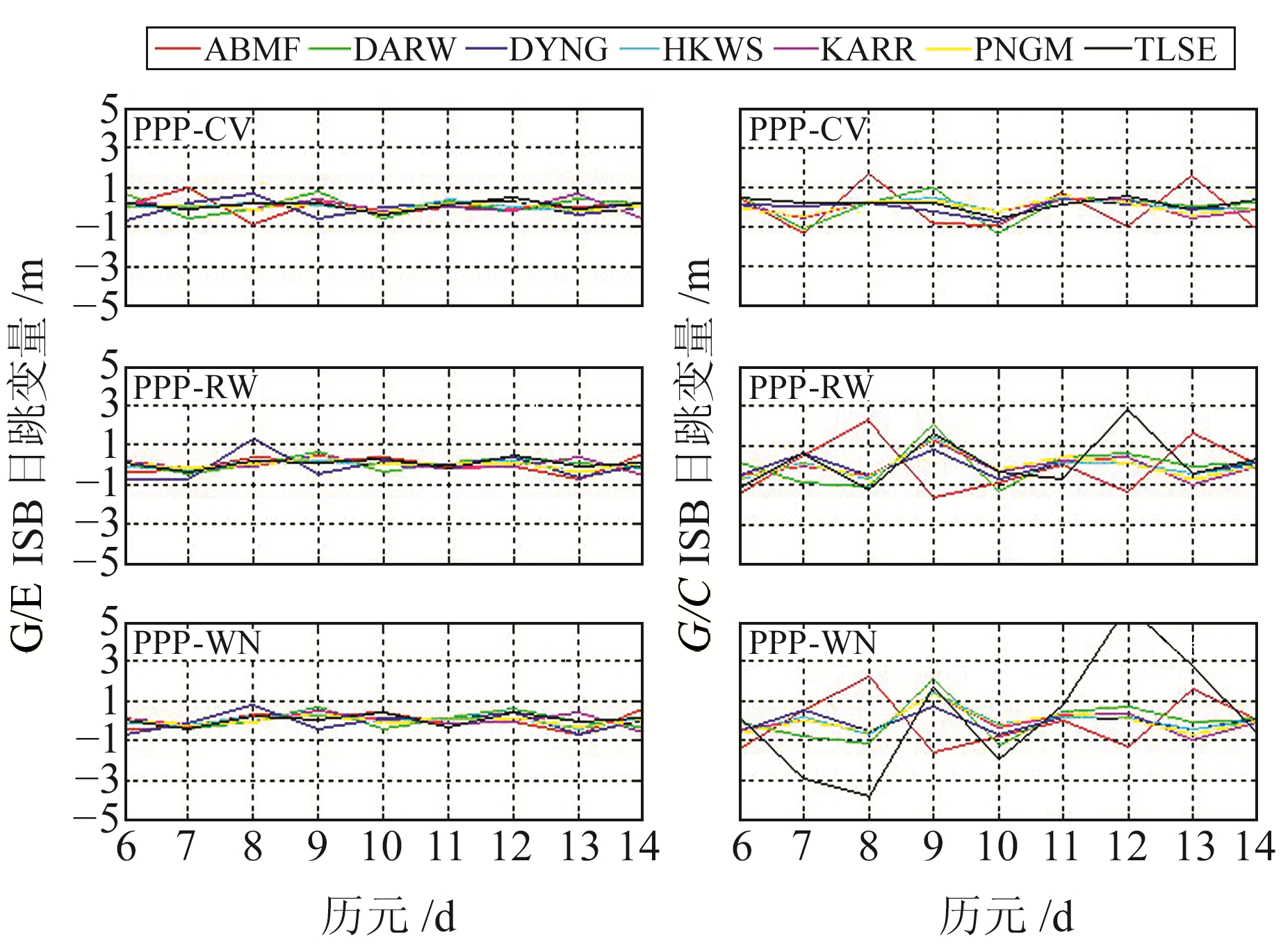
图 4为7个测站3种ISB模型的日跳变量,从图中可以看出,G/E的日跳变量相比于G/C更稳定,3种模型的日跳变量都较小,最大值约为1 m。PPP-CV模型的日跳变量最小,普遍小于1 m;PPP-RW模型和PPP-WN模型的日跳变量变化较大,其中PPP-WN模型的日跳变量最大,在TLSE测站最大日跳变量可达到5 m。
|
图 4 3种ISB模型日跳变量 Fig. 4 Daily variation of three different ISB models |
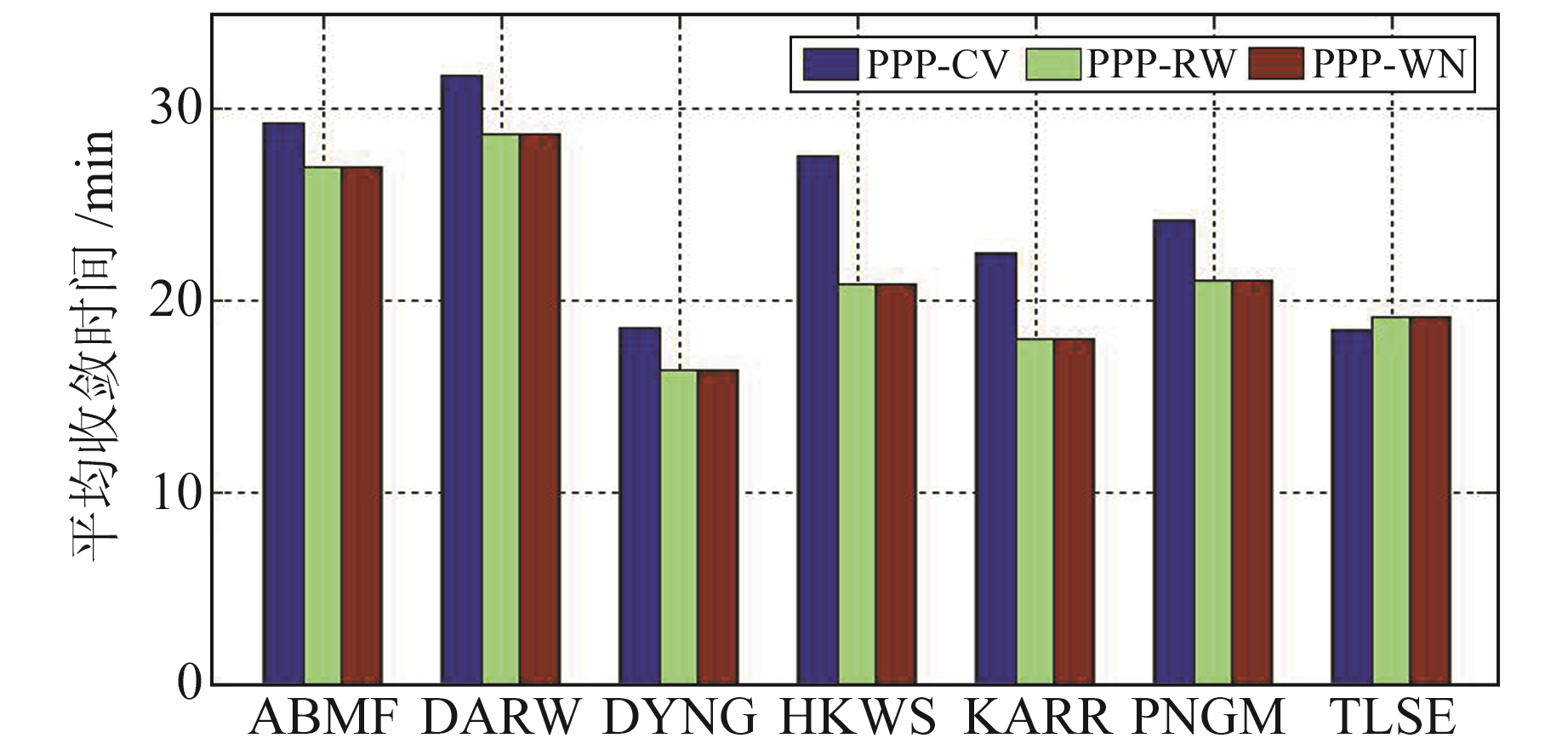
静态实验采用2019年doy 5~14数据,GPS采用L1和L2频点数据,BDS采用B1和B2频点数据,Galileo采用E1和E5频点数据。图 5为静态条件下7个测站10 d的平均收敛时间,从图中可以看出,PPP-RW模型和PPP-WN模型均优于PPP-CV模型,可提升2~7 min;PPP-RW模型和PPP-WN模型的收敛效果相当。
|
图 5 各测站静态收敛时间 Fig. 5 Static convergence time of each stations |
表 2为测站10 d静态定位结果的RMS,从表中可以看出,相比于PPP-CV模型,PPP-RW模型和PPP-WN模型在N方向上的定位精度相当,都收敛到mm级,在E、U方向却有显著提升,E方向平均提高2.2 cm,提升约77.7%,U方向平均提高0.6 cm,提升约32.2%。
|
|
表 2 不同模型静态PPP精度 Tab. 2 Static PPP accuracy of different models |
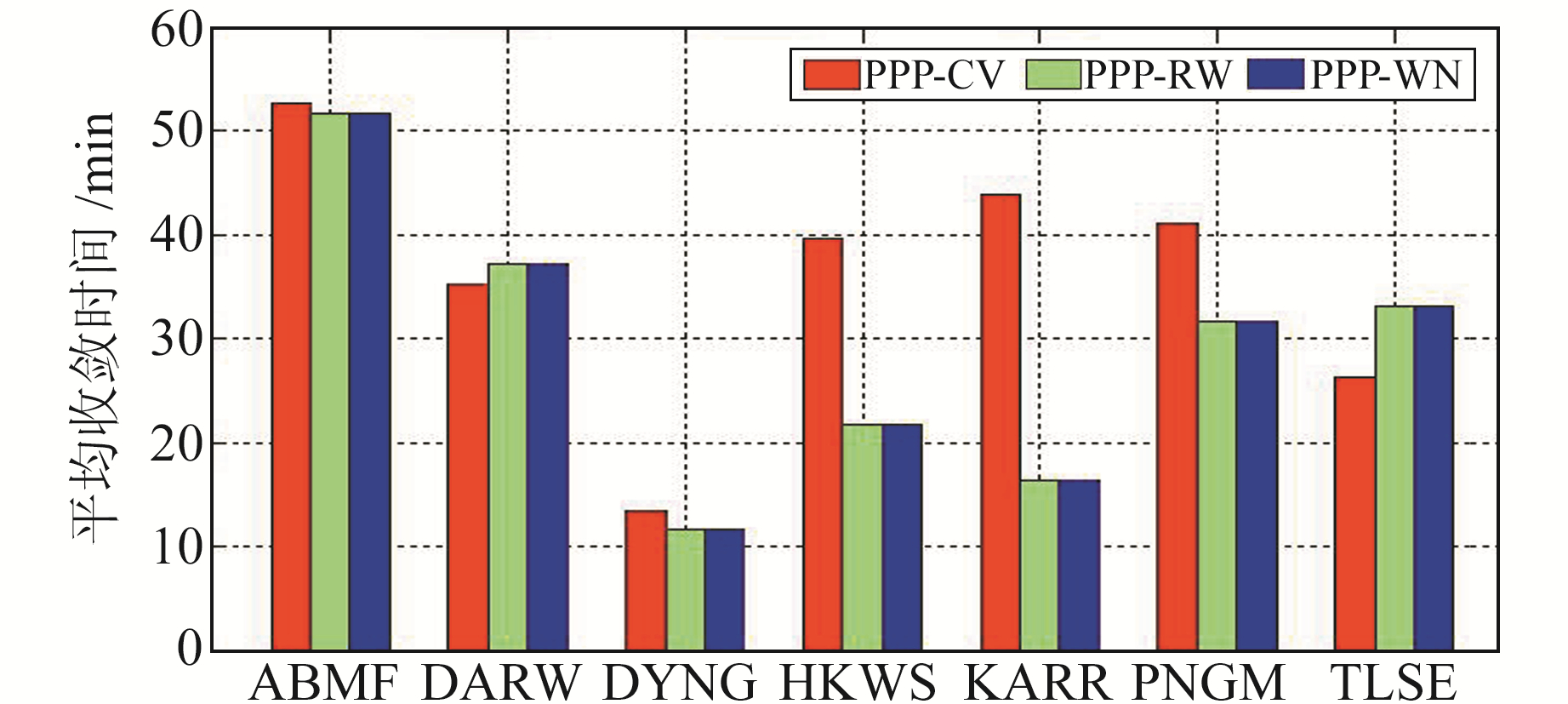
仿动态实验分析时将ISB采取与静态同样的处理策略。图 6为仿动态环境下7个测站10 d的平均收敛时间,从图中可以看出,PPP-RW模型和PPP-WN模型的收敛时间整体上优于PPP-CV模型,在ABMF、DYNG、HKWS、KARR、PNGM等5个测站平均提升约13 min。
|
图 6 各测站仿动态PPP收敛时间 Fig. 6 Simulated dynamic PPP convergence time of each stations |
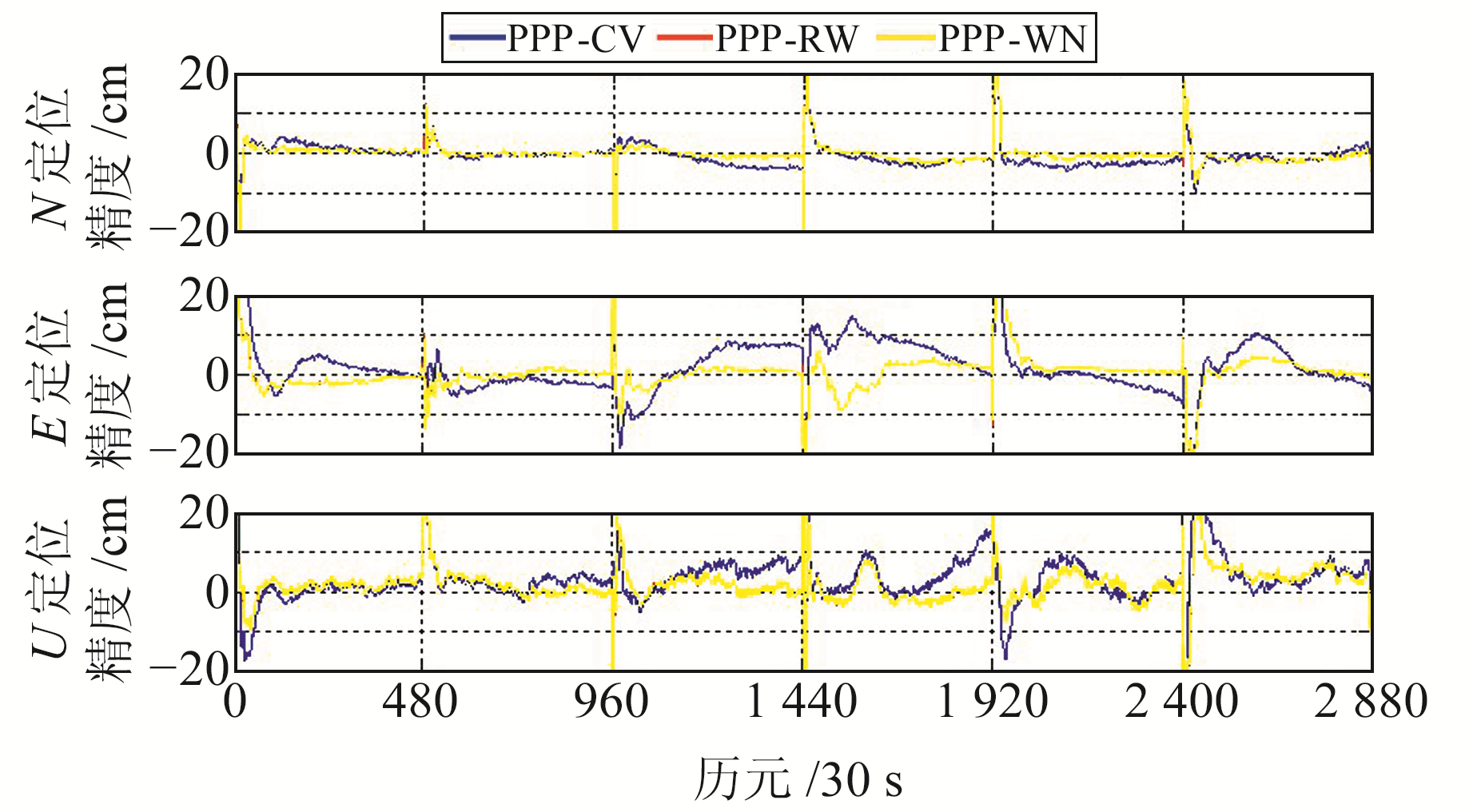
将HKWS测站1 d观测数据分为6个观测弧段,图 7为3个方向的定位结果。从图中可以看出,PPP-RW模型和PPP-WN模型在N、E方向可收敛到约0.5 cm,U方向可收敛到约2 cm;PPP-CV模型在N方向可收敛到0.6 cm,E方向可收敛到2 cm,U方向可收敛到约3 cm。在E、U方向上,PPP-RW模型和PPP-WN模型的定位精度均优于PPP-CV模型,其中E方向精度提升最为明显,但3种模型在N方向的定位精度相当。
|
图 7 HKWS仿动态定位精度 Fig. 7 Simulated dynamic positioning accuracy of HKWS station |
表 3为基于3种模型10 d仿动态定位精度的RMS,从表中可以看出,PPP-RW模型和PPP-WN模型在N、E、U、3D方向的定位精度相当,且均优于PPP-CV模型。PPP-RW模型和PPP-WN模型在N、E方向的定位精度均优于1.5 cm,在U方向上优于3 cm,3D方向优于5 cm。PPP-CV模型在N方向的定位精度优于2 cm,在E方向上优于4 cm,在U方向上优于6 cm。相比于PPP-CV模型,PPP-RW模型和PPP-WN模型在E、U方向上的精度提升最为明显,在N方向上效果相当,仿动态模型整体变化趋势与静态模型一致。
|
|
表 3 不同模型仿动态PPP精度 Tab. 3 Simulated dynamic PPP accuracy of different models |
将ISB设计成3种不同模型进行处理,通过实验得出以下结论:
1) 相比于G/B ISB模型,G/E ISB模型的日跳变量变化较小,表明GPS与Galileo系统的ISB模型更加稳定。
2) 在收敛时间方面,PPP-RW模型和PPP-WN模型的收敛时间相当,总体上优于PPP-CV模型,在静态模式下可提升15.4%,在仿动态模式下可提升29.4%。
3) 在定位精度方面,PPP-RW模型和PPP-WN模型的定位精度与静态模式基本一致,但均优于PPP-CV模型,E和U方向的定位精度分别提升约77.7%和32.2%。在仿动态条件下,相比于PPP-CV模型,PPP-RW模型和PPP-WN模型在E和U方向提升约66%和43.5%。在静态模式和仿动态模式下,3种ISB模型在N方向的定位精度相当。
在使用GFZ发布的精密产品时,将ISB作为白噪声模型和随机游走模型,在定位精度和收敛时间上均优于常量模型。
| [1] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research Solid Earth, 1997, 102(B3): 5 005-5 017 DOI:10.1029/96JB03860
(  0) 0) |
| [2] |
Kouba J, Hérous P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28 DOI:10.1007/PL00012883
(  0) 0) |
| [3] |
屈利忠, 赵齐乐, 郭靖, 等. GNSS融合动态精密单点定位性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 298-302 (Qu Lizhong, Zhao Qile, Guo Jing, et al. Performance Analysis on Multi-GNSS Kinematic Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 298-302)
(  0) 0) |
| [4] |
Colombo O, Sutter A W, Evans A G. Evaluation of Precise, Kinematic GPS Point Positioning[C]. The 17th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2004), Long Beach, 2004
(  0) 0) |
| [5] |
EI-Mowafy A, Deo M, Rizos C. On Biases in Precise Point Positioning with Multi-Constellation and Multi-Frequency GNSS Data[J]. Measurement Science and Technology, 2016, 27(3)
(  0) 0) |
| [6] |
Torre A D, Caporali A. An Analysis of Intersystem Biases for Multi-GNSS Positioning[J]. GPS Solutions, 2015, 19(2): 297-307 DOI:10.1007/s10291-014-0388-2
(  0) 0) |
| [7] |
Jiang N, Xu Y, Xu T H, et al. GPS/BDS Short-Term ISB Modeling and Prediction[J]. GPS Solution, 2017, 21(1): 163-175
(  0) 0) |
| [8] |
Bakker P F, Tiberius C C J M. Real-Time Multi-GNSS Single-Frequency Precise Point Positioning[J]. GPS Solutions, 2017, 21(4): 1 791-1 803 DOI:10.1007/s10291-017-0653-2
(  0) 0) |
| [9] |
Zhou F, Dong D A, Li P, et al. Influence of Stochastic Modeling for Inter System Biases on Multi GNSS Undifferenced and Uncombined Precise Point Positioning[J]. GPS Solutions, 2019, 23(3): 59 DOI:10.1007/s10291-019-0852-0
(  0) 0) |
| [10] |
Liu X X, Jiang W P, Chen H, et al. An Analysis of Inter-System Biases in BDS/GPS Precise Point Positioning[J]. GPS Solutions, 2019, 23(4): 116 DOI:10.1007/s10291-019-0906-3
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

