2. 山东省煤田地质局物探测量队, 济南市经十东路33699号, 250104
随着空间测量技术的不断发展,利用GPS速度场描绘地壳运动状态的方法被广泛应用于地震监测预报等研究领域。国内外学者利用GPS数据大量开展了针对地壳形变的分析研究,包括采用GAMIT或Bernese软件求取单天解、分析连续观测时间序列、获取速度场及应力应变信息等[1-3],其中单天解坐标分量中误差一般优于3 mm[4-5]。GPS流动观测作为连续观测的有力补充,可有效解决GPS站点密度偏低的问题,同时可准确、全面地刻画大陆地壳细部运动特征,但也存在观测周期长、干扰因素多等问题。本文利用连续观测站点的时间序列提高GPS流动观测的定位精度,并分析了GPS流动观测结果的可靠性。
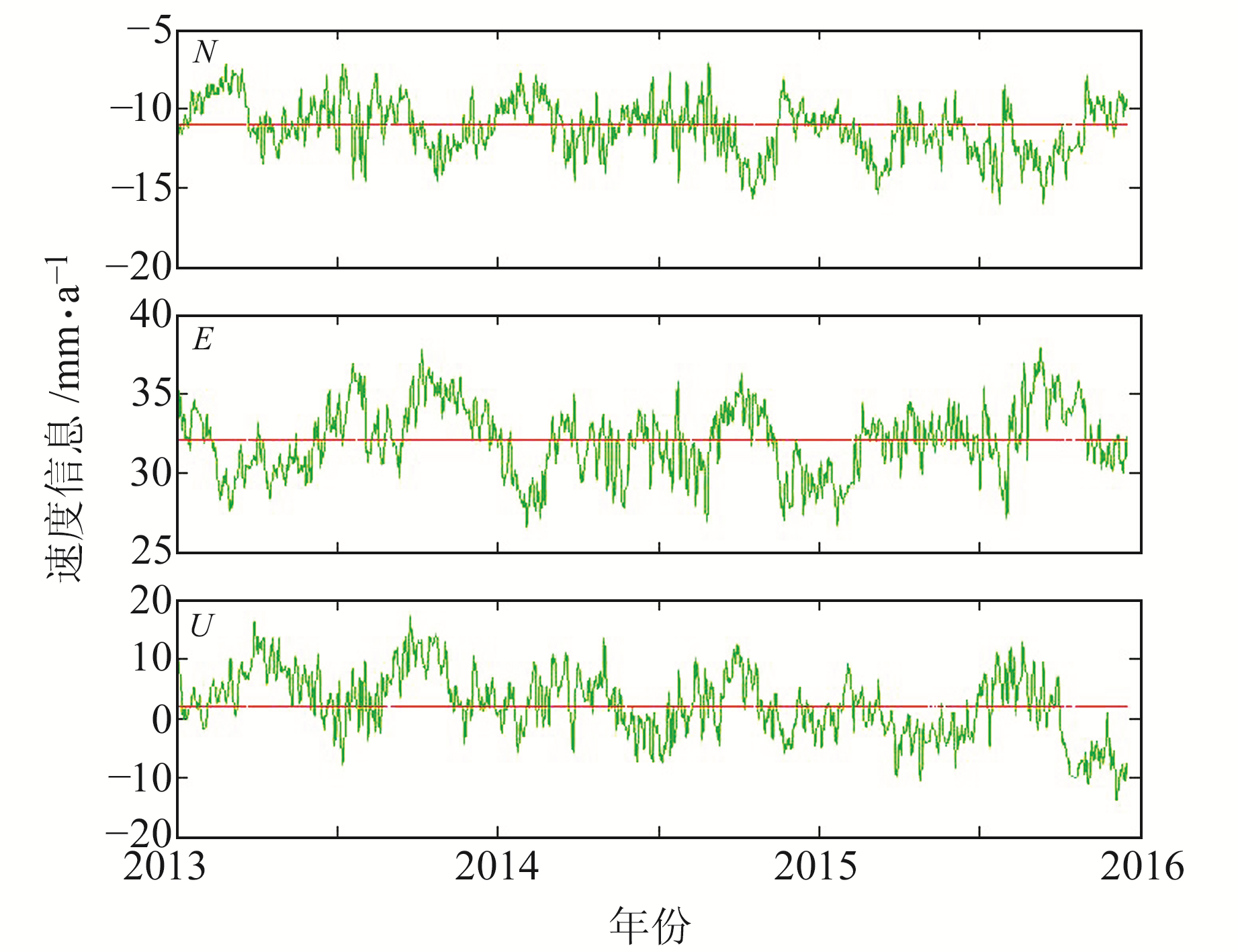
1 流动观测可靠性分析流动观测每期大多间隔1~3 a,每期观测3~4 d。利用陆态网络连续运行站点数据,分析通过流动观测获取速度场信息的可靠性,站点位置如图 1所示。以TAIN站点为例,将连续观测时间序列按每期间隔1 a、连续3期、每期3 d截取为流动观测数据,将求取的结果标记为该组观测数据起始观测时间点的速度信息,则2013年至2019-04连续观测数据截取的流动观测结果标记时间为2013年至2016-04。图 2为N、E、U三分量速度信息,其中红线为连续观测解算的速度信息。
|
图 1 本文所用山东地壳运动观测网GPS站点分布 Fig. 1 Distribution of GPS stations of CMONOSD used in this paper |
|
图 2 TAIN站点流动观测获取的速度信息 Fig. 2 Velocity of TAIN station obtained by mobile observation |
从图 2可以看出,不同时间点连续3 a、固定间隔1 a观测策略的速度信息解算结果与连续6 a观测的速度信息解算结果偏差较大,且不具备固定规律。为保证结果的准确性,通常采用增加观测次数、延长观测时间等方法,但也会影响流动测量的时效性并增大外业工作量。
2 基于周期项参数模型的GPS流动观测改正方法GPS时间序列一般可利用包含年周期项和半年周期项的参数模型进行拟合,其表达式为:
| $ \begin{array}{l} y\left( t \right) = a + bt + c\sin \left( {2\pi t} \right) + d\cos \left( {2\pi t} \right) + \\ \;\;\;\;\;\;\;e\sin \left( {4\pi t} \right) + f\cos \left( {4\pi t} \right) + \varepsilon \end{array} $ | (1) |
式中,t为时间,a为常数项,b为速度,c和d为年周期运动振幅,e和f为半年周期运动振幅,ε为残差项。年周期项和半年周期项主要由地球表面物质随时间变化所产生的负荷效应造成[6],如果不考虑特殊事件对时间序列的影响,残差项ε具有闪烁噪声和白噪声的特征[7],同时包含某种与时空相关的误差[8-13],即共模误差。
利用流动观测数据求取站点的速度信息,对站点的年周期项和半年周期项稳定性要求较高。以TAIN站点为例,受地表负载物变化的影响,部分年份GPS时间序列偏离参数模型拟合值较大,导致流动观测计算的速度信息偏离真实值。
式(1)中年周期项和半年周期项的差异会随测站距离的减小而逐渐缩小,如图 3所示,距离TAIN站点200 km以内的XINT、LAIW、QUFU站点表现出与TAIN站点类似的年周期和半年周期波动特征。当站点距离较小时,流动站可利用相邻连续站点的年周期项和半年周期项平均值减小周期误差的影响,并利用空间距离内插求取残差值,减小共模误差的影响。周期项误差影响表达式为:

|
图 3 TAIN站点200 km范围内站点的连续观测时间序列 Fig. 3 Time series of continuous observation of stations within 200 km of TAIN station |
| $ \begin{array}{l} Z\left( t \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^n \left( {{c_n}\sin \left( {2\pi t} \right) + {d_n}\cos \left( {2\pi t} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{e_n}\sin \left( {4\pi t} \right) + {f_n}\cos \left( {4\pi t} \right)} \right) \end{array} $ | (2) |
式中,Z(t)为流动站周边连续观测站点周期误差平均值,n为流动站附近连续观测站点个数,cn和dn为相应连续观测站点年周期项,en和fn为相应连续观测站点半年周期项。
残差项表达式为:
| $ {\rm{ \mathsf{\tilde ε} }} = \frac{1}{{\mathop \sum \nolimits\limits_{i = 1}^n {D_n}}}\mathop \sum \limits_{i = 1}^n \left( {{D_n} \cdot {{\rm{ \mathsf{ ε} }}_n}} \right) $ | (3) |
式中,n为流动站附近连续观测站点个数,Dn为流动站与连续观测站点距离,εn为相应连续观测站点残差项。
由式(1)可得流动观测站点表达式为:
| $ \tilde y\left( t \right) = a + bt + Z\left( t \right) + \tilde \varepsilon $ | (4) |
根据式(4)可求取流动站速度信息b。
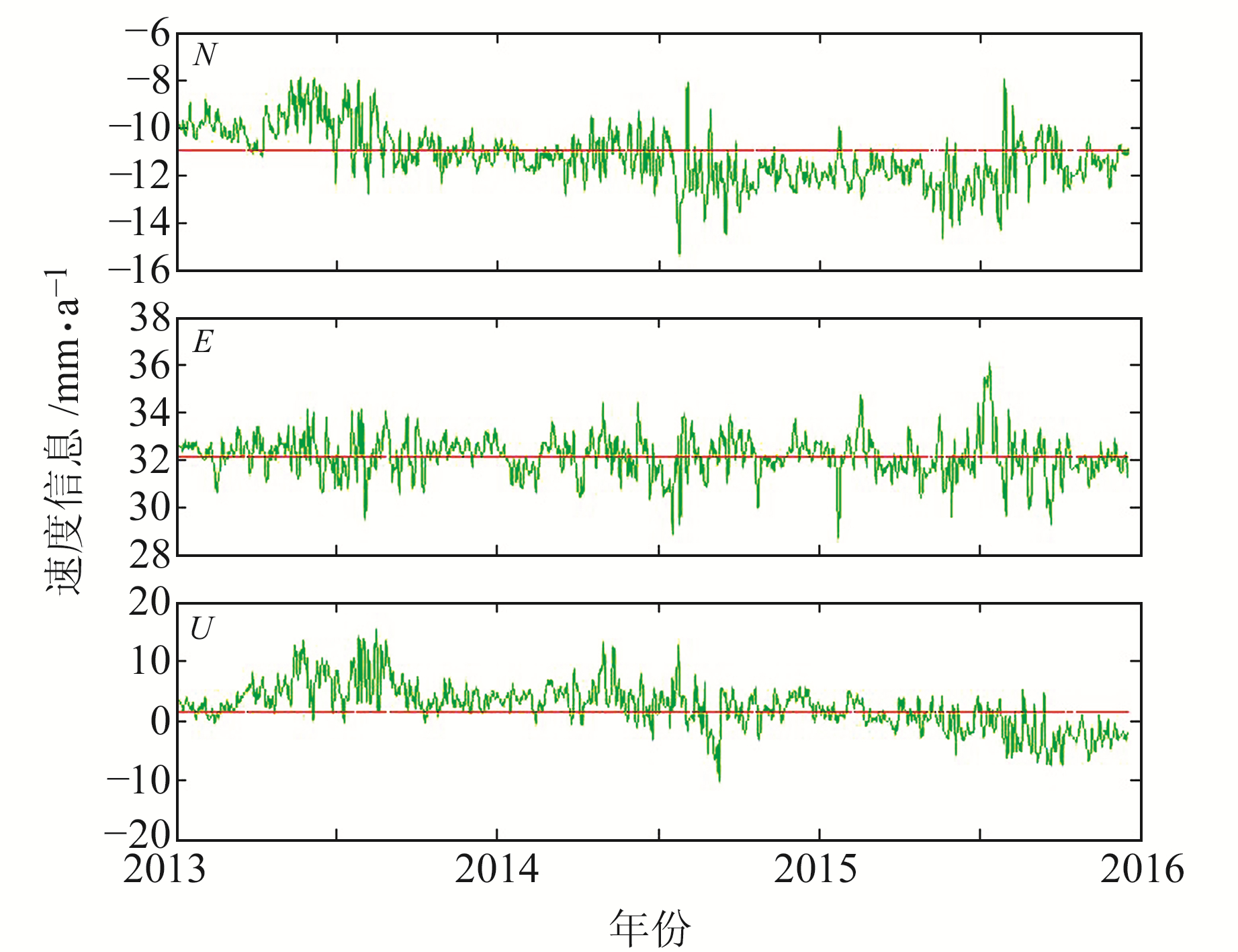
3 流动观测改正方法有效性分析将陆态网络中TAIN站点的时间序列按每期间隔1 a、连续3期、每期3 d截取为流动观测数据,利用站点周边200 km范围内山东地壳运动观测网站点的时间序列获取周期项和残差项,然后根据式(4)求解站点速度信息。滑动获取所有可能的流动观测方案,并利用截取的流动观测数据求取站点的速度信息。图 4为TIAN站点改正后求取的速度信息,其中红线为6 a连续观测解算的速度信息。
|
图 4 TAIN站点改正后流动观测速度信息 Fig. 4 Velocity of TAIN station by mobile observation after correction |
对比图 4和2可知,对周边站点进行改正后,流动测量求取的站点速度信息与真实值的偏差更小,波动明显减小。将陆态网络中TAIN、WUDI、CASH等3个站点的时间序列按连续观测3 a、每期间隔1 a、每期3 d截取为流动观测数据,滑动获取所有可能的流动观测方案,并利用截取的流动观测数据求取站点的速度信息。表 1为获取的站点速度信息与连续6 a观测求取的速度信息的差值区间统计。
|
|
表 1 流动观测与连续观测速度对比 Tab. 1 Velocity comparison of mobile observation and continuous observation |
从表 1可看出,改正前观测结果离散度较大,3 mm以上偏差出现的概率较大,利用200 km范围内连续观测站点改正周期项和残差项后偏差整体减小。为提高研究结果的可信度,分析山东地壳运动观测网中其他4个站点的数据,表 2为其周期项与残差项改正前后的标准差。由表 2可知,改正后周期项和残差项的标准差整体减小。利用本文流动观测改正方法可使流动观测站点速度测量值与连续观测结果差值标准差平均减小37.97%。
|
|
表 2 流动观测改正前后速度标准差 Tab. 2 Standard deviation of velocity obtained by mobile observation before and after correction |
为进一步核实流动观测改正方法的有效性,在山东地壳运动观测网络中TAIN、CASH两个站点2 km范围内同址架设流动站,连续观测3 a、每期观测4 d,结果如图 5所示。

|
图 5 流动观测站改正前后时间序列图 Fig. 5 Time series of mobile observation before and after correction |
表 3为流动观测站改正前后的统计结果。从表中可以看出,将连续观测求取的速度值作为站点的真实速度,流动站改正后观测数据求取的速度值与真实值偏离更小,TAIN、CASH两个站点同址流动站改正后的偏离值平均减小38.9%。
|
|
表 3 TAIN、CASH两个站点同址流动站改正前后偏离值 Tab. 3 Deviation values of mobile observation at TAIN and CASH stations before and after correction |
利用流动站200 km范围内站点的连续观测时间序列改正流动观测数据可有效提高测量结果的质量,连续观测站点改正周期项和残差项后,流动观测站的速度测量值与连续观测结果差值的标准差平均减小37.97%。实测结果显示,同址流动站改正后偏离值平均减小38.9%。
| [1] |
朱成林, 甘卫军, 贾媛, 等. GPS测定沂沭断裂带两侧块体的相对运动状态[J]. 大地测量与地球动力学, 2016, 36(1): 57-61 (Zhu Chenglin, Gan Weijun, Jia Yuan, et al. Measuring the Relative Motion State between the Two Sides' Blocks of Yishu Fault Zone by GPS[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 57-61)
(  0) 0) |
| [2] |
王伟, 杨少敏, 赵斌, 等. 中国大陆现今地壳运动速度场[J]. 大地测量与地球动力学, 2012, 32(6): 29-32 (Wang Wei, Yang Shaomin, Zhao Bin, et al. Present-Day Crustal Movement Velocity Field in Chinese Mainland[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 29-32)
(  0) 0) |
| [3] |
殷海涛, 肖根如, 张磊, 等. TRACK高频GPS定位中震时参考站的选取方法[J]. 大地测量与地球动力学, 2012, 32(4): 15-19 (Yin Haitao, Xiao Genru, Zhang Lei, et al. Study on Method for Selecting Reference Station in High Rate GPS Positioning Using Track during Earthquake[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 15-19)
(  0) 0) |
| [4] |
王琪, 张培震, 马宗晋. 中国大陆现今构造变形GPS观测数据与速度场[J]. 地学前缘, 2002, 9(2): 415-429 (Wang Qi, Zhang Peizhen, Ma Zongjin. GPS Database and Velocity Field of Contemporary Tectonic Deformation in Continental China[J]. Earth Science Frontiers, 2002, 9(2): 415-429)
(  0) 0) |
| [5] |
马下平, 赵立都. 陆态网络GNSS基准站地壳运动速度场分析[J]. 测绘科学, 2018, 43(8): 1-6 (Ma Xiaping, Zhao Lidu. Analysis of Crustal Movement Velocity Field Based on GNSS Base Stations in CMONOC[J]. Science of Surveying and Mapping, 2018, 43(8): 1-6)
(  0) 0) |
| [6] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052 (Wang Min, Shen Zhengkang, Dong Danan. Effects of Non-Tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1045-1052)
(  0) 0) |
| [7] |
黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33 (Huang Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31-33)
(  0) 0) |
| [8] |
Williams S D P, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research Solid Earth, 2004, 109(B3)
(  0) 0) |
| [9] |
Altamimi Z, Métivier L, Collilieux X. ITRF2008 Plate Motion Model[J]. Journal of Geophysical Research Solid Earth, 2012, 117(B7)
(  0) 0) |
| [10] |
胡良晨, 周义炎, 王伟. 陆态网络共模误差的提取研究[J]. 测绘科学, 2019, 44(5): 37-42 (Hu Liangchen, Zhou Yiyan, Wang Wei. Study on the Extraction of Common-mode Errors in CMONOC[J]. Science of Surveying and Mapping, 2019, 44(5): 37-42)
(  0) 0) |
| [11] |
王健, 许安安, 周伯烨. 顾及共模误差的大区域GPS网坐标时间序列噪声分析[J]. 测绘通报, 2018(4): 6-9 (Wang Jian, Xu An'an, Zhou Boye. Noise Analysis of the Coordinate Time Series of the Large-Scale GPS Network with Consideration of Common Mode Error[J]. Bulletin of Surveying and Mapping, 2018(4): 6-9)
(  0) 0) |
| [12] |
常金龙, 甘卫军, 梁诗明, 等. 大华北地区GPS时间序列共模误差的确定与分析[J]. 地震研究, 2018, 41(3): 430-437 (Chang Jinlong, Gan Weijun, Liang Shiming, et al. The Determination and Analysis of GPS Time Series Common Mode Error in the North China Region[J]. Journal of Seismological Research, 2018, 41(3): 430-437)
(  0) 0) |
| [13] |
刘宗强, 党亚民, 杨强, 等. 顾及共模误差的四川连续GPS基准站坐标时间序列噪声分析[J]. 大地测量与地球动力学, 2018, 38(5): 510-515 (Liu Zongqiang, Dang Yamin, Yang Qiang, et al. Noise Analysis of Coordinate Time Series of Sichuan GPS Reference Stations with Common Mode Error[J]. Journal of Geodesy and Geodynamics, 2018, 38(5): 510-515)
(  0) 0) |
2. Geophysical Prospecting and Surveying Team of Shandong Coal Geology Bureau, 33699 East-Jingshi Road, Jinan 250104, China
 2020, Vol. 40
2020, Vol. 40

