卫星信号在传输过程中易受电离层和对流层延时、多路径等的影响,其测距精度很难满足终端区飞机精密进近着陆对导航性能的需求,因此需要进行系统增强[1-2]。GBAS是一种基于伪距测量的差分导航系统,增加了一系列监测过程以提高导航系统的完好性[3-4]。目前,GBAS作为未来唯一能够支持终端区CAT Ⅲ精密进近着陆的卫星导航增强系统,受到欧美等航空强国的高度重视,基于GPS L1 C/A码的GBAS已获得国际民航组织(ICAO)CAT Ⅰ运行许可认证[5]。但系统性能表明,单频GBAS不能满足终端区CAT Ⅲ导航性能的需求,为此国内外学者开展了多星座/双频GBAS技术研究。Sung等[6]对基于GPS/BDS双频/双星座的GBAS载波相位平滑伪距算法进行研究,分析了无码载偏离和无电离层延时两种Hatch滤波器的性能。Song等[7]对CAT Ⅲ GBAS信号质量监测算法进行研究,分析了双频信号质量的监测性能。国内许多研究机构也在开展CAT Ⅰ GBAS的研究工作,并逐步向CAT Ⅲ原型系统演进,围绕完好性监测[8]、机载差分定位[9]等展开研究,也有学者向电离层风暴监测、性能评估、相位平滑伪距等方向展开技术攻关[10-12],为GBAS的研究领域提供了理论与应用支撑。
目前GBAS中已有的研究工作主要集中在完好性监测、差分定位等方面,并未对可能涉及的非完好性事件进行分析,如机载端“虚警”和“漏警”产生的原因及相应的处理方法等。本文对GBAS机载端完好性算法进行研究,给出H0和H1假设下机载端保护级计算过程,并对“虚警”和“漏警”两类非完好性事件进行分析,认为可见卫星几何布局、电离层风暴等是引起这两类非完好性事件的主要误差源。利用GBAS进行验证实验,并通过模拟误差源的方式对“虚警”和“漏警”两类非完好性事件进行了仿真,结果与理论分析具有一致性,为CAT Ⅲ GBAS原理样机的研制提供了理论基础。
1 机载端完好性算法实际飞行中真实导航系统误差(NSE)无法实时量化,因此需要建立理论上的置信界限,称为保护级(PL)。PL表示系统NSE的置信概率为1-p的上限,即
| $ {\rm Prob\left( {NSE > PL} \right)} < p $ | (1) |
式中,p为所允许的完好性风险,与飞机进近着陆阶段的运行需求相关。PL可分为侧向保护级(LPL)和垂直保护级(VPL)两个分量,其大小由卫星几何分布、差分校正后残余伪距测量误差标准差等决定。
利用最小二乘法进行线性逼近可以得到机载端位置和接收机钟差,线性化迭代方程为:
| $ \Delta \mathit{\boldsymbol{\vec y}} = \mathit{\boldsymbol{G}}\Delta \mathit{\boldsymbol{\vec x}} + \mathit{\boldsymbol{\vec \varepsilon }} $ | (2) |
式中,Δ${\mathit{\boldsymbol{\vec y}}}$为N维向量,N为可见卫星个数,由差分校正后的伪距测量值与基于卫星位置和用户位置(${\mathit{\boldsymbol{\vec x}}}$)计算的距离作差求得;Δ${\mathit{\boldsymbol{\vec x}}}$为真实四维位置与计算得到的四维位置的差分量;${\mathit{\boldsymbol{\vec \varepsilon }}}$为N维误差向量;G为机载端接收机的几何矩阵,可表示为:
| $ \begin{array}{l} {\mathit{\boldsymbol{G}}_i} = \left[ { - \cos \left( {{\theta _i}} \right)\cos \left( {{\alpha _i}} \right)\;\cos \left( {{\theta _i}} \right)\sin \left( {{\alpha _i}} \right)\;\;} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - \sin \left( {{\theta _i}} \right),\;1} \right] \end{array} $ | (3) |
式中,i的取值范围为1~N,Gi为第i行向量,θi、αi分别为第i颗卫星的俯仰角和方位角。
利用加权最小二乘法进一步可得Δ${\mathit{\boldsymbol{\vec x}}}$的最优解为:
| $ \Delta \mathit{\boldsymbol{\vec x}} = \left( {{\mathit{\boldsymbol{G}}^{\rm T}}\mathit{\boldsymbol{WG}}} \right){}^{ - 1}{\mathit{\boldsymbol{G}}^{\rm T}}\mathit{\boldsymbol{W}}\Delta \mathit{\boldsymbol{\vec y}} = \mathit{\boldsymbol{S}}\Delta \mathit{\boldsymbol{\vec y}} $ | (4) |
式中,S=(GTWG)-1GTW为加权最小二乘投影矩阵,W为伪距经差分校正后的剩余误差协方差矩阵,其逆矩阵可表示为:
| $ {\mathit{\boldsymbol{W}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {\sigma _1^2}&0& \cdots &0\\ {0}&{\sigma _2^2}& \cdots &0\\ \vdots & \vdots & \ddots &0\\ 0&0&0&{\sigma _N^2} \end{array}} \right] $ | (5) |
式中,σi2=σair, i2+σpr_gnd, i2+σiono, i2+σtropo, i2,σair, i为机载端伪距测量噪声的标准差,σpr_gnd, i为地面系统伪距校正值的误差标准差,σiono, i、σtropo, i分别为伪距差分校正后残余电离层和对流层的误差标准差。
机载端分别计算H0假设和H1假设下的LPL和VPL,并有:
| $ {\rm{LPL}} = \max \left\{ {{\rm{LP}}{{\rm{L}}_{{H_0}}},\;{\rm{LP}}{{\rm{L}}_{{H_1}}}} \right\} $ | (6) |
| $ {\rm{VPL}} = \max \left\{ {{\rm{VP}}{{\rm{L}}_{{H_0}}},\;{\rm{VP}}{{\rm{L}}_{{H_1}}}} \right\} $ | (7) |
H0假设下的LPL和VPL计算方法为:
| $ {\rm{LP}}{{\rm{L}}_{{H_0}}} = {K_{{\rm{ffmd}}}}\sqrt {\sum\limits_{i = 1}^N {s_{{\rm{lat}},i}^2} \times \sigma _i^2} $ | (8) |
| $ {\rm{VP}}{{\rm{L}}_{{H_0}}} = {K_{{\rm{ffmd}}}}\sqrt {\sum\limits_{i = 1}^N {s_{{\rm{vert}},i}^2} \times \sigma _i^2} $ | (9) |
式中,Kffmd为无故障漏检系数,slat, i和svert, i分别为第i颗卫星测距源误差在侧向和垂直方向上的投影。
H1假设下的LPL和VPL计算方法为:
| $ {\rm{LP}}{{\rm{L}}_{{H_1}}} = \max \left\{ {{\rm{LP}}{{\rm{L}}_{{H_1},j}}} \right\} $ | (10) |
| $ {\rm{VP}}{{\rm{L}}_{{H_1}}} = \max \left\{ {{\rm{VP}}{{\rm{L}}_{{H_1},j}}} \right\} $ | (11) |
式中,j为GBAS地面系统接收机编号。LPLH1, j和VPLH1, j的计算方法为:
| $ {\rm{LP}}{{\rm{L}}_{{H_1},j}} = \left| {{B_{j,{\rm{lat}}}}} \right| + {K_{{\rm{md}}}}{\sigma _{{\rm{lat}},{H_1}}} $ | (12) |
| $ {\rm{VP}}{{\rm{L}}_{{H_1},j}} = \left| {{B_{j,{\rm{vert}}}}} \right| + {K_{{\rm{md}}}}{\sigma _{{\rm{vert}},{H_1}}} $ | (13) |
式中,Kmd为地面子系统存在故障时的漏检系数,Bj, lat、Bj, vert分别为基准站接收机引起的侧向和垂直方向误差,σlat, H1、σvert, H1分别为侧向和垂直方向误差的标准差,其计算过程为:
| $ {B_{j,{\rm{lat}}}} = \sum\limits_{i = 1}^N {{s_{{\rm{lat}},i}}{B_{i,j}}} $ | (14) |
| $ {B_{j,{\rm{vert}}}} = \sum\limits_{i = 1}^N {{s_{{\rm{vert}},i}}{B_{i,j}}} $ | (15) |
| $ \sigma _{{\rm{lat}},{H_1}}^2 = \sum\limits_{i = 1}^N {s_{{\rm{lat}},i}^2 \times \sigma _{i,{H_1}}^2} $ | (16) |
| $ \sigma _{{\rm{vert}},{H_1}}^2 = \sum\limits_{i = 1}^N {s_{{\rm{vert}},i}^2 \times \sigma _{i,{H_1}}^2} $ | (17) |
| $ \sigma _{i,{H_1}}^2 = \frac{{M\sigma _{{\rm{pr}}\_{\rm{gnd}},i}^2}}{{M - 1}} + \sigma _{{\rm{air}},i}^2 + \sigma _{{\rm{iono}},i}^2 + \sigma _{{\rm{tropo}},i}^2 $ | (18) |
式中,M为地面系统基准接收机总数;Bi, j为第j个基准接收机上计算得到的第i颗卫星的B值,其计算方法为:
| $ {B_{i,j}} = \frac{1}{M}\sum\limits_{k = 1}^M {{\rm{PR}}{{\rm{c}}_{i,k}}} - \frac{1}{{M - 1}}\mathop {\sum\limits_{k = 1}^M {} }\limits_{k \ne j} {\rm{PR}}{{\rm{c}}_{i,k}} $ | (19) |
式中,PRci, k为第k个基准站接收机计算得到的第i颗卫星伪距的校正值。
2 非完好性事件分析“虚警”和“漏警”是GBAS中两类典型非完好性事件,会引起导航系统性能的降低,因此需要对这两类非完好性事件进行分析,为CAT Ⅲ GBAS的研制提供理论依据。
“虚警”即为机载端计算得到的保护级超出规定的告警门限,而实际的导航系统误差却在告警门限以内,会导致系统的连续性和可用性降低。以H0假设下的垂直保护级计算为例,由式(9)可知,影响保护级计算结果的主要因素有卫星几何分布结构及伪距差分校正后残余误差标准差等。由于空间卫星几何分布随时间变化,可见卫星个数在不同时间段内存在差异,因此当卫星个数较少且分布较差时,计算得到的保护级也会变大,易引起非完好性事件中的“虚警”现象。
“漏警”即为实际的导航系统误差超出规定的告警门限,但机载端计算得到的保护级却在告警门限以内,没能及时向机载端发出告警指示,即出现危险的虚假信息(HMI),引起较大的完好性风险。根据分析可知,电离层风暴是引起非完好性事件中“漏警”现象发生的主要误差源,下面以斯坦福大学提出的电离层风暴模型为例,对“漏警”现象进行分析。
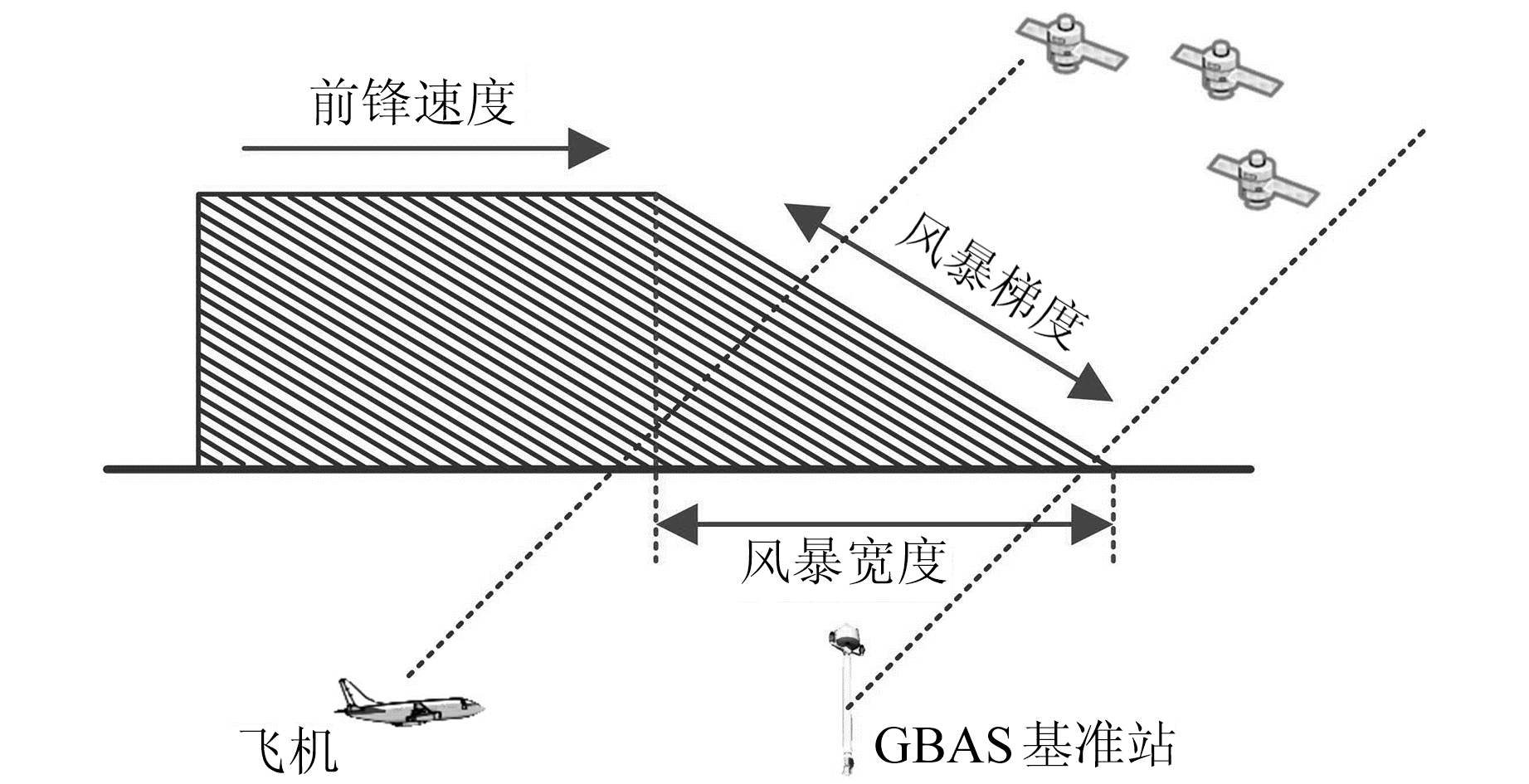
图 1为斯坦福大学电离层风暴模型。由图 1可以看出,该电离层风暴模型由4个典型参数表征,分别为风暴梯度(30~400 mm/km)、宽度(15~200 km)、前锋速度(0~1 000 m/s)及前锋前进方向与飞机接近方向的夹角(0°~360°)。例如,当电离层风暴梯度为200 mm/km、飞机飞行速度为70 m/s时,引起的瞬时电离层时间梯度为14 mm/s。当机载端受电离层风暴影响时,地面基准站与机载端所受电离层的延时具有不一致性,导致差分后的机载端伪距误差偏大,从而引起较大的位置误差。
|
图 1 斯坦福大学电离层风暴模型 Fig. 1 Ionospheric storm model of Stanford University |
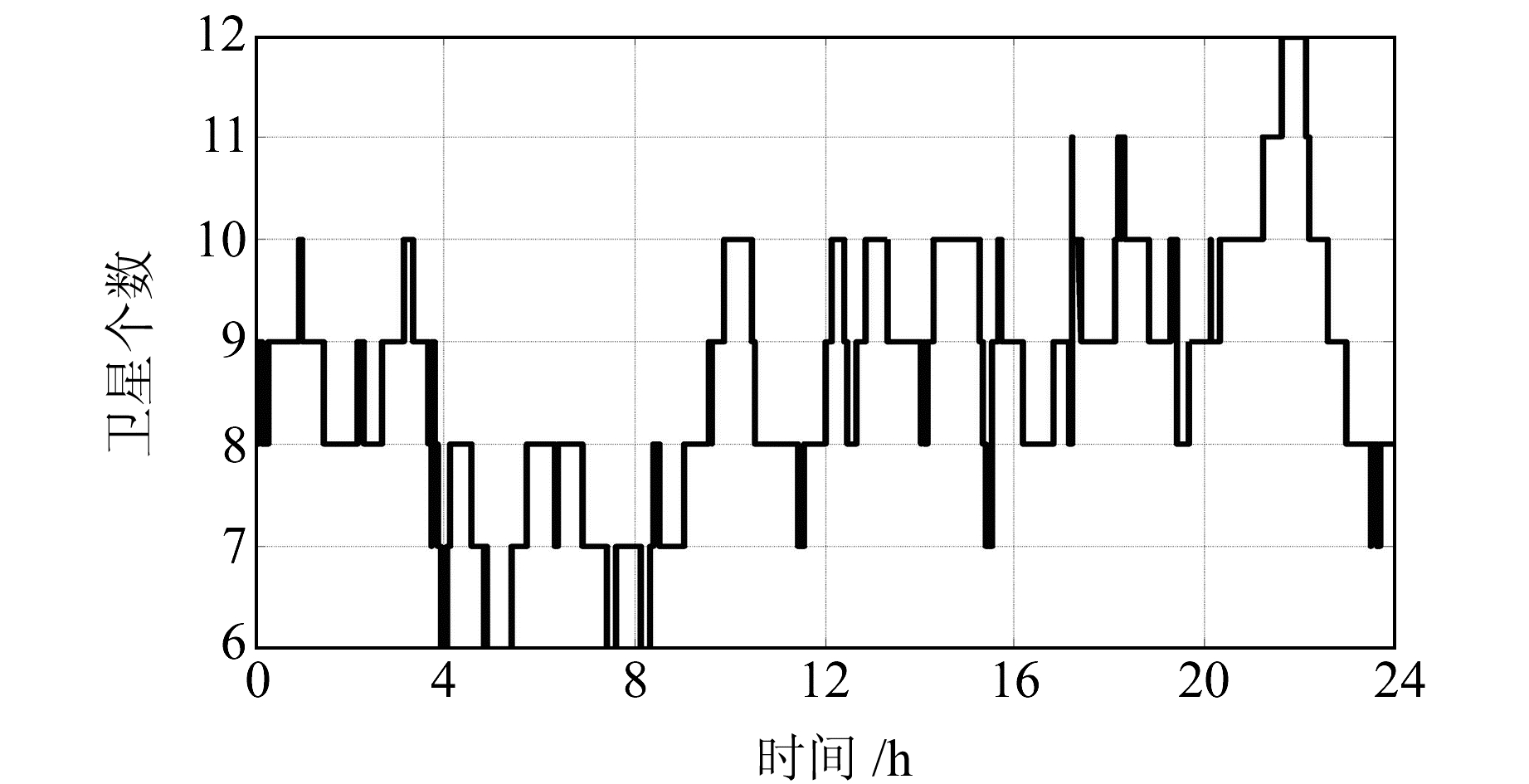
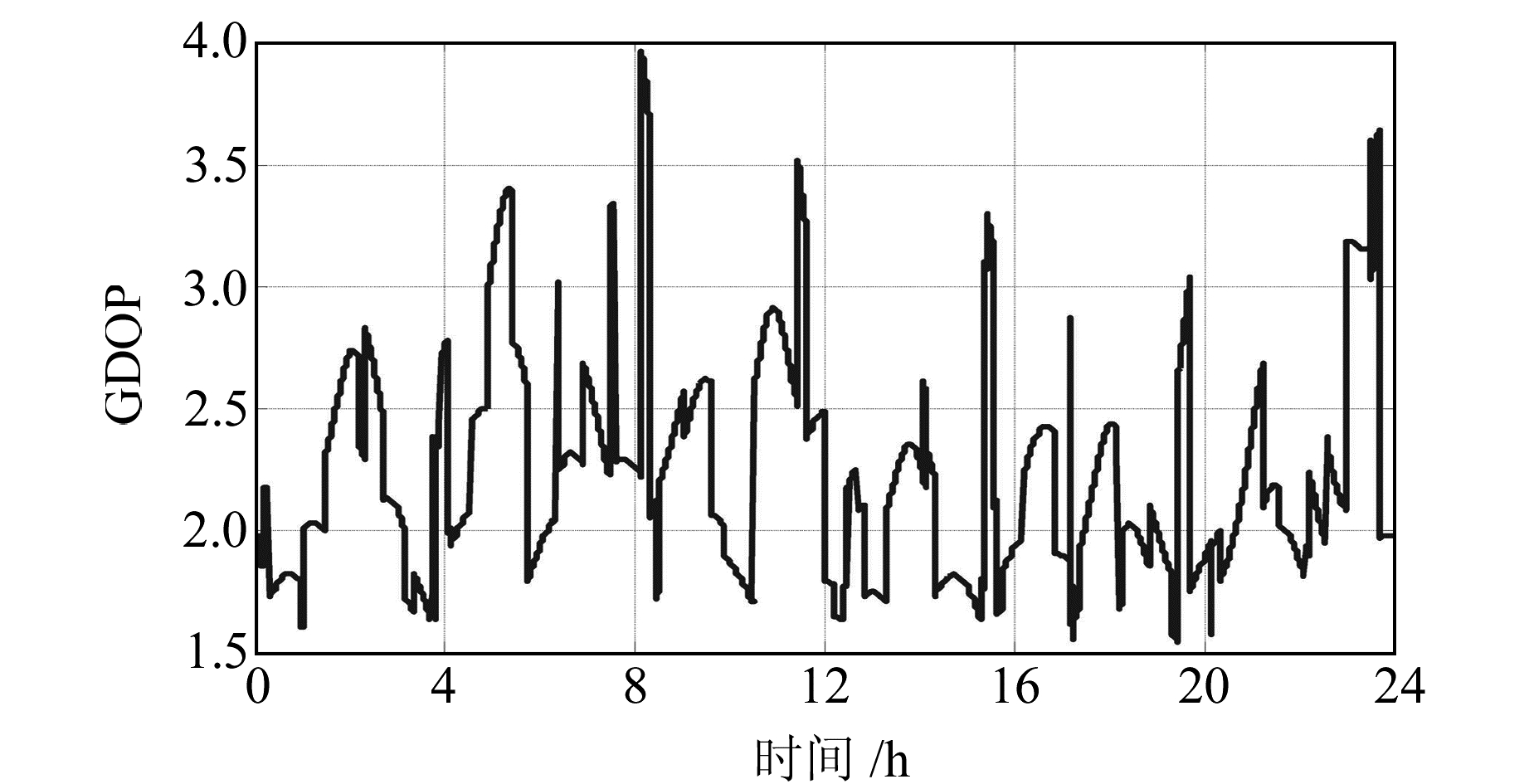
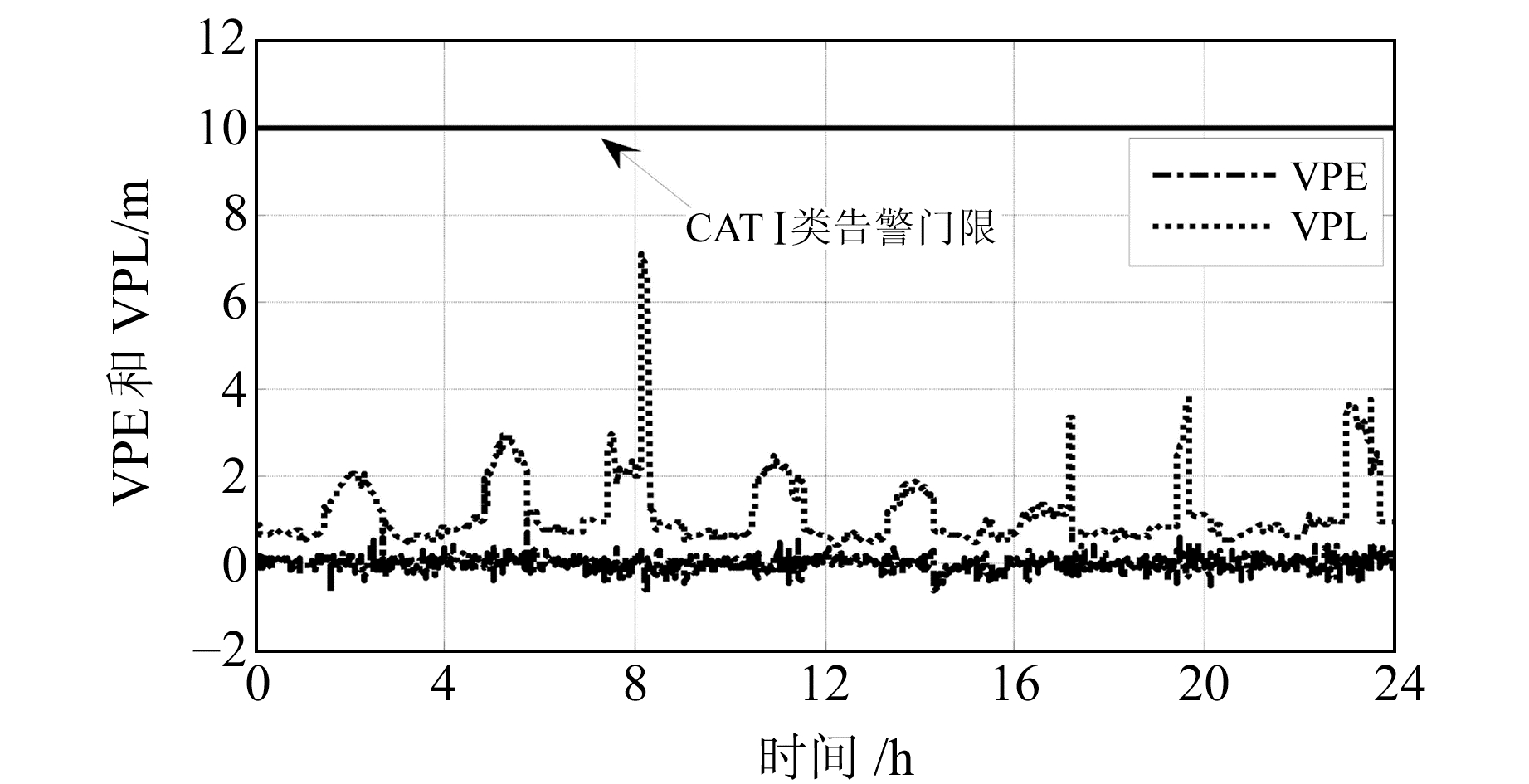
利用GBAS原理样机进行了24 h长时间验证实验,图 2为卫星截止高度角为10°时24 h内可见卫星的个数,图 3为可见卫星几何精度因子(GDOP)曲线。由于飞机精密进近着陆过程中对垂直方向的精度和完好性要求最为苛刻,因此以垂直方向为例,图 4给出了机载端垂直位置误差(VPE)和VPL随时间的变化曲线,表 1(单位m)为VPE和VPL的数值统计。
|
图 2 24 h内可见卫星个数 Fig. 2 Number of visible satellite in 24 hours |
|
图 3 可见卫星几何精度因子 Fig. 3 GDOP of visible satellite |
|
图 4 垂直误差和保护级 Fig. 4 Vertical position error and protection level |
|
|
表 1 VPE和VPL数值统计 Tab. 1 Numerical statistics of VPE and VPL |
由图 2可以看出,当卫星截止高度角为10°时,24 h内机载端接收机可见卫星个数最少为6颗,最多为12颗,满足位置解算需求(可见卫星个数大于等于4颗)。由图 3可以看出,当卫星个数较少时,对应的GDOP值相对较大,与理论分析结果具有一致性。
由图 4和表 1可以看出,实验室研制的GBAS原理样机能够满足ICAO附件10所规定的飞机CAT Ⅰ精密进近着陆导航的完好性需求(VAL=10 m),24 h内系统无非完好性事件发生。对比图 2和4可以看出,当可见卫星个数为6颗且卫星几何分布较差时,VPL会出现突变,最大差值达到7.098 m,使得该时间段内不能满足飞机CAT Ⅲ精密进近着陆导航的完好性需求(VAL=5.3 m)。
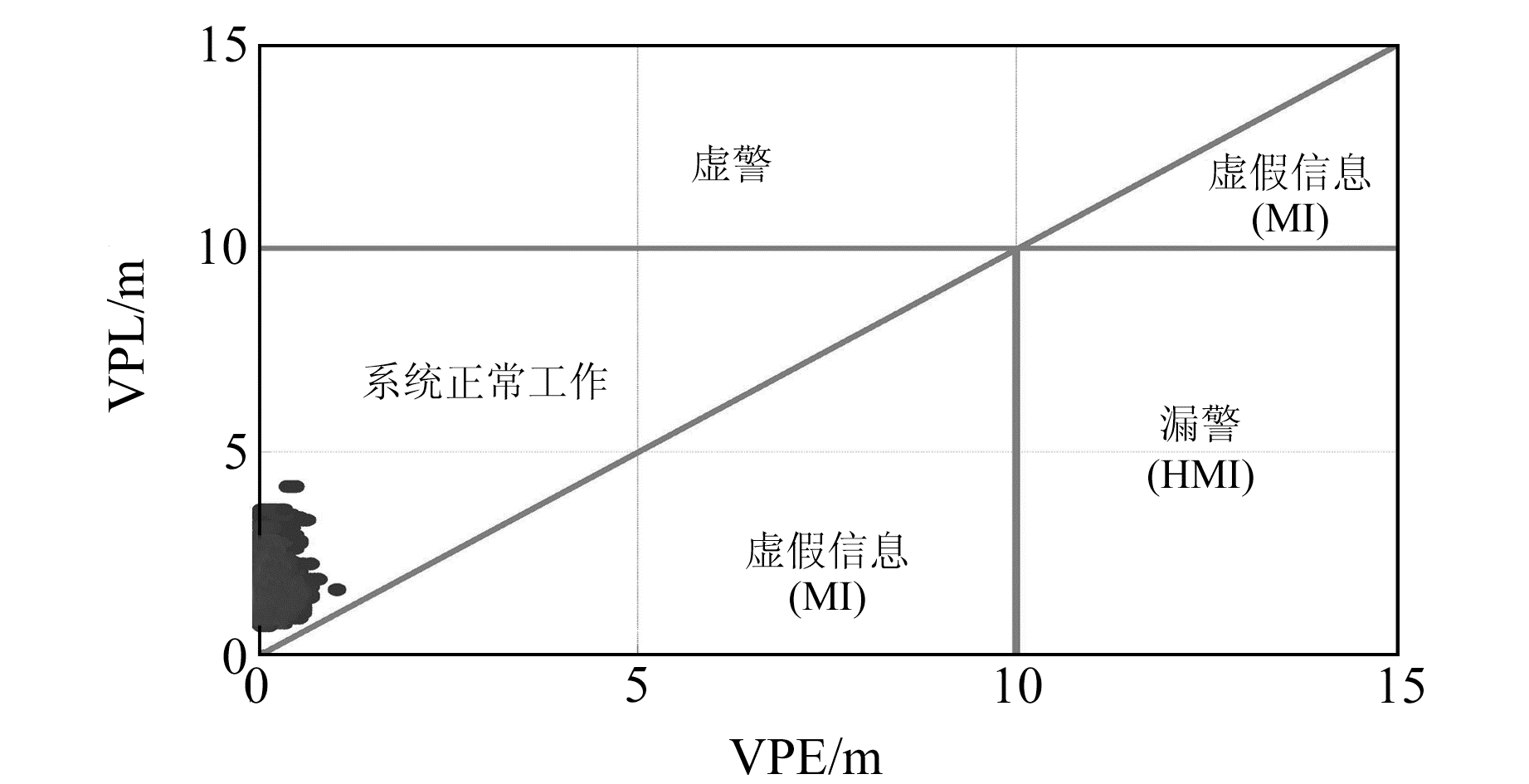
图 5为VPL与VPE所对应的Stanford图(Stanford chart),由此可以对系统在CAT Ⅰ标准下的可用性进行定量分析。
|
图 5 CAT Ⅰ标准Stanford图 Fig. 5 Stanford chart for category Ⅰ standard |
由图 5可以看出,VPE和VPL的比值小于1,说明系统无虚假信息(MI),计算得到的保护级能够包络位置误差,且系统无危险虚假信息。同时还可以看出,24 h内系统可用性大于99.999 9%,满足CAT Ⅰ精密进近着陆导航性能的需求。
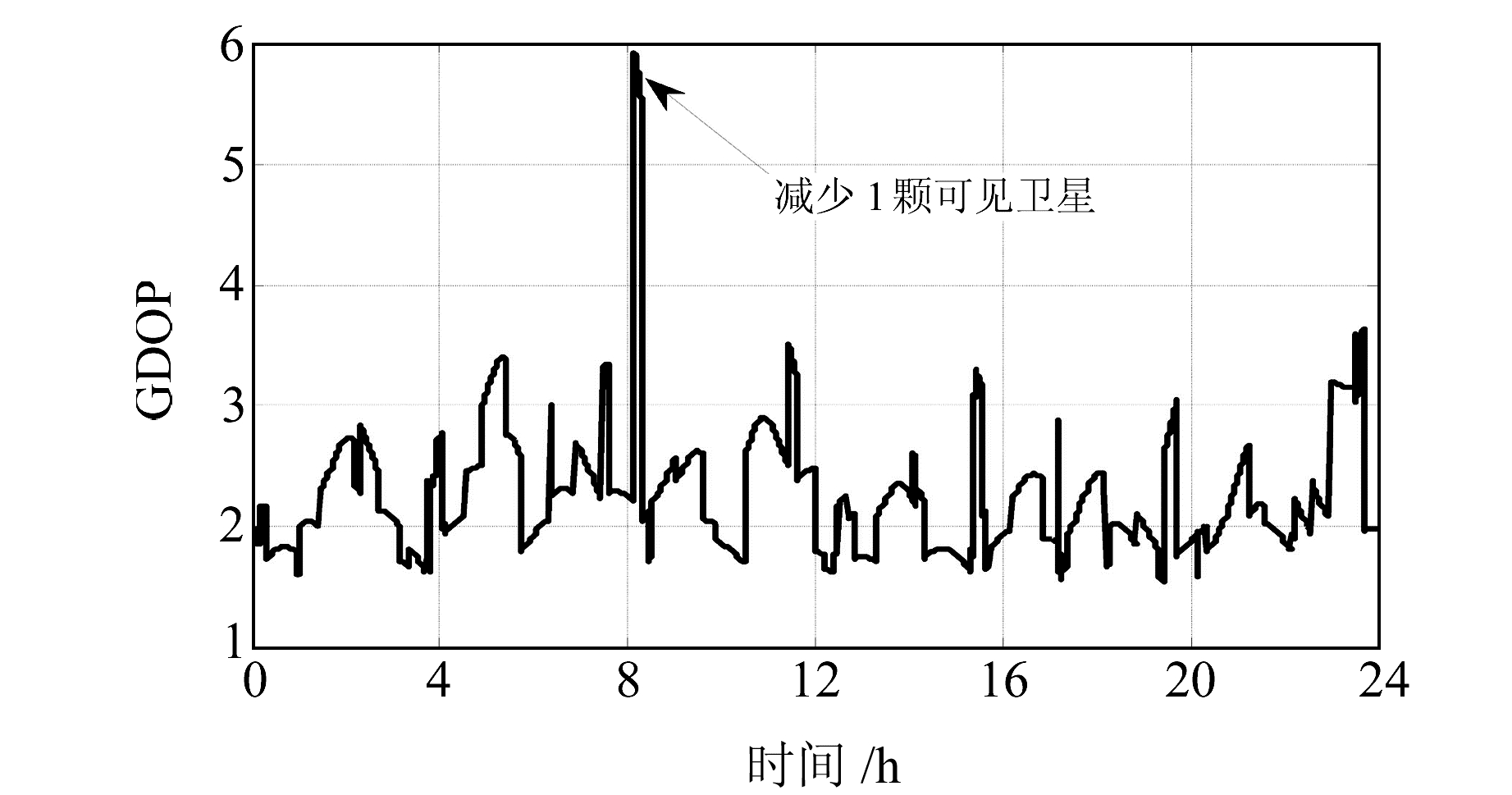
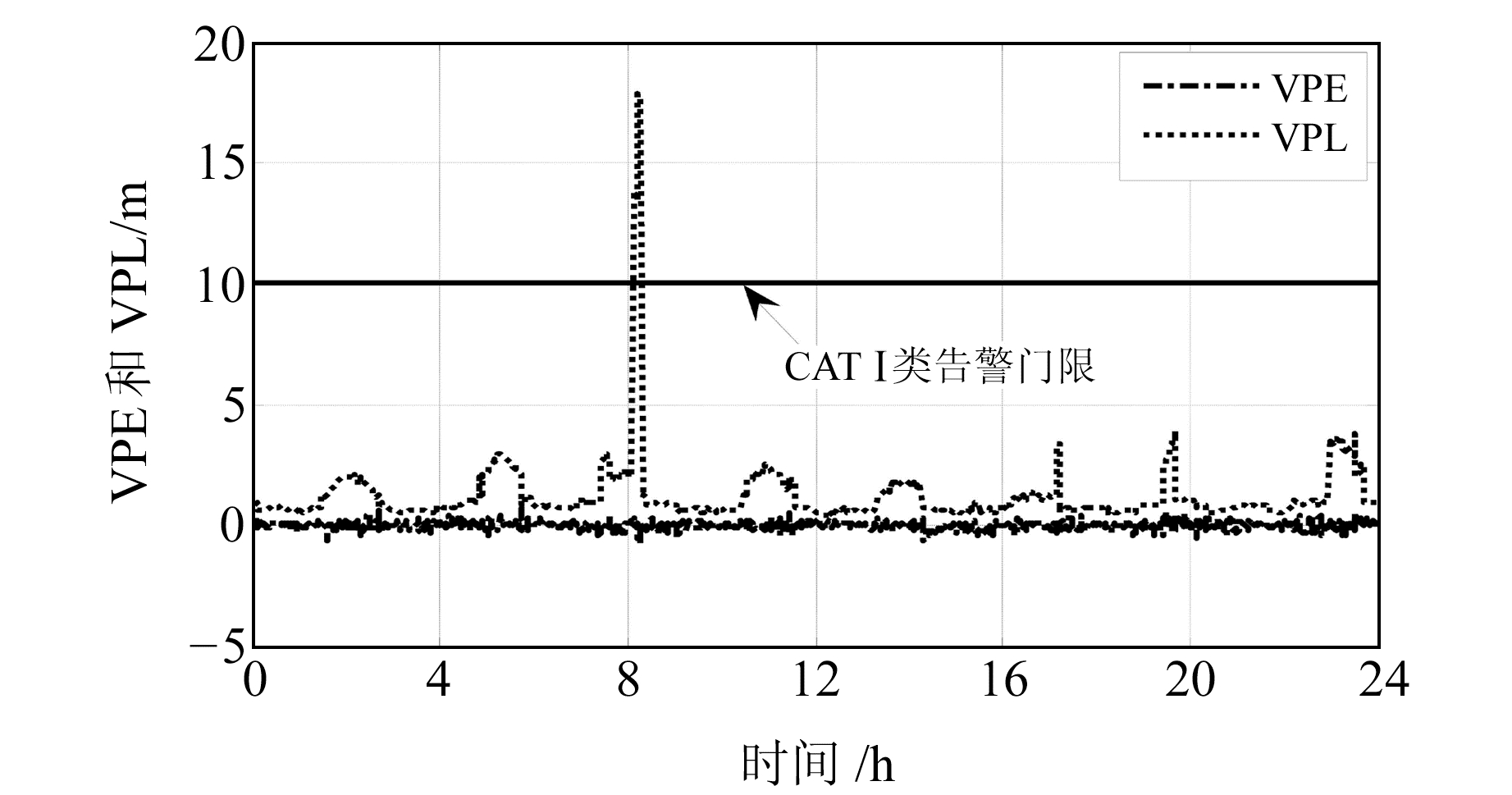
3.2 非完好性事件仿真 3.2.1 虚警模拟仿真由于GBAS原理样机中的模拟机载端与地面基准站间隔较近(两者相距小于20 m),机载端可见卫星的个数与地面基准站具有一致性。而实际中,GBAS的作用域在50 km范围以内,因此机载端可见卫星个数小于等于地面基准站的可见卫星个数,特别是当基准站可见卫星个数较少时,机载端计算得到的保护级易超出告警门限。因此,以§3.1实验数据为例,假设历元在29 343~29 890之间,机载端的可见卫星个数由6颗减少为5颗,通过模拟仿真的方式验证可见卫星个数对导航系统完好性的影响。图 6为GDOP曲线,图 7为VPE和VPL随时间变化的曲线。
|
图 6 可见卫星几何精度因子 Fig. 6 GDOP of visible satellite |
|
图 7 垂直误差和保护级 Fig. 7 Vertical position error and protection level |
由图 6可以看出,当历元在29 343~29 890之间、机载端可见卫星个数由6颗减少为5颗时,对应的GDOP最大值由3.97变为5.92。由图 7可以进一步看出,VPL最大值由7.098变为17.82,从而引起“虚警”的发生,使得系统的可用性降低。由此说明,可见卫星个数及其几何分布对保护级计算结果的影响较大,因此CAT Ⅲ GBAS需要在现有GBAS基础上将单星座扩展为包括北斗在内的多星座,以增加可见卫星个数,提高导航系统的可用性水平。
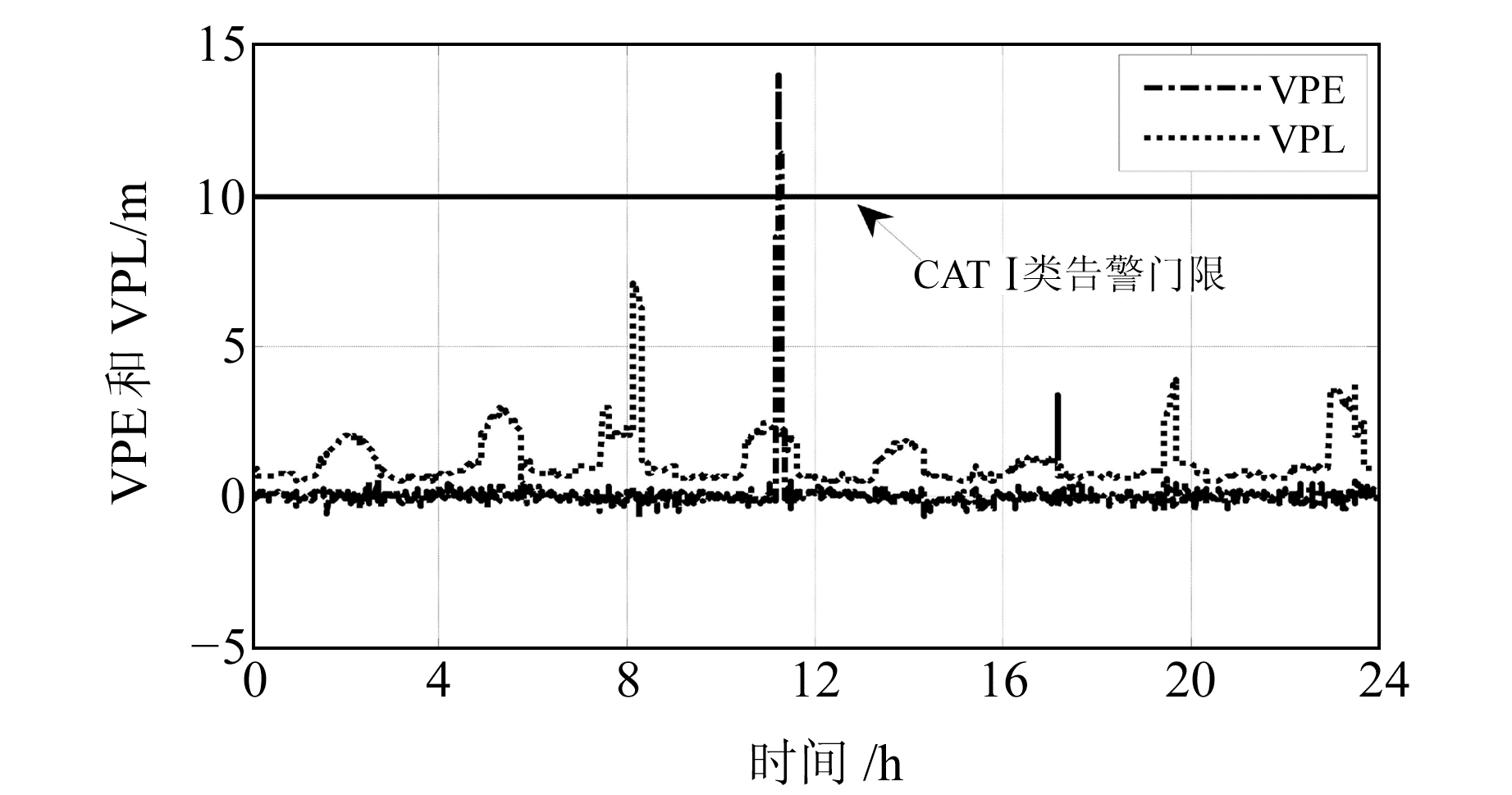
3.2.2 漏警模拟仿真由于GBAS原理样机中的模拟机载端静止不动,且正常情况下大气电离层较为平稳(电离层发生异常的概率在10-7~10-8量级),因此机载端经差分校正后的残余电离层误差近乎为零。为验证系统在极端恶劣环境下的导航性能,同样以§3.1实验数据为例,通过注入伪距和载波相位观测误差的方式模拟机载端受电离层风暴的影响。假设观测历元在32 143~32 843之间,电离层风暴梯度为200 mm/km,飞机飞行速度为70 m/s,则机载端受到的电离层延时变化率为14 mm/s,通过模拟仿真的方式验证电离层风暴对导航系统精度的影响。图 8为VPE和VPL随时间变化的曲线。
|
图 8 垂直误差和保护级 Fig. 8 Vertical position error and protection level |
由图 8可以看出,当在机载端注入异常电离层,且飞机处于飞行状态时,地面基准站电离层误差与机载端具有不一致性,从而使得机载端差分校正后的残余电离层误差偏大,导致VPE超过告警门限,引起“漏警”现象。由此说明,在GBAS使用过程中需实时监测电离层风暴,且未来CAT Ⅲ GBAS需在现有GBAS基础上将单频升级为双频,利用双频测量值对电离层延时进行实时测定,使得伪距差分校正值中不包含电离层误差,从而高系统的导航性能。
4 结语本文对GBAS机载端完好性算法进行研究,给出H0和H1假设下机载端保护级的计算方法,并对GBAS完好性中“虚警”和“漏警”两类典型非完好性事件进行分析。利用研制的GBAS原理样机进行验证实验,结果表明,原理样机性能能够满足飞机CAT Ⅰ精密进近着陆导航性能的需求。同时,通过模拟仿真典型场景对“虚警”和“漏警”两类非完好性事件进行验证,结果表明,未来GBAS需将单星座扩展为包括北斗在内的多星座,将单频升级为双频。多星座可以优化可见卫星的几何布局,提高系统的可用性,而双频则可以抑制电离层风暴的影响,提高机载端位置的解算精度。
| [1] |
Felux M, Dautermann T, Becker H. GBAS Landing System-Precision Approach Guidance after ILS[J]. Aircraft Engineering and Aerospace Technology, 2012, 85(5): 382-388
(  0) 0) |
| [2] |
Lee J, Pullen S, Dattabarua S, et al. Real-Time Ionospheric Threat Adaptation Using a Space Weather Prediction for GNSS-Based Aircraft Landing Systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(7): 1 752-1 761 DOI:10.1109/TITS.2016.2627600
(  0) 0) |
| [3] |
Pullen S, Pervan B, Enge P, et al. A Comprehensive Integrity Verification Architecture for on-Airport LAAS Category Ⅲ Precision Landing[C]. ION GPS, Salt Lake City, 1996
(  0) 0) |
| [4] |
Wang Z P, Macabiau C, Zhang J, et al. Prediction and Analysis of GBAS Integrity Monitoring Availability at Linzhi Airport[J]. GPS Solutions, 2014, 18: 27-40 DOI:10.1007/s10291-012-0306-4
(  0) 0) |
| [5] |
Dautermann T, Mayer C, Antreich F, et al. Non-Gaussian Error Modeling for GBAS Integrity Assessment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 693-706 DOI:10.1109/TAES.2012.6129664
(  0) 0) |
| [6] |
Sung Y T, Lin Y W, Yeh S J, et al. A Dual-Frequency Ground Based Augmentation System Prototype for GPS and BDS[C]. ION GNSS+, Miami, 2019
(  0) 0) |
| [7] |
Song J, Milner C, Selmi L, et al. Assessment of Dual-Frequency Signal Quality Monitor to Support CAT Ⅱ/Ⅲ GBAS[C]. ION GNSS+, Miami, 2019
(  0) 0) |
| [8] |
Xing Z D, Zhao J B, Wang Z H, et al. Analysis and Improvement to Ionosphere Grads Integrity Monitoring Algorithm in Ground Based Augmentation System[C]. CSNC, Xi'an, 2015
(  0) 0) |
| [9] |
Hu J, Sun Q W, Shi X Z. Differential Positioning Algorithm for GBAS Based on Extended Kalman Filtering[C]. WCICA, Changsha, 2018
(  0) 0) |
| [10] |
Wang Z P, Wang S J, Zhu Y B, et al. Assessment of Ionospheric Gradient Impacts on Ground-Based Augmentation System(GBAS) Data in Guangdong Province, China[J]. Sensors, 2017, 17: 1-23 DOI:10.1109/JSEN.2017.2761499
(  0) 0) |
| [11] |
Zhu Y B, Liu Y, Wang Z P, et al. Evaluation of GBAS Flight Trials Based on BDS and GPS[J]. IET Radar, Sonar and Navigation, 2020, 14(2): 233-241 DOI:10.1049/iet-rsn.2019.0284
(  0) 0) |
| [12] |
Xue R, Zhang J, Zhu Y B. Cascade Dual Frequency Smoothing for Local Area Augmentation System[J]. Chinese Journal of Aeronautics, 2009, 22(1): 49-55 DOI:10.1016/S1000-9361(08)60068-0
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

