2. 地理信息工程国家重点实验室, 西安市雁塔路中段1号, 710054;
3. 西安测绘研究所, 西安市雁塔路中段1号, 710054
北斗三号系统(BDS-3)在星座设计、卫星载荷、信号体制和系统服务等方面较北斗二号均有大幅改进[1],并可提供覆盖全球、性能更优的服务。国内部分学者已对其信号质量[2-4]、卫星定轨和钟差性能[5-6]、授时精度[7]、星间链路性能[7-9]及定位服务[10-11]等进行了初步的验证分析,但随着BDS-3组网建设的不断完善,其相关服务性能仍有待进一步评估。
SISRE是评估空间信号精度的重要指标之一,可描述由广播星历轨道和卫星钟差误差引起的用户距离误差统计不确定度,对GNSS的定位精度和完好性具有重要影响。目前针对BDS空间信号精度的研究主要集中在BDS-2[12-14],而针对BDS-3空间信号精度评估的研究较少[15],且研究数据有限,分析结果具有一定的局限性。本文采用2019-01~08的数据,以包含BDS-3的精密星历和钟差产品为基准,对BDS-3中18颗MEO卫星广播星历的轨道误差、钟差误差和SISRE精度进行较为全面的分析。
1 空间信号精度评估方法 1.1 轨道比较基准的统一北斗广播星历轨道与精密星历轨道所采用的坐标框架不同,精密星历基于ITRF框架,而广播星历采用北斗坐标系(Beidou coordinate system, BDCS)。BDCS的定义与CGCS2000坐标系一致,其与ITRF之间的差异为cm级,对广播星历的精度而言可忽略不计[15]。由于广播星历的计算结果为卫星天线相位中心坐标,而精密星历为卫星质心坐标[12],在比较前需对精密星历轨道进行卫星天线相位中心偏差改正,使两者统一到卫星天线相位中心。
设广播星历计算得到的卫星天线相位中心坐标为${\mathit{\boldsymbol{\vec r}}_b}$,精密星历计算得到的卫星质心坐标为${\mathit{\boldsymbol{\vec r}}_s}$,星固坐标系下的卫星天线相位中心改正PCO为${\mathit{\boldsymbol{\vec p}}_{{\rm{co}}}}$= [xp yp zp]T,则广播星历轨道在径向(radial)、切向(along-track)和法向(cross-track)的误差可表示为:
| $ \begin{array}{l} \Delta {{\mathit{\boldsymbol{\vec r}}}_{{\rm{rac}}}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\vec e}}}_R^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_A^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_C^{\rm{T}}}} \end{array}} \right]\left( {\left( {{{\mathit{\boldsymbol{\vec r}}}_b} - {{\mathit{\boldsymbol{\vec r}}}_s}} \right) - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_x}}&{{\mathit{\boldsymbol{e}}_y}}&{{\mathit{\boldsymbol{e}}_z}} \end{array}} \right]{{\mathit{\boldsymbol{\vec p}}}_{{\rm{co}}}}} \right) = \\ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\vec e}}}_R^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_A^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_C^{\rm{T}}}} \end{array}} \right]\left( {{{\mathit{\boldsymbol{\vec r}}}_b} - {{\mathit{\boldsymbol{\vec r}}}_s}} \right) - \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\vec e}}}_R^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_A^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_C^{\rm{T}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_x}}&{{\mathit{\boldsymbol{e}}_y}}&{{\mathit{\boldsymbol{e}}_z}} \end{array}} \right]{{\mathit{\boldsymbol{\vec p}}}_{{\rm{co}}}} \end{array} $ | (1) |
式中,[ex ey ez]为星固系坐标轴在地固系中的单位向量,$\left[{\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\vec e}}}_R}}&{{{\mathit{\boldsymbol{\vec e}}}_A}}&{{{\mathit{\boldsymbol{\vec e}}}_C}} \end{array}} \right]$为卫星轨道坐标系坐标轴在地固系中的单位向量,具体计算公式可参考文献[16]。则PCO对广播星历轨道R、A、C方向误差的影响$\Delta {\mathit{\boldsymbol{\vec r}}_{{\rm{pc}}{{\rm{o}}_ - }{\rm{rac}}}}$可表示为:
| $ \begin{array}{l} \Delta {{\mathit{\boldsymbol{\vec r}}}_{{\rm{pco\_rac}}}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\vec e}}}_R^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_A^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_C^{\rm{T}}}} \end{array}} \right]\Delta {{\mathit{\boldsymbol{\vec r}}}_{\rm pco\_xyz}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\vec e}}}_R^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_A^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\vec e}}}_C^{\rm{T}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_x}}&{{\mathit{\boldsymbol{e}}_y}}&{{\mathit{\boldsymbol{e}}_z}} \end{array}} \right]·\\ \;\;\;\;\;{{\mathit{\boldsymbol{\vec p}}}_{{\rm{co}}}} = \left[ {\begin{array}{*{20}{c}} 0&0&1\\ {{{\mathit{\boldsymbol{\vec e}}}_A^{\rm{T}}}{\mathit{\boldsymbol{e}}_x}}&{{{\mathit{\boldsymbol{\vec e}}}_A^{\rm{T}}}{\mathit{\boldsymbol{e}}_y}}&0\\ {{{\mathit{\boldsymbol{\vec e}}}_C^{\rm{T}}}{\mathit{\boldsymbol{e}}_x}}&{{{\mathit{\boldsymbol{\vec e}}}_C^{\rm{T}}}{\mathit{\boldsymbol{e}}_y}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_p}}\\ {{y_p}}\\ {{z_p}} \end{array}} \right] \end{array} $ | (2) |
由几何关系可得:$\mathit{\boldsymbol{\vec e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_x} = \mathit{\boldsymbol{\vec e}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{e}}_y}, \mathit{\boldsymbol{\vec e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_y} = \mathit{\boldsymbol{\vec e}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{e}}_x}$。设$\mathit{\boldsymbol{\vec e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_x}$=cos(θ),θ为轨道切向与地心、卫星和太阳三者所在平面的夹角,则:
| $ \begin{array}{l} \Delta {{\mathit{\boldsymbol{\vec r}}}_{{\rm{pco\_rac}}}} = \left[ {\begin{array}{*{20}{c}} 0&0&1\\ {\cos \theta }&{\sin \theta }&0\\ {\sin \theta }&{\cos \theta }&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_p}}\\ {{y_p}}\\ {{z_p}} \end{array}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{z_p}}\\ {{x_p}\cos \theta + {y_p}\sin \theta }\\ {{x_p}\sin \theta + {y_p}\cos \theta } \end{array}} \right] \end{array} $ | (3) |
由式(3)可知,天线PCO中zp仅对广播星历轨道的径向误差产生影响,误差可达m级,而对法向和切向误差无影响。当zp的改正值不准确时,径向误差中会出现明显的系统性偏差。在实际改正时,BDS-2卫星的PCO改正参数取其卫星出厂时的标定值[18],BDS-3卫星的PCO改正参数采用IGS发布的参考值。
1.2 钟差比较基准的统一北斗广播星历的钟差采用北斗时(BDT),而精密星历的钟差则基于GPST,在比较前需将两者统一到GPST。由于北斗系统广播星历钟差与精密星历钟差的频率基准和时标基准均不同,在比较前需对其进行统一。广播星历钟差的频率基准为B3频点,本文所采用的BDS-2和BDS-3精密星历钟差产品的频率基准均为B1Ⅰ/B3Ⅰ消电离层组合,因此在比较前需对广播星历钟差进行设备时间延迟(TGD)改正,将频率基准改正到B1Ⅰ/B3Ⅰ消电离层组合,即钟差比较值可表示为:
| $ \Delta T_b^i = T_s^i - T_b^i = T_s^i - T_{{\rm{brdm}}}^i + \frac{{f_{{\rm{B}}1}^2}}{{f_{{\rm{B}}1}^2 - f_{{\rm{B}}3}^2}}{\rm{tgd}}_1^i $ | (4) |
式中,Tsi为精密星历钟差,Tbrdmi为广播星历钟差,Tbi为经过TGD改正后的广播星历钟差,fB1和fB3分别为B1频点和B3频点的频率,tgd1i为B1频率的TGD改正值。
由于广播星历钟差和精密星历钟差的时标基准不同,ΔTbi中包含一个系统性的时标基准偏差,该时标基准偏差随历元变化,且对同一系统中的卫星取值相同,可采用取均值的方式获得。为了剔除粗差影响,本文采用抗差估计方法[17]对其进行估计,计算公式为:
| $ \hat b\left( k \right) = \frac{{\sum\limits_{i = 1}^n {{{\bar p}_i} \cdot \Delta T_b^i\left( k \right)} }}{{\sum\limits_{i = 1}^n {{{\bar p}_i}} }} $ | (5) |
式中,$\hat b$ (k)为时标基准偏差估计值,pi为ΔTbi(k)的等价权,n为有效卫星数。计算中采用中位数作为抗差估计的初值,选取IGGⅢ等价权函数[17],通过迭代计算得到时标基准偏差的估计值$\hat b$ (k),此时广播星历钟差误差可表示为:
| $ \delta {T^i}\left( k \right) = \Delta T_b^i\left( k \right) - \hat b\left( k \right) $ | (6) |
在计算时标基准偏差估计值时,本文将BDS-2和BDS-3作为2个系统进行处理,分别计算其卫星的时标基准差。后文中计算结果也表明,BDS-2和BDS-3卫星存在时标基准偏差。
1.3 SISRE计算方法轨道误差Δ${\mathit{\boldsymbol{\vec r}}}$rac= ΔrR ΔrA ΔrC对用户距离误差的影响为其在用户到卫星方向上的投影,设用户到卫星方向的单位向量为${\mathit{\boldsymbol{\vec e}}}$,则该用户的SISRE可表示为Δ${\mathit{\boldsymbol{\vec r}}}$racT${\mathit{\boldsymbol{\vec e}}}$。显然,SISRE随用户位置的变化而改变,因此仅受轨道影响的空间信号距离误差(orbit-only SISRE, O-SISRE)可用卫星可视区域内所有用户的空间信号距离误差的平均值表示,计算公式为[12]:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{O - SISRE}}\\ = \sqrt {w_R^2 \cdot \Delta r_R^2 + w_{A,C}^2 \cdot \left( {\Delta r_A^2 + \Delta r_C^2} \right)} \end{array} $ | (7) |
式中,wR和wA, C为广播星历轨道径向误差及切向和法向误差对SISRE的贡献因子,该值与卫星的轨道高度有关,具体取值和计算方法见文献[18]。
北斗广播星历钟差采用双向卫星时间与频率传递方法进行估计[19],这会削弱卫星钟差与广播星历轨道的相关性。受轨道和钟差误差影响的全球平均空间信号距离误差(global-average SISRE, GA-SISRE)可表示为:
| $ \begin{array}{l} \,\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{GA - SISRE = }}\\ \sqrt {w_R^2 \cdot \Delta r_R^2 + w_{A,C}^2 \cdot \left( {\Delta r_A^2 + \Delta r_C^2} \right) + {{\left( {c\delta T} \right)}^2}} \end{array} $ | (8) |
由于空间信号距离误差受用户位置的影响,因此存在SISRE最差值(worst SISRE, W-SISRE)[13],W-SISRE可采用数值搜索和解析分析2种方法求取,本文采用文献[12]中的解析方法进行计算。
2 数据简介与预处理本文选用2019-01-01~08-07的数据进行分析,其中北斗广播星历数据可从MGEX提供的brdm文件中获取,精密星历数据采用武汉大学最新发布的包含BDS-3的精密星历和钟差产品,该产品均基于B1I/B3I频点消电离层组合进行计算,且将BDS-2和BDS-3作为一个系统进行处理。实际处理时每15 min计算一组数据,以精密星历数据为基准进行评估。由于武汉大学精密星历数据中仅包含BDS-3基本系统的18颗MEO卫星,故本文仅分析BDS-3基本系统卫星的空间信号精度。
在进行评估计算前,对广播星历和精密星历进行以下预处理以获取有效的星历数据:
1) 合并广播星历中的重复数据,剔除星历健康标志为1的不健康广播星历数据;
2) 广播星历间隔大于2 h时不进行评估,即|tk-toe|>2 h或|tk-toc|>2 h,其中toe为星历参考时刻,toc为钟差参考时刻;
3) 精密星历缺失或钟差为999 999.999 9时不进行评估。
3 计算与分析 3.1 广播轨道误差分析图 1~3为C05、C06、C11和C25卫星广播星历轨道径向、切向和法向误差及其日均值序列,从图中可以看出:

|
图 1 广播星历轨道径向误差及日均值序列 Fig. 1 Radial error of BDS broadcast ephemeris orbit and daily mean value sequence |

|
图 2 广播星历轨道切向误差及日均值序列 Fig. 2 Along-track error of BDS broadcast ephemeris orbit and daily mean value sequence |
|
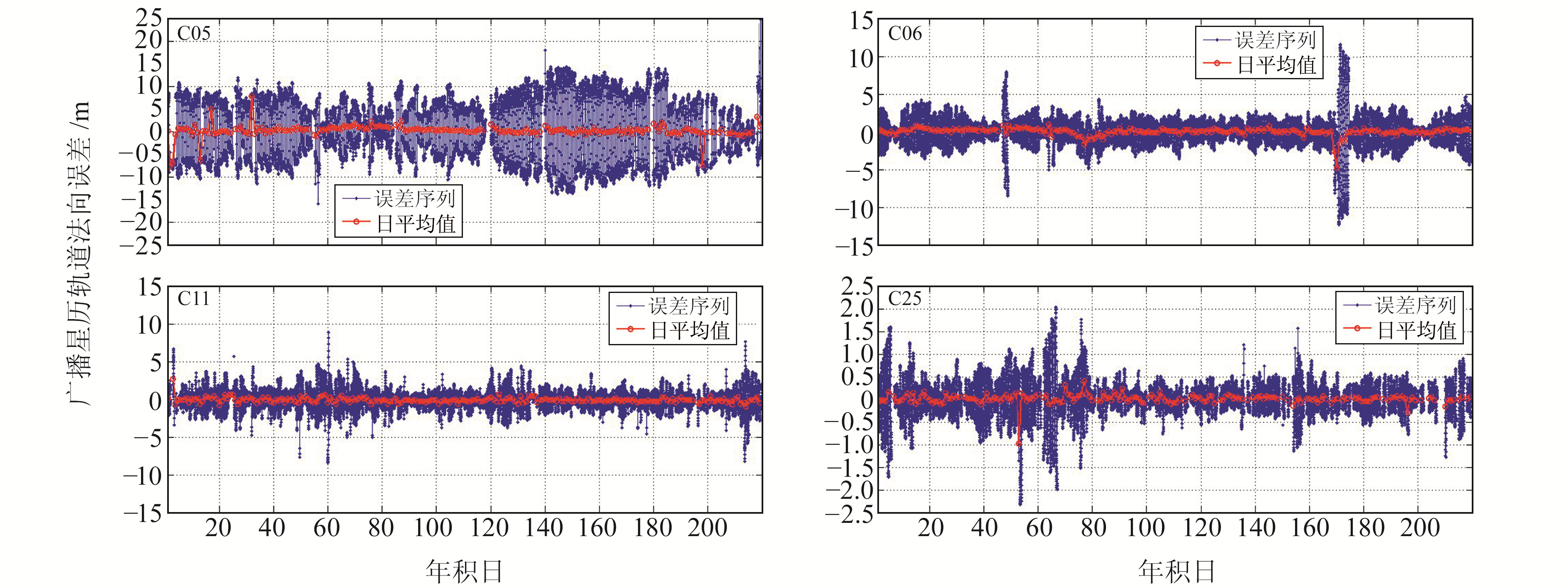
图 3 广播星历轨道法向误差及日均值序列 Fig. 3 Cross-track error of BDS broadcast ephemeris orbit and daily mean value sequence |
1) 各卫星广播星历轨道误差序列中均存在部分时段轨道误差较大,可能为卫星机动或星蚀期影响造成。
2) BDS-2 GEO卫星广播星历轨道误差较大,IGSO和MEO卫星的轨道精度均优于GEO卫星。GEO卫星的径向误差序列总体小于3 m,但切向和法向误差序列部分可达10 m,其主要原因为GEO卫星广播星历轨道精度观测站分布的几何结构较差,且卫星基本处于静止状态,观测量对切向和法向的变化不敏感。
3) BDS-3卫星广播星历轨道误差明显小于BDS-2同类卫星,其中径向误差最小,基本小于0.5 m,切向和法向误差基本小于2 m,较BDS-2卫星均有显著提升,这与BDS-3卫星间链路观测的支持和轨道测定策略的优化有关。
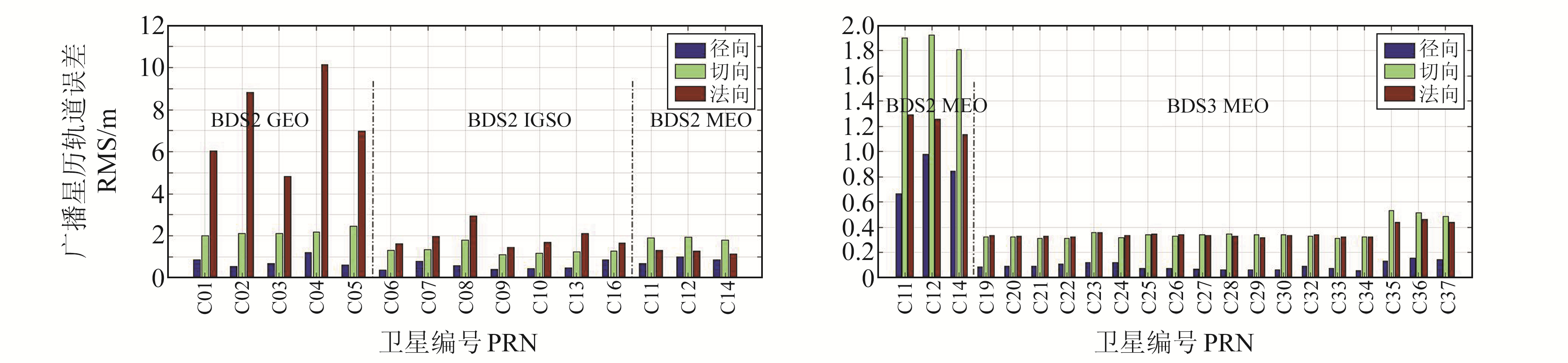
图 4为BDS-2和BDS-3卫星广播星历轨道误差相对于零均值的RMS统计精度,从图中可以看出,BDS-3卫星广播星历轨道径向RMS优于0.18 m,切向和法向RMS均优于0.6 m,其中C35、C36和C37卫星由于数据缺失较为严重,统计结果较其他BDS-3卫星稍差。BDS-2 MEO卫星广播星历轨道径向、切向和法向RMS统计精度分别约为0.8 m、2 m和1.3 m,均差于BDS-3 MEO卫星。
|
图 4 北斗系统广播星历轨道误差RMS统计值 Fig. 4 RMS values of BDS broadcast ephemeris orbit error |
根据§1.2的方法分别计算各卫星广播星历钟差误差,图 5为C05、C07、C11和C28卫星广播星历钟差误差及日均值序列,图 6为BDS-2和BDS-3卫星广播星历钟差误差RMS和95%统计精度。从图中可以看出:

|
图 5 北斗系统广播星历钟差误差及日均值序列 Fig. 5 BDS broadcast ephemeris clock error and daily mean value sequence |
|
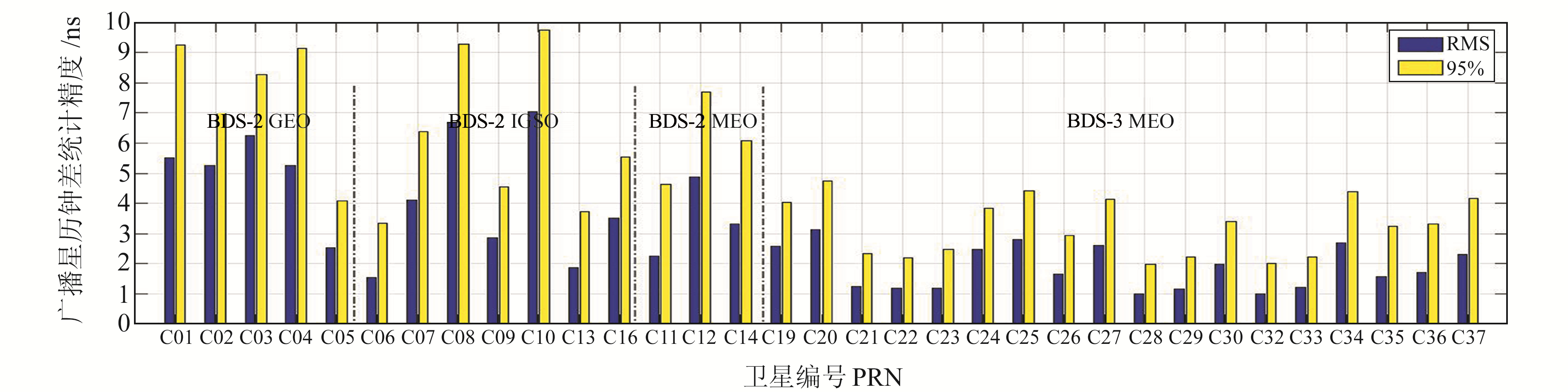
图 6 北斗系统广播星历钟差精度统计 Fig. 6 Accuracy of BDS broadcast ephemeris clock error |
1) BDS-2卫星广播星历钟差序列一般小于10 ns,平均RMS统计精度约为4.2 ns,平均95%统计精度为6.6 ns,对用户距离误差的影响均在1 m以上。
2) BDS-3广播星历钟差误差序列绝大部分小于5 ns,较BDS-2卫星变化较为平稳,其平均RMS统计精度约为1.86 ns,平均95%统计精度为3.23 ns,均优于BDS-2卫星。这与BDS-3卫星采用新氢原子钟和更高精度的铷原子钟有重要关系。
3.3 SISRE分析根据§1.3中的方法分别计算各卫星的SISRE,图 7~9分别为C11和C25卫星的O-SISRE、GA-SIS RE和W-SISRE序列及日均值,从图中可以看出:

|
图 7 北斗系统O-SISRE及日均值序列 Fig. 7 O-SISRE of BDS and daily mean value sequence |
|
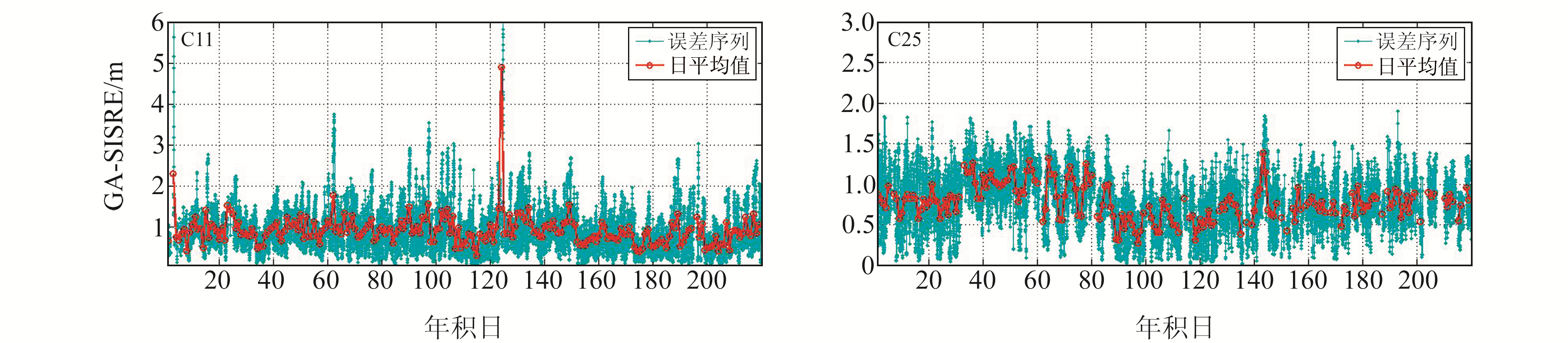
图 8 北斗系统GA-SISRE及日均值序列 Fig. 8 GA-SISRE of BDS and daily mean value sequence |

|
图 9 北斗系统W-SISRE及日均值序列 Fig. 9 W-SISRE of BDS and daily mean value sequence |
1) BDS-3卫星的O-SISRE明显小于BDS-2卫星,C25卫星的O-SISRE序列基本小于0.5 m,而C11卫星的O-SISRE序列最大可达2 m,明显大于C25卫星(图 7)。由于O-SISRE主要受径向轨道误差的影响,该结果进一步说明BDS-3卫星广播星历的轨道径向精度较BDS-2有较大提升。
2) BDS-3卫星的GA-SISRE主要受钟差误差影响,C25卫星的GA-SISRE序列在2 m内变化(图 8),较O-SISRE大幅增大,其增大部分主要受钟差误差影响。该结果表明,钟差精度是制约BDS-3空间信号精度提升的主要因素。
3) BDS-3卫星的W-SISRE序列基本小于2 m,而BDS-2卫星的W-SISRE序列部分可达3 m。该结果表明,用户距离精度(URA)取值2 m可较好地描述BDS-3卫星的URA精度,但对于BDS-2卫星则过于乐观。
表 1(单位m)为BDS-2卫星的SISRE精度统计,表 2(单位m)为BDS-3卫星的SISRE精度统计,从表中可以看出:
|
|
表 1 北斗二号卫星SISRE精度统计 Tab. 1 Accuracy of BDS-2 satellites SISRE |
|
|
表 2 北斗三号卫星SISRE精度统计 Tab. 2 Accuracy of BDS-3 satellites SISRE |
1) BDS-2卫星的O-SISRE、GA-SISRE和W-SISRE平均RMS统计精度分别为0.79 m、1.53 m和1.83 m,对应的95%统计精度分别为1.39 m、2.30 m和2.78 m。
2) BDS-3卫星O-SISRE、GA-SISRE和W-SISRE的平均RMS统计精度分别为0.12 m、0.58 m和0.60 m,对应的95%统计精度分别为0.22 m、0.99 m和1.02 m,均明显小于BDS-2卫星。
4 结语基于2019-01-01~08-07数据,以精密星历为基准,对比分析BDS-2和BDS-3卫星广播星历的轨道精度、钟差精度及3类SISRE精度的变化情况,结果表明:
1) BDS-3 MEO卫星广播星历的轨道精度明显优于BDS-2同类卫星,其径向RMS精度优于0.18 m,切向和法向RMS精度优于0.6 m;
2) BDS-3卫星广播星历的钟差误差基本小于5 ns,较BDS-2卫星变化更为平稳,其平均RMS统计精度为1.86 ns,平均95%统计精度为3.23 ns,均优于BDS-2卫星;
3) BDS-3卫星3类SISRE精度均优于BDS-2卫星,且主要受钟差误差的制约,轨道误差对其影响较小。BDS-3卫星O-SISRE、GA-SISRE和W-SISRE的平均RMS统计精度分别为0.12 m、0.58 m和0.60 m,对应的95%统计精度分别为0.22 m、0.99 m和1.02 m,均明显小于BDS-2卫星。
本文仅对BDS-3基本系统组网卫星的空间信号精度进行分析,随着BDS-3的进一步完善和相应精密产品的发布,其空间信号的精度仍需进一步分析。
| [1] |
Yang Y X, Gao W G, Guo S R, et al. Introduction to Beidou-3 Navigation Satellite System[J]. Navigation, 2019, 66(1): 7-18
(  0) 0) |
| [2] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测——试验验证数据分析[J]. 中国科学:地球科学, 2018, 48(5): 584-594 (Yang Yuanxi, Xu Yangyin, Li Jinlong, et al. Progress and Performance Evaluation of Beidou Global Navigation Satellite System:Data Analysis Based on BDS-3 Demonstration System[J]. Science China Earth Science, 2018, 48(5): 584-594)
(  0) 0) |
| [3] |
Zhang X H, Wu M K, Liu W K, et al. Initial Assessment of the COMPASS/Beidou-3:New-Generation Navigation Signals[J]. Journal of Geodesy, 2017, 91(10): 1225-1240 DOI:10.1007/s00190-017-1020-3
(  0) 0) |
| [4] |
Lu M G, Li W Y, Yao Z, et al. Overview of BDS-3 New Signals[J]. Navigation, 2019, 66(4): 19-35
(  0) 0) |
| [5] |
Zhao Q L, Wang C, Guo J, et al. Precise Orbit and Clock Determination for Beidou-3 Experimental Satellites with Yaw Attitude Analysis[J]. GPS Solutions, 2018, 22(4)
(  0) 0) |
| [6] |
Li X X, Yuan Y Q, Zhu Y T, et al. Precise Orbit Determination for BDS-3 Experimental Satellites Using iGMAS and MGEX Tracking Networks[J]. Journal of Geodesy, 2019, 93(1): 103-117
(  0) 0) |
| [7] |
陈金平, 胡小工, 唐成盼, 等. 北斗新一代试验卫星星钟及轨道精度初步分析[J]. 中国科学:物理学力学天文学, 2016, 46(11) (Chen Jinping, Hu Xiaogong, Tang Chengpan, et al. Orbit Determination and Time Synchronization for New-Generation Beidou Satellites: Preliminary Results[J]. Science Sinica Physica, Mechanica and Astronomica, 2016, 46(11))
(  0) 0) |
| [8] |
Yang D N, Yang J, Li G, et al. Globalization Highlight: Orbit Determination Using Beidou Inter-satellite Ranging Measurements[J]. GPS Solutions, 2017, 21(5): 1395-1404
(  0) 0) |
| [9] |
Xie X, Geng T, Zhao Q L, et al. Precise Orbit Determination for BDS-3 Satellites Using Satellite-Ground and Inter-Satellite Link Observations[J]. GPS Solutions, 2019, 23(2)
(  0) 0) |
| [10] |
Zhang Z T, Li B F, Nie L W, et al. Initial Assessment of Beidou-3 Global Navigation Satellite System: Signal Quality, RTK and PPP[J]. GPS Solutions, 2019, 23(4)
(  0) 0) |
| [11] |
Wang M H, Wang J X, Dong D N, et al. Performance of BDS-3: Satellite Visibility and Dilution of Precision[J]. GPS Solutions, 2019, 23(2)
(  0) 0) |
| [12] |
Montenbruck O, Steigenberger P, Hauschild A. Broadcast Versus Precise Ephemerides:A Multi-GNSS Perspective[J]. GPS Solution, 2015, 19(2): 321-333
(  0) 0) |
| [13] |
Wu Y, Liu X L, Liu W K, et al. Long-Term Behavior and Statistical Characterization of Beidou Signal-in-Space Errors[J]. GPS Solutions, 2017, 21(1): 1907-1922
(  0) 0) |
| [14] |
张柔, 胡志刚, 陶钧, 等. 顾及不同天线相位中心改正模型的北斗空间信号精度评估方法[J]. 武汉大学学报:信息科学版, 2019, 44(6): 806-813 (Zhang Rou, Hu Zhigang, Tao Jun, et al. BDS Signal-in-Space User Range Error Evaluation Considering Different Antenna Phase Center Offset Models[J]. Geomatics and Information Science of Wuhan University, 2019, 44(6): 806-813)
(  0) 0) |
| [15] |
郭树人, 蔡洪亮, 孟轶男, 等. 北斗三号导航定位技术体制与服务性能[J]. 测绘学报, 2019, 48(7): 810-821 (Guo Shuren, Cai Hongliang, Meng Yinan, et al. BDS-3 RNSS Technical Characteristics and Service Performance[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 810-821)
(  0) 0) |
| [16] |
唐成盼.融合多种观测数据计算北斗导航卫星的高精度广播星历[D].上海: 中国科学院上海天文台, 2017 (Tang Chengpan. Generation of Precise Broadcast Orbits for Beidou Navigation Satellites with Multiple Tracking Measurements[D]. Shanghai: Shanghai Astronomical Observatory, CAS, 2017)
(  0) 0) |
| [17] |
杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2017 (Yang Yuanxi. Adaptive Navigation and Kinematic Positioning[M]. Beijing: Surveying and Mapping Press, 2017)
(  0) 0) |
| [18] |
Montenbruck O, Steigenberger P, Hauschild A. Multi-GNSS Signal-in-Space Range Error Assessment-Methodology and Results[J]. Advances in Space Research, 2018, 61(12): 3020-3038 DOI:10.1016/j.asr.2018.03.041
(  0) 0) |
| [19] |
Su K, Jin S G. Triple-Frequency Carrier Phase Precise Time and Frequency Transfer Models for BDS-3[J]. GPS Solutions, 2019, 23(3)
(  0) 0) |
2. State Key Laboratory of Geographic Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China
 2020, Vol. 40
2020, Vol. 40

