2. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室, 武汉市徐东大街340号, 430077
目前学术界对BDS卫星钟性能的评估较为完善,但仍存在一些不足:1)对BDS-2卫星钟性能的评估主要集中在卫星在轨运行的初期和中期,针对设计年限末期的卫星钟性能分析研究较少;2)目前普遍使用IGS多模GNSS实验项目(MGEX)的精密钟差产品进行卫星钟性能评估[1-4],很少采用iGMAS钟差产品进行分析[5]。针对这些问题,本文采用iGMAS 2018年共365 d的精密钟差数据,将Score检验量引入钟差异常探测,并结合中位数(MAD)法进行数据质量控制,较为全面地剔除了粗差数据;然后,利用处理后的钟差数据计算频率准确度、频率漂移率、频率稳定度、模型拟合残差、周期特性及噪声类型等6项指标,对现阶段BDS-2卫星钟的相关性能进行全面的评估与分析。
1 卫星钟性能评估模型与方法 1.1 粗差探测模型由于空间环境干扰及信号异常等的影响,卫星钟在轨运行过程中获取的钟差序列常常出现粗差和数据中断等情况[6-7],在进行卫星钟性能评估时需先对钟差数据进行质量控制。目前普遍采用MAD法[3, 6]进行粗差探测,但其探测效果较依赖于经验阈值的选取,探测结果不够客观且存在部分粗差漏探的现象[8]。基于广义似然比的Score检验量是统计诊断的一种重要方法,对时间序列中的粗差历元十分敏感,且探测结果较为客观[9-10]。本文在MAD法探测钟差数据的基础上,提出一种MAD法与Score检验量相结合的粗差探测模型,对iGMAS钟差数据进行质量控制。
BDS-2卫星钟多为铷原子钟,本文的基本钟差模型为顾及其频漂特性的二次多项式模型[6],表达式为:
| $ \begin{array}{l} {L_i} = {a_0} + {a_1}({t_i} - {t_0}) + {a_2}{({t_i} - {t_0})^2} + {\Delta _i},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1,2, \cdots ,n \end{array} $ | (1) |
式中,Li为历元时刻ti的卫星钟差;a0、a1、a2分别为卫星钟参数,即相位、钟速(频率)和钟漂(频漂);t0为卫星钟参考时间;Δi为钟差模型残差;n为钟差观测量个数。式(1)对应的方差膨胀模型见文献[9]。
钟差观测值Score检验量的具体原理及求解方法见文献[9-10],本文结合MAD法和Score检验量的粗差探测模型的关键在于Score检验量的建立与求解,其具体探测步骤为:
1) 以d为单位,采用MAD法对原始钟差数据进行探测,对探测出的粗差历元进行剔除;
2) 计算经过MAD法处理后钟差数据的Score检验量SCi;
3) 根据给定的显著性水平α求得分位数值χα2(1),若第i个钟差观测值的SCi>χα2(1),则认为该钟差历元处含有粗差;
4) 剔除步骤3)探测出的粗差历元,对处理后的钟差数据进行滑动线性插值[6]。
1.2 时域性能评估方法卫星钟时域性能的评估指标主要包括频率准确度、频率漂移率、频率稳定度及钟差周期项,其中卫星钟差周期项可通过频谱分析[6]提取。
频率准确度描述了实际频率相对于标称值的一致性程度,频率漂移率反映了卫星钟受各种相关因素影响造成输出频率值的单调变化。基于最小二乘法拟合钟差序列,便可求得T时间段内的频率准确度KT和频率漂移率DT:
| $ {K_T} = \frac{{\sum\limits_{i = 1}^n {({L_i} - \bar L)({t_i} - \bar t)} }}{{\sum\limits_{i = 1}^n {{{({t_i} - \bar t)}^2}} }} $ | (2) |
| $ {D_T} = \frac{{\sum\limits_{i = 1}^n {({y_i}(T) - \bar y(T))({t_i} - \bar t)} }}{{\sum\limits_{i = 1}^n {{{({t_i} - \bar t)}^2}} }} $ | (3) |
式中,T为取样时间间隔,t、L、y分别为T时间段内测量的钟差时刻、钟差数据和相对频率值的均值。
频率稳定性是描述卫星钟输出频率受噪声影响而产生的随机起伏情况,表征了卫星钟授时的稳定性。本文采用能够较好地消除频漂影响的重叠哈达玛方差来计算BDS-2卫星钟的频率稳定度,基于钟差(相位)数据的重叠哈达玛方差计算公式为:
| $ \begin{array}{l} H{\sigma _y}^2(\tau ) = \frac{1}{{6{\tau ^2}(N - 3m)}} \times \\ \sum\limits_{i = 1}^{n - 3m} {[{L_{i + 3m}} - 3{L_{i + 2m}} + } 3{L_{i + m}} - {L_i}{]^2} \end{array} $ | (4) |
式中,τ=mτ0为平滑时间;τ0为相邻钟差数据的采样间隔;m为平滑因子,一般取1≤m≤int[(n-1)/3]。
1.3 频域性能评估方法频域性能分析通常用于描述噪声能量随频率的变化,可以反映原子频标受噪声影响的本质。噪声的功率谱密度与边带频率的关系为[11]:
| $ {S_y}(f) = \sum\limits_{\alpha = - 2}^2 {{h_\alpha }} {f^\alpha } $ | (5) |
式中,f为边带频率;hα为噪声指数α的能量谱噪声强度系数,而α取值-2、-1、0、1、2分别对应调频随机游走噪声(RWFM)、调频闪烁噪声(FFM)、调频白噪声(WFM)、调相闪烁噪声(FPM)和调相白噪声(WPM)。
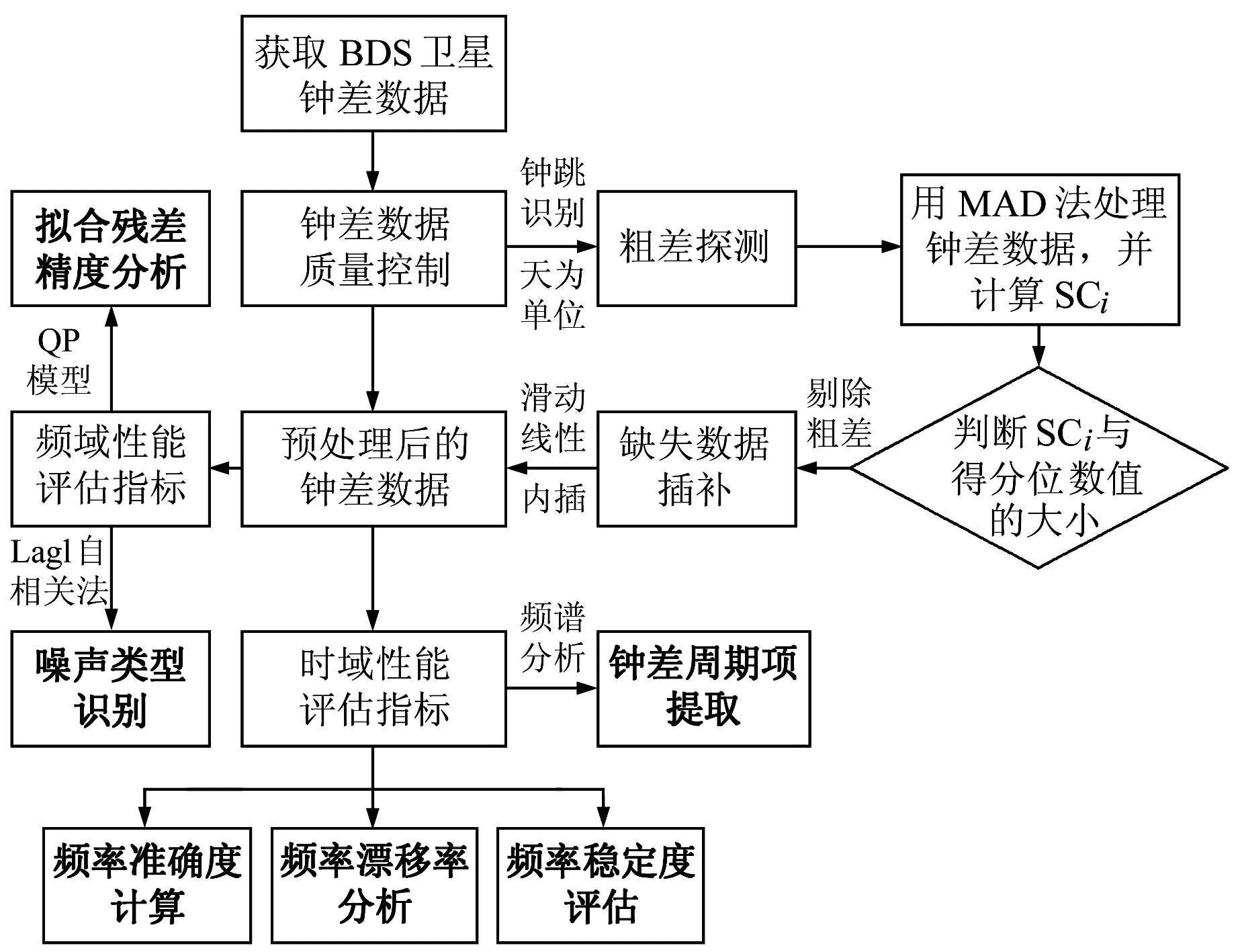
本文采用识别性能稳定的Lag1自相关法对BDS卫星钟进行噪声识别[11],图 1为BDS卫星钟性能评估与分析流程,图中加粗的部分为性能评估时采用的性能指标。
|
图 1 性能评估与分析流程 Fig. 1 Process of performance evaluation and analysis |
本文采用iGMAS中心通过多星联合定轨解算的钟差产品,数据选取时段为2018-01-01~12-31(MJD58 119~58 484)共365 d,采样间隔为5 min。针对iGMAS钟差数据的特点,本文钟差序列的质量控制策略主要包括钟跳识别、粗差探测及缺失数据插补等。
1) 钟跳识别。相位跳变对应于频率峰值,可设定合适的阈值,通过一次差分识别钟跳历元并确定钟跳位置。若单天钟差数据出现钟跳,则进行分段处理。
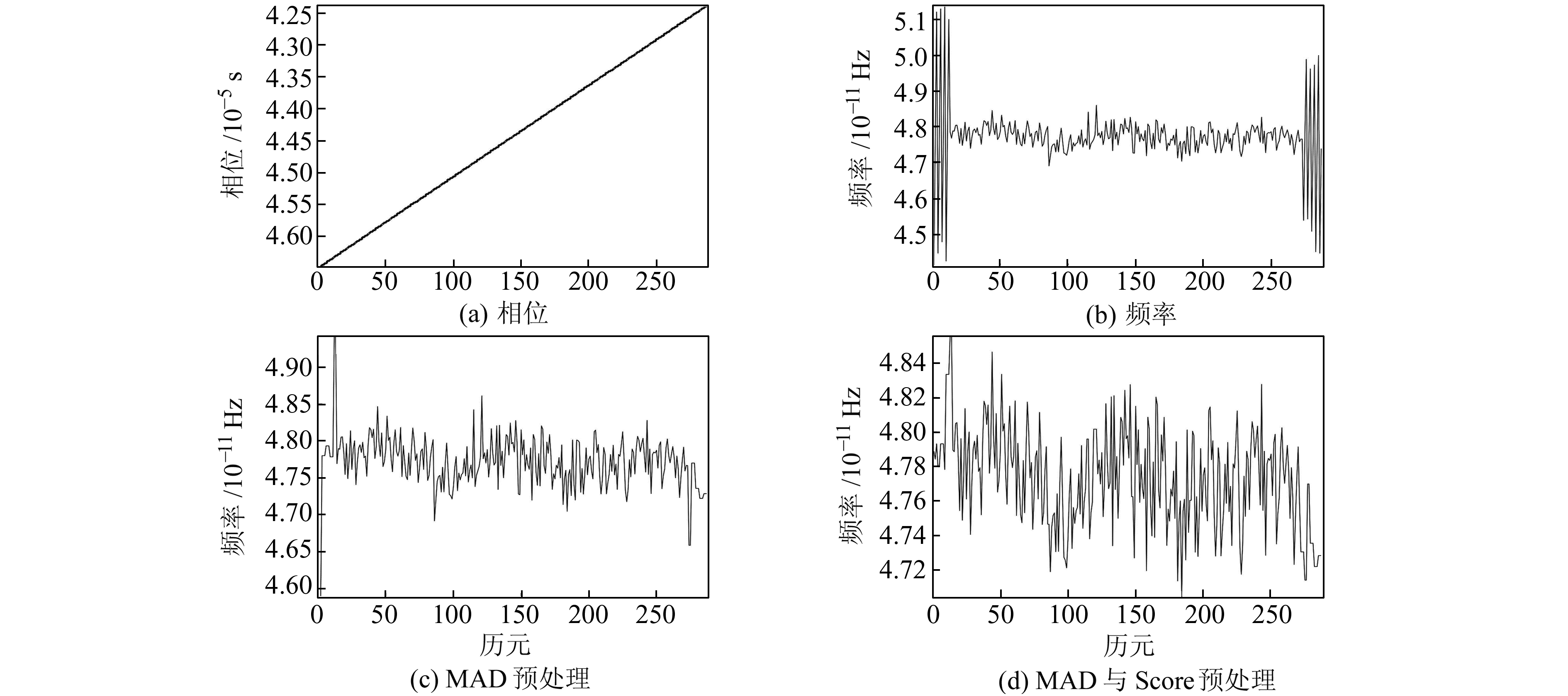
2) 粗差探测。识别钟跳后,结合MAD法(参数n取3)[6]和Score检验量的探测模型(显著性水平α取0.01)[10]对钟差数据进行粗差探测,通过对比新模型与MAD法处理后钟差频率数据来表征粗差探测的效果。以C01卫星为例,图 2为12-01其钟差数据探测的结果。对比图 2(a)和2(b)可以看出,BDS卫星的原始钟差数据值相对较大,容易掩盖其所含粗差,而频率数据可以很好地显示出相位数据中较大的粗差点。由图 2(c)和2(d)可以看出,MAD法在进行粗差探测时会遗漏部分粗差历元,而Score检验量探测模型弥补了这个不足,因此采用MAD法与Score检验量相结合的粗差探测模型可以更全面地剔除钟差数据中的粗差。
|
图 2 12-01 C01卫星原始钟差数据与预处理后频率数据 Fig. 2 Original clock offsets data and pre-processed frequency data of C01 satellite on December 1 |
3) 缺失数据插补。若原始钟差序列单天内缺失少量数据,采取滑动线性插值处理;若缺失数据过多,则直接剔除该天数据。
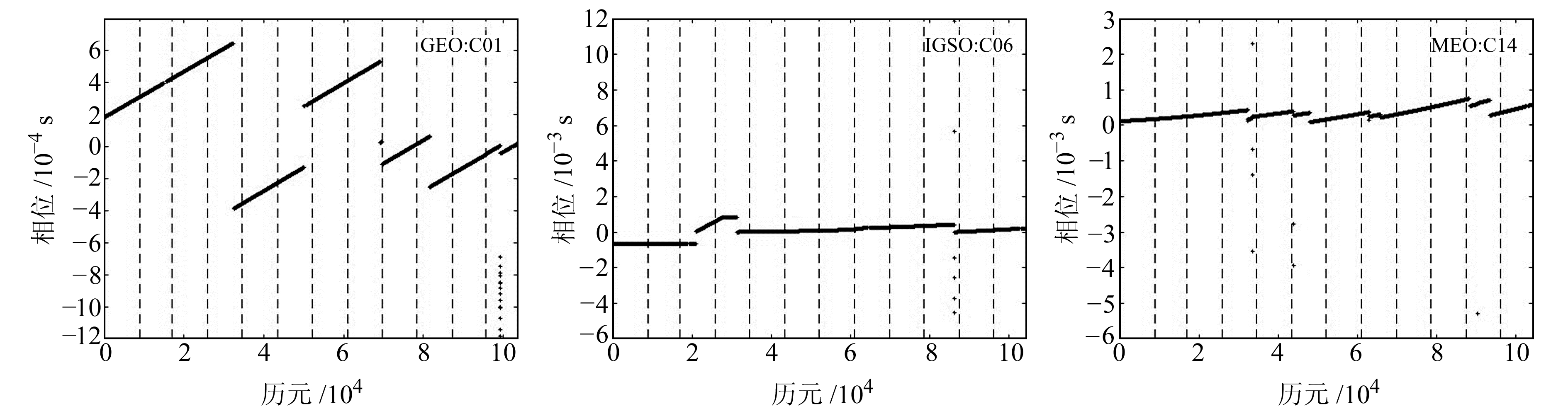
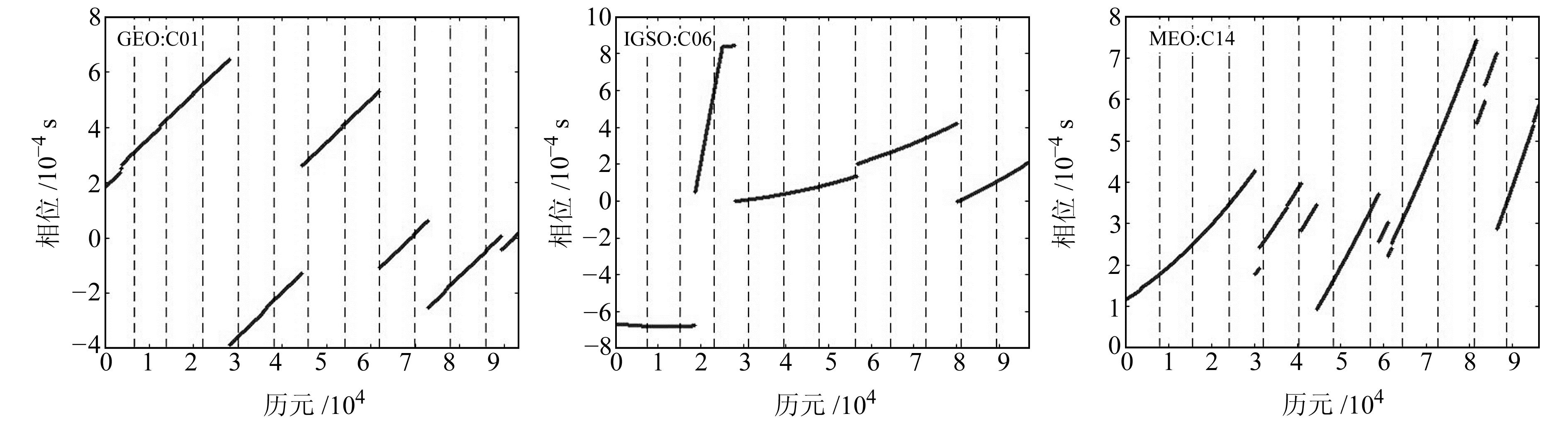
通过上述钟差数据质量控制策略,依次处理单天的钟差数据,并合并为长期卫星钟差序列。以C01、C06、C14卫星为例,图 3和4给出了质量控制前后钟差数据的变化情况(图中纵向虚线为年数据按照月进行的划分)。
|
图 3 BDS卫星原始钟差数据 Fig. 3 BDS satellite original clock offsets data |
|
图 4 BDS卫星预处理后钟差数据 Fig. 4 BDS satellite preprocessed clock offsets data |
结合图 2~4可以看出,iGMAS北斗精密卫星钟差数据中存在较多的粗差,且粗差历元多出现在每天钟差数据的两端临界处,经本文质量控制后能够有效探测并处理钟差数据中的异常。质量控制后钟差序列的实际变化过程得到显现,发现BDS卫星钟在长期运行过程中存在一定次数的相位跳变,可能是由卫星钟切换、地面监控站调相操作或卫星钟差数据解算时基准钟调整引起的[12-16]。多颗卫星相位数据均在4月和10月发生跳变,说明BDS卫星钟在该时段内可能进行了多次调相操作,其中C04卫星钟相位跳变最为频繁,而频繁的相位调整会使钟差数据的连续性和稳定性变差。
3 卫星钟性能分析BDS-2星载卫星钟的设计年限为8 a[14],根据中国卫星导航系统管理办公室测试评估研究中心(http://www.csno-tarc.cn/index/index)提供的星座状态,表 1给出截至2018-01-01 BDS-2在轨卫星的相关信息(其中C03和C13分别由第23颗和第22颗北斗导航卫星切换而来,切换后C13属于IGSO)。
由表 1可知,目前除C03和C13卫星外,BDS-2在轨卫星的卫星钟均已处于系统设计年限末期,其中C01、C04、C06和C07卫星钟的在轨运行时间已超过7 a,即将到达设计年限。本文将着重评估处于设计年限末期的BDS卫星钟性能,同时对比BDS卫星钟的各项系统设计指标,以探究BDS-2卫星钟在当前阶段的运行状态及性能情况。
|
|
表 1 BDS-2卫星相关信息 Tab. 1 The information of BDS-2 satellite |
采用质量控制后的钟差序列,利用式(2)以d为采样时间间隔,计算得到频率准确度序列,并对其平均值(年平均值取绝对值均值)进行统计,结果见图 5。
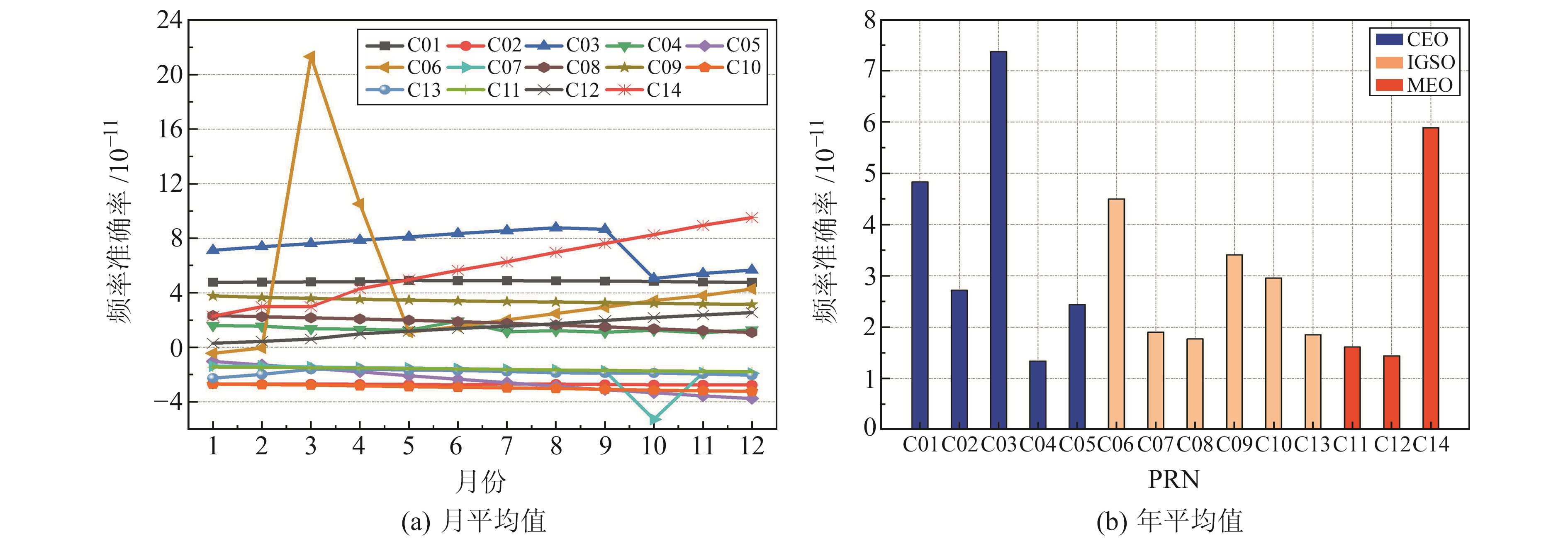
|
图 5 BDS卫星钟频率准确度 Fig. 5 Frequency accuracy of BDS satellite clocks |
从图 5可以看出,目前BDS在轨卫星钟频率准确度整体处于10-11量级。在实验时段内,GEO的C03卫星钟、IGSO的C06与C07卫星钟及MEO的C14卫星钟频率准确度均存在一定次数的跳变,其中C06卫星钟频率准确度在3月和4月发生较大异常,达到10-10量级。C03、C06、C12及C14卫星钟频率准确度均呈线性增大趋势,其余卫星钟除跳变外,全年整体变化较为平稳。C02、C05、C08、C09、C10、C11及C12卫星钟频率准确度的年平均值在3.5×10-11以下,全年频率准确度较好,并未出现较大异常,但C06和C07卫星钟的频率准确度全年波动范围较大且跳变频繁,可能与硬件设备老化造成的校准调相有关。
3.2 频率漂移率分析以月为处理单元,利用式(3)计算卫星钟的频率漂移率,再将结果转化为日漂移率,并对日漂移率序列绝对值的平均值进行统计,结果见图 6。
由图 6可知,BDS在轨卫星钟日漂移率整体处于10-13量级。C02、C08、C09、C11及C12卫星钟日漂移处于10-14量级,且全年频率漂移率较小;C04和C06卫星钟日漂移率波动范围较大,且C04卫星钟在9月出现明显的频漂异常,日漂移率达到10-12量级;C03、C05、C06、C08、C09和C11等6颗卫星的卫星钟在10月均发生日漂移率跳变,多颗卫星的卫星钟漂移率同时跳变可能与地面监测站的调频操作有关。在GEO中,C02、C03及C05卫星钟日漂移率相差不大,远好于C01和C04卫星钟;在IGSO中,C08、C09及C10卫星钟日漂移率较小,年平均值均在1.5×10-13以下;在MEO卫星中,C14卫星钟日漂移率最差,一直在2×10-13以上,远大于其余MEO卫星。与BDS-2日漂移率设计指标(10-13量级)[16]相比,各类型卫星钟频率漂移率均处在较好水平,但C01、C04及C06卫星钟因运行时间较长导致频率漂移率波动范围较大。

|
图 6 BDS卫星钟频率日漂移率 Fig. 6 Frequency daily drift rate of BDS satellite clocks |
以d为处理单元,平滑因子取50[3],利用式(4)计算重叠哈达玛方差,统计重叠哈达玛方差平方根序列平均值,以表征卫星钟在平滑15 000 s下的稳定度[3, 12](万秒稳),结果见图 7。
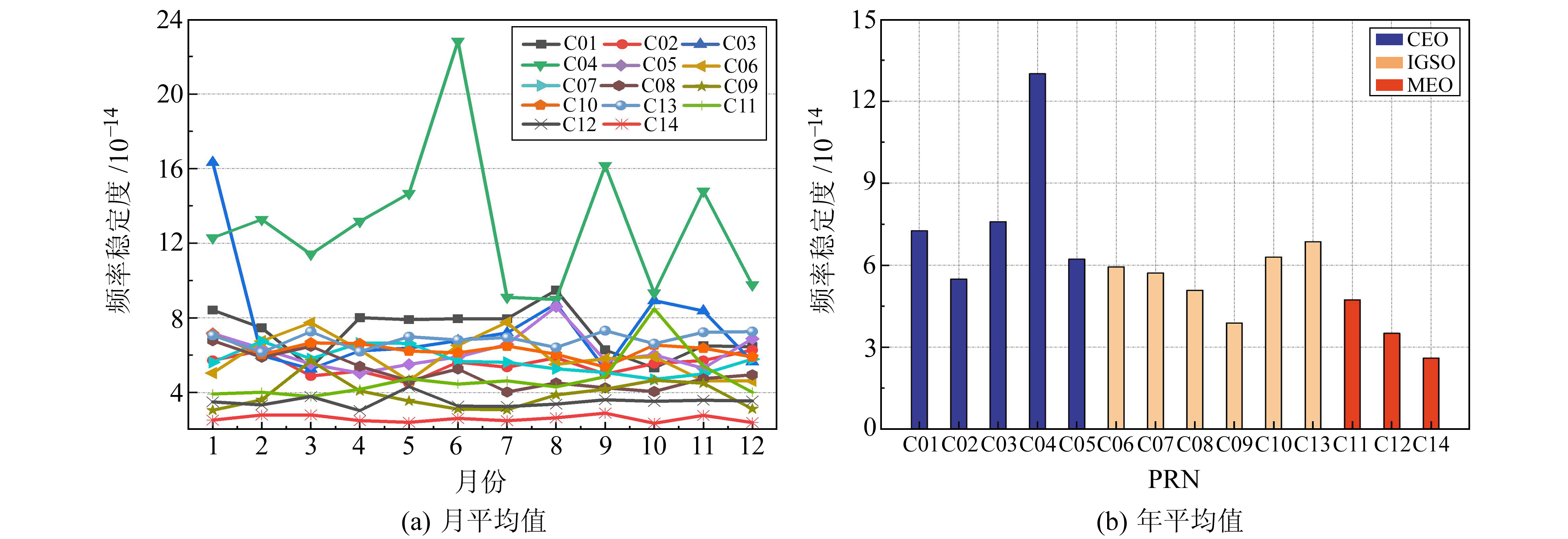
|
图 7 BDS卫星钟万秒稳定度 Fig. 7 Frequency stability of BDS satellite clocks in ten thousand seconds |
从图 7可以看出,当前阶段BDS在轨卫星钟万秒稳整体处于10-14量级。所有卫星中,C04卫星钟频率稳定性明显差于其他卫星,且波动范围较大,全年万秒稳处于10-13量级;C03、C05、C06、C08、C09及C11卫星钟在10月万秒稳与日漂移率一样也发生跳变,推测监测站在该时段内对卫星钟进行了相关的调频操作;C02、C05、C08及C09卫星钟频率稳定度年平均值在各自类型的卫星中均保持较高水平;对比C09和C13卫星钟的万秒稳发现,C09卫星钟在实验时段内的稳定性优于C13卫星钟,说明发射早的卫星钟频率稳定度并不一定差;C14卫星钟日漂移率较差,但其频率稳定性却较好,全年万秒稳一直在2.6×10-14左右,是所有卫星钟中频率稳定性最好的。目前,BDS卫星钟万秒稳全年波动范围较大,但整体仍在10-14量级,BDS-2卫星钟的频率稳定度并未因其运行时间过长而存在显著异常。
为全面评估BDS卫星钟的频率稳定性,利用钟差数据质量较好的MJD58 300~58 330(2018-07)时段,对平滑1 d时间内卫星钟的频率稳定度进行分析,结果见图 8。
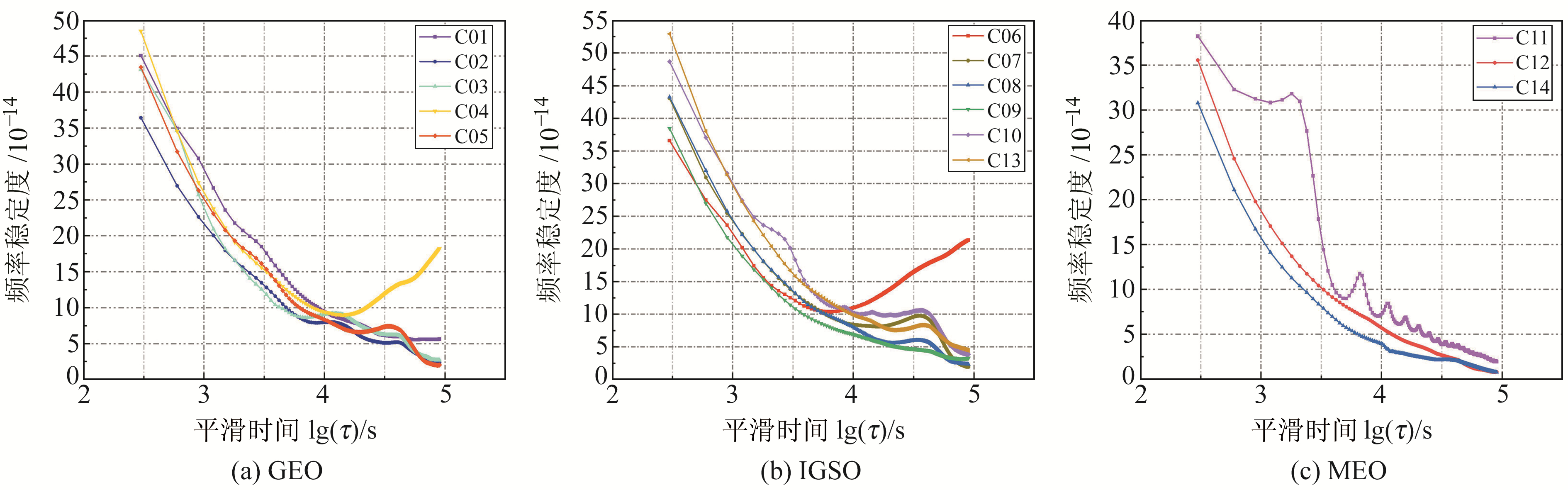
|
图 8 BDS卫星钟平滑1 d时间内的频率稳定度 Fig. 8 Frequency stability of BDS satellite clock smoothing in one day |
由图 8可以看出,随着平滑时间的增加,卫星钟的频率稳定度近似呈指数形式下降,C04和C06卫星钟在平滑时间达到104s后频率稳定度呈明显的上升趋势,可见BDS部分卫星钟因运行时间过长导致维持高水准频率稳定度的时间变短。总的来看,目前BDS-2卫星钟的千秒稳处于10-13量级,万秒稳处于10-14量级,天稳处于10-14量级(C04和C06卫星钟除外),3类稳定度的量级均符合BDS卫星钟的设计指标[16]。
3.4 模型拟合残差利用式(1)以d为单元对钟差数据进行拟合,得到对应的拟合残差序列,统计全时段的拟合残差精度(RMS),结果见图 9。

|
图 9 钟差模型拟合残差序列和精度统计 Fig. 9 Fitting residual sequence of clock offsets model and accuracy statistics |
从图 9可以看出,除C04卫星钟外,BDS卫星钟差模型的拟合精度均处于亚ns量级,其中MEO卫星钟差模型拟合精度最高,IGSO次之,GEO最差,依次为0.284 ns、0.585 ns和0.797 ns。从拟合残差的分布来看,GEO卫星中C03、C04和IGSO中C06卫星钟差模型残差分布的波动性显著,其余卫星钟残差分布较为平稳,同时C02、C05、C09、C10、C12及C14等6颗卫星的卫星钟残差分布呈显著的周期性特征,存在以大约0.5 a为周期的长周期项。不论是残差分布还是拟合精度,MEO卫星钟均优于GEO和IGSO卫星钟,且BDS各卫星钟的拟合残差并未因卫星钟运行时间的增加而存在显著的异常。
3.5 周期特性分析针对卫星钟残差分布呈现出的周期性,利用频谱分析[15]对拟合残差序列进行周期特性分析。为保证周期项提取的准确性和有效性,只提取每颗卫星钟差数据中前4个显著周期项,结果见表 2(其中周期项按照显著程度依次给出,单位h),图 10为C01、C10和C14卫星钟差频谱分析结果。
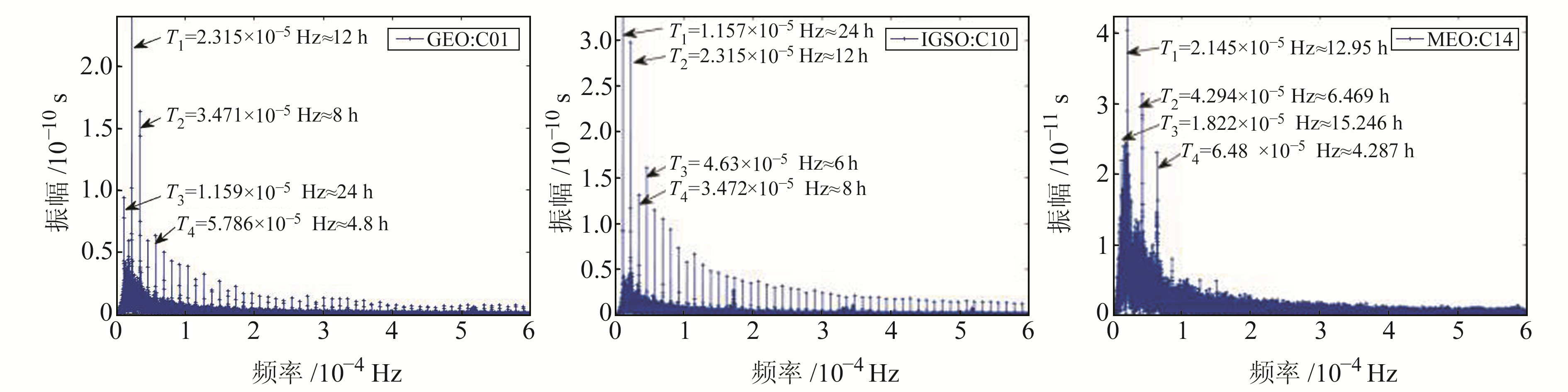
|
图 10 BDS钟差数据频谱分析结果 Fig. 10 Spectrum analysis results of BDS clock offsets data |
结合表 2和图 10可以看出,BDS三类卫星钟差数据存在显著的周期项,其中第1主周期和第2主周期与各自卫星的轨道周期相关。GEO与IGSO卫星钟差的第1、2主周期分别为12 h和24 h(C01卫星钟除外),与轨道周期(23 h 56 min,约23.933 h)的0.5倍和1倍对应;MEO卫星钟差的前2个显著周期项差别不大,也与轨道周期(12 h 53 min,约12.883 h)的1倍及0.5倍对应。GEO卫星中C03与C05卫星钟差的第1主周期项为24 h,与其余3颗卫星不同,同时C01与C02卫星钟差出现了4.8 h的显著周期项;IGSO卫星中C06卫星钟差存在15.49 h与7.91 h的周期项;MEO卫星钟差中前2个显著周期项整体在12.9 h和6.4 h左右,但后2个显著周期项差异较大。所有卫星中,C01和C06卫星钟差的显著周期项与文献[3]及文献[15]的分析结果有所不同,可能是卫星钟运行时间过长引起光压模型改变而造成的。
|
|
表 2 BDS卫星钟差数据周期项提取结果 Tab. 2 The results of extracting periodic items from BDS clockoffsets data |
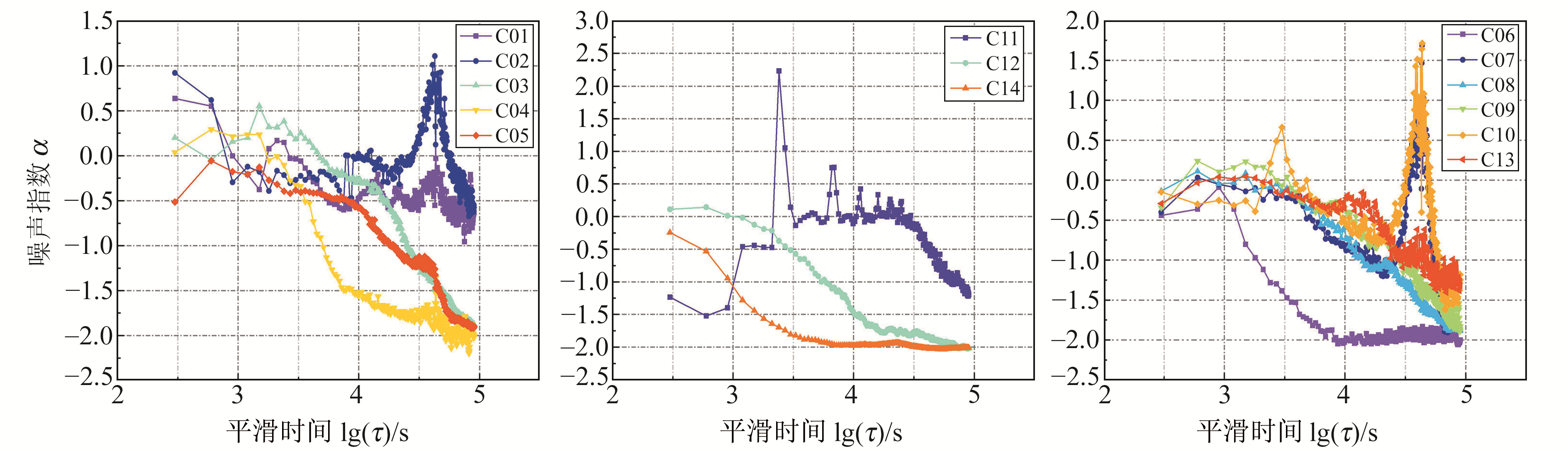
采用Lag1自相关法对MJD58 300~58 330时段内的BDS卫星钟差数据进行较长平滑时间的噪声分析,结果见图 11。
|
图 11 BDS卫星钟噪声分析 Fig. 11 BDS satellite clocks noise analysis |
从图 11可以看出,随着平滑时间的增加,BDS卫星钟的噪声类型会发生变化。当平滑时间小于103 s时,GEO卫星钟主要受调相闪烁噪声和调频白噪声的影响,IGSO卫星钟主要受调频白噪声和调频闪烁噪声的影响,MEO卫星中C11和C14卫星钟主要受调频闪烁噪声和调频随机游走噪声的影响,C12卫星钟主要受调频白噪声的影响;当平滑时间在103~104 s之间时,GEO卫星钟的主要噪声类型变为调频白噪声和调频闪烁噪声,IGSO卫星中C06卫星钟的主要噪声类型变为调频闪烁噪声和调频随机游走噪声,其余卫星钟的噪声类型仍为调频白噪声和调频闪烁噪声,MEO卫星中C11卫星钟的噪声指数发生大的跳变后趋于稳定,3颗卫星的卫星钟主要噪声类型为调频白噪声、调频闪烁噪声和调频随机游走噪声;当平滑时间大于104 s时,GEO、IGSO和MEO卫星钟的噪声类型基本一致,都受调频白噪声、调频闪烁噪声和调频随机游走噪声的影响。总的来看,在不同平滑时间下,BDS卫星钟主要受调频白噪声(WFM)、调频闪烁噪声(FFM)和调频随机游走噪声(RWFM)的影响,对比各卫星钟的噪声类型发现,BDS卫星钟运行时间的长短并不会引起噪声类型发生显著变化。
为进一步分析BDS卫星钟的性能,表 3统计了频率准确度、日漂移率、万秒稳的均值和模型拟合残差序列的RMS,其中频率准确度和漂移率取绝对值的均值。
|
|
表 3 BDS卫星钟性能分析指标统计值 Tab. 3 Statistics of BDS satellite clock performance analysis indicators |
由表 3可知,当前阶段BDS-2卫星钟的频率准确度为3.15×10-11,日漂移率为1.59×10-13,万秒稳为5.72×10-14,拟合残差平均精度为0.596 ns。与BDS-2系统设计指标(频率准确度10-11,日漂移率10-13,万秒稳10-14)[1-2, 3-5, 11-12, 16]对比发现,处于设计年限末期的BDS-2卫星钟虽在轨运行时间较长,但各项性能指标仍符合设计要求。
4 结语本文基于iGMAS中心2018年共365 d的精密钟差数据,将Score检验量引入钟差异常探测,并结合MAD法进行数据质量控制,弥补了MAD法部分粗差漏探的缺陷,再从频率准确度、频率漂移率、频率稳定度、模型拟合残差、周期特性及噪声类型等6个方面对当前阶段BDS-2卫星钟的相关性能进行全面评估与分析。结果表明:
1) 目前BDS卫星钟频率准确度整体处于10-11量级,全时段所有卫星中IGSO卫星钟频率准确度平均值最好,MEO卫星钟次之,GEO卫星钟最差,频率准确度平均值依次为2.73×10-11、2.98×10-11和3.74×10-11。C06和C07卫星钟频率准确度全年波动范围较大且跳变频繁,可能与硬件设备老化造成的校准调相有关。
2) BDS卫星钟日漂移率处于10-13量级,其中GEO卫星钟全年日漂移率平均值最差,IGSO与MEO卫星钟均值相当,日漂移率平均值依次为2.19×10-13、1.38×10-13和1.19×10-13。BDS三类卫星钟频率漂移率均在较好水平,但可以看出,C01、C04和C06卫星钟因运行时间较长导致频漂明显,且频率漂移率波动范围更大。
3) MEO卫星钟全年频率稳定性最好,IGSO卫星钟次之,GEO卫星钟最差,万秒稳平均值依次为3.61×10-14、5.63×10-14和7.91×10-14,BDS-2卫星钟万秒频率稳定度全年变化较大,但整体仍在10-14量级。通过对平滑1 d时间内BDS卫星钟频率稳定度进行分析可知,处于设计年限末期的部分卫星钟因运行时间过长导致维持高水准频率稳定度的时间变短。
4) BDS卫星钟差模型拟合精度整体处于亚ns量级,GEO、IGSO和MEO卫星钟差的拟合精度依次为0.797 ns、0.585 ns和0.284 ns。不论是残差分布还是拟合精度,MEO卫星钟均优于GEO和IGSO卫星钟,BDS各卫星钟的拟合残差并未因运行时间的增加而存在显著的异常。对拟合残差进行频谱分析发现,BDS卫星钟差数据中存在显著的周期项,3类卫星钟差的第1、2主周期分别与各自卫星轨道周期的1倍和0.5倍对应。
5) 随着平滑时间的增加,BDS卫星钟的噪声类型会发生变化,但影响BDS卫星钟的噪声均为WFM、FFM和RWFM。进一步分析发现,BDS卫星钟运行时间的长短并不会引起噪声类型发生显著变化。
总的来看,处于设计年限末期的BDS-2卫星钟的性能会变差,但各项性能指标仍符合系统设计要求,存在超期服役的可能。本文性能评估的结果说明,现阶段BDS-2在轨卫星的原子钟运行状况正常,可继续为BDS-2系统的精稳运行提供可靠保障,同时希望本文评估结果能为BDS-3系统的建设和维护提供参考。
致谢: 感谢iGMAS中心提供的数据支持。
| [1] |
刘帅, 贾小林, 孙大伟. GNSS星载原子钟性能评估[J]. 武汉大学学报:信息科学版, 2017, 42(2): 277-284 (Liu Shuai, Jia Xiaolin, Sun Dawei. Performance Evaluation of GNSS on-Board Atomic Clock[J]. Geomatics and Information Science of Wuhan University, 2017, 42(2): 277-284)
(  0) 0) |
| [2] |
毛亚, 王潜心, 胡超, 等. 北斗在轨卫星广播星历精度分析[J]. 宇航学报, 2018, 39(9): 1013-1021 (Mao Ya, Wang Qianxin, Hu Chao, et al. Precision Analysis of Beidou Satellites Broadcast Ephemeris[J]. Journal of Astronautics, 2018, 39(9): 1013-1021)
(  0) 0) |
| [3] |
黄观文, 余航, 郭海荣, 等. 北斗在轨卫星钟长期钟差特性分析[J]. 武汉大学学报:信息科学版, 2017, 42(7): 982-988 (Huang Guanwen, Yu Hang, Guo Hairong, et al. Analysis of the Mid-Long Term Characterization for BDS on-Orbit Satellite Clocks[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 982-988)
(  0) 0) |
| [4] |
王宇谱, 吕志平, 王宁. BDS星载原子钟长期性能分析[J]. 测绘学报, 2017, 46(2): 157-169 (Wang Yupu, Lü Zhiping, Wang Ning. The Long-Term Performance Analysis for on-Board Atomic Clock of BDS[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 157-169)
(  0) 0) |
| [5] |
毛亚, 王潜心, 胡超, 等. 北斗三号试验卫星的钟差评估及预报[J]. 天文学报, 2018, 59(1): 58-71 (Mao Ya, Wang Qianxin, Hu Chao, et al. Performance Analysis and Prediction of Clock Offsets for the BDS-3 Test Satellites[J]. Acta Astronomica Sinica, 2018, 59(1): 58-71)
(  0) 0) |
| [6] |
郭海荣.导航卫星钟时频特性分析理论与方法研究[D].郑州: 信息工程大学, 2006 (Guo Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D].Zhengzhou: Information Engineering University, 2006) http://cdmd.cnki.com.cn/article/cdmd-90008-2007051629.htm
(  0) 0) |
| [7] |
Huang G W, Zhang Q, Li H, et al. Quality Variation of GPS Satellite Clocks on-Orbit Using IGS Clock Products[J]. Advances in Space Research, 2013, 51(6): 978-987 DOI:10.1016/j.asr.2012.09.041
(  0) 0) |
| [8] |
张倩倩, 韩松辉, 杜兰, 等. 星地时间同步钟差异常处理的Bayesian方法[J]. 武汉大学学报:信息科学版, 2016, 41(6): 772-777 (Zhang Qianqian, Han Songhui, Du Lan, et al. Bayesian Methods for Outliers Detection and Estimation in Clock Offset Measurements of Satellite-Ground Time Transfer[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 772-777)
(  0) 0) |
| [9] |
时正华, 袁永生, 印凡成. 一般均值漂移模型的Score检验统计量[J]. 数学杂志, 2010, 30(2): 283-288 (Shi Zhenghua, Yuan Yongsheng, Yin Fancheng. The Score Test Statistic of General Mean-Shift Model[J]. Journal of Mathematics, 2010, 30(2): 283-288)
(  0) 0) |
| [10] |
归庆明, 宫轶松, 李国重, 等. 基于方差膨胀模型的多个粗差的探测[J]. 测绘科学, 2006, 31(4): 28-29 (Gui Qingming, Gong Yisong, Li Guozhong, et al. Detection of Multiple Gross Errors Based on Variance Expansion Model[J]. Science of Surveying and Mapping, 2006, 31(4): 28-29)
(  0) 0) |
| [11] |
罗璠, 李建文, 黄海, 等. 北斗卫星钟稳定性分析及噪声识别[J]. 测绘科学技术学报, 2014, 31(1): 34-37 (Luo Fan, Li Jianwen, Huang Hai, et al. Frequency Stability Analysis and Noise Identification of BD Satellite Clock[J]. Journal of Geomatics Science and Technology, 2014, 31(1): 34-37)
(  0) 0) |
| [12] |
Huang G W, Cui B B, Zhang Q, et al. Switching and Performance Variations of on-Orbit BDS Satellite Clocks[J]. Advances in Space Research, 2018, 63(5): 1681-1696
(  0) 0) |
| [13] |
Huang G W, Cui B B, Xu Y, et al. Characteristics and Performance Evaluation of Galileo on-Orbit Satellites Atomic Clocks during 2014-2017[J]. Advances in Space Research, 2018, 63(9): 2899-2911
(  0) 0) |
| [14] |
崔博斌. GNSS卫星钟时频特性及预报算法研究[D].西安: 长安大学, 2018 (Cui Bobin. Research on Time-Frequency Characteristics and Prediction Algorithm of GNSS Satellite Clock[D]. Xi'an: Chang'an University, 2018) http://cdmd.cnki.com.cn/Article/CDMD-10710-1018792407.htm
(  0) 0) |
| [15] |
周佩元, 杜兰, 路余, 等. 多星定轨条件下北斗卫星钟差的周期性变化[J]. 测绘学报, 2015, 44(12): 1299-1306 (Zhou Peiyuan, Du Lan, Lu Yu, et al. Periodic Variations of Beidou Satellite Clock Offsets Derived from Multi-Satellite Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1299-1306)
(  0) 0) |
| [16] |
李文涛, 边少锋, 任青阳, 等. 基于粒子群优化核极限学习机的北斗超快速钟差预报[J]. 宇航学报, 2019, 40(9): 1080-1088 (Li Wentao, Bian Shaofeng, Ren Qingyang, et al. Kernel Extreme Learning Machine Based on Particle Swarm Optimization for Prediction of Beidou Ultra-Rapid Clock Offset[J]. Journal of Astronautics, 2019, 40(9): 1080-1088)
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China
 2020, Vol. 40
2020, Vol. 40

