2. 武汉地震计量检定与测量工程研究院有限公司,武汉市洪山侧路40号,430071
地面激光扫描仪是20世纪90年代出现的一种新型测量设备,它通过旋转高速激光进行脉冲或相位测量,可以快速获取被测对象表面的空间点位信息,为建立物体的三维数字模型提供了一种全新的技术手段。为了评估地面激光扫描仪的实际计量性能,国家市场监督总局在2013年颁布了《JJF 1406-2013地面激光扫描仪校准规范》,要求使用空间距离校准装置对地面激光扫描仪的空间坐标测量性能进行评价。
空间距离标准装置的球形标靶的空间距离坐标测量是该标准的难点之一。因为无法直接测量标靶球的球心,需要依靠“球心坐标的估计”,比如利用最小二乘球心拟合方法[2]进行估计。目前,主流的地面激光扫描仪(以Leica C10为例)的标称标靶测量精度为2 mm,角度测量精度约为0.003°。根据规范[1]的要求,空间距离标准装置的距离测量精度要优于0.5 mm。
规范[1]中没有给出空间距离标准装置的推荐校准方法。Boehler[3]提出使用类似的4个球体的平面式空间距离的标准装置来校准,但是没有给出标准装置的测量方法;邓向瑞等[4]给出径向距离校准装置的校准方法和不确定度分析;李金鑫[5]提出使用经纬仪工业测量系统测量空间校准装置,但是没有估算其测量的精度水平,对计量机构的不确定度评定缺乏指导意义;徐寿志等[6]用高精度全站仪直接测量校准标靶的空间坐标,但是没有给出空间坐标的测量方法和精度;梁建军等[7]以激光跟踪仪为标准,将经纬仪交会测量法、全站仪无棱镜直接测量球心法和全站仪无棱镜测量拟合球心法进行精度对比,证明用全站仪免棱镜模式精度较低,不满足空间距离标准装置的校准要求,推荐采用激光跟踪仪或前方交会测量方式来测量,但是没有给出具体的数据处理方法,最后评估的3个方向总均方根误差(以激光跟踪仪为标准)为0.596 mm,低于对空间距离标准装置的准确度要求。
国内许多计量机构的空间距离标准装置采用的是激光跟踪仪测量法。欧阳健飞等[8]在三坐标机上安置标准标靶球,用静态测量方法评价激光跟踪仪接触测量的坐标拟合精度,在3.59 m和6.72 m处,激光跟踪仪的坐标测量标准差分别为0.038 7 mm和0.068 1 mm,和孙海丽[9]的实验精度水平一致。考虑到跟踪仪在动态测量下精度有所降低,且标靶球圆度误差约为0.1 mm,总体精度水平能满足校准激光扫描仪的要求。王东伟[10]从电子经纬仪交汇测量的原理出发,分析测量中的误差因素,通过实验证明,在实验室环境中交汇角度不大的情况下,工业经纬仪交会测量精度达到0.1 mm,也能够满足空间距离标准装置的测量精度要求。但是用全站仪进行交会测量,对空间距离标准装置进行校准测量却没有找到相关案例。为此,本文基于全站仪交汇方法给出一种空间距离标准装置的非接触式测量和数据处理方法,通过精度评估,能够满足规程[1]的计量性能要求。
1 测量方法与数据处理 1.1 整体思路常用的空间距离校准装置有平面式、空间式和球棒式3种,其中平面式空间距离校准装置以其空间要求低、建设方便、造价低和稳定性高等特点在计量机构里应用最为广泛。通常选在一块约5 m(宽)×3 m(高)的稳定墙面上固定安置不少于9个磁性基座,形成一个“+”型,然后将球形标靶安装在磁性基座上,即可完成空间距离标准装置的建立。在实验室环境下,温湿度环境相对稳定,整套系统采用刚性连接,装置的稳定性很高。
本文的处理思路如图 1所示。要测量空间距离标准装置的坐标,首先通过基于反射片/棱镜模式的多台高精度全站仪后方交会确立3台全站仪的相对概略坐标,然后再通过全站仪免棱镜测量模式测量基准尺基准坐标,归化后球心的概略坐标、测量标靶球的水平角和天顶距作为原始观测值。设全站仪的天顶方向为垂直方位基准,通过3台全站仪无穷远互瞄建立一个空间三角形的“水平角定向基准”,然后通过全站仪对标靶球、基线尺分别进行高精度的角度交汇测量,确立一个不含尺度因子的空间三角网。全站仪、基线尺、标靶球的坐标都是待求参数,再以概略坐标为基础,用基线尺的长度确定空间结构的尺度因子,定权时考虑基准尺的长度精度,将所有的测角观测数据进行整体平差,得到各个点的坐标和精度。
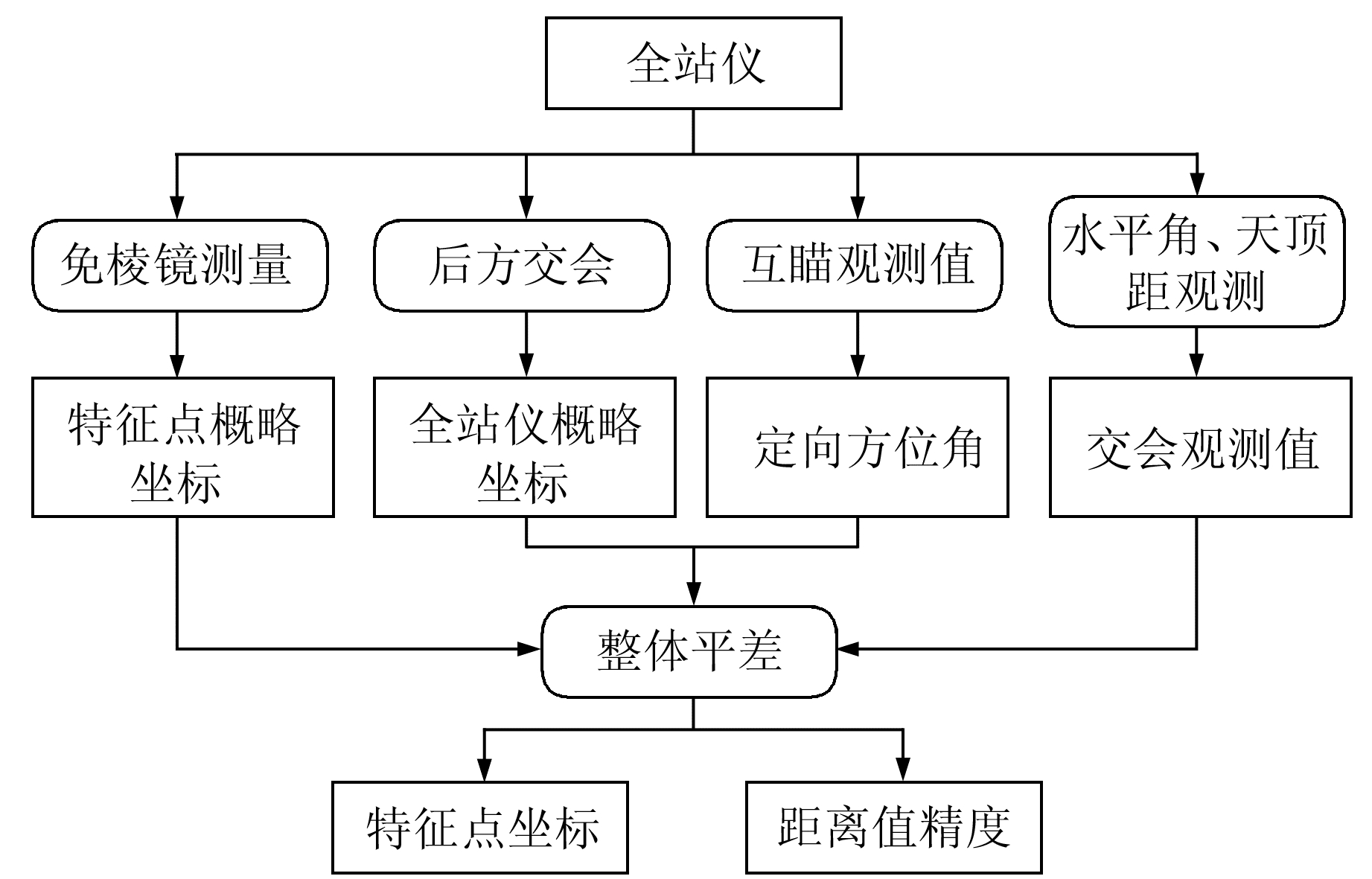
|
图 1 测量及数据处理流程 Fig. 1 Flow chart of measurement and data processing |
这样处理的优点有3个:一是测量时只需全站仪视线平行,避免测量过程的“精确互瞄”(互瞄过程中全站仪视线要通过仪器中心,即横轴线与竖轴线的虚拟交点),因为这个过程需要使用带内觇标的工业经纬仪或外觇标精调[11],对人员和仪器的要求比较高;二是通过全站仪的内置功能直接测得高精度概略坐标,避免概略坐标推算造成误差积累,当初始概略坐标误差过大时,迭代计算结果不收敛;三是数据处理采用整体平差,可以充分利用交会测量的观测条件,避免结果精度的不均匀性,平差结果更优。
1.2 测量方法如图 2所示,标靶球1~10构成一套平面式空间距离标准装置,RE1、RE2、RE3为反射片公共点,在标靶球附近布置一根铟钢水准尺,在位置1、2、3上各架设一台0.5″带免棱镜测量功能的高精度全站仪。测量前,需要对基线尺的标志间长度进行校准,还需要将全站仪的物镜调至无穷远,在全站仪的目镜上打光以方便照准,在互瞄过程中不能调焦,互瞄测量需要采用盘左、盘右观测两个测回,记录互瞄的水平角观测值。

|
图 2 平面式空间距离标准装置测量方法布置示意图 Fig. 2 Schematic layout of measurement method for plane space distance standard device |
互瞄完成后,利用全站仪的后方交会功能获得每台全站仪的概略坐标。如图 2所示,可以先用位置1的全站仪测量出反射片RE1、RE2、RE3的坐标,然后用位置2、位置3的全站仪以后方交会设站的方式得到其设站的坐标。基准尺上的标志概略坐标直接用位置1的全站仪以免棱镜模式测得。
在观测标靶球时用全站仪的横丝中心分别观测球的上下边缘,用竖丝中心观测球的左右边缘,这样可以避免象限法在标靶球距离比较近的时候在望远镜内无法观测到球的整体,每个球观测两个测回,取两个测回上下边缘、左右边缘平均值作为标靶球球心的水平角、天顶距的角度观测值。然后用全站仪在盘左时将水平角和天顶距的度盘调至该标靶球的球心角度值,用全站仪免棱镜模式测量得到标靶球表面的距离L,再用公式(1)计算球心概略坐标:
| $ \left\{ \begin{array}{l} R = \frac{{{\rm{sin}}\alpha /2}}{{1 - {\rm{sin}}\alpha /2}}L{\rm{sin}}V\\ x = {x_i} + (R + L){\rm{sin}}V{\rm{cos}}{H_z}\\ y = {y_i} + (R + L){\rm{sin}}V{\rm{cos}}{H_z}\\ z = {z_i} + (R + L){\rm{cos}}V \end{array} \right. $ | (1) |
式中,α是标靶球的左右边缘对应的水平角角度值,R为球半径,(x,y,z)为球心坐标,(xi,yi,zi)为全站仪测量的球外表面坐标,Hz、V分别为全站仪球心瞄准方向的水平角与天顶距。测量完所有球心概略坐标后,用剩下的全站仪测量每个标靶球心方向的水平角和天顶距。
1.3 整体平差与精度估计得到概略坐标后,需要对整个观测体(包括全站仪、标靶球和基准尺)进行整体平差。首先需要确定平差的一个基准点和两个基准方向,以任意一个标靶球的坐标为固定点P,天顶方向为z轴方向,任意一个互瞄方向为方位角起始方向,可以得到下面的已知条件。
已知位置1上点P坐标,算得:
| $ {x_P} = {X_P} - X_P^0, {y_P} = {Y_P} - Y_P^0, {z_P} = {Z_P} - Z_P^0 $ |
已知方位角:
| $ \begin{array}{l} {\rm{tan}}{A_{mn}} = \frac{{{X_n} - {X_m}}}{{{Y_n} - {Y_m}}} \Rightarrow {\rm{tan}}{A_{mn}}\left( {{y_n} - {y_m}} \right) - \\ \;\;\;\;\;\;\;\left( {{x_n} - {x_m}} \right) = \Delta X_{mn}^0 - \Delta Y_{mn}^0{\rm{tan}}{A_{mn}} \end{array} $ |
若tanAmn接近无穷大,则使用下面的公式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{\rm{tan}}\left( {\frac{\pi }{2} - {A_{mn}}} \right) = \frac{{{Y_n} - {Y_m}}}{{{X_n} - {X_m}}} \Rightarrow \\ {\rm{tan}}\left( {\frac{\pi }{2} - {A_{mn}}} \right)\left( {{x_n} - {x_m}} \right) - \left( {{y_n} - {y_m}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta Y_{mn}^0 - \Delta X_{mn}^0{\rm{tan}}\left( {\frac{\pi }{2} - {A_{mn}}} \right) \end{array} $ |
根据4类观测值,列出观测方程组。
1) 水平方向观测值:
| $ {\widehat{L}}_{mn}={\rm arctan}\left(\frac{{\widehat{X}}_{n}-{\widehat{X}}_{m}}{{\widehat{Y}}_{n}-{\widehat{Y}}_{m}}\right)-{\widehat{\rm{SA}}}_{k} $ | (2a) |
2) 天顶距观测值:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat T}_{mn}} = \frac{\pi }{2} - \\ {\rm{arctan}}\left( {\frac{{{{\hat Z}_n} - {{\hat Z}_m}}}{{\sqrt {{{\left( {{{\hat X}_n} - {{\hat X}_m}} \right)}^2} + {{\left( {{{\hat Y}_n} - {{\hat Y}_m}} \right)}^2}} }}} \right) \end{array} $ | (2b) |
3) 起始方位角差观测值:
| $ {\widehat {{\rm{DA}}}_{kl}} = {\widehat {{\rm{SA}}}_k} - {\widehat {{\rm{SA}}}_l} $ | (2c) |
4) 距离观测值:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat S}_{{{mn}}}} = \\ \sqrt {{{\left( {{{\hat X}_n} - {{\hat X}_m}} \right)}^2} + {{\left( {{{\hat Y}_n} - {{\hat Y}_m}} \right)}^2} + {{\left( {{{\hat Z}_n} - {{\hat Z}_m}} \right)}^2}} \end{array} $ | (2d) |
式中,
根据观测方程组(2)可以推导出误差方程组:
| $ \left\{ \begin{array}{l} {V_{L_{mn}}} = \frac{{\Delta X_{mn}^0}}{{{{\left( {{\rm{SH}}_{mn}^0} \right)}^2}}}{y_m} - \frac{{\Delta Y_{mn}^0}}{{{{\left( {{\rm{SH}}_{mn}^0} \right)}^2}}}{x_m} - \\ \;\;\;\frac{{\Delta X_{mn}^0}}{{{{\left( {{\rm{SH}}_{mn}^0} \right)}^2}}}{y_n} + \frac{{\Delta Y_{mn}^0}}{{{{\left( {{\rm{SH}}_{mn}^0} \right)}^2}}}{x_n} - {a_k} - {l_{mn}} + \\ \;\;\;{\rm{arctan}}\left( {\frac{{\Delta X_{mn}^0}}{{\Delta Y_{mn}^0}}} \right) - SA_k^0\\ {V_{T_{mn}}} = \frac{{\Delta Z_{mn}^0\Delta X_{mn}^0}}{{{{\left( {S_{mn}^0} \right)}^2}{\rm{SH}}_{mn}^0}}{x_n} - \frac{{\Delta Z_{mn}^0\Delta X_{mn}^0}}{{{{\left( {S_{mn}^0} \right)}^2}{\rm{SH}}_{mn}^0}}{x_m} + \\ \;\;\;\frac{{\Delta Z_{mn}^0\Delta Y_{mn}^0}}{{{{\left( {S_{mn}^0} \right)}^2}{\rm{SH}}_{mn}^0}}{y_n} - \frac{{\Delta Z_{mn}^0\Delta Y_{mn}^0}}{{{{\left( {S_{mn}^0} \right)}^2}{\rm{SH}}_{mn}^0}}{y_m} - \\ \;\;\;\frac{{{\rm{SH}}_{mn}^0}}{{{{\left( {S_{mn}^0} \right)}^2}}}{z_n} + \frac{{{\rm{SH}}_{mn}^0}}{{{{\left( {S_{mn}^0} \right)}^2}}}{z_m} + \frac{\pi }{2} - \\ \;\;\;\;{\rm{arctan}}\left( {\frac{{\Delta Z_{mn}^0}}{{{\rm{SH}}_{mn}^0}}} \right) - {t_{mn}}\\ {V_{{\rm{d}}{{\rm{a}}_{kl}}}} = {a_k} - {a_l} + A_k^0 - A_l^0 - {\rm{d}}{{\rm{a}}_{kl}}\\ {V_{{S_{mn}}}} = \frac{{\Delta X_{mn}^0}}{{S_{mn}^0}}{x_n} - \frac{{\Delta X_{mn}^0}}{{S_{mn}^0}}{x_m} + \frac{{\Delta Y_{mn}^0}}{{S_{mn}^0}}{y_n} - \\ \;\;\;\;\;\;\;\frac{{\Delta Y_{mn}^0}}{{S_{mn}^0}}{y_m} + \frac{{\Delta Z_{mn}^0}}{{S_{mn}^0}}{z_n} - \frac{{\Delta Z_{mn}^0}}{{S_{mn}^0}}{z_m} + S_{mn}^0 - {{\rm{s}}_{mn}} \end{array} \right. $ | (3) |
误差方程组可写成:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{Bx}} + \mathit{\boldsymbol{l}} $ | (4) |
其中待求参数为:
| $ \begin{array}{l} \mathit{\boldsymbol{x}} = ({x_1}\;\;{y_1}\;\;{z_1}\;\;{x_2}\;\;{y_2}\;\;{z_2}\;\; \cdots \\ \;\;\;\;\;\;\;\;\;{x_N}\;\;{y_N}\;\;{z_N}\;\;{a_{k1}}\;\;{a_{k2}}\; \cdots \;\;{a_{kM}}{)^{\rm{T}}} \end{array} $ |
根据已知条件有:
| $ \mathit{\boldsymbol{Gx}} = \mathit{\boldsymbol{t}} $ |
对G作奇异值分解(SVD):
| $ \mathit{\boldsymbol{G}} = \mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{H}}^{\rm{T}}} = \left( {{\mathit{\boldsymbol{U}}_{{r}}}} \right)\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_r}}&{{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_0}} \end{array}} \right){\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_r}}&{{\mathit{\boldsymbol{H}}_0}} \end{array}} \right)^{\rm{T}}} $ |
存在一组独立参数y (比未知参数x少4个),使得
| $ \mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{H}}_0}\mathit{\boldsymbol{y}} + \mathit{\boldsymbol{w}} $ |
其中, w为方程组Gw = t的一个特解,可由下式构造:
| $ \mathit{\boldsymbol{w}} = {\mathit{\boldsymbol{H}}_r}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_r^{ - 1}\mathit{\boldsymbol{U}}_r^{\rm{T}}\mathit{\boldsymbol{t}} $ |
代入误差方程组(4),得:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{H}}_0}\mathit{\boldsymbol{y}} + \mathit{\boldsymbol{Bw}} + \mathit{\boldsymbol{l}}\\ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{y}} {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}} = - {\left( {{\mathit{\boldsymbol{H}}_0}^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{H}}_0}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}_0}^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{Bw}} + \mathit{\boldsymbol{l}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}} = \\ \;\;\;\mathit{\boldsymbol{w}} - {\mathit{\boldsymbol{H}}_0}{\left( {{\mathit{\boldsymbol{H}}_0}^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{H}}_0}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}_0}^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{Bw}} + \mathit{\boldsymbol{l}}} \right)\\ \mathit{\boldsymbol{x}}\left| {{\rm{min}}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}}}) \right. = {\mathit{\boldsymbol{H}}_r}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_r^{ - 1}\mathit{\boldsymbol{U}}_r^{\rm{T}}\mathit{\boldsymbol{t}} - {\mathit{\boldsymbol{H}}_0}{\left( {{\mathit{\boldsymbol{H}}_0}^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{H}}_0}} \right)^{ - 1}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{H}}_0}^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{H}}_r}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_r^{ - 1}\mathit{\boldsymbol{U}}_r^{\rm{T}}\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{l}}} \right) \end{array} $ | (5) |
式中,P为权阵。以1 s为单位权中误差,距离观测值的权按下式确定:
| $ {p_s} = {\left( {\frac{S}{{\rho ''{\sigma _s}}}} \right)^2} $ | (6) |
式中,σs为基线尺特征点校准的精度。
两点间距离为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{S_{{{mn}}}} = \\ \sqrt {{{\left( {{X_m} - {X_n}} \right)}^2} + {{\left( {{Y_m} - {Y_n}} \right)}^2} + {{\left( {{Z_m} - {Z_n}} \right)}^2}} \end{array} $ |
一阶展开,得到误差方程:
| $ \begin{array}{l} {S_{{{mn}}}} = \frac{{\Delta X_{mn}^0}}{{S_{mn}^0}}{x_n} - \frac{{\Delta X_{mn}^0}}{{S_{mn}^0}}{x_m} + \frac{{\Delta Y_{mn}^0}}{{S_{mn}^0}}{y_n} - \\ \;\;\;\;\;\;\frac{{\Delta Y_{mn}^0}}{{S_{mn}^0}}{y_m} + \frac{{\Delta Z_{mn}^0}}{{S_{mn}^0}}{z_n} - \frac{{\Delta Z_{mn}^0}}{{S_{mn}^0}}{z_m} + S_{mn}^0 \end{array} $ |
根据误差传播定律,有:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{D}}_{SS}}{\rm{ = }}\\ \left( {\frac{{\Delta X_{mn}^0}}{{S_{mn}^0}}, - \frac{{\Delta X_{mn}^0}}{{S_{mn}^0}}, \frac{{\Delta Y_{mn}^0}}{{S_{mn}^0}}, - \frac{{\Delta Y_{mn}^0}}{{S_{mn}^0}}, \frac{{\Delta Z_{mn}^0}}{{S_{mn}^0}}, - \frac{{\Delta Z_{mn}^0}}{{S_{mn}^0}}} \right) \cdot \\ {\mathit{\boldsymbol{D}}_{XX}}{\left( {\frac{{\Delta X_{mn}^0}}{{S_{mn}^0}}, \frac{{\Delta X_{mn}^0}}{{S_{mn}^0}}, \frac{{\Delta Y_{mn}^0}}{{S_{mn}^0}}, \frac{{\Delta Y_{mn}^0}}{{S_{mn}^0}}, \frac{{\Delta Z_{mn}^0}}{{S_{mn}^0}}, \frac{{\Delta Z_{mn}^0}}{{S_{mn}^0}}} \right)^{\rm{T}}} \end{array} $ | (7) |
可以根据上式来进行坐标间距离的精度评定,其中,DXX是向量(xn, xm, yn, ym, zn, zm)T的协方差阵:
| $ {\mathit{\boldsymbol{D}}_{XX}} = {\hat \sigma _0}^2{\mathit{\boldsymbol{Q}}_{xx}} $ |
式中,后验单位权中误差
用本文测量方法对某平面式空间距离标准装置进行测量,标准装置高2.9 m、宽4.4 m,由9个反射率为90%的粗糙面标靶球组成,标靶球的直径为139 mm。基准尺选用3 m铟钢水准尺,在水准尺上选取4个特征标志点,用双频激光干涉仪测量特征点扩展不确定度为±35 μm(k=2)。用3台Leica TS60型0.5″的全站仪按本文方法进行测量,然后进行最小约束平差和距离精度统计。
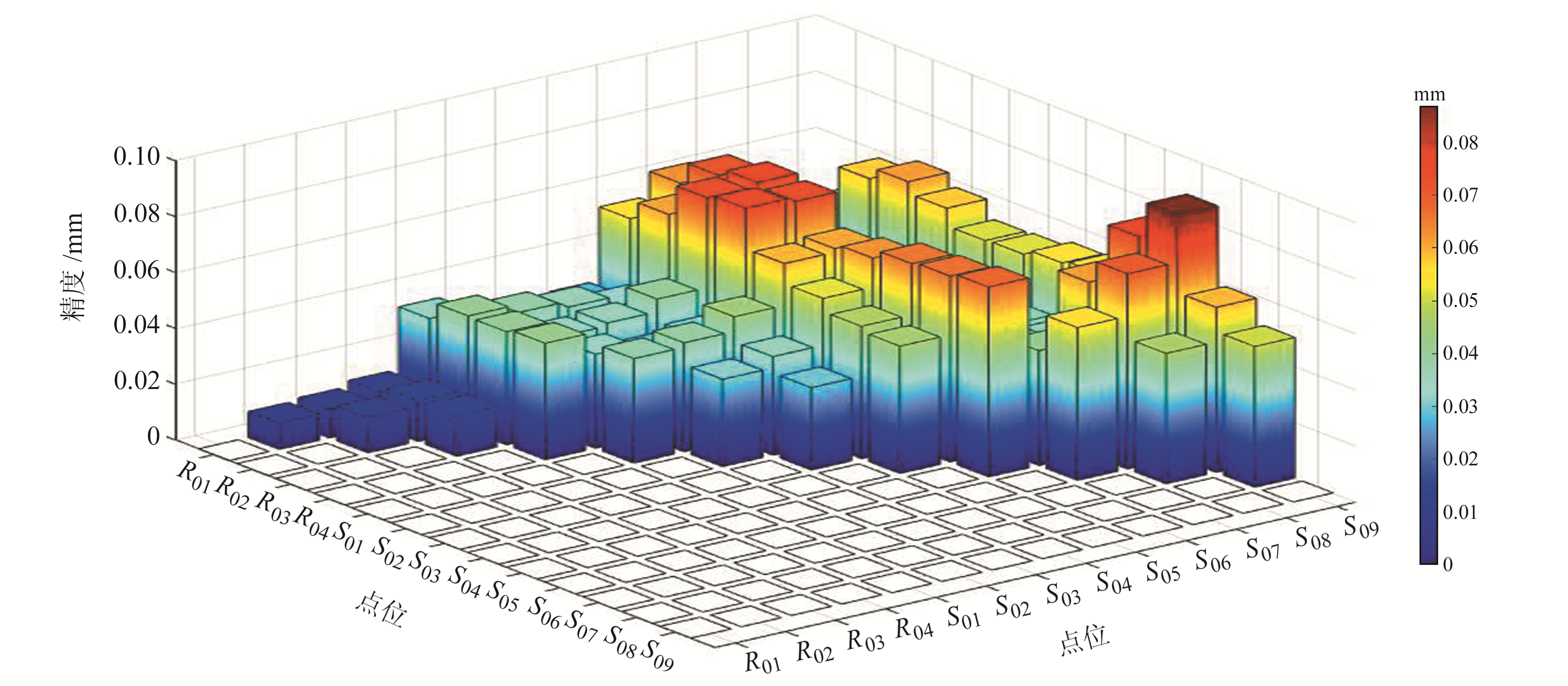
概略坐标空间示意图如图 3所示,R01~R04为基准尺上的4个标志,S01~S09为9个标靶球,S1、S2、S3为全站仪的3个架设点位。通过平差和精度统计(图 3~5)可以看出:1)从点位精度来说,绝大多数点位的x、y、z三个方向的精度都优于0.1 mm,全站仪的架设点位精度相对较低,原因是由于互瞄时调焦运行误差会带来一定的影响;2)点位精度分布呈现出所有点位在z轴方向(天顶方向)上精度最高、x轴(标靶平面水平方向)精度次之、y轴(标靶平面垂直方向)最低,原因是互瞄时x方向的交会角度远大于y方向,而z轴向有高精度的尺度控制,因此精度最高;3)在整体平差的框架下,所有的距离观测值的精度都优于0.1 mm,距离精度基本遵循距离越远精度越低的规律,最弱边为S06-S09,为左右最远距离;4)基准尺上6段距离约束后的精度都优于0.01 mm。

|
图 3 点位概略坐标示意图 Fig. 3 A schematic diagram of the outline coordinate |

|
图 4 点位坐标精度统计 Fig. 4 Statistics of coordinate accuracy |
|
图 5 空间距离精度统计 Fig. 5 Statistics for spatial distance accuracy |
为进一步验证本方法的准确性与可靠性,将上述空间距离标准装置的各个点位距离与API激光跟踪仪的测量值进行比较。测量方式采用激光跟踪仪动态测量,用空心球棱镜接触测量,然后进行球心拟合(每个标靶球观测不少于5个点)。由于S01在墙面最高点,考虑到人员安全,标靶球S01只测量5个点,测量点都位于标靶球的中下部。每个标靶球拟合的精度如表 1所示,空间测量值与交会测量结果的比较如表 2所示。
|
|
表 1 标靶球观测拟合点数及拟合精度 Tab. 1 Numbers of every target sphere observations and fitting accuracy |
|
|
表 2 交会测量与激光跟踪仪测量结果比较 Tab. 2 Comparisons between intersection measurements and laser tracker measurements |
通过表 1可以看出,除了S01标靶球,激光跟踪仪的多点球心拟合后的球圆度标准差都不大于0.13 mm,能够满足规范[1]的要求。由于S01点位置比较高,激光跟踪仪测量不方便,观测点比较少,且测量点都位于球的中下部,所以拟合精度明显低于其他标靶球。
通过表 2可以看出,从垂直测线S01-S05和水平测线S06-S09这两条全组合测线观测结果来看,交会测量结果和激光跟踪仪的测量结果基本一致,互差较大的是S01-S02、S01-S04和S06-S09,分别达到0.47 mm、0.43 mm和-0.42 mm。分析其影响因素主要有两个:一是S01标靶激光跟踪仪坐标测量误差的影响,由于S01点不便于激光跟踪仪观测,且观测点比较少,造成S01的激光跟踪仪坐标精度不高,这一点可以通过S01同S02-S05等标靶球的互差一致性判断出来;另外是由于交会测量时,S06-S09位于两端,交会角度较小,会影响交会测量的精度,这与空间距离精度统计的结果是一致的。
3 结语1) 用全站仪交会测量后整体平差的方法可以用于地面激光扫描仪空间距离标准装置的校准,内符合精度优于0.1 mm,精度和激光跟踪仪相当。由于交会测量属于非接触测量,对于空间范围很大的空间距离标准装置校准来说,比激光跟踪仪更加安全、更方便操作。若使用激光跟踪仪测量,要充分考虑测量点的稳定性和分布。
2) 和工业经纬仪测量系统相比,全站仪使用广泛、价格便宜,使得建立工业测量系统更加便捷。用全站仪测量大尺度的空间标准距离,可以利用全站仪的免棱镜、后方交会等功能来直接测量概略坐标,更加直观、便捷,还可避免坐标推算造成的系统误差积累。
3) 交会测量后用整体平差法可以更好地利用全站仪的技术特点,直接使用补偿后的天顶方向为坐标纵轴,直接互瞄后(不需要内外觇标)得到水平角观测值,方法更加简便,精度一致性、可靠性都能满足工业测量的要求,可以用于更多室内精密测量的场景。
| [1] |
全国几何量长度委员会.JJF 1406-2013地面激光扫描仪校准规范[S].北京: 国家质量监督检疫总局, 2013 (National Geometric Length Committee.JJF 1406-2013 Calibration Specification for Terrestrial Laser Scanners[S].Beijing: General Administration of Quality Supervision, Inspection and Quarantine of the PRC, 2013)
(  0) 0) |
| [2] |
杨占立, 范百兴, 西勤, 等. TLS算法在参考球标定场中的应用[J]. 测绘工程, 2016, 25(9): 40-43 (Yang Zhanli, Fan Baixing, Xi Qin, et al. Application of TLS to the Reference Ball Calibration Field[J]. Engineering of Surveying and Mapping, 2016, 25(9): 40-43)
(  0) 0) |
| [3] |
Boehler W, Marbs A. Investigating Laser Scanner Accuracy[C]. Sixth CIPA Symposium, 2003
(  0) 0) |
| [4] |
邓向瑞, 钱征宇, 周志春. 地面三维激光扫描仪距离校准装置及测量不确定度评定[J]. 计量学报, 2010, 31(增2): 157-159 (Deng Xiangrui, Qian Zhengyu, Zhou Zhichun. Terrestrial Laser Scanner Ranging Calibration Equipment and Evaluation of Measurement Uncertainty[J]. Acta Metrologica Sinica, 2010, 31(S2): 157-159)
(  0) 0) |
| [5] |
李金鑫.基于室内规范检定场的地面三维激光扫描仪检校技术研究[D].青岛: 山东科技大学, 2017 (Li Jinxin.The Research of Terrestrial Laser Scanner Calibration Technology Based on Indoor Standard Field[D]. Qingdao: Shandong University of Science and Technology, 2017) http://cdmd.cnki.com.cn/Article/CDMD-10424-1017295190.htm
(  0) 0) |
| [6] |
徐寿志, 程鹏飞, 张玉, 等. 地面三维激光扫描仪的检校与测量精度评定[J]. 测绘通报, 2016(2): 79-83 (Xu Shouzhi, Cheng Pengfei, Zhang Yu, et al. Calibration and Accuracy Evaluation of Terrestrial Laser Scanner[J]. Bulletin of Surveying and Mapping, 2016(2): 79-83)
(  0) 0) |
| [7] |
梁建军, 范百兴, 邓向瑞, 等. 三维激光扫描仪球形靶标测量方法与精度评定[J]. 工程勘察, 2011, 39(2): 81-84 (Liang Jianjun, Fan Baixing, Deng Xiangrui, et al. Measurement Method and Precision Evaluation of Spherical Targets in 3D Laser Scanner[J]. Geotechnical Investigation and Surveying, 2011, 39(2): 81-84)
(  0) 0) |
| [8] |
欧阳健飞, 刘万里, 闫勇刚, 等. 激光跟踪仪坐标测量精度的研究[J]. 红外与激光工程, 2008(增1): 15-18 (Ouyang Jianfei, Liu Wanli, Yan Yonggang, et al. Coordinate Measuring Accuracy of Laser Tracker[J]. Infrared and Laser Engineering, 2008(S1): 15-18)
(  0) 0) |
| [9] |
孙海丽, 姚连璧, 周跃寅, 等. 激光跟踪仪测量精度分析[J]. 大地测量与地球动力学, 2015, 35(1): 177-181 (Sun Haili, Yao Lianbi, Zhou Yueyin, et al. Analysis of Measurement Accuracy of Laser Tracker[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 177-181)
(  0) 0) |
| [10] |
王东伟, 姜黎, 陈晓晖, 等. 电子经纬仪测量系统交会测量误差分析[J]. 宇航计测技术, 2014(6): 4-8 (Wang Dongwei, Jiang Li, Chen Xiaohui, et al. Analysis of Electronic Theodolite Measurement System on Intersection Measurement Error[J]. Journal of Astronautic Metrology and Measurement, 2014(6): 4-8)
(  0) 0) |
| [11] |
李广云, 李宗春. 工业测量系统原理与应用[M]. 北京: 测绘出版社, 2011 (Li Guangyun, Li Zongchun. The Principles and Applications of Industrial Measuring Systems[M]. Beijing: Surveying and Mapping Press, 2011)
(  0) 0) |
2. Wuhan Seismic Metrological Verification and Surveying Engineering Institute Co Ltd, 40 Hongshance Road, Wuhan 430071, China
 2020, Vol. 40
2020, Vol. 40

