2. 中国地震局地壳应力研究所武汉科技创新基地,武汉市洪山侧路40号,430071
环境噪声和地面振动是许多精密仪器进一步提高精度的制约因素[1]。在高精度绝对重力测量领域,无论是采用角锥棱镜自由下落的FG5型绝对重力仪,还是采用原子下落的原子干涉型重力仪,都需对其中的参考棱镜或光学反射镜进行隔振。目前应用于绝对重力仪中的隔振系统主要有超长弹簧隔振系统(superspring)[2-3]、主动式磁悬浮隔振系统[4]、由加速度计和单极弹簧组成的主动隔振系统[5-9]、基于零长弹簧的单级隔振系统[10-11]和基于两级摆杆的两级隔振系统[12-13]。
目前常用的隔振系统为弹簧-质量振子系统,该系统本质上为一个低通滤波器,可有效隔离超过其固有频率的振动噪声,但无法隔离低于其固有频率的振动噪声。弹簧-质量振子系统固有频率f0=(1/2π)
目前最为成熟的超低频隔振系统为应用在FG5绝对重力仪上的超长弹簧隔振系统,该系统采用两级弹簧结构,利用主动反馈补偿技术让一级弹簧跟随二级弹簧运动,最终使得整个系统等效于一个固有周期长达60 s的弹簧-质量振子系统,从而实现超低频隔振[2]。本文拟对应用于绝对重力仪中的两级隔振系统进行理论研究,主要分析两级隔振系统的传递函数,根据分析结果选择合适的反馈方式,分析各个反馈参数对系统的影响,并通过仿真对分析结果进行验证,从而为自行设计隔振系统提供理论指导。
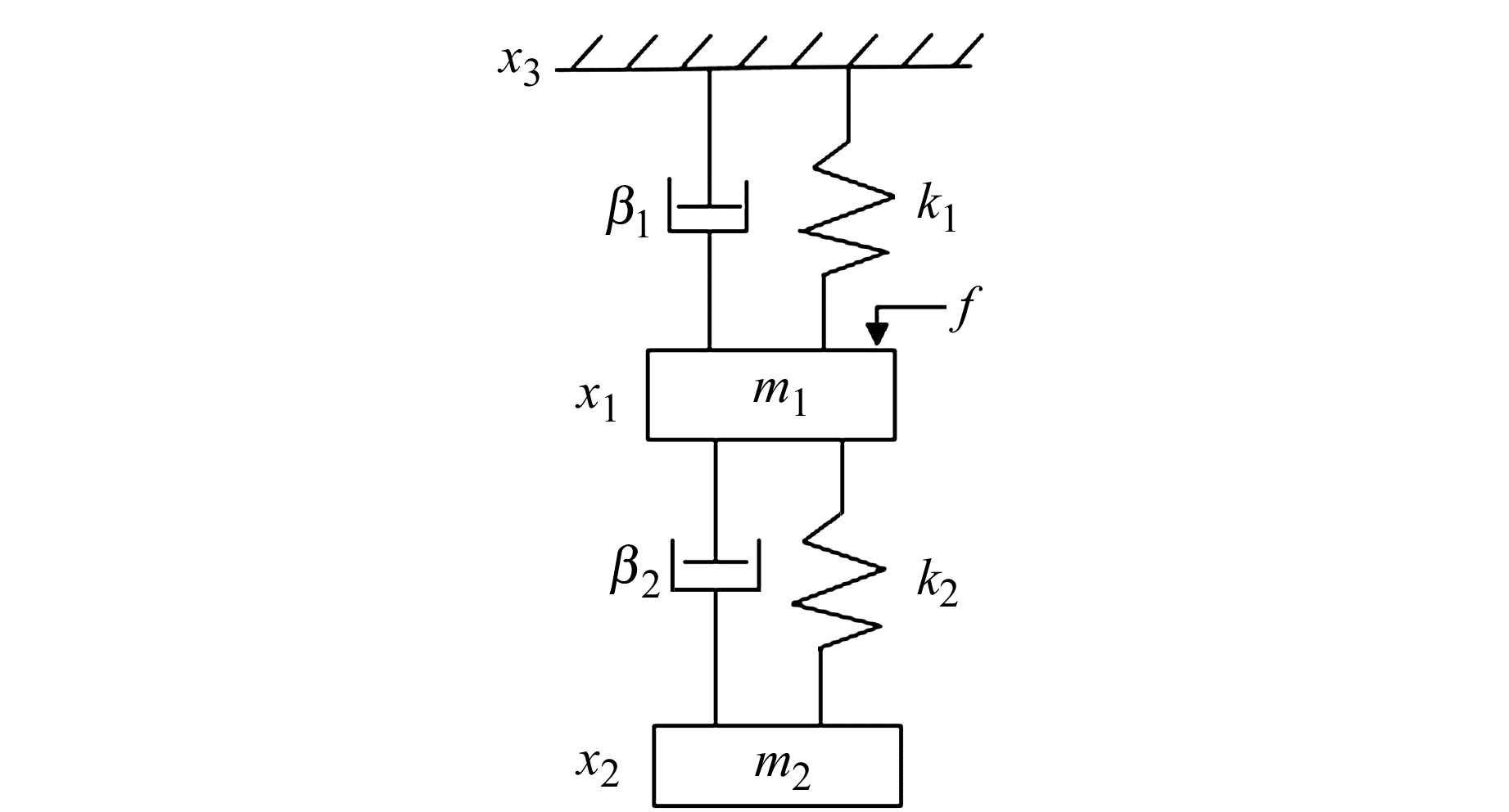
1 两级隔振系统运动模型图 1为两级隔振系统的运动模型,其中,k1、k2分别代表一级弹簧和二级弹簧的弹性系数,β1、β2分别代表一级弹簧和二级弹簧的阻尼系数,m1、m2分别为一级隔振平台和二级隔振平台的质量,x1、x2、x3分别为一级隔振平台、二级隔振平台(绝对重力仪中参考棱镜)以及系统支撑框架(或地面)的绝对位移,f为作用在一级隔振平台上的反馈力。
|
图 1 两级隔振系统示意图 Fig. 1 Diagram of two-stage vibration isolation system |
开环时,分别列出一级和二级摆时域中的运动方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{m_1}{{\ddot x}_1} = {k_1}\left( {{x_3} - {x_1}} \right) + {\beta _1}\left( {{{\dot x}_3} - {{\dot x}_1}} \right) + {k_2}\left( {{x_2} - {x_1}} \right) + {\beta _2}\left( {{{\dot x}_2} - {{\dot x}_1}} \right)}\\ {{m_2}{{\ddot x}_2} = {k_2}\left( {{x_1} - {x_2}} \right) + {\beta _2}\left( {{{\dot x}_1} - {{\dot x}_2}} \right)} \end{array}} \right. $ | (1) |
对式(1)进行拉普拉斯变换,将时域函数x1(t)、x2(t)、x3(t)转换到频域函数X1(s)、X2(s)、X3(s),并求出两级隔振系统在频域的开环传递函数,即参考棱镜与地面运动的位移比为:
| $ \frac{{X}_{2}\left(s\right)}{{X}_{3}\left(s\right)}=\frac{\left({\beta }_{1}{s}+{k}_{1}\right)\left({\beta }_{2}{s}+{k}_{2}\right)}{\left({m}_{1}{s}^{2}+{\beta }_{1}{s}+{k}_{1}\right)\left({m}_{2}{s}^{2}+{\beta }_{2}{s}+{k}_{2}\right)+{m}_{1}{s}^{2}\left({\beta }_{2}{s}+{k}_{2}\right)} $ | (2) |
闭环时,参考超长弹簧的设计原理,令一级弹簧跟随二级弹簧运动,即以(x2-x1)作为反馈量,f(t)为反馈函数,分别列出一级和二级摆时域中的运动方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{m_1}{{\ddot x}_1} = {k_1}\left( {{x_3} - {x_1}} \right) + {\beta _1}\left( {{{\dot x}_3} - {{\dot x}_1}} \right) + {k_2}\left( {{x_2} - {x_1}} \right) + {\beta _2}\left( {{{\dot x}_2} - {{\dot x}_1}} \right) + f\left( t \right)\left( {{x_2} - {x_1}} \right)}\\ {{m_2}{{\ddot x}_2} = {k_2}\left( {{x_1} - {x_2}} \right) + {\beta _2}\left( {{{\dot x}_1} - {{\dot x}_2}} \right)} \end{array}} \right. $ | (3) |
对式(3)进行拉普拉斯变换,求出两级隔振系统在频域的开环传递函数为:
| $ \frac{{{X_2}\left( s \right)}}{{{X_3}\left( s \right)}} = \frac{{\left( {{\beta _1}s + {k_1}} \right)\left( {{\beta _2}s + {k_2}} \right)}}{{\left( {{m_1}{s^2} + {\beta _1}s + {k_1}} \right)\left( {{m_2}{s^2} + {\beta _2}s + {k_2}} \right) + {m_1}{s^2}\left( {{\beta _2}s + {k_2} + f\left( s \right)} \right)}} $ | (4) |
令σ1=β1/m1,σ2=β2/m2,σ12=β2/m1,ω12=k1/m1,ω22=k2/m2,ω122=k2/m1,代入式(4)并展开得:
| $ \frac{{{X_2}\left( s \right)}}{{{X_3}\left( s \right)}} = \frac{{{\sigma _1}{\sigma _2} + {\sigma _1}{\omega _2}^2 + {\sigma _2}{\omega _1}^2 + {\omega _1}^2{\omega _2}^2}}{{{s^4} + \left( {{\sigma _1} + {\sigma _2} + {\sigma _{12}}} \right){s^3} + \left[ {f\left( s \right)/{m_1} + {\omega _1}^2 + {\omega _2}^2 + {\omega _{12}}^2 + {\sigma _1}{\sigma _2}} \right]{s^2} + \left( {{\sigma _1}{\omega _2}^2 + {\sigma _2}{\omega _1}^2} \right)s + {\omega _1}^2{\omega _2}^2}} $ | (5) |
超长弹簧隔振系统采用PD反馈,反馈函数表达式为:
| $ f(s) = {k_p} + {k_d}s $ | (6) |
将式(6)代入式(5)并展开得:
| $ \frac{{{X_{\rm{2}}}(s)}}{{{X_{\rm{3}}}(s)}} = \frac{{{\sigma _1}{\sigma _{\rm{2}}} + {\sigma _1}{\omega _{\rm{2}}}^2 + {\sigma _2}{\omega _{\rm{1}}}^2 + {\omega _{\rm{1}}}^2{\omega _{\rm{2}}}^2}}{{{s^4} + ({\sigma _1} + {\sigma _2} + {\sigma _{12}} + {\sigma _d}){s^3} + ({\omega _p}^2 + {\omega _{\rm{1}}}^2 + {\omega _{\rm{2}}}^2 + {\omega _{{\rm{12}}}}^2 + {\sigma _1}{\sigma _{\rm{2}}}){s^2} + ({\sigma _1}{\omega _{\rm{2}}}^2 + {\sigma _2}{\omega _{\rm{1}}}^2)s + {\omega _{\rm{1}}}^2{\omega _{\rm{2}}}^2}} $ | (7) |
式中,ωp=kp/m1,σd=kd/m1。为提高隔振效果,一般需要降低隔振系统的等效固有频率,则反馈需要较高的增益,即ωp2≫ω12, ωp2≫ω22, ωp2≫ω122, ωp2≫σ1σ2, σd≫σ1, σd≫σ2, σd≫σ12。参考文献[2]超长弹簧的分析方法,式(7)可近似表示为:
| $ \frac{{{X_2}(s)}}{{{X_3}(s)}} \approx \frac{{({\sigma _1}s + {\omega _1}^2)({\sigma _2}s + {\omega _2}^2)}}{{({s^2} + {\sigma _d}s + {\omega _p}^2)({s^2} + {C_1}s + {\omega _1}^2{\omega _2}^2/{\omega _p}^2)}} $ | (8) |
其中,
| $ {C_1} \approx \frac{{{\sigma _1}{\omega _2}^2 + {\sigma _2}{\omega _1}^2}}{{{\omega _p}^2}} - {\sigma _d}\frac{{{\omega _1}^2{\omega _2}^2}}{{{\omega _p}^4}} $ | (9) |
式(8)即为简化后的两级隔振系统的传递函数。对隔振系统而言,重要的是传递函数的幅频响应,根据式(8)可得:
| $ \left| {{H_{{\rm{j}}w}}} \right| = \left| {\frac{{{X_2}({\rm{j}}w)}}{{{X_3}({\rm{j}}w)}}} \right| \approx \frac{{{\omega _1}^2{\omega _2}^2/{\omega _p}^2}}{{\sqrt {{{({\omega _1}^2{\omega _2}^2/{\omega _p}^2 - {\omega ^2})}^2} + {C_1}^2{\omega ^2}} }} $ | (10) |
由式(10)可以看出,闭环两级隔振系统的幅频响应与单级弹簧-质量振子幅频响应具有相同的形式,通过类比可得到闭环两级隔振系统的等效阻尼系数为C1,等效固有频率为:
| $ {\omega _0} = {\omega _1}{\omega _2}/{\omega _p} = \sqrt {\frac{{{k_1}{k_2}}}{{{k_p}{m_2}}}} $ | (11) |
式中,k1、k2、m2分别为一级摆弹簧刚度系数、二级摆弹簧刚度系数和二级摆的质量,这些参数一旦确定即为固定值。为了使两级隔振系统获得较长的等效固有周期,需要增大反馈比例系数kp。对式(9)进行分析可知,由于σ1、σ2非常小,而σd、ωp比较大,因此C1小于0,即系统的阻尼系数为负值,系统不稳定。超长弹簧系统需要采用非常复杂且配合良好的结构设计和电路设计来解决此问题。
结合对系统传递函数的分析,可通过改变反馈方式来解决系统易自激振荡的问题,拟采用PID反馈代替超长弹簧的PD反馈方式,此时反馈函数表达式为:
| $ f(s) = {k_p} + {k_d}s + {k_i}/s $ | (12) |
采取同样的分析方法,采用PID反馈时系统传递函数为:
| $ \frac{{{X_{\rm{2}}}(s)}}{{{X_{\rm{3}}}(s)}} = \frac{{{\sigma _1}{\sigma _{\rm{2}}} + {\sigma _1}{\omega _{\rm{2}}}^2 + {\sigma _2}{\omega _{\rm{1}}}^2 + {\omega _{\rm{1}}}^2{\omega _{\rm{2}}}^2}}{{{s^4} + ({\sigma _1} + {\sigma _2} + {\sigma _{12}} + {\sigma _d}){s^3} + ({\omega _p}^2 + {\omega _{\rm{1}}}^2 + {\omega _{\rm{2}}}^2 + {\omega _{{\rm{12}}}}^2 + {\sigma _1}{\sigma _{\rm{2}}}){s^2} + ({\sigma _1}{\omega _{\rm{2}}}^2 + {\sigma _2}{\omega _{\rm{1}}}^2 + {\sigma _i})s + {\omega _{\rm{1}}}^2{\omega _{\rm{2}}}^2}} $ | (13) |
式中,ωp=kp/m1,σd=kd/m1,σi=ki/m1,简化得:
| $ \frac{{{X_2}(s)}}{{{X_3}(s)}} = \frac{{({\sigma _1}s + {\omega _1}^2)({\sigma _2}s + {\omega _2}^2)}}{{({s^2} + {\sigma _d}s + {\omega _p}^2)({s^2} + {C_2}s + {\omega _1}^2{\omega _2}^2/{\omega _p}^2)}} $ | (14) |
此时,系统的幅频响应与采用PD反馈时相同,而等效阻尼系数为:
| $ {C_2} \approx \frac{{{\sigma _1}{\omega _2}^2 + {\sigma _2}{\omega _1}^2 + {\sigma _i}}}{{{\omega _p}^2}} - {\sigma _d}\frac{{{\omega _1}^2{\omega _2}^2}}{{{\omega _p}^4}} $ | (15) |
对比式(15)与式(9)可知,采用PID反馈代替PD反馈后,系统的等效阻尼系数由负值变为由积分项和微分项共同调节的量,且调节过程中积分项占主导地位,能轻易地将等效阻尼系数调整为正值。即采用PID反馈后,系统能轻易实现稳定状态,无需像超长弹簧一样设计复杂的机械结构并配合良好的电路。
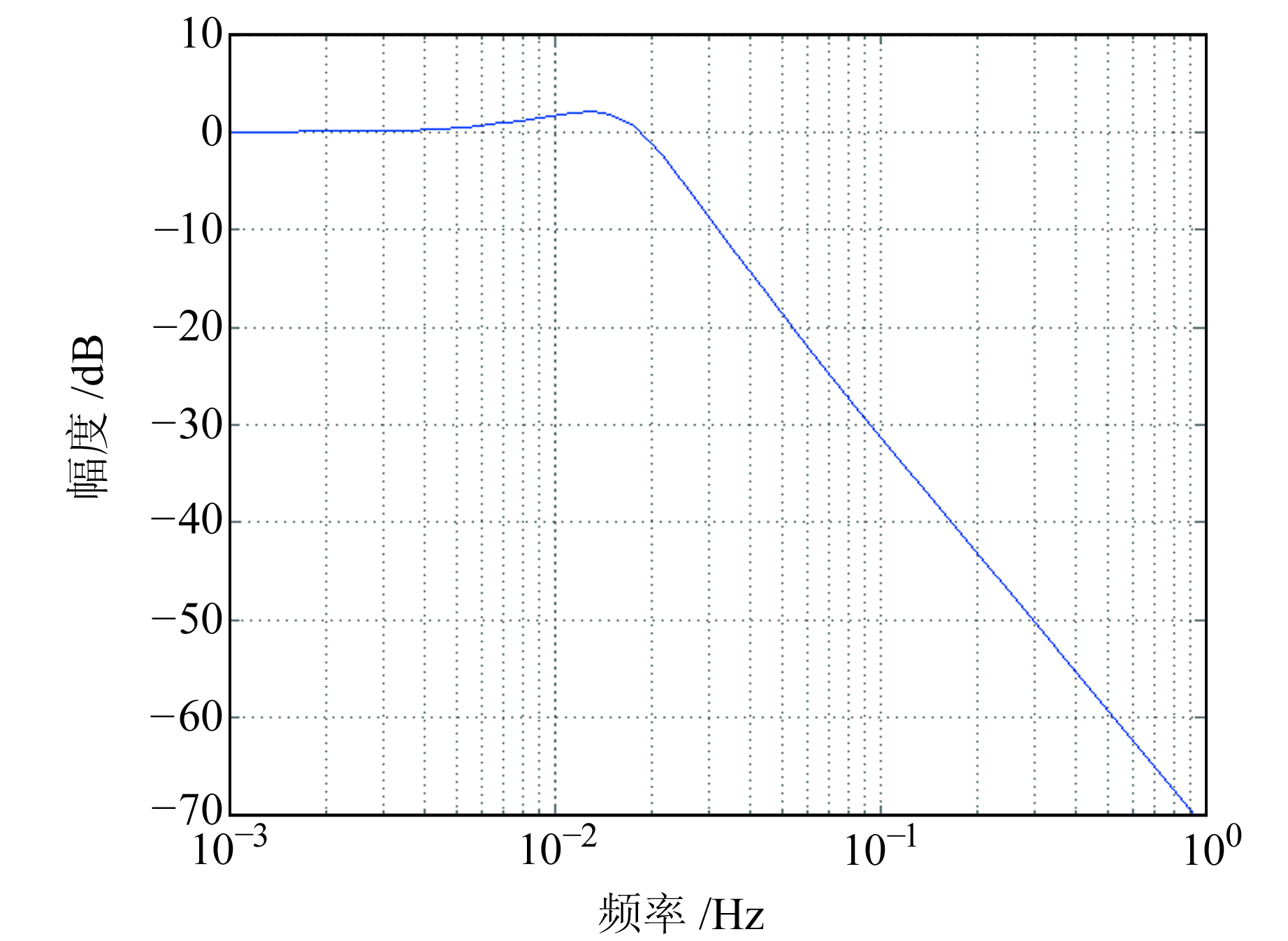
3 两级隔振系统仿真 3.1 隔振特性仿真为验证闭环系统的隔振特性,选取典型参数(表 1),将其代入两级隔振闭环传递函数式(5)。根据式(11)和式(15)选择合适的反馈参数(比例系数kp=2.2×105、微分系数kd=1.0×103、积分系数ki=2.0×104,此时系统等效固有周期约为60 s,且能保持稳定),利用Matlab绘制出该传递函数的Bode图,即可得到该系统的频率响应曲线,从而得出隔振特性。图 2为选择上述参数绘制的系统Bode图,由图可见,系统在1 Hz处隔振效果优于-70 dB。
|
|
表 1 隔振系统典型参数 Tab. 1 Typical parameters of the vibration isolation system |
|
图 2 闭环两级隔振系统Bode图 Fig. 2 The Bode diagram of closed-loop two-stage vibration isolation system |
为验证上述分析中各反馈参数对系统的影响,采用改变单一变量法对系统进行仿真。仿真过程中,改变单个参数,其他参数保持不变,从而得出该参数对两级隔振系统的影响。
为验证反馈参数中比例系数kp对系统等效固有周期的影响,选取ki=1.0×104、kd=1.0×103,kp分别取1.5×105、2.0×105、2.5×105,利用Matlab绘制时域下的阶跃响应曲线图(图 3)。由图可知,当kp分别取1.5×105、2.0×105、2.5×105时,对应的等效固有周期分别约为52.1 s、58.9 s、65.7 s,等效固有周期随比例系数kp的增大而增大。

|
图 3 反馈比例系数kp对系统的影响 Fig. 3 The influence of the feedback scale factor kp on the system |
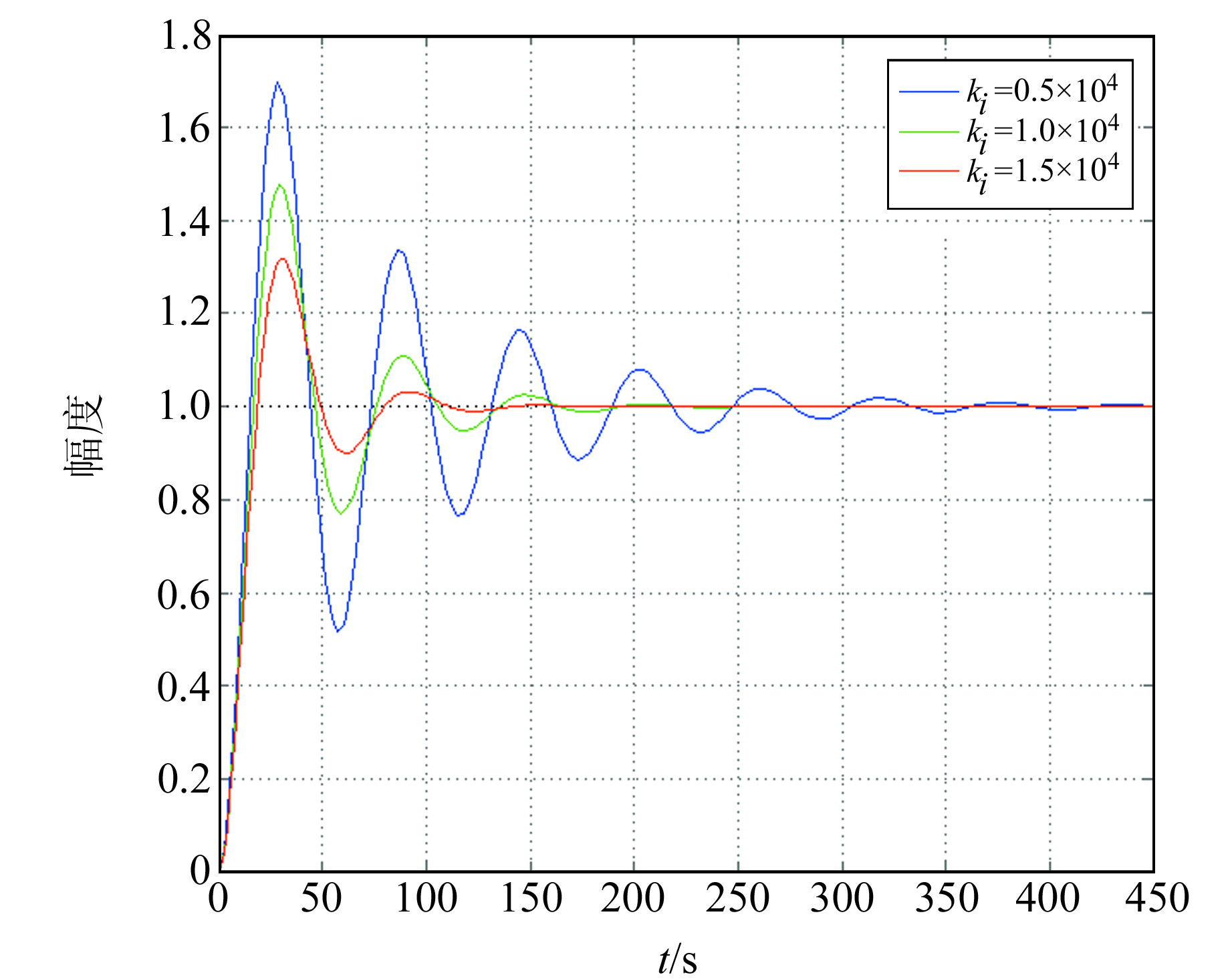
为验证反馈参数中积分系数ki对系统等效固有周期的影响,选取kp=2.0×105、kd=1.0×103,ki分别取0.5×104、1.0×104、1.5×104,利用Matlab绘制时域下的阶跃响应曲线图(图 4)。由图可知,随着积分系数ki的增大,系统的阻尼变大,趋于稳定。
|
图 4 反馈积分系数ki对系统的影响 Fig. 4 The influence of the feedback integral coefficient ki on the system |
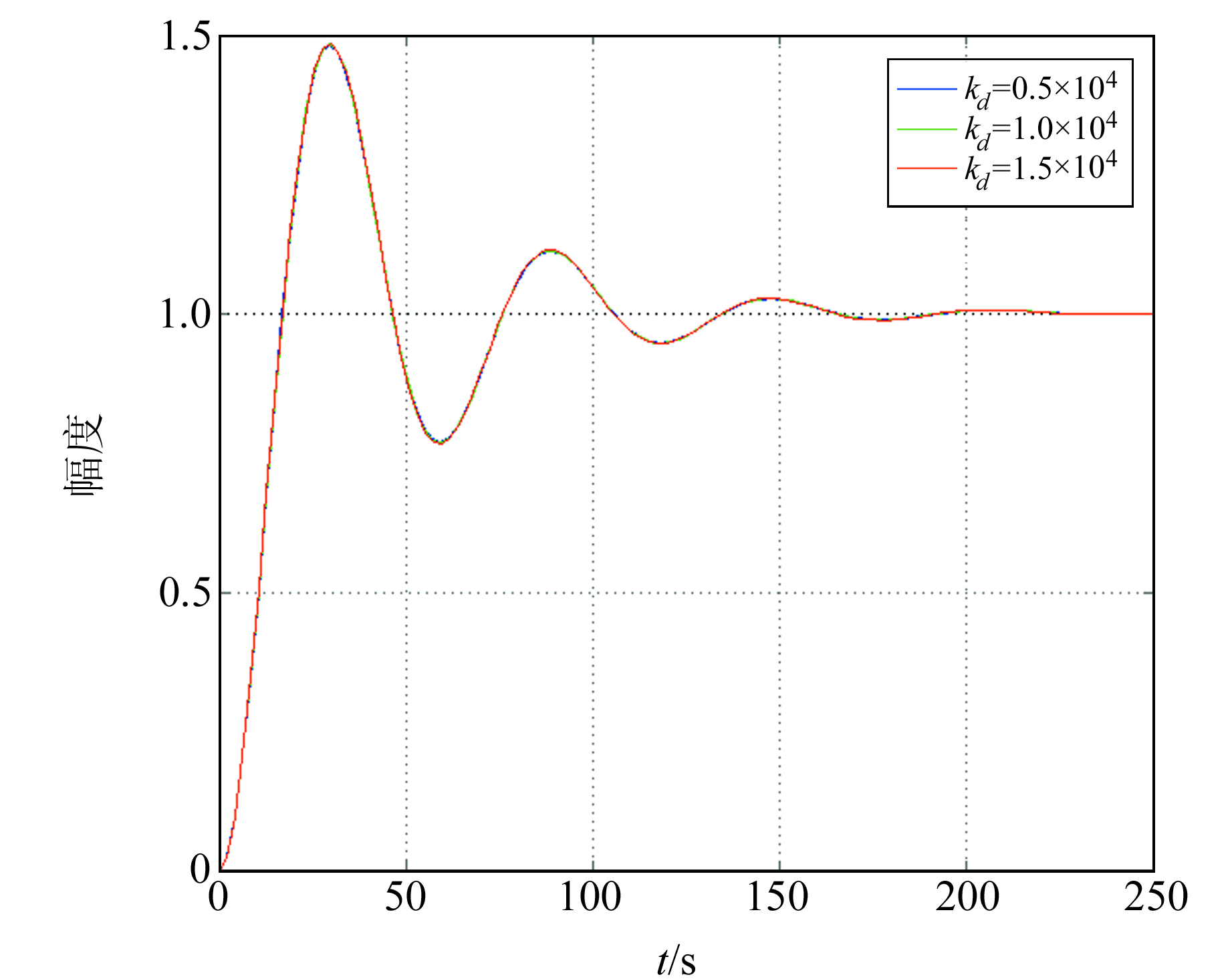
为验证反馈参数中微分系数kd对系统等效固有周期的影响,选取kp=2.0×105、ki=1.0×104,kd选择数值较小的微分系数组合分别为0.5×104、1.0×104、1.5×104,利用Matlab绘制时域下的阶跃响应曲线图(图 5)。
|
图 5 反馈微分系数kd对系统的影响(kd取值较小) Fig. 5 The influence of the feedback differential coefficient kd on the system (kd is small) |
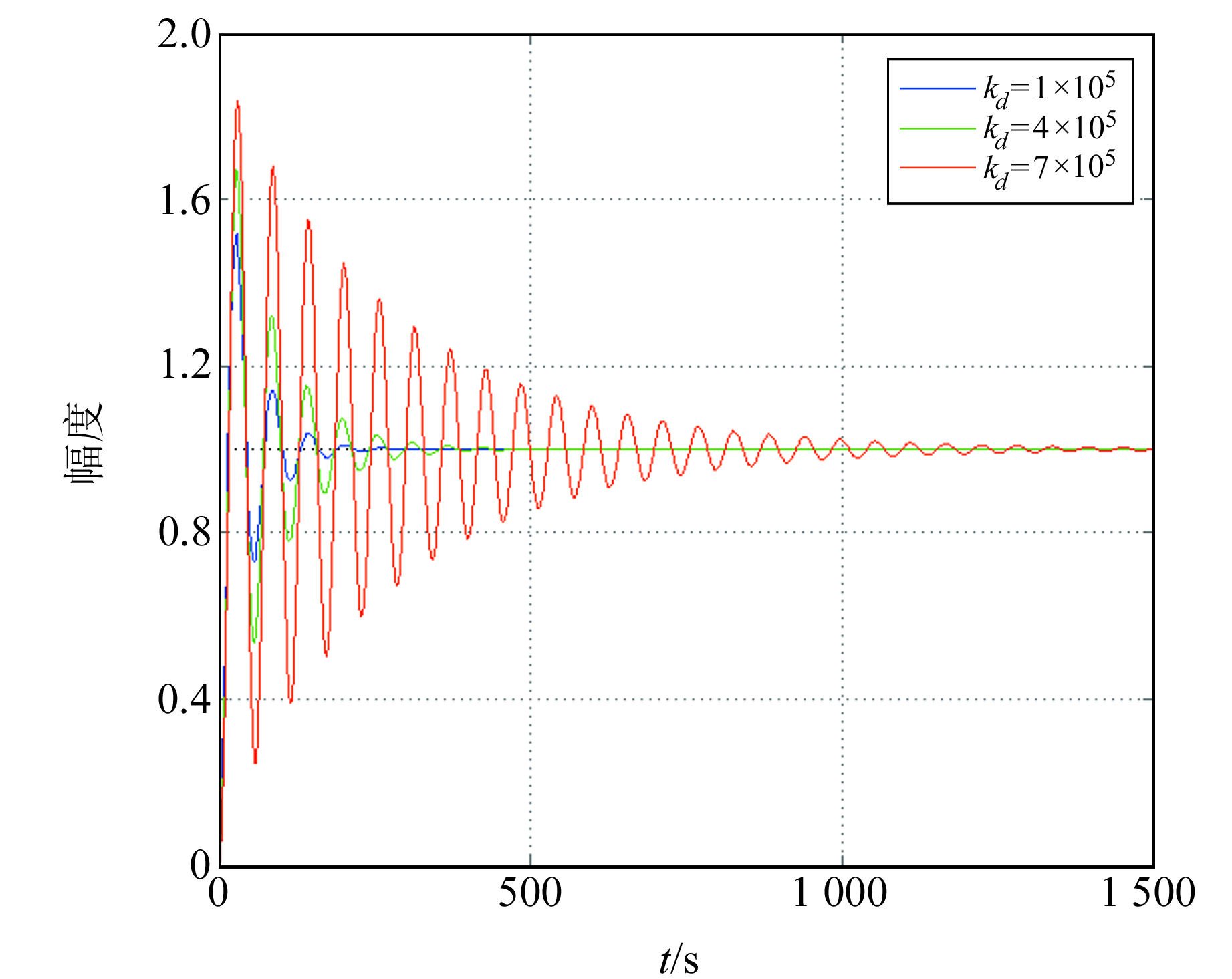
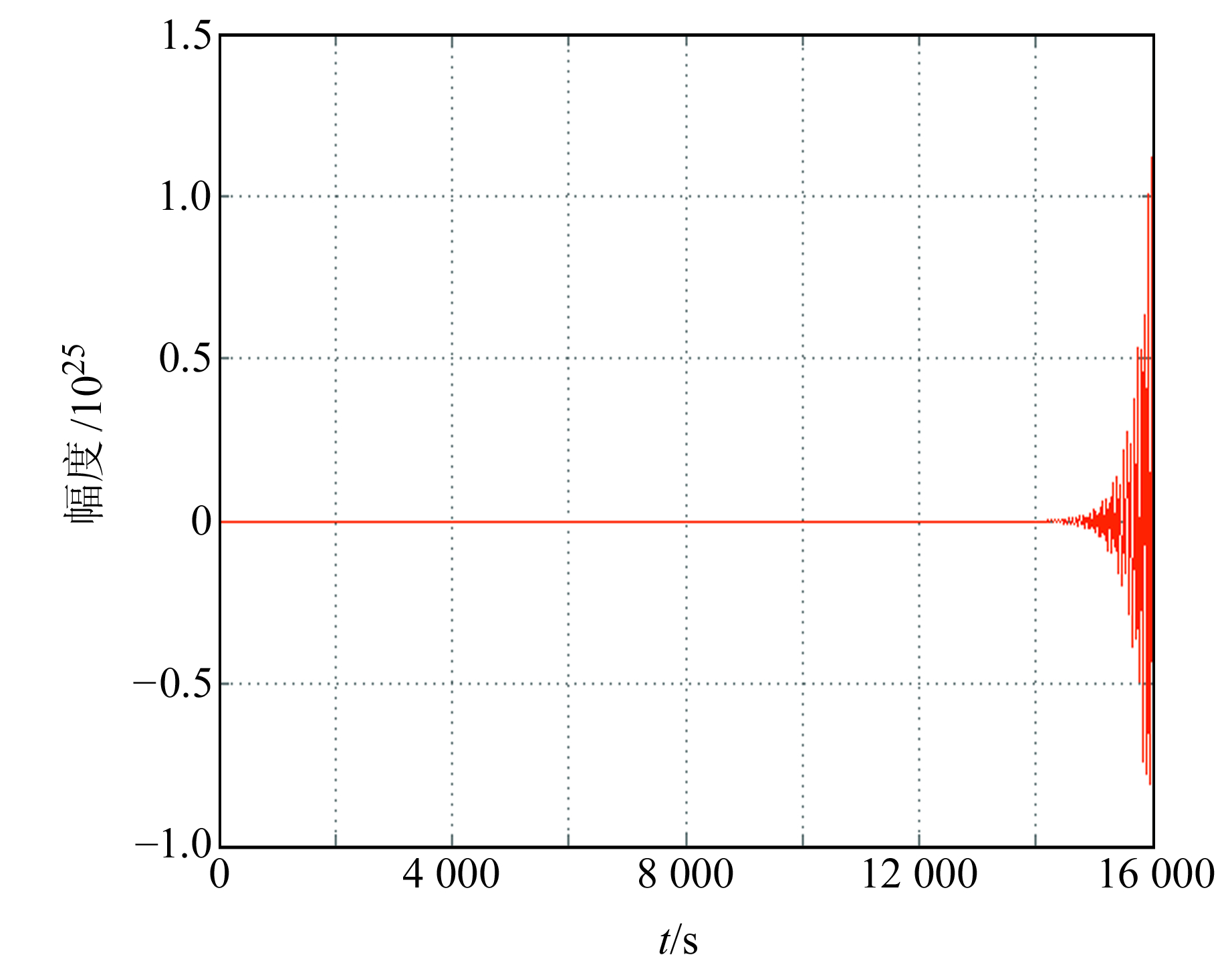
从图 5可以明显看出,当反馈参数中比例系数kp和积分系数ki固定时,微分系数kd取值较小(与积分系数ki相同量级),对系统基本无影响;而当kp与ki不变,kd选取数值较大的微分系数组合分别为1×105、4×105、7×105,可得到如图 6所示的阶跃响应曲线。由图可知,随着微分系数kd的增大,系统阻尼逐渐变小,系统的稳定性变差。进一步增大微分系数,当kd取值比ki高2个量级时(即取kd=1.0×106),系统在时域下的阶跃响应曲线如图 7所示,表明系统发散。
|
图 6 反馈微分系数kd对系统的影响(kd取值较大) Fig. 6 The influence of the feedback differential coefficient kd on the system (kd is large) |
|
图 7 反馈微分系数kd过大时系统发散 Fig. 7 The system diverges when the feedback differential coefficient kd is too large |
根据式(15)等效阻尼系数表达式可分析产生上述现象的原因。当微分项与积分项相比很小或两者差别不大时,等式右边第1项分母为ωp2,而第2项分母为ωp4,仍然是积分项占主导地位,微分项对系统阻尼的影响可以忽略,此时等效阻尼为正,系统稳定;随着微分项增大到一定程度,等式右边两项相减后逐渐减小,等效阻尼不断变小,系统的稳定性变差;当微分系数远大于积分系数时,等式右端两项相减小于0,此时等效阻尼系数由正值变为负值,系统变得不稳定。
4 结语1) 应用于绝对重力仪中的两级超低频隔振系统,采用PID反馈代替PD反馈,可更方便地调节系统等效阻尼系数,有效避免等效阻尼系数为负值,从而有利于在调试过程中实现系统的稳定。
2) 两级隔振系统采用PID反馈方式时,等效固有周期主要受比例系数kp影响,kp越大,等效固有周期越长,隔振效果越好。选取合适的kp后,积分系数ki和微分系数kd共同影响整个系统的阻尼,且ki占主导地位,决定系统的稳定性。
综上所述,应用于绝对重力仪中的两级超低频隔振系统,采用PID反馈可获得较好的等效阻尼系数调节功能,选取合适的参数时,等效固有周期可达70 s,在1 Hz处隔振性能可达-70 dB。
| [1] |
Ju L W, Blair D G. Low Resonant Frequency Cantilever Spring Vibration Isolator for Gravitational Wave Detectors[J]. Review of Science Instruments, 1994, 65(11): 3 482-3 488 DOI:10.1063/1.1145218
(  0) 0) |
| [2] |
Lee R R. SuperSpring: A New Type of Low Frequency Vibration Isolator[D]. Boulder: University of Corolado, 1983
(  0) 0) |
| [3] |
Niebauer T M, Sasagawa G S, Faller J E, et al. A New Generation of Absolute Gravimeters[J]. Metrologia, 2005, 32(3): 159-180
(  0) 0) |
| [4] |
张兵, 滕云田, 邢丽莉, 等. 激光干涉绝对重力仪参考棱镜隔振系统仿真[J]. 地球物理学报, 2017, 60(11): 4 221-4 230 (Zhang Bing, Teng Yuntian, Xing Lili, et al. The Simulation of Reference Corner Cube Vibration Isolation System of Laser Interference Absolute Gravimeter[J]. Chinese Journal of Geophysics, 2017, 60(11): 4 221-4 230)
(  0) 0) |
| [5] |
Hensley J M, Peters A, Chu S. Active Low Frequency Vertical Vibration Isolation[J]. Review of Science Instruments, 1999, 70(6): 2 735-2 741 DOI:10.1063/1.1149838
(  0) 0) |
| [6] |
Fteier C. Measurement of Local Gravity Using Atom Interferometer[D]. Berlin: Humboldt University, 2010
(  0) 0) |
| [7] |
Zhou M K, Hu Z K, Duan X C, et al. Performance of a Cold-Atom Gravimeter with an Active Vibration Isolator[J]. Physical Review A, 2012, 86(4): 43 630 DOI:10.1103/PhysRevA.86.043630
(  0) 0) |
| [8] |
Tang B, Zhou L, Xiong Z Y, et al. A Programmable Broadband Low Frequency Active Vibration Isolation System for Atom Interferometry[J]. Review of Science Instruments, 2014, 85(9): 93 109 DOI:10.1063/1.4895911
(  0) 0) |
| [9] |
张华兴, 田蔚, 丁国龙. 绝对重力仪中几种隔振系统的对比测试[J]. 大地测量与地球动力学, 2017, 37(7): 767-770 (Zhang Huaxing, Tian Wei, Ding Guolong. Comparison Experiments of Several Kinds of Vibration Isolation Systems in Absolute Gravimeter[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 767-770)
(  0) 0) |
| [10] |
李刚, 胡华, 伍康, 等. 基于零长弹簧的超低频垂直隔振系统研究[J]. 振动与冲击, 2015, 34(7): 33-37 (Li Gang, Hu Hua, Wu Kang, et al. Ultra-Low Frequency Vertical Vibration Isolation System Based on Zero-Length Spring[J]. Journal of Vibration and Shock, 2015, 34(7): 33-37)
(  0) 0) |
| [11] |
Li G, Hu H, Wu K, et al. Ultra-Low Frequency Vertical Vibration Isolator Based on LaCoste Spring Linkage[J]. Review of Scientific Instruments, 2014, 85(10): 104 502 DOI:10.1063/1.4897488
(  0) 0) |
| [12] |
王观, 胡华, 伍康, 等. 基于两级摆杆结构的超低频垂直隔振系统[J]. 物理学报, 2016, 65(20): 44-50 (Wang Guan, Hu Hua, Wu Kang, et al. Ultra-Low-Frequency Vertical Vibration Isolator Based on a Two-Stage Beam Structure[J]. Acta Physica Sinica, 2016, 65(20): 44-50)
(  0) 0) |
| [13] |
Wang G, Wu K, Hu H, et al. Ultra-Low-Frequency Vertical Vibration Isolator Based on a Two-Stage Beam Structure for Absolute Gravimetry[J]. Review of Scientific Instruments, 2016, 87(10): 105 101 DOI:10.1063/1.4963676
(  0) 0) |
| [14] |
Peterson J.Observations and Modeling of Seismic Background Noise[R]. Albuquerque: Department of Interior Geological Survey, 1993
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2020, Vol. 40
2020, Vol. 40


