大地震中由垂直同震地壳运动激发的地表声波、瑞利波面波及重力波会产生同震电离层扰动(CID)现象[1-2]。2015-04-25 UT 06:11:26尼泊尔发生MW7.8地震,震中28.147°N、84.708°E,震源深度15 km。目前已有学者对尼泊尔MW7.8地震的同震电离层扰动展开研究[3-6]。本文选取少量位于震中附近且分布较为集中的GPS站,利用尼泊尔MW7.8地震的GPS观测数据计算相应的高精度电离层TEC,处理分析各测站的同震电离层扰动序列。通过比对TEC扰动的时间序列、时间-距离曲线及电离层穿刺点轨迹,分析电离层TEC扰动的时空分布特征并确定水平传播速率,同时结合FFT频谱的频段与扰动速率范围探究可能引起同震电离层扰动的地震波类型。
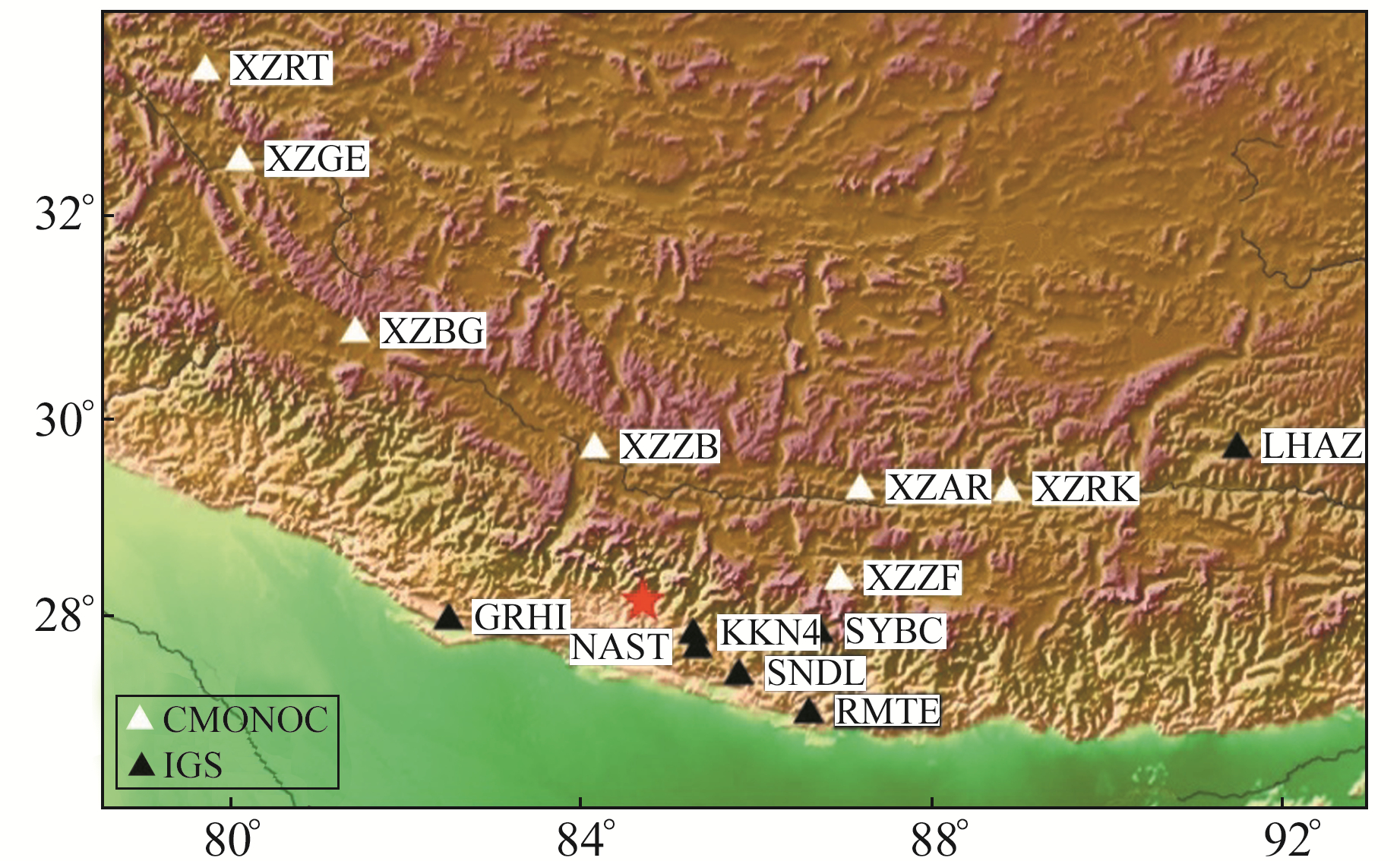
1 数据与处理 1.1 GPS TEC解算GPS观测数据采用中国地壳运动观测网络(CMONOC)与IGS提供的RENIX格式观测数据。选取距离震中最近的7个IGS测站与7个位于西藏的陆态网测站,位置分布如图 1所示。其中部分IGS测站原始数据采样频率为1 Hz,预先将高频GPS数据的采样率转化为30 s,对所有测站的卫星数据剔除粗差,并以多项式拟合法探测并修复周跳[7]。本文分析对象为短时间内电离层TEC随时间的波动趋势,因此仅需考虑TEC的相对变化部分,故可利用载波相位观测值直接解算电离层穿刺点处的电离层TEC,基本公式为:
| $ {\rm{TEC = - }}\frac{c}{{{\rm{40}}{\rm{.26}}}}\frac{{f_{{\rm{1}}}^{{\rm{2}}}{f_2}}}{{{\rm{}}\left( {{\rm{}}f_{\rm{1}}^{\rm{2}}{\rm{ - }}f_{{\rm{2}}}^{\rm{2}}} \right)}}\left( {{\mathit{\Phi }_{{\rm{2}}}} - {\rm{}}\frac{{{f_2}}}{{{f_1}}}{\mathit{\Phi }_{{\rm{1}}}}{\rm{ + }}{N_{\varphi }}} \right) $ | (1) |
| $ {N_{\varphi}} = {N_2} - \frac{{{f_2}}}{{{f_1}}}{N_1} $ | (2) |
|
图 1 GPS测站分布 Fig. 1 Distribution of GPS stations |
式中,Фi为载波相位观测值,Ni为未知的整周模糊度(i=1, 2)。已知载波L1与L2的精度分别约为1.9 mm和2.5 mm,在分析相对TEC时忽略整周模糊度线性组合Nφ,根据误差传播定律可知,相对TEC精度约为0.005 TECu(1 TECu =1016/m2),可满足电离层TEC扰动精度分析的需要。
1.2 TEC扰动序列获取对已经获取的电离层TEC采用Savitzky-Golay滑动滤波进行平滑处理,通过移动一定长度的窗口进行拟合,基于最小二乘原理,计算简单快速,并且能保留数据相对极大值、极小值和宽度等分布特性。基本公式为:
| $\overline {{\rm{TEC}}\left( t \right)} = \mathop \sum \limits_{i = m}^n {a_i}{\rm{TEC}}\left( {t + i} \right)$ | (3) |
| $\Delta {\rm{TEC}}\left( t \right) = {\rm{TEC}}\left( t \right) - {\rm{}}\overline {{\rm{TEC}}\left( t \right)} $ | (4) |
式中,t为当前历元,m和n分别为滤波窗口前后的历元个数,滤波窗口的长度为m+n-1,ai为滤波系数。根据TEC原始值与式(3)可计算当前历元电离层TEC趋势值
根据上述处理方法解算获得各测站的电离层TEC扰动时间序列。图 2为从各跟踪站观测数据中提取的扰动较为明显的4颗卫星(PRN16、PRN23、PRN26和PRN31)的平滑TEC时间序列。将不同测站的TEC数据按照震中距从上到下递增排列[8],每条TEC曲线右侧标注各测站名称及其震中距(单位km),红色竖直虚线表示地震发生时间UT 06:11:26。距离震中位置较近、观测数据时间最长且可观测卫星数目最多的测站为KKN4、NAST及SYBC。从图 2(a)中可以明显看出,PRN16卫星观测到的扰动异常波形基本一致,从地震发生时刻起约5 min后扰动序列开始出现区别于常态波动的增大趋势,到达峰值后骤降并再次大幅增加,正峰值为0.122 TECu(KKN4测站),负峰值可达-0.160 TECu(SYBC测站),扰动异常持续约6 min后恢复正常。图 2(b)中NAST测站出现扰动异常峰值的位置距震中85.968 km,为最近的扰动峰值震中距;SYBC测站波动起伏较大,TEC异常值最大为0.083 TECu,最小为-0.105 TECu,异常持续时间约10 min。卫星PRN26和PRN31包含较多测站数据,随着各测站震中距逐渐增加,扰动异常发生的时间出现约1 min的短暂延迟。从图 2(c)中可以看出,XZGE(震中距最近测站)和LHAZ(震中距最远测站)出现扰动峰值时的距离最大,分别为726.411 km和948.717 km。XZZF测站振幅最大为-0.1 TECu,为4个测站的最小幅值。PRN26在有限的数据内出现两段振幅相近的扰动异常,从测站XZBG、NAST与SYBC的时间序列中可清晰地看到,第2段异常于UT 07:18开始,最大振幅分别为0.350 TECu、0.348 TECu和0.667 TECu。SYBC测站的两次扰动异常均大于初次异常幅值0.532 TECu,其余两个测站均小于初次异常,分别为0.603 TECu和0.540 TECu。从图 2(d)可以看出,PRN31的时间序列较为特殊,异常持续时间更长,NAST测站在有限的观测数据内异常时间达到40 min;LHAZ测站的波形与PRN26一致且峰值最大,振幅为0.126 TECu。

|
图 2 部分测站观测的同震电离层扰动时间序列 Fig. 2 CID time series observed from different stations |
从整体上看,TEC时间序列在震后5 min开始出现扰动异常,持续时间大于6 min,且异常波形呈现增大-减小-增大的变化趋势,最大正异常为0.667 TECu,最小负异常为-0.160 TECu。
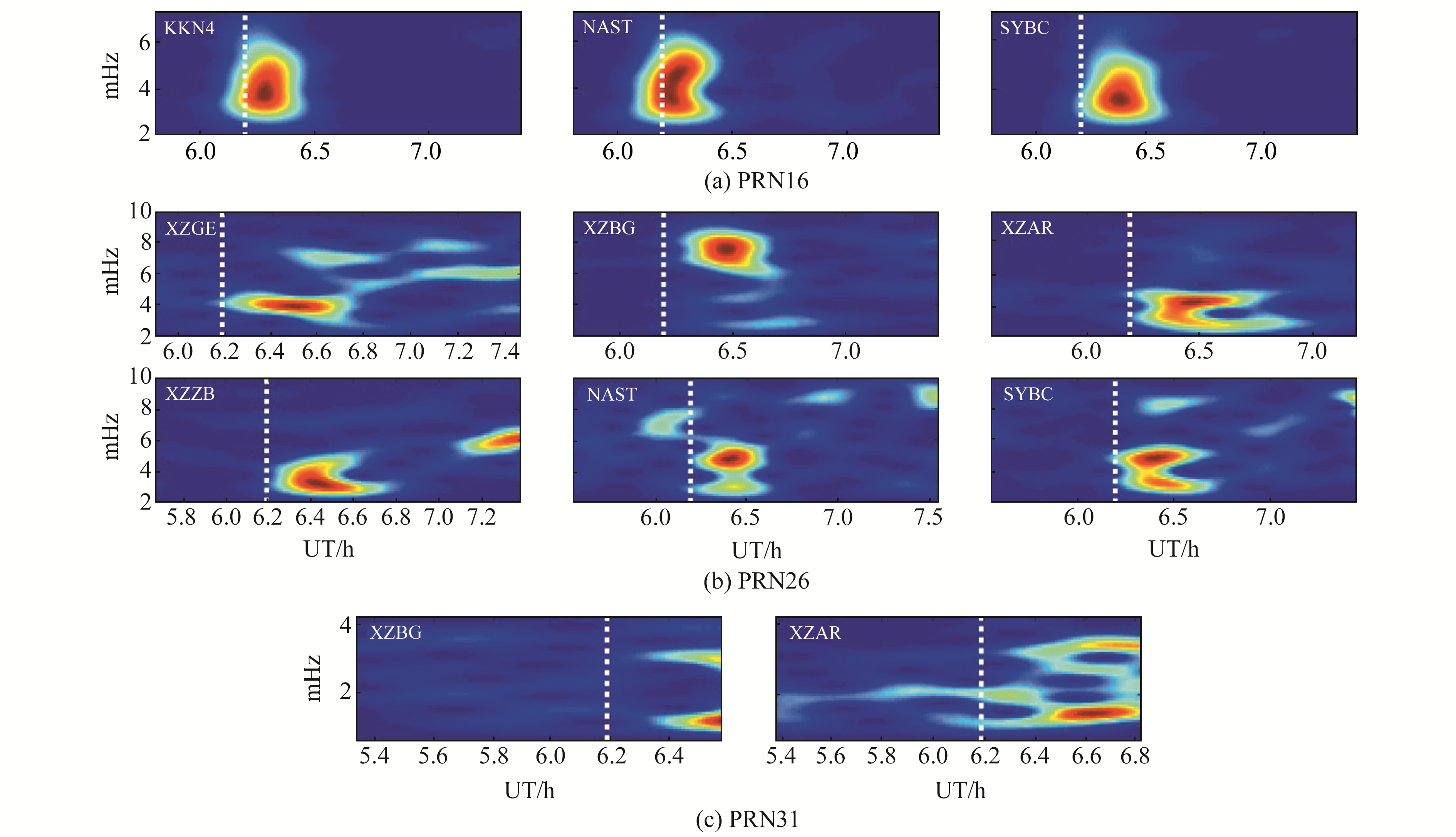
2.2 TEC扰动频谱分析从地震当天的TEC扰动时间序列中选取异常幅值较大的CID序列进行时频分析,在频率域内研究扰动异常。选取卫星PRN16中NAST、KKN4、SYBC测站,卫星PRN26中XZGE、XZBG、XZAR、XZZB、NAST和SYBC测站以及卫星PRN31中XZBG、XZAR测站的扰动序列,采用长度为60 min、重叠度为59 min的Hamming窗口进行短时傅里叶变换[4, 8-10],生成FFT频谱分布图(图 3,白色点线为地震发生时刻),图中亮度越大表示频率梯度越大,即变化越剧烈。
|
图 3 PRN16、PRN26与PRN31卫星观测的同震电离层扰动FFT频谱图 Fig. 3 FFT spectrograms of CID observed from PRN16, PRN26 and PRN31 |
PRN16卫星观测到的KKN4、NAST、SYBC三个测站的扰动频谱中深红色表示扰动中心频率,其中KKN4测站的中心频率为3.68~4.32 mHz,扰动异常出现于UT 06:14;NAST的中心频率为3.52~4.96 mHz,异常出现时刻为UT 06:11;SYBC的中心频率为3.44~3.85 mHz,对应时刻为UT 06:20。3个测站的频谱整齐,频谱峰值为两种扰动异常中心频率的混合值。
在PRN26卫星中除XZBG测站外均出现两组或多组异常频谱。XZGE测站在UT 06:29的异常中心频率为4.06 mHz,在UT 07:28的中心频率约为6.09 mHz;XZBG测站在UT 06:34的中心频率为7.66 mHz;XZAR测站在UT 06:28的中心频率为3.28~4.22 mHz;XZZB测站在UT 06:23时出现的扰动异常的中心频率为3.13~3.76 mHz,在UT 07:23的中心频率约为6.28 mHz;NAST测站中首次频率峰值为3.13 mHz和4.86 mHz,于UT 06:24同时出现,第2次峰值为8.75 mHz,对应时刻为UT 07:32;SYBC与NAST测站现象类似,在UT 06:25时出现的首次异常的中心频率分别为4.86 mHz和3.29 mHz,后者存在2 min延迟,第2次异常约为8.59 mHz,对应时刻为UT 07:27。
在PRN31卫星观测结果中,XZBG于UT 06:34同时出现3.28 mHz和7.34 mHz两处中心频率;XZAR测站自UT 06:35起存在持续时间大于6 min的中心频率3.75 mHz和占比较小的5.00 mHz、6.72 mHz及8.28 mHz共4处中心频率。
通过上述分析可知,峰值频率最小为3.13 mHz,最大值为9.06 mHz,基本处于3~7 mHz范围内,个别测站出现大于7 mHz但不超过10 mHz的中心频率。
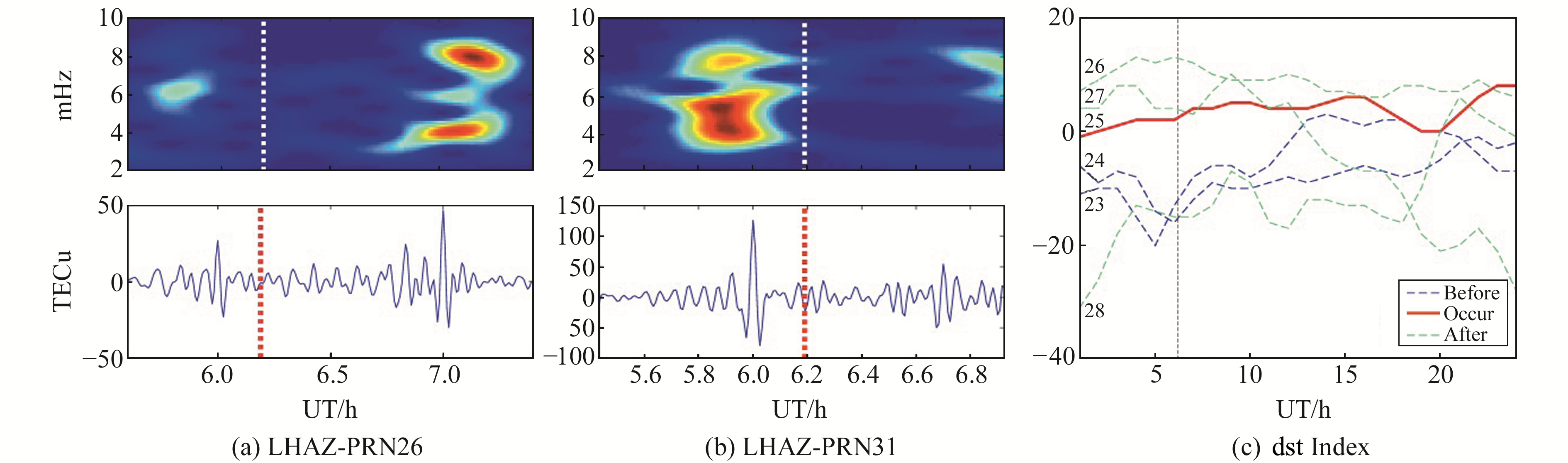
考虑到LHAZ测站为唯一位于中国境内的IGS测站,并且该测站在有限的时间序列内两个扰动异常峰值的时间间隔最长(不低于1 h),获得LHAZ测站在PRN26和PRN31观测下的扰动序列及对应的FFT频谱(图 4)。由图可知,PRN26卫星在震前UT 05:52的异常中心频率为6.25 mHz,震后UT 07:04起出现4.06 mHz、5.93 mHz和7.97 mHz的异常中心频率;PRN31卫星在震前UT 05:53~05:55出现的3处异常的中心频率分别为4.38 mHz、5.47 mHz和7.81 mHz,由于数据所限仅可得出震后06:56 UT的中心频率为7.66 mHz。根据地磁活动dst指数图像可知,震前2 d的dst指数均处于较低水平,基本为负值,最低值可达-20;地震当天dst指数出现攀升,数值大于0;震后1.5 d仍保持较高水平,并且出现最高峰值16;震后1.5~3 d逐渐回落到负值。LHAZ测站震中距为61.146 km,但在PRN26、PRN31卫星观测下均发现震前扰动。上述分析表明,地震当天该测站周边地区可能存在地磁活动等干扰因素。综合图 3、4可知,测站同震电离层扰动的中心频率值为3~7 mHz,符合震中附近探测到以声波与瑞利波相关波形式传播的3~7 mHz的扰动[5, 11],同时也存在更高频率(7~15 mHz)的干扰[5]。
|
点线为地震发生时刻;图(c)红色实线为地震当天,蓝色虚线为震前2d,绿色虚线为震后3d 图 4 测站LHAZ观测的电离层TEC扰动时频曲线及dst指数曲线 Fig. 4 Time series and spectrograms of ionospheric TEC of LHAZ station and dst index curves |
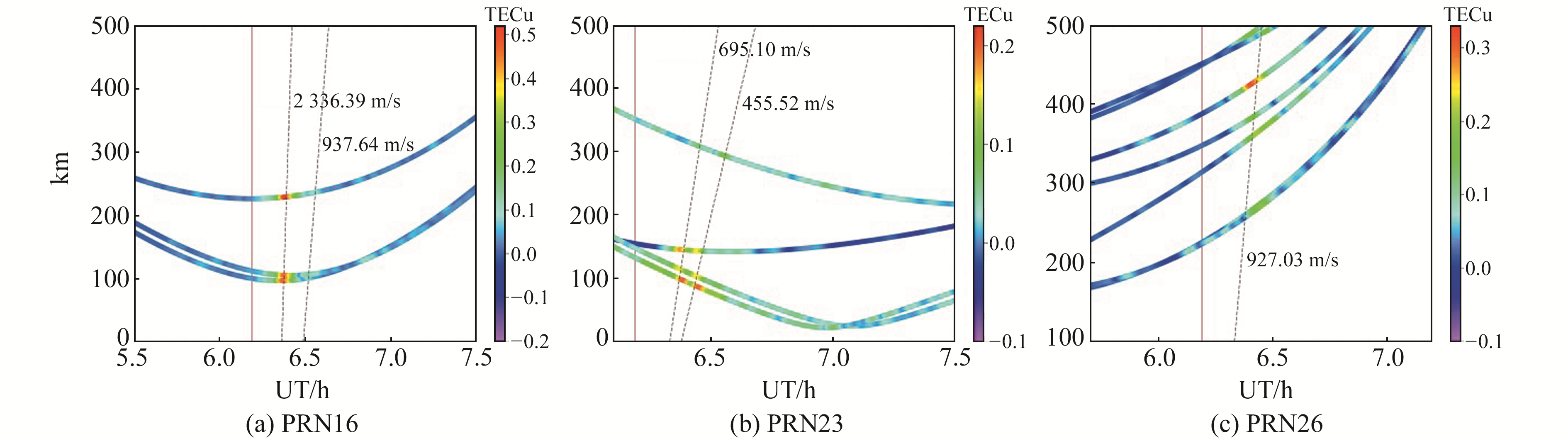
电离层扰动通常与震后引发的瑞利波(2~3 km/s)、声波(1 km/s)及飓风生成的重力波有关,并以每秒几百米到几千米的速率从震中沿各方向传播[12]。对震后前两次异常峰值所在位置利用异常出现的时间、距离进行线性拟合,拟合直线的斜率即为波传播的水平相速度[13],即近场扰动的传播速率。
首先对TEC值进行Hilbert变换以便于瞬时信号的提取与分析,公式为:
| $\begin{array}{l} \;\;\;\;\;\;\;\;\widehat {s\left( t \right)} = h\left( t \right)*\Delta {\rm{TEC}}\left( t \right) = \\ \mathop \smallint \limits_{ - \infty }^\infty \Delta {\rm{TEC}}\left( \tau \right)h\left( {t - \tau } \right){\rm{d}}\tau = \frac{1}{\pi }\mathop \smallint \limits_{ - \infty }^\infty \frac{{\Delta {\rm{TEC}}\left( \tau \right)}}{{t - \tau }}{\rm{d}}\tau \end{array}$ | (5) |
| $s\left( t \right) = 2\left| {\widehat {s\left( t \right)}} \right|$ | (6) |
式中,
|
图 5 卫星PRN16、PRN23与PRN26观测到近场扰动的时间-距离曲线 Fig. 5 Distance-time curves of near-field disturbance observed from satellite PRN16, PRN23 and PRN26 |
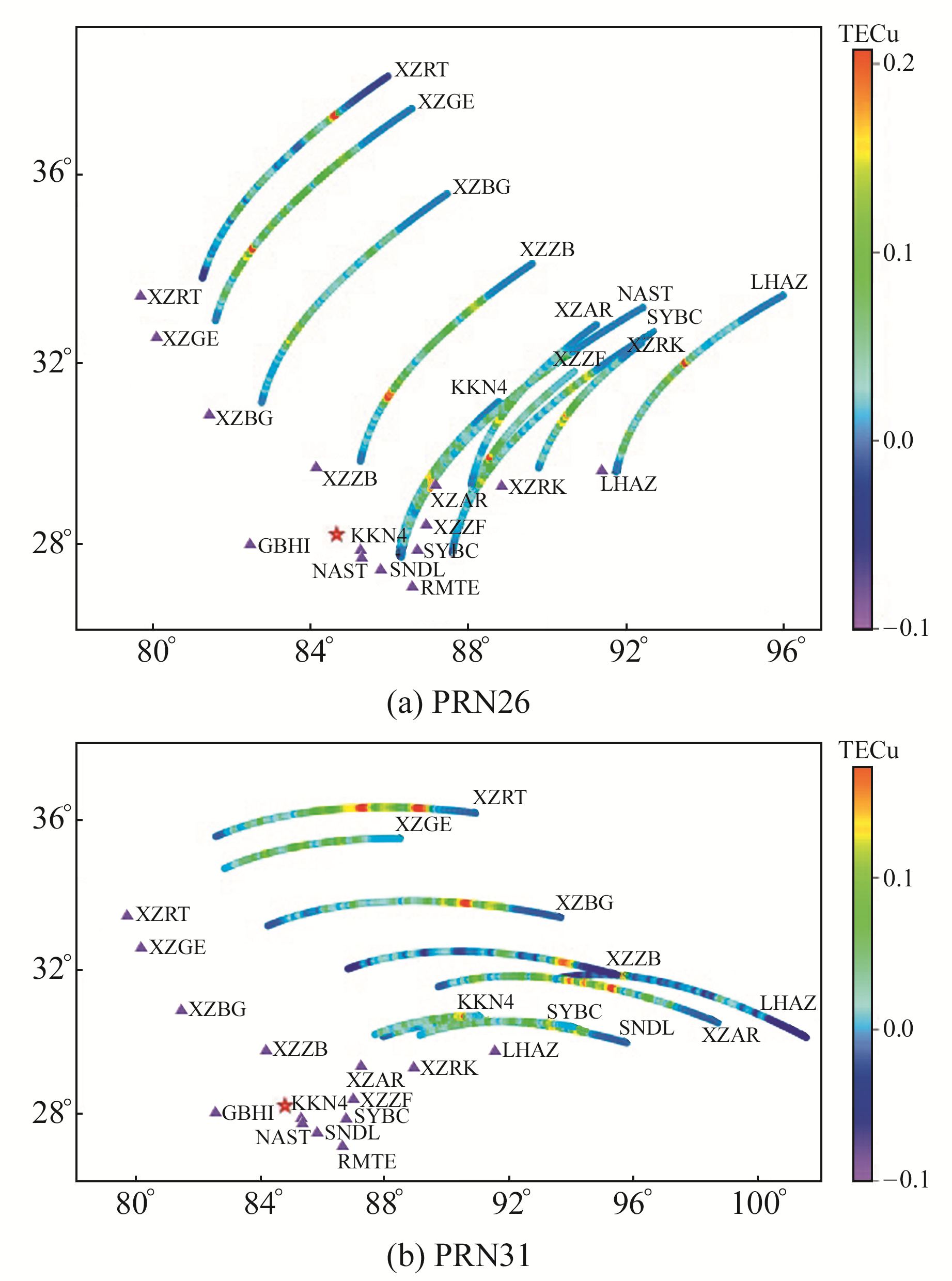
为分析电离层扰动的传播方向,图 6为穿刺点在经纬度坐标下的轨迹分布。由图可见,PRN26卫星的扰动沿西南向东北方向传播,PRN31的扰动向东及东南方向传播。测站XZZF序列中红色部分扰动异常最为突出,s(t)峰值可达0.312 TECu,其余测站序列出现异常时扰动水平约为0.1 TECu。PRN16、PRN23卫星的扰动序列轨迹方向为西、东南等方向。总体来看,各卫星观测的扰动由震中沿多个方向传播。
|
图 6 PRN26、PRN31的穿刺点轨迹分布 Fig. 6 IPP traces distribution of PRN26 and PRN31 |
本文基于GPS观测数据分析2015尼泊尔MW7.8地震引起的同震电离层扰动序列,探究CID的波动变化规律。结果表明,从发震时刻起5 min后陆续出现异常扰动,扰动时间序列整体呈现增大-减小-增大的趋势;TEC扰动的主要频率为3~7 mHz,个别测站为7~10 mHz,与瑞利波和声波的频段一致;震后电离层扰动的传播速率为2 336.36 m/s和455.52~937.64 m/s,推测为地震引发的瑞利波与声波波速;电离层扰动向东、东北、东南等不同方向传播。
致谢: 感谢中国地壳运动观测网络提供GPS观测数据以及加利福尼亚大学圣迭戈分校(UCSD)提供IGS测站数据。
| [1] |
Heki K, Ping J S. Directivity and Apparent Velocity of the Coseismic Ionospheric Disturbances Observed with a Dense GPS Array[J]. Earth and Planetary Science Letters, 2005, 236(3-4): 845-855 DOI:10.1016/j.epsl.2005.06.010
(  0) 0) |
| [2] |
Heki K, Otsuka Y, Choosakul N, et al. Detection of Ruptures of Andaman Fault Segments in the 2004 Great Sumatra Earthquake with Coseismic Ionospheric Disturbances[J]. Journal of Geophysical Research Solid Earth, 2006, 111(B9)
(  0) 0) |
| [3] |
Chen P, Yao Y B, Yao W Q. On the Coseismic Ionospheric Disturbances after the Nepal MW7.8 Earthquake on April 25, 2015 Using GNSS Observations[J]. Advances in Space Research, 2017, 59(1): 103-113 DOI:10.1016/j.asr.2016.09.021
(  0) 0) |
| [4] |
李哲, 唐龙, 张小红. 利用GPS TEC探测2015年尼泊尔地震激发的电离层扰动[J]. 大地测量与地球动力学, 2016, 36(9): 757-760 (Li Zhe, Tang Long, Zhang Xiaohong. Ionospheric Disturbances Triggered by 2015 Nepal Earthquake Detected by GPS TEC[J]. Journal of Geodesy and Geodynamics, 2016, 36(9): 757-760)
(  0) 0) |
| [5] |
Jin S G, Jin R, Li J H. Pattern and Evolution of Seismo-Ionospheric Disturbances Following the 2011 Tohoku Earthquakes from GPS Observations[J]. Journal of Geophysical Research Space Physics, 2014, 119(9): 7 914-7 927 DOI:10.1002/2014JA019825
(  0) 0) |
| [6] |
Liu J Y, Chen C H, Lin C H, et al. Ionospheric Disturbances Triggered by the 11 March 2011 M9.0 Tohoku Earthquake[J]. Journal of Geophysical Research Space Physics, 2011, 116(A6)
(  0) 0) |
| [7] |
万军. GNSS周跳探测与修复融合算法研究[D].北京: 中国测绘科学研究院, 2016 (Wan Jun. Research on Fusion Algorithm of Cycle Slip Detection and Correction for GNSS[D]. Beijing: Chinese Academy of Surveying and Mapping, 2016) http://cdmd.cnki.com.cn/Article/CDMD-86001-1016143255.htm
(  0) 0) |
| [8] |
Reddy C D, Sunil A S, González G, et al. Near-Field Co-Seismic Ionospheric Response due to the Northern Chile MW8.1 Pisagua Earthquake on April 1, 2014 from GPS Observations[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2015, 134: 1-8 DOI:10.1016/j.jastp.2015.09.006
(  0) 0) |
| [9] |
Dautermann T, Calais E, Mattioli G S. Global Positioning System Detection and Energy Estimation of the Ionospheric Wave Caused by the 13 July 2003 Explosion of the Soufrière Hills Volcano, Montserrat[J]. Journal of Geophysical Research Solid Earth, 2009, 114(B2)
(  0) 0) |
| [10] |
Dautermann T, Calais E, Lognonné P, et al. Lithosphere-Atmosphere-Ionosphere Coupling after the 2003 Explosive Eruption of the Soufriere Hills Volcano, Montserrat[J]. Geophysical Journal International, 2009, 179(3): 1 537-1 546 DOI:10.1111/j.1365-246X.2009.04390.x
(  0) 0) |
| [11] |
Matsumura M, Saito A, Lyemori T, et al. Numerical Simulations of Atmospheric Waves Excited by 2011 off the Pacific Coast of Tohoku Earthquake[J]. Earth, Planets and Space, 2011, 63(7): 885-889 DOI:10.5047/eps.2011.07.015
(  0) 0) |
| [12] |
Heki K, Otsuka Y, Choosakul N, et al. Detection of Ruptures of Andaman Fault Segments in the 2004 Great Sumatra Earthquake with Coseismic Ionospheric Disturbances[J]. Journal of Geophysical Research Solid Earth, 2006, 111(B9)
(  0) 0) |
| [13] |
Bowling T, Calais E, Haase J S. Detection and Modelling of the Ionospheric Perturbation Caused by a Space Shuttle Launch Using a Network of Ground-Based Global Positioning System Stations[J]. Geophysical Journal International, 2013, 192(3): 1 324-1 331 DOI:10.1093/gji/ggs101
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


