2. 华南师范大学地理科学学院,广州市中山大道西55号,510631;
3. 广东省智慧国土工程技术研究中心,广州市中山大道西55号,510631
随着全球卫星导航定位技术的发展及连续运行参考站的广泛应用,使获得高精度的基于WGS84参考椭球的大地高成为可能,但我国目前使用的高程系统仍是正常高系统。为了将大地高进行正常高的高精度转换,以获得高精度、高分辨率的区域似大地水准面,许多学者提出了不同的大地水准面精化模型[1-4]。其中,应用最广泛的转换模型为移去-恢复模型,该方法可在缺少重力资料、地形资料等情况下得到较高精度的正常高,方便快捷。为了探讨几种常用的移去-恢复模型在不同地形条件下的适用性和选取问题,本文构建了二次曲面-RBF、二次曲面-多面函数、二次曲面-Shepard、EGM2008-RBF、EGM2008-多面函数和EGM2008-Shepard等6种移去-恢复模型,并结合平原地区和高原山区两个工程实例进行大地水准面拟合与精度对比分析。
1 单一高程转换模型 1.1 二次曲面拟合法二次曲面拟合法是一种局部逼近法,根据区域内已知的GNSS水准联测点建立高程异常拟合曲面,再内插出其他点位的高程异常值。其函数模型为:
| $ {\xi _{{i}}}{\rm{ = }}{\alpha _0} + {\alpha _1}{x_i} + {\alpha _2}{y_i} + {\alpha _3}x_i^2 + {\alpha _4}y_i^2 + {\alpha _5}{x_i}{y_i} $ | (1) |
式中,(xi, yi)为点的平面坐标,ξi为高程异常值,α0、α1、…、α5为二次曲面拟合模型待定系数。求解待定系数时,只需选择6个以上均匀分布的GNSS水准联测点,通过最小二乘平差即可计算出结果。
1.2 RBF神经网络拟合RBF神经网络是由输入层、隐含层和输出层构成的3层前馈反向传播网络,可以逼近任意非线性函数。输入层至隐含层为直接连接,隐含层至输出层为权连接,隐含层中的激励函数是径向基函数,是对中心点径向对称且衰减的非负非线性函数[4]。RBF神经网络结构如图 1所示,在GNSS高程转换过程中,RBF神经网络的输入层数据为点的平面坐标(xi, yi),输出层为高程异常ξi。
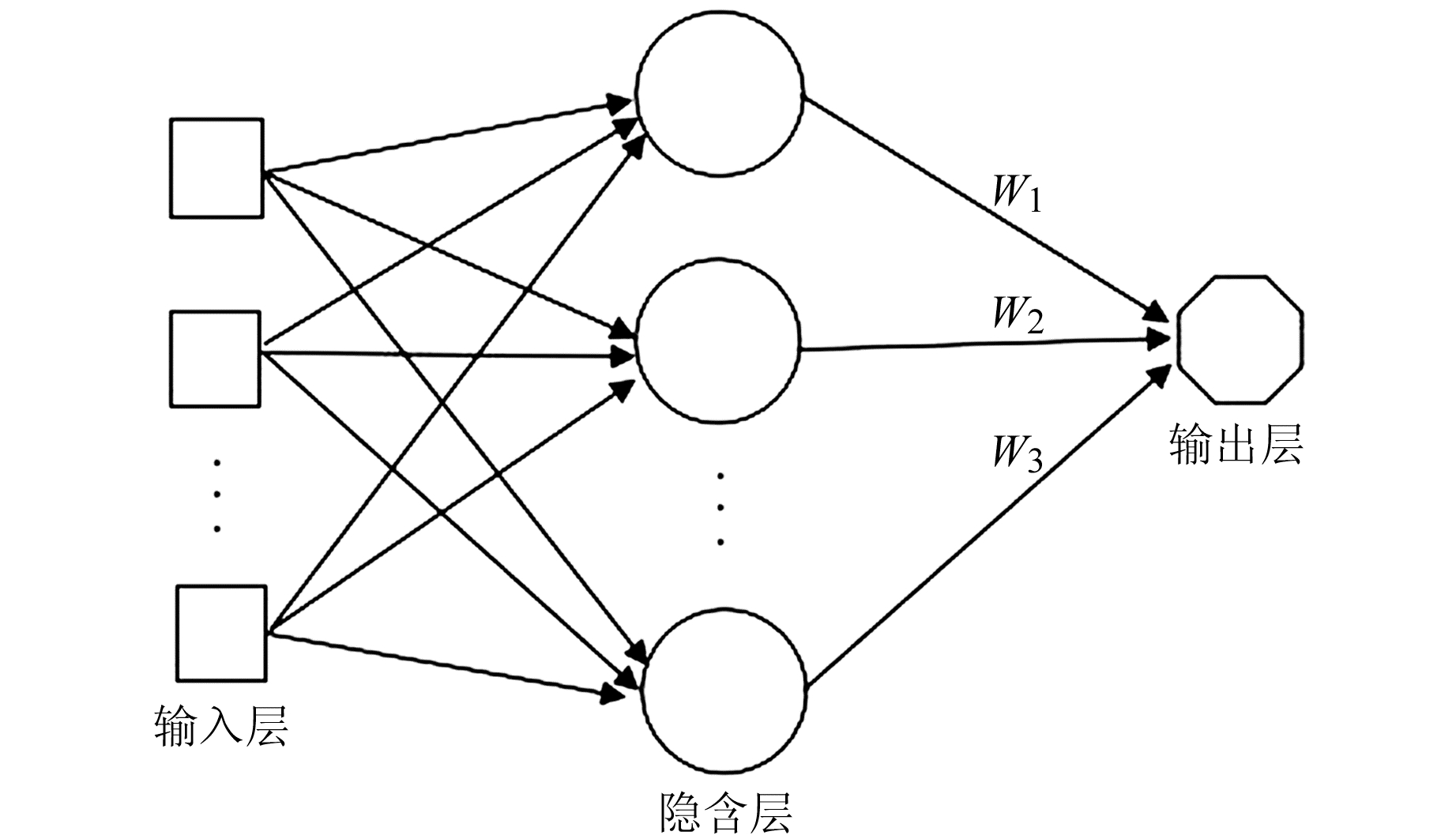
|
图 1 RBF神经网络结构 Fig. 1 The structure of RBF neural network |
多面函数拟合法由Hardy于1977年首先提出,其主要思想为:任何数学表面和不规则圆滑表面总可用一系列规则的数学表面总和以任意精度逼近[5]。其基本模型为:
| $ \xi \left( {x, y} \right){\rm{ = }}\sum\limits_{j = 1}^n {{\alpha _j}Q\left( {x, y, {x_j}, {y_j}} \right)} $ | (2) |
式中,αj为待定系数,n为节点数,(xj, yj)为中心点,Q(x, y, xj, yj)为关于平面坐标x和y的核函数(本文取正双曲面函数作为核函数)。
如果有n个GNSS水准点,将其全部作为核函数的中心点,可列误差方程为:V=QA-ξ。根据最小二乘原理求得待定系数矩阵A=(QTQ)-1QTξ,最后将系数矩阵代入式(2),便可求出任意一点的高程异常。
1.4 Shepard曲面拟合法Shepard曲面拟合法是一种改进的加权平均法[6]。如果有n个GNSS水准联测点,(xj, yj)为其平面坐标,ξi为高程异常值,则待求点高程异常的求解公式为:
| $ \xi \left( {x, y} \right) = \left\{ \begin{array}{l} \frac{{\sum\limits_{i = 1}^n {{\xi _i}{{\left( {\rho \left( {{r_i}} \right)} \right)}^u}} }}{{\sum\limits_{i = 1}^n {{{\left( {\rho ({r_i})} \right)}^u}} }}, {r_i} \ne 0\\ {\xi _i}, {r_i} = 0 \end{array} \right. $ | (3) |
式中,u为拟合度,取大于1的常数;ri为待求点至各已知点的距离,ρ(ri)为各点关于距离的权函数,并将拟合点的影响区域设为一个以R为半径的圆形区域。
1.5 EGM2008重力模型法EGM2008地球重力场模型是由美国国家地理空间情报局利用先进的建模技术与算法,以PGM2007B为参考,结合卫星重力数据、测高数据、地形数据等得到的全球超高阶地球重力场模型[7-9]。该模型可提供2 159次、2 190阶的球谐系数,基本空间分辨率为5′×5′,最高分辨率为1′×1′。模型高程异常计算公式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;{\xi _{{\rm{GM}}}}(\rho , \psi , \lambda ) = \frac{{{\rm{GM}}}}{{\rho r}}\sum\limits_{n = 2}^N {(\frac{a}{\rho }} {)^n} \cdot \\ \sum\limits_{m = 0}^n {({{\overline C }_{n, m}}\cos m\lambda + {{\overline S }_{n, m}}\sin m\lambda )} \cdot ({\overline P _{n, m}}(\sin \psi )) \end{array} $ | (4) |
式中,ρ为计算点地心向径,ψ、λ分别为余纬和经度,GM为地心引力常数,a为椭球长半径,Cn, m和Sn, m为完全规格化位系数,r为计算点的正常重力值,Pn, m(sinψ)为完全规格化缔合函数。
2 移去-恢复模型根据物理大地测量学理论,高程异常ξ包含3个分量[10],其公式为:
| $ {\xi _{}}{\rm{ = }}{\xi _{{\rm{长}}}}{\rm{ + }}{\xi _{{\rm{中}}}}{\rm{ + }}{\xi _{{\rm{短}}}} $ | (5) |
式中,ξ长、ξ中、ξ短分别为长波、中波、短波分量。在高程异常值中,中长波分量(中波分量和长波分量之和)变化较小,趋势较为平缓;短波分量则受局部地形起伏影响较大。
移去-恢复算法的主要思想为:首先将高程异常中的中长波分量移除,然后对剩余值进行拟合并通过插值计算出待求点上的数值,最后再在待定点上恢复中长波分量[11]。
如果有N个GNSS水准联测点,则移去-恢复模型的具体操作步骤为:
1)移去:首先求出N个点的高程异常值,并用数学模型或重力场模型计算出这些点上的中长波分量,然后求出高程异常值与中长波分量的差值。
2)拟合:以这N个点的平面坐标、高程异常与中长波分量的差值为起始数据,构建数学拟合模型,进而计算出待求点的高程异常值与中长波分量的差值。
3)恢复:利用步骤1)中的数学模型或重力场模型计算出待求点的中长波分量,再加上步骤2)中该点高程异常与中长波分量的差值,便可得到待求点的高程异常值。
3 实验分析 3.1 工程概况实例1 大地水准面精化项目区位于哈尔滨市,地势较为平坦,属于平原地区,测区面积约1 100 km2。项目以GPS连续观测站及高精度GPS网为基础,利用GPS技术和水准测量技术,建立集GPS和水准测量于一体的74个GPS C级网点和二等水准网点[12]。其中,最低点高程为116.026 m,最高点高程为200.321 m。本文采用这74个点的数据进行GPS水准高程拟合研究,点位分布见图 2。
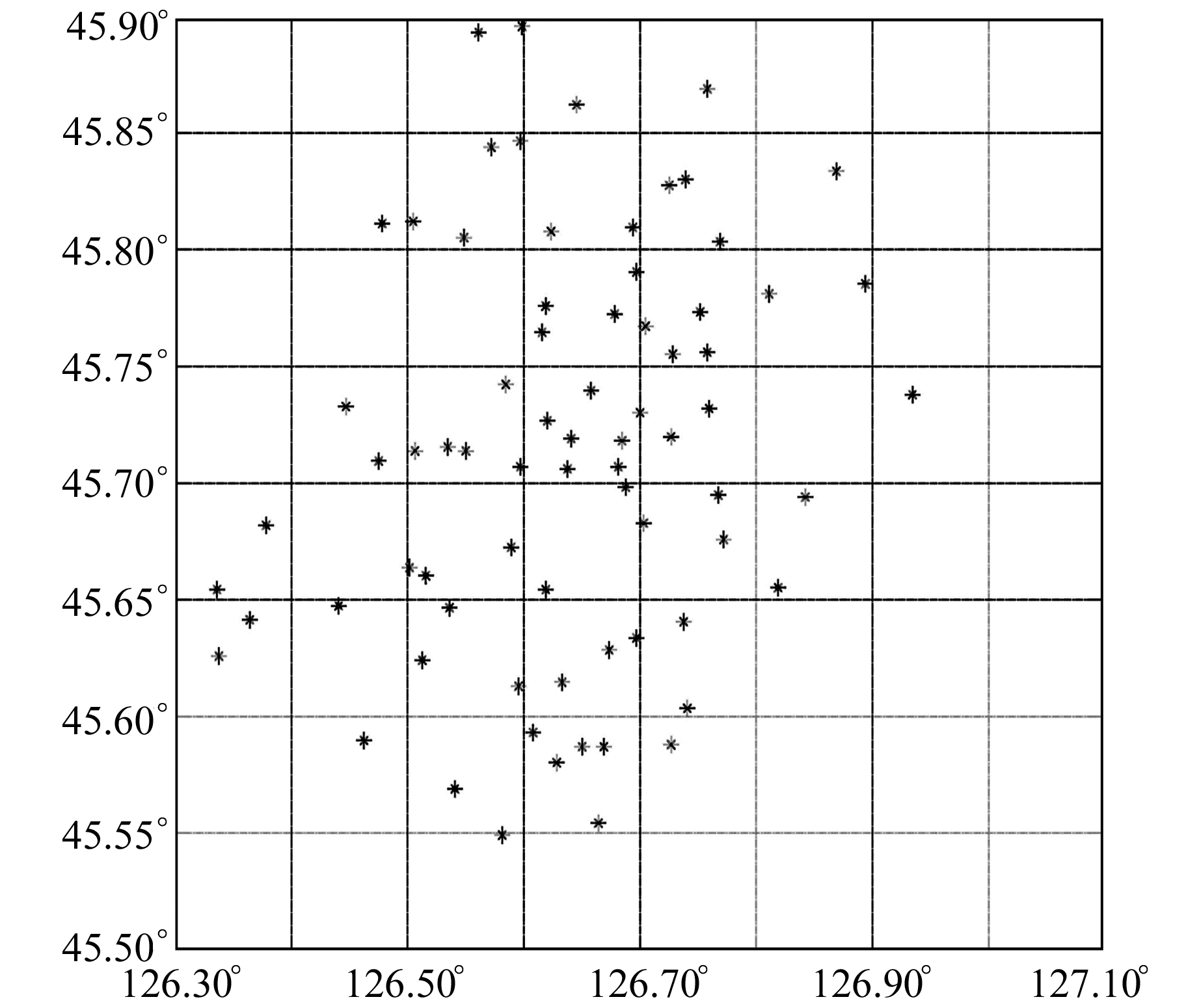
|
图 2 平原地区点位分布 Fig. 2 Distribution of points in plains |
实例2 项目区位于云南省,地形起伏较大,属于典型的高原山区地形,测区总面积约为300 km2。区内共布设25个三等GPS控制点,其中有10个控制点为二等水准点,其余各点均进行了四等水准测量[13]。最低点高程为1 924.033 m,最高点高程为2 589.462 m,点位分布见图 3。
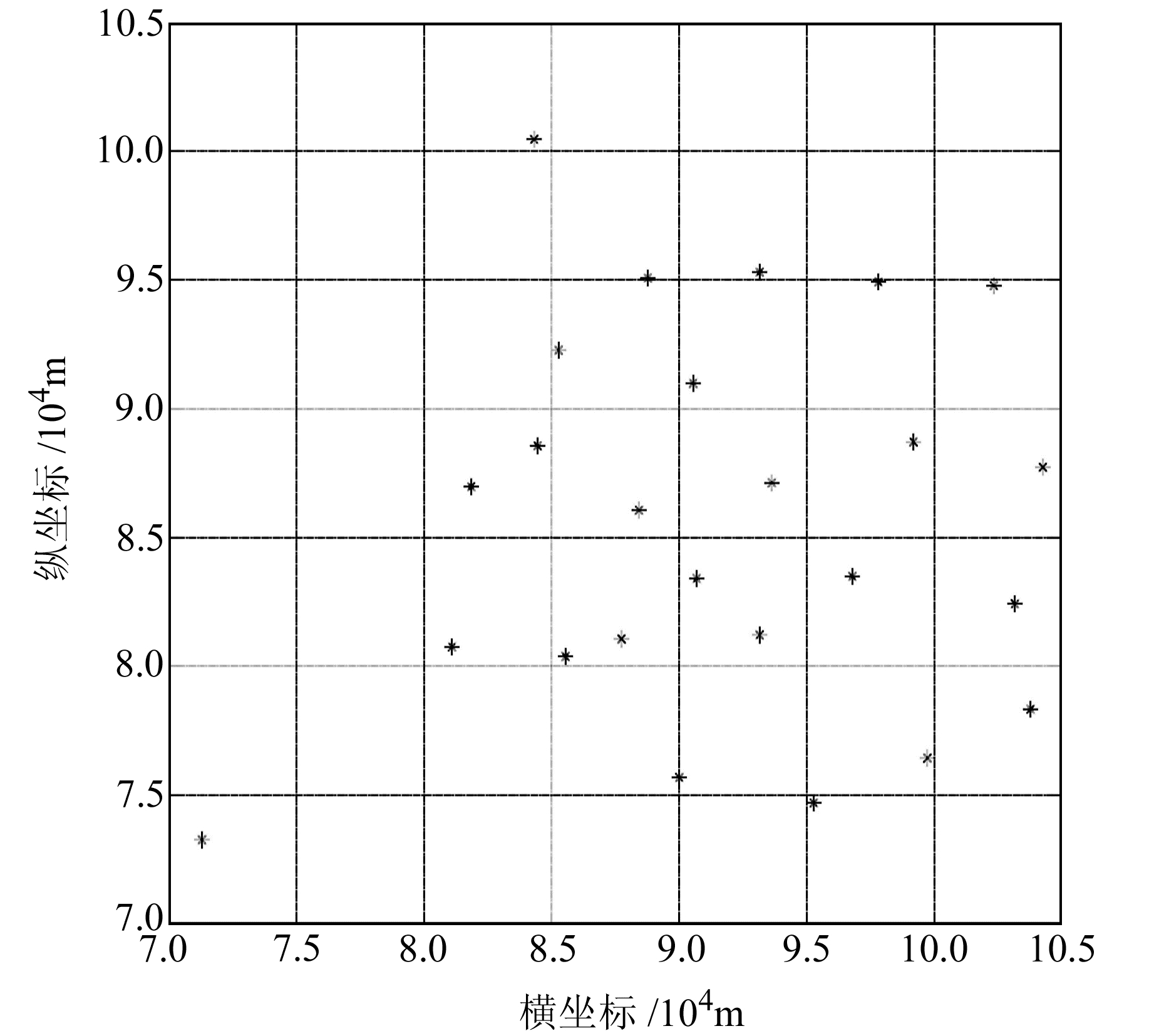
|
图 3 高原山区点位分布 Fig. 3 Distribution of points in plateau mountainous areas |
本文采用检测点的外符合精度作为模型的评定指标,即
| $ \delta {\rm{ = }} \pm \sqrt {\left[ {\mathit{\Delta \Delta }} \right]/(n - 1)} $ | (6) |
式中,n为检测点个数,Δ为检测点的高程异常拟合值与已知值之差。
3.3 参数选取利用RBF神经网络、多面函数和Shepard曲面拟合建模时,为获得较好的泛化效果,需确定模型的参数。RBF神经网络的参数为网络扩展常数Spread,多面函数的参数为平滑因子k,Shepard曲面拟合的参数为拟合度u和拟合半径R。本文在确定参数时先给定参数范围,再在该范围中寻找使检测样本误差最小的值作为建模参数。为防止获得的参数为局部最优,要结合经验将参数范围尽量设大,搜索步长尽量设小,同时通过循环操作使寻优过程遍历每一个节点。在实验中,spread的范围设定为[0.000 01, 3],搜索步长为0.005;k的范围设定为[0.001, 400],搜索步长为0.005;u和R的范围分别为[1, 50]和[0.1, 20],搜索步长分别为1和0.02。
3.4 实验对比分析为避免单次实验结果的偶然性,使实验结果更加可靠,本文在实例1中分别选取7、9、13、17、21、25、39、51个均匀分布的联合点作为拟合点,在实例2中分别选取7、9、11、13、16、19个均匀分布的点作为拟合点,剩余点作为实验的检测点。同时,为获得高精度的计算结果,在实验前对数据进行归一化处理。
本文分别采用二次曲面-RBF、二次曲面-多面函数、二次曲面-Shepard、EGM2008-RBF、EGM2008-多面函数和EGM2008-Shepard等6种移去-恢复模型进行似大地水准面精化实验。
由表 1(单位m)可知,在平原地区,当拟合点数为7和9时,EGM2008-多面函数和EGM2008-RBF模型外符合精度均为0.029 m和0.025 m,优于其他模型;当拟合点数增至13、17和21时,EGM2008-多面函数、二次曲面-RBF和二次曲面-多面函数模型的外符合精度数值一致,略优于其他模型;当拟合点数增加至25、39、51时,6种模型的外符合精度基本相同。可以看出,随着拟合点数的增加,EGM2008-多面函数模型的外符合精度始终优于或等于其他模型。图 4为各模型在不同拟合点数情况下的外符合精度平均值,EGM2008-多面函数模型的精度平均值为0.022 m,优于其他模型。由此可见,在平原地区的似大地水准面精化实验中,相比其他5种模型,EGM2008-多面函数模型的高程转换精度较高,可靠性较强。
|
|
表 1 平原地区移去-恢复模型计算结果对比 Tab. 1 The comparison of calculation results of remove-restore models in plains |
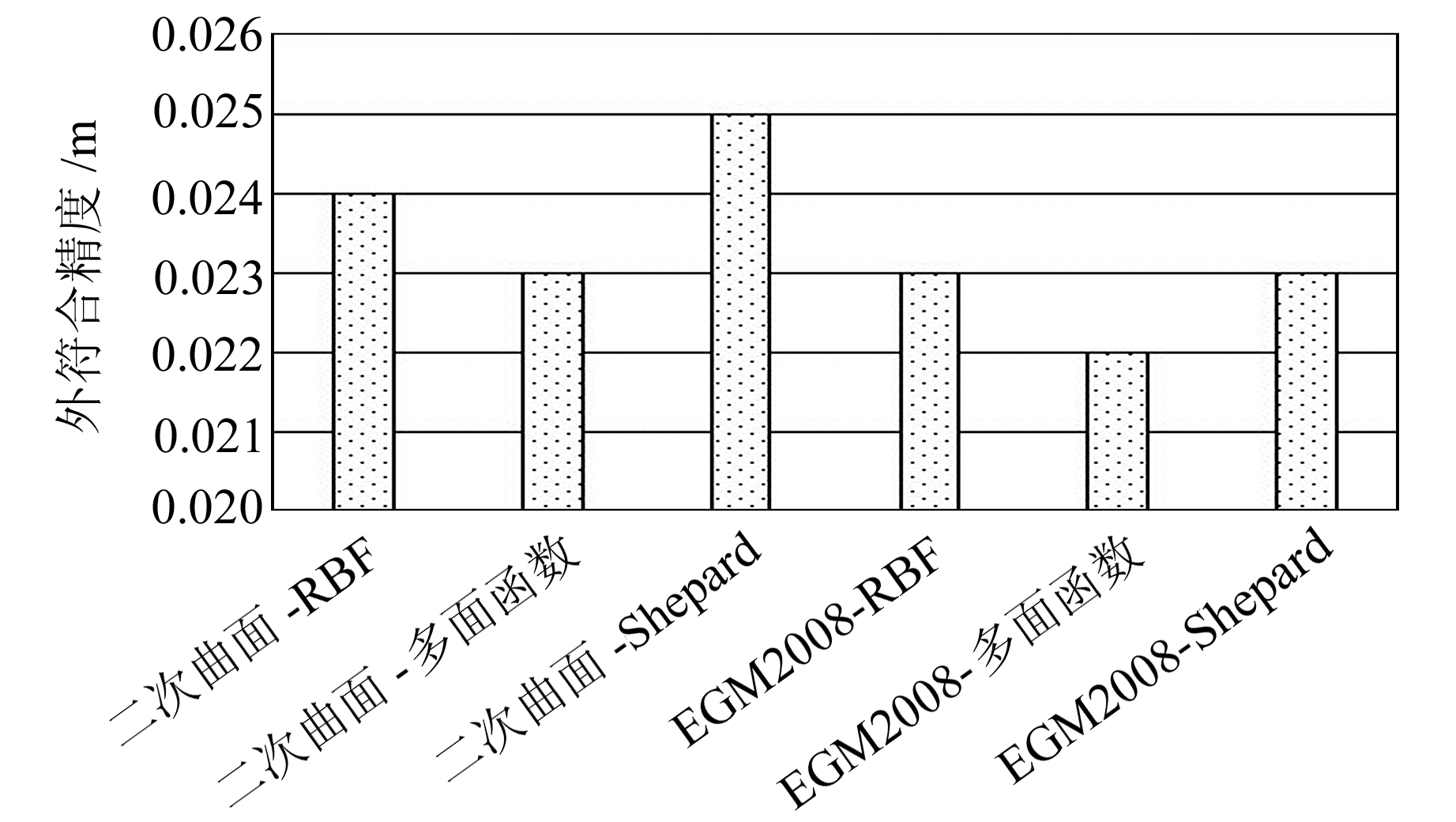
|
图 4 平原地区各模型外符合精度均值 Fig. 4 The mean value of outer precision of each model in plains |
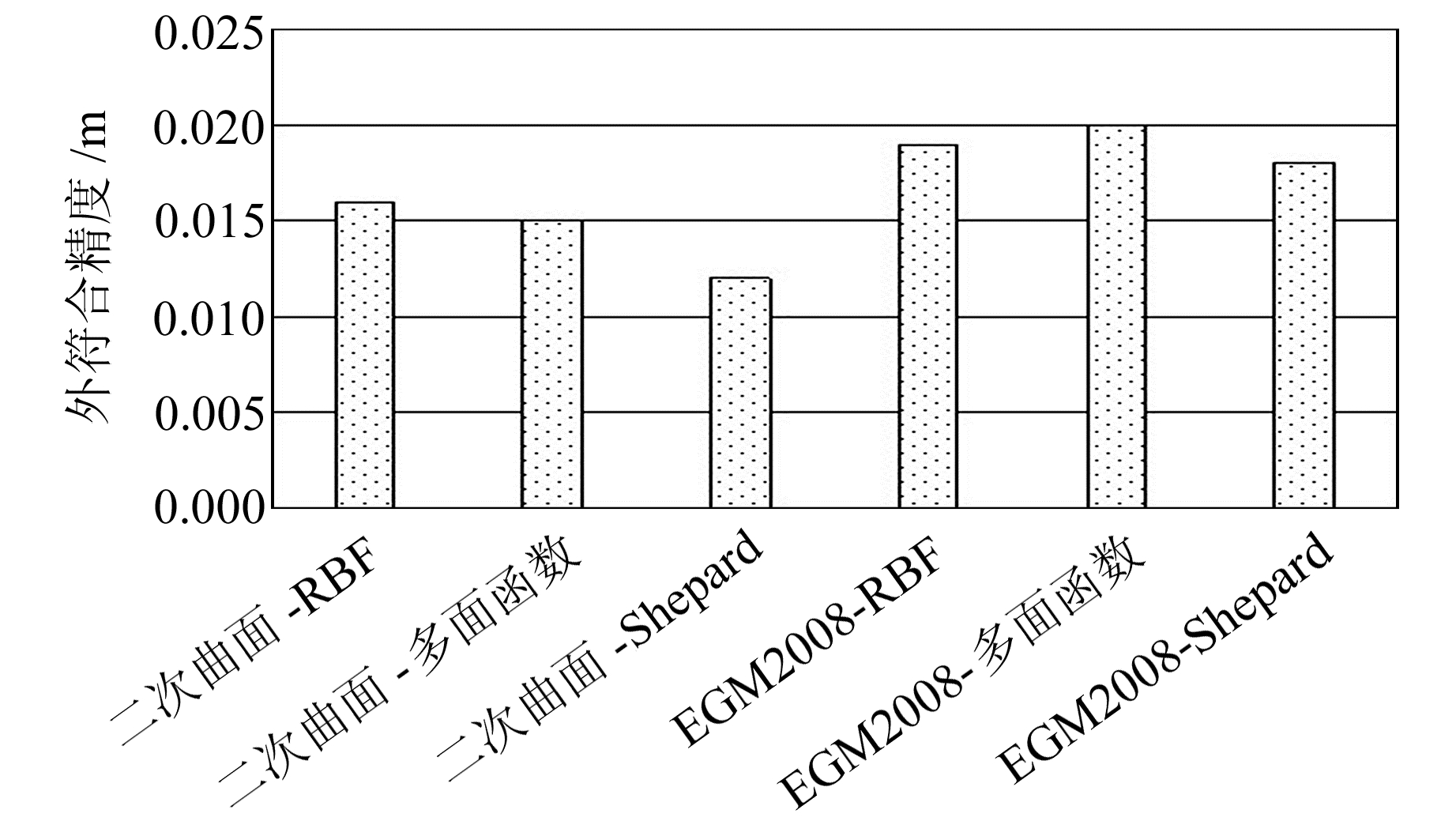
由表 2(单位m)可知,在高原山区,当拟合点数为7时,EGM2008-多面函数和EGM2008-Shepard模型的外符合精度均为0.031 m,小于其他4种模型,精度最优;当拟合点数为9、11、13、16和19时,二次曲面-Shepard模型的外符合精度分别为0.015 m、0.013 m、0.013 m、0.013 m和0.004 m,小于其他5种模型的对应数值。图 5为各模型在拟合点数为9、11、13、16和19时的外符合精度平均值,可以看出,二次曲面-Shepard模型的精度平均值为0.012 m,低于其他5种模型。由此可见,在高原山区的似大地水准面精化实验中,当拟合点数较少时,EGM2008-多面函数和EGM2008-Shepard模型的转换结果较好;随着拟合点数目的增加,二次曲面-Shepard模型具有较高的转换精度和较强的可靠性。
|
|
表 2 高原山区移去-恢复模型计算结果对比 Tab. 2 The comparison of calculation results of remove-restore models in in plateau mountainous areas |
|
图 5 高原山区各模型部分外符合精度均值 Fig. 5 The mean value of outer precision of each model in plateau mountainous areas |
另外,在平原地区,当拟合点数从7增加至51时,二次曲面-RBF、二次曲面-多面函数、二次曲面-Shepard、EGM2008-RBF、EGM2008-多面函数和EGM2008-Shepard模型的外符合精度分别从0.038 m、0.038 m、0.036 m、0.029 m、0.029 m和0.030 m逐步提高至0.015 m、0.014 m、0.014 m、0.014 m、0.013 m和0.012 m;在高原山区,当拟合点数从7增加至19时,6种模型的外符合精度分别从0.056 m、0.034 m、0.050 m、0.035 m、0.031 m和0.031 m逐渐提高至0.013 m、0.011 m、0.004 m、0.008 m、0.011 m和0.009 m。随着拟合点数的增加,部分模型由于拟合点位的选择、地形等因素,外符合精度局部出现小幅度增加,但6种模型自身的整体转换精度是逐渐提高的。
4 结语本文构建了二次曲面-RBF、二次曲面-多面函数、二次曲面-Shepard、EGM2008-RBF、EGM2008-多面函数和EGM2008-Shepard等6种移去-恢复模型,并结合平原地区和高原山区两个工程实例进行似大地水面精化实验,得出以下结论:
1)当拟合点数较少时,无论在平原地区还是高原山区,基于EGM2008的移去-恢复模型转换精度略优于基于二次曲面的移去-恢复模型。
2)随着拟合点数的增加,各个移去-恢复模型的整体转换精度逐渐增高。
3)在平原地区,EGM2008-多面函数模型的高程转换精度略优于其他5种模型;在高原山区,当拟合点数较少时,EGM2008-多面函数和EGM2008-Shepard模型的转换精度较高,而当拟合点数较多时,二次曲面-Shepard模型的高程转换精度优于其他5种模型。
| [1] |
蒲伦, 唐诗华, 刘银涛, 等. 利用蚁群遗传算法改进高程异常拟合模型[J]. 测绘科学, 2019, 44(7): 46-52 (Pu Lun, Tang Shihua, Liu Yintao, et al. Improved Elevation Anomaly Fitting Model Based on Ant Colony Genetic Algorithm[J]. Science of Surveying and Mapping, 2019, 44(7): 46-52)
(  0) 0) |
| [2] |
杨帆, 于奇. 遗传小波神经网络的GPS高程拟合模型[J]. 导航定位学报, 2017, 5(2): 131-134 (Yang Fan, Yu Qi. GPS Elevation Fitting Based on Genetic Wavelet Neural Network Model[J]. Journal of Navigation and Positioning, 2017, 5(2): 131-134)
(  0) 0) |
| [3] |
刘斌, 郭际明, 史俊波, 等. 利用EGM2008模型与地形改正进行GPS高程拟合[J]. 武汉大学学报:信息科学版, 2016, 41(4): 554-558 (Liu Bin, Guo Jiming, Shi Junbo, et al. A GPS Height Fitting Method Based on the EGM2008 Model and Terrain Correction[J]. Geomatics and Information Science of Wuhan University, 2016, 41(4): 554-558)
(  0) 0) |
| [4] |
郭辉. 组合模型的GPS高程转换及精度分析[J]. 测绘科学, 2018, 43(2): 34-38 (Guo Hui. Transformation of GPS Height and Accuracy Analysis Based on Combination Model[J]. Science of Surveying and Mapping, 2018, 43(2): 34-38)
(  0) 0) |
| [5] |
田晓, 郑洪艳, 许明元, 等. 一种改进的适用于不同地形的GPS高程拟合模型[J]. 测绘通报, 2017(1): 35-38 (Tian Xiao, Zheng Hongyan, Xu Mingyuan, et al. An Improved GPS Elevation Fitting Model for Different Terrain[J]. Bulletin of Surveying and Mapping, 2017(1): 35-38)
(  0) 0) |
| [6] |
钟波, 罗志才. GPS水准综合模型的应用研究[J]. 测绘通报, 2007(6): 5-7 (Zhong Bo, Luo Zhicai. Research on Application of Combined Model for GPS Leveling[J]. Bulletin of Surveying and Mapping, 2007(6): 5-7)
(  0) 0) |
| [7] |
马艳鸽, 郭春喜, 张盼盼. 组合重力场模型的精度及其适用性分析[J]. 测绘工程, 2018, 27(7): 18-23 (Ma Yange, Guo Chunxi, Zhang Panpan. Analysis of the Accuracy and Applicability of Combined Gravity Field Model[J]. Engineering of Surveying and Mapping, 2018, 27(7): 18-23)
(  0) 0) |
| [8] |
康靖玉.综合EGM2008、剩余地势模型及地面重力数据的大地水准面精化[D].长春: 吉林大学, 2017 (Kang Jingyu. Geoid Refinement Based on EGM2008, Residual Terrain Model and Ground Gravity Data[D]. Changchun: Jilin University, 2017) http://cdmd.cnki.com.cn/Article/CDMD-10183-1017148791.htm
(  0) 0) |
| [9] |
Agren J. Evaluation of EGM2008 and PGM2007A over Sweden[J]. Newton's Bulletin, 2009(4): 99-109
(  0) 0) |
| [10] |
董书晓, 甘淑. 不同地形条件下多种GPS高程拟合模型的适应性研究[J]. 大地测量与地球动力学, 2014, 34(6): 126-130 (Dong Shuxiao, Gan Shu. Study on Adaptability of GPS Elevation Fitting Models Under Different Terrains[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 126-130)
(  0) 0) |
| [11] |
罗陶荣, 王中元, 梁宁, 等. 利用EGM2008模型与加权组合模型进行高程异常拟合[J]. 测绘通报, 2018(1): 28-32 (Luo Taorong, Wang Zhongyuan, Liang Ning, et al. Height Anomaly Fitting Based on EGM2008 Model and Weighted Composite Model[J]. Bulletin of Surveying and Mapping, 2018(1): 28-32)
(  0) 0) |
| [12] |
朱君俊.基于重力场模型EGM 2008的高程拟合方法研究[D].呼和浩特: 内蒙古农业大学, 2012 (Zhu Junjun.Study on Elevation Fitting Method Based on EGM2008 Model[D].Hohhot: Inner Mongolia Agricultural University, 2012) http://d.wanfangdata.com.cn/thesis/D340300
(  0) 0) |
| [13] |
董书晓.局部大地水准面精化组合模型对比研究[D].昆明: 昆明理工大学, 2014 (Dong Shuxiao.Comparative Study on the Combination Model of Local Geoid Surface Refinement[D].Kunming: Kunming University of Science and Technology, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10674-1014353079.htm
(  0) 0) |
2. School of Geography, South China Normal University, 55 West-Zhongshan Road, Guangzhou 510631, China;
3. Guangdong Provincial Center for Smart Land Research, 55 West-Zhongshan Road, Guangzhou 510631, China
 2020, Vol. 40
2020, Vol. 40

