青藏高原是中国大陆现今构造运动和地震活动最为强烈的区域之一,对其重力变化的监测有助于了解现代高原隆起、深部物质迁移以及地震的孕育和发生过程。
国内学者在利用地面重复重力观测资料监测地震孕育和发生过程方面取得了较大进展[1-4]。不过,地面重力测量获得的重力变化信号包含了多种地球物理场过程的综合响应,如地表流体质量再分布和深部物质迁移等。青藏高原包括构造运动、地震活动和地表流体质量变化等在内的地球物理场特征异常复杂,其中,地表流体的质量再分布可对地面重力的观测结果造成显著影响。因此,系统性地分析地表流体的重力效应不仅有利于对青藏高原地区绝对重力控制网和流动重力观测网数据的精细化处理,也有利于对该地区地震孕育和发生过程的深入分析与解释[4-5]。
地表流体质量变化引起的重力效应可分为:1)地表流体质量的直接效应;2)地表流体质量负荷作用下的地球形变以及由此导致的地球内部质量再分布引起的附加引力位变化,也就是间接效应。传统上,可利用地表流体质量变化与负荷格林函数的全球褶积计算分析重力效应[6-7]。而随着空间观测技术的发展,数值模式、再分析资料以及全球时变重力场模型逐渐累积和完善,为进一步分析地表流体质量变化的重力效应提供了丰富的基础数据。本文利用近区地形优化的负荷格林函数和时变重力场反演方法系统分析青藏高原地区大尺度地表流体的的重力效应特征,为该区域重力场的时空演化特征分析提供参考。
1 数据与数据处理方法 1.1 模式与再分析资料及数据处理土壤水和积雪模式数据由GSFC/NCEP全球陆面过程同化系统GLDAS Noah、Mosaic和CLM驱动生成,时间分辨率为1个月,空间分辨率为0.25°×0.25°。三维大气再分析数据(包括从地面开始到1 hPa的37个等压层的高程、位势高度、比湿、大气压、气温等)由ECMWF Interim提供,时间分辨率为1个月,水平空间分辨率为0.125°×0.125°。以上两类数据的时间跨度均为2002~2017年。另外,考虑到青藏高原远离海洋区域,本文忽略了海洋非潮汐变化的重力效应影响。
根据Farrell[6]的地球表面负荷函数理论,地表流体对观测点重力负荷影响可用流体质量和负荷格林函数的褶积积分计算求得:
| $ L({\theta _0}, {\lambda _0}, t) = \iint\limits_s {\rho (\theta , \lambda , t)h(\theta , \lambda , t)G(\psi )}{\rm{d}}s $ | (1) |
式中,θ0与λ0分别为观测点的纬度和经度;ρ为积分面元的流体密度;h为积分面元的高程;ψ为观测点到积分面元的角距;G(ψ)为重力负荷格林函数,可表示为:
| $ \begin{array}{l} G(\psi ) = {G^N}(\psi ) + {G^D}(\psi ) = \frac{g}{M}\sum\limits_{n = 0}^\infty {n{P_n}(\cos \psi ) + } \\ \;\;\;\;\;\;\;\;\;\;\frac{g}{M}\sum\limits_{n = 0}^\infty {\left[ { - (n + 1){k_n} + 2{h_n}} \right]{P_n}(\cos \psi )} \end{array} $ | (2) |
式中,g为地表平均重力,M为地球质量,Pn(cosψ)为勒让德函数,kn和hn为PREM地球模型计算给出的负荷勒夫数[8],GN(ψ)为质量变化引起的牛顿引力项直接效应,GD(ψ)为质量负荷作用下弹性地球产生的形变和地球形变使内部质量重新分布而引起的弹性项间接效应。
本文将观测点周围划分为近区(ψ<1°)、中区(1°<ψ<20°)和远区(ψ>20°)3个部分,依次计算地表流体质量的重力负荷效应。对近区而言,理论分析表明,质量负荷引起的牛顿引力直接效应gN较间接效应gD要大得多,且会受到地形起伏的显著影响。因此,本文首先对观测点近区的高程数据采用空间分辨率为90 m的SRTM DEM进行修正。对于二维网格的水文质量负荷,可由引力位公式径向求导给出其牛顿引力直接效应gN:
| $ {g^N}({r_s}, {\theta _s}, {\lambda _s}) = G\frac{{[{d^2} + {{(R + {h_s})}^2} - {{(R + {h_p})}^2}]}}{{2{d^3}(R + {h_s})}} $ | (3) |
式中,G为引力常数,hs为观测点高程,hp为计算点高程,d为观测点与计算点之间的距离,R为地球平均半径。
对于三维大气质量负荷,本文采用泰勒级数展开二阶近似给出其Tesseroid单元体下对观测点的牛顿引力直接效应gN[9-10]:
| $ \begin{array}{l} {g^N}({r_s},{\theta _s},{\lambda _s}) = G\rho \Delta r\Delta \theta \Delta \lambda [{L_{000}} + \\ \;\frac{1}{{24}}({L_{200}}\Delta {r^2} + {L_{020}}\Delta {\theta ^2} + {L_{002}}\Delta {\lambda ^2})] \end{array} $ | (4) |
式中,Lijk为与观测点和计算点位置相关的一阶和二阶系数;地表及各规定等压层的大气密度ρ可根据流体静力平衡方程表示为:
| $ \rho = \frac{p}{{{R_L}T(1 + 0.608q)}} $ | (5) |
式中,p为大气压,RL=287.05 J/kg ·K为干空气对应的比气体常数,T为大气温度,q为大气比湿。
1.2 GRACE数据及数据处理GRACE时变重力场模型是由CSR、GFZ和JPL三家机构提供的Level2 RL06版本GSM数据,包括2002-08~2017-06共160个月的观测数据。本文对每月的GRACE模型依次进行如下处理:替换C20项[11],扣除时间段内球谐系数的平均值,作组合滤波处理(250 km高斯滤波[12]和去相关滤波P5M11[13])。经过上述处理后,研究区域内各网格点上的重力异常时间序列可表示为:
| $ \begin{array}{l} \Delta g(r, \theta , \lambda ) = \frac{{{\rm{GM}}}}{{{R^2}}}\sum\limits_{n = 0}^{{n_{\max }}} {(n - 1)} \sum\limits_{m = 0}^n {{{\overline P }_{nm}}(\cos \theta )} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;[\Delta {C_{nm}}\cos (m\lambda ) + \Delta {S_{nm}}\sin (m\lambda )] \end{array} $ | (6) |
式中,θ和λ分别为地心余纬和经度,ΔC和ΔS分别为经过预处理的月时变重力场模型球谐系数,Pnm(cosθ)为正则化缔合勒让德函数。
2 结果与分析 2.1 模式及再分析资料结果分析图 1为2002~2017年ECMWF Interim扣除季节项前后青藏高原及其周边1°×1°网格上的三维大气重力效应。从图 1(a)看出,在全球范围内,三维大气质量变化对青藏高原重力变化的影响峰对峰介于1.9~10.7 μGal之间,影响较大的区域主要位于青藏高原西部的帕米尔高原、喀喇昆仑山和西昆仑山地区(表 1),其次是沿昆仑山向东延伸至青藏高原内陆的地区。从空间分布特征上看,西风环流带的控制影响可能是导致上述地区大气重力效应呈现较大变化的主要原因。另外,本文利用ECMWF Interim内插提取出各网格的气压变化数据,并采用大气导纳方法[14](大气导纳值取为-0.303 7 μGal/hPa)计算大气负荷对青藏高原重力变化的影响。从结果看,由大气导纳方法与本文方法给出的青藏高原重力差值结果的标准差介于0.2~2.6 μGal,表明前者会低估该区域大气重力效应的影响。图 1(b)给出了ECMWF Interim扣除周年项和半年项之后的青藏高原大气重力效应。可以看出,青藏高原大气重力效应的年际变化相对较小,峰对峰变化介于1.1~4.6 μGal之间,表明该区域大气重力效应主要表现为季节性变化。

|
图 1 ECMWF Interim扣除季节项前后青藏高原重力峰对峰变化 Fig. 1 The gravity peak to peak change before and after deducting seasonal term from ECMWF Interim |
|
|
表 1 地表流体重力效应扣除季节项前后的最大峰对峰值 Tab. 1 The maximum gravity peak to peak before and after deducting seasonal term |
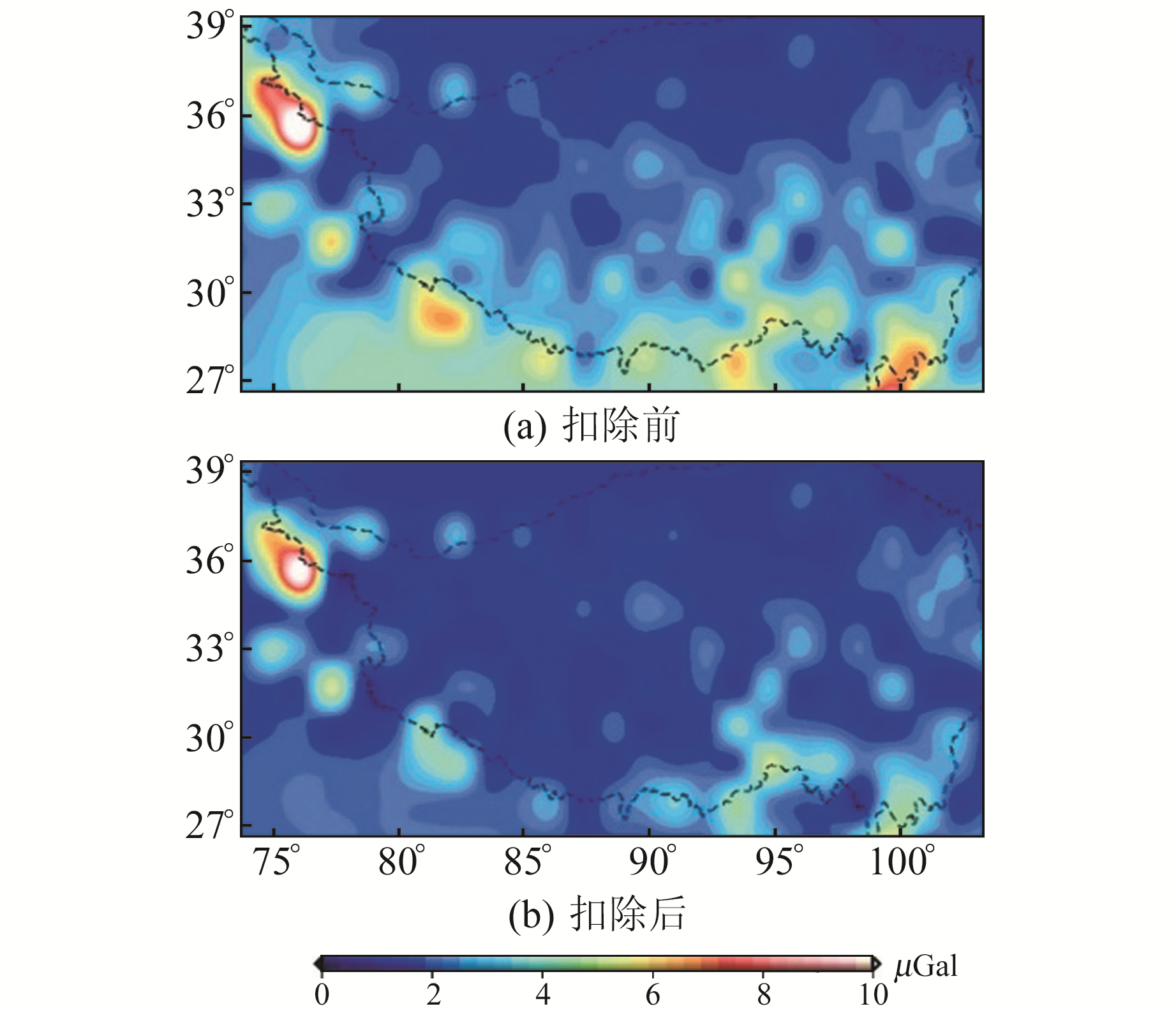
图 2为2002~2017年GLDAS Noah扣除季节项前后青藏高原及其周边1°×1°网格上的土壤水和积雪重力效应。从图 2(a)看出,在全球范围内,土壤水和积雪质量变化对青藏高原重力变化的影响峰对峰变化介于0.9~9.9 μGal之间,影响较大的区域主要位于青藏高原西部的帕米尔高原、喀喇昆仑山地区(表 1),其次是沿喜马拉雅山和念青唐古拉山一带的青藏高原南部地区。从空间分布特征上看,西风环流带、印度季风和东亚季风的控制影响可能是导致上述地区土壤水和积雪重力效应呈现较大变化的主要原因。图 2(b)给出了GLDAS Noah扣除周年项和半年项之后青藏高原土壤水和积雪重力效应,其峰对峰变化介于0.7~8.3 μGal之间,且在青藏高原西部和南部某些局部地区仍存在较大变化,表明该区域土壤水和积雪重力效应存在显著的年际变化特征。
|
图 2 GLDAS Noah扣除季节项前后青藏高原重力峰对峰变化 Fig. 2 The gravity peak to peak change before and after deducting seasonal term from GLDAS Noah |
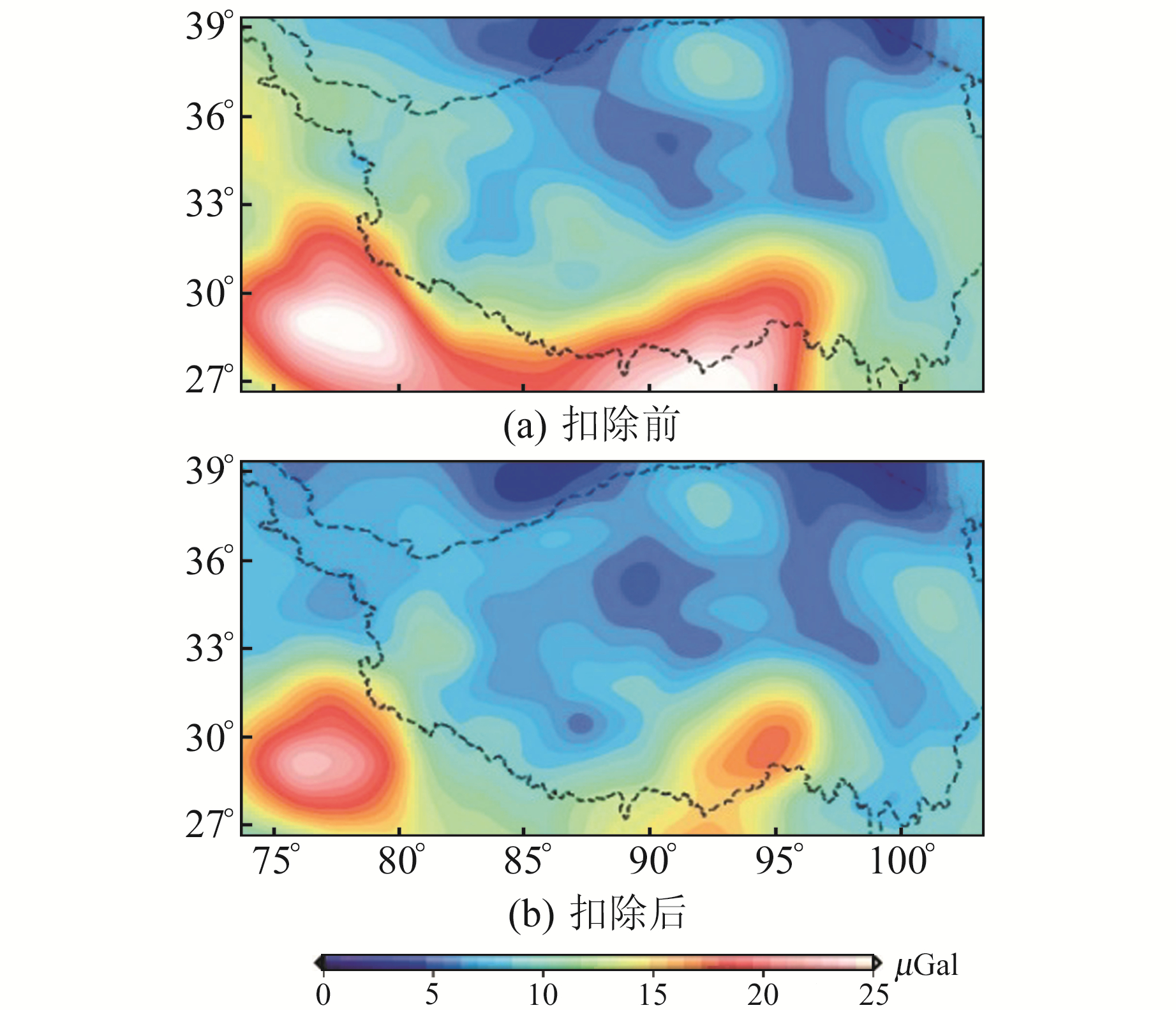
图 3为2002~2017年GRACE数据扣除季节项前后青藏高原及其周边1°×1°网格上的重力峰对峰变化。由GRACE反演得到的时变重力场信号主要反映了青藏高原地区冰川、土壤水、积雪、地下水和湖泊等陆地水文以及构造运动等综合地球物理信号的影响,在季节性或年际变化上其反映的主要是陆地水文的变化特征。从图 3(a)可以看出,青藏高原GRACE时变重力场的峰对峰变化介于4.4~24.1 μGal之间,变化最大的区域主要位于青藏高原南部(表 1)。图 3(b)给出了GRACE扣除周年项和半年项之后青藏高原时变重力场变化特征,其峰对峰变化介于3.4~18.3 μGal之间,年际变化较大的区域主要分布于喜马拉雅山东段及念青唐古拉山一带。
|
图 3 GRACE扣除季节项前后青藏高原重力峰对峰变化 Fig. 3 The gravity peak to peak change before and after deducting seasonal term from GRACE |
对土壤水和积雪重力效应与GRACE时变重力场的结果进行比较分析和讨论。另外,考虑到GRACE GAA产品与ECMWF Interim大气再分析资料采用的数据是相同的,两者给出的结果也基本一致,因此对两者不再进行详细的比较分析。图 4给出了GRACE扣除GLDAS Noah影响之后青藏高原及其周边地区的重力变化特征。可以看出,GRACE-GLDAS Noah扣除季节项前后青藏高原地区重力的峰对峰变化分别介于4.6~24.3 μGal和3.6~23.9 μGal之间,变化最大的区域主要位于青藏高原南部地区(表 1)。对于GRACE与GLDAS Noah的结果差异,影响其不确定性的因素主要包括GRACE与模式资料观测误差、GRACE构造运动影响和GRACE信号泄漏误差。

|
图 4 GRACE-GLDAS Noah扣除季节项前后青藏高原重力峰对峰变化 Fig. 4 The gravity peak to peak change before and after deducting seasonal term from GRACE-GLDAS Noah |
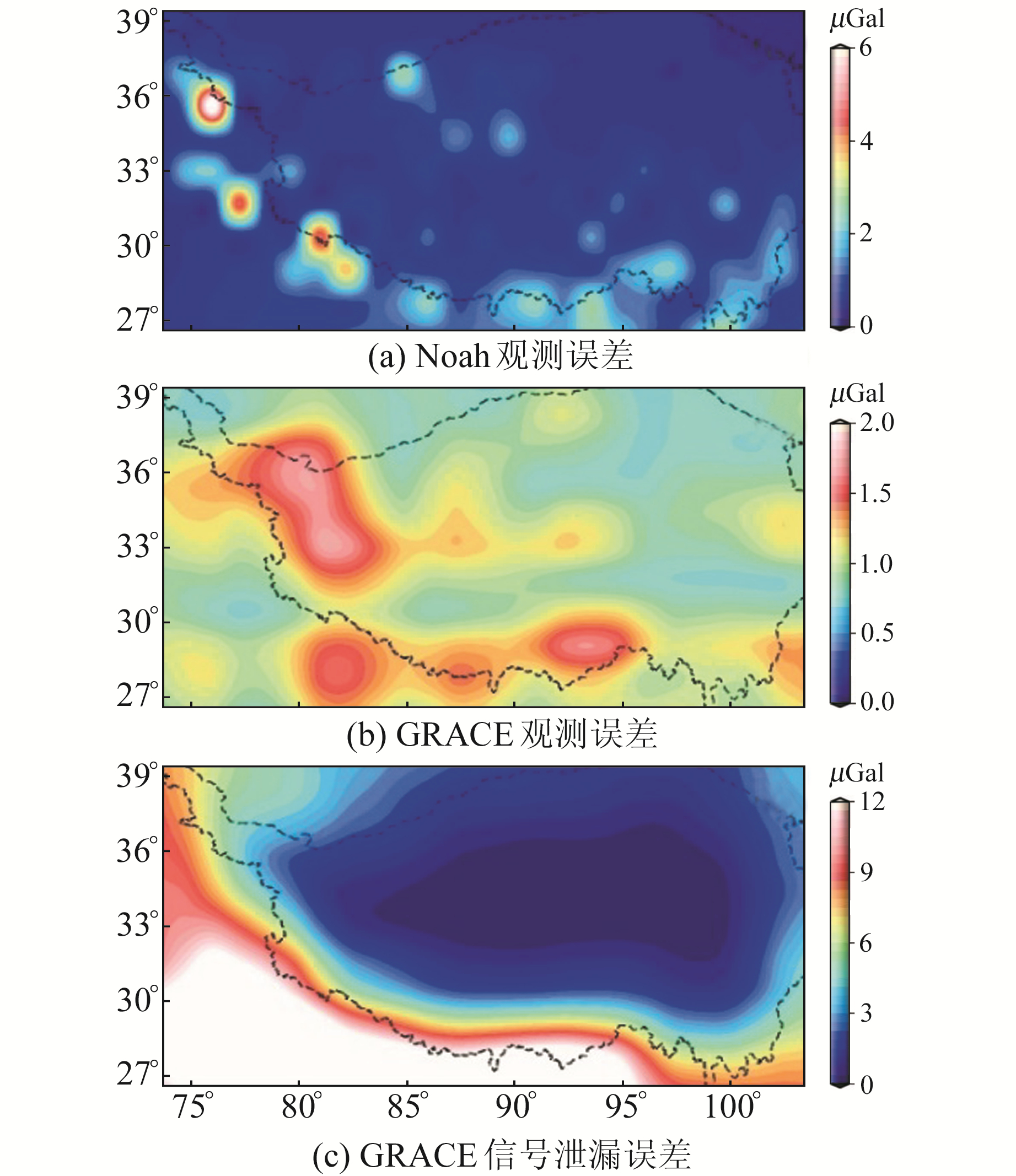
1) 观测误差。本文联合CSR、JPL和GFZ等3种卫星重力数据以及GLDAS Noah、Mosaic和CLM等3种陆面过程水文模式数据,采用经典的三角帽方法[15]评估了CSR GRACE和GLDAS Noah数据的观测误差(图 5(a)、5(b))。结果表明,在青藏高原地区GLDAS Noah和CSR GRACE数据的观测误差分别介于0.3~6.3 μGal和0.7~1.8 μGal之间。
|
图 5 青藏高原地区GLDAS Noah观测误差、GRACE观测误差及GRACE信号泄漏误差 Fig. 5 The observation error of GLDAS Noah, observation error of GRACE and leakage error of GRACE in Qinghai-Tibet plateau |
2)GRACE构造运动影响。青藏高原在印度板块碰撞作用下会出现地壳隆升与底部增厚,地壳隆升和底部增厚速率分别取1.4 mm/a和3.9 cm/a[16],地幔和地壳的平均密度分别取2.8 g/cm3和3.4 g/cm3,据此估算构造运动对GRACE观测结果的影响为1.2 μGal/a。
3)GRACE信号泄漏误差。本文对青藏高原以外的GRACE掩膜网格数据再次经过球谐系数展开和高斯滤波处理,以此估算由于球谐系数截断和滤波处理导致的区域外部信号泄漏误差(图 5(c))。结果表明,在青藏高原地区GRACE信号泄漏误差介于0.1~13.8 μGal,影响较大的区域主要分布于青藏高原南部邻近印度等北部平原地下水信号变化较为剧烈的地区。
综合以上分析,对于GRACE-GLDAS Noah给出的重力变化结果,其空间分布特征及变化量级受各种不确定因素的影响非常有限,总体上其主要反映了青藏高原地区冰川、湖泊和地下水等多种地表流体质量的负荷影响。
3 结语本文基于2002~2017年的大气再分析资料、水文模式及卫星重力数据,利用负荷格林函数和卫星重力反演方法分析青藏高原大尺度地表流体的负荷重力效应。结果表明,大尺度地表流体的质量再分布对青藏高原地面重力观测的影响不可忽视。即使地面重力选择在相同的季节进行观测,地表流体重力效应年际变化的影响也不可避免。因此,对青藏高原地面重力观测结果进行地表流体重力效应改正,可进一步提高其重力场变化分析和研判的可信度。今后可进一步借助多源观测技术来提高地面重力点位周边流体数据的观测精度,改善其重力效应改进的效果。
| [1] |
李辉, 申重阳, 孙少安, 等. 中国大陆近期重力场动态变化图像[J]. 大地测量与地球动力学, 2009, 29(3): 1-10 (Li Hui, Shen Chongyang, Sun Shaoan, et al. Dynamic Gravity Change in Recent Years in China Continent[J]. Journal of Geodesy and Geodynamics, 2009, 29(3): 1-10)
(  0) 0) |
| [2] |
申重阳, 李辉, 孙少安, 等. 重力场动态变化与汶川MS8.0地震孕育过程[J]. 地球物理学报, 2009, 52(10): 2 547-2 557 (Shen Chongyang, Li Hui, Sun Shaoan, et al. Dynamic Variations of Gravity and the Preparation Process of the Wenchuan MS8.0 Earthquake[J]. Chinese Journal of Geophysics, 2009, 52(10): 2 547-2 557)
(  0) 0) |
| [3] |
祝意青, 梁伟锋, 湛飞并, 等. 中国大陆重力场动态变化研究[J]. 地球物理学报, 2012, 55(3): 804-813 (Zhu Yiqing, Liang Weifeng, Zhan Feibing, et al. Study on Dynamic Change of Gravity Field in China Continent[J]. Chinese Journal of Geophysics, 2012, 55(3): 804-813)
(  0) 0) |
| [4] |
Chen S, Liu M, Xing L L, et al. Gravity Increase before the 2015 MW7.8 Nepal Earthquake[J]. Geophysical Research Letters, 2016, 43(1): 111-117 DOI:10.1002/2015GL066595
(  0) 0) |
| [5] |
康开轩, 李辉, 刘少明, 等. 尼泊尔MS8.1地震前我国西藏及周边区域的重力长期变化[J]. 大地测量与地球动力学, 2015, 35(5): 742-746 (Kang Kaixuan, Li Hui, Liu Shaoming, et al. Long-Term Gravity Changes in Tibet and Its Vicinity before the Nepal MS8.1 Earthquake[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 742-746)
(  0) 0) |
| [6] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797
(  0) 0) |
| [7] |
Mikolaj M, Meurers B, Güntner A. Modelling of Global Mass Effects in Hydrology, Atmosphere and Oceans on Surface Gravity[J]. Computers and Geosciences, 2016, 93: 12-20 DOI:10.1016/j.cageo.2016.04.014
(  0) 0) |
| [8] |
Wang H S, Xiang L W, Jia L L, et al. Load Love Numbers and Green's Functions for Elastic Earth Models PREM, iasp91, ak135, and Modified Models with Refined Crustal Structure from Crust 2.0[J]. Computers and Geosciences, 2012, 49: 190-199 DOI:10.1016/j.cageo.2012.06.022
(  0) 0) |
| [9] |
Neumeyer J, Hagedoorn J, Leitloff J, et al. Gravity Reduction with Three-Dimensional Atmospheric Pressure Data for Precise Ground Gravity Measurements[J]. Journal of Geodynamics, 2004, 38(3): 437-450
(  0) 0) |
| [10] |
Heck B, Seitz K. A Comparison of the Tesseroid, Prism and Point-Mass Approaches for Mass Reductions in Gravity Field Modelling[J]. Journal of Geodesy, 2007, 81(2): 121-136
(  0) 0) |
| [11] |
Cheng M K, Tapley B D. Variations in the Earth's Oblateness During the Past 28 Years[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B9)
(  0) 0) |
| [12] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection using GRACE[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B12): 30 205-30 229 DOI:10.1029/98JB02844
(  0) 0) |
| [13] |
Chen J L, Wilson C R, Tapley B D, et al. GRACE Detects Coseismic and Postseismic Deformation from the Sumatra-Andaman Earthquake[J]. Geophysical Research Letters, 2007, 34(13)
(  0) 0) |
| [14] |
罗少聪.大气负荷效应问题研究[D].武汉: 中国科学院测量与地球物理研究所, 2003 (Luo Shaocong. Study on the Loading Effects on the Atmospheric Pressure[D]. Whuhan: Institute of Geodesy and Geophysics, CAS, 2003) http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB200402017.htm
(  0) 0) |
| [15] |
邢乐林, 孙文科, 李辉, 等. 用拉萨点大地测量资料检测青藏高原地壳的增厚[J]. 测绘学报, 2011, 40(1): 41-44 (Xing Lelin, Sun Wenke, Li Hui, et al. Present-Day Crust Thickness Increasing Beneath the Qinghai-Tibetan Plateau by Using Geodetic Data at Lhasa Station[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 41-44)
(  0) 0) |
| [16] |
Ferreira V G, Montecino H D C, Yakubu C I, et al. Uncertainties of the Gravity Recovery and Climate Experiment Time-Variable Gravity-Field Solutions Based on Three-Cornered Hat Method[J]. Journal of Applied Remote Sensing, 2016, 10(1)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

