2. 安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽省淮南市泰丰大街168号,232001;
3. 安徽理工大学矿区环境与灾害协同监测煤炭行业工程研究中心,安徽省淮南市泰丰大街168号,232001
构建地表下沉预测模型是矿山开采的难点,但对于由开采沉陷引发的地质环境灾害的防治具有重要意义[1]。目前,针对沉降预测的方法有模糊神经网络[2]、灰色模型[3]、支持向量机[4]、径向基神经网络[5]、组合预报模型[6]、多核相关向量机[7-8]、时间序列分析[9]和智能算法优化的BP神经网络[10]等。但利用上述方法进行建模时,模糊神经网络的隶属函数带有一定的主观性,灰色模型精度较低,支持向量机的核函数的参数较难确定,径向基神经网络容易陷入局部最优解(结果不稳定),组合预报模型权系数难以确定,多核相关向量机的核函数难以选择,时间序列分析精度较低,智能算法优化BP神经网络时间较长(迭代次数不易确定)。针对上述问题,BP-Adaboost在寻找全局最优解方面有一定的优势[11]。因为地下开采引起的地表下沉具有显著的混沌特性和非线性特性,本文针对BP-Adaboost没有考虑残差而导致精度降低并且不稳定的问题,运用混沌理论对下沉残差序列进行分析和预测,提出一种新的融合混沌残差的BP-Adaboost预测模型。
1 融合混沌残差的BP-Adaboost模型预测原理BP神经网络和BP-Adaboost神经网络原理见文献[10-11]。
1.1 混沌残差序列的预测客观事物的运动除了周期、准周期和定常以外,还存在一种更具普遍意义的运动形式,即混沌。混沌具有如下特征:内部似随机性、整体稳定局部不稳定性、初值敏感性、短期可预测长期不可预测性、奇异吸引子、轨道稳定性及分岔、普适性等。混沌残差序列的预测分为3个步骤,分别是残差序列的相空间重构、混沌特性的识别、混沌残差的预测。
1.1.1 残差序列的相空间重构相空间重构理论是混沌序列的基础,可用坐标延迟法对混沌序列进行相空间重构。对于残差序列{d1, d2, d3, …, dn}可以重构一个m维的相空间:
| $ \begin{array}{c} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_1}}&{{\mathit{\boldsymbol{X}}_2}}& \cdots &{{\mathit{\boldsymbol{X}}_K}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{d_1}}&{{d_2}}& \cdots &{{d_K}}\\ {{d_{1 + \tau }}}&{{d_{2 + \tau }}}& \cdots &{{d_{K + \tau }}}\\ {{d_{1 + 2\tau }}}&{{d_{2 + 2\tau }}}& \cdots &{{d_{K + 2\tau }}}\\ {}& \vdots & \vdots & \vdots \\ {{d_{1 + \left( {m - 1} \right)\tau }}}&{{d_{2 + \left( {m - 1} \right)\tau }}}& \cdots &{{d_{K + \left( {m - 1} \right)\tau }}} \end{array}} \right] \end{array} $ | (1) |
式中,m为嵌入维数,τ为坐标延迟时间,K为相点个数,X为相点,K=n-(m-1)τ。运用G-P算法可以获取混沌序列的关联维(G),而如果嵌入维数m≥2G+1, 则系统原始状态变量构成的相空间和一维观测值重构相空间的动力学行为等价,即获得了所有状态变量演变的全部信息,从而可获得下一时刻的预测值,同时嵌入维数可以通过G-P算法获得[12]。残差序列的τ取1。
1.1.2 残差序列混沌特性的识别常见判断残差序列混沌特性的方法有最大Lyapunov指数法和关联维分数判别法,下面主要介绍关联维分数判别法。关联维数为分数则说明该系统的动力行为可能具有混沌特征,只要相空间重构的维数足够大,就能描述出系统的混沌吸引子,表示出传统方法无法展示的系统运动规律。但是在实际测算中也可能出现关联维没有饱和的情况,其原因有两种可能:1)m不够大,所以应继续增大m; 2)该序列没有无特征尺度区[13]。
1.1.3 一阶加权局域预测法常用的混沌时间序列的预测方法有零阶局域预测法、加权零阶局域预测法、一阶局域预测法、加权一阶局域预测法、全局预测方法和最大Lyapunov指数法等,下面主要介绍一阶加权局域预测法。局域法是将相空间轨迹的最后一点作为中心点, 把离中心点最近的若干轨迹点作为相关点, 然后对这些相关点进行拟合, 再估计轨迹下一点的走向, 最后从预测出的轨迹点的坐标中分离出所需要的预测值, 其原理即“寻找历史上情况最相似之处”。对于状态空间中重构的状态矢量,假设中心点为Xm, Xmi(i=1, 2, …,q, q是邻近点的个数)到Xm的距离是disi,其中的最小值是dismin,Xmi的权值表示为:
| $ {\rm{p}}{{\rm{d}}_i} = \frac{{{\rm{exp}}( - c({\rm{di}}{{\rm{s}}_i} - {\rm{di}}{{\rm{s}}_{{\rm{min}}}}))}}{{\sum\limits_{i = 1}^q {{\rm{exp}}( - c({\rm{di}}{{\rm{s}}_i} - {\rm{di}}{{\rm{s}}_{{\rm{min}}}}))} }} $ | (2) |
式中,c为参数,一般取c=1。一阶加权的拟合表达式为:
| $ \mathit{\boldsymbol{X}}{_{mi + 1}} = \alpha \mathit{\boldsymbol{e}} + b{\mathit{\boldsymbol{X}}_{mi}} $ | (3) |
式中,a、b是拟合系数,e=(1, 1, …, 1)T, Xmi+1是通过 Xmi预测的值。
通过加权最小二乘求取拟合系数a、b,其表达式为:
| $ \sum\limits_{i = 1}^q {{\rm{p}}{{\rm{d}}_i}{{({\mathit{\boldsymbol{X}}_{mi + 1}} - \alpha \mathit{\boldsymbol{e}} + b{\mathit{\boldsymbol{X}}_{mi}})}^2} = {\rm{min}}} $ | (4) |
求解出a、b的值,代入(3)式即可求出混沌序列的预测值。
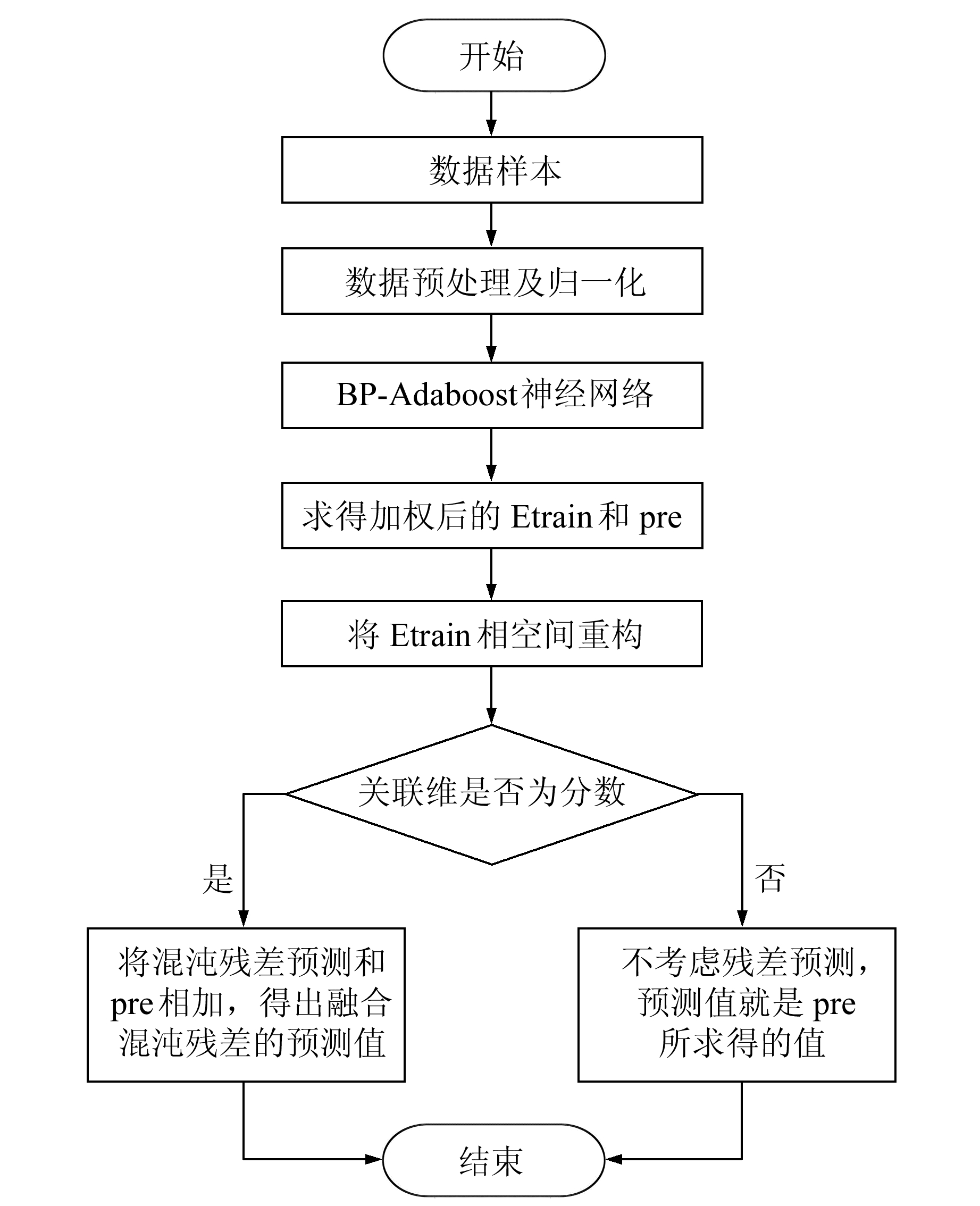
1.2 融合混沌残差的BP-Adaboost模型预测原理将BP-Adaboost神经网络模型的残差d代入式(1),再由式(4)得出拟合系数a、b,代入式(3)得到残差,最终将每个预测对应的残差和BP-Adaboost神经网络模型的预测值pre累加就得到了融合混沌残差的预测值。融合混沌残差的BP-Adaboost预测算法流程如图 1所示,图中Etrain为训练误差矩阵。
|
图 1 融合混沌残差的BP-Adaboost预测算法流程 Fig. 1 Flow chart of BP-Adaboost algorithm fused with chaotic residuals |
融合混沌残差的BP-Adaboost预测算法的表达式为:
| $ y = {\rm{pre}} + \varepsilon $ | (5) |
式中,ε是残差预测值。
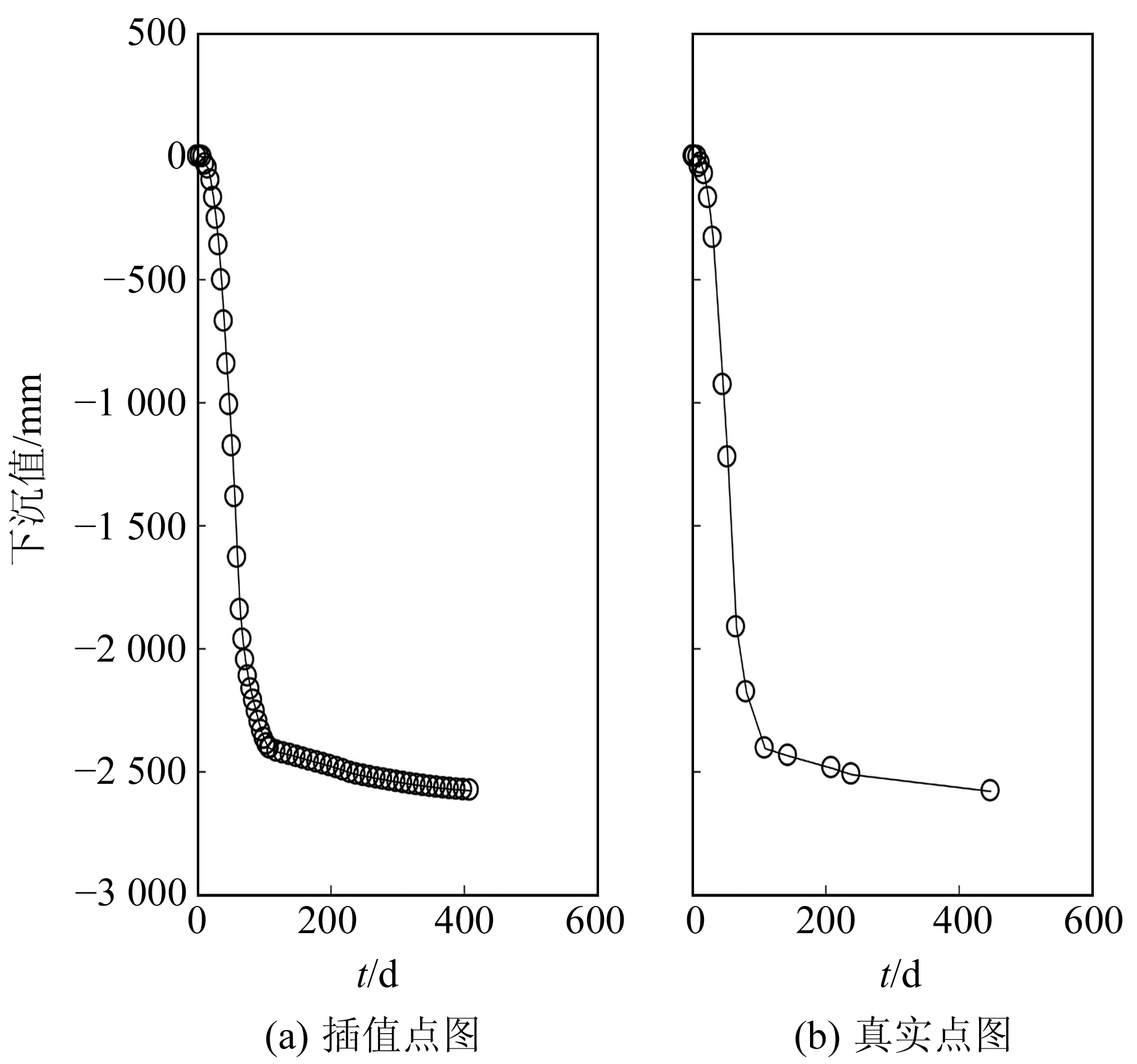
2 工程实例 2.1 工程应用以淮南顾北煤矿1312(1)工作面的最大下沉点为研究对象, 经过数据预处理,以下沉速度1.6 mm/d为临界速度,将下沉点的下沉进程分为开始期、活跃期和稳定期。开始期和活跃期以4 d为一个三次样条插值,稳定期以10 d为一个三次样条插值,最终得到开始期的天数是1~7 d,活跃期的天数是8~108 d,稳定期的天数是109~409 d。获得的最大下沉点MS23的图像如图 2所示。
|
图 2 最大下沉点MS23下沉图 Fig. 2 MS23 sinking plot |
以最大相对中误差(error1)、平均相对中误差(error2)、均方根误差(error3)和最大误差绝对值(error4)为指标,对BP神经网络模型、BP-Adaboost神经网络模型和融合混沌残差的BP-Adaboost模型进行精度评价。其中网络的输入为活跃期前7个三次样条插值下沉数据,输出为活跃期输入值下一个三次样条插值的下沉数据,隐含层的节点个数是8,网络的拓扑结构是7-8-1,预测最后5个三次样条插值。重复计算10次后,下沉平均值的模型精度比较如表 1所示。
|
|
表 1 最大下沉点的活跃期单步预测精度比较 Tab. 1 Comparison of one-step prediction accuracy for maximum sinking point |
从表 1可以看出,融合混沌残差的BP-Adaboost模型在4种精度评判指标中精度均最好,其次是BP-Adaboost神经网络模型,BP神经网络最差。
BP-Adaboost模型拟合下沉值残差的嵌入维和相关维的值如表 2所示。从表 3可以看出,在进行多步预测的时候,3种模型的预测精度均有所下降,BP神经网络模型精度最低,然后是BP-Adaboost神经网络模型,融合混沌残差的BP-Adaboost模型精度最高。融合混沌残差的BP-Adaboost模型在BP-Adaboost神经网络模型的基础上略微有所提高,两者精度相差不大的原因在于,混沌序列只能进行短期预测,不能进行长期预测,同时又没有顾及数据的新鲜度。
|
|
表 2 BP-Adaboost模型拟合下沉值残差的嵌入维和相关维 Tab. 2 The residual embedding dimension and correlation dimension of sinking values fitted by BP-Adaboost model |
|
|
表 3 最大下沉点的活跃期多步预测精度比较 Tab. 3 Comparison of multi-step prediction accuracy for maximum sinking point for the active period |
用3种模型进行最大观测点稳定期的预测,同样用上节中4个指标进行精度评价。其中网络的输入为稳定期前7个插值的下沉数据,输出为下一个三次样条插值的下沉数据,隐含层的节点个数是8,网络的拓扑结构是7-8-1,预测后5个三次样条插值的下沉值。重复计算10次后,下沉平均值的模型精度比较如表 4所示。
|
|
表 4 最大下沉点的稳定期单步预测精度比较 Tab. 4 Comparison of the stability period step prediction accuracy of the maximum sinking point |
从表 4可以看出,在最大下沉点的稳定期单步预测时,3种模型的预测精度均很高,原因在于稳定期下沉值变化相比于活跃期不是很大。其中BP神经网络模型和BP-Adaboost神经网络模型精度差不多,融合混沌残差的BP-Adaboost模型效果最好,具有明显的优势。
从表 5可以看出,在最大下沉点的稳定期多步预测时,3种模型的预测精度均很高,其中BP神经网络模型最差,BP-Adaboost神经网络模型和融合混沌残差的BP-Adaboost模型结果精度相差不大,再次说明混沌序列只适合短期预测,由于没有顾及下沉数据的新鲜度,所以精度只是略有提高。
|
|
表 5 最大下沉点的稳定期多步预测精度比较 Tab. 5 Comparison of multi-step prediction accuracy of the maximum sink point for the stability period |
最大下沉点的稳定期多步BP-Adaboost预测残差如表 6所示。
|
|
表 6 最大下沉点的稳定期多步BP-Adaboost预测残差 Tab. 6 Multi-step BP-Adaboost prediction residuals for maximum sinking point for the stability period |
为提高地下开采引起地表下沉预测结果的精度,本文提出融合混沌残差的BP-Adaboost地表下沉预测模型。通过对顾北矿1312(1)实测最大下沉值的预测发现,融合混沌残差的BP-Adaboost地表下沉预测模型单步预测和多步预测精度均高于BP神经网络模型和BP-Adaboost神经网络模型, 尤其在对单步预测的时候,精度提高最为明显。
| [1] |
李培现.深部开采地表沉陷规律及预测方法研究[D].徐州: 中国矿业大学, 2012 (Li Peixian. Study on Regularity and Prediction Method of Surface Subsidence Due to Deep Mining[D]. Xuzhou: China University of Mining and Technology, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10290-1012032583.htm
(  0) 0) |
| [2] |
Ding D X, Zhang Z J, Bi Z W. A New Approach to Predicting Mining Induced Surface Subsidence[J]. Journal of Central South University of Technology, 2006, 13(4): 438-444 DOI:10.1007/s11771-006-0064-y
(  0) 0) |
| [3] |
何君, 杨国东. 灰色预测理论在建筑物沉降中的应用研究[J]. 测绘通报, 2012(3): 63-64 (He Jun, Yang Guodong. On the Application of Grey Theory in Building Settlement[J]. Bulletin of Surveying and Mapping, 2012(3): 63-64)
(  0) 0) |
| [4] |
Li L, Wu K, Zhou D W. Extraction Algorithm of Mining Subsidence Information on Water Area Based on Support Vector Machine[J]. Environmental Earth Sciences, 2014, 72(10): 3 991-4 000 DOI:10.1007/s12665-014-3288-4
(  0) 0) |
| [5] |
谭洋, 牛雪峰, 王明常. 径向基神经网络在沉降预测中的应用[J]. 测绘科学, 2016, 41(4): 33-36 (Tan Yang, Niu Xuefeng, Wang Mingchang. Application of Radial Basis Function Neural Networks in Settlement Predictive Model[J]. Science of Surveying and Mapping, 2016, 41(4): 33-36)
(  0) 0) |
| [6] |
魏博文, 熊威, 李火坤, 等. 融合混沌残差的大坝位移蛙跳式组合预报模型[J]. 武汉大学学报:信息科学版, 2016, 41(9): 1 272-1 278 (Wei Bowen, Xiong Wei, Li Huokun, et al. Dam Deformation Forecasting of Leapfrog Combined Model Merging Residual Errors of Chaos[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1 272-1 278)
(  0) 0) |
| [7] |
Blekas K, Likas A. Sparse Regression Mixture Modeling with the Multi-Kernel Relevance Vector Machine[J]. Knowledge and Information Systems, 2014, 39(2): 241-264
(  0) 0) |
| [8] |
罗亦泳, 姚宜斌, 赵庆志, 等. 利用优化的组合核相关向量机算法构建地表下沉预测模型[J]. 武汉大学学报:信息科学版, 2018, 43(9): 1 295-1 301 (Luo Yiyong, Yao Yibin, Zhao Qingzhi, et al. Prediction of Surface Subsidence of Underground Mining Based on HIOA and MK-RVM[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1 295-1 301)
(  0) 0) |
| [9] |
王晶晶, 尹晖. 一种建筑沉降叠加预测方法[J]. 测绘科学, 2019, 44(3): 107-113 (Wang Jingjing, Yin Hui. A Method of Building Settlement Superposition Prediction Based on ARMA Model[J]. Science of Surveying and Mapping, 2019, 44(3): 107-113)
(  0) 0) |
| [10] |
李苋兰, 张顶, 黄晞. 基于BP-AdaBoost神经网络的多参数掌静脉图像质量评价法[J]. 计算机系统应用, 2020, 29(3): 20-28 (Li Xianlan, Zhang Ding, Huang Xi. Multi-Parameter Palm Vein Image Quality Evaluation Method Based on BP-AdaBoost Neural Network[J]. Computer Systems and Applications, 2020, 29(3): 20-28)
(  0) 0) |
| [11] |
刘艳丽, 陈跃东. 基于BP-Adaboost的目标跟踪算法应用研究[J]. 河北工程大学学报:自然科学版, 2012, 29(3): 99-102 (Liu Yanli, Chen Yuedong. The Applied Research of Motive Object Tracking Based on BP[J]. Adaboost Algorithm:Natural Science Edition, 2012, 29(3): 99-102)
(  0) 0) |
| [12] |
董春娇, 邵春福, 张辉, 等. 基于G-P算法的快速路交通流参数相空间重构[J]. 吉林大学学报:工学版, 2012, 42(3): 594-599 (Dong Chunjiao, Shao Chunfu, Zhang Hui, et al. Phase Space Reconstruction of Traffic Flow Parameters on Expressway Based on G-P Algorithm[J]. Journal of Jilin University:Engineering and Technology Edition, 2012, 42(3): 594-599)
(  0) 0) |
| [13] |
张安兵.动态变形监测数据混沌特性分析及预测模型研究[D].徐州: 中国矿业大学2009 (Zhang Anbing. Study on Chaotic Characteristic and Prediction Model of Dynamic Deformation Monitoring Data[D]. Xuzhou: China University of Mining and Technology, 2009) http://cdmd.cnki.com.cn/Article/CDMD-10290-2009222856.htm
(  0) 0) |
2. Key Laboratory of Aviation-Aerospace-Ground Cooperative Monitoring and Early Warning of Coal Mining-Induced Disasters of Anhui Higher Education Institutes, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China;
3. Coal Industry Engineering Research Center of Mining Area Environmental and Disaster Cooperative Monitoring, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China
 2020, Vol. 40
2020, Vol. 40


