卫星导航系统实时导航定位的精度与星载原子钟的钟差预报结果具有紧密联系,提高钟差预报的可靠性以及准确性,有利于提高卫星导航系统的服务质量[1-2]。目前常用的钟差预报模型有二次多项式模型(QP)[3-4]、灰色模型(GM(1, 1))[5-8]、卡尔曼滤波[9-11]、人工神经网络[12-14]和谱分析法[15]等,但每种模型都具有其自身局限性[13],从而导致预报结果精度不足。鉴于灰色模型建模简单、建模速度较快等优点,许多学者在其基础上构建新的预报模型[6-8, 16-19]。本文在此前研究基础上,构建基于GM(1, 1)模型和AR模型的循环式钟差预报模型,该方法可及时更新建模钟差序列,同时可顾及预报历元与前一历元之间的相关性,预报精度较普通组合模型有所提高,但耗时与计算量也明显增加。以往研究中在钟差预报时并未考虑原始钟差序列长度对预报精度的影响,过长的钟差序列虽然包含的信息量较多,但对短期预报结果的影响也较大。通过设计不同的实验方案,研究利用不同长度的钟差序列构建模型对不同星载原子钟预报精度的影响,以期为后续研究提供一定参考。
1 钟差预报模型 1.1 GM(1, 1)模型GM(1, 1)模型是应用最为广泛的灰色模型,由一个仅包含单变量的一阶微分方程构成。设卫星钟差原始数据序列为X(0)={x(0)(1), x(0)(2), …, x(0)(n)},对原始序列进行累加形成序列X(1)={x(1)(1), x(1)(2), …, x(1)(n)},对X(1)可建立微分方程:
| $ \frac{{{\rm{d}}{x^{(1)}}}}{{{\rm{d}}t}} + a{x^{(1)}} = b $ | (1) |
式中,a为模型发展系数,b为灰色作用量,可通过最小二乘法进行求解。
根据式(1)的响应函数,可得X(1)的预报模型为:
| $ {x^{(1)}}(k + 1) = [{x^{(0)}}(1) - \frac{b}{a}]{e^{ - ak}} + \frac{b}{a} $ | (2) |
式中,k为参与建模的原始数据个数。对预报的x(1)(k)序列依次进行累减即可得到原始序列的预测结果。
在建立GM(1, 1)模型前需检验原始数据的正负性是否一致,若不一致则需给原始序列数据增加一个常数,以保证原始数据的符号一致。根据上述原理建立GM(1, 1)模型进行预报,然后从预报结果中减去所加常数即为最终的预报结果[5]。
1.2 AR模型自回归模型(auto regressive model)是利用前面若干期数据的线性组合来描述以后某时刻变量的线性回归模型,为一种时间序列形式。假设存在平稳时间序列zt(t=1, 2, …, n),其p阶AR模型可表示为[11]:
| $ {z_t} = \sum\limits_{i = 1}^p {{\varphi _i}{z_{t - i}}} + {a_t} $ | (3) |
式中,φi为AR模型自回归系数,at表示均值为0、方差为σ的白噪声。
利用最小二乘法求解系数φi。令B=[φ1 φ2 … φp]T,则当
模型阶数是影响预报结果的关键元素之一,常用的定阶方法有自相关函数和偏自相关函数定阶法、AIC准则和BIC准则,其中AIC准则和BIC准则应用较广[21]。AIC准则和BIC准则均在模型中引入与模型参数个数相关的惩罚项,以达到降低模型参数、避免过拟合的目的。AIC准则在样本数据量较大时,由于似然函数值较大而超过模型参数的影响,因此通常会失效;而在BIC准则中加大与模型参数个数相关的惩罚力度,在样本数量较大时可有效控制模型的复杂度,即模型参数的个数[22-23]。基于所用原始钟差序列长度,本文选用BIC准则来确定模型阶数。
BIC准则定义为[22]:
| $ {\rm{BIC}}(p) = p\ln n - 2\ln L $ | (4) |
式中,p为模型参数个数,n为样本量,L为似然函数。
1.3 改进的钟差短期预报策略GM(1, 1)模型单独进行预报时,由于其稳定性较低而导致预报风险较大,在实际应用中一般无法满足使用要求[18]。采用AR模型对GM(1, 1)模型预报残差进行修正,可进一步提高预报效果,但随着预报时间增加,预报精度下降较快[24]。为提高钟差预报精度,提出基于GM(1, 1)模型和AR模型的循环式钟差预报模型,记为GM(1, 1)+AR循环模型。
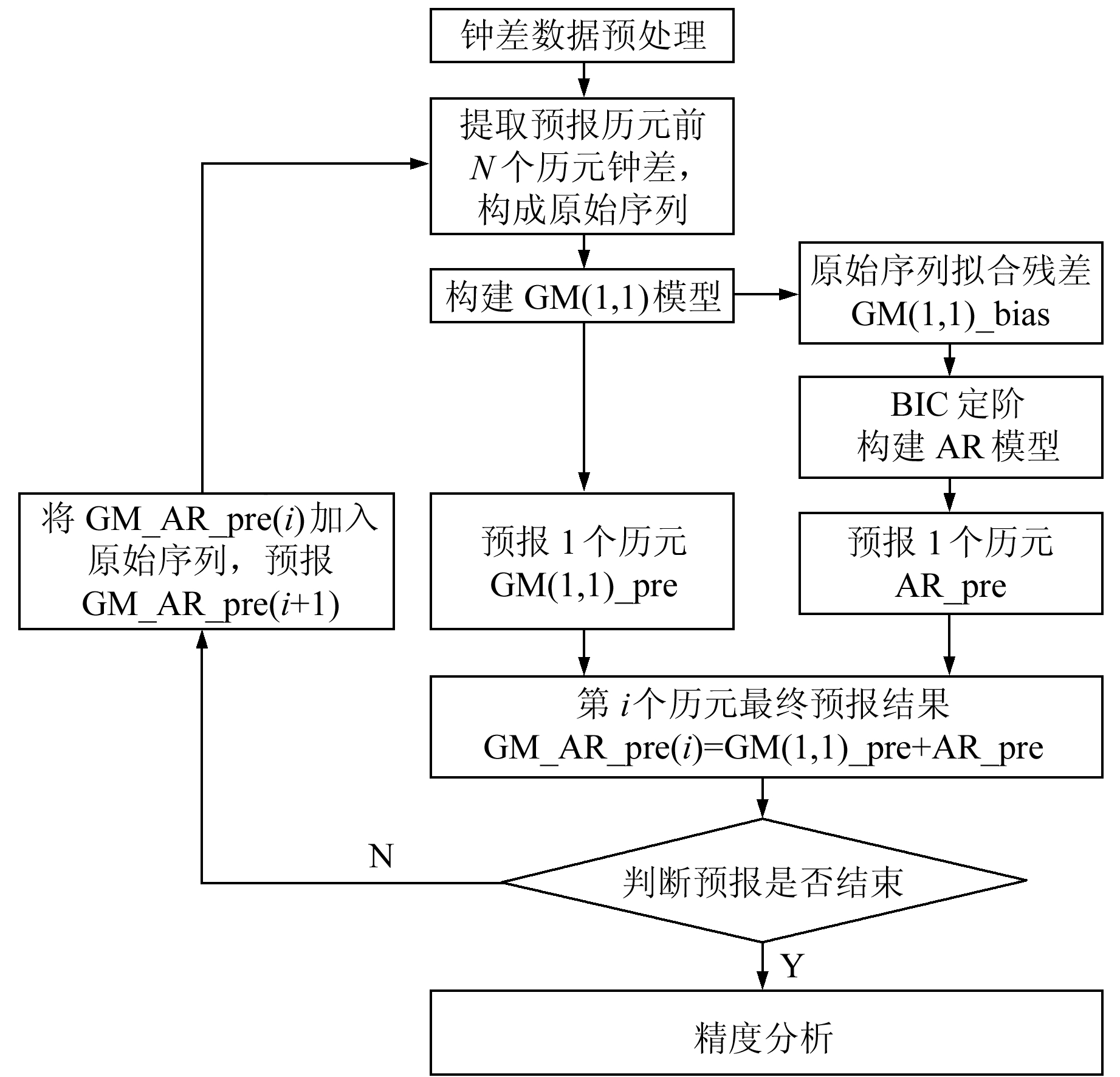
GM(1, 1)+AR循环模型预报钟差思路如下:1)利用原始钟差序列构建GM(1, 1)模型,并向外预报1个历元,预报结果记为GM(1, 1)_pre,通过对比可得原始钟差序列与GM(1, 1)模型拟合序列之差,记为GM(1, 1)_bias;2)利用BIC准则确定合适的阶数,对GM(1, 1)_bias序列构建AR模型,并向外预报1个历元,预报结果记为AR_pre;3)取GM(1, 1)_pre与AR_pre之和为下一个历元的最终预报结果,即GM_AR_pre(i)= GM(1, 1)_pre+AR_pre;4)将GM_AR_pre(i)添加至原始钟差序列中最后一位并剔除钟差序列的首位数据,形成新的原始钟差序列。重复执行上述步骤,直至预报结束。具体预报流程见图 1。
|
图 1 GM(1, 1)+AR循环模型的预报流程 Fig. 1 Prediction process of GM(1, 1)+AR cycle model |
构建预报模型时,AR模型具有明确的定阶指标要求,而GM(1, 1)模型对建模数据量大小并无明确规定。当原始序列长度不同时,GM(1, 1)模型系数及后续预报结果也会存在差异,因此在建模前需确定原始钟差序列的长度。本文拟预报24 h的钟差,分别采用前2 h、6 h、12 h和24 h的钟差序列作为原始序列构建GM(1, 1)模型,分析采用不同长度的原始序列构建GM(1, 1)模型对预报精度的影响。
2 实验与分析为比较本文算法的预报精度,分别使用QP模型、GM(1, 1)模型、GM(1, 1)+AR组合模型和GM(1, 1)+AR循环模型进行预报,实验数据来源于IGS发布的最终钟差产品,采样间隔为5 min。选取2016-08-08~08-21的钟差数据作为实验数据,同时为验证原始钟差序列长度对钟差预报的影响,分别使用前一天2 h、6 h、12 h和24 h的钟差数据进行建模,预报后一天(共288个历元)的钟差。如使用08-08最后2 h(22:00~23:55)、6 h(18:00~23:55)、12 h(12:00~23:55)和24 h(0:00~23:55)的钟差数据分别对08-09全天的钟差进行预报,不同长度的原始序列各预报13期,并将预报结果与IGS发布的结果进行对比,采用绝对最大值(max)、平均值(mean)和均方根误差(RMS)作为统计量来检验模型的预报结果。根据GPS星载原子钟的类型,选取PRN02(IIR RB)、PRN08(IIF CS)、PRN26(IIF RB)和PRN31(IIR-MRB)进行实验。
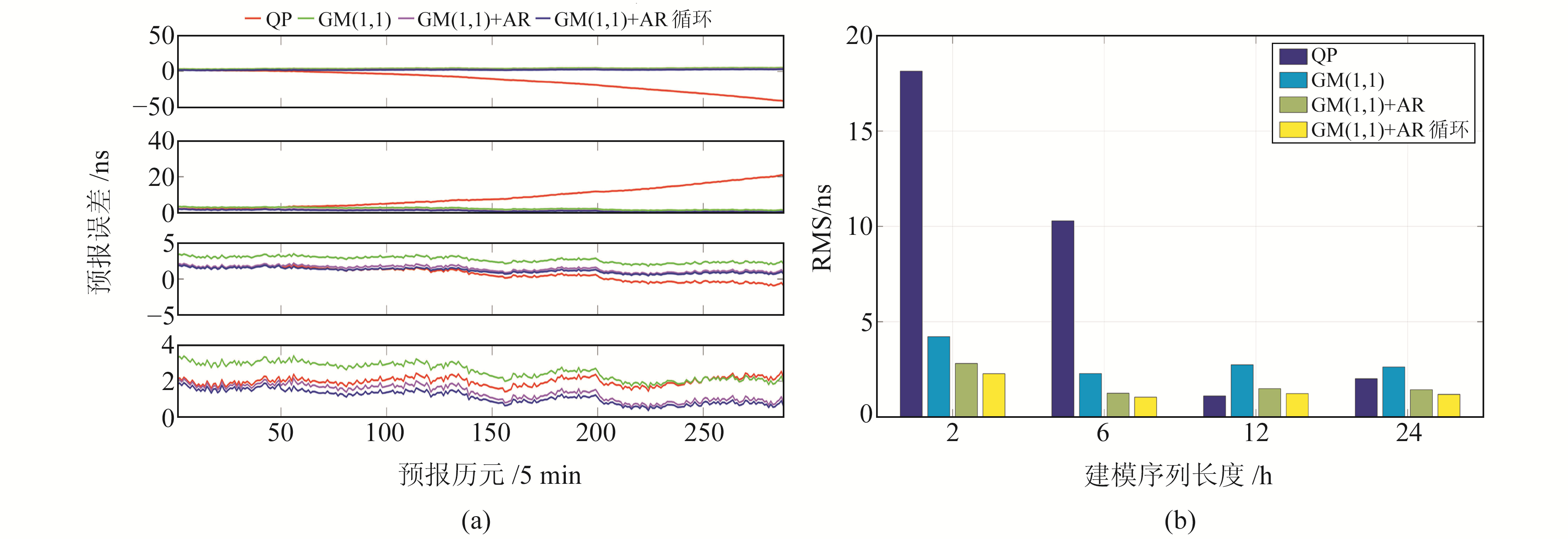
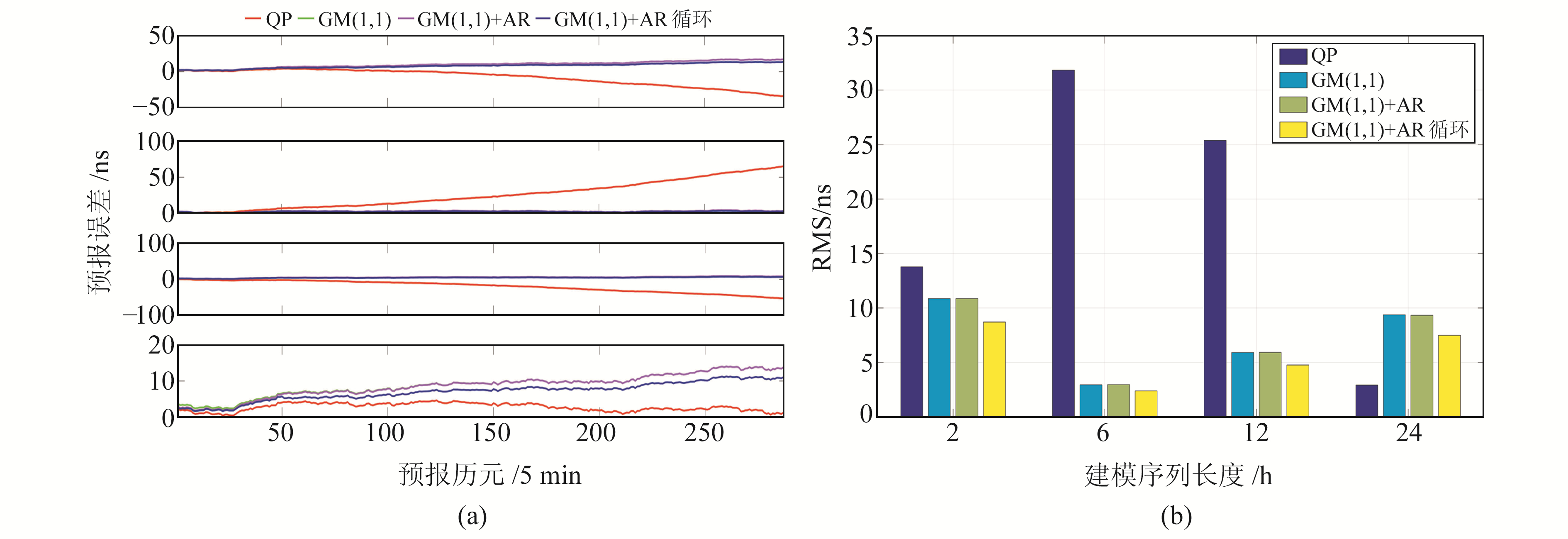
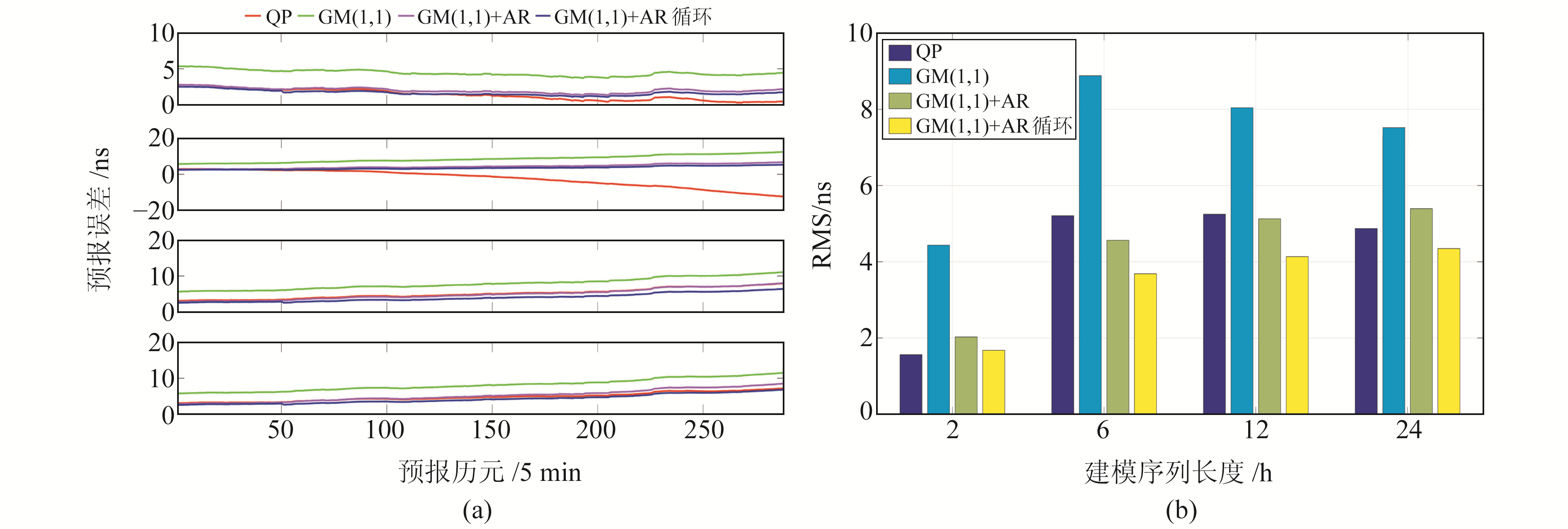
图 2~5和表 1(单位ns)为预报结果及精度统计,图 2~5中图(a)从上至下分别表示建模序列为2 h、6 h、12 h和24 h的预报误差,图(b)为不同情况下的精度统计。对图 2~5及表 1进行分析可知:
|
图 2 PRN02钟差预报结果 Fig. 2 Clock bias prediction results of PRN02 |
|
图 3 PRN08钟差预报结果 Fig. 3 Clock bias prediction results of PRN08 |
|
图 4 PRN26钟差预报结果 Fig. 4 Clock bias prediction results of PRN26 |

|
图 5 PRN31钟差预报结果 Fig. 5 Clock bias prediction results of PRN31 |
|
|
表 1 不同模型钟差预报结果统计 Tab. 1 Statistics of clock bias prediction results of different model |
1) GM(1, 1)+AR循环模型预报效果总体上优于GM(1, 1)+AR组合模型、GM(1, 1)模型和QP模型,仅PRN26在2 h钟差序列长度下的预报结果略低于QP模型。随着预报历元的增加,4种模型的预报误差均逐渐增大,GM(1, 1)+AR循环模型预报误差增大速度较慢,多数情况下QP模型增速最快,部分情况下GM(1, 1)模型增速最快。
2) 随着预报历元的增加,组合模型较GM(1, 1)模型预报精度有一定提高,这是由于组合模型可提高单一模型的稳定性,减少单一模型的预报风险。GM(1, 1)+AR循环模型预报结果趋势与GM(1, 1)+AR组合模型相似,但随着预报历元的增加,精度较组合模型有一定提高,原因为循环模型可利用更多的原始序列信息,同时反复构建模型也使最终的模型系数更为有效。但这种重复建模预报的方式会导致计算复杂度不断提高,如序列长度为N时,GM(1, 1)+AR组合模型的计算复杂度为O(N),则此时循环模型的计算复杂度为O(N)+O(N+1)+O(N+2)+…+O(N+k-1)(k为预报历元数)。
3) 由钟差预报误差可知,不同模型的预报结果与原始钟差序列长度具有较大关系,对于不同卫星,QP模型预报精度受建模序列长度影响最大。以PRN02为例,2 h建模长度预报的max和RMS分别为41.183 ns和18.143 ns,12 h建模长度预报的max和RMS分别为2.082 ns和1.109 ns,精度提高较为明显。统计分析4颗卫星QP模型预报结果可知,PRN02的最优长度为12 h,PRN08和PRN31的最优长度为24 h,PRN26的最优长度为2 h,从总体上看,建模序列较长的预报效果会更好。GM(1, 1)模型、GM(1, 1)+AR组合模型与GM(1, 1)+AR循环模型的预报精度受原始钟差序列长度的影响类似,PRN02和PRN08的最优长度为6 h,PRN26的最优长度为2 h,PRN31的最优长度为24 h,这是因为3种模型都是由GM(1, 1)模型的预报结果主导。
4) 对比Rb钟(PRN02、PRN26、PRN32)和Cs钟(PRN08)的max、mean和RMS可知,Rb钟的预报精度总体上优于Cs钟,仅当原始序列长度为6 h时,Cs钟的预报精度与Rb的预报精度相当。在预报结果较好的情况下,Rb钟预报误差的波动范围多在4 ns以内,而Cs钟的波动范围多在5 ns以上,这是由于Cs钟的短期稳定性较差。目前北斗卫星均搭载Rb钟,这也从侧面反映出Rb钟的稳定性和精度较高,可为用户提供更好的导航和授时等服务。
5) 在使用组合模型进行预报时,AR模型的阶数在向外预报时会发生变化,即各预报时刻的最优阶数存在差异,这也从侧面反映出星载原子钟较为敏感,易受外界或自身因素的影响。
3 结语针对传统GM(1, 1)+AR组合模型的缺点,提出一种循环式钟差预报模型。该模型可使用AR模型对GM(1, 1)模型预报残差进行修正,同时还可及时更新建模序列以提高预报精度。与GM(1, 1)模型和GM(1, 1)+AR组合模型对比可知,GM(1, 1)+AR循环模型能充分利用原始钟差序列信息,有效改善钟差预报精度,并且随着预报历元增多,精度提高越明显,但会增加计算复杂度和耗时。原始钟差序列长度与建模预报精度分析结果表明,原始建模序列长度对预报精度有一定影响。QP模型的预报效果受原始序列长度变化影响最大,GM(1, 1)模型、GM(1, 1)+AR组合模型和GM(1, 1)+AR循环模型的预报效果受原始钟差序列长度的影响类似。在短期预报时,Rb钟的预报精度总体上优于Cs钟,这与Cs钟的短期稳定性较差有关。后续研究中将会增加实验方案,分析不同类型原子钟在进行钟差预报时原始序列长度与预报长度的关系,以形成一套合理的原始序列长度选择机制。
| [1] |
魏亚静, 袁海波, 董绍武, 等. BDS星钟预报误差分析及对授时性能的影响[J]. 时间频率学报, 2016, 39(4): 301-307 (Wei Yajing, Yuan Haibo, Dong Shaowu, et al. Error Analysis of BDS Satellite Clock Difference Prediction and Its Impact on Performance[J]. Journal of Time and Frequency, 2016, 39(4): 301-307)
(  0) 0) |
| [2] |
雷雨, 赵丹宁. 基于经验模式分解和最小二乘支持向量机的卫星钟差预报[J]. 天文学报, 2014, 55(3): 216-227 (Lei Yu, Zhao Danning. The Satellite Clock Bias Forecast Based on Empirical Mode Decomposition and Least Squares Support Vector Machines[J]. Acta Astronomica Sinica, 2014, 55(3): 216-227)
(  0) 0) |
| [3] |
王向磊. 钟差预报模型的分析和比较[J]. 全球定位系统, 2018, 43(2): 84-90 (Wang Xianglei. The Analysis and Comparision of Clock Error Prediction Models[J]. GNSS World of China, 2018, 43(2): 84-90)
(  0) 0) |
| [4] |
王宇谱, 吕志平, 孙大双, 等. 一种改进钟差二次多项式模型的导航卫星钟差预报方法[J]. 天文学报, 2016, 57(1): 78-90 (Wang Yupu, Lü Zhiping, Sun Dashuang, et al. A New Navigation Satellite Clock Bias Prediction Method Based on Modified Clock-Bias Quadratic Polynomial Model[J]. Acta Astronomica Sinica, 2016, 57(1): 78-90)
(  0) 0) |
| [5] |
崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报:信息科学版, 2005, 30(5): 447-450 (Cui Xianqiang, Jiao Wenhai. Grey System Model for the Satellite Clock Error Prediction[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 447-450)
(  0) 0) |
| [6] |
于烨, 黄默, 王小青, 等. 利用最小一乘法改进的灰色模型的导航卫星钟差预报[J]. 测绘通报, 2019(4): 1-6 (Yu Ye, Huang Mo, Wang Xiaoqing, et al. Navigation Satellite Clock Bias Prediction Based on Grey Model Improved by Least Absolute Deviations[J]. Bulletin of Surveying and Mapping, 2019(4): 1-6)
(  0) 0) |
| [7] |
张清华, 隋立芬, 牟忠凯, 等. 利用改进灰色模型的钟差预报算法及其精度分析[J]. 测绘科学, 2012, 37(1): 54-56 (Zhang Qinghua, Sui Lifen, Mou Zhongkai, et al. A Prediction Method of the Clock Errors Based on Modified Grey Model[J]. Science of Surveying and Mapping, 2012, 37(1): 54-56)
(  0) 0) |
| [8] |
梁月吉, 任超, 杨秀发, 等. 基于一次差的灰色模型在卫星钟差预报中的应用[J]. 天文学报, 2015, 56(3): 264-277 (Liang Yueji, Ren Chao, Yang Xiufa, et al. Grey Model Based on First Difference in the Application of the Satellite Clock Bias Prediction[J]. Acta Astronomica Sinica, 2015, 56(3): 264-277)
(  0) 0) |
| [9] |
孙启松, 王宇谱. 基于方差递推法的Kalman滤波在钟差预报中的应用[J]. 测绘与空间地理信息, 2016, 39(6): 93-95 (Sun Qisong, Wang Yupu. Clock Bias Prediction by Application of Kalman Filter Based on Recursive Variance Method[J]. Geomatics and Spatial Information Technology, 2016, 39(6): 93-95)
(  0) 0) |
| [10] |
Huang G W, Zhang Q. Real-Time Estimation of Satellite Clock Offset Using Adaptively Robust Kalman Filter with Classified Adaptive Factors[J]. GPS Solutions, 2012, 16(4): 531-539 DOI:10.1007/s10291-012-0254-z
(  0) 0) |
| [11] |
朱祥维, 肖华, 雍少为, 等. 卫星钟差预报的Kalman算法及其性能分析[J]. 宇航学报, 2008, 29(3): 966-970 (Zhu Xiangwei, Xiao Hua, Yong Shaowei, et al. The Kalman Algorithm Used for Satellite Clock Offset Prediction and Its Performance Analysis[J]. Journal of Astronautics, 2008, 29(3): 966-970)
(  0) 0) |
| [12] |
王宇谱, 吕志平, 陈正生, 等. 卫星钟差预报的小波神经网络算法研究[J]. 测绘学报, 2013, 42(3): 20-28 (Wang Yupu, Lü Zhiping, Chen Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 20-28)
(  0) 0) |
| [13] |
黄观文, 崔博斌, 张勤, 等. 附加周期和神经网络补偿的实时钟差预报模型[J]. 宇航学报, 2018, 39(1): 83-88 (Huang Guanwen, Cui Bobin, Zhang Qin, et al. Real-Time Clock Offset Prediction Model with Periodic and Neural Network Corrections[J]. Journal of Astronautics, 2018, 39(1): 83-88)
(  0) 0) |
| [14] |
Wang Y P, Lü Z P, Qu Y Y, et al. Improving Prediction Performance of GPS Satellite Clock Bias Based on Wavelet Neural Network[J]. GPS Solutions, 2016, 21(2): 523-534
(  0) 0) |
| [15] |
黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报:信息科学版, 2008, 33(5): 496-499 (Huang Guanwen, Zhang Qin, Xu Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 496-499)
(  0) 0) |
| [16] |
Huang G W, Zhang Q, Xu G C. Real-Time Clock Offset Prediction with an Improved Model[J]. GPS Solutions, 2014, 18(1): 95-104 DOI:10.1007/s10291-013-0313-0
(  0) 0) |
| [17] |
李晓宇, 杨洋, 胡晓粉, 等. 基于改进灰色ARMA模型的卫星钟差短期预报研究[J]. 大地测量与地球动力学, 2013, 33(1): 59-63 (Li Xiaoyu, Yang Yang, Hu Xiaofen, et al. Research on Short-Term Prediction of Satellite Clock Errors Based on Improved Grey ARMA Model[J]. Journal of Geodesy and Geodynamics, 2013, 33(1): 59-63)
(  0) 0) |
| [18] |
雷雨, 赵丹宁. 基于灰色模型和最小二乘支持向量机的卫星钟差预报[J]. 天文研究与技术, 2014, 11(1): 39-45 (Lei Yu, Zhao Danning. Prediction of Satellite Clock Errors with a Combination of the Grey Model and the Least-Squares Support Vector Machines[J]. Astronomical Research and Technology, 2014, 11(1): 39-45)
(  0) 0) |
| [19] |
黄飞江, 陈演羽, 李廷会, 等. 基于灰色模型和混沌时间序列的卫星钟差预测算法[J]. 电子学报, 2019, 47(7): 1 416-1 424 (Huang Feijiang, Chen Yanyu, Li Tinghui, et al. A Satellite Clock Bias Prediction Algorithm Based on Grey Model and Chaotic Time Series[J]. Acta Electronica Sinica, 2019, 47(7): 1 416-1 424)
(  0) 0) |
| [20] |
许雪晴.地球定向参数高精度预报方法研究[J].天文学报, 2015, 56(5): 526-527 (Xu Xueqing. Research on High Accuracy Prediction Methods of Earth Orientation Parameters[D].Acta Astronomica Sinica, 2015, 56(5): 526-527) http://www.cnki.com.cn/Article/CJFDTotal-TWXB201505012.htm
(  0) 0) |
| [21] |
席超, 蔡成林, 李思敏, 等. 基于ARMA模型的导航卫星钟差长期预报[J]. 天文学报, 2014, 55(1): 78-89 (Xi Chao, Cai Chenglin, Li Simin, et al. Long-Term Satellite Clock Bias Prediction Based on ARMA Model[J]. Acta Astronomica Sinica, 2014, 55(1): 78-89)
(  0) 0) |
| [22] |
刘伟峰, 杨爱兰. 基于BIC准则和Gibbs采样的有限混合模型无监督学习算法[J]. 电子学报, 2011, 39(增): 134-139 (Liu Weifeng, Yang Ailan. Unsupervised Learning for Finite Mixture Models Based on BIC Criterion and Gibbs Sampling[J]. Acta Electronica Sinica, 2011, 39(S): 134-139)
(  0) 0) |
| [23] |
陈晓锋. AIC准则及其在计量经济学中的应用研究[D].天津: 天津财经大学, 2012 (Chen Xiaofeng. Akaike Information Criterion and Its Application in Econometrics[D]. Tianjin: Tianjin University of Finance and Economics, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10070-1013169106.htm
(  0) 0) |
| [24] |
韩保民, 郭振华. 改进的精密卫星钟差预报法[J]. 辽宁工程技术大学学报:自然科学版, 2013, 32(9): 1 265-1 268 (Han Baomin, Guo Zhenhua. Improved Algorithm for Prediction of Precise Satellite Clock Bias[J]. Journal of Liaoning Technical University:Natural Science, 2013, 32(9): 1 265-1 268)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


