2. 西安测绘研究所,西安市雁塔路中段1号,710054
目前全球主要卫星导航系统采用的广播电离层修正模型和发播参数各异,其中,北斗全球系统同时播发BDGIM和BDS Klobuchar两种电离层修正模型。学者们对多种广播电离层模型的修正效果进行了对比分析[1-4],但针对BDGIM模型精度评估的研究较少[5]。为满足北斗用户的需求,本文对各类广播电离层模型的特点进行分析,在此基础上,以IGS分析中心CODG格网电离层模型为精度评估标准,将BDGIM与其他3种广播电离层模型进行比较分析,为实际应用提供参考。
1 广播电离层模型差异分析GPS Klobuchar模型采用电离层薄层假设,在地磁坐标系下利用八参数余弦函数表达式进行计算,反映电离层周日振幅和相位变化[6]。但Klobuchar模型属于统计经验模型,仅能反映电离层平稳期的周日平均特性,全球平均改正效果较差。
Galileo系统采用的NeQuickG模型为三维电离层电子密度半经验模型,该模型基于电离层剖面公式,将电离层分为底部和顶部两个部分。由于模型涉及路径电子含量数值积分运算,在公式及计算时效性上较Klobuchar模型复杂[7]。Galileo NeQuickG模型采用与地磁纬度有关的有效电离因子代替NeQuick模型中的输入参数F10.7,以满足实时修正需求。
BDS在B1I、B3I频点播发的改进Klobuchar电离层修正模型同样以Klobuchar为基础模型。与GPS Klobuchar模型相比,BDS Klobuchar模型采用日固地理坐标系,其地理经度与时间具有良好的一致性,能够更好地反映电离层的周日变化[8],在计算系数限值上也与GPS Klobuchar模型略有不同。BDS Klobuchar模型最早服务于北斗区域卫星导航系统,因此其将高精度修正区域设定在中国及周边区域。
BDS在B1C、B2a频点播发的BDGIM模型以改进的球谐函数为基础,模型计算简单,可有效满足用户计算效率与性能的需求。模型发播参数个数可调,综合考虑发播通信容量限制、布站条件、更新频率及模型修正精度等多个因素,目前选择9个更新发播参数。BDGIM数学结构式为:
| $ {T_{{\rm{ion}}}} = {M_F}\cdot\frac{{40.28 \times {{10}^{16}}}}{{{f^2}}}\cdot\left[ {{A_0} + \sum\limits_{i = 1}^9 {{\alpha _i}{A_i}} } \right] $ | (1) |
式中,MF为投影函数;f为当前信号对应的载波频率;αi(i=1, 9)为BDGIM模型的发播参数,可根据北斗基准站观测数据计算得到,并通过导航电文发播给用户;A0为根据固化于用户接收机的非发播电离层参数、用户日固坐标系下穿刺点地磁经纬度及观测时刻计算得到的预报值;Ai(i=1, 9)为根据用户穿刺点位置及观测时刻计算得到的函数值。
2 评估方法目前常用的广播电离层模型精度评定方法主要有两种:1)以利用监测站双频实测GNSS下行数据获得电离层穿刺点处的垂直电离层总电子含量(VTEC)值作为评价准则进行广播电离层精度评估[9];2)采用IGS分析中心提供的IONEX格式的后处理电离层格网图(GIM),通过对比各格网点处GIM和广播电离层模型计算的VTEC值的差异进行精度评定[3]。考虑到第1种方法受限于GNSS监测站的分布和观测数据的测量精度,本文选用第2种方法。
欧洲定轨中心(CODE)提供的全球电离层格网图(CODG)精度高、信息完整,被广泛应用于GNSS电离层研究中[10]。本文将全球划分为纬度2.5°、经度5°间隔的格网,利用后处理CODG计算每个格网点的VTEC,采用均方根误差(RMS)和修正百分比(per)两个指标进行评估。在修正百分比统计中,将单历元修正百分比小于0的结果作为粗差进行剔除。具体计算公式如下:
| $ {\rm{RMS}} = \sqrt {\frac{{\sum\limits_{i = 0}^N {{{({\rm{VTEC}}_{{\rm{model}}}^i - {\rm{VTEC}}_{{\rm{ref}}}^i)}^2}} }}{N}} $ | (2) |
| $ \left\{ \begin{array}{l} {\rm{pe}}{{\rm{r}}_i} = \left( {1 - \frac{{|{\rm{VTEC}}_{{\rm{model}}}^i - {\rm{VTEC}}_{{\rm{ref}}}^i|}}{{{\rm{VTEC}}_{{\rm{ref}}}^i}}} \right) \times 100\% \\ {\rm{per}} = (\frac{{\sum\limits_{i = 1}^{{N_{({\rm{pe}}{{\rm{r}}_i} \ge 0)}}} {{\rm{pe}}{{\rm{r}}_i}} }}{{{N_{({\rm{pe}}{{\rm{r}}_i} \ge 0)}}}}) \times 100\% \end{array} \right. $ | (3) |
式中,VTECmodel为广播电离层模型计算值,VTECref为评价基准参考值,N为参与评估的历元数。
3 BDGIM模型修正精度分析为评估上述4种广播电离层模型在不同纬度带的电离层延迟修正精度,对比4种模型在中国区域的修正效果,分析修正精度随时间的变化情况。本文采用2019-01~09后处理全球电离层图对4种模型的修正精度进行评估。
3.1 纬度带修正精度分析按纬度带对全球进行划分,设定低、中、高纬度范围分别为-30°~30°、±(30°~55°)、±(55°~90°)。采用全球电离层格网图对上述4种广播电离层模型精度进行评估,结果见表 1。
|
|
表 1 广播电离层模型全球精度统计 Tab. 1 Global accuracy statistics of broadcast ionosphere models |
从表 1可以看出,4种模型在北半球的修正精度普遍高于南半球,一方面由于在计算生成模型参数时南半球采用的监测站数量及分布相对北半球略有不足;另一方面由于南北半球测站数量与分布的差异,用作评估参考的CODG在南半球的精度低于北半球。高纬度地区NeQuickG模型修正精度最优,但在低纬度地区偏差较大。在中低纬度地区,BDGIM模型具有良好的修正效果,修正百分比可达74%以上,显著优于其他3种模型。GPS Klobuchar模型修正百分比随纬度降低而逐渐升高,BDS Klobuchar模型在中纬度地区比GPS Klobuchar模型更具优势,这是由于BDS Klobuchar主要设计服务于我国及周边地区,在北斗重点服务区内拥有较多的高性能监测站用于辅助发播模型参数的生成计算。
3.2 中国区域修正精度对比以CODG全球电离层格网为评价标准,对4种模型在中国区域(0°~55°N,70°~135°E)的电离层修正精度进行统计。从表 2可以看出,在中国区域内,与其他3种模型相比,BDGIM模型的修正精度可提高1.57~2.2 TECu,具有明显的优势,修正百分比达77.01%,可有效保证中国及周边区域的服务性能。
|
|
表 2 广播电离层模型区域精度统计 Tab. 2 Regional accuracy statistics of broadcast ionosphere models |
以CODG电离层格网为评价标准,评估全球范围内广播电离层模型修正精度及修正百分比随时间的变化情况(图 1、2)。BDS Klobuchar模型不具备高纬度地区的修正能力,因此未考虑。
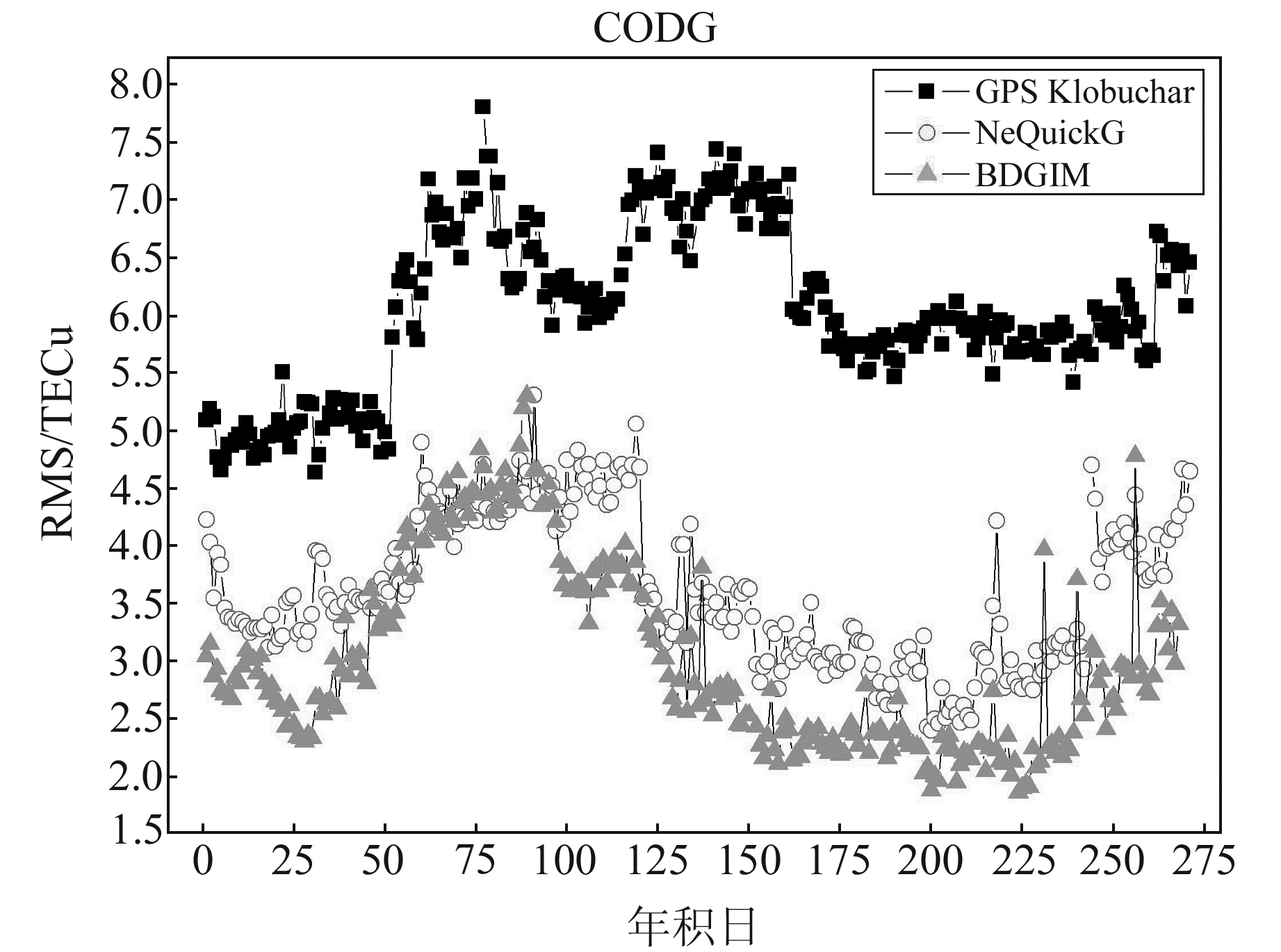
|
图 1 修正精度单天统计时间序列 Fig. 1 Time series diagram of single-day corrected precision statistic |
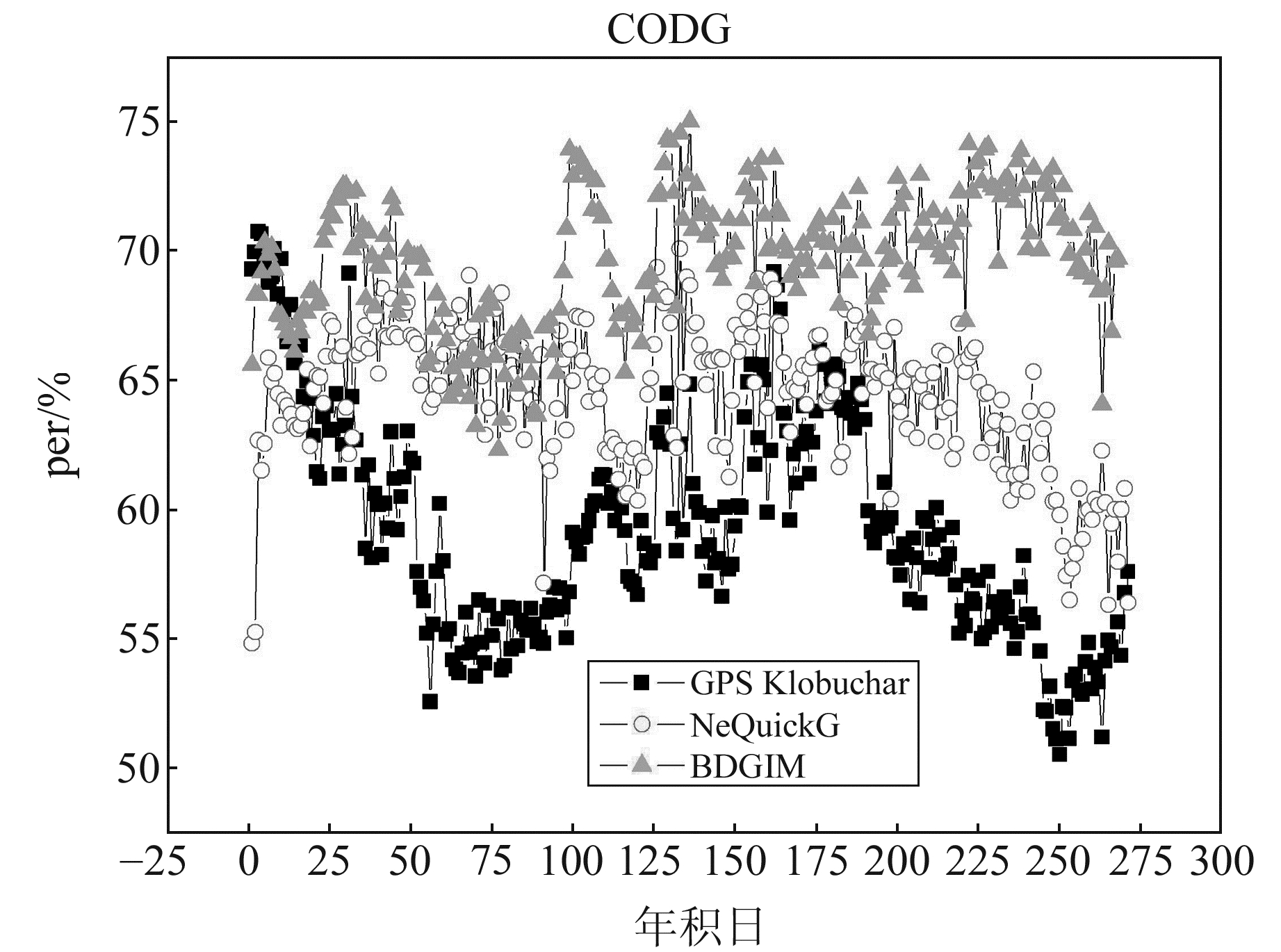
|
图 2 修正百分比单天统计时间序列 Fig. 2 Time series diagram of single-day corrected percentage statistic |
从图 1和图 2可以看出,3种全球电离层修正模型的修正精度存在明显的季节性变化。3~4月修正精度逐渐下降后又上升,在3月下旬达到最低值,这与地球绕日公转而产生的地球与太阳间的相对位置变化有关。图中结果表明,NeQuickG模型1~9月全球范围内平均修正精度为3.61 TECu,修正百分比为64.40%;BDGIM模型1~9月全球范围内平均修正精度为3.04 TECu,修正百分比为69.69%;GPS Klobuchar模型1~9月全球范围内平均修正精度为6.06 TECu,修正百分比为59.33%。
3.4 不同格网模型评估结果对比GIM可由全球监测站观测数据中的电离层信息获得。由于不同分析中心所采用的监测站数量和分布不同,使用的电离层格网处理方式也存在差异,导致GIM在全球的格网精度并不完全相同。目前电离层分析中心主要包括欧洲定轨中心(CODE)、美国喷气推进实验室(JPL)、中国科学院(CAS)等。CODE采用球谐函数展开式描述全球电离层总电子含量的时空分布;JPL采用电离层多层模型及全球三角格网模型计算GIM[11];CAS综合采用球谐函数和广义三角级数模型,可同时保障有、无观测数据覆盖区域的格网精度。本文分别以CODG、JPLG、CASG和产品综合生成的IGSG为评估参考值,对BDGIM模型进行对比评估,分析其差异性。图 3、4为1~9月单天全球范围内统计结果时间序列,表 3为不同格网模型评估结果对比。

|
图 3 不同格网模型修正精度时间序列 Fig. 3 Time series of single-day corrected accuracy using different grid models |
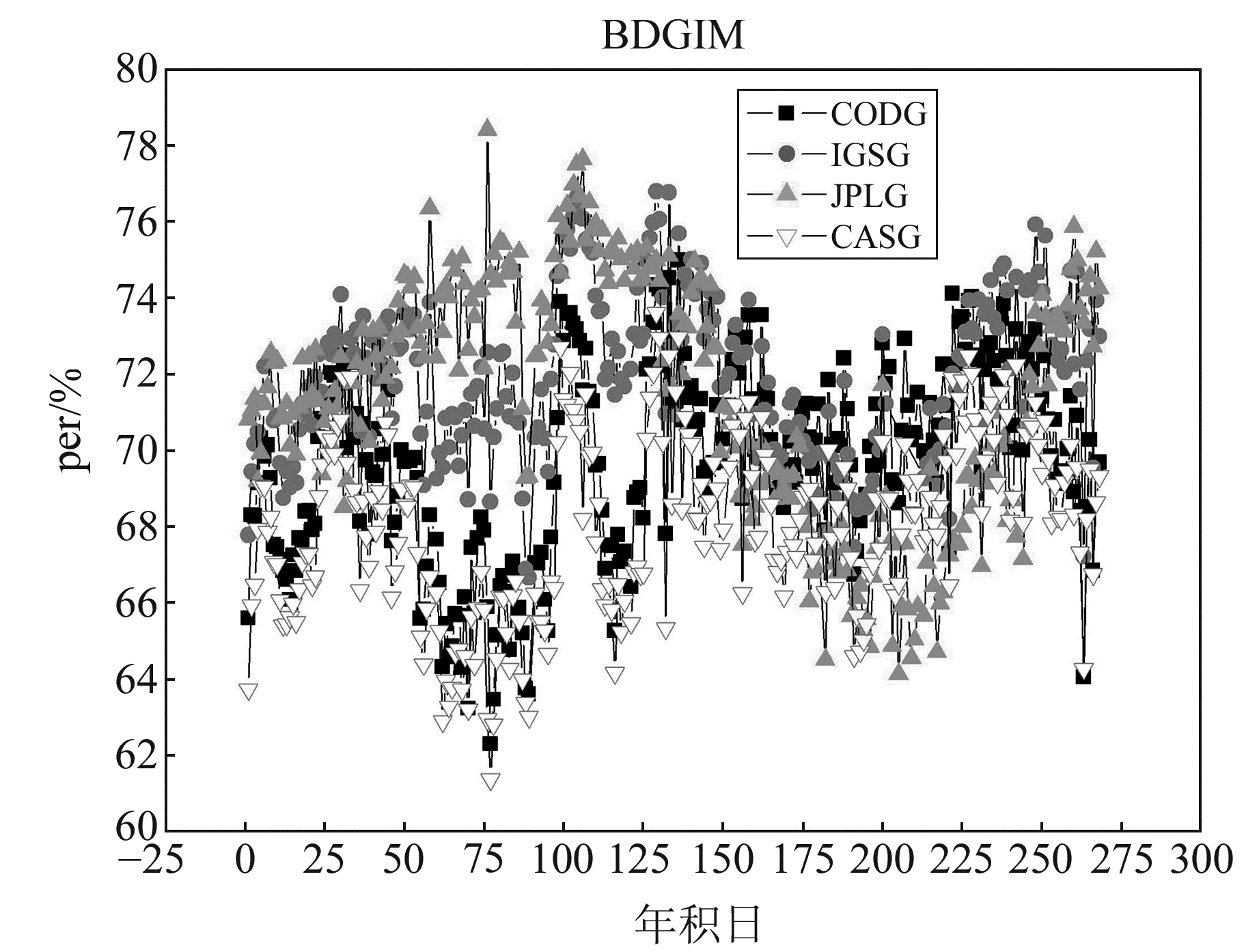
|
图 4 不同格网模型修正比时间序列 Fig. 4 Time series of single-day corrected percentage using different grid models |
|
|
表 3 不同格网模型评估结果对比 Tab. 3 Comparison of evaluation results using different grid models |
从上述图表中可以看出,4种电离层格网模型对BDGIM的评估结果差异较小,评估精度差异在0.3 TECu以内,修正百分比差异在3.86%以内。BDGIM与IGSG模型评估结果最为接近。
4 结语1) BDS Klobuchar模型和GPS Klobuchar模型计算简便,但全球平均改正效果较差。
2) 高纬度地区NeQuickG模型修正精度最优,但在低纬度地区偏差较大。
3) 在中低纬度地区,BDGIM模型具有良好的修正效果,显著优于其他3种模型。尤其在中国及周边区域修正百分比达77.01%,可有效保证北斗重点服务区的电离层修正效果。
4) 采用不同后处理电离层格网图进行精度评估的结果差异较小,BDGIM模型与IGSG模型最为接近。
| [1] |
程娜. GNSS广播电离层精度监测评估方法研究[D].西安: 长安大学, 2015 (Cheng Na. Study on Methods of Precision Monitoring and Assessment of Broadcast Ionospheric Model of GNSS[D]. Xi'an: Chang'an University, 2015) http://cdmd.cnki.com.cn/Article/CDMD-10710-1015802666.htm
(  0) 0) |
| [2] |
王宁波, 袁运斌, 李子申, 等. 不同NeQuick电离层模型参数的应用精度分析[J]. 测绘学报, 2017, 46(4): 421-429 (Wang Ningbo, Yuan Yunbin, Li Zishen, et al. Performance Analysis of Different NeQuick Ionospheric Model Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 421-429)
(  0) 0) |
| [3] |
刘帅, 贾小林. GNSS电离层模型改正精度评估与分析[J]. 空间科学学报, 2016, 36(3): 297-304 (Liu Shuai, Jia Xiaolin. Correction Accuracy Evaluation and Analysis for GNSS Ionosphere Model[J]. Chinese Journal of Space Science, 2016, 36(3): 297-304)
(  0) 0) |
| [4] |
孙满, 喻金, 胡艳, 等. 北斗电离层模型改正精度分析[J]. 测绘科学技术学报, 2015, 32(1): 27-31 (Sun Man, Yu Jin, Hu Yan, et al. Correction Accuracy Analysis on Ionospheric Model of Beidou System[J]. Journal of Geomatics Science and Technology, 2015, 32(1): 27-31)
(  0) 0) |
| [5] |
Yuan Y B, Wang N B, Li Z S, et al. The Beidou Global Broadcast Ionospheric Delay Correction Model(BDGIM) and Its Preliminary Performance Evaluation Results[J]. Navigation, 2019, 66(1): 55-69
(  0) 0) |
| [6] |
杨哲, 宋淑丽, 薛军琛, 等. Klobuchar模型和NeQuick模型在中国地区的精度评估[J]. 武汉大学学报:信息科学版, 2012, 37(6): 704-707 (Yang Zhe, Song Shuli, Xue Junchen, et al. Accuracy Assessment of Klobuchar Model and NeQuick Model in China[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6): 704-707)
(  0) 0) |
| [7] |
李施佳, 蔡昌盛, 戴吾蛟, 等. NeQuick2电离层改正模型的性能评估[J]. 测绘工程, 2015, 24(1): 40-43 (Li Shijia, Cai Changsheng, Dai Wujiao, et al. Performance Evaluation of NeQuick2 Ionosphere Model[J]. Engineering of Surveying and Mapping, 2015, 24(1): 40-43)
(  0) 0) |
| [8] |
张强, 赵齐乐, 章红平, 等. 北斗卫星导航系统Klobuchar模型精度评估[J]. 武汉大学学报:信息科学版, 2014, 39(2): 142-146 (Zhang Qiang, Zhao Qile, Zhang Hongping, et al. Evaluation on the Precision of Klobuchar Model for Beidou Navigation Satellite System[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 142-146)
(  0) 0) |
| [9] |
陈秀德, 贾小林, 朱永兴. 广播电离层模型性能评估及分析[J]. 导航定位学报, 2017, 5(1): 18-23 (Chen Xiude, Jia Xiaolin, Zhu Yongxing. Performance Estimation and Analysis on Broadcast Ionospheric Model[J]. Journal of Navigation and Positioning, 2017, 5(1): 18-23)
(  0) 0) |
| [10] |
陈秀德, 贾小林, 朱永兴, 等. 不同电离层格网产品的精度分析[J]. 大地测量与地球动力学, 2017, 37(8): 849-855 (Chen Xiude, Jia Xiaolin, Zhu Yongxing, et al. Analysis the Accuracy of Different Ionospheric Grid Products[J]. Journal of Geodesy and Geodynamics, 2017, 37(8): 849-855)
(  0) 0) |
| [11] |
李子申, 王宁波, 李敏, 等. 国际GNSS服务组织全球电离层TEC格网精度评估与分析[J]. 地球物理学报, 2017, 60(10): 3 718-3 729 (Li Zishen, Wang Ningbo, Li Min, et al. Evaluation and Analysis of the Global Ionospheric TEC Map in the Frame of International GNSS Services[J]. Chinese Journal of Geophysics, 2017, 60(10): 3 718-3 729)
(  0) 0) |
2. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China
 2020, Vol. 40
2020, Vol. 40

