2. 中国测绘科学研究院,北京市莲花池西路28号,100830;
3. 同济大学测绘与地理信息学院,上海市四平路1239号,200092;
4. 中国科学院上海天文台,上海市南丹路80号,200030;
5. 中国地震局地球物理研究所,北京市民族大学南路5号,100081
随着我国北斗技术全球覆盖进程的加快推进,以及地基基准站网的加密和升级,大规模GNSS网迎来了新的发展机遇。然而在GNSS原始观测信息不断丰富的同时,也给相关专业人员在大规模数据的预处理、组织管理、基准站选取、数据处理策略、分区方案、质量检核与评估等方面提出了一系列挑战[1-3]。同时为了满足高精度数据处理的需要,通常需要采用专门的数据处理软件(如GAMIT、GIPSY和Bernese)[4]进行解算。其中GAMIT/GLOBK具备可免费申请获取、开放源代码、更新速度快、解算精度高、自动化处理程度高等优点,在国内应用比较广泛[2]。
另外,随着mm级现代化大地测量技术的不断发展,高精度速度场日益成为精密定位不可或缺的基本要素之一。中国大陆构造环境监测网络(crustal movement observation network of China,CMONOC,简称陆态网)是目前推算中国大陆速度场的主要数据来源,已有不少学者利用陆态网数据开展中国大陆速度场的研究。魏子卿等[5]系统论述基于2000国家大地坐标系构建速度场模型的方法,对比了全局欧拉矢量法、局部欧拉矢量法和格网均值法的适用范围和精度;刘经南等[6]研究中国大陆区域在ITRF97框架下的速度场,并提出采用多面函数法拟合速度场;任雅奇[7]、于亮等[8]基于陆态网数据研究对比常用的数值拟合方法的精度。但是,由于使用的数据较少、数据连续性不强、缺乏明确的应用背景以及数据现势性不强等原因,现有研究成果在实用性方面仍有一定的局限。
鉴于此,本文首先基于中国陆态网260多个基准站2011~2017年的观测数据,使用GAMIT/GLBOK软件探讨大规模GNSS网高精度数据处理一体化方案,对数据处理过程中的几个关键点进行阐述,并给出解算成果质量检核与评估方法,以期为大规模GNSS网的数据解算提供相关借鉴;然后,基于陆态网速度场成果构建当代中国大陆水平格网速度场格网模型,并利用国内IGS站和区域站进行模型外符合精度检核。
1 陆态网测站与观测数据简介中国地壳运动观测网络主要由均匀分布在全国的260多个连续运行基准站和2 000多个不定期观测区域站构成。为将陆态网连续基准站同国际IGS站进行联合解算,需选取国内及周边的IGS站进行约束。基于连续性、稳定性和高精度性等原则,本文挑选17个IGS站进行处理。2 000多个区域站、260基准站和17个IGS站的分布见图 1。

|
图 1 陆态网测站与周边IGS测站分布 Fig. 1 Distribution of CMONOC and its surrounding IGS stations |
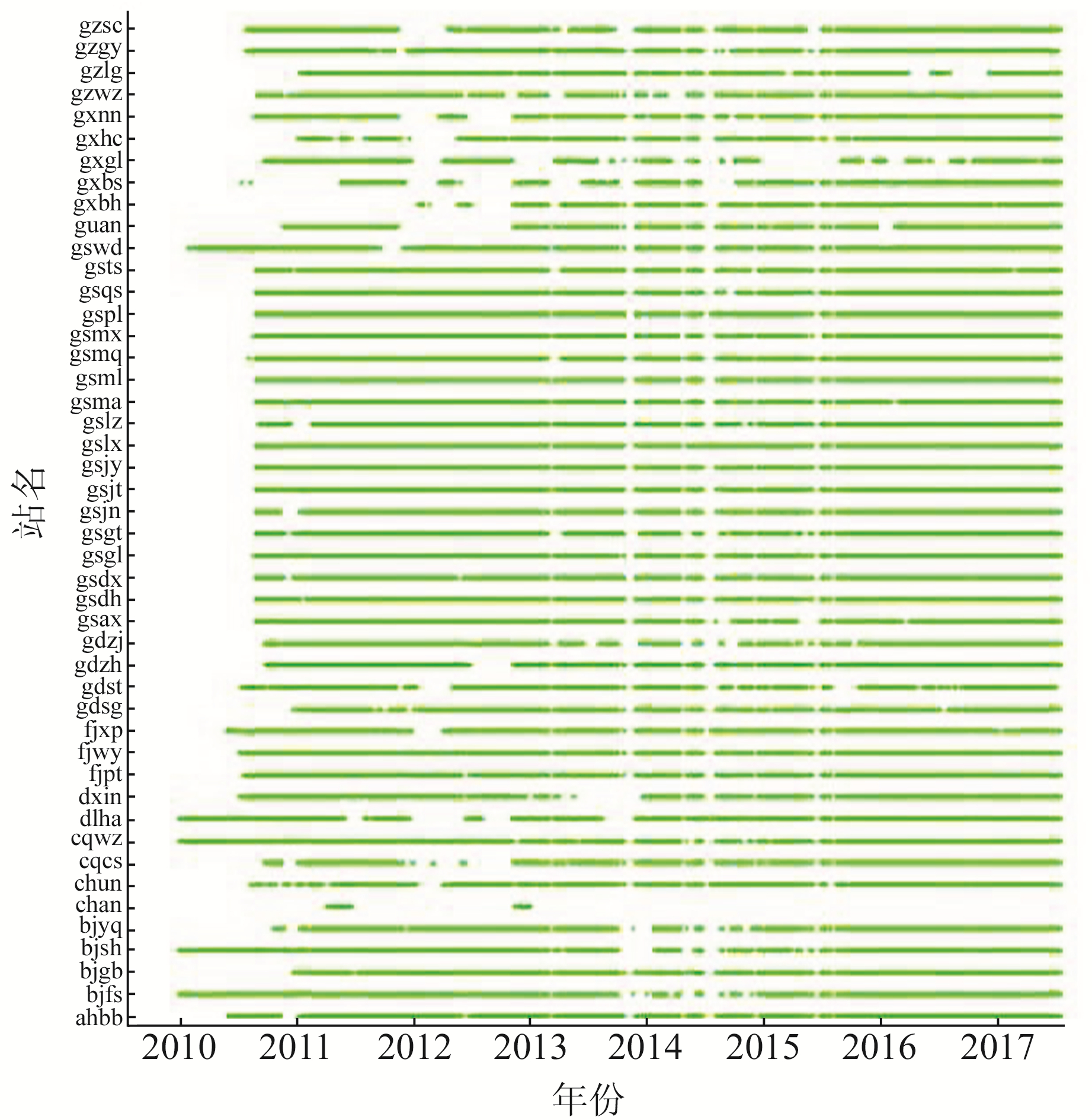
数据预处理主要包括格式标准化、完整性检查和质量检核。统计陆态网260多个基准站观测数据收集情况,有助于直观分析数据的完整性和连续性。本文统计了2011~2017年部分测站的数据收集情况(图 2),可以看出,2011年前陆态网处于初步完善中,因此测站数据缺失率较高;2011年后陆态网连续运行站除个别出现故障外,总体数据连续性良好。
|
图 2 部分陆态网CORS站观测数据连续性统计 Fig. 2 Continuity of observation data from some CORS stations |
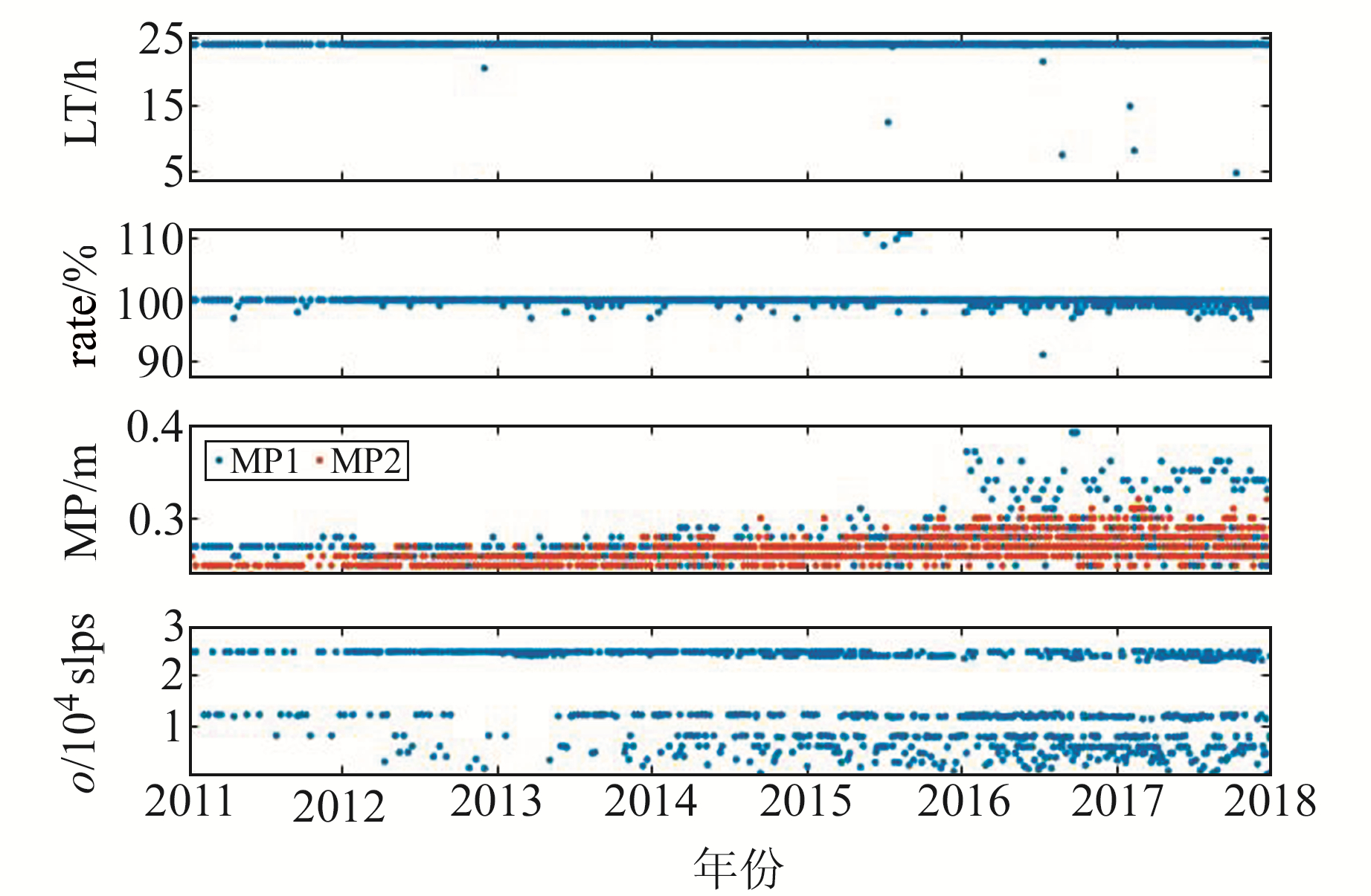
对观测数据进行质量检核,便于分析数据的电离层延迟、多路径影响、卫星信号信噪比等信息[9]。以BJFS站为例,质量检核统计结果如图 3所示,可以看出,2011~2017年BJFS站99%以上的单日观测时长为24 h;单日数据利用率在100%附近,最小利用率不低于90%;L1、L2载波相位观测值上的多路径效应分别小于0.4 m、0.3 m,但在2016年后多路径效应有明显的变大趋势;观测数据与周跳比总体小于30 000。以上分析表明,BJFS站观测数据质量良好,可用于解算分析。
|
图 3 BJFS站观测文件的质量检核结果 Fig. 3 Quality of observation data at BJFS station |
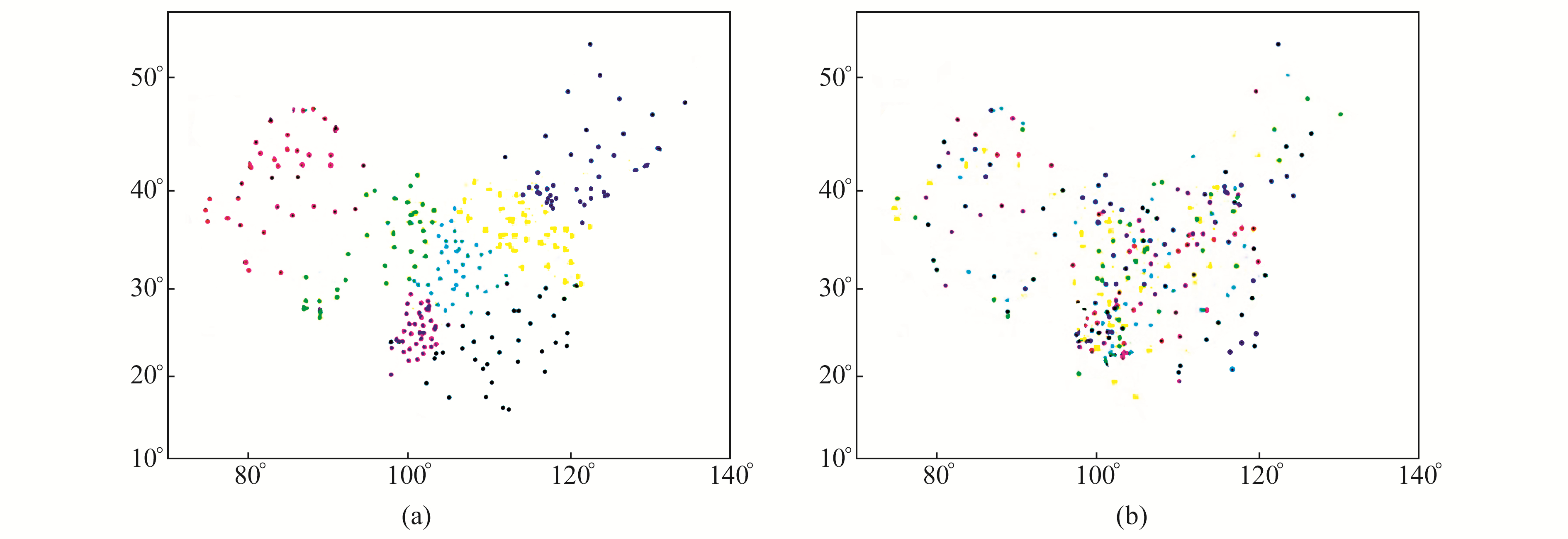
受计算机软件和硬件的限制,目前大多数GNSS数据处理软件只能同时处理少于100个测站的数据,通常采用的策略是将一个大规模GNSS基准站网分成若干子网,各子网独立解算后再联合处理得到最终结果。在采用子网解算大规模GNSS基准站网数据时,如何划分子网与选取公共站对解算结果存在一定的影响。子网划分方案大体分为两类[10]:一类是按地理属性进行区域划分,如图 4(a)所示;一类是按分布状态的均匀性原则进行划分,如图 4(b)所示。
|
图 4 陆态网基准站子网划分示意图 Fig. 4 Sub-network division of CMONOC stations |
由于GAMIT是基于双差原理进行基线解算的,若长短基线混合时采取针对中长基线的解算策略,则会造成短基线解算精度较低的现象。均匀划分法中的间距分区方案可以使测站分布更加均匀,避免了短基线的存在,而区域子网划分方案中会存在很多短基线,因此解算精度低于间距分区方案。本文采用间距分区方案将陆态网基准站划分为7个子网(图 4(b)),中国大陆周边的17个IGS站作为各分区的公共连接点。
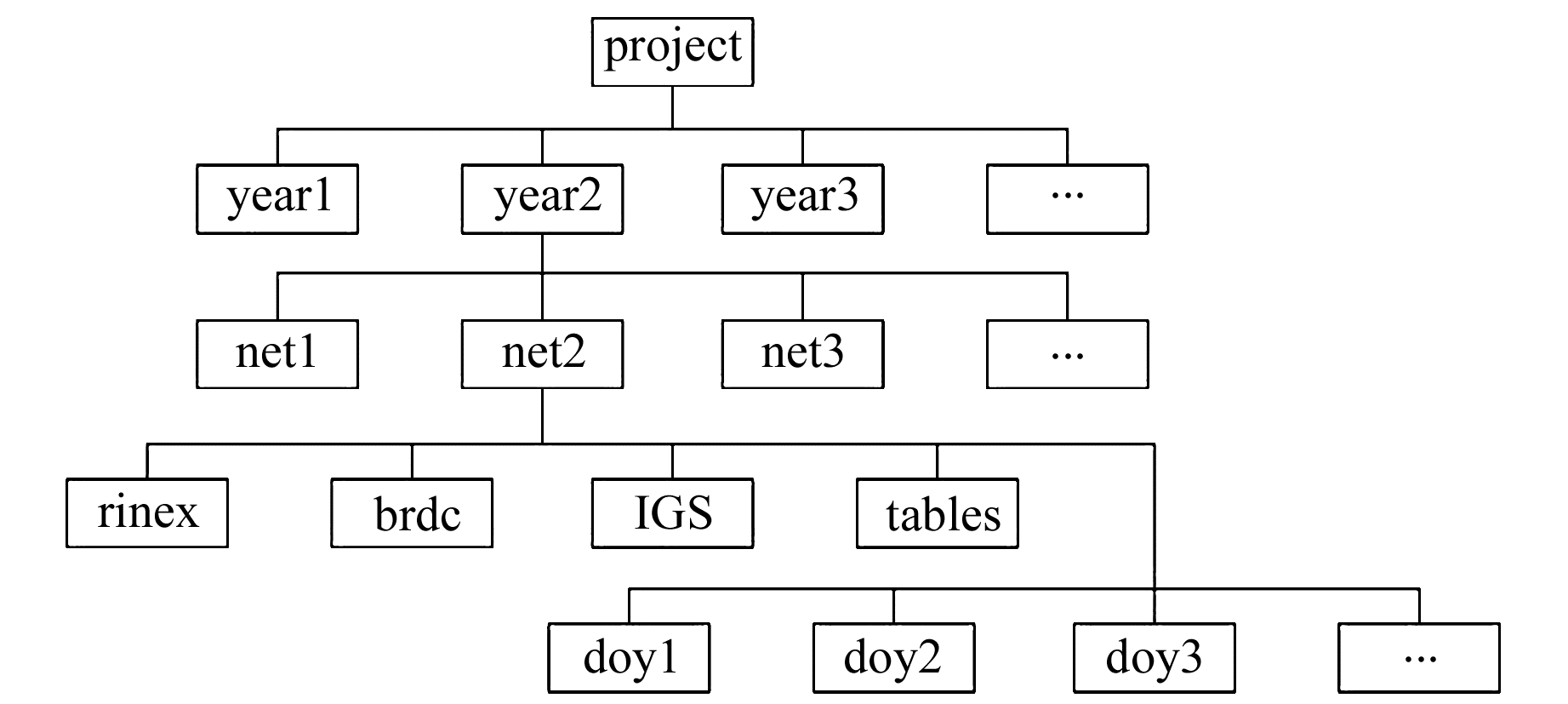
2.1.3 相关文件准备与数据整理下载对应时间段的国内及周边17个IGS站观测文件、广播星历和精密星历文件,更新GAMIT解算所需的表文件,配置GAMIT解算所需的控制文件(测站信息文件、测站信息控制文件、测段信息控制文件和近似坐标等文件)。另外,合理地组织数据有利于数据的处理,本文按年为二级目录组织数据文件(图 5)。
|
图 5 陆态网分区解算的数据组织结构 Fig. 5 Data organization of CMONOC partition solution |
采用GAMIT进行陆态网基线解算时,解算设置(基线处理模式、观测值组合模式、坐标参考框架、对流层改正模型、海潮模型改正等设置)的不同会对基线结果造成一定程度的影响[11]。本文数据处理的优化方案主要参数[11-12]设置见表 1。
|
|
表 1 基线解算优化设置 Tab. 1 Optimization settings of baseline solution |
组织并配置好基线解算所需的目录和文件后,使用GAMIT进行基线批处理[11-12],并根据图 5所示的项目数据组织结构,在三级目录中分别计算各年各分区的数据,解算得到的单天解文件存放在年积日文件夹下。
2.3 高精度GNSS网平差的优化方案GLOBK平差步骤较为繁琐,需人为干预和调试才能得到理想的结果。优化方案[13]总结如下:1)将单日解法方程文件转换为二进制文件,通过时序平差获得各分区测站坐标的时间序列;2)通过时间序列分析,确认具有异常域的特定站或特定历元并予以删除;3)将各分区的单日解文件合并为一个包含陆态网基准站坐标、卫星轨道和极移等参数的单日解文件;4)下载全球IGS站各分区的单日解文件,连同以上3个步骤得到的结果,合并得到包含IGS站坐标、卫星轨道和极移等参数的单日解文件;5)将包含全球IGS核心站信息和陆态网基准站信息的单日整体松弛解文件合并为一个整体单日解,同时得到测站坐标的时间序列,再次进行时间序列分析,检查是否含有粗差并剔除;6)挑选全球均匀分布的IGS核心站,将测站坐标约束至ITRF2014框架,最终平差获得陆态网基准站的坐标和速度。
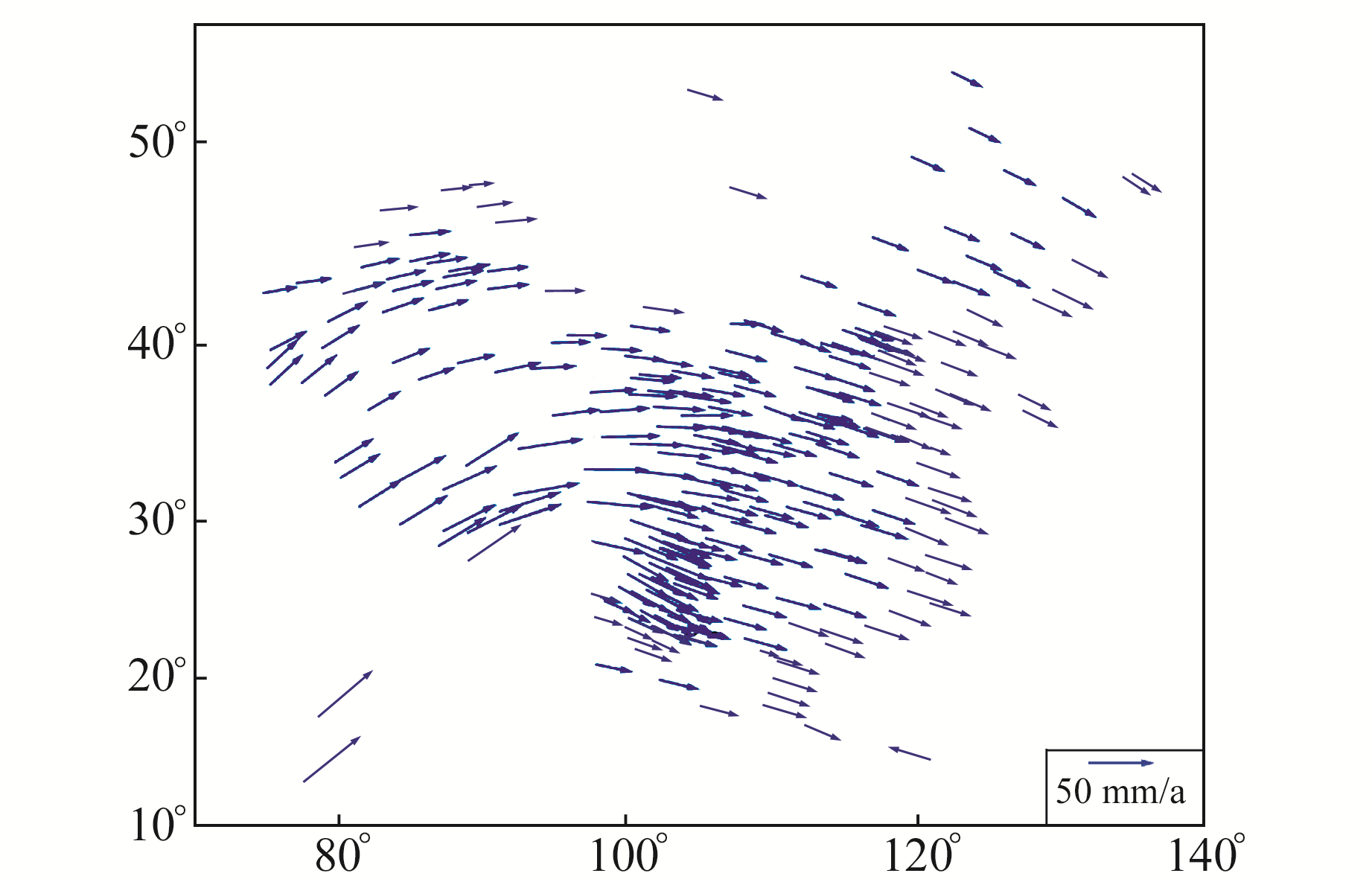
绘制陆态网基准站的速度场矢量图,如图 6所示。
|
图 6 陆态网基准站速度场矢量图 Fig. 6 Velocity field of CMONOC reference stations |
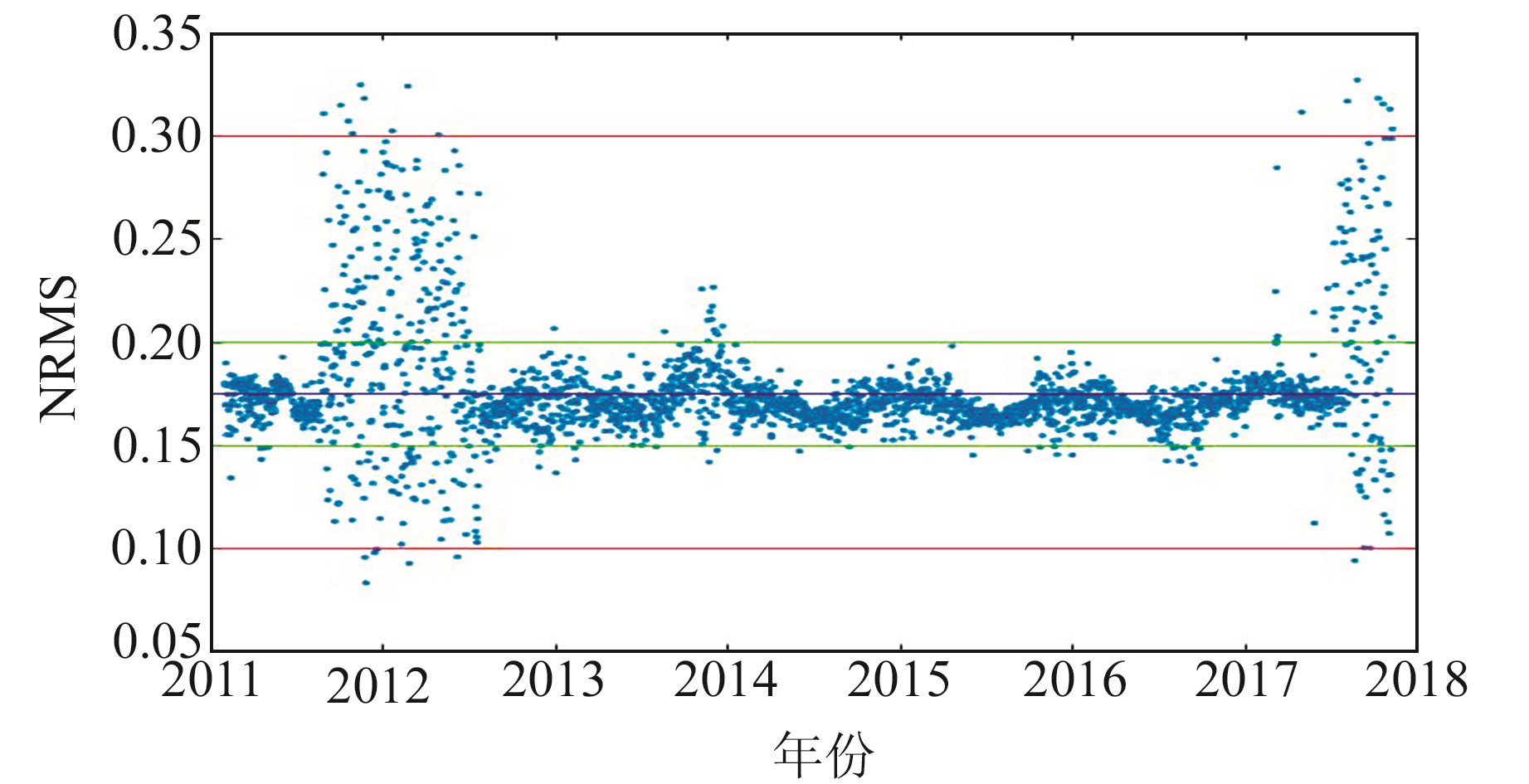
以陆态网net1子网为例,统计并绘制2011~2017年基线单日解的NRMS值图。由图 7可见,各单日解NRMS最大值不超过0.35,均值在0.18附近,除个别值偏离平均值较大外,总体上NRMS值在0.10~0.30之间,其中,在2012年和2017年底附近,由于观测数据质量较差而导致NRMS浮动较大,但总体符合基线解的精度要求。
|
图 7 陆态网net1子网基线单日解NRMS值统计 Fig. 7 NRMS of baseline single-day solution in subnet net1 |
对net1子网各基线的坐标重复性、基线重复性和基线相对重复性[10]的分析可知,基线解的相对精度能达到10-9左右,短基线的精度优于1 mm,符合基线解的精度要求,且重复性与基线长度有明显的线性关系,线性回归拟合求出重复性的常数部分和比例系数分别为0.000 6、6.6×10-10。
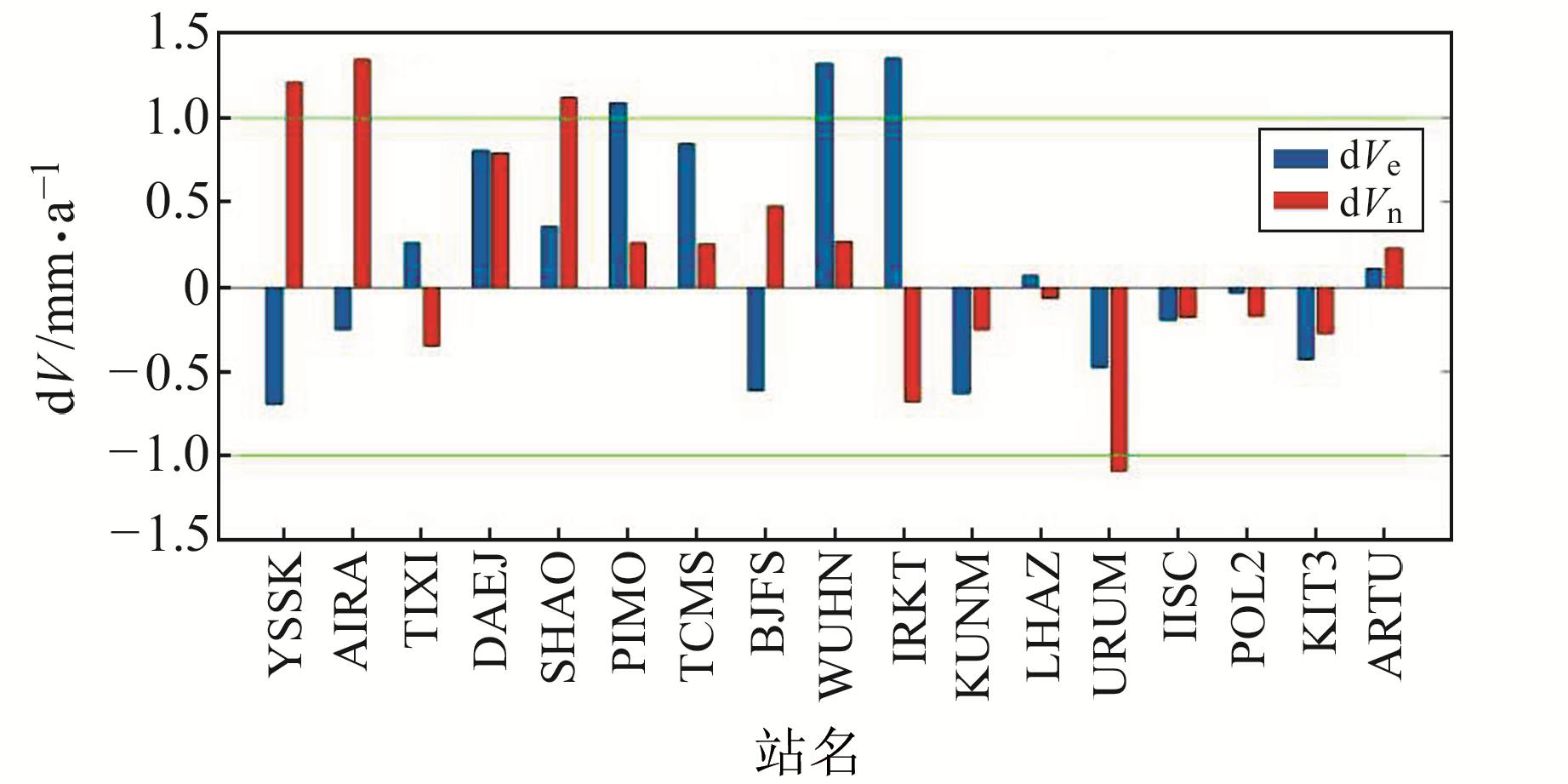
3.2 网平差结果的质量评估 3.2.1 国内及周边IGS站速度解的精度分析为了检验陆态网基准站速度场解算成果,首先以国内及周边的17个IGS站作为外部检核点,对比测站速度解算值与ITRF2014公布的速度值,得到速度残差(图 8)。统计其外符合精度信息可得,17个外部检核点东、北方向速度残差绝对值的最大值不超过1.5 mm/a,且绝对值的平均值不超过0.6 mm/a,中误差不超过0.7 mm/a,完全满足高精度解算要求。
|
图 8 IGS站的水平速度残差柱状图 Fig. 8 Horizontal velocity residuals of each IGS station |
求取测站速度的主要目的是通过某一历元时刻的坐标递推至任意历元的坐标,因此速度的精度对于坐标递推结果的精度具有重要意义。通过对实验解算的国内IGS站进行坐标递推结果的精度验证,以进一步分析陆态网速度场产品的精度和可靠性。
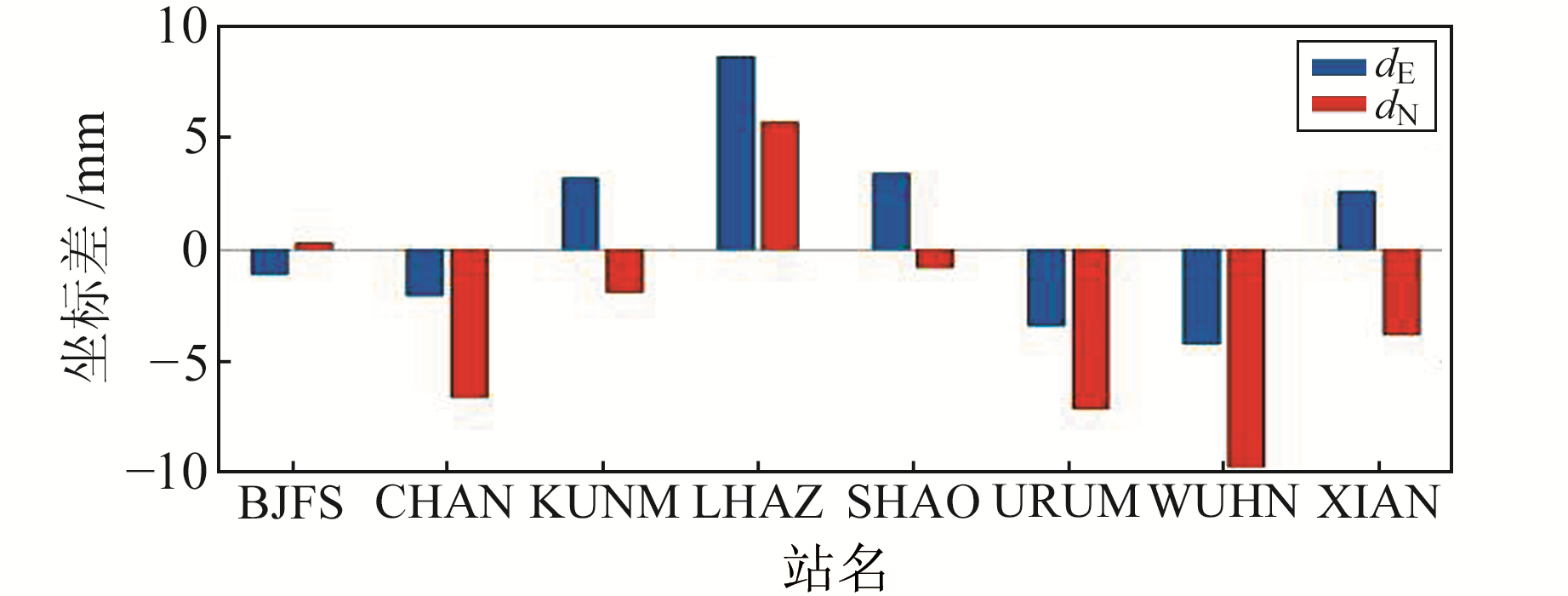
取8个IGS站2012.0历元时刻的坐标作为初值,利用解算的速度值计算2017.0历元时刻测站的坐标,与SOPAC网站获取的2017.0历元时刻的精确坐标作对比,东、北方向的坐标差如图 9所示。可以看出,3个测站水平方向的坐标差绝对值最大不超过10 mm,东、北方向坐标差的平均误差分别为3.6 mm、4.5 mm,中误差分别为4.3 mm、4.8 mm。
|
图 9 速度推算的坐标与SOPAC发布的坐标之间差异统计 Fig. 9 Difference between the calculated coordinate using velocity and that provide by SOPAC |
目前,中国地震局GNSS数据产品服务平台也提供陆态网连续运行基准站的水平速度场文件。为了进一步验证本文解算的中国大陆速度场产品的精度和可靠性,有必要与现有速度场产品进行对比分析,同时起到两套速度场相互检验的作用。将260多个陆态网基准站的两套速度场作差,得到每个站点东、北方向的速度残差值(图 10)。
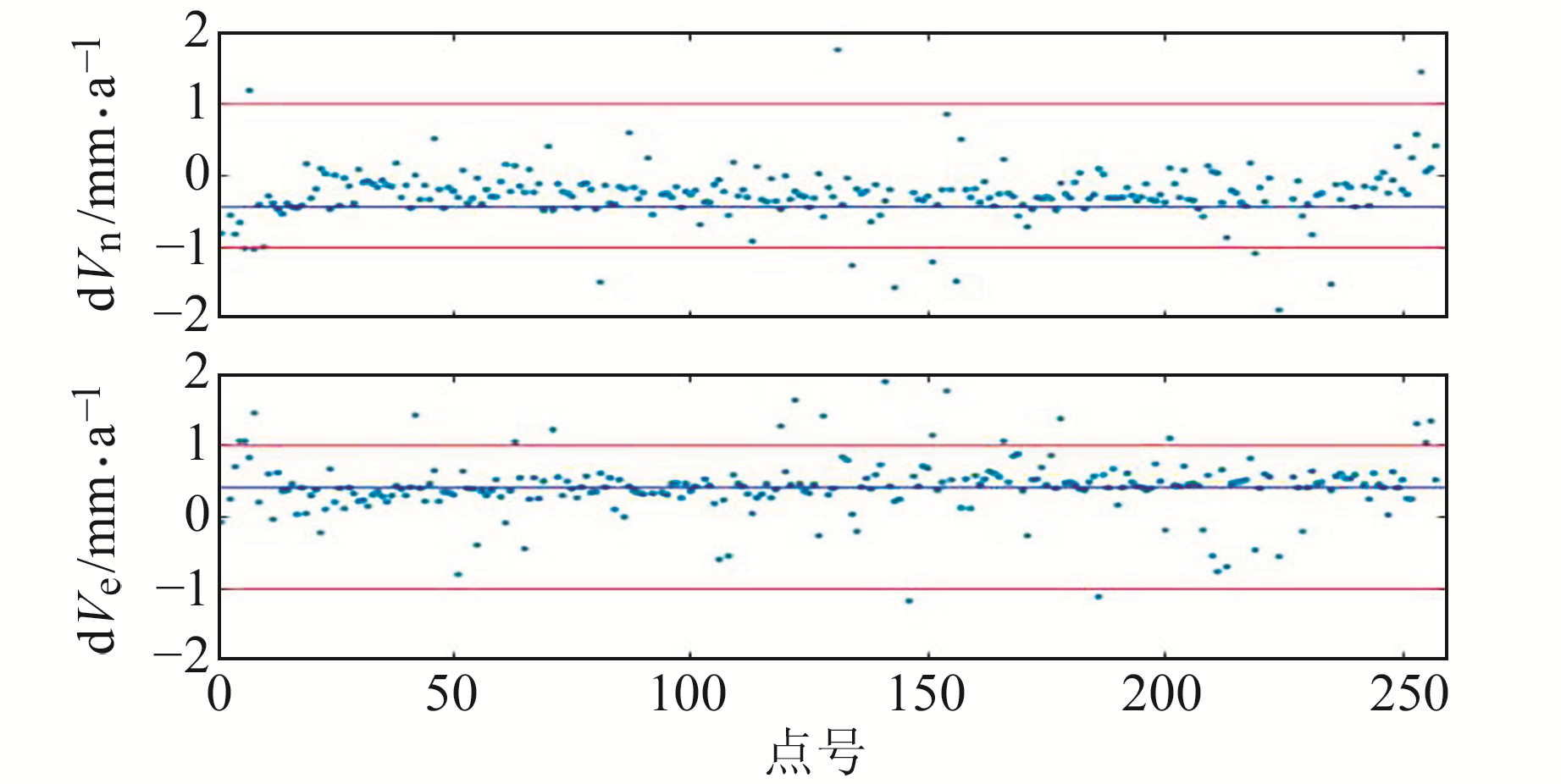
|
图 10 陆态网连续运行站的水平速度残差 Fig. 10 Horizontal velocity residuals of all CMONOC reference stations |
由图 10可知,连续运行基准站的两套速度场产品东、北方向的速度残差绝对值的最大值不超过2 mm/a,绝对值的平均值不超过0.5 mm/a,中误差不超过0.7 mm/a。由于中国地震局发布的速度场产品是基于1999年至今的GPS观测数据解算得到的,其代表的是测站近20 a来的平均速度值,而本文速度解是基于2011~2017年的观测数据解算得到的,同时数据解算成果受解算方案等多种因素的影响,因此两套速度场产品不可避免地存在差异。
3.3.2 对比时序分析得到的速度场产品由于受到仪器变更、地震等因素的影响,原始时间序列通常存在阶跃,而且距离地震近的测站还存在显著的震后形变的影响[14]。此外,GNSS观测站还记录到了受地表质量迁移引起的季节性负荷形变的影响。因此,在进行时间序列分析时,有必要对上述非构造形变进行参数估计,测站的周期性变化主要考虑周年和半年变化[14]。
对阶跃的处理,现有的分段线性探测法往往忽略了非线性信号的影响,且无法准确地确定阶跃发生的历元。利用奇异谱分析对GPS测站坐标序列进行预处理,可以准确地探测粗差,并确定阶跃发生的历元时刻与对应的阶跃值;然后根据时序分析基本方程构建误差方程,并求取最小二乘参数解[14-15]。通过时序分析提取陆态网基准站的速度项,与文中使用GLOBK解算的速度场产品进行对比分析,可进一步检验速度场解算的精度与可靠性。由图 11可知,两套速度场产品东、北方向的速度残差绝对值的最大值不超过1.8 mm/a,绝对值的平均值不超过0.3 mm/a,中误差不超过0.5 mm/a。这些精度指标再次验证,本文解算的速度场成果具有高精度和高可靠性。
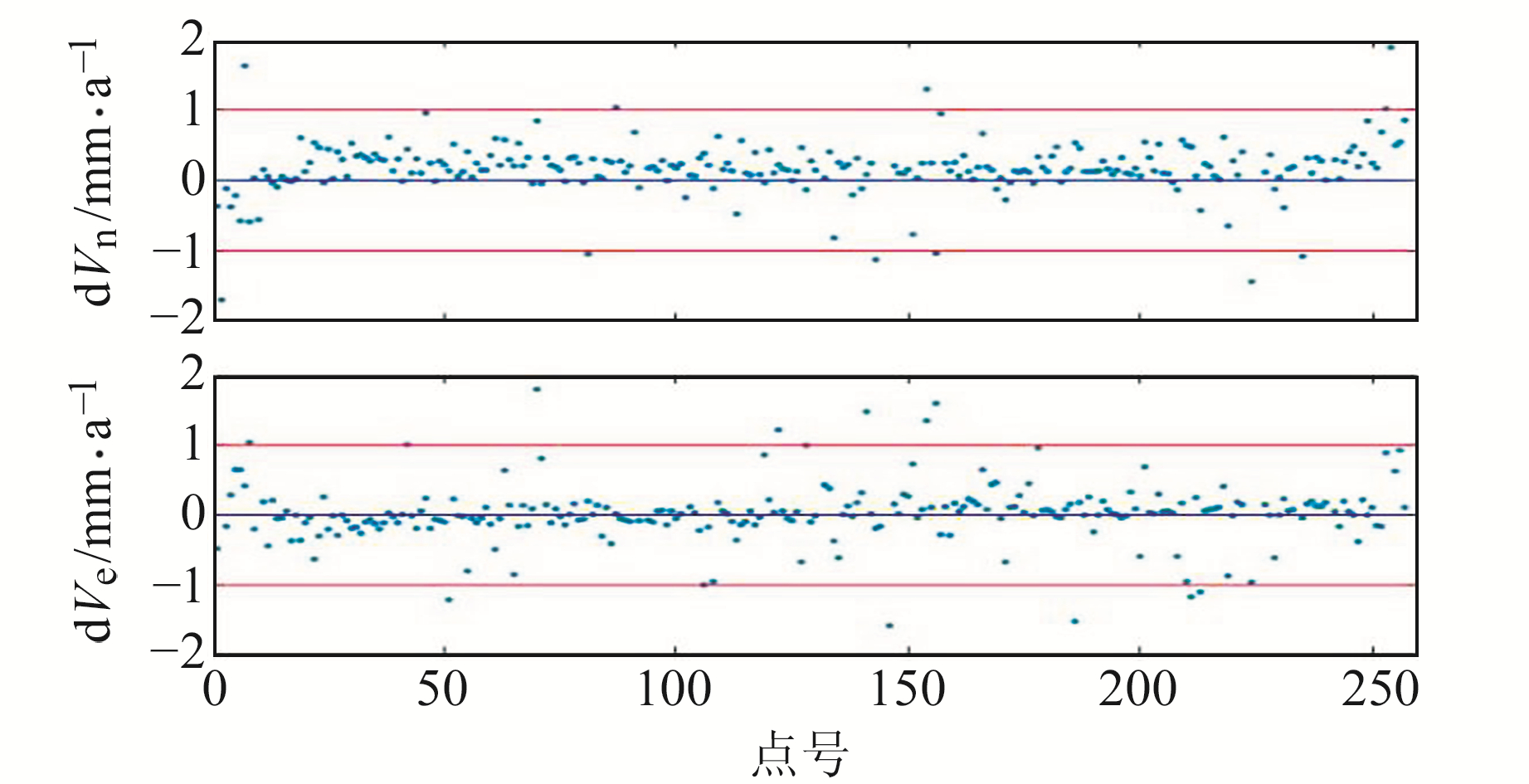
|
图 11 陆态网连续运行站的水平速度残差 Fig. 11 Horizontal velocity residuals of all CMONOC reference stations |
克里金法[16]作为地理统计常用的一种方法,其模型以变异函数理论和结构分析理论为基础,是在有限区域内对区域化变量进行线性无偏最优估计的一种方法。克里金法同时考虑了随机数据的期望和方差等信息,因此精度较为可靠。由于克里金插值公式复杂,本文仅介绍基于普通克里金法进行速度插值的主要步骤。
1) 计算陆态网基准站的数据集Qi(xi, yi, zi)(i=1, 2, …, n,xi、yi为经、纬度信息,zi为速度信息)中任意两点之间的距离和速度半方差值为:
| $ {d_{ij}} = \sqrt {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2}} $ | (1) |
| ${r_{ij}} = \frac{1}{2}{\left( {{z_i} - {z_j}} \right)^2}, \left( {i, j = 1, 2, \cdots , n} \right) $ | (2) |
2) 在数据对(dij, rij)中寻找最优拟合函数,拟合两者之间的函数关系,得到最优拟合函数关系式为:
| $ r = r\left( d \right) $ | (3) |
3) 根据最优拟合函数计算得到所有已知离散点集之间的半方差rij;
4) 对未知点z0,根据最优拟合函数计算得到未知点到已知点之间的半方差ri0;
5) 代入式(4),利用最小二乘原理求解最优权重系数λi:
| $ \left\{ {\begin{array}{*{20}{l}} {{r_{k0}} - \mathop \sum \limits_{j = 1}^n {\lambda _j}{r_{kj}} + u = 0, k = 1, 2, \cdots , n}\\ {\mathop \sum \limits_{i = 1}^n {\lambda _i} = 1} \end{array}} \right. $ | (4) |
式中,u为拉格朗日乘子;
6) 求出权重系数λi后,代入目标方程,求出待定点速度值
| $ {\hat z_0} = \mathop \sum \limits_{i = 1}^n {\lambda _i}{r_{i0}} $ | (5) |
为了便于速度场模型的发布和使用,首先将中国大陆区域按照1°×1°的格网间隔分为1 000个左右的格网,然后以上文解算得到的陆态网基准站的速度场产品为已知值,采用克里金插值分别计算出每个格网中心点的东、北方向的速度值,并绘制中国大陆水平格网速度场图(图 12)。

|
图 12 中国大陆水平格网速度场成果示意图 Fig. 12 Horizontal grid velocity field in Chinese mainland |
为了初步检验中国大陆水平格网速度场模型的精度,利用ITRF2014公布的国内8个IGS测站的速度值作为真实观测值,与本文构建的ITRF2014下1°×1°水平格网速度场模型的插值结果作比较,得到8个IGS站东、北方向速度差值(图 13)。除CHAN站东方向的速度残差值较大外,其余各测站的水平方向速度残差均在2 mm/a左右。统计IGS站东、北方向的速度残差的平均误差分别为1.41 mm/a、1.21 mm/a,东、北方向的速度残差的中误差分别为1.75 mm/a、1.38 mm/a。8个IGS站的站址和速度见表 2。
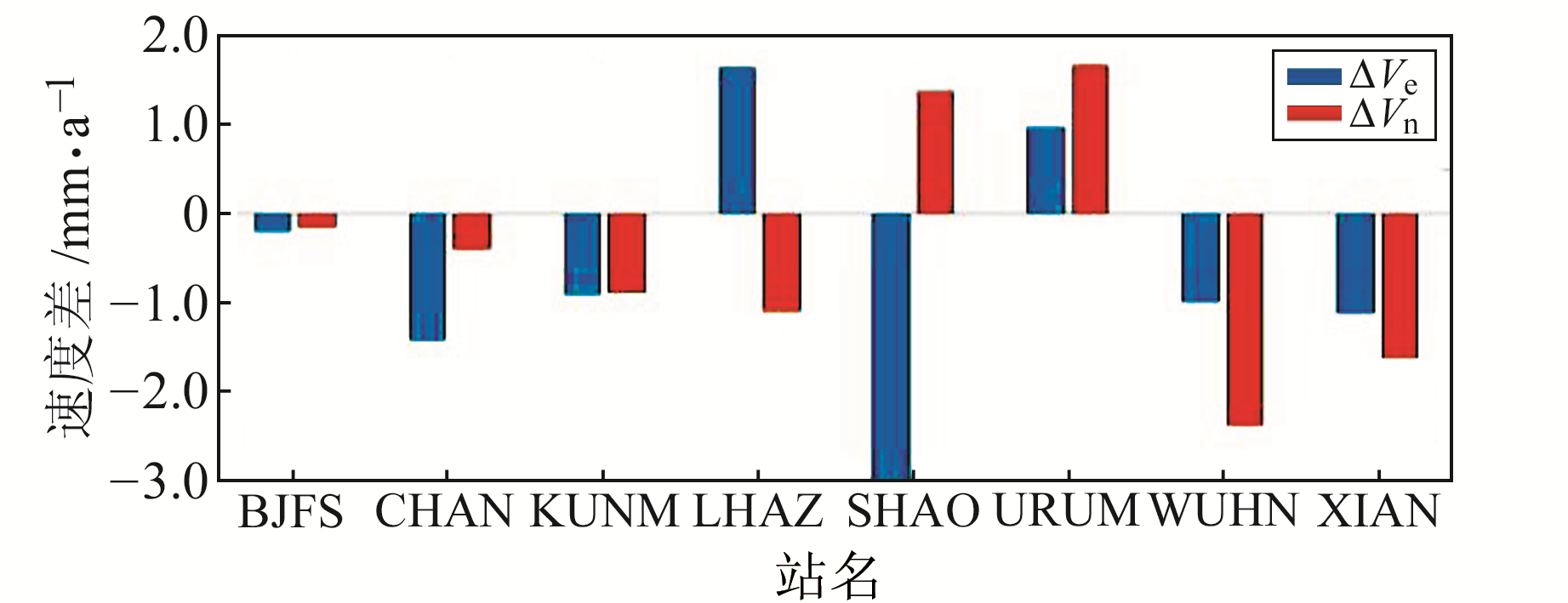
|
图 13 中国大陆IGS站水平方向速度残差 Fig. 13 Horizontal velocity residuals of each IGS station in Chinese mainland |
|
|
表 2 中国大陆IGS站址和速度 Tab. 2 Location and velocity of each IGS station in Chinese mainland |
为了进一步评估中国大陆水平格网速度场模型的精度与实用性,利用中国大陆范围内观测时段较长的1 800多个区域站点的实测精确速度作为真实观测值,与本文构建的ITRF2014框架下1°×1°格网速度场模型的插值结果进行比较,得到陆态网区域站东、北方向速度残差(图 14)。由图可知,大部分区域站东、北方向的速度残差范围在-2~2 mm/a之间;少量测站速度残差的绝对值超过4 mm/a,该部分站点主要集中于西藏和新疆地区,这些地区所布设的基准站数量较少,且同时受地壳活动频繁剧烈等因素影响,从而导致该地区的水平格网速度场模型精度略低。大陆整体区域站东、北方向的速度残差的平均误差分别为1.27 mm/a、1.02 mm/a,对应的中误差分别为1.65 mm/a、1.44 mm/a。
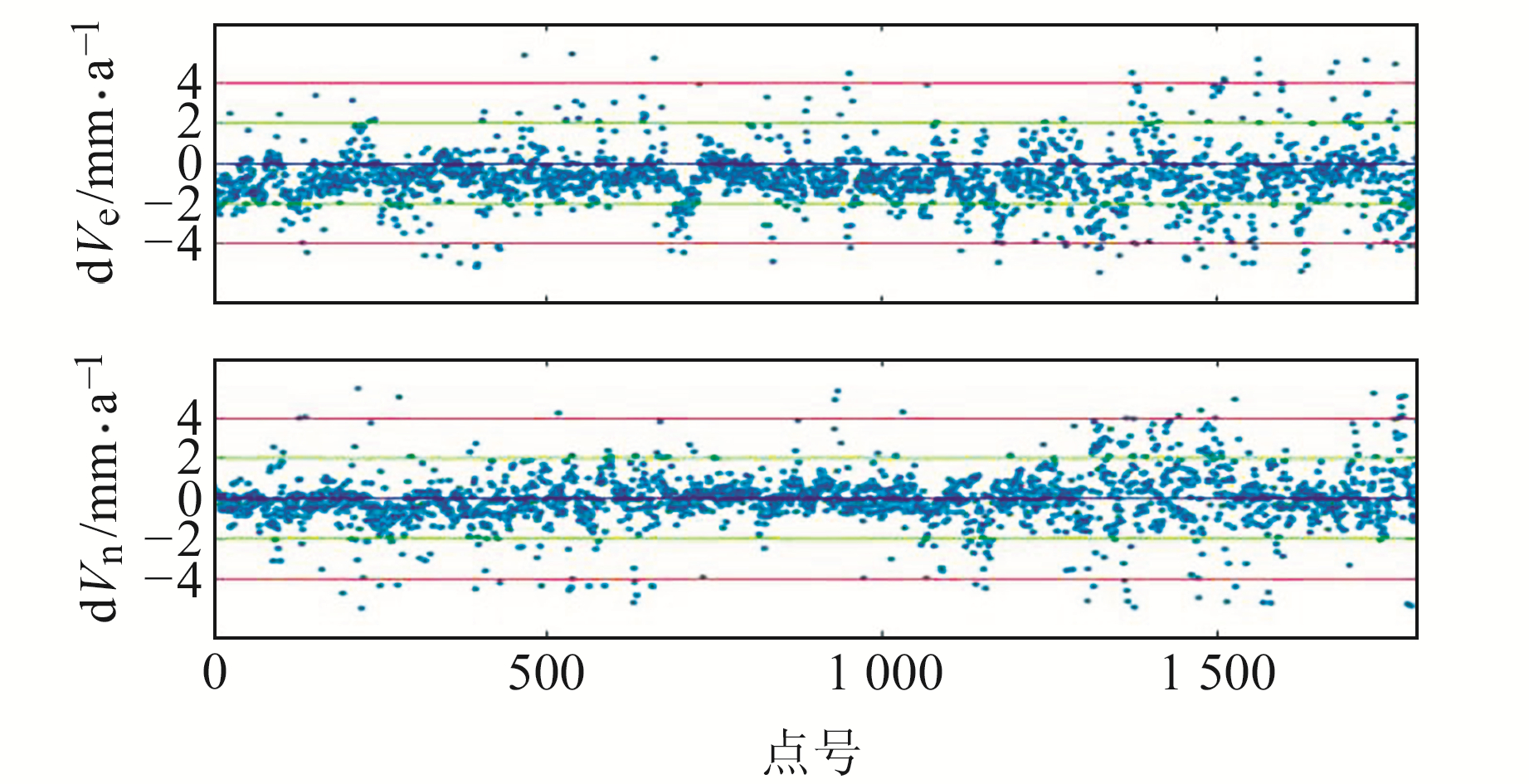
|
图 14 陆态网区域站水平方向速度残差 Fig. 14 Horizontal velocity residuals of all CMONOC regional stations |
由以上分析得出,本文建立的基于ITRF2014框架的1°×1°水平格网速度场模型具有较高的精度和可信度,无论是采用国内IGS站还是陆态网区域站作为检核数据,两者的检核精度均优于2 mm/a,完全满足当代mm级大地测量工作的精度需求,同时该格网模型具有使用简单、便于更新的优点。
5 结语针对当前大规模GNSS网面临的一系列挑战和现有研究中速度场模型所存在的局限性,本文以陆态网基准站观测数据为例,首先从数据准备与预处理、基线解算和网平差3个方面介绍大网数据处理一体化方案,给出适用于大网解算的优化处理原则;其次归纳基线与平差解算成果的质量检核方案,验证陆态网解算成果的高精度;然后提出不同速度场产品的对比评估方案,验证中国大陆速度场产品的高精度性;最后采用克里金法构建当代中国大陆水平格网速度场模型,并利用国内IGS站和区域站验证该模型的精度和可靠性。本文介绍的连续运行基准站数据处理一体化与质量评估方案对大规模GNSS站网的数据解算具有借鉴和参考意义。
随着我国地基基准站的不断加密与升级,大规模GNSS网将迎来新的机遇,如何通过改进算法和模型及采用并行计算技术来提高GNSS大网的解算效率,也值得进一步探讨和研究。另外,本文利用普通克里金法插值得到的中国大陆水平格网速度场模型在大陆西部地壳活动剧烈的新疆和西藏等地区精度略低,可通过改进克里金法或利用局域无缝三角网法来进一步提高并验证大陆西部格网速度场的精度。同时,随着观测数据的不断积累和更新,中国大陆格网速度场模型也需要不断进行优化与修正,以满足当代mm级大地测量技术的需求。
致谢: 感谢中国大陆构造环境监测网络提供部分数据支撑。
| [1] |
Ren Y, Wang J, Wang H, et al. Accuracy Analysis of BDS/GPS Navigation Position and Service Performance Based on Non/Double Differential Mode[C].China Satellite Navigation Conference, Singapore, 2019 https://link.springer.com/chapter/10.1007/978-981-13-7751-8_35
(  0) 0) |
| [2] |
姜卫平. GNSS基准站网数据处理方法与应用[M]. 武汉: 武汉大学出版社, 2016 (Jiang Weiping. Data Processing Method and Application of GNSS Base Station Network[M]. Wuhan: Wuhan University Press, 2016)
(  0) 0) |
| [3] |
李林阳, 张学东, 黄娴, 等. 大规模GNSS网发展及数据处理现状[J]. 测绘通报, 2018(10): 1-5 (Li Linyang, Zhang Xuedong, Huang Xian, et al. Development of Large-Scale GNSS Network and Current Status of Data Processing[J]. Bulletin of Surveying and Mapping, 2018(10): 1-5)
(  0) 0) |
| [4] |
李军, 高咏梅. GAMIT、GIPSY和BERNESE软件解算结果的比较研究[J]. 全球定位系统, 2010, 35(3): 5-9 (Li Jun, Gao Yongmei. Comparative Study on the Solution Results of GAMIT, GIPSY and BERNESE Software[J]. GNSS World of China, 2010, 35(3): 5-9)
(  0) 0) |
| [5] |
魏子卿, 刘光明, 吴富梅. 2000中国大地坐标系:中国大陆速度场[J]. 测绘学报, 2011, 40(4): 403-410 (Wei Ziqing, Liu Guangming, Wu Fumei. 2000 China Earth Coordinate System: Velocity Field in China[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 403-410)
(  0) 0) |
| [6] |
刘经南, 姚宜斌, 施闯. 中国地壳运动整体速度场模型的建立方法研究[J]. 武汉大学学报:信息科学版, 2002(4): 331-336 (Liu Jingnan, Yao Yibin, Shi Chuang. Study on the Method of Establishing the Whole Velocity Field Model of Chinese Crustal Movement[J]. Geomatics and Information Science of Wuhan University, 2002(4): 331-336)
(  0) 0) |
| [7] |
任雅奇.基于GPS数据的中国地壳运动速度场模型的建立[D].郑州: 信息工程大学, 2012 (Ren Yaqi. Establishment of Velocity Field Model of China's Crustal Movement Based on GPS Data[D]. Zhengzhou: Information Engineering University, 2012) http://cdmd.cnki.com.cn/Article/CDMD-90005-1013161053.htm
(  0) 0) |
| [8] |
于亮, 朱璇, 陈永祥, 等. 基于CMONOC建立和评估中国大陆地壳运动速度场模型[J]. 大地测量与地球动力学, 2017, 37(7): 704-708 (Yu Liang, Zhu Xuan, Chen Yongxiang, et al. Establishment and Evaluation of Crustal Velocity Field Model Based on CMONOC in China[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 704-708)
(  0) 0) |
| [9] |
张亦梅, 特木其勒, 刘可, 等. 应用TEQC对湖北省陆态网络连续站的观测数据进行质量分析[J]. 大地测量与地球动力学, 2011, 31(增1): 94-97 (Zhang Yimei, Temuqile, Liu Ke, et al. Quality Analysis of Observation Data of Continuous Network Stations in Hubei Province Using TEQC[J]. Journal of Geodesy and Geodynamics, 2011, 31(S1): 94-97)
(  0) 0) |
| [10] |
郝美云, 孙宪坤, 丁倩云, 等. K-means++分区法在密集型测站中的应用研究[J]. 全球定位系统, 2018, 43(3): 17-24 (Hao Meiyun, Sun Xiankun, Ding Qianyun, et al. Application of K-means++ Partitioning Method in Intensive Station[J]. GNSS World of China, 2018, 43(3): 17-24)
(  0) 0) |
| [11] |
马飞虎, 孙喜文, 贺小星. 基于GAMIT的IGS站基线可靠性处理与分析[J]. 华东交通大学学报, 2018, 35(4): 124-132 (Ma Feihu, Sun Xiwen, He Xiaoxing. Baseline Reliability Processing and Analysis of IGS Station Based on GAMIT[J]. Journal of East China Jiaotong University, 2018, 35(4): 124-132)
(  0) 0) |
| [12] |
Herring T A, King R W, Floyd M A, et al. GAMIT Refrence Manual: GPS Analysis at MIT.Releasr10.6[Z].Massachusetts Institute of Technology, 2018
(  0) 0) |
| [13] |
Herring T A, King R W, Floyd M A, et al. GLOBK Reference Manual: Global Kalman Filter VLBI and GPS Analysis Program. Releasr10.7[Z]. Massachusetts Institute of Technology, 2015
(  0) 0) |
| [14] |
Ren Y, Lian L, Wang J, et al. Preprocessing of GPS Coordinate Sequence Based on Singular Spectrum Analysis[C].IOP Conference Series: Earth and Environmental Science, 2019
(  0) 0) |
| [15] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Establishment and Analysis of Coordinate Time Series Noise Model for Regional IGS Base Stations in China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China;
3. College of Surveying and Geo-Informatics, Tongji University, 1239 Siping Road, Shanghai 200092, China;
4. Shanghai Astronomical Observatory, CAS, 80 Nandan Road, Shanghai 200030, China;
5. Institute of Geophysics, CEA, 5 South-Minzudaxue Road, Beijing 100081, China
 2020, Vol. 40
2020, Vol. 40

