2. 武汉地震工程研究院有限公司,武汉市洪山侧路40号,430071
混凝土结构实时动态的健康监测,尤其是监测裂缝的产生和变化过程,越来越受到重视。压电陶瓷材料集传感与驱动功能于一体,具有频响宽、响应快、成本低等优点,近年来已被许多学者用于混凝土裂缝损伤的监测和识别[1-6]。但这些研究均基于室内模型实验来验证所提方法的有效性和可行性,而使用有限元软件模拟压电主动传感法监测裂缝的研究较少。本文采用ABAQUS软件建立压电-预置裂缝混凝土梁机电耦合模型,通过预设不同跨中垂直裂缝和支座处斜裂缝,分析其损伤工况,探明压电主动传感法识别混凝土裂缝的原理及裂缝演化对应力波传播的影响,从裂缝宽度和深度2个方面分析应力波信号值和小波包能量值的变化特征。该仿真研究方法有利于分析应力波在病损混凝土内部传播与衰减的机理,能有效检测基于压电应力波的混凝土裂缝损伤程度。
1 压电主动传感理论Wang等[7]最早将压电主动传感理论应用于复合材料冲击损伤检测,正逆压电效应是压电主动传感实现的前提。在线弹性范围内选取机械应力场σ和电场强度E为主动变量,其d型压电本构方程可写为:
| $ \mathit{\boldsymbol{D = d\sigma + }}{\mathit{\boldsymbol{\varepsilon }}^\sigma }\mathit{\boldsymbol{E}} $ | (1) |
| $ \mathit{\boldsymbol{S}} = {\mathit{\boldsymbol{s}}^E}\mathit{\boldsymbol{\sigma }} + {\mathit{\boldsymbol{d}}^{\rm{T}}}\mathit{\boldsymbol{E}} $ | (2) |
式中,D、S分别为在电场E和应力场σ同时作用下压电材料产生的电位移向量和应变向量,d为压电应变常数矩阵,ε σ为应力场等于0时压电材料的介电常数矩阵,s E为电场强度等于0时压电材料的弹性柔顺常数矩阵。
压电材料具有各向异性,其材料属性在ABAQUS软件中一般可定义为应力型或应变型,本文选取类型为应变型,则式(1)、(2)在ABAQUS软件中可表示为:
| $ \mathit{\boldsymbol{q}}_i^{} = \mathit{\boldsymbol{d}}_{ijk}^{}\mathit{\boldsymbol{\sigma }}_{jk}^{} + {\mathit{\boldsymbol{D}}^\sigma }_{ij}^{}\mathit{\boldsymbol{E}}_j^{} $ | (3) |
| $ {\mathit{\boldsymbol{\varepsilon }}_{ij}} = {({\mathit{\boldsymbol{D}}^E}_{ijkl})^{ - 1}}{\mathit{\boldsymbol{\sigma }}_{kl}} + \mathit{\boldsymbol{d}}_{ijk}^{\rm{T}}{\mathit{\boldsymbol{E}}_j} $ | (4) |
式中,q i、ε ij分别为电位移分量和应变分量,E j、σ jk分别为电场强度分量和应力分量,d ijk为压电应变常数分量,(D ijklE)-1为弹性常数逆矩阵的分量,D ijσ为介电常数分量。本文采用文献[8]中压电陶瓷材料,各矩阵方程式可参考文献中数据。
2 压电-预置裂缝混凝土梁机电耦合数值模型 2.1 数值模型建立本文研究采用ABAQUS软件建立2类裂缝形式模型,即35个跨中预设垂直裂缝和40个支点处预设斜裂缝的混凝土梁有限元模型,压电片(PZT)尺寸为20 mm×20 mm×1 mm,混凝土梁尺寸为550 mm×150 mm×150 mm。模型中裂缝形式参考同尺寸梁三点受弯实验中的实际裂缝,深度和宽度大小可人为设定,并在中心轴高度处适当增加工况。跨中垂直裂缝和支座处斜裂缝的宽度均分别设为1 mm、2 mm、3 mm、4 mm、5 mm,前者深度为2 cm、4 cm、6 cm、7 cm、9 cm、11 cm、13 cm,后者深度为1 cm、5 cm、9 cm、13 cm、14 cm、18 cm、22 cm、26 cm,支座处斜裂缝演化方向与水平面夹角为30°。考虑到模型具有几何、材料及约束条件的对称性,裂缝以对称形式演化,故取1/2模型。同时,为进一步降低计算时间成本,模型以10 :1比例缩尺(图 1),表 1为模型材料参数。
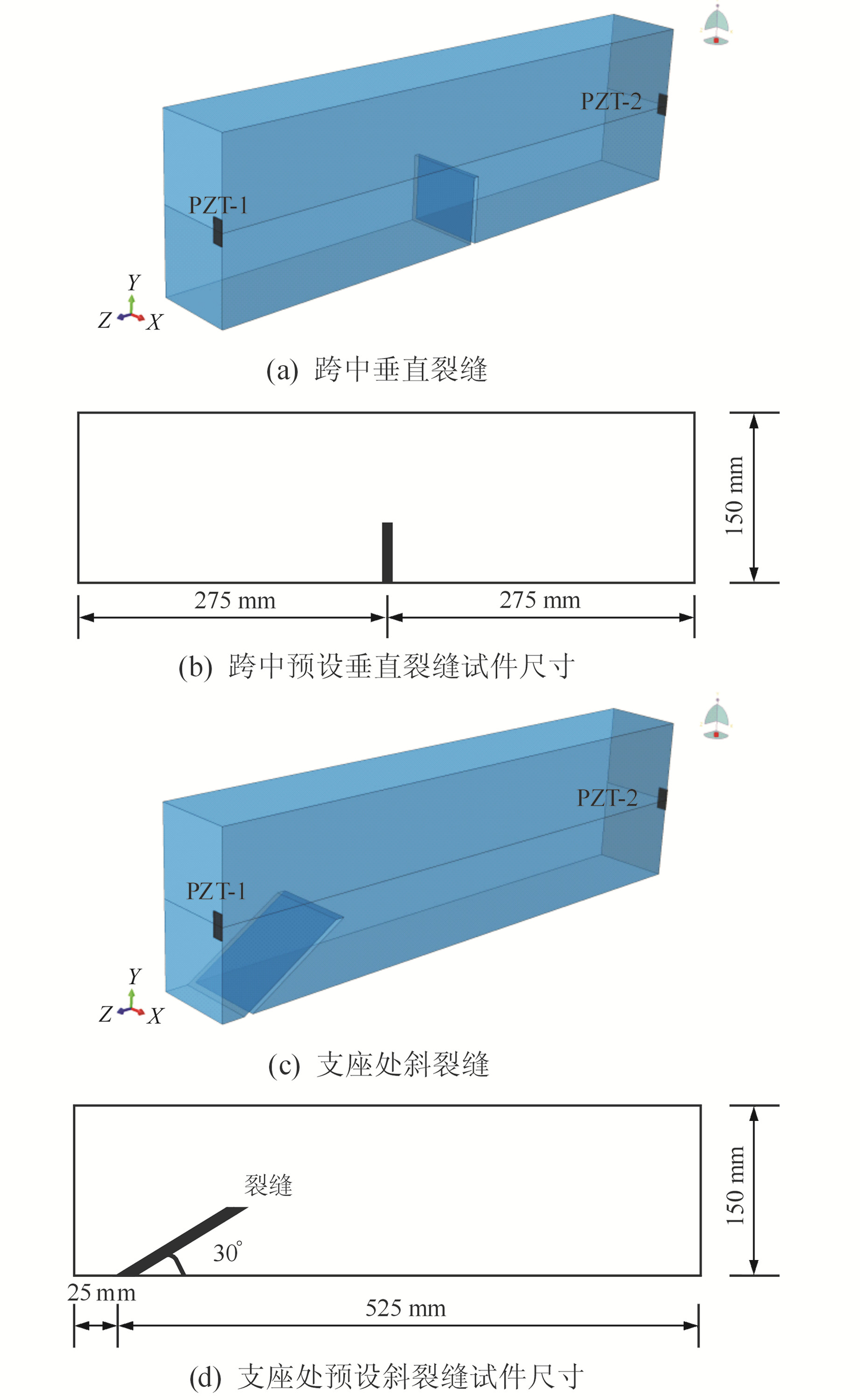
|
图 1 预设裂缝混凝土梁模型示意图 Fig. 1 Schematic diagram of preset crack of concrete beam model |
|
|
表 1 模型材料参数 Tab. 1 Material parameters of the model |
由于压电材料具有各向异性,在模型设置前需通过建立局部坐标系来确定压电材料极化方向[9]。为真实模拟压电激励/传感器的工作状态,采用绑定约束以实现PZT与混凝土梁之间的耦合连接(图 2)。

|
图 2 压电片极化方向 Fig. 2 Polarization direction of piezoelectric patch |
将PZT绑定在混凝土梁端面中心,通过电极面上电压与变形之间的转换,模拟激发和接收应力波信号。PZT-1和PZT-2下电极面均为零电势面,PZT-1上电极面输入扫频余弦电压信号,扫频范围为10~100 kHz,持续时间为2 ms,电压幅值为50 V,由MATLAB程序chirp命令(t, 10 000, 0.002, 100 000)生成信号(图 3)。PZT-2上电极面输出的电压信号为接收到的应力波。
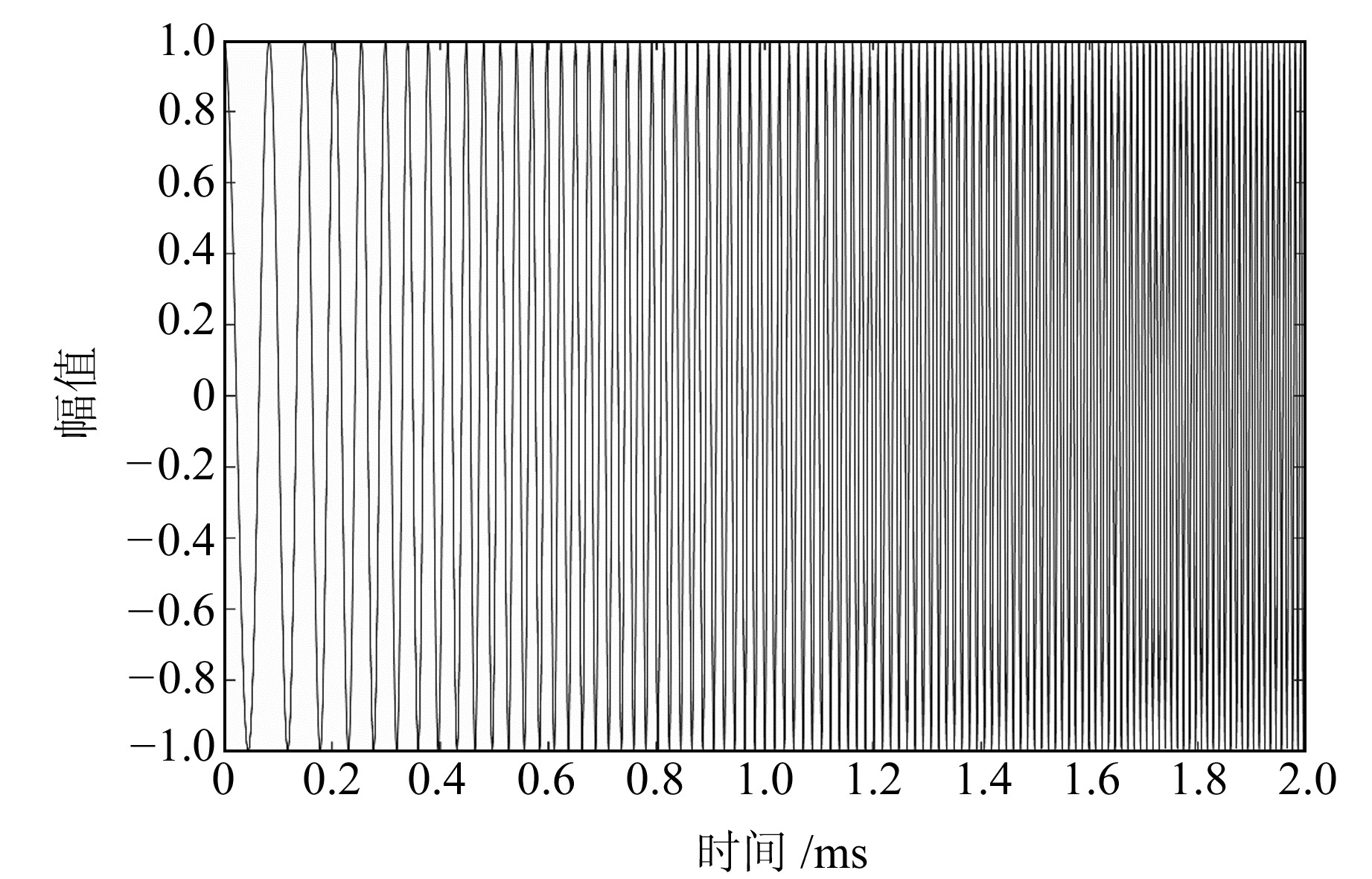
|
图 3 单位扫频信号波形 Fig. 3 Waveform of unit sweeping signal |
有限元软件ABAQUS在分析波动效应时,采用动力隐式分析步类型,分析步长与PZT-1输入扫频信号时长一致。增量步长依据预设扫频信号的最大频率来设定[10]:
| $ t \le \frac{1}{{20 \times {f_{{\rm{max}}}}}} $ | (5) |
式中,fmax为信号最大频率,t为增量步长。本研究中扫频信号最大频率为100 kHz,故增量步长为5×10-7 s。
2.4 网格划分原则为精确模拟应力波在混凝土中的传播过程,模型的网格尺寸一般应小于应力波在材料中传播波长的1/8[11],即
| $ t\le {{\lambda }_{min}}/8 $ | (6) |
式中,λmin为最小波长。根据文献[12]可计算出应力波在混凝土中传播的最小波长为37.2 mm。本文模型单元最大尺寸为1 mm,且在裂缝处会适当减小,故单元尺寸满足要求。模型中以八结点线性压电六面体单元(C3D8E)模拟压电片,以八结点线性六面体单元(C3D8R)模拟混凝土(图 4)。

|
图 4 模型网格划分 Fig. 4 Grid division of the model |
本文模型中压电片属于伸缩型,由泊松效应可知,沿其厚度方向的伸缩变形会导致其长度方向也发生变形。在扫频信号作用下,混凝土梁左端压电片激发的应力波由纵波和剪切波耦合而成。根据材料特性可确定纵波波速高于剪切波[13],这与Mises应力云图中初始应力波为半球形并逐渐发展为尖峰形一致(图 5)。应力波以沿梁体纵向中心轴向右端传播为主,仅剪切波沿截面横向传播。当应力波传播至裂缝边界处,部分波发生反射并与向右传播而来的应力波叠加;另一部分通过裂缝的应力波继续向前传播,但强度因裂缝的阻碍作用而发生衰减,最终被梁体右端压电片感知接收。由于裂缝的深度和宽度不同,接收到的电压时程信号会存在差异。
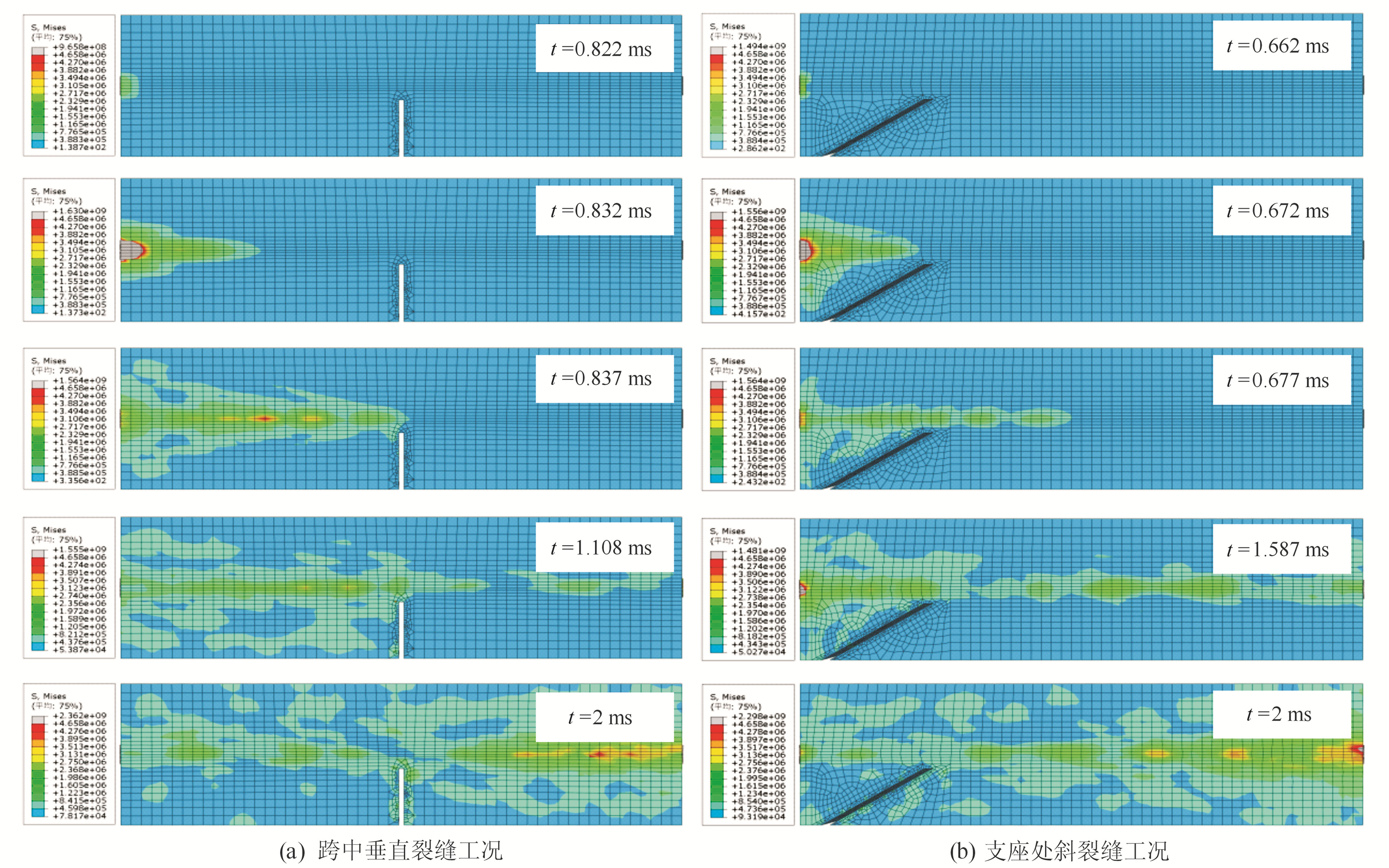
|
图 5 应力波传播示意图 Fig. 5 Schematic diagram of stress wave propagation |
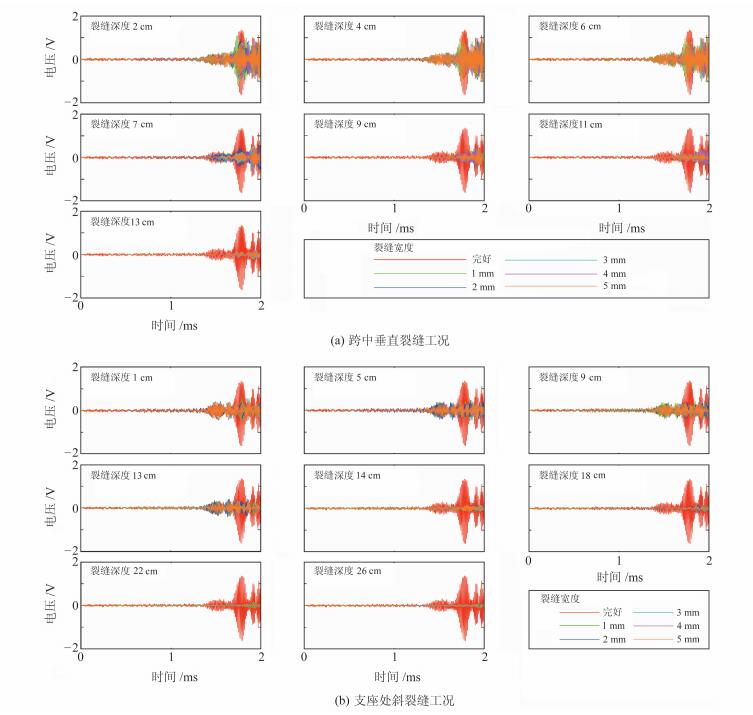
图 6为将同一裂缝宽度工况下数值模拟输出的电压时程曲线叠加的结果。可以看出,2类裂缝的信号值几乎都随裂缝深度的增加逐渐减小,呈明显的负相关性。当跨中裂缝深度由6 cm增至7 cm、支座斜裂缝由13 cm增至14 cm时,信号值显著减小,之后趋于稳定。
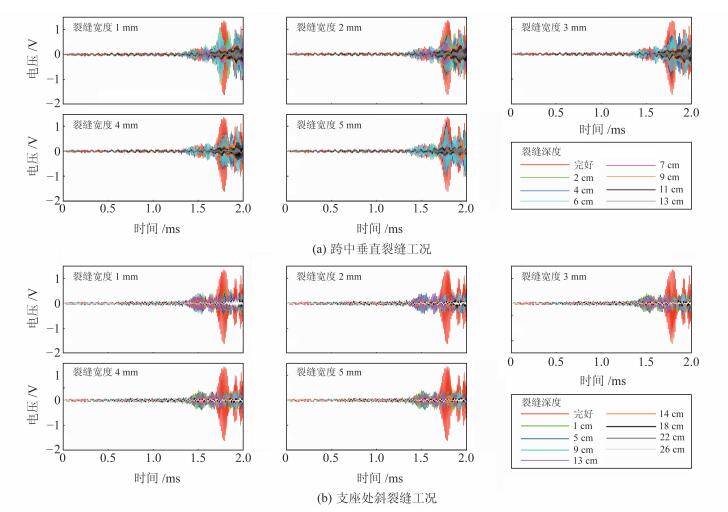
|
图 6 应力波随裂缝深度的变化 Fig. 6 Stress wave changes with crack depth |
对于相同深度的裂缝,当裂缝宽度增至2~3 mm时,信号值减小较为显著,之后信号值变化不再明显。当裂缝深度逐渐增加时,宽度变化对接收到的信号值几乎无影响(图 7)。
|
图 7 应力波随裂缝宽度的变化 Fig. 7 Stress wave changes with crack width |
运用压电主动传感法进行结构健康监测时,通常以压电传感器所采集的应力波信号S的能量值大小作为评定结构损伤程度的依据。小波包能量法能有效提取到信号的局部特征,以小波包分解信号S后,将各频段信号能量总和作为信号的能量指标,该方法适用于分析主动传感器所采集的非平稳应力波信号[14],其表达式为:
| $ \begin{array}{c} \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{X}}_1^{} + \mathit{\boldsymbol{X}}_2^{} + \cdots + \mathit{\boldsymbol{X}}_i^{} + \cdots + {\mathit{\boldsymbol{X}}_{{2^n} - 1}} + \mathit{\boldsymbol{X}}_{{2^n}}^{},\\ i = 1,2, \cdots ,{2^n} \end{array} $ | (7) |
| $ \begin{array}{l} \mathit{\boldsymbol{X}}_i^{} = {\rm{ [}}x_i^{},x_i^{},_2^{} \cdots x_i^{},_j^{} \cdots x_i^{},_{m - 1}^{}x_i^{},_m^{}],\\ i = 1,2, \ldots ,{2^n},j{\rm{ }} = 1,2, \ldots ,m \end{array} $ | (8) |
| $ {{P}_{i}}=\sum\limits_{j=1}^{m}{{{x}^{2}}_{i}}\text{, }i\text{ }=1, 2, \cdots , {{2}^{n}} $ | (9) |
| $ P\text{ }=\sum\limits_{i=1}^{{{2}^{n}}}{{{P}_{i}}} $ | (10) |
式中,n为小波包分解层数,Xi为分解后第i个频段信号,xi, j为第i个频段第j个离散点信号值,Pi为信号频段X i能量值,P为各频段能量值之和。
若以无损伤状态下应力波能量值Ph作为基准值,Pk为损伤状态下所采集信号的能量值,将信号能量值进行归一化处理,计算公式为:
| $ {{D}_{k}}=\frac{{{P}_{k}}}{{{P}_{h}}} $ | (11) |
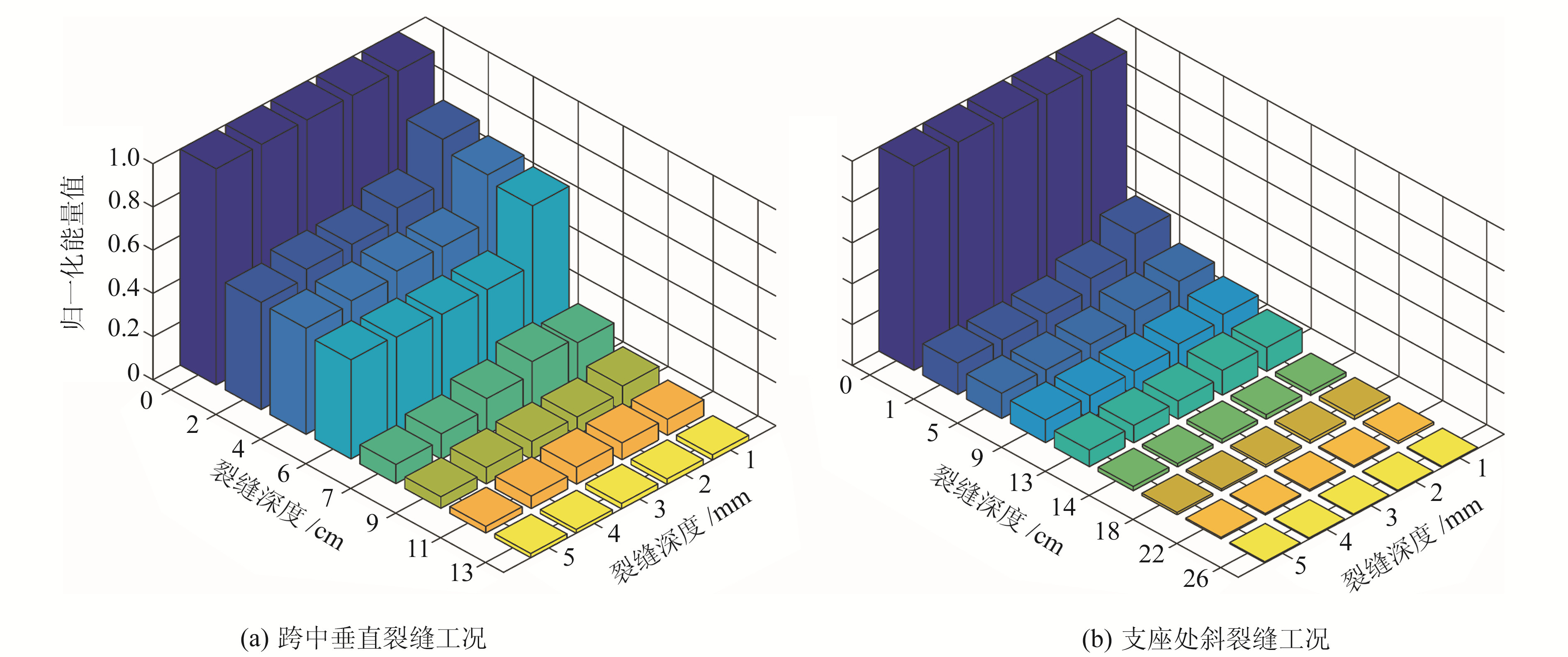
式中,相对能量值Dk为损伤程度因子。当结构无损伤时,Dk=1,接收信号能量无损;当结构完全破坏时,Dk=0,接收信号能量为0。图 8为本文仿真中各裂缝工况的应力波能量值归一化处理结果。
|
图 8 归一化应力波能量值 Fig. 8 Normalization of stress wave energy values |
与接收信号值随裂缝深度变化的趋势相同,当裂缝深度增加时,信号相对能量值呈现下降趋势。裂缝深度的变化会对相对能量值产生明显影响,当混凝土梁跨中裂缝深度达7 cm或支座处斜裂缝深度达14 cm时,信号相对能量值减小最为显著。当裂缝深度一定时,信号相对能量值受裂缝宽度影响较小,裂缝宽度为2~3 mm时存在一定程度的减小,这与应力波信号值随裂缝宽度变化的规律一致。
从上述信号值和相对能量值的变化中可以发现,在混凝土梁跨中垂直裂缝和支座处斜裂缝深度分别增至7 cm和14 cm时,两者的归一化能量值均明显减小。裂缝可作为应力波在混凝土梁中的反射面,会增强混凝土对应力波强度的耗散作用。在本文模型中,激发应力波的压电激励器固定在混凝土梁端面中心位置,应力波主要沿梁体纵向中心轴传播,其高度在跨中垂直裂缝和支座处斜裂缝的深度演化方向上分别对应7 cm和14 cm,当裂缝增加到此深度时会阻断应力波的传播路径,信号值和相对能量值均会显著减小。
4 结语本文采用有限元分析软件ABAQUS建立不同裂缝工况的压电-混凝土梁机电耦合数值模型,模拟压电主动传感法中应力波激发、传播和接收等一系列混凝土梁裂缝识别过程,并对所采集的信号进行分析,得到以下结论:
1) 压电应力波的信号值随裂缝深度的增加而减小,裂缝宽度增至2~3 mm时信号值明显降低,随后宽度变化对其影响不明显;裂缝沿深度方向演化对应力波强度的削弱作用明显高于其沿宽度方向的演化。
2) 应力波的主要传播路径与激发应力波的压电激励器布设位置紧密相关,文中压电激励器安装于混凝土梁端面中心,故当裂缝演化至梁体纵向中心轴高度时,裂缝对应力波传播的阻碍作用最明显。
3) 以应力波接收信号值和能量大小为判据,将相对能量值作为混凝土梁损伤程度因子,可有效识别裂缝损伤及演化状况。
| [1] |
Song G B, Gu H C, Mo Y L. Smart Aggregates: Multi-Functional Sensors for Concrete Structures——A Tutorial and a Review[J]. Smart Materials and Structures, 2008, 17(3): 033001
(  0) 0) |
| [2] |
李宏男, 赵晓燕. 压电智能传感结构在土木工程中的研究和应用[J]. 地震工程与工程振动, 2004, 24(6): 165-172 (Li Hongnan, Zhao Xiaoyan. Research and Application of Piezo-Intelligent Sensors in Civil Engineering[J]. Earthquake Engineering and Engineering Vibration, 2004, 24(6): 165-172 DOI:10.3969/j.issn.1000-1301.2004.06.029)
(  0) 0) |
| [3] |
Feng Q, Kong Q Z, Huo L S, et al. Crack Detection and Leakage Monitoring on Reinforced Concrete Pipe[J]. Smart Materials and Structures, 2015, 24(11): 115020 DOI:10.1088/0964-1726/24/11/115020
(  0) 0) |
| [4] |
Song G B, Gu H C, Mo Y L, et al. Concrete Structural Health Monitoring Using Embedded Piezoceramic Transducers[J]. Smart Materials and Structures, 2007, 16(4): 959-968
(  0) 0) |
| [5] |
郑合营.基于压电智能骨料的混凝土结构损伤主动监测研究[D].大连: 大连理工大学, 2016 (Zheng Heying. The Study of Active Damage Monitoring for Concrete Structures Based on Piezoelectric Smart Aggregate[D]. Dalian: Dalian University of Technology, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10141-1016217111.htm
(  0) 0) |
| [6] |
Hughi D, Marzouk H. Crack Width Monitoring System for Reinforced Concrete Beams Using Piezo-Ceramic Sensors[J]. Journal of Civil Structural Health Monitoring, 2015, 5(1): 57-66
(  0) 0) |
| [7] |
Wang C S, Chang F K. Diagnosis of Impact Damage in Composite Structures with Built-in Piezoelectrics Network[C]. Smart Structures and Materials 2000: Smart Electronics and MEMS, Newport Beach, 2000
(  0) 0) |
| [8] |
Markovic N, Nestorovic T, Stojic D. Numerical Modeling of Damage Detection in Concrete Beams Using Piezoelectric Patches[J]. Mechanics Research Communications, 2015, 64: 15-22 DOI:10.1016/j.mechrescom.2014.12.007
(  0) 0) |
| [9] |
杜国锋, 刘向东, 何明星, 等. 基于压电陶瓷的混凝土柱应力监测模拟研究[J]. 混凝土, 2016(9): 29-33 (Du Guofeng, Liu Xiangdong, He Mingxing, et al. Simulation Study on Dynamic Stress Monitoring with Embedded Piezoceramic for Concrete Column[J]. Concrete, 2016(9): 29-33)
(  0) 0) |
| [10] |
杜文卫, 江刚, 朱彬占, 等. 基于瑞利波法对混凝土表面裂缝检测的数值研究[J]. 土木建筑与环境工程, 2018, 40(4): 151-158 (Du Wenwei, Jiang Gang, Zhu Binzhan, et al. Numerical Simulation on Detection of Concrete Surface Crack Based on Rayleigh Wave Method[J]. Journal of Civil, Architectural and Environmental Engineering, 2018, 40(4): 151-158)
(  0) 0) |
| [11] |
魏灯莱.基于压电阻抗特征频率偏移的螺栓轴向力监测[D].武汉: 武汉科技大学, 2018 (Wei Denglai. Axial Force Monitoring of Bolts Based on the Shift of Characteristic Frequency of Piezoelectric Impedance[D]. Wuhan: Wuhan University of Science and Technology, 2018)
(  0) 0) |
| [12] |
Karaiskos G, Deraemaeker A, Aggelis D G, et al. Monitoring of Concrete Structures Using the Ultrasonic Pulse Velocity Method[J]. Smart Materials and Structures, 2015, 24(11): 113001 DOI:10.1088/0964-1726/24/11/113001
(  0) 0) |
| [13] |
Wang Z J, Wei L, Cao M S. Damage Quantification with Embedded Piezoelectric Aggregates Based on Wavelet Packet Energy Analysis[J]. Sensors, 2019, 19(2): 425
(  0) 0) |
| [14] |
梁亚斌.大跨斜拉桥的局部损伤监测和环境因素影响分离[D].大连: 大连理工大学, 2016 (Liang Yabin. Local Damage Detection and Elimination of Environmental Effects for Long-Span Cable-Stayed Bridge[D]. Dalian: Dalian University of Technology, 2016)
(  0) 0) |
2. Wuhan Institute of Earthquake Engineering Co Ltd, 40 Hongshance Road, Wuhan 430071, China
 2020, Vol. 40
2020, Vol. 40


