宽城地震台是定点形变台站,建台以来各测项观测资料质量较好。通过分析观测日志可知,在宽城台定点形变资料的干扰因素中,自然环境干扰是主因,其中气压干扰出现的频率较高。本文分析宽城台定点形变仪器的观测资料,选取各测项相同时间段受气压干扰的典型事件,利用小波分析方法将潮汐波分解成不同频段的信息,通过识别分析高频和低频信息,得出能够被清晰辨别的固体潮畸变信息成分与受干扰噪声成分[1-2],再采用小波阈值去噪消除气压的影响,从而提高观测数据的质量,对地震前兆异常的识别有一定的作用。
1 台站基本情况宽城地震台位于河北省宽城满族自治县宽城镇岔沟路,海拔310 m,属燕山构造带,受马兰峪大背斜控制,位于宽城盆地边缘。台站基岩岩性为震旦系硅质灰岩,走向近EW,沿节理透水,地貌上为高山区。仪器所处山洞的洞顶覆盖层厚度为20~40 m,有少量植被,洞内年温差为0.5 ℃[3]。
宽城台的定点形变观测仪器共有5套,分别为DSQ水管倾斜仪、VS垂直摆倾斜仪、VP垂直摆倾斜仪,SS-Y伸缩仪和TJ-2体应变仪,其中伸缩仪和水管仪于2015-12由“九五”公用数据采集器升级为“十五”智能化仪器,VP型垂直摆倾斜仪安装于2016-11。各仪器基本信息见表 1。
|
|
表 1 宽城台定点形变仪器基本信息 Tab. 1 Basic information of fixed pointdeformational instruments of Kuancheng station |
气压变化影响一般来自于气温的变化,气温变化使大气压产生波动,导致洞腔内的空气出现振荡,从而使形变观测仪器的数据发生变化[4]。通过对宽城台定点形变观测数据的观察与分析可知,其观测曲线受气压影响的主要变化形态为不同幅度的抖动。

|
图 1 宽城台山洞平面图 Fig. 1 Ichnography of Kuancheng station cave |
对连续小波变换进行离散化处理可以增加计算的可行性,离散小波变换通常只对尺度因子a及平移因子τ进行离散化处理[5]。在连续小波变换的计算中,通常将小波母函数表示为:
| $ {\psi _a}{,_\tau }\left( t \right) = \frac{1}{{\sqrt a }}\psi \left[ {\left( {t - \tau } \right)/a} \right] $ | (1) |
式中,a、τ∈R, a≠0,ψ为可容许的。设定a>0,相容性条件的表达式变为:
| $ {{C}_{\psi }}={{\int\limits_{-\infty }^{+\infty }{\frac{\left| \psi \left( \omega \right) \right|}{\omega }}}^{2}}d\omega <\infty $ | (2) |
将离散小波变换中的尺度因子a和连续平移因子τ表示为:
| $ a=a_{0}^{j}, \tau =ka_{0}^{j}{{\tau }_{0}}, j\in Z $ | (3) |
式中,a0为扩展步长。假设a0>1,且为常数,则对应的离散小波函数ψj, k(t)的表达式为:
| $ {{\psi }_{j, k}}(t)=a_{0}^{-\frac{j}{2}}\psi \left( \frac{t-ka_{0}^{j}{{\tau }_{0}}}{a_{0}^{j}} \right)=a_{0}^{-\frac{j}{2}}\psi (a_{0}^{-j}t-k{{\tau }_{0}}) $ | (4) |
离散小波变换的系数表达式为:
| $ {{C}_{j, k}}=\int\limits_{-\infty }^{+\infty }{f(t)\psi _{j, k}^{*}}(t)dt=\left\langle f, {{\psi }_{j, k}} \right\rangle $ | (5) |
小波分析首先要选取适合的小波基函数,不同的小波基函数会对信号处理的结果产生不同的影响。在实际应用中,较为常用的小波基函数有Haar小波、Daubechies小波、Biorthogonal小波、Coiflet小波、Symlet小波、Morlet小波和Meyer小波等,选择小波基函数的一般原则为紧支撑性、对称性和正则性(光滑性)[6]。本文利用定点形变观测仪器1 d的分钟值数据,根据数据特点将其处理后的重构信号与原始信号的误差大小进行判定,选取最优的小波基函数。选取水管仪北南分量数据,分别采用不同的小波基进行计算,得出不同小波基重构后的平均误差,结果见表 2。由表可知,Haar小波在时域上是不连续的;Meyer小波不是紧支撑的,误差较大;Daubechies小波(db5)与Symlet小波(sym5)具备较好的正则性,在连续性、支集长度、滤波器长度方面表现较好,能够在一定程度上减少信号分析和重构时的相位失真,误差较小。选取db族小波不同长度的滤波器进行计算,结果见表 3。由表可知,db1~db3小波紧支撑长度较小,光滑度不够,重构误差较大;db4~db6小波误差较小,能够较好地顾及正交小波的紧支集和平滑性;db7~db9小波紧支集区间变大,重构结果较为光滑,但小波基的局部性下降,误差也逐渐增大。综上所述,选取db5小波为小波基函数。
|
|
表 2 不同小波基的误差结果 Tab. 2 Error results of different wavelet bases |
|
|
表 3 db族小波误差结果 Tab. 3 Error results of db family wavelet |
选取宽城台水管仪北南分量的分钟值数据,利用db5小波基函数进行离散小波变换,分解为8个层次,并对其进行重构,结果见图 2。由图可知,原始数据和重构后的数据曲线形态一致,只有微小的误差,表明本文选用的小波基具有一定的紧支集、平滑性和对称性,符合小波变换的要求。

|
图 2 水管仪北南分量分钟值小波重构及其误差 Fig. 2 Wavelet reconstruction and error of the minute value of water tube tiltmeter of NS component |
选取宽城台4套定点形变观测资料中受气压干扰的典型事件为研究对象,利用小波分析方法分析气压干扰因素。根据前兆处理系统的记录日志,选择宽城台2017-06-02数据,该观测日内各测项观测资料均因气压变化产生了不同程度的干扰。分别对受气压变化影响的各测项观测数据进行小波分析,对结果中不同频段的细节与原始曲线进行对比,结果见图 3。根据结果可知:1)VS垂直摆北南向气压干扰频段主要分布在细节3~7,东西向气压干扰频段主要分布在细节2~6;2)水管仪北南向气压干扰频段主要分布在细节2~7,东西向气压干扰频段主要分布在细节3~6;3)伸缩仪北南向气压干扰频段主要分布在细节3~7,东西向气压干扰频段主要分布在细节3~7;4)VP垂直摆北南向气压干扰频段主要分布在细节2~6,东西向气压干扰频段主要分布在细节4~6。经过小波分析细节可以看出,宽城台各定点形变测项的气压干扰变化特征存在较强的一致性,受干扰的细节频段大致相同,摆式仪器受气压干扰程度较小。

|
图 3 各观测仪器受气压干扰原始曲线及小波分析细节 Fig. 3 Wavelet analysis details and original curves affected by atmospheric pressure of all instruments |
小波阈值去噪是利用信号频率与噪声频率的不同进行去噪处理。在对原始信号进行小波分解时,分解后的有效信号小波系数较大,噪声的小波系数较小,因此需选取一个合适的阈值,将大于阈值的小波系数认为是分解后的有效信号予以保留,小于阈值的小波系数则认为是噪声置零,从而达到去噪的目的[7]。由上述分析可知,正常观测数据的频率较低,信号比较平稳;气压干扰的频率较高,含干扰的部分基本都分布在细节2~7中。对不同频率的小波细节采用不同的阈值进行处理,再对信号进行重构就可去除原始信号中的噪声[8]。
小波阈值去噪处理的基本步骤为:
1) 采用db5小波对原始信号进行小波分解,由于气压干扰的频率较宽,故将小波分解为8层,得到不同频率的小波细节。
2) 不同的阈值选取有不同的去噪效果,结合不同阈值的去噪效果和干扰信号的特点选取固定形式阈值(fixed form threshold),公式为:
| $ {\rm{thr}} = \sqrt {2\lg (n) \cdot \sigma } $ | (6) |
式中,n为信号长度,σ为噪声强度。
3) 阈值函数是修正小波系数的规则,不同的阈值函数体现了不同的小波系数处理策略[9]。为保留更多的细节,本文选用软阈值函数。
4) 由于定点形变仪器数据格值不同,且受气压变化影响的程度不同,结合上述小波分解受干扰细节,尽可能保留固体潮和背景噪声,得出不同仪器在不同细节的阈值(表 4)。
|
|
表 4 定点形变仪器小波阈值 Tab. 4 Threshold of fixed-point deformational instrument |
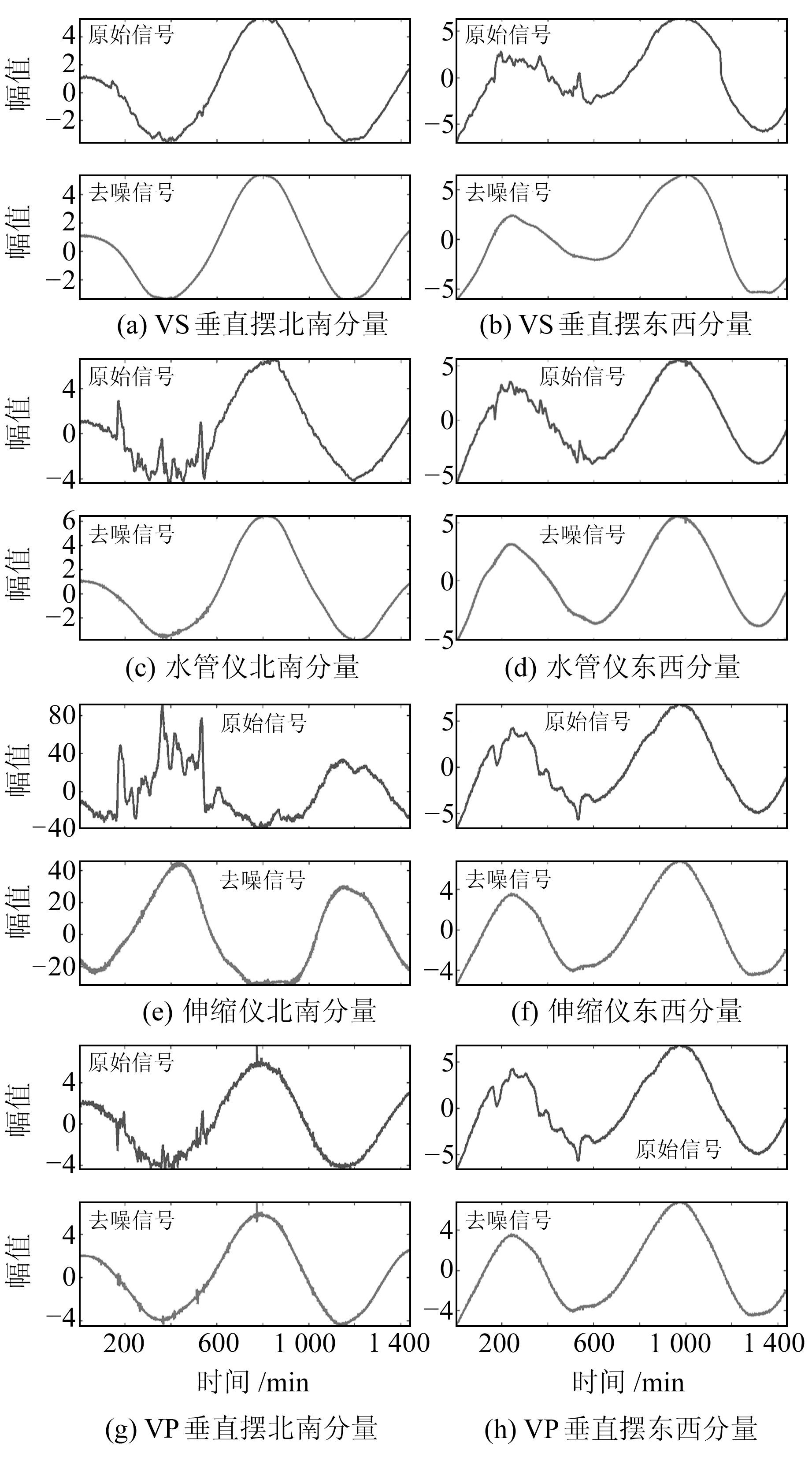
5) 将经过处理之后的小波系数进行重构,获得去噪之后的信号,如图 4所示。
|
图 4 各观测仪器受气压干扰原始信号及去噪信号对比 Fig. 4 Comparison of original signals and denoising signals affected by atmospheric pressure of all instruments |
由图 4可知,通过小波阈值去噪后的信号基本去掉了气压干扰对原始信号的影响,去噪效果很好,去噪后的信号光滑度高,基本抑制了噪声的高频信号,保留了仪器的背景有效高频信号,能观测到清晰的固体潮等有效信息。
4 结语由宽城台定点形变仪器各测项小波分析的结果可知,小波分解后的各频段数据基本都与同频段上的气压变化特征存在较强的一致性;各测项的观测数据受干扰的细节频段大致相同;利用小波阈值去噪后的信号基本去掉了气压干扰对原始信号的影响,去噪效果显著,去噪后的信号曲线光滑度高,基本抑制了噪声的高频信号,保留了仪器的背景有效高频信号,具有更好的视觉效果,能清晰观测出固体潮等有效信息,对定点形变观测资料的前兆信息识别有一定的作用。
| [1] |
王勇, 刘备, 刘严萍, 等. 基于小波变换的GPS水汽与气象要素相关性分析[J]. 大地测量与地球动力学, 2017, 37(7): 721-725 (Wang Yong, Liu Bei, Liu Yanping, et al. Correlation Analysis of GPS PWV and Meteorological Elements Based on Wavelet Transform[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 721-725)
(  0) 0) |
| [2] |
茅远哲, 马栋, 张国苓, 等. 河北形变观测中大气环境干扰因素频谱特征研究[J]. 四川地震, 2016(4): 35-40 (Mao Yuanzhe, Ma Dong, Zhang Guoling, et al. The Frequency Spectrum of Atmospheric Environmental Interference in Hebei Tidal Deformation Observation[J]. Earthquake Research in Sichuan, 2016(4): 35-40)
(  0) 0) |
| [3] |
任俊峰, 孙澎涛, 袁国旭, 等. 宽城地震台水管倾斜仪端点一致性分析[J]. 地震地磁观测与研究, 2016, 37(4): 111-116 (Ren Junfeng, Sun Pengtao, Yuan Guoxu, et al. The Endpoints Consistency Analysis of Water Tube Tiltmeter at Kuancheng Seismic Station[J]. Seismological and Geomagnetic Observation and Research, 2016, 37(4): 111-116)
(  0) 0) |
| [4] |
马栋, 牛安福, 袁淑芳, 等. 据频谱特征分析短时气压波动对体应变的影响[J]. 内陆地震, 2011, 25(3): 67-74 (Ma Dong, Niu Anfu, Yuan Shufang, et al. Analysis on the Influence of Short-Term Atmospheric Pressure Fluctuation on Body Strain Data Based on Spectrum Characteristics[J]. Inland Earthquake, 2011, 25(3): 67-74)
(  0) 0) |
| [5] |
刘建明, 李志海, 孙甲宁, 等. 基于小波分析提取地倾斜异常特征[J]. 地震, 2016, 36(1): 38-48 (Liu Jianming, Li Zhihai, Sun Jianing, et al. Extraction of Ground Tilt Anormalies Based on Wavelet Analysis[J]. Earthquake, 2016, 36(1): 38-48 DOI:10.3969/j.issn.1000-3274.2016.01.005)
(  0) 0) |
| [6] |
曾宪伟, 赵卫明, 师海阔, 等. 利用小波包变换对地震信号进行时频分析时小波基函数的选取[J]. 地震研究, 2010, 33(4): 323-328 (Zeng Xianwei, Zhao Weiming, Shi Haikuo, et al. Selection of Wavelet Basis Function in Process of Time-Frequency Analysis of Earthquake Signals using Wavelet Packet Transform[J]. Journal of Seismological Research, 2010, 33(4): 323-328 DOI:10.3969/j.issn.1000-0666.2010.04.012)
(  0) 0) |
| [7] |
王旭, 王昶. 一种改进小波阈值去噪方法的研究[J]. 大地测量与地球动力学, 2017, 37(10): 1 038-1 041 (Wang Xu, Wang Chang. Improved Wavelet Threshold De-Noising Method Research[J]. Journal of Geodesy and Geodynamics, 2017, 37(10): 1 038-1 041)
(  0) 0) |
| [8] |
郭思, 郭科, 陈聆, 等. 基于小波变换新阈值函数的地震资料去噪方法[J]. 成都理工大学学报:自然科学版, 2014, 41(3): 378-381 (Guo Si, Guo Ke, Chen Ling, et al. Seismic Data De-Noising Method Based on a New Threshold Function of Wavelet Transformation[J]. Journal of Chengdu University of Technology:Science and Technology Edition, 2014, 41(3): 378-381)
(  0) 0) |
| [9] |
李英, 张淑贞, 许康生. 小波降噪方法在地震信号处理中的应用[J]. 西北地震学报, 2006, 28(2): 159-162 (Li Ying, Zhang Shuzhen, Xu Kangsheng. Application of Wavelet Transfer in Seismic Signal Denoise[J]. Northwestern Seismological Journal, 2006, 28(2): 159-162)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

