监测构造应力场的变化是地震预报研究的基本任务和重要手段[1]。钻孔体应变仪工作原理简单,观测精度达到10-9,相比于一般的形变仪,能记录到清晰的应变固体潮和同震响应,与大尺度的GPS和地震仪在观测频段上互补[1]。“十五”期间江苏省地震局使用国产TJ-2型体应变仪在地震重点监测区布设了8个测点,初步建成江苏省的地壳应变监测网,获得较为可靠的连续观测资料,能有效监测测区应力状态变化,为研究地壳应力应变场、地球动力学和地震预报提供基础资料。
根据DB/T 8.2-2020《地震台站建设规范地形变台站第2部分:钻孔地倾斜和地应变台站》,体应变仪安装时需要进行钻孔工程的施工,松散层孔段正循环无芯钻进,岩石井段采用Ø159 mm金刚石取芯钻头取芯钻进,依据取样及岩芯岩样划分地层,在预安装井下传感器的岩芯区间段根据岩芯状况进一步确定准确的安装位置,井下传感器与观测层岩石耦合采用膨胀水泥固结方式。因井下传感器埋于钻孔内,故仪器记录到的M2波潮汐因子与钻孔条件、岩芯的物理力学性质有着密切的关系。早在1950年,Nishimura[2]就提出了地球潮汐响应能反映地壳介质的弹性参数。Beaumont等[3]进一步揭示了潮汐振幅受到地壳介质的影响,并运用有限元模拟了潮汐振幅的变化和地壳物质的泊松比以及体积模量之间的关系。池顺良等[4]、张斯奇等[5]和周江存等[6]通过开展数值模拟研究发现,潮汐因子与理论模型相比有很大的离散性及有规律的方位各向异性,认为潮汐传播与断层、深度和弹性参数有关。李进武等[7]通过回归分析发现,M2波潮汐因子受高程、纬度的影响基本可以忽略,定性分析认为,其受到基岩岩石性质的影响较大。有研究认为,钻孔环境也是井下地形变连续观测仪器的一个不可或缺的组成部分,岩石的硬度(如剪切模量和杨氏模量)与潮汐振幅呈负相关,围岩的裂隙降低了弹性模量和强度极限,造成岩石力学性质分布不均匀,对观测产生一定的影响,并且用数值模拟了裂隙的影响范围[8-11]。以上研究表明,M2波潮汐因子的主要影响因素可能为井下环境和基岩岩性,而大部分研究以数值模拟为主,岩芯分析仅停留在对岩芯的人工识别、进行定性分析层面上。
目前国内体应变仪观测井的岩芯标本还没有进行单轴抗压强度和弹性模量的测定,在进行数值模拟计算时,往往缺少理论值与实测值的比较。本文首次通过对体应变仪观测层岩芯进行单轴压缩试验,获得M2波视潮汐因子与弹性模量的关系,从岩石力学角度定量分析岩芯的力学参数对M2波视潮汐因子的影响。
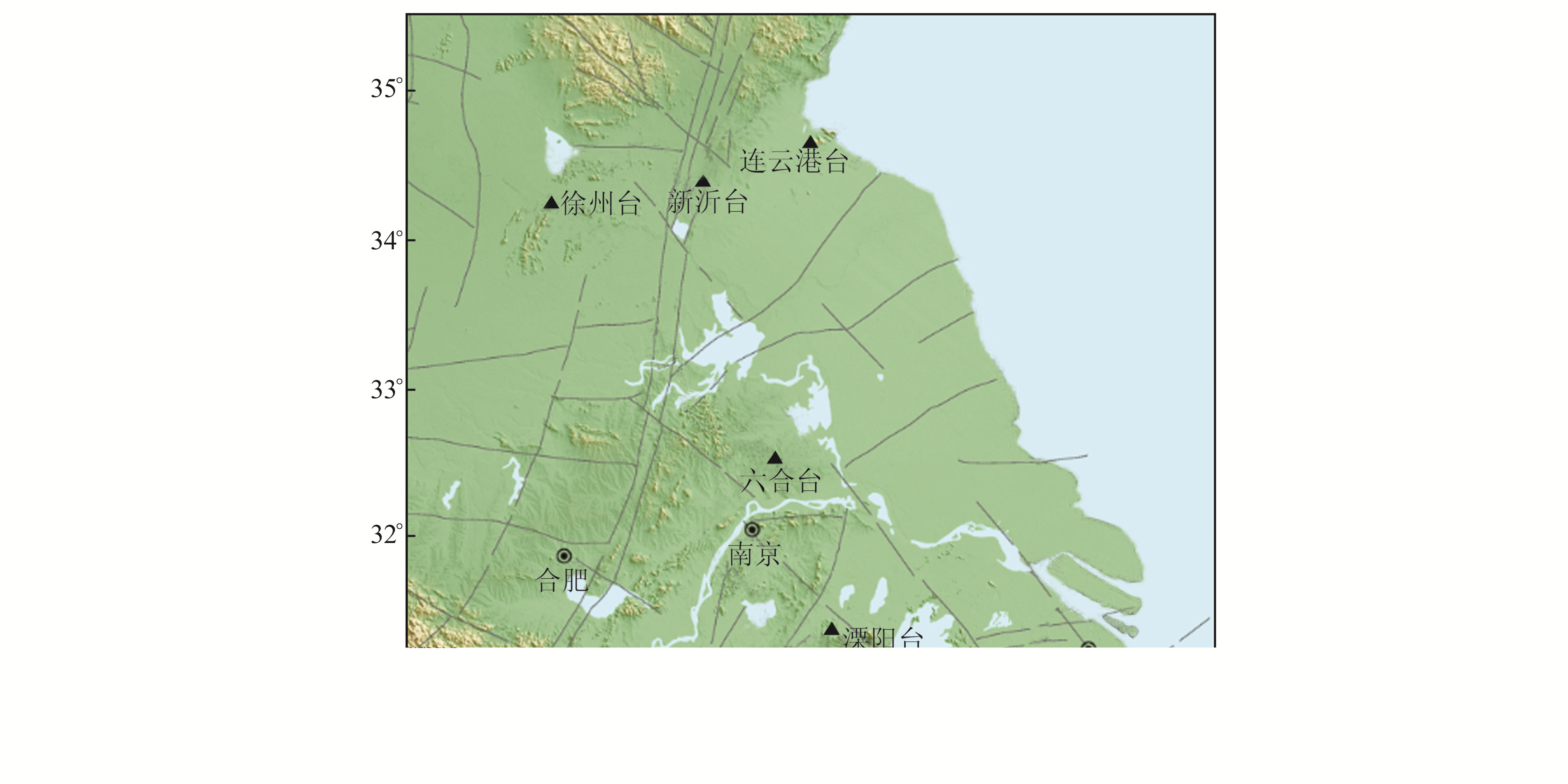
1 观测概况进行试验的有溧阳台、六合台、徐州台、新沂台和连云港台的体应变仪钻孔岩芯,台站主要围绕着江苏省区域内活动性较强且与现代地震有密切关系的2条重要断裂带(郯庐断裂带江苏段和茅东断裂带)分布(图 1)。新沂台观测点位于郯庐断裂带中南段F1与F4段之间,台基岩性为上白垩统王氏组紫红色砂岩层。徐州台和连云港台分别在郯庐断裂带西南侧和北东侧,距新沂台分别为113.2 km和83.1 km,台基岩性分别为寒武纪灰岩层和前寒武系云台山组的白云斜长片麻岩层。溧阳台和六合台分别位于茅东断裂带北侧和东南侧,台基岩性分别为安山玄武岩层和震旦系白云岩。
|
图 1 台站分布 Fig. 1 Distribution of stations |
六合台在2012-07因雷击造成仪器故障停测,2015年恢复观测,但是2016-06再次遭遇雷击造成仪器故障。六合台位于六合区冶山镇冶山林场内,推测由于仪器安装的海拔较高(104 m),并且距离冶山铁矿仅2 km,震旦系白云岩台基穿插了多种燕山期中酸性火成岩,导致六合台容易遭受雷击,井下传感器一旦遭雷击故障恢复难度较大,需重新打井安装,周期较长。
因此,统一选取2015-07~2016-06的体应变观测记录来进行研究。图 2(a)为2016-03典型的月分钟值曲线图,图 2(b)为2016-03-02 20:49在印尼苏门答腊岛海域(4.9°S, 94.2°E)发生的M7.8地震的同震记录,该地震与各个台站的震中距在4 900 km左右,属于远震。

|
图 2 各台2016-03-11~31体应变分钟值观测曲线和印尼M7.8地震同震记录 Fig. 2 The change curves of minute value of body strain at 5 stations during March 11 to 31, 2016 and coseismic records of Indonesia M7.8 earthquake |
可以看出:1)由于地下岩体存在相互耦合过程,压性背景成为体应变仪的主要背景趋势,月观测曲线呈现出显著的大潮和小潮的周期性,呈“梭形”变化,日观测曲线呈现出较明显的峰谷变化。2)潮汐形态各不相同,徐州台、六合台和连云港台形态光滑,徐州台固体潮清晰,幅值也明显大于六合台和连云港台;溧阳台和新沂台因覆盖层薄,受气压干扰明显,固体潮形态毛刺较多。3)各台均能清晰地记录印尼苏门答腊岛海域发生的M7.8地震,但是同震形态不同,六合台在初动过后出现阶跃,其他台站均为清晰的类地震波,幅值以新沂台最小。
体应变仪能观测记录到清晰的固体潮汐变化,潮汐波以半日和周日变化为主,其中月亮的主半日波M2的振幅最大,具有最大的信噪比,因此在潮汐波的研究中主要考虑M2波的潮汐因子。考虑到体应变仪的直接观测值为套筒内面积的改变,本文仅对直接观测值进行分析和处理,将直接观测值与理论应变的比值作为M2波视潮汐因子[12]。日常观测曲线上的畸变、脉冲等瞬时的扰动性变化与气压、降雨等干扰有关,以短周期的正向干扰影响为主,在时间上往往表现为准同步。台站环境固定的干扰源,如一定距离内的湖泊、饮水井等,通过地下水的作用造成观测数据的规律性变化,影响时间尺度较长。气压、降雨、固定干扰源和地震等因素仅对体应变仪的观测精度存在一定的影响,基本不影响M2波视潮汐因子,运行稳定的体应变仪M2波视潮汐因子整体变化幅度基本稳定在3%以内。
2 M2波视潮汐因子选取上述5个地震台体应变仪2015-07~2016-06的体应变观测记录,数据采样率为1 min/次,观测数据的连续性和稳定性较好,能记录到清晰的固体潮。M2波视潮汐因子用整时值与分钟值计算结果比较接近, 相差在2%以内,因此用整时值计算潮汐参数即可。本文对部分观测数据消除仪器或人为干扰所产生的线性漂移、阶变和缺数等,进行去除线性趋势和线性内插等处理,提取整点值后,应用Venedikow调和分析方法计算M2波视潮汐因子,结果见表 1。
|
|
表 1 体应变观测资料计算结果 Tab. 1 The calculation results of body strain |
试验样品取自江苏省5套体应变仪钻孔岩芯,取样段为体应变仪地下传感器安装位置,具体钻孔分布见图 1,岩芯信息见表 2。5个钻孔共取得5组钻孔岩芯,根据技术规范[13],将取回的岩芯(直径为150 mm)制成圆柱体试样,端面在平面磨床上磨平磨光,使其长度、外表面光洁度、两端面光滑度以及平行度都达到国际岩石力学学会(ISRM)规定的要求。每套体应变仪钻孔岩芯均制成2个圆柱体试样,直径分别为Ø31.23 mm和Ø31.5 mm,高度为40.33~116.46 mm(表 2)。
|
|
表 2 取样岩芯深度、尺寸及岩石名称 Tab. 2 The microcrack depth and size of rock samples |
本次试验加载设备采用WAW-D1000型电液伺服万能试验机,对标准圆柱形岩样进行单轴压缩试验(图 3)。为保证数据的可靠性,另考虑到应变片容易损坏,在试样上贴了2组应变片。为获取到样品内详细的微破裂信息,单轴压缩试验采用荷载速率加载控制,加载速率为0.1 kN/s,持续加载直至试样破坏。通过单轴压缩试验的应力-应变曲线得到力学参数单轴抗压强度σc和弹性模量E。整个试验在中国地震局地质研究所地震动力学国家重点实验室完成。

|
图 3 单轴压缩试验照片 Fig. 3 Photo of uniaxial compression test |
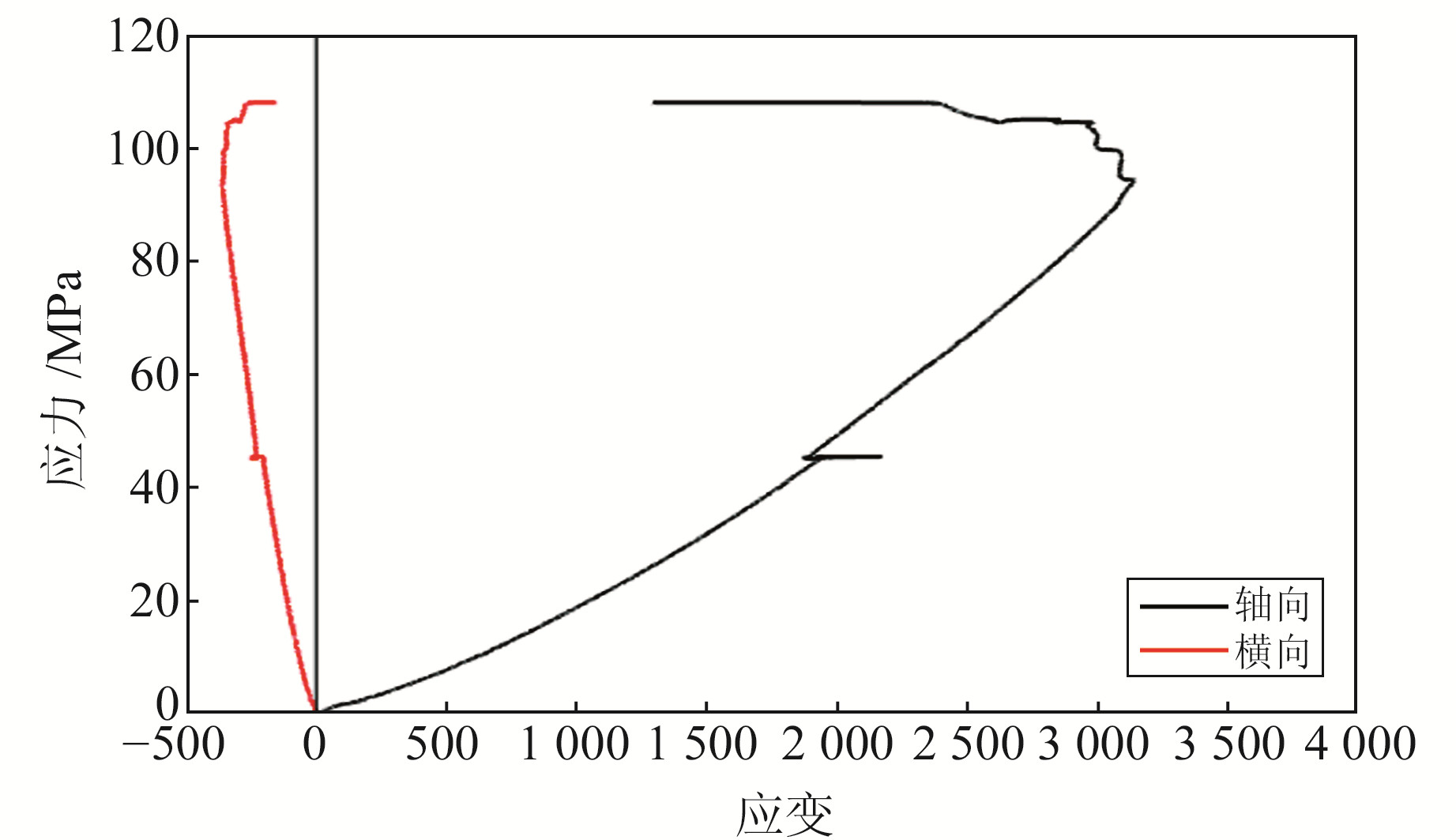
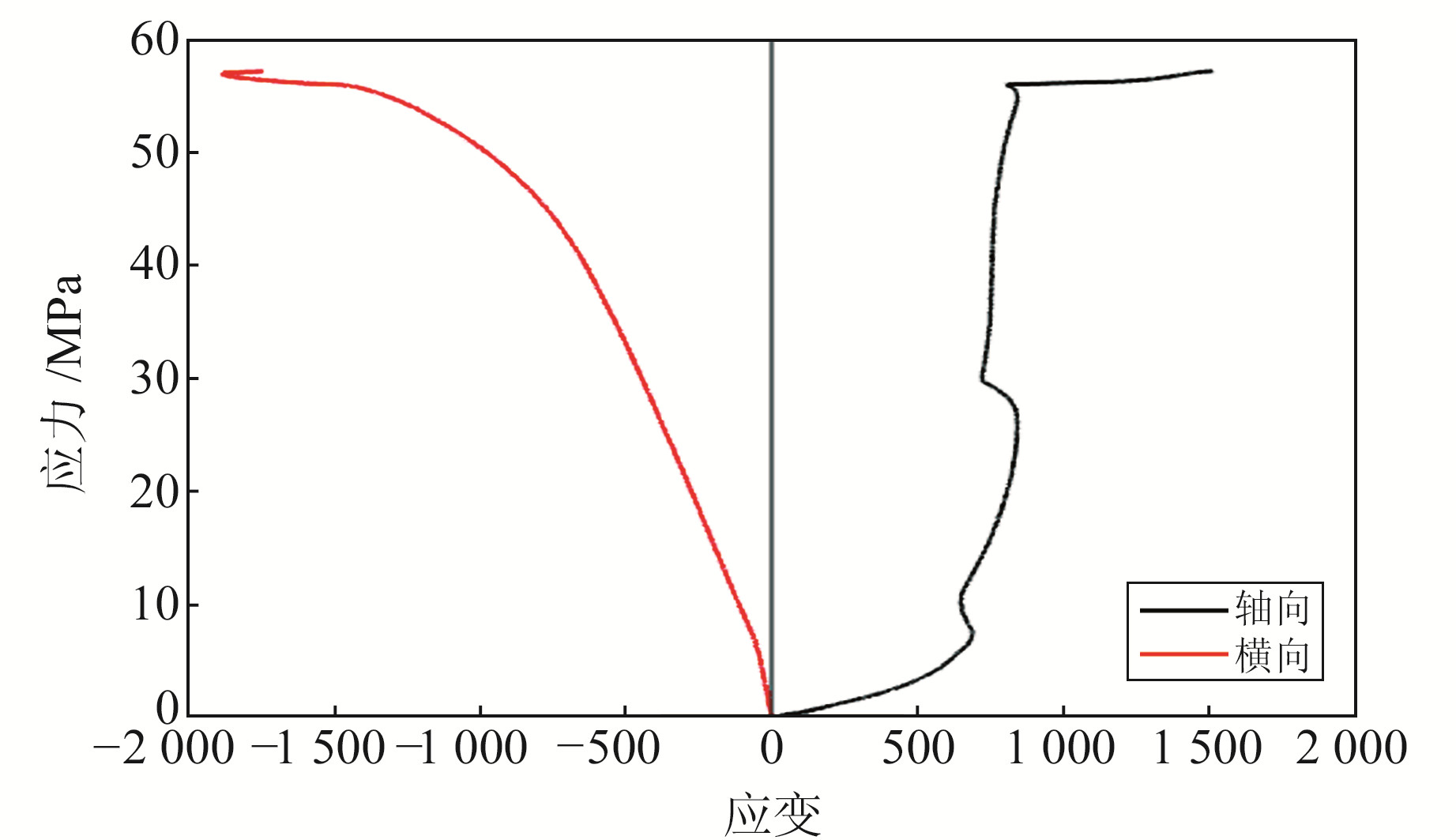
图 4和图 5为选取的部分代表性岩芯试样在单轴压缩条件下的应力-应变关系曲线,能反映出从加压到最终破坏整个受压试验过程中岩石所表现出的特性,呈现细节虽有区别但大致阶段相似[14]。试验过程大致可以分为4个阶段:初始压密阶段、弹性阶段、扩容阶段和破坏阶段。在压密阶段,试样JS05-10维持的时间较长,内凹明显,片麻岩内部存在的层理在该阶段有扩展;而JS03-6在压密阶段内凹不太明显,压密阶段几乎与弹性阶段重合,可能原因是JS03-6灰岩试样致密完整,无明显裂隙,导致其在压应力的作用下产生量非常微小,在很短的时间内即完成了试样的压密过程。在弹性阶段,图 4中JS03-6试样横向应变与轴向应变相比较小,即横向膨胀较小。由于受负荷控制加载方式的影响,JS03-6在弹性阶段维持的时间较长,在此阶段内,岩石试样JS03-6内部原有微孔隙、裂隙在较大压应力作用下基本完成了闭合,整个过程在弹性阶段中表现出较好的线性。在临近峰值时,岩石试样开始充分受力,轴向应变迅速增加,达到其抗压强度后突然破坏,粘贴在试样表面的电阻应变片被完全崩裂破坏。JS05-10试样在弹性阶段还是受到了层理的影响,维持时间不长,应力-应变曲线比标准样要复杂很多。JS03-6轴向应变在达到最大值后出现折回的现象,在该阶段微破裂继续扩展,轴向应力并非直接跌落,而是在较小的应力下呈“峰后阶梯式扰动”,岩石强度不断下降,已有宏观破裂面形成,岩石破裂成数块。
|
图 4 单轴压缩条件下JS03-6应力-应变曲线 Fig. 4 Stress-strain curves of JS03-6 samples in uniaxial compression test |
|
图 5 单轴压缩条件下JS05-10应力-应变曲线 Fig. 5 Stress-strain curves of JS05-10 samples in uniaxial compression test |
通过上述方法,获得各岩样的M2波视潮汐因子和力学参数,如表 3所示。
|
|
表 3 各岩样M2波视潮汐因子和力学参数 Tab. 3 The microcrack M2 apparent and mechanical parameters of rock samples |
对比M2波视潮汐因子与单轴抗压强度之间的关系发现,二者离散性较大,没有规律可循,随着单轴抗压强度的增大,没有表现出明显的变化趋势,这可能是由于岩石试件尺寸效应导致的随机性等因素造成的。考虑到本次试验的岩芯比较复杂,含有许多节理、裂隙等,因此制造圆柱体试样的过程中尺寸无法实现统一。另由表 2可知,60%的试样高径比为3,高径比为2和高径比为1的试样各占20%。陈瑜等[15]认为,尽管岩石参数计算方法本身很严格,但是不能忽略岩体力学性质的尺寸效应,因此需对单轴抗压强度对比尺寸效应进一步分析。

|
图 6 M2波视潮汐因子与单轴抗压强度之间的关系 Fig. 6 The relationship between the uniaxial compressive strength and M2 |
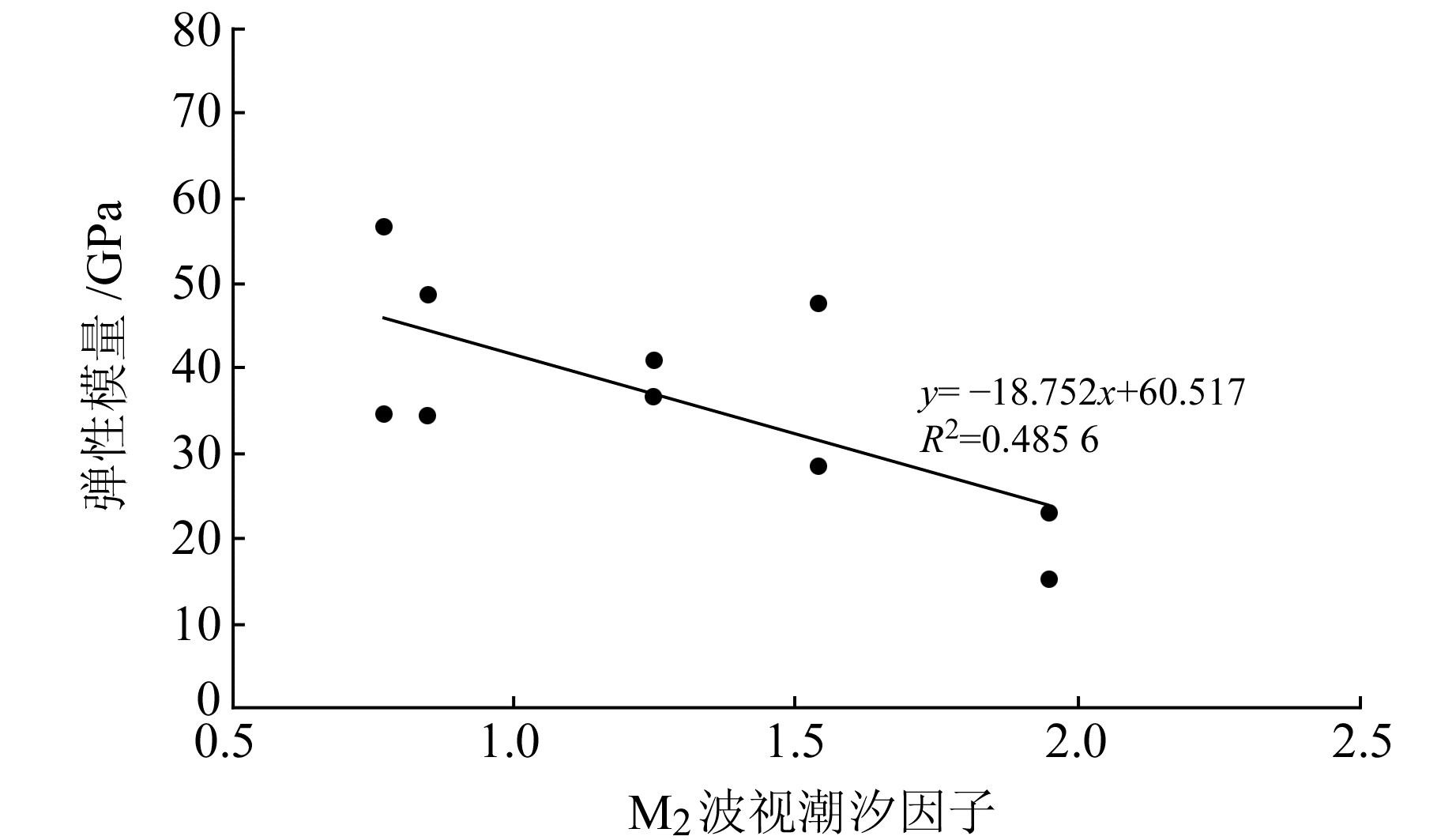
对比M2波视潮汐因子与弹性模量发现,试样表现出M2波视潮汐因子随着弹性模量的减小而增大的总体趋势。从图 7可以看出,两者之间基本呈现线性函数关系,拟合M2波视潮汐因子(N)与弹性模量(E)的关系,得:
| $ E = {\rm{ - 18}}{\rm{.752}}N{\rm{ + 60}}{\rm{.517,}}{R^2} = 0.4{\rm{85 \ 6}} $ |
|
图 7 M2波视潮汐因子与弹性模量之间的关系 Fig. 7 The relationship between deformation modulus and M2 |
1) 江苏省的经纬度范围在5°以内,而在大尺度范围内,理论应变固体潮在全省范围内M2波视潮汐因子基本相同。但由表 3可知,各个台站之间的M2波视潮汐因子差别较大,最大的徐州台为1.948 3,最小的六合台为0.771 9。
2) 通过单轴压缩试验,获得了5个台站的岩芯的主要力学性质,单轴抗压强度为15.42~205.05 MPa, 弹性模量为15.3~56.5 GPa。
3) 计算10组岩芯试样强度和弹性模量,并绘制出关系曲线,在不考虑试样的尺寸效应下,单轴抗压强度对M2波视潮汐因子的影响是随机的,离散性较大,不具规律。单轴抗压强度需要进一步考虑尺寸效应,本文不就此展开分析。根据试验结果可以看出,M2波视潮汐因子与试样的弹性模量有明确的相关性,前者随后者的减小而增大,这可解释为岩芯试样抵抗单位量所需的外力越小,即弹性模量越小,相对应的岩芯受潮汐引力作用越大,量越显著,M2波视潮汐因子越大。
4) 目前在运行的体应变仪之所以记录到的M2波视潮汐因子差异较大,多是由于钻孔岩芯力学性质的差异性造成的,因此对井下传感器附近的岩芯进行取样测试,获取弹性模量,对观测数据有一定的预期,可避免观测值的不可预见性,也是更进一步研究的重要基础。
| [1] |
中国地震局监测预报司.地形变测量[M].北京:地震出版社, 2008 (Monitoring and Forecasting Department of CEA. Ground Deformation Measurement[M].Beijing:Seismological Press, 2008)
(  0) 0) |
| [2] |
Nishimura E. On Earth Tides[J]. American Geophysical Union Transactions, 1950, 31(3): 357-376 DOI:10.1029/TR031i003p00357
(  0) 0) |
| [3] |
Beaumont C, Berger J. Earthquake Prediction: Modification of the Earth Tide Tilts and Strains by Dilatancy[J]. Geophysical Journal of the Royal Astronomical Society, 1974, 39(1): 111-121 DOI:10.1111/j.1365-246X.1974.tb05441.x
(  0) 0) |
| [4] |
池顺良, 武红岭, 骆鸣津. 钻孔应变观测中潮汐因子离散性与各向异性原因探讨——"十五"数字地震观测网络分量钻孔应变仪首批观测资料分析解释[J]. 地球物理学进展, 2007, 22(6): 1 746-1 753 (Chi Shunliang, Wu Hongling, Luo Mingjin. Discussion on Strain Tidal Factor Separation and Anisotropy-Analysis of First Data of Borehole Component Strain-Meter of China's Digital Seismological Observational Networks[J]. Progress in Geophysics, 2007, 22(6): 1 746-1 753)
(  0) 0) |
| [5] |
张斯奇, 张怀, 石耀霖. 固体潮应变各向异性研究[J]. 地震, 2013, 33(4): 190-195 (Zhang Siqi, Zhang Huai, Shi Yaolin. A Study on Anisotropy of Solid-Tidal Strain[J]. Earthquake, 2013, 33(4): 190-195 DOI:10.3969/j.issn.1000-3274.2013.04.020)
(  0) 0) |
| [6] |
周江存, 孙和平, 徐建桥, 等. 地球内部应变与应力固体潮[J]. 地球物理学报, 2013, 56(11): 3 779-3 787 (Zhou Jiangcun, Sun Heping, Xu Jianqiao, et al. Tidal Strain and Tidal Stress in the Earth's Interior[J]. Chinese Journal of Geophysics, 2013, 56(11): 3 779-3 787)
(  0) 0) |
| [7] |
李进武, 邱泽华. 钻孔应变仪观测的面应变潮汐因子初步分析[J]. 地球物理学进展, 2014, 29(5): 2 013-2 018 (Li Jinwu, Qiu Zehua. Analysis on Strain Tidal Factor Observed Borehole Strainmeters[J]. Progress in Geophysics, 2014, 29(5): 2 013-2 018)
(  0) 0) |
| [8] |
Asai Y, Ishii H, Aoki H. Comparison of Tidal Strain Changes Observed at the Borehole Array Observation System with In Situ Rock Properties in the Tono Region, Central Japan[J]. Journal of Geodynamics, 2009, 48(3-5): 292-298 DOI:10.1016/j.jog.2009.09.024
(  0) 0) |
| [9] |
何斌, 田韬, 王恒知. 基于钻孔特性的体应变观测相关性研究[J]. 地震工程学报, 2018, 40(1): 153-158 (He Bin, Tian Tao, Wang Hengzhi. Study on Correlation of Volume Strain Observation Based on Borehole Features[J]. China Earthquake Engineering Journal, 2018, 40(1): 153-158 DOI:10.3969/j.issn.1000-0844.2018.01.153)
(  0) 0) |
| [10] |
姚瑞, 杨树新, 王迪. 裂隙对四分量钻孔应力-应变观测影响的数值模拟分析[J]. 岩土工程学报, 2016, 38(2): 331-335 (Yao Rui, Yang Shuxin, Wang Di. Numerical Simulation Analysis of Effects of Cracks on 4-Component Borehole Observation of Stress-Strain[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(2): 331-335)
(  0) 0) |
| [11] |
王恒知, 周昱辰, 何斌, 等. 溧阳地区强震动台站场地特征研究[J]. 防灾减灾工程学报, 2019, 39(6): 1 005-1 009 (Wang Hengzhi, Zhou Yuchen, He Bin, et al. Study on Site Characteristics of Strong Motion in Liyang City[J]. Journal of Disaster Prevention and Mitigation Engineering, 2019, 39(6): 1 005-1 009)
(  0) 0) |
| [12] |
邱泽华. 钻孔应变观测理论和应用[M]. 北京: 地震出版社, 2017 (Qiu Zehua. Borehole Strain Monitoring: Theory and Application[M]. Beijing: Seismological Press, 2017)
(  0) 0) |
| [13] |
中国电力企业联合会. GB/T 50266-2013工程岩体试验方法标准[S].北京: 中国计划出版社, 2013 (China Electricity Council. GB/T 50266-2013 Standard for Test Methods of Engineering Rock Mass[S]. Beijing: China Planning Press, 2013))
(  0) 0) |
| [14] |
王文星. 岩石力学[M]. 长沙: 中南大学出版社, 2004 (Wang Wenxing. Rock Mechanics[M]. Changsha: Central South University Press, 2004)
(  0) 0) |
| [15] |
陈瑜, 黄永恒, 曹平, 等. 不同高径比时软岩强度与尺寸效应试验研究[J]. 中南大学学报:自然科学版, 2010, 41(3): 1-1 078 (Chen Yu, Huang Yongheng, Cao Ping, et al. Size Effect Experimental Study of Strength and Deformation in Different Height-to-Diameter Ratio Soft Rocks[J]. Journal of Central South University:Science and Technology, 2010, 41(3): 1-1 078)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


