2. 中国科学院大学,北京市玉泉路19号甲,100049;
3. 中国地震台网中心,北京市三里河南横街5号,100045
重力仪噪声水平是评估重力数据质量和观测台站周围环境优良与否的重要指标[1]。固定台站重力仪噪声水平的研究对于重力仪仪器性能、仪器运行状况以及重力台站选址等诸多问题具有重要参考意义[2]。超导重力仪(superconducting gravimeter, SG)和gPhone重力仪等多种类型重力仪被广泛布设于中国大陆[3],用来监测中国大陆重力场连续重力变化和观测各种长周期地球动力学信号[4]。高精度连续观测相对重力仪不仅可以观测到固体潮信号,也能够观测到地震频段的地震信号,如体波、面波和自由振荡等[5-7]。
目前国内对超导重力仪和gPhone重力仪观测噪声水平的研究多与新低噪声模型(new low noise model,NLNM)进行比较,而NLNM是全球地震仪观测台站噪声水平的下包络线[8],即代表仪器性能和台站综合条件最好的地震仪台站的噪声水平。但是每个地震仪台站的具体噪声水平不尽相同,不同台站仪器的噪声水平除了与仪器自身有关外,也受台站所处地理位置和周围环境等因素的影响。因此,对比同址观测的重力仪和地震仪噪声水平,可以排除地理位置和台站周围环境等因素的影响,得到不同观测仪器对相同的台站环境噪声响应的差异,从而能更合理地对不同类型的仪器噪声水平进行评定。
SNM是用来描述地震频段噪声大小的无量纲参数[9-10],可用其来评定台站地震频段噪声水平的高低,SNM值越大,表明地震频段的噪声水平越高。Rosat等[11]曾给出不同超导重力仪台站SNM值随年份的变化,发现SNM值变化较为平缓。但其使用的是分钟采样观测数据,而超导重力仪1 s采样间隔的原始观测数据被减采样到1 min采样间隔时,所使用的低通滤波器会压制数百秒周期信号的振幅。另外,不同台站仪器使用的低通滤波器也不尽相同[12]。考虑到SNM定义在200~600 s周期范围,因此使用分钟采样数据进行SNM计算时会产生一定的偏差。同时,前人的研究一般只计算得到每年的SNM值,很少研究SNM值在更短时间范围内的变化。综合考虑以上问题,本文采用1 s采样间隔的重力仪数据和同址观测的地震仪数据研究SNM值随月份的变化。
本文利用实测数据计算拉萨台超导重力仪、恩施和昆明台gPhone重力仪在地震频段的噪声水平,并分别与同址观测的STS-1和STS-2.5地震仪的噪声水平进行比较,最后分析每台仪器SNM值随时间的变化特征。
1 数据处理研究使用的仪器及其台站信息见表 1,其中拉萨台超导重力仪和地震仪相距约11 km,而恩施和昆明台仪器距离均不超过3 km,因此同一台站的各类仪器可以当作同址观测[13]。每台仪器均包含2013~2017年的连续观测数据。根据前人的研究,超导重力仪对周期大于100 s的信号的振幅响应为1,即可忽略仪器响应对100 s以上周期信号振幅的影响[14-15]。对于超导重力仪观测数据,将采样间隔从1 s减采样到1 min时,所使用的低通滤波器会对数百秒周期范围的信号振幅产生衰减作用[12]。因此,为了保证计算结果的可靠性,采用1 s采样间隔的重力仪数据和地震仪LHZ分量数据计算各类仪器在地震频段的噪声水平和SNM值。不同于地震仪和超导重力仪,gPhone重力仪数据观测系统使用的是北京时间,因此在处理数据前需要统一调整到格林尼治时间。
|
|
表 1 所用仪器及其台站信息 Tab. 1 Information of the instruments and stations |
用重力仪数据计算SNM的步骤为:1)将1 s采样间隔的连续重力数据分割成单天数据段;2)利用格值因子将电压值转换成重力值(nm/s2);3)去除均值和线性趋势;4)扣除重力潮汐理论值;5)扣除拟合得到的9阶多项式,以去除残余潮汐和仪器漂移等长周期项;6)人工剔除单天异常数据(间断、尖峰、阶跃以及地震等异常);7)计算单天数据的均方根RMS;8)选取每个月中RMS值最小的3 d数据作为该月的平静期数据;9)计算选取的3 d平静期数据的平均功率谱,并作为该月的噪声水平;10)计算每个月的SNM值。
用地震仪数据计算SNM的流程为:1)将原始观测数据分割成单天数据段;2)去除仪器响应并转换成加速度值(nm/s2);3)去除均值和线性趋势;4)人工剔除单天异常数据(间断、尖峰、阶跃以及地震等异常);5)采用高通滤波(0.1 mHz)扣除长周期项;6)计算单天数据的均方根RMS;7)选取每个月中RMS值最小的3 d数据作为该月平静期数据;8)计算选取的3 d平静期数据的平均功率谱,并作为该月的噪声水平;9)计算每个月的SNM值。
Peterson[8]计算NLNM时并没有扣除气压的影响,为保证重力仪和地震仪结果具有完全可比性,本研究对两类数据也不作气压改正处理。考虑到地震事件和仪器异常等因素会对地震频段噪声水平估计产生较大影响,使用人工方法检查波形数据,扣除异常数据。SNM值的计算采用Banka等[9]等给出的定义:
| $ \text{SNM=lg(meanPSD }\!\![\!\!\text{ }\frac{{{\text{(nm/}{{\text{s}}^{\text{2}}}\text{)}}^{\text{2}}}}{\text{mHz}}\text{ }\!\!]\!\!\text{ )+3}\text{.5} $ | (1) |
式中,meanPSD表示最平静期数据的平均功率谱在200~600 s频率范围内的求和。因为本研究使用的功率谱单位为(nm/s2)2/mHz,因此式(1)需要加上常数值3.5,该常数值能保证由NLNM计算得到的SNM值为0。因此在后面的比较中,SNM值大于0表示噪声水平高于NLNM。
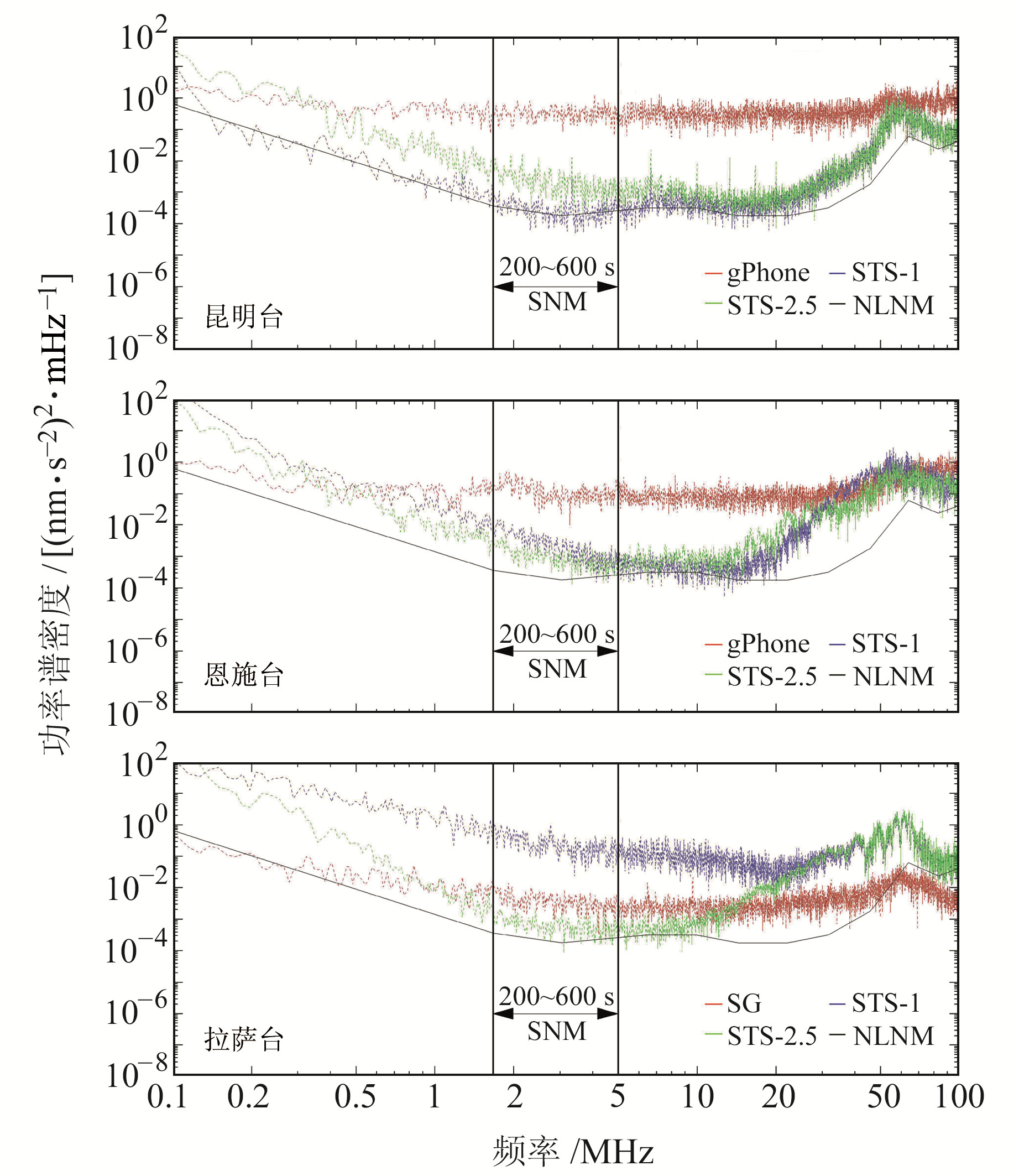
2 噪声水平估计和SNM值随月份的变化首先给出根据RMS值选取的2013~2017年最平静5 d数据功率谱的平均值作为5 a的噪声水平估计(图 1)。结果表明,对于拉萨台,在1~10 mHz频率范围,STS-2.5地震仪具有最低的噪声水平,超导重力仪噪声水平略高于STS-2.5地震仪,而STS-1地震仪具有异常高的噪声水平,3台仪器的噪声水平均高于NLNM;在0.1~1 mHz频率范围,超导重力仪噪声水平明显低于STS-1和STS-2.5地震仪;在15 mHz以上频率范围,超导重力仪噪声水平比地震仪更低,这是因为超导重力仪将模拟信号转换成数字信号时使用的抗混叠滤波器对10 mHz以上的高频信号具有振幅衰减作用[14-15]。对于恩施台,在0.1~100 mHz整个频率范围内,STS-1和STS-2.5地震仪噪声水平较为接近;同址观测的gPhone重力仪噪声水平在0.1~0.5 mHz频率范围内略低于地震仪,而在0.5 mHz以上具有更高的噪声水平;3台仪器在0.1~100 mHz频率范围内的噪声水平都要高于NLNM。对于昆明台,STS-1地震仪在0.1~20 mHz频率范围噪声水平与NLNM符合较好,STS-2.5地震仪噪声水平略高于STS-1地震仪,gPhone重力仪噪声水平最高。值得注意的是,在50~100 mHz(10~20 s)频率范围,各台站STS-1和STS-2.5地震仪均能观测到明显的谱峰,该谱峰被称为第一类地脉动,主要成分为海洋和固体地球耦合激发的瑞利面波信号[16]。在拉萨台超导重力仪噪声谱上也能观测到该谱峰,但在其他2个台站的gPhone重力仪结果图中该谱峰不太明显,这是由gPhone重力仪在此频段的较高噪声水平造成的。
|
图 1 2013~2017年最平静5 d的噪声水平 Fig. 1 Noise levels of 5 quietest days during 2013 to 2017 |
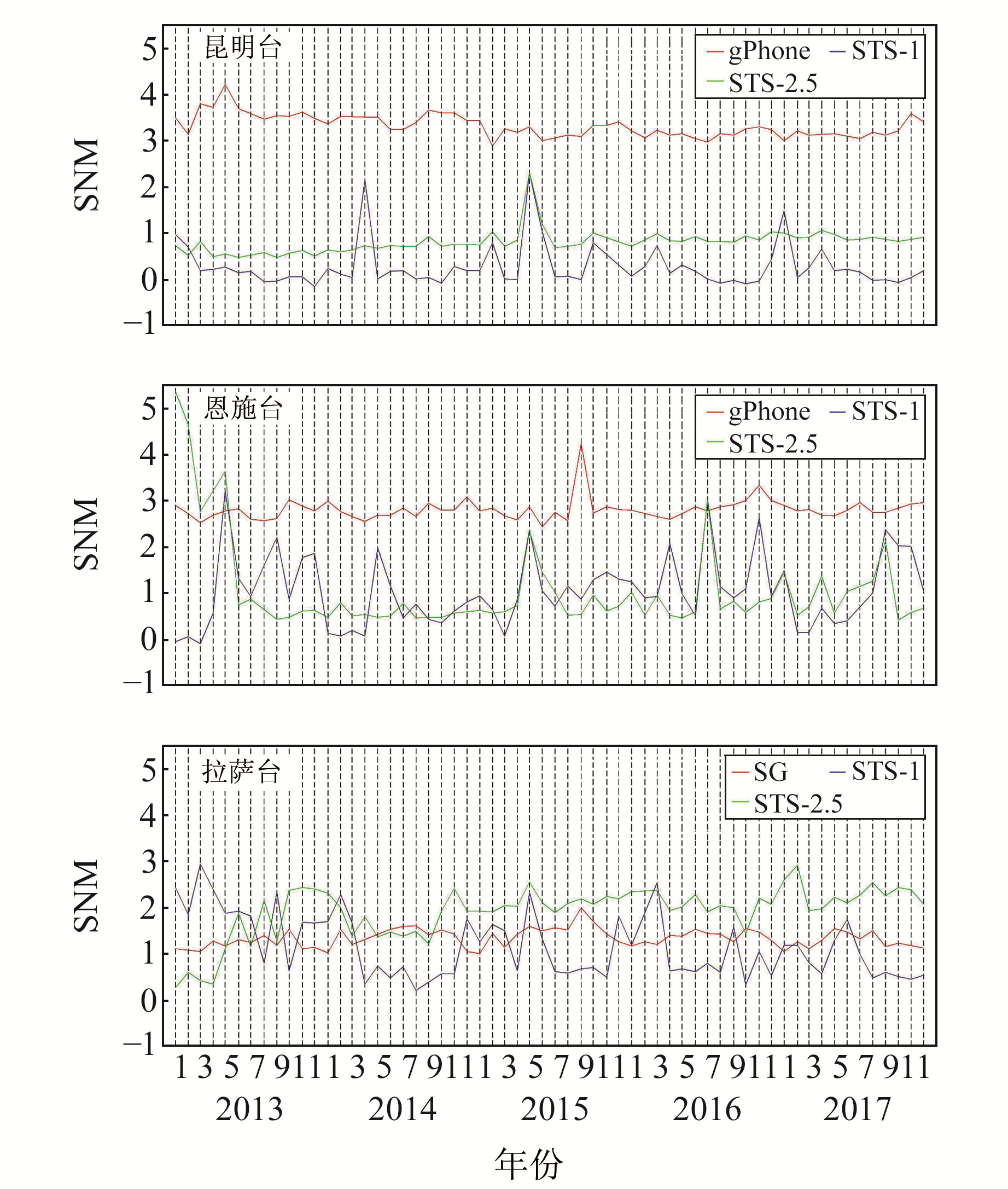
计算得到SNM值随月份的变化见图 2,结果表明,除了恩施台gPhone重力仪在2015-09出现一个较大的峰值外(SNM=4.23),其余重力仪的SNM值随月份变化相对较为平缓。但对地震仪来说,3个台站的STS-1和STS-2.5地震仪的SNM值随月份变化的波动均较为剧烈,且不具有明显的规律性。拉萨台超导重力仪的SNM值在随月份的变化中一直介于同址的STS-1和STS-2.5地震仪的结果之间。而昆明和恩施台gPhone重力仪每个月的SNM值都要明显大于STS-1和STS-2.5地震仪的结果。整体上,3个台站STS-2.5地震仪的SNM值在大部分月份都要大于同址观测的STS-1地震仪的结果。
|
图 2 SNM值随月份的变化 Fig. 2 Variations of the monthly SNM values |
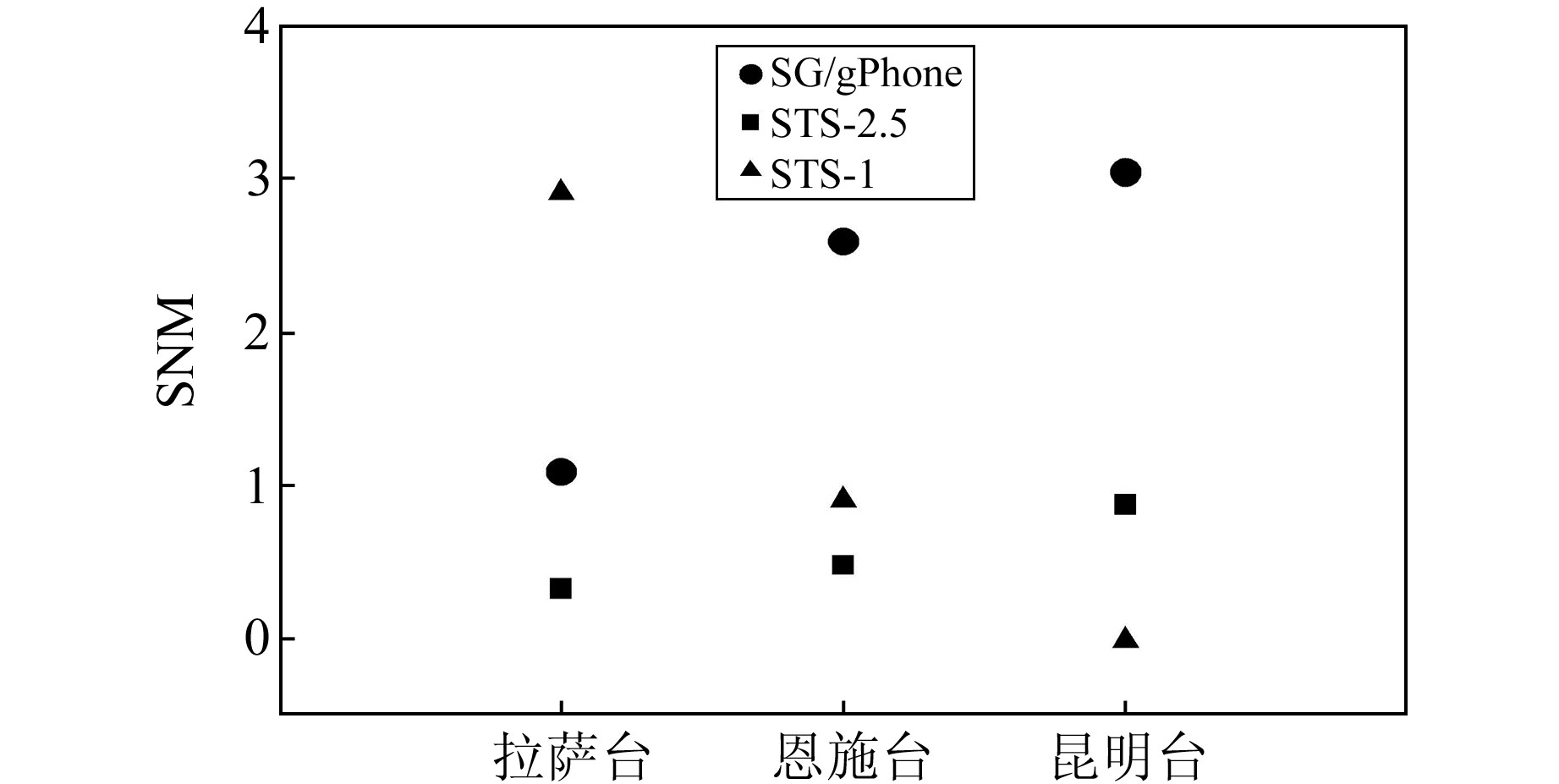
为了保证分析结果的完整性,给出由2013~2017年最平静的5 d数据计算得到的SNM值(图 3)。结果表明,拉萨台超导重力仪的SNM值为1.09,恩施和昆明台gPhone重力仪的SNM值分别为2.59、3.04,与前人的研究结果基本一致[1-2, 17]。对于恩施和昆明台,gPhone重力仪的SNM值要明显大于同址观测的2种地震仪的结果。但对于拉萨台STS-1地震仪来说,计算得到的SNM值明显过大(SNM=2.91),这与图 1中拉萨台STS-1地震仪噪声水平明显过高的异常现象一致。
|
图 3 2013~2017年各台站仪器最平静5 d的SNM值 Fig. 3 SNM values of 5 quietest days during 2013 to 2017 for different instruments at all stations |
对比图 2、3可知,对于拉萨台STS-1地震仪,图 2中有些月份的最平静期SNM值要小于图 3中连续5 a数据得到的平静期SNM值,说明从5 a的连续观测数据中获得的5 d最平静期数据并不完全是从这些在单月中出现的明显更加平静的平静期数据中选取的。仔细对比其他各台仪器结果,同样可以发现该问题的存在。
仔细检查数据处理流程发现,在计算SNM值时是利用扣除9阶多项式后的重力残差直接计算RMS,然后选出RMS值最小的几天数据作为最平静期数据。但是扣除9阶多项式后的残差数据中包含了大量的非SNM频率范围(SNM频率范围为200~600 s)的噪声能量(图 1),而SNM频段是0.1~100 mHz频率范围内能量最小的频段,该频段能量在计算时间域波形RMS值时所占的比重要小于其他频段。这种情况下使用包含0.1~100 mHz整个频段能量计算得到RMS值,并从中选取RMS最小值作为最平静期结果时,选取的是整个频段的RMS最小值,而不是SNM频段对应的RMS最小值,所以才会出现上述问题[10]。因此,在分析1 s采样间隔的观测数据时,仅采用9阶多项式处理极有可能会造成获得的SNM值不是真正的最小值。
3 带通滤波(200~600 s)方法选取的最平静期噪声水平和SNM值采用带通滤波的方法解决上述问题(将上一节使用的方法称为未滤波方法)。对于重力数据,先对扣除9阶多项式后的重力残差信号进行带通滤波(通带范围200~600 s,即SNM所定义的频段范围),然后再计算RMS,选取RMS最小的5 d数据作为2013~2017年最平静期数据,或者选择单月中RMS最小的3 d数据作为当月的最平静期数据。对于地震仪数据,将高通滤波替换为带通滤波(200~600 s),然后计算RMS,并选取最平静期数据。
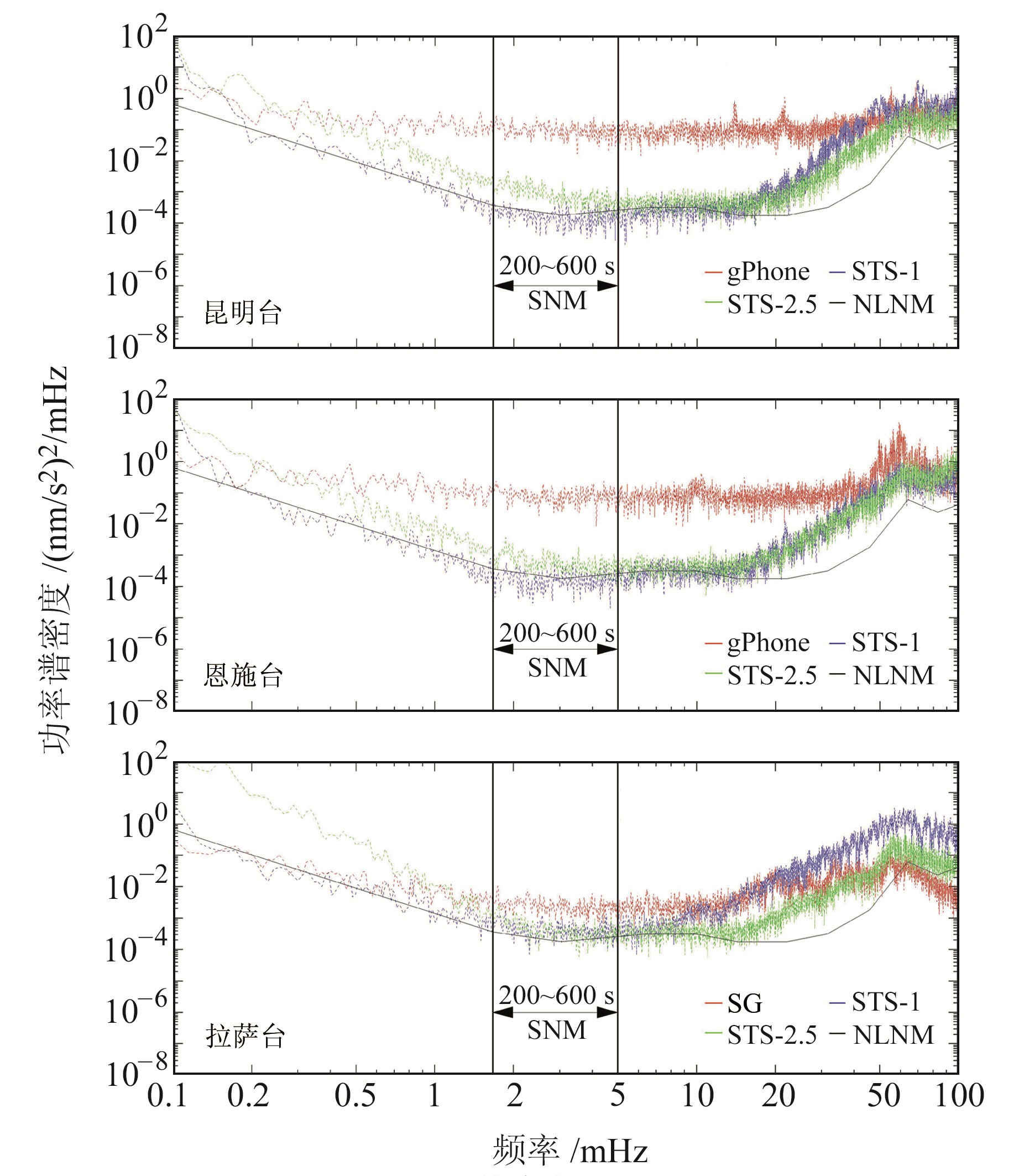
图 4为采用带通滤波方法重新选取的2013~2017年5 d最平静期数据计算得到的平均功率谱。对比图 1可知,拉萨和恩施台的2种地震仪在SNM频段(200~600 s)的噪声水平均得到明显降低。而3个台站的重力仪噪声水平变化较小,这与重力仪在0.1~100 mHz频段噪声能量分布相对较为均匀有关。对于所有台站,STS-1地震仪在小于10 mHz频段具有比STS-2.5地震仪更低的噪声水平,而在10 mHz以上频段2种仪器噪声水平相当。
|
图 4 带通滤波方法选取的2013~2017年最平静5 d的噪声水平 Fig. 4 Noise levels of 5 quietest days during 2013 to 2017(with bandpass filtering) |
利用带通滤波方法选取的最平静期时段数据计算SNM值随月份的变化(图 5)。相比于图 2,图 5中最大的变化是所有仪器的SNM值随月份的变化变得更加平缓,说明先对数据进行带通滤波,然后再计算SNM值的方法是有效的。图 2中恩施台gPhone重力仪在2015-09出现的SNM极大值,经过带通滤波处理后大幅减小,变得和邻近月份的SNM值较为接近。从图 5中还可以发现,带通滤波处理对地震仪SNM值随时间变化曲线的平滑作用比重力仪更为明显,这同样与重力仪观测数据在0.1~100 mHz整个频率范围内噪声能量分布比地震仪更为均匀有关。

|
图 5 带通滤波方法计算的SNM随月份的变化 Fig. 5 Variations of the monthly SNM values (with bandpass filtering) |
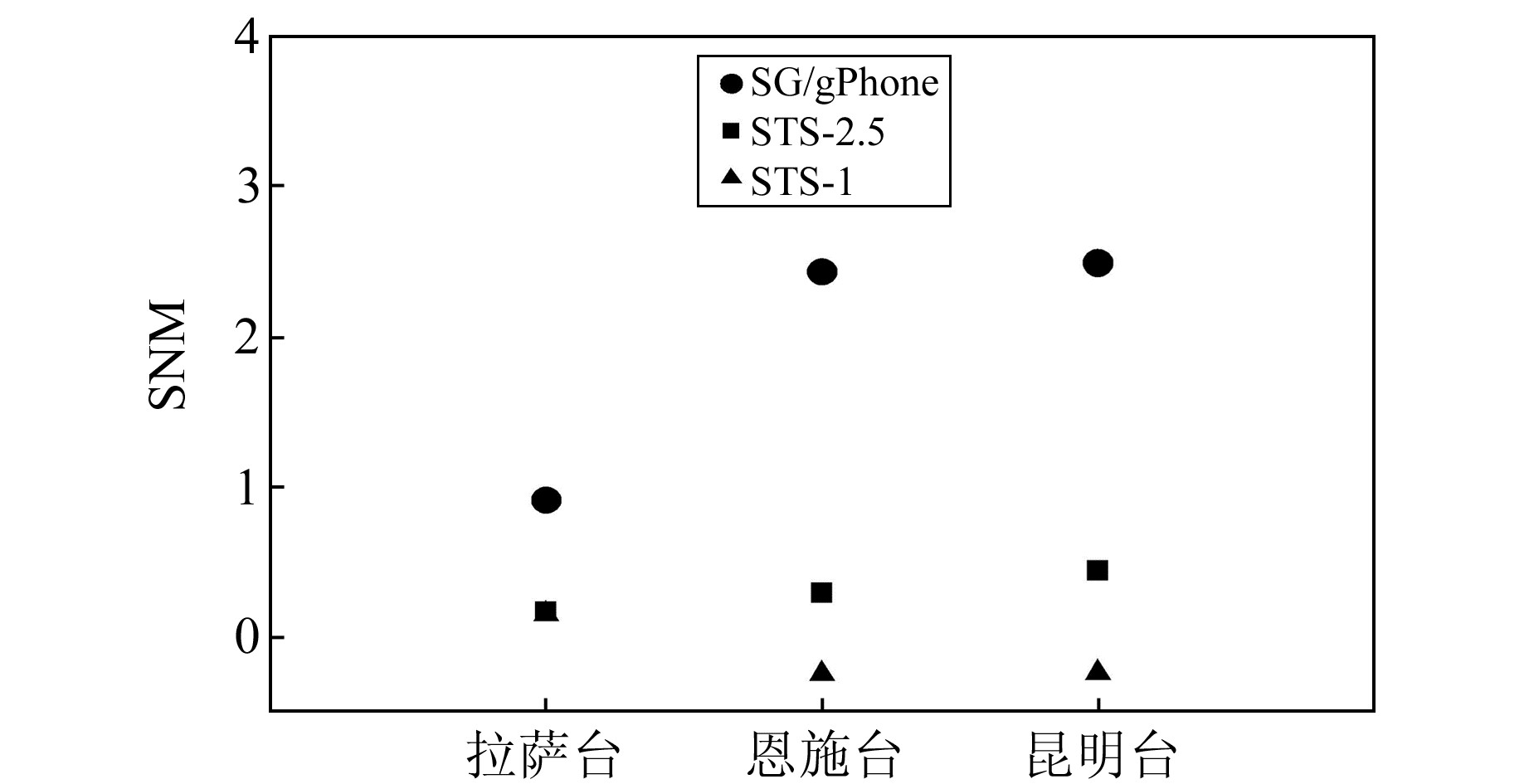
同样给出由带通滤波方法选取的2013~2017年最平静5 d数据计算得到的SNM值(图 6)。结果表明,经过带通滤波处理后,拉萨台STS-1地震仪的SNM值和STS-2.5地震仪的结果极为接近(在图 6中是重合的)。未滤波方法和带通滤波方法计算得到的SNM具体数值在表 2中给出。从图 6和表 2可以看出,带通滤波方法可以明显地减小SNM值,这表明只有直接对200~600 s频段数据计算得到的最小RMS所在的日期才能代表SNM频段的最平静期。恩施和昆明台STS-1地震仪数据经带通滤波后计算得到的SNM值小于0,表明2个台站的STS-1地震仪噪声水平在200~600 s频段要低于NLNM,这一结论同样可以从图 4结果中得到,这说明部分性能较好的STS-1地震仪的噪声水平要低于NLNM[18]。
|
图 6 带通滤波方法选取的各台站仪器2013~2017年最平静5 d的SNM值 Fig. 6 SNM values of 5 quietest days during 2013 to 2017 for different instruments at all stations(with bandpass filtering) |
|
|
表 2 带通滤波和未滤波2种方法计算得到的SNM值的对比 Tab. 2 Comparison of SNM values computed with bandpass filtering and without bandpass filtering |
最后给出各台站仪器由未滤波和带通滤波2种方法选取的2013~2017年5 d最平静期(表 3)。可以看出,对于同一台仪器,2种数据处理方法选取的最平静期差异较大,很少有重合的日期。这也再次表明,SNM频率范围200~600 s对应的最平静期不同于整个频率范围0.1~100 mHz(10~10 000 s)对应的最平静期。
|
|
表 3 带通滤波和未滤波2种方法选取的最平静期的对比 Tab. 3 Quietest days obtained with bandpass filtering and without bandpass filtering |
1) 地震频段1 mHz以上时,超导重力仪噪声水平略高于同址观测的2种地震仪噪声水平,而1 mHz以下时则相反。0.5 mHz以上时,gPhone重力仪噪声水平高于同址观测的2种地震仪噪声水平,0.1~0.5 mHz频率范围与地震仪结果接近。10 mHz以下时,STS-1地震仪噪声水平低于STS-2.5地震仪,而10 mHz以上时,2种仪器的噪声水平相当。
2) 使用未滤波方法计算得到的最平静期的SNM值并不是SNM所在频段(200~600 s)的最小值,采用带通滤波方法计算得到的最平静期的SNM值才是真正的最小值。后者计算得到的SNM值随月份的变化比前者更为平缓。
| [1] |
张苗苗. 超导重力仪台站背景噪声水平评估及信号提取[J]. 测绘学报, 2017, 46(4): 535 (Zhang Miaomiao. Estimation of the Background Noise Levels and Extraction of Signals at SG Stations[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 535)
(  0) 0) |
| [2] |
Zhang X T, Jiang Y, Zhang K, et al. The Influence of Observation Environment on Background Noise Level of gPhone Gravimeter[J]. Geodesy and Geodynamics, 2017, 8(6): 443-447
(  0) 0) |
| [3] |
甘卫军, 李强, 张锐, 等. 中国大陆构造环境监测网络的建设与应用[J]. 工程研究, 2012, 4(4): 324-331 (Gan Weijun, Li Qiang, Zhang Rui, et al. Construction and Application of Tectonic and Enviromental Observation Network of Mainland China[J]. Journal of Engineering studies, 2012, 4(4): 324-331)
(  0) 0) |
| [4] |
Sun H P, Zhang H K, Xu J Q, et al. Influences of the Tibetan Plateau on Tidal Gravity Detected by Using SGs at Lhasa, Lijiang and Wuhan Stations in China[J]. Terrestrial, Atmospheric and Oceanic Sciences, 2019, 30(1): 139-149 DOI:10.3319/TAO.2019.02.14.01
(  0) 0) |
| [5] |
江颖, 胡小刚. 利用芦山地震自由振荡信号检验中国大陆超导重力仪的高频特性[J]. 武汉大学学报:信息科学版, 2017, 42(5): 583-588 (Jiang Ying, Hu Xiaogang. Investigation of High-Frequency Noise for Superconducting Gravimeters of China Using Normal Modes of Lushan Earthquake[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 583-588)
(  0) 0) |
| [6] |
Niebauer T M, MacQueen J, Aliod D, et al. Monitoring Earthquakes with Gravity Meters[J]. Geodesy and Geodynamics, 2011, 2(3): 71-75
(  0) 0) |
| [7] |
Camp M. Measuring Seismic Normal Modes with the GWR C021 Superconducting Gravimeter[J]. Physics of the Earth and Planetary Interiors, 1999, 116(1): 81-92
(  0) 0) |
| [8] |
Peterson J R. Observations and Modeling of Seismic Background Noise[R]. USGS, Reston, 1993 https://www.researchgate.net/publication/236946018_Observations_and_Modeling_of_Seismic_Background_Noise
(  0) 0) |
| [9] |
Banka D, Crossley D J. Noise Levels of Superconducting Gravimeters at Seismic Frequencies[J]. Geophsical Journal International, 1999, 139(1): 87-97 DOI:10.1046/j.1365-246X.1999.00913.x
(  0) 0) |
| [10] |
Rosat S, Hinderer J, Crossley D J. A Comparison of the Seismic Noise Levels at Various GGP Stations[J]. Bull Inf Marées Terrestres, 2002, 135: 10 699-10 700
(  0) 0) |
| [11] |
Rosat S, Hinderer J. Noise Levels of Superconducting Gravimeters: Updated Comparison and Time Stability[J]. Bulletin of the Seismological Society of America, 2011, 101(3): 1 233-1 241 DOI:10.1785/0120100217
(  0) 0) |
| [12] |
Rosat S, Hinderer J, Crossley D J, et al. The Search for the Slichter Mode: Comparison of Noise Levels of Superconducting Gravimeters and Investigation of a Stacking Method[J]. Physics of the Earth and Planetary Interiors, 2003, 140(1): 183-202
(  0) 0) |
| [13] |
Marion F, Hinderer J, Trampert J. Comparative Study of Superconducting Gravimeters and Broadband Seismometers STS-1 / Z in Seismic and Subseismic Frequency Bands[J]. Physics of the Earth and Planetary Interiors, 1997, 101(3): 203-217
(  0) 0) |
| [14] |
Camp M, Wenzel H G, Schott P, et al. Accurate Transfer Function Determination for Superconducting Gravimeters[J]. Geophysical Research Letters, 2000, 27(1): 37-40 DOI:10.1029/1999GL010495
(  0) 0) |
| [15] |
Francis O, Lampitelli C, Camp M, et al. Comparison between the Transfer Functions of Three Superconducting Gravimeters[J]. Marées Terrestres Bulletin Dinformations, 2011, 147: 11 857-11 868
(  0) 0) |
| [16] |
Kiwamu N. Ambient Seismic Wave Field[J]. Proceedings of the Japan Academy, Series B, 2017, 93(7): 423-448 DOI:10.2183/pjab.93.026
(  0) 0) |
| [17] |
Zhang K, Liu Z W, Zhang X T, et al. Comparison of Noise-Levels between Superconducting Gravimeter and gPhone Gravimeter[J]. Geodesy and Geodynamics, 2018, 9(6): 498-503
(  0) 0) |
| [18] |
Jonathan B, Davis P, EkstrÖm G. Ambient Earth Noise: A Survey of the Global Seismographic Network[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B11)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. China Earthquake Networks Center, 5 Nanheng Street, Sanlihe, Beijing 100045, China
 2020, Vol. 40
2020, Vol. 40


