台湾处于菲律宾海和欧亚板块交界处,其间有多个活动断层,地理位置特殊,地质构造复杂。采用GNSS观测资料探测台湾地区可能的地球物理信号,有助于了解台湾区域各种物理现象对GNSS站点坐标时间序列的贡献,分析GNSS站点时间序列,了解各种物理现象的变化,为后续研究提供更加可靠的数据基础。本文采用PCA方法进行台湾地区空间滤波,提取共模误差(CME),对比分析空间滤波前后站点长期速度项的不确定度及噪声特点等。
1 数据与方法 1.1 cGPS数据台湾地区由各单位建立了大量的连续运行GPS站点(continues GPS,cGPS)。本文采用GIPSY/OASIS Ⅱ(v6.4)软件精密单点定位模式[1]解算其1996-01-07~2011-06-01的GPS观测数据。为保证数据的质量,在后续处理中将剔除一部分不在岛内和数据长度太短的测站。图 1(a)给出了所有站点的数据可用性,其中空白处表示数据缺失, 图 1(b)为站点数目随时间的变化、站点分布以及对应站点的数据长度、台湾地区的地形信息。

|
图 1 台湾cGPS数据可用性和站点分布及其数目随时间的变化 Fig. 1 Data availability, the distribution and number variation of cGPS stations in Taiwan |
共模误差是一种空间相关的误差,因此先剔除不在台湾主岛上的站点。为了避免数据缺失和早期的数据质量对结果的影响,仅选取2005-07-20以后的时间序列,并选取数据长度超过总长度(2005-07-20~2011-06-01)80%的站点。对于每一个站点,考虑到仪器维护以及地震事件引起的间断、阶跃及跳变会影响速度、周期等参数的准确估计,并且人工判读优于自动或半自动[2]判读,因此本文采用目视探测的方法。
每个站点的时间序列y(ti)可以写为[3]:
| $ \begin{gathered} y({t_i}) = a + b{t_i} + c\sin (2\pi {t_i}) + d\cos (2\pi {t_i}) + \hfill \\ e\sin (4\pi {t_i}) + f\sin (4\pi {t_i}) + \sum\limits_{j = 1}^{{n_g}} {{g_i}H({t_i} - {T_{gi}}) + {v_i}} \hfill \\ \end{gathered} $ | (1) |
式中,ti为历元,H(ti-Tgi)为阶梯函数,当ti≥Tgi时, 其值为1否则为0;gi为速率从ti=Tgi开始的变化;a、b分别为站点位置和速率;c、d分别为周年项系数;e、f分别为半周年项系数;vi为残差项。根据式(1),采用最小二乘的方法拟合原始时间序列,扣除线性趋势项和季节项(周年项和半周年项),得到残差坐标时间序列。
1.3 PCA法空间滤波PCA法滤波的中心思想是数据降维,同时尽可能保留数据集中存在的变化特征[4]。假设在GPS区域网中有n个测站、m个历元,其坐标序列分量组成矩阵形式:
| $ X({t_i}, {x_j}) = [{X_1}, {X_2}, {X_3}, ..., {X_n}] $ |
| $ i = 1,2,3, \cdots ,m;j{\rm{ }} = 1,2,3, \cdots ,n $ | (2) |
| $ X({t_i},{x_j}) = \sum\limits_{k = 1}^n {{a_k}({t_i})} {v_k}({x_j}) $ | (3) |
其中,
| $ {{\rm{a}}_k}({t_i}) = \sum\limits_{j = 1}^n {X({t_i},{x_j})} {v_k}({x_j}) $ | (4) |
ak(ti)称作X(ti, xj)与时间相关的第k阶主成分分量(kth principal component, PCk),vk(xj)为其对应的与站点有关的空间响应特征向量。
通常前几个主成分分量就代表了该观测网络绝大部分的共同变化模式,它们反映了整个网的变化规律;而越靠后面的高阶主成分分量通常反映的整个网的信息很少,它们往往反映的是单个站点自身变化的特点甚至是噪声[5-6]。
2 结果 2.1 PCA滤波结果将cGPS坐标时间序列的3个分量分解为时间分量和其对应的空间响应,为了增强可比性,将每个空间响应向量除以绝对值最大的空间响应向量,使得每个空间响应的数值都在-100%~100%内。限于篇幅,这里仅给出第1主成分及其空间响应。如图 2所示,线条代表正响应,从左到右依次为N、E、U方向。

|
图 2 方向缩放后的第1主成分及其空间响应 Fig. 2 The first scaled PC and(bottom) its normalized spatial response for the N, E and U direction |
可以看到,各个站点N、E、U方向第1主成分的空间响应几乎在所有站都表现出一致性,平均空间响应分别为66%、77%和68%,表明第1主成分能代表绝大部分的共模主成分。
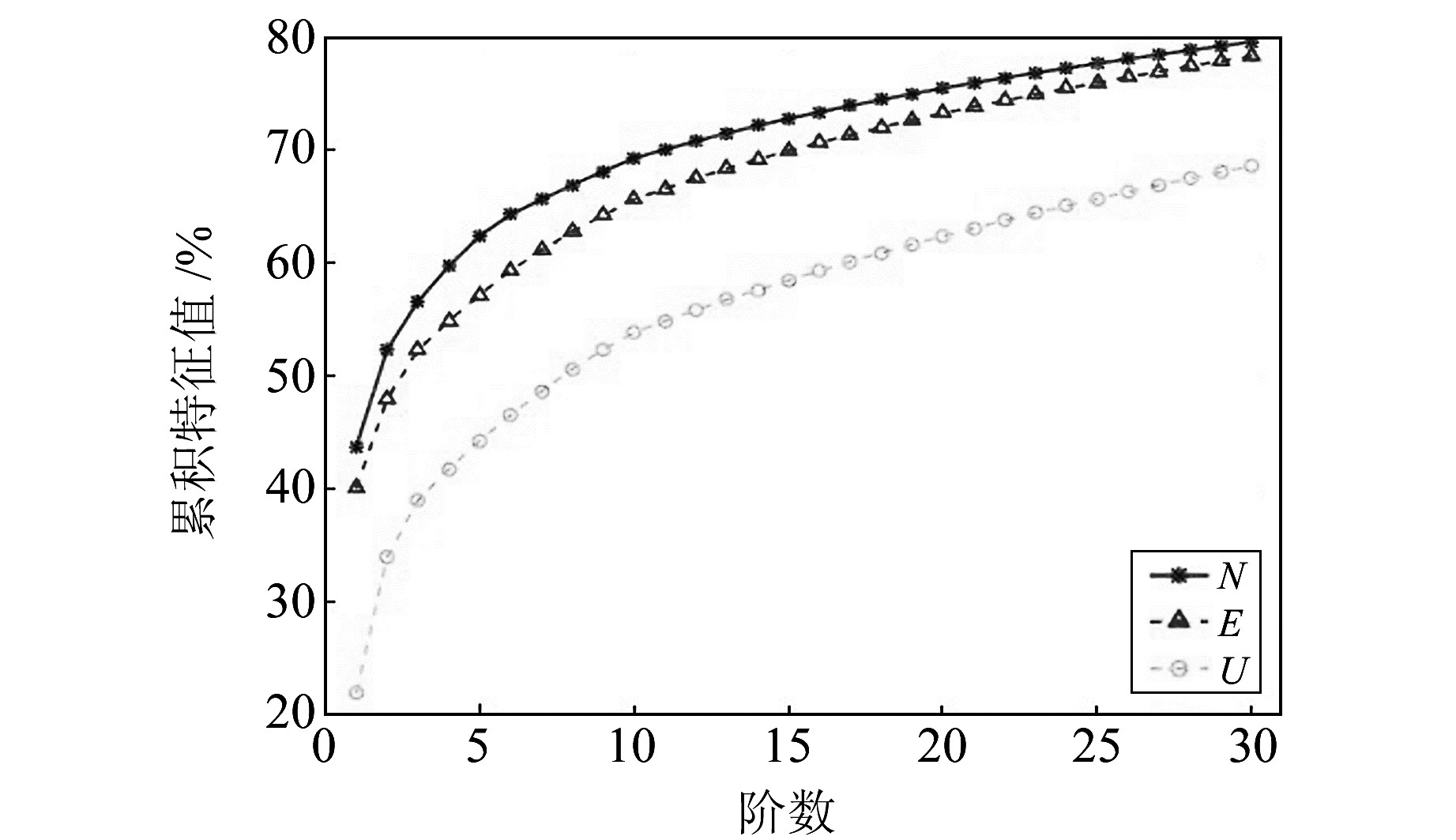
图 3给出了前30阶主成分的累积贡献率(特征值),N、E、U分量第1主成分分别占到43.7%、40.0%和21.9%。值得注意的是,第2主成分甚至更高阶主成分占到了较高的贡献率,但空间响应没有呈现出很好的区域一致性。根据前述原理,在定义共模误差、选取前几个主成分分量的时候,需要考虑到前几个主成分分量能够代表整个cGPS网络的大部分信息,因此可以根据前几个主成分分量的贡献率和空间响应模式是否一致来定义共模误差取前几个主成分分量。考虑到站点空间响应的一致性,本文将第1主成分分量定义为整个网的CME[5],即
|
图 3 前30阶主成分累积特征值 Fig. 3 Cumulative percentage of the first 30 PCs eigenvalues |
| $ {\varepsilon _i}({t_i}) = \sum\limits_{k = 1}^p {{a_k}} {v_k}({x_j}), (p = 1) $ | (5) |
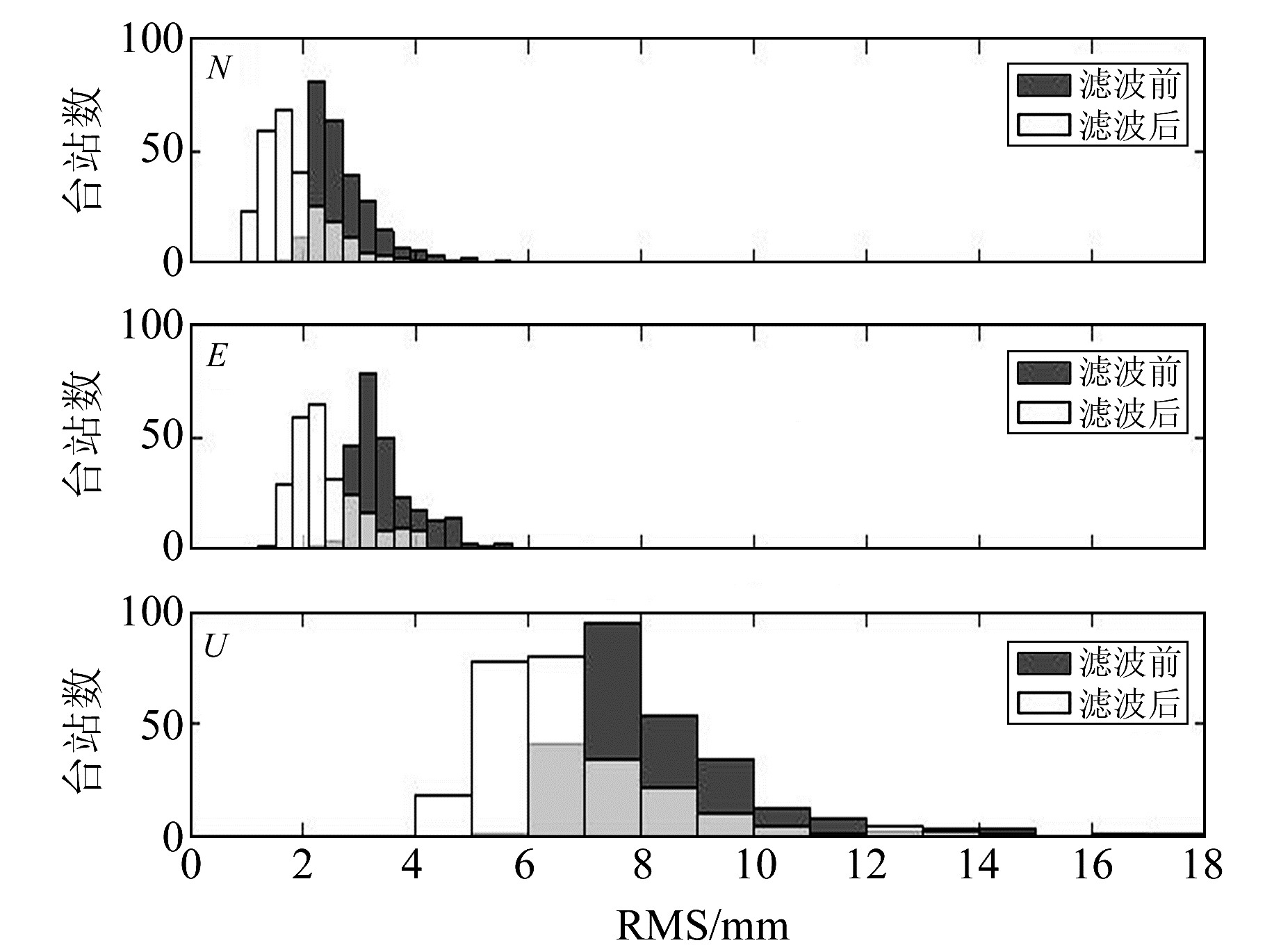
根据式(5)可以计算CME,并进行滤波处理。滤波的效果可以用残差时间序列RMS的降低率进行描述。图 4给出经过滤波后残差时间序列RMS值减小百分比的分布情况,图 5给出滤波前后RMS的直方图统计结果。

|
图 4 PCA滤波后残差序列的RMS减小百分比 Fig. 4 RMS reduction rates of residual time series after PCA filtering |
|
图 5 N、E、U组分的RMS直方图 Fig. 5 The histogram of RMS for N, E, and U component |
噪声是影响时间序列精度的特性之一,为了了解滤波对坐标时间序列噪声特性的改正效果,采用基于最大似然估计方法的Hector软件[7]对滤波前后的时间序列进行处理。本文采用幂律噪声(power law noise, PLN)[8]加白噪声(white noise, WN)组合模型在估计时间序列周期项、速度项等的同时估计各个站点的噪声性质(包括谱指数和噪声振幅)。
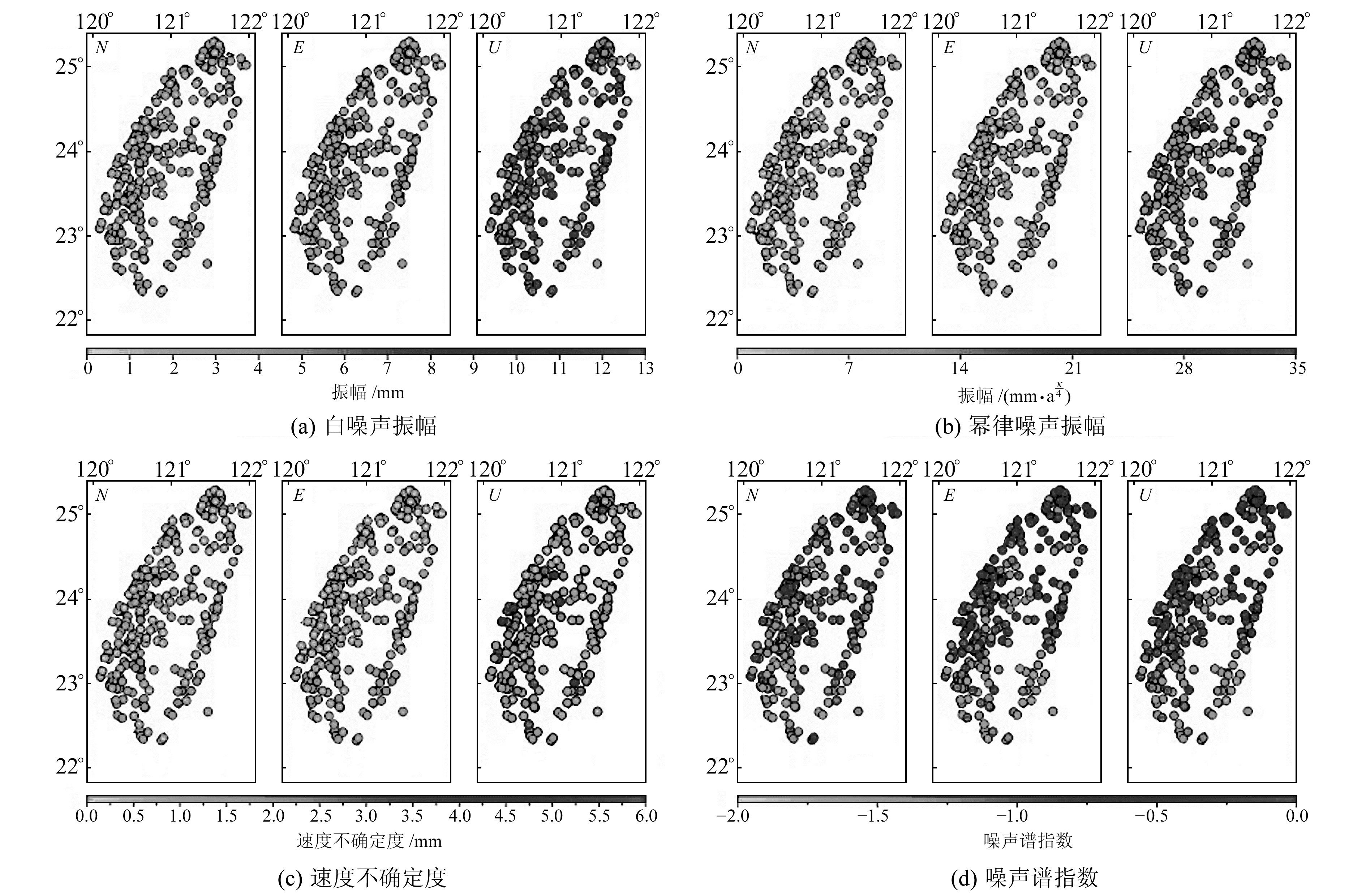
图 6为滤波后白噪声振幅(σwn)、幂律噪声振幅(σpl)、谱指数(κ)、速度不确定度(σvel)和RMS等指标的空间分布,表 1为滤波前后各项指标的对比。
|
图 6 PCA滤波后N、E、U的白噪声振幅、幂律噪声振幅、速度不确定度以及噪声谱指数 Fig. 6 The WN amplitude, PLN amplitude, velocity uncertainty and spectral indices for N, E and U component after filtering |
|
|
表 1 滤波前后对比 Tab. 1 Comparison between before and after filtering |
滤波的效果可以根据站点坐标序列的RMS值降低率表征。从图 4可以看出,残差的RMS均有所降低。由表 1可以看出,N、E方向降低率略高于U方向,分别为33%、31%、19%。垂直方向比水平方向有更大的周期项振幅,而滤波前的残差时间序列中已经去掉了季节项(周年项和半周年项)。因此,在去除共模误差后,水平方向的效果更加明显。从图 5可以看出,PCA滤波后时间序列的RMS在N、E、U方向上均有所减小。
从图 4还可以看出,PCA滤波效果在台湾的东、西两侧存在明显的差异,东侧N、E、U方向RMS减小比率相对较小,且在U方向上体现更加明显。从图 1(b)地形情况及台站分布看出,台湾东侧以山脉居多,台站分布较为稀疏,而西侧相对比较平坦,台站分布比较密集;此外,台湾的西南部分由于地下水的抽取存在整体下沉的现象[9],而东部由于造山运动,存在地形隆起现象[10]。另外注意到,主成分的贡献率比较分散。限于篇幅,这里仅给出第2主成分,如图 7(粗线代表正响应,细线代表负响应),第3~5主成分基本与第2主成分类似。这些成分的站点响应呈现明显的局部变化特征,表明台湾地区cGPS站点时间序列所反映的信号十分复杂。站点坐标时间序列在垂直分量上共性特征不如水平方向明显,也就是说,垂直时间序列中更多反映的是与站点局部变化相关的信号。因此,滤波结果在台湾东、西部分的差异可能与地形起伏有关,背后的变化机制需进一步研究确定。

|
图 7 N、E、U第2主成分及其空间响应 Fig. 7 The second scaled PC and its normalized spatial response for the N, E and U component |
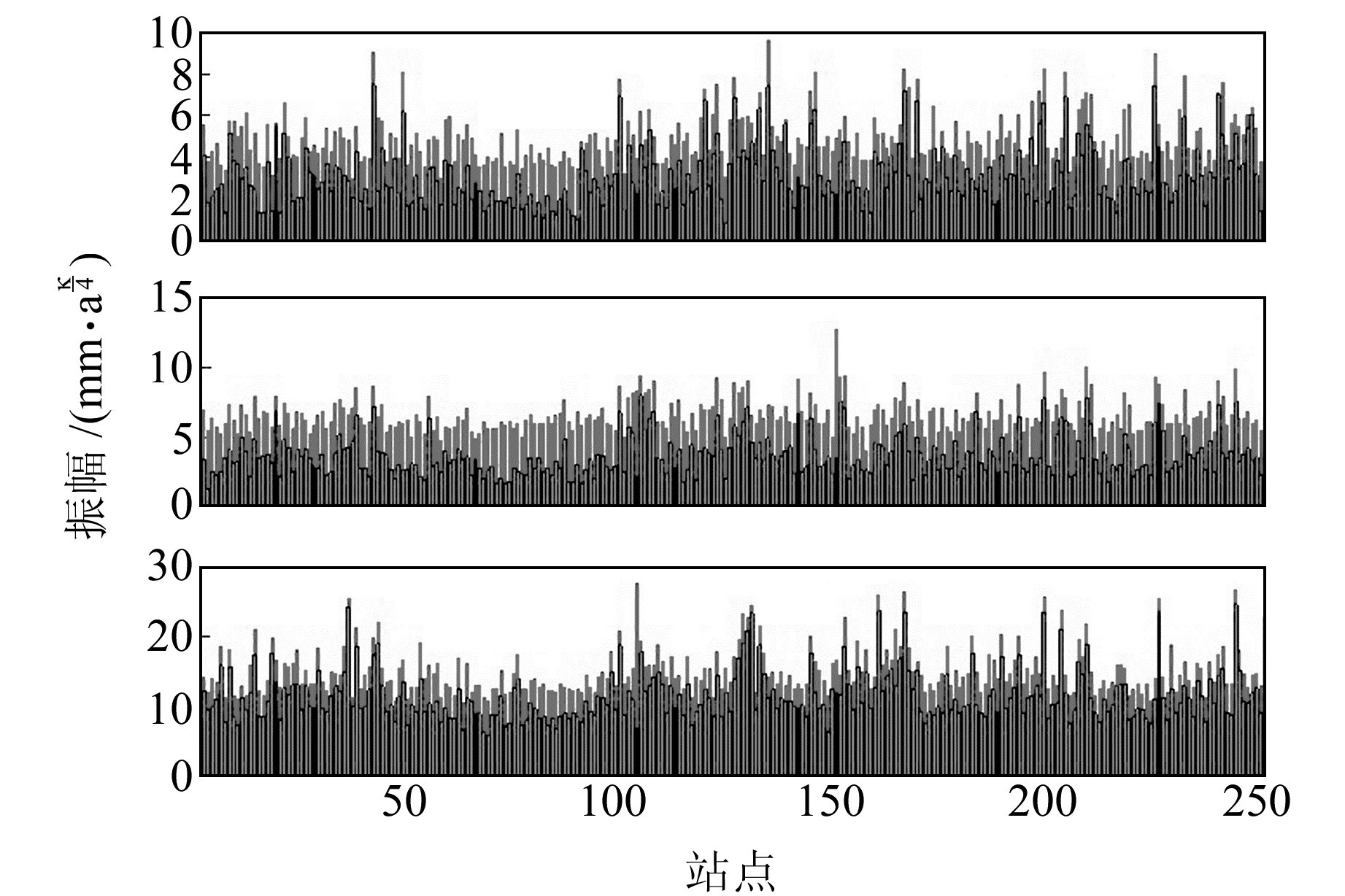
图 8给出滤波前后幂律噪声的振幅变化结果,上端表示滤波前的幂律噪声振幅,下端表示滤波后的幂律噪声振幅。可以看出,幂律噪声振幅在所有站点上均有所减小;滤波后幂律噪声的振幅在N、E、U方向分别下降约36%、43%、23%,表明滤波对噪声的抑制起到了一定作用。
|
图 8 滤波前后幂律噪声振幅 Fig. 8 The amplitude of PLN before and after filtering |
从表 1可以看出,在N、E、U方向上,滤波后RMS的平均值分别从2.7 mm、3.5 mm、8.4 mm下降到1.8 mm、2.4 mm、6.8 mm;滤波对部分站点速度估计的不确定度有一定的改善,但改善效果并不明显,这可能跟站点的时间序列长度有关,对比站点时间长度分布和速度不确定度分布可以发现这一点。说明站点的时间序列长度对于站点速度的估计有重要影响,对于站点线性项的估计需要采用更长时间跨度的数据。
4 结语本文针对台湾地区256个GPS站点2005~2011年的数据,采用PCA方法进行区域空间滤波提取CME,并采用最大似然估计方法定量估计滤波前后坐标时间序列的噪声特性。结果表明,总体上,PCA提取到的CME在台湾区域呈现出一致性的变化模式,但滤波效果在东西部存在明显差异,且水平方向的滤波效果好于垂直方向,这可能主要与站点地形变化有关。经过PCA滤波后,残差时间序列在N、E、U方向RMS平均减小33%、31%、19%;基于幂律噪声模型的振幅在所有站点均有所下降,水平方向下降最大达到36%,垂直方向下降最大达到23%。说明PCA滤波能够很好地抑制有色噪声振幅,并提高速度估计的精度和信噪比,有利于发现细微的地球物理信号。
| [1] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 005-5 017 DOI:10.1029/96JB03860
(  0) 0) |
| [2] |
Gazeaux J, Williams S D, King M A, et al. Detecting Offsets in GPS Time Series: First Results from the Detection of Offsets in GPS Experiment[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(5): 2 397-2 407 DOI:10.1002/jgrb.50152
(  0) 0) |
| [3] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California San Diego, 2002 https://www.researchgate.net/publication/234355464_Observation_of_Geodetic_and_Seismic_Deformation_with_the_Global_Positioning_System
(  0) 0) |
| [4] |
Jolliffe I T. Principle Component Analysis[M]. Berlin: Springer-Verlag, 2003
(  0) 0) |
| [5] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3): B03405
(  0) 0) |
| [6] |
Yuan L G, Ding X L, Chen W, et al. Characteristics of Daily Position Time Series from the Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5): 976-990
(  0) 0) |
| [7] |
Bos M S, Fernandes R M S, Williams S D P, et al. Fast Error Analysis of Continuous GPS Observations[J]. Journal of Geodesy, 2008, 82(3): 157-166
(  0) 0) |
| [8] |
Williams S D P. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3): B03412
(  0) 0) |
| [9] |
Hu J C, Chu H T, Hou C S, et al. The Contribution to Tectonic Subsidence by Groundwater Abstraction in the Pingtung Area, Southwestern Taiwan as Determined by GPS Measurements[J]. Quaternary International, 2006, 147(1): 62-69 DOI:10.1016/j.quaint.2005.09.007
(  0) 0) |
| [10] |
Hsu Y J, Lai Y R, You R J, et al. Detecting Rock Uplift across Southern Taiwan Mountain Belt by Integrated GPS and Leveling Data[J]. Tectonophysics, 2018, 275-284
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


