2. 上海宝冶集团有限公司,上海市庆安路77号,200941;
3. 中国测绘科学研究院,北京市莲花池西路28号,100830
多面函数法的观点是任意一个数学曲面或不规则的平滑曲面总可以用一系列简单规则的曲面进行叠加,并以任意精度逼近[1]。多面函数法用于GPS高程拟合需要解决3个关键问题[2],即核函数结点的选取、核函数阶数和平滑因子的确定,本文统称为多面函数参数的选取。目前多面函数参数的选取主要采用经验性方法,如王文利等[3]采用一般性原则选取多面函数参数对地壳垂直运动速率面进行拟合,但不能保证最终的拟合模型精度为最优,因此需要研究更具通用性的参数自适应选取方法。在核函数结点的选取方面,已有一些自适应选取算法,如蚁群算法[4]、正交化算法[5]、地形熵聚类分析法[6]等。其中,蚁群算法先寻找山谷线或山脊线附近的特征点作为结点,对于区域内地势平缓的部分则用均匀格网法补充结点;正交化算法是将多面函数系数矩阵正交化,按各点对曲面拟合贡献大小得到结点组合;地形熵聚类分析法以各点之间距离与地形熵的比值为指标选出结点。在平滑因子的确定方面,其最佳取值也有相关的分析与研究,如引入Tikhonov正则化系数代替平滑因子[7],以及利用模糊集合理论对平滑因子进行优选[8]。但这些方法通常只解决了多面函数拟合中部分参数的自适应选取,其他参数仍采用经验性方法。为此,本文在分析多面函数参数对模型拟合精度的影响特征的基础上,提出综合利用正交化算法选取核函数结点和采用二维粒子群算法确定核函数阶数与平滑因子,从而实现多面函数参数的完全自适应选取。最后,选取2个GPS高程拟合的工程实例进行计算,并与传统的多面函数方法进行比较分析,验证本文方法的正确性和有效性。
1 多面函数法的数学模型 1.1 多面函数的一般形式| $ \xi (x,y) = \sum\limits_{i = 1}^n {{c_i}} [q({x_{0i}},{y_{0i}},x,y)] $ | (1) |
式中,ci为待定系数;(x0i, y0i)为核函数结点;n为核函数结点个数;ξ(x, y)为坐标(x, y)对应的高程异常值;q(x0i, y0i, x, y)为核函数,其一般形式为:
| $ \begin{gathered} q({x_{0i}}, {y_{0i}}, x, y) = {[{(x - {x_{0i}})^2} + {(y - {y_{0i}})^2} + {\delta ^2}]^u} \hfill \\ \hfill \\ \end{gathered} $ | (2) |
式中,δ为多面函数的平滑因子,具有平滑核函数的作用;u为核函数阶数,一般取值为0.5或-0.5,即核函数为正双曲面或倒双曲面。
设共有m个已知点参与多面函数模型的拟合,则可将式(1)写成矩阵形式:
| $ {{\mathbf{\xi }}_{m}}{{_{\times }}_{\mathbf{1}}}={{\boldsymbol{Q}}_{m}}{{_{\times }^{{}}}_{n}}{{\boldsymbol{C}}_{n}}{{_{\times }}_{1}} $ | (3) |
当m≥n时,利用最小二乘原理可得待定系数:
| $ \boldsymbol{C}={{({{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{Q})}^{-1}}{{\boldsymbol{Q}}^{\text{T}}}\mathbf{\xi } $ | (4) |
求解出待定系数矩阵C后,已知一点的坐标(x, y),利用式(1)即可求得相应高程异常ξ(x, y)。
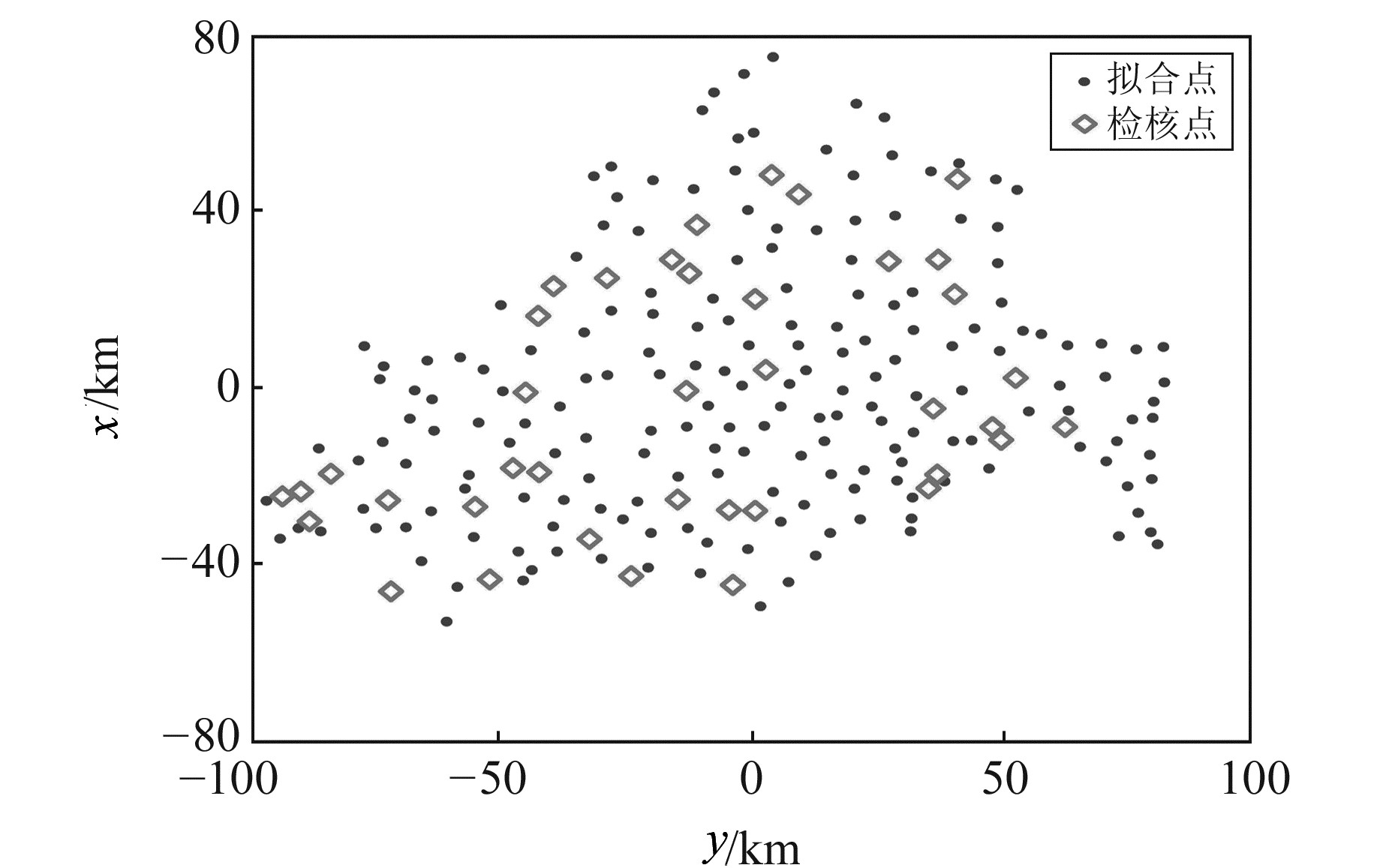
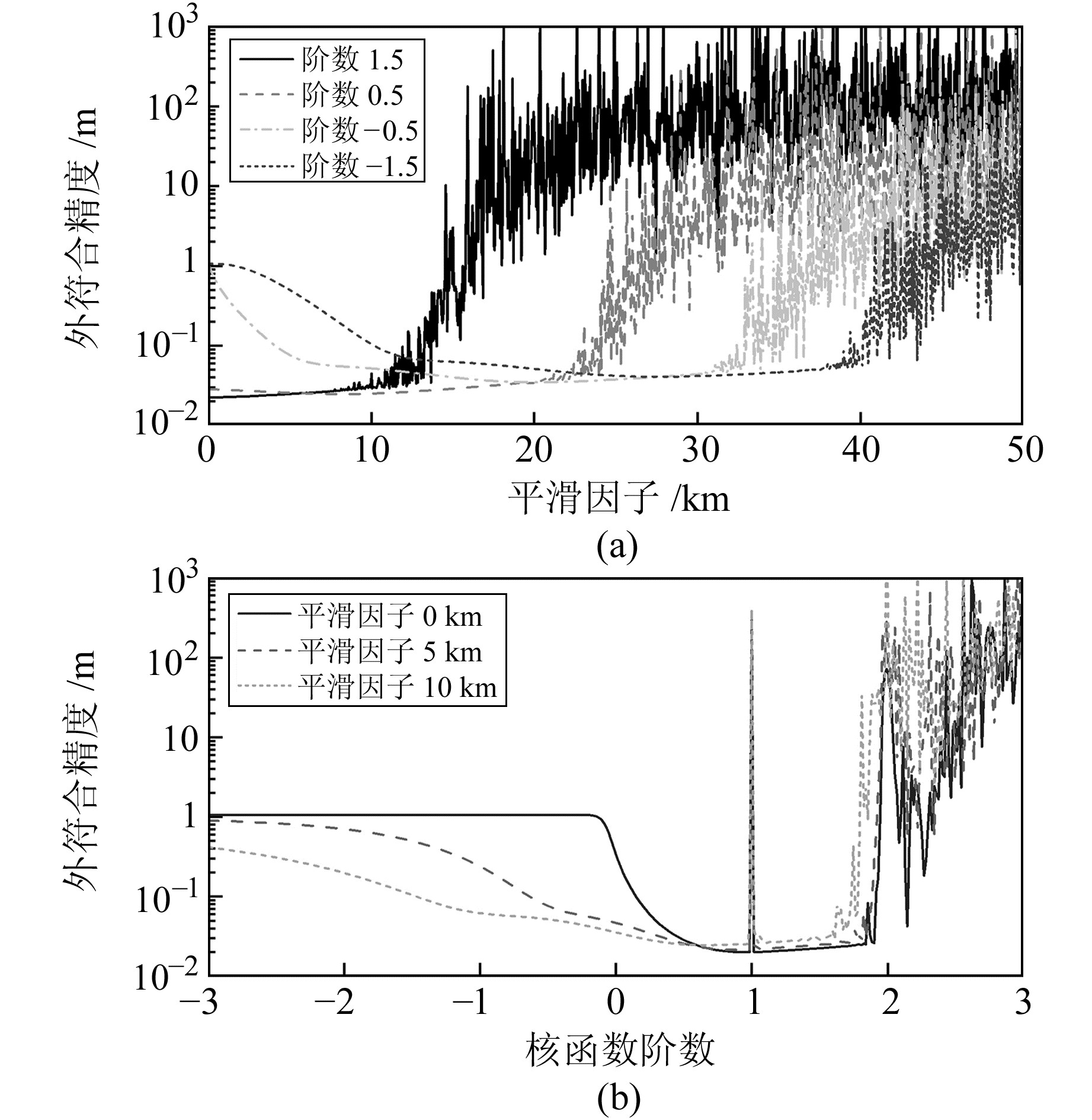
1.2 多面函数参数的影响分析多面函数参数自适应选取的目的是使多面函数拟合模型与实际似大地水准面更加匹配,从而提高拟合模型的精度与可靠性。以我国西部某地区GPS水准数据为例,采用多面函数法拟合区域似大地水准面,分析多面函数参数取值对模型拟合精度的影响。该测区共有228个分布较为均匀的GPS水准点,测区面积约为23 000 km2,最大高程异常为6.3 m,地形起伏较大,根据点位分布情况设置189个拟合点和39个检核点(下文称其为测区1,点位分布见图 1)。将多面函数参数中的核函数结点设置为全部拟合点,计算给定核函数阶数(平滑因子)下不同平滑因子(核函数阶数)对应的拟合精度,得到拟合模型的外符合精度随平滑因子和核函数阶数的变化曲线(图 2)。
|
图 1 测区1点位数据分布 Fig. 1 Distribution of GPS leveling data of test area 1 |
|
图 2 多面函数不同参数取值对应的拟合模型外符合精度 Fig. 2 External coincidence accuracy of fitting model for different multiquadric function parameters |
由图 2(a)可知,选取适当的平滑因子可以提高拟合模型的外符合精度,而过度平滑时将使核函数的空间信息影响减弱、平滑因子的影响增强,从而导致拟合模型的外符合精度随平滑因子增大而降低,且不稳定。总体上看,随着平滑因子的增大,外符合精度呈现出先逐渐提高直至最优,然后又逐渐降低的趋势。由图 2(b)可知,当平滑因子设置为0时,若阶数在负数范围内,分数形式的核函数使得Q矩阵对角线上元素为极大值,进而外符合精度几乎不受阶数变化影响;阶数为1时,核函数与距离平方项线性相关导致拟合效果变差;阶数大于2的Q矩阵病态趋势更加明显,导致阶数对外符合精度的影响更不稳定。总体上看,外符合精度最优阶数的取值范围大致在0~2之间。综合图 2(a)和2(b)可知,平滑因子和核函数阶数均存在最优取值,根据两者对外符合精度的影响规律,可以选择合适的寻优算法,以检核点为样本训练,得到两者的最优取值,从而实现多面函数参数中平滑因子和核函数阶数的自适应选取。
此外,对于核函数结点的选择,需要同时考虑结点的数量及其位置分布情况。在保证一定数量的拟合点作为多余观测数据,并使结点的分布尽可能反映高程异常的变化特征时,才能提高拟合模型的精度和可靠性。
2 多面函数参数自适应方法 2.1 核函数结点选择的正交化算法对于核函数结点选取的自适应方法,可利用正交化算法[5]分解式(3)中的列向量,依据结点对应的列向量对拟合模型的贡献大小来自适应选择结点。正交化算法自适应选取核函数结点可在模型内符合精度无太大损失的前提下,保证具有足够的多余观测值,并使得结点分布能够更好地反映高程异常的变化特征,因而使拟合模型能够更加逼近实际的似大地水准面。
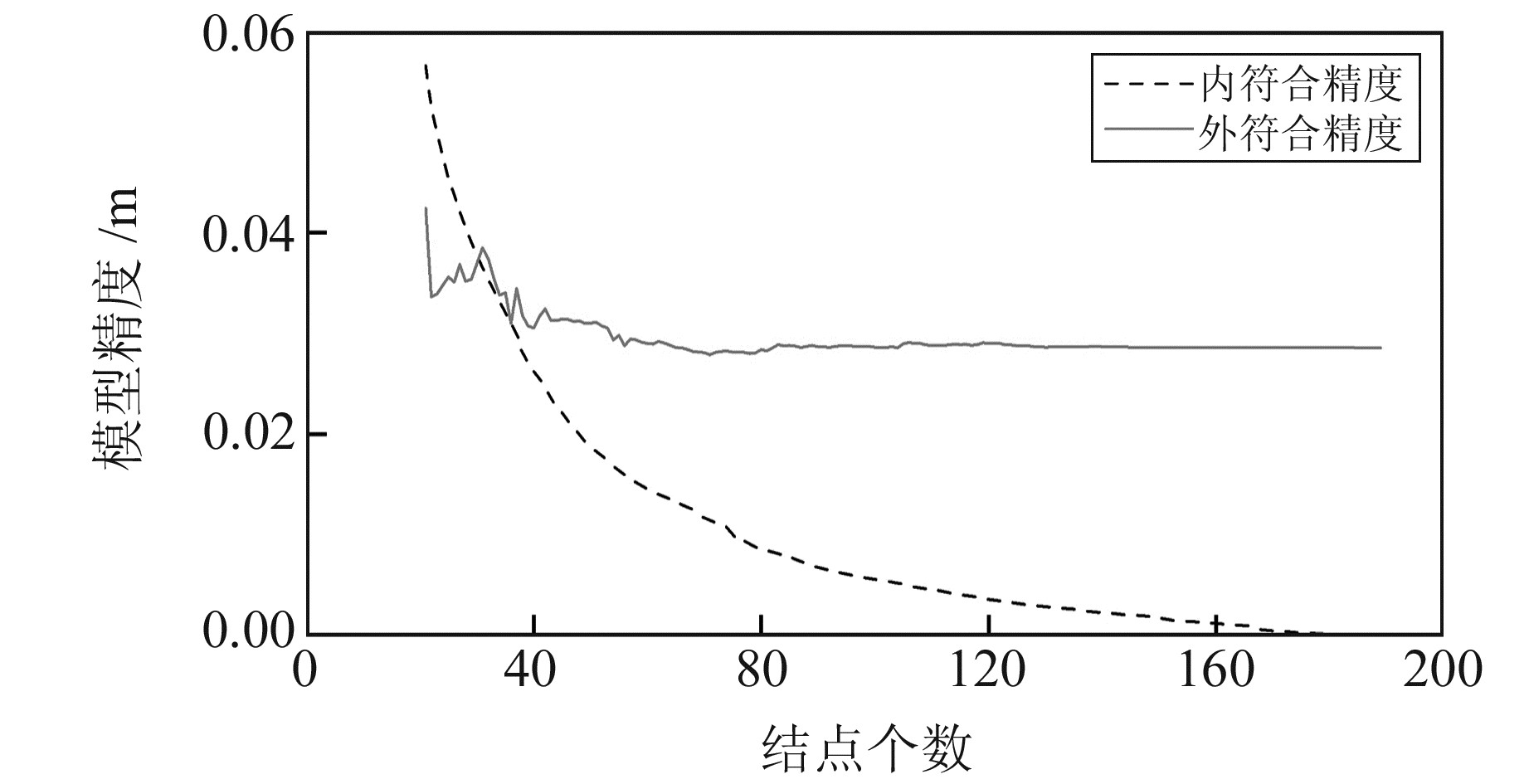
为使正交化算法自适应确定合适的核函数结点数量,以测区1数据为例,设置正交化算法选择的结点数量从20个增加至189个,设置平滑因子为0,阶数为0.5(正双曲面核函数),进行多面函数法拟合,得到不同结点数对应的拟合模型内、外符合精度变化曲线(图 3)。可以看出,拟合模型精度随结点个数的增加而逐渐提高,当结点个数为189时,其内符合精度为0;当结点个数大于80以后,外符合精度开始趋于稳定,此时再增加结点个数对外符合精度的改进已不明显。因此,正交化算法选取的结点数量可以依据外符合精度趋于稳定且有足够高的内符合精度为标准来自适应确定。
|
图 3 正交化算法选择不同结点个数对应的拟合精度 Fig. 3 Fitting accuracy for different numbers of nodes selected by orthogonalization method |
由于核函数阶数和平滑因子会对彼此的最佳取值产生影响,可以使用二维粒子群算法同时对两者进行寻优,得到在一定取值范围内都达到最佳取值的核函数阶数和平滑因子。在保证算法运行效率的基础上,为减少二维粒子群算法陷入局部最优的情况,可以采用动态改变惯性权的粒子群算法[9],以达到前期收敛速度快、后期收敛精度高的效果。本文将该算法的粒子位置设置为核函数阶数和平滑因子,速度范围根据相对应的位置范围分别设置,而粒子位置的不同将影响模型拟合的效果,因此将粒子的适应度设置为多面函数拟合得到的外符合精度:
| $ f\left( {u, \delta } \right) = {\text{ }}\hat \sigma {\text{ }} = {\text{ }}\sqrt {\frac{{\left[ {\Delta \Delta } \right]}}{{t - 1}}} {\text{ }} $ | (5) |
式中,f(u, δ)为粒子适应度;u为核函数阶数;δ为平滑因子
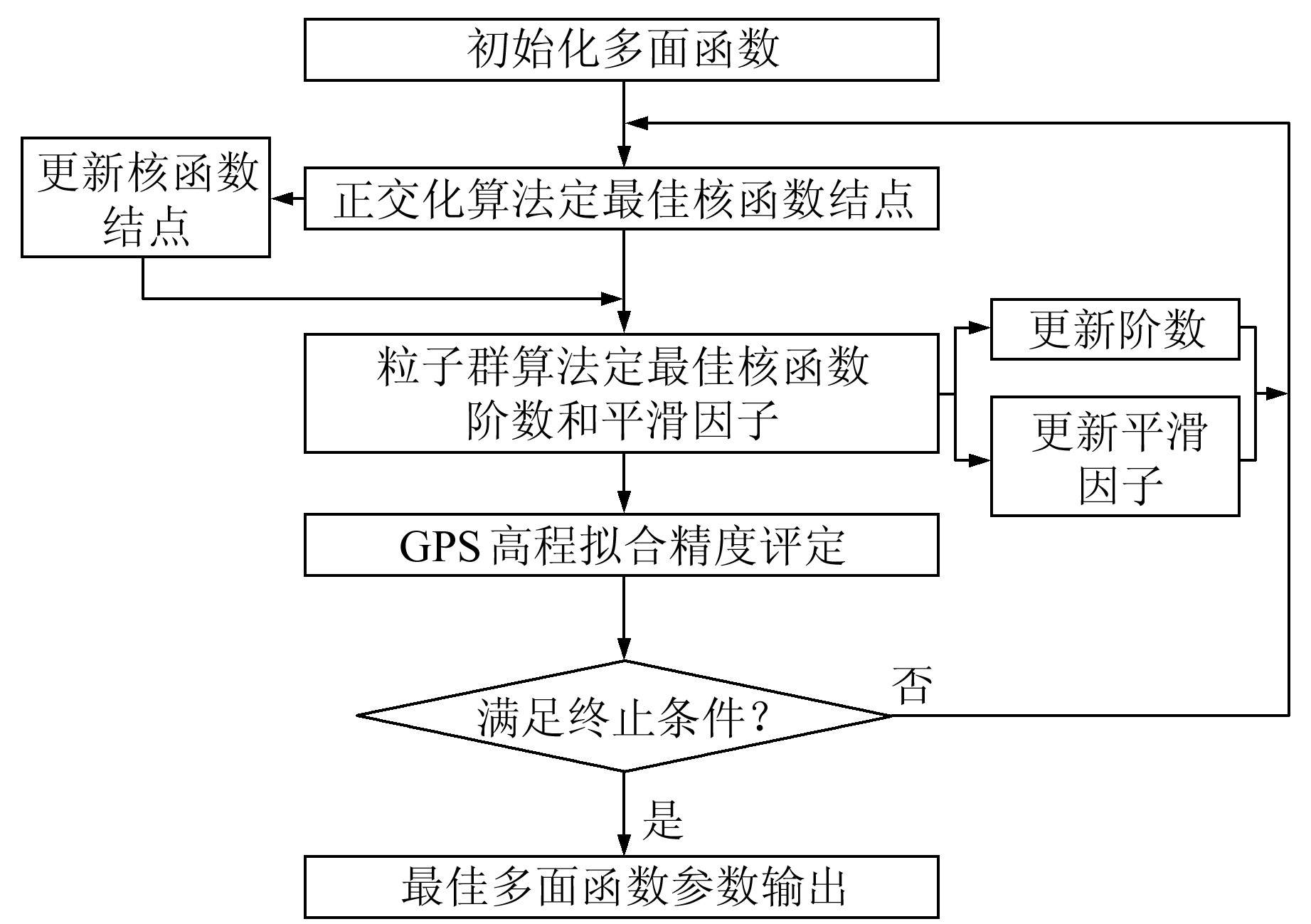
正交化算法可以自适应选择核函数结点,二维粒子群算法可以自适应确定核函数阶数和平滑因子,将两者综合就可以同时解决这3种参数的自适应选取问题。具体过程为:先初始化多面函数参数,完成核函数结点的自适应后,利用二维粒子群算法完成平滑因子和核函数阶数的自适应确定;再用更新后的多面函数参数继续参与适应性选择步骤,反复迭代,终止条件为参数的变化所引起的模型精度变化远低于模型的精度要求。具体计算流程如图 4所示。
|
图 4 综合的多面函数参数自适应选取流程 Fig. 4 Process of integrated self-adaptive parameter selection for multiquadric function |
需注意的是,将2种自适应方法综合并直接将一种自适应算法的最优结果用于另一种自适应算法时,并不能保证逐次迭代的结果会趋于稳定,还需对第2次及以后多次迭代中的正交化算法更新的核函数结点作一定的修改,以降低核函数结点变动的速度。具体的过程为:
1) 第n-1次迭代中用正交化算法得到的核函数结点按提取的先后顺序存储在结点组中,假定为Gn-1,用Gn-1参与二维粒子群算法得到当前最佳核函数阶数un-1和最佳平滑因子δn-1。
2) 在第n次迭代中,将un-1和δn-1用于正交法选择结点时,同样按结点提取的先后顺序存储在结点组中,假定为Gn0。
3) 比较Gn-1和Gn0中结点的排列顺序情况,在Gn0中依先后顺序找到最先提取出来的且不在Gn-1中的结点,假定为a。用un-1、δn-1、Gn-1以及拟合点生成多面函数系数矩阵Q和高程异常矩阵ξ,找到Q中与ξ向量方向最接近正交角度的列向量,假定对应的结点为b。
4) 用a替换Gn-1中的b,此时得到第n次迭代中正交化算法最终得到的核函数结点组合Gn。再以该结点组合进入下一次迭代过程,重复步骤1)~4),直至结点组合Gn-1和Gn0相同。
以上修改的意义为,每次迭代仅更新核函数结点中影响最大的一个结点,从而保证在循环中多面函数参数的变化是趋于稳定的。
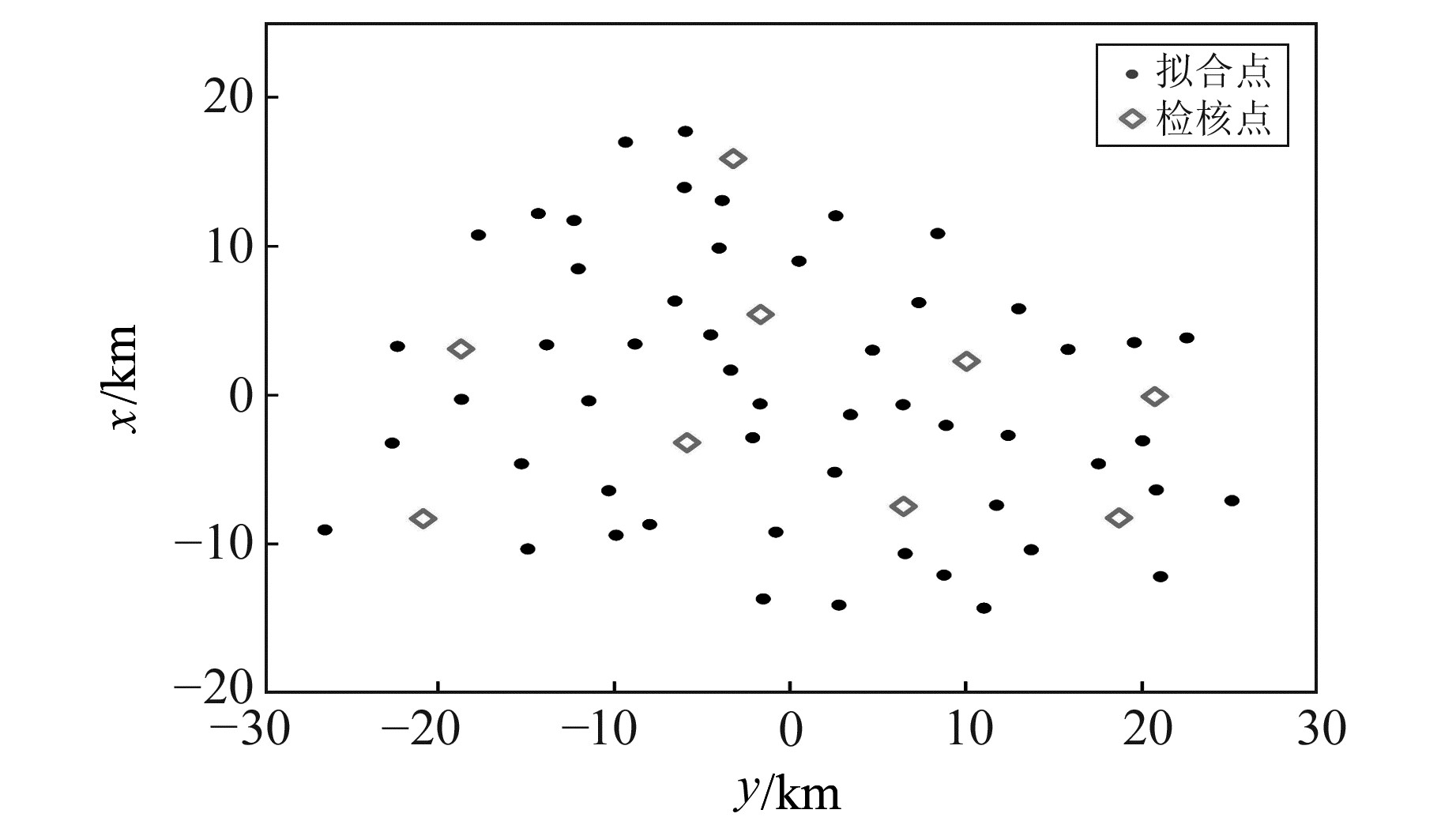
3 算例与分析使用2组不同地区的GPS水准数据对参数自适应选取方法进行验证,其中测区1与§1.2参数影响分析中的测区数据一致;测区2为我国中部某地区,该测区共有62个分布较为均匀的GPS水准点,测区面积约为1 200 km2,最大高程异常为1.4 m,地形起伏较小,根据点位分布情况设置53个拟合点和9个检核点(图 5)。
|
图 5 测区2点位数据分布 Fig. 5 Distribution of GPS leveling data of test area 2 |
分别采用4种不同的方案确定以上2个测区的多面函数参数,比较多面函数参数自适应选取方法与常规参数选择方法的拟合效果。制定的4种参数选取方案分别为:1)常规多面函数参数选择方法,记为MQ_N,将所有拟合点作为核函数结点,设置平滑因子为0,核函数阶数为0.5;2)基于正交化算法的多面函数参数选择方法,记为MQ_O,利用正交化方法选取核函数的结点,设置平滑因子为0,核函数阶数为0.5;3)基于二维粒子群算法的多面函数参数选择方法,记为MQ_P,将所有拟合点作为核函数结点,寻找平滑因子和核函数阶数的最佳取值,其中平滑因子的查找范围为0 km至测区拟合点间最远距离,阶数的查找范围为-3~3;4)基于正交化算法和二维粒子群算法的多面函数参数选择方法,记为MQ_OP,综合正交化算法和二维粒子群算法的参数自适应选取方法,初始的多面函数参数采用MQ_N方案的设置,二维粒子群算法的设置与MQ_P方案相同。
利用4种不同的选取方案确定多面函数参数,并拟合区域似大地水准面,得到的模型拟合精度统计如表 1所示。比较MQ_N和MQ_O方案,在测区1中,正交化算法自适应选取核函数结点得到的外符合精度略低于拟合点全选为结点的方法;而在测区2中,正交化算法得到的拟合模型的外符合精度略高。分析其原因,对于地形起伏较大的测区1,需要更多的特征点来描述高程异常的变化特征,当正交化算法选择的结点不足时,拟合模型与实际似大地水准面的匹配程度反而会降低;对于地形起伏较小的测区2,正交化算法选择的结点可以足够反映高程异常的变化特征,而常规方法选择全部拟合点为结点,反而会由于非特征点本身的误差导致拟合模型出现偏差。
|
|
表 1 4种参数选取方案的拟合精度比较 Tab. 1 Comparison of fitting accuracies for the four parameter selection schemes |
比较MQ_N和MQ_P方案看出,利用二维粒子群算法得到的最优平滑因子和核函数阶数,相比于常规方法,在地形起伏较大的测区1中,其外符合精度提高近30%,而对于地形起伏小的测区2,外符合精度也提高近5%,说明该自适应参数选取方法具有很好的效果。
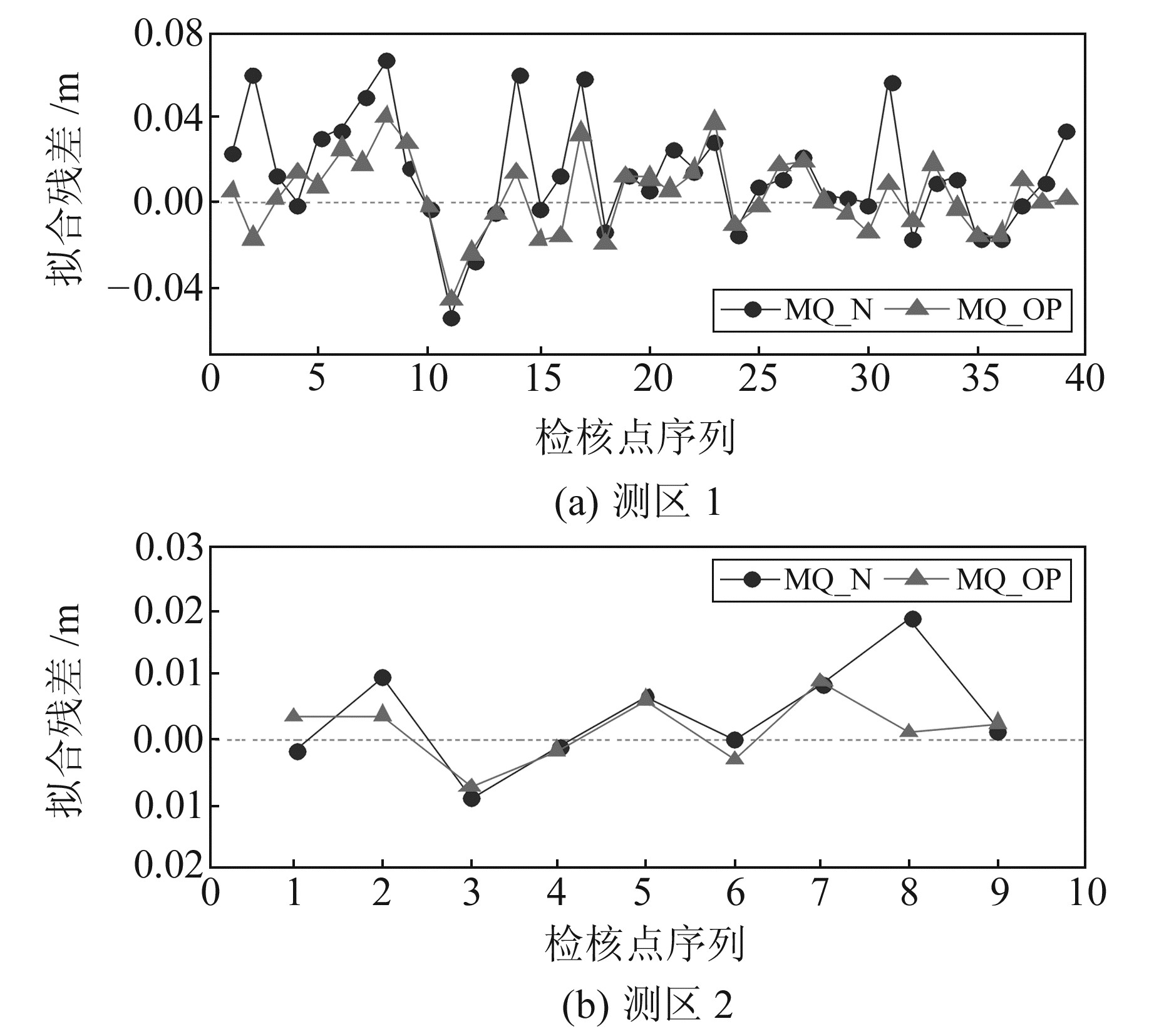
比较MQ_N和MQ_OP方案,两者检核点的拟合残差如图 6所示。对于综合的多面函数参数自适应选取方法,其得到的检核点拟合残差明显小于常规方法,特别是在常规方法得到的拟合残差较大的检核点,如测区1的2、8、14、17、31、39号点和测区2的2、8号点,其改进效果更为明显。另外,从表 1中MQ_OP方案和MQ_N方案拟合的外符合精度来看,在测区1中, MQ_OP方案得到的95个结点、平滑因子0.29 km和阶数0.91用于多面函数拟合,其外符合精度提高约30%;在测区2中,MQ_OP方案得到的30个结点、平滑因子0.40 km和阶数1.62用于多面函数拟合,其外符合精度提高约38%,并且与MQ_O和MQ_P等部分参数的自适应选择方法相比,其精度也有明显的提高。
|
图 6 MQ_N方案和MQ_OP方案的检核点拟合残差 Fig. 6 Fitting residuals of check points for MQ_N and MQ_OP |
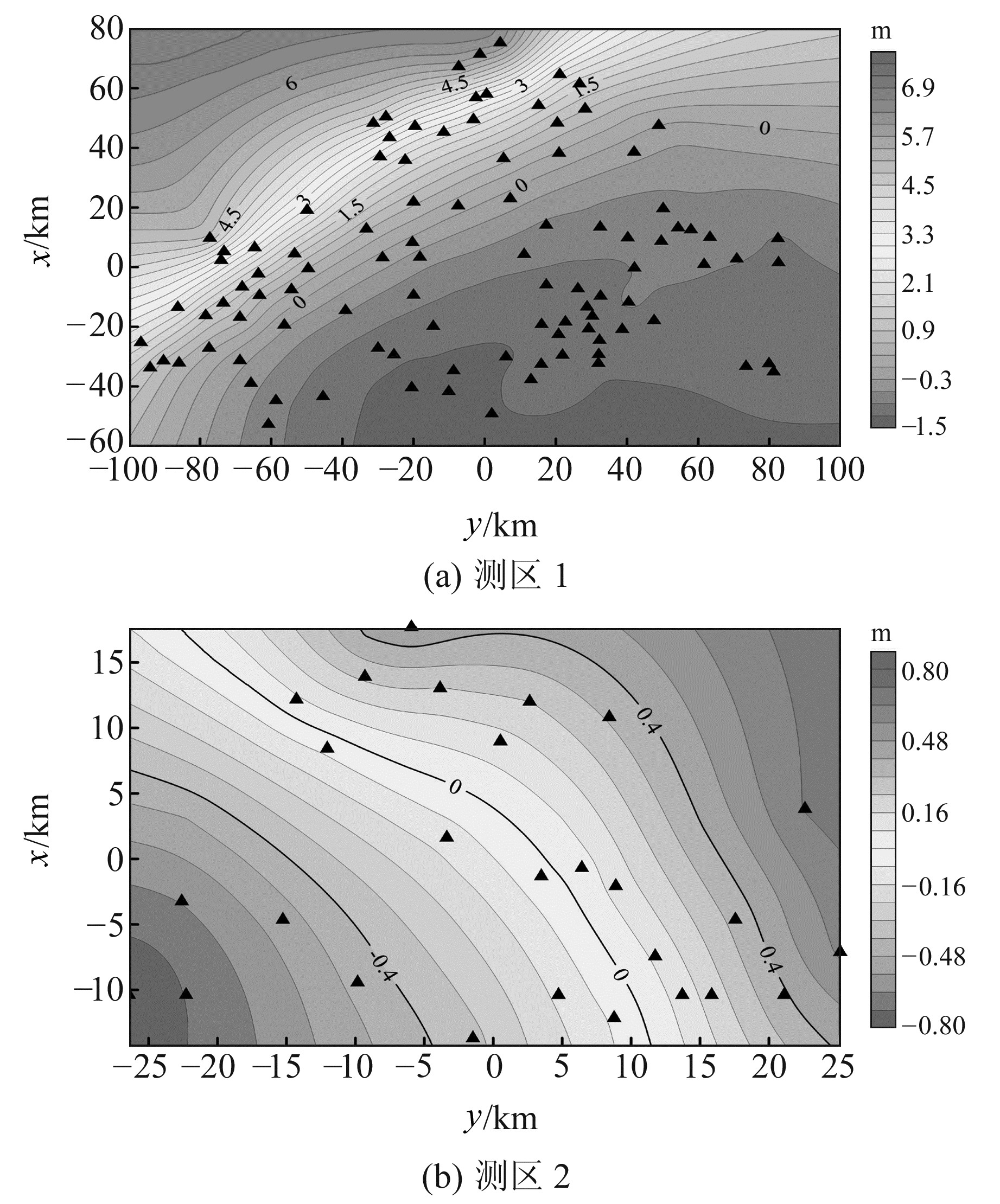
图 7为MQ_OP方案在2个测区选取得到的核函数结点分布情况。可以看出,通过正交化算法选取的结点主要分布在高程异常起伏较大或者局部变化不均匀的地方,说明该方法在地形起伏大或者地形平滑的地区均可以很好地选取高程异常分布的特征点,从而使拟合模型能够更好地反映实际似大地水准面的起伏。
|
图 7 MQ_OP方案中确定的核函数结点分布 Fig. 7 Distribution of kernel nodes for MQ_OP |
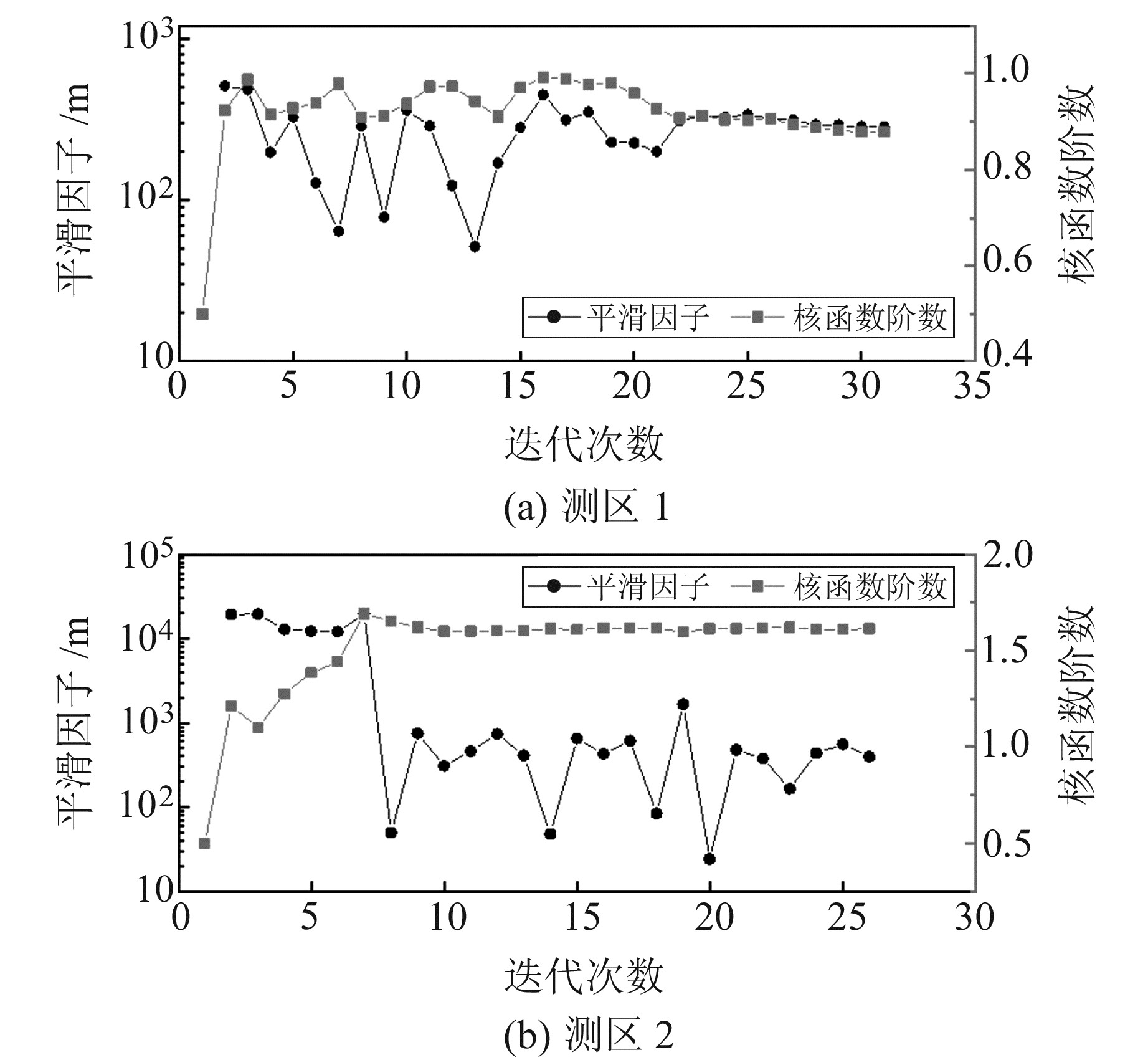
对于MQ_OP方案的迭代过程,核函数阶数和平滑因子的变化情况如图 8所示。可以看出,测区2采用综合的自适应参数选取方法经过约10次迭代后,核函数阶数和平滑因子基本趋于稳定,而测区1由于其面积更大、拟合点更多的原因,经过约27次迭代后,其参数变化幅度明显减小并逐渐趋于稳定。当二维粒子群算法得到的平滑因子和核函数阶数稳定后,正交化算法选取的核函数结点也趋于稳定(图 7为趋于稳定后的核函数结点),说明该综合的参数自适应选取方法可以保证参数选取的稳定性。
|
图 8 核函数阶数和平滑因子随迭代次数的变化 Fig. 8 Changes of order and smoothing factor with the number of iterations |
为了进一步分析多面函数参数自适应选取方法对GPS高程拟合综合模型[10]的优化效果,采用基于二次曲面的多面函数方法对以上2个测区进行拟合计算。同样选取前文的4种参数选择方法进行计算,其精度统计如表 2所示。从表 2可以看出,多面函数参数的自适应选取方法对于该综合模型方法依然有效,各种模型的拟合精度情况与表 1类似,并且比较MQ_N方案和MQ_OP方案可以看出,综合的自适应参数选取方法在测区1得到的93个结点、平滑因子0.23 km和阶数1.23用于多面函数拟合,其外符合精度比常规方法提高约20%,而在测区2则提高约32%。以上分析说明,综合的多面函数参数自适应选取方法比常规方法及部分参数自适应选取方法拟合得到的似大地水准面模型精度及可靠性更优。
|
|
表 2 基于二次曲面的多面函数不同参数选取方案的拟合精度比较 Tab. 2 Comparison of fitting accuracies for different schemes of quadratic-multifaceted function |
本文综合正交化算法和二维粒子群算法,实现了多面函数参数(核函数结点、核函数阶数和平滑因子)的完全自适应选取。该方法相比传统的经验性参数选择方法更具有理论支撑,可以有效地使参数趋于稳定并达到最优。将综合的参数自适应选取方法应用于2个地形起伏不同的测区,分别采用多面函数法和基于二次曲面的多面函数法进行GPS高程拟合,结果表明,本文提出的多面函数参数完全自适应选取方法比经验性参数选择方法或部分参数自适应选取方法的拟合精度更优,验证了其正确性与有效性。
| [1] |
Hardy R L. Multiquadric Equations of Topography and Other Irregular Surfaces[J]. Journal of Geophysical Research, 1971, 76(8): 1 905-1 915 DOI:10.1029/JB076i008p01905
(  0) 0) |
| [2] |
陶本藻. GPS水准似大地水准面拟合和正常高计算[J]. 测绘通报, 1992(4): 14-18 (Tao Benzao. Quasigeoid Fitting by Using GPS Leveling and Normal Height Calculation[J]. Bulletin of Surveying and Mapping, 1992(4): 14-18)
(  0) 0) |
| [3] |
王文利, 陈士银, 董鸿闻, 等. 利用多面函数拟合中国陆地垂直运动速率图[J]. 测绘通报, 2002(8): 6-8 (Wang Wenli, Chen Shiyin, Dong Hongwen, et al. China Vertical Crustal Movement Rate Chart Made by Multiple-Surface Function Fitting[J]. Bulletin of Surveying and Mapping, 2002(8): 6-8 DOI:10.3969/j.issn.0494-0911.2002.08.002)
(  0) 0) |
| [4] |
蒲伦, 唐诗华, 张紫萍, 等. 一种基于蚁群算法的山区GPS高程异常拟合方法[J]. 测绘通报, 2018(8): 26-31 (Pu Lun, Tang Shihua, Zhang Ziping, et al. A GPS Height Anomaly Fitting Method in Mountainous Area Based on Ant Colony Algorithm[J]. Bulletin of Surveying and Mapping, 2018(8): 26-31)
(  0) 0) |
| [5] |
张菊清, 刘平芝. 抗差趋势面与正交多面函数结合拟合DEM数据[J]. 测绘学报, 2008, 37(4): 526-530 (Zhang Juqing, Liu Pingzhi. Combining Fitting Based on Robust Trend Surface and Orthogonal Multiquadrics with Application in DEM Fitting[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 526-530 DOI:10.3321/j.issn:1001-1595.2008.04.021)
(  0) 0) |
| [6] |
孙佳龙, 郭淑艳, 龙冰心, 等. 地形熵聚类下利用多面函数拟合高程异常[J]. 测绘通报, 2018(11): 86-89 (Sun Jialong, Guo Shuyan, Long Bingxin, et al. A Polyhedral Function Fitting Method of Elevation Anomaly with Terrain Entropy and Clustering[J]. Bulletin of Surveying and Mapping, 2018(11): 86-89)
(  0) 0) |
| [7] |
彭钊, 陈志遥, 李赫. 一种基于Tikhonov正则化的改进多面函数拟合法[J]. 大地测量与地球动力学, 2019, 39(3): 285-289 (Peng Zhao, Chen Zhiyao, Li He. A Refined Multiquadric Function Fitting Method Based on Tikhonov Regularization[J]. Journal of Geodesy and Geodynamics, 2019, 39(3): 285-289)
(  0) 0) |
| [8] |
邱斌, 朱建军. 基于模糊集合理论的GPS高程多面函数拟合模型平滑因子优选[J]. 测绘工程, 2004, 13(3): 35-38 (Qiu Bin, Zhu Jianjun. Choiceness of Smooth Factor of GPS Elevation Multiquadric Function Fit Model Based on Fuzzy Set Theory[J]. Engineering of Surveying and Mapping, 2004, 13(3): 35-38 DOI:10.3969/j.issn.1006-7949.2004.03.011)
(  0) 0) |
| [9] |
张选平, 杜玉平, 秦国强, 等. 一种动态改变惯性权的自适应粒子群算法[J]. 西安交通大学学报, 2005, 39(10): 1 039-1 042 (Zhang Xuanping, Du Yuping, Qin Guoqiang, et al. Adaptive Particle Swarm Algorithm with Dynamically Changing Inertia Weight[J]. Journal of Xi'an Jiaotong University, 2005, 39(10): 1 039-1 042)
(  0) 0) |
| [10] |
钟波, 罗志才. GPS水准综合模型的应用研究[J]. 测绘通报, 2007(6): 5-7 (Zhong Bo, Luo Zhicai. Research on Application of Combined Model for GPS Leveling[J]. Bulletin of Surveying and Mapping, 2007(6): 5-7 DOI:10.3969/j.issn.0494-0911.2007.06.002)
(  0) 0) |
2. Shanghai Baoye Group Co Ltd, 77 Qing'an Road, Shanghai 200941, China;
3. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China
 2020, Vol. 40
2020, Vol. 40

