2. 矿山采动灾害空天地协同监测与预警安徽省高校重点实验室,安徽省淮南市泰丰大街168号,232001;
3. 矿区环境与灾害协同监测煤炭行业工程研究中心,安徽省淮南市泰丰大街168号,232001;
4. 北京航天宏图信息技术股份有限公司,北京市杏石口路65号,100195
在使用Kalman滤波进行PPP参数估计时,参数估计的质量往往取决于Kalman滤波对于状态异常以及观测异常扰动的认知和控制[1-2]。在PPP数据预处理时对粗差、周跳等进行探测和处理、精化误差模型,可以较好地控制观测异常扰动。而动力学模型异常是由于难以追踪载体运动,导致模型无法描述实际物理情况[3-4],主要表现在模型噪声方差矩阵和量测噪声方差矩阵理解不够准确,增益矩阵不足以修正滤波器导致滤波发散,影响参数估计质量,在PPP解算中体现为定位精度下降、收敛时间延长[5]。
自适应Kalman滤波通过构造观测等价权和反映真实动力学模型误差的统计量来获取更加可靠的自适应因子,进而控制动力学模型异常对Kalman滤波解的影响。反映真实动力学模型误差的统计量有多种,如状态不符值统计量、方差分量比统计量和预测残差统计量,这些统计量都能可靠地判别动力学模型预测信息与载体实际物理情况的差异,为更准确地构造自适应因子提供基础[6]。基于以上动力学模型异常的统计量构造的自适应因子函数包括三段函数[7]、两段函数[8]和指数函数[9]。
以上讨论均基于单因子的自适应Kalman滤波,当状态参数向量中参数类型不同,且各类参数的动力学模型可靠性不同时,若仍采用单一的自适应因子调节,那么对于可靠的预测状态参数会损失效率,对于误差较大的预测参数又因为其他可靠参数的平衡使其权重得不到有效降低,对相应参数的不利影响得不到应有的控制[10]。
鉴于此,有关多因子自适应滤波的研究受到学者关注。欧吉坤等[10]考虑到不破坏载波相位模糊度参数的整数特性,即模糊度参数的自适应因子应为1,提出参数选权自适应因子函数。郝明等[11]对自适应选权拟合法进行研究并应用到精密单点定位中,提高PPP收敛速度。郭斐[12]将改进的抗差自适应Kalman滤波应用到PPP参数估计中,实验表明,该方法对状态异常扰动具有较强的控制能力,特别适用于高动态、机动性较复杂的载体的动态精密单点定位。
本文在标准Kalman滤波研究的基础上,将新息向量作为模型异常统计量,以位置相关为条件对PPP待估计参数进行分类,针对不同类别的参数,选取两段函数构造分类因子自适应Kalman滤波,以更好地适用于精密单点定位参数估计。
1 PPP的自适应Kalman滤波模型 1.1 异常判别统计量构造新息向量Vk, k-1是状态预测信息Xk, k-1与当前历元观测信息Lk的函数,即
| $ {\mathit{\boldsymbol{V}}_{k,k - 1}} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_{k,k - 1}} - {\mathit{\boldsymbol{L}}_k} $ | (1) |
当Lk可靠时,Vk, k-1的大小主要反映Xk, k-1的可靠性,而Xk, k-1是通过动力学模型预测的状态信息,因此Vk, k-1能够反映动力学模型的误差。故以预测残差Vk, k-1为变量构造状态模型误差的判别统计量Δ Vk, k-1,表达式为:
| $ \Delta {\mathit{\boldsymbol{V}}_{k,k - 1}} = \sqrt {\frac{{\mathit{\boldsymbol{V}}_{k,k - 1}^{\rm{T}}{\mathit{\boldsymbol{V}}_{k,k - 1}}}}{{tr({\mathit{\boldsymbol{Q}}_{{V_{k,k - 1}}}})}}} $ | (2) |
其中,
| $ {\mathit{\boldsymbol{Q}}_{{V_{k,k - 1}}}} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k,k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k} $ | (3) |
式中,QVk, k-1为新息残差的协方差矩阵,tr(QVk, k-1)为新息向量协方差矩阵的迹,Rk为观测噪声协方差矩阵。
1.2 分类自适应因子确定在PPP参数估计中,状态参数向量Xk包含位置参数(X、Y、Z)、对流层延迟误差T、接收机钟差δt和模糊度参数NiLi:
| $ {\mathit{\boldsymbol{X}}_k} = {\left[ {X,Y,Z,T,{\rm{ }}\delta {\rm{ }}{t_r},N_{{L_1}}^1, \cdots ,N_{{L_1}}^n,N_{{L_2}}^1, \cdots ,N_{{L_2}}^n} \right]^{\rm{T}}} $ | (4) |
由于Xk包含的参数类型不同,各类参数不符值对动力学模型异常的描述特性也不相同,即动力学模型异常对于预测状态向量中各参数的误差影响量级不同,接收机位置及位置相关参数不符值对于动力学模型异常较敏感,动力学模型异常对于预测状态向量中位置相关参数的影响量级明显。若仍采用单一的自适应因子进行调节,对于误差较大的预测参数,因为其他可靠参数的平衡作用,使得相应参数的不利影响得不到应有的控制。因此,采用分类因子自适应滤波,对模型预测状态向量各分量根据各自的误差影响量级分组确定自适应因子。
精密单点定位中,动力学模型异常主要体现在Xk中与位置相关的参数。因此,将Xk的参数以位置相关为条件分类,由于对流层延迟误差与位置具有相关性,所以可以分为两类[13],一类为位置参数(X、Y、Z)和T,另一类为δt和NiLi。此时,自适应因子可表示为:
| $ {\mathit{\boldsymbol{\alpha }}_k} = \left[ {\begin{array}{*{20}{c}} {{\alpha _{{X_k}}}}&0&0\\ 0&{{\alpha _{{d_t}}}}&0\\ 0&0&{{\alpha _N}} \end{array}} \right] $ | (5) |
式中,αXk为位置相关参数根据新息向量构造异常判别统计量确定的自适应因子,表达式如式(6),αdt、αN为与位置不相关参数的自适应因子,分别为接收机钟差、模糊度参数确定的自适应因子,因为与位置不相关且不体现动力学模型异常信息,所以此类自适应因子设置为固定值1,不对此类参数进行修正调节,即式(7):
| $ {\alpha _{{X_{\rm{k}}}}} = \left\{ \begin{array}{l} 1,\left| {\Delta {\mathit{\boldsymbol{V}}_{k,k - 1}}} \right| \le c\\ \frac{c}{{\left| {\Delta {\mathit{\boldsymbol{V}}_{k,k - 1}}} \right|}},\left| {\Delta {\mathit{\boldsymbol{V}}_{k,k - 1}}} \right| \ge c \end{array} \right. $ | (6) |
式中,c为常数,选取经验值1[14]。
| $ {{\alpha }_{{{d}_{t}}}}\text{ = 1}, {{\alpha }_{N}}\text{ = 1} $ | (7) |
在进行参数分类后,分类因子的自适应Kalman滤波递推公式为:
| $ \begin{array}{l} \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat X}}}_{k.k - 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}{{\mathit{\boldsymbol{\hat X}}}_{k - 1,k - 1}}\\ {\mathit{\boldsymbol{P}}_{k,k - 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}{\mathit{\boldsymbol{P}}_{k - 1,k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_{k - 1}}\\ {{\mathit{\boldsymbol{P'}}}_{k,k - 1}} = \mathit{\boldsymbol{\alpha }}_k^{1/2}{\mathit{\boldsymbol{P}}_{k,k - 1}}\mathit{\boldsymbol{\alpha }}_k^{1/2}\\ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{k,k - 1}}\mathit{\boldsymbol{H}}_K^{\rm{T}}{\left( {_K^\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{P}}_{k.k - 1}} + {\mathit{\boldsymbol{R}}_k}} \right)^{ - 1}}\\ {{\mathit{\boldsymbol{\hat X}}}_{k,k}} = {{\mathit{\boldsymbol{\hat X}}}_{k,k - 1}} + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{L}}_k} - {\mathit{\boldsymbol{H}}_k}{{\mathit{\boldsymbol{\hat X}}}_{k,k - 1}}} \right)\\ {\mathit{\boldsymbol{P}}_{k,k}} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_k}} \right){\mathit{\boldsymbol{P}}_{k,k - 1}} \end{array} \right.\\ \end{array} $ | (8) |
式中,αk为确定的分类自适应因子,Rk为符合高斯分布的观测噪声,Hk为观测方程系数矩阵,Φk, k-1为状态转移矩阵,
分别使用标准Kalman滤波和构建自适应Kalman滤波进行静态PPP解算分析。选取6个IGS站(REDU、WARK、JFNG、NNOR、REUN、KIRU)2018年年积日356~358的数据,采样率为30 s。数据处理时,以2 h的观测数据为1个弧段,对每个弧段分别采用2种方式进行静态PPP解算,最后对N、E、U方向偏差及收敛时间进行统计分析。同时,选取PALM站24 h弧段数据进行仿动态解算,验证算法的有效性。
2.2 实验结果分析为直观地表现构建的自适应Kalman滤波对PPP动力学模型异常的修正作用,选取GMSD站12 h弧段数据进行PPP解算,分别从N、E、U方向偏差序列及滤波过程中的状态预测协方差观察自适应Kalman滤波相对于标准Kalman滤波的修正过程。
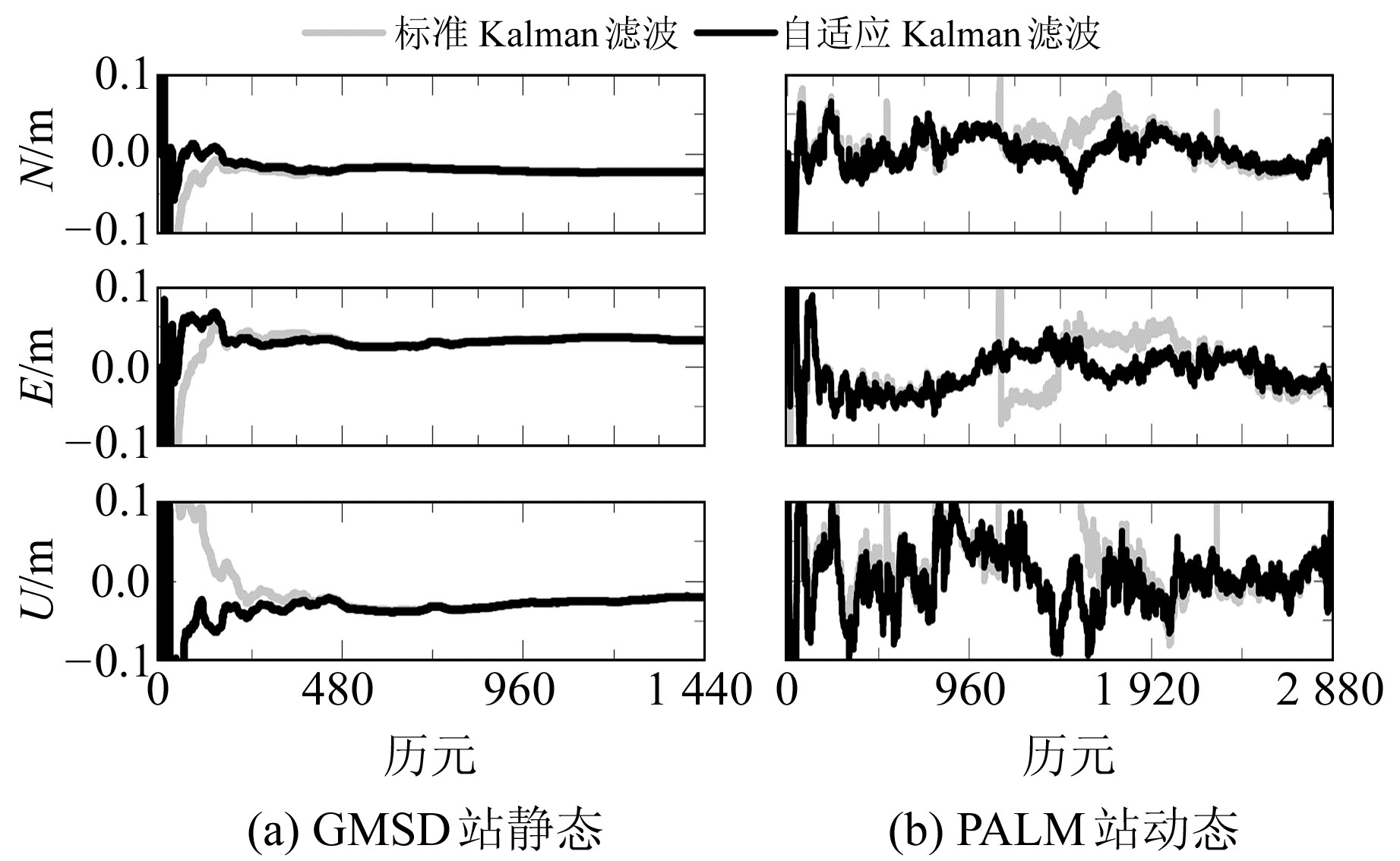
图 1(a)为2种滤波方法下静态PPP解算N、E、U方向偏差序列。可以看出,相较于标准Kalman滤波,构建的自适应Kalman滤波在滤波初期能够不断修正方向偏差,使序列更快地趋于平稳。图 1(b)为仿动态实验。可以看出,相较于标准Kalman滤波,构建的自适应Kalman滤波能够很好地修正滤波过程中的发散和异动。
|
图 1 2种滤波情况下N、E、U方向偏差序列 Fig. 1 The deviation sequence of N, E and Udirection of two filtering cases |
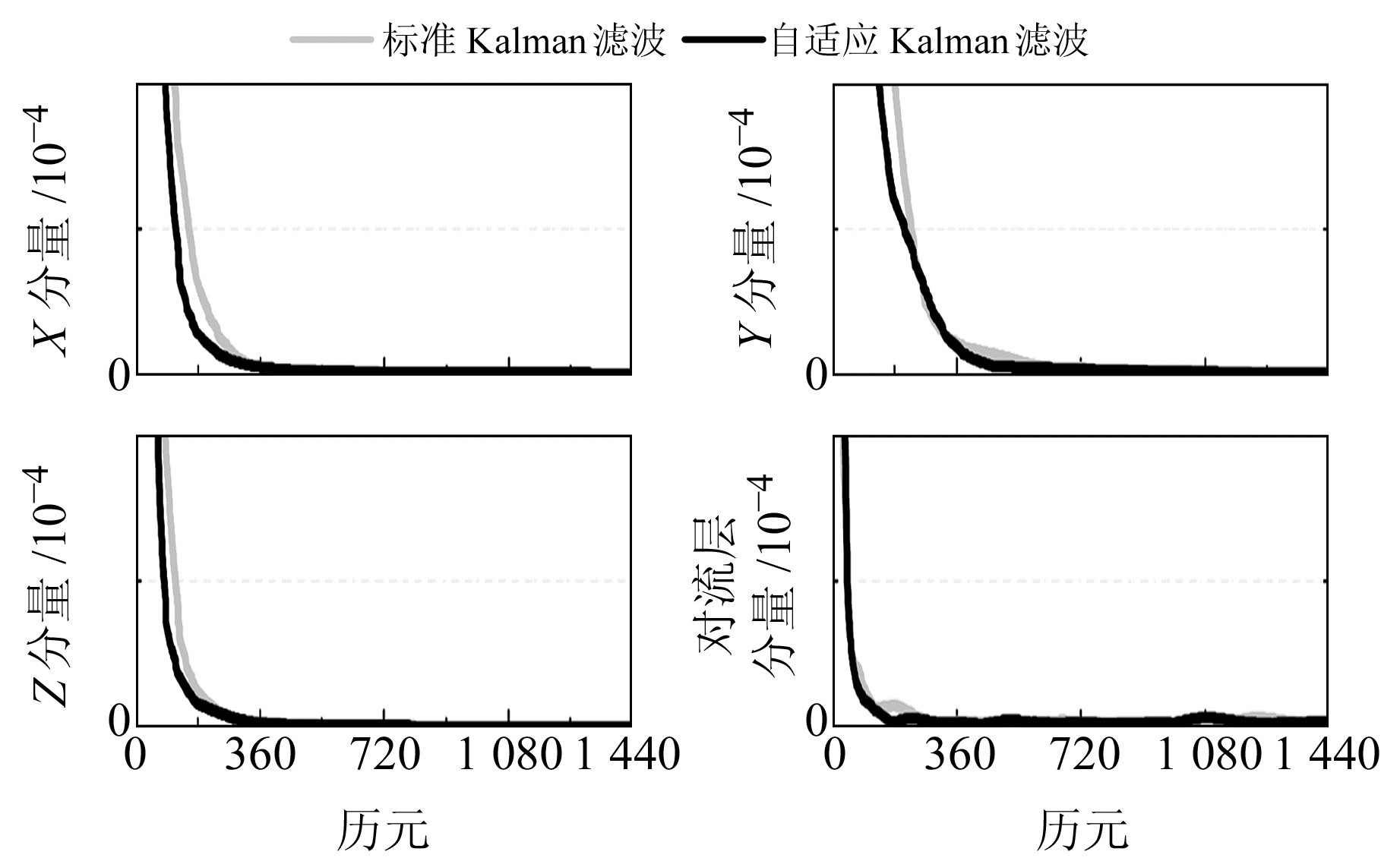
图 2为静态模式下2种滤波情况时各分量的状态预测协方差。由于自适应因子通过修正状态预测协方差获取更优的增益矩阵,达到对异常的控制效果,因此,随着滤波的不断推进,增益矩阵会趋于稳定,当状态预测协方差过大或过小时,会增加增益矩阵趋于稳定的时间,增加状态参数的收敛时间。由图 2可看出,相较于标准Kalman滤波,构建的自适应Kalman滤波在自适应因子调节下,状态预测协方差能够较快地收敛;从对流层分量的状态预测协方差可以看出,在标准Kalman滤波中对流层分量状态预测协方差出现异常波动时,自适应Kalman滤波能够很好地修正波动,使趋势表现更加平稳。
|
图 2 静态模式下2种滤波情况时各分量状态预测协方差 |
为了进一步验证构建的自适应Kalman滤波的性能,采用2种滤波方法对6个IGS站(REDU、WARK、JFNG、NNOR、REUN、KIRU) 2018年年积日356~358的数据以2 h为一个弧段进行PPP解算。分别从N、E、U方向偏差、收敛时间方面对实验数据进行统计分析,结果见图 3、4。
|
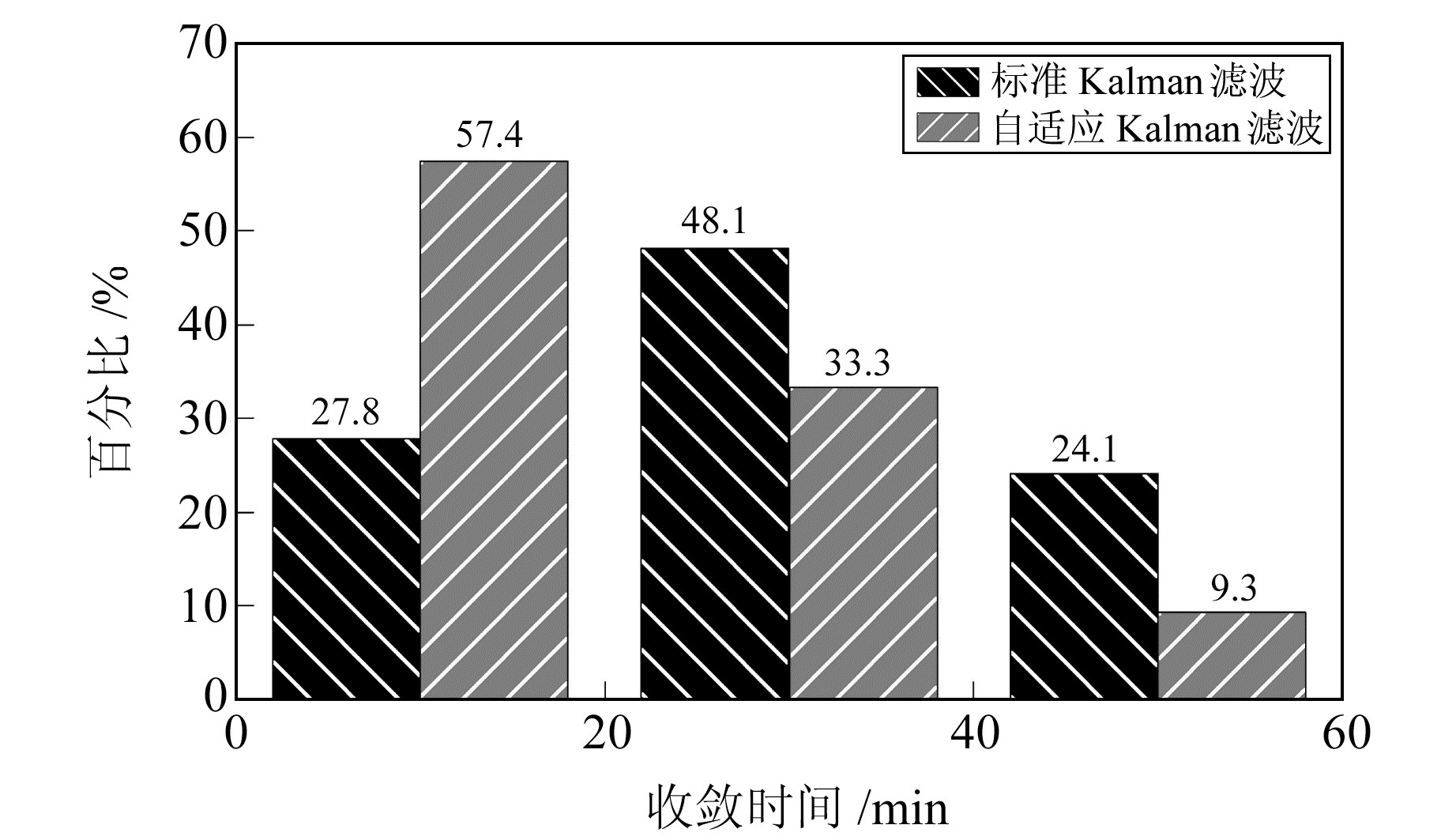
图 3 静态模式下2种滤波情况时收敛时间统计 Fig. 3 Statistics of convergence time of two filtering cases in static model |
|
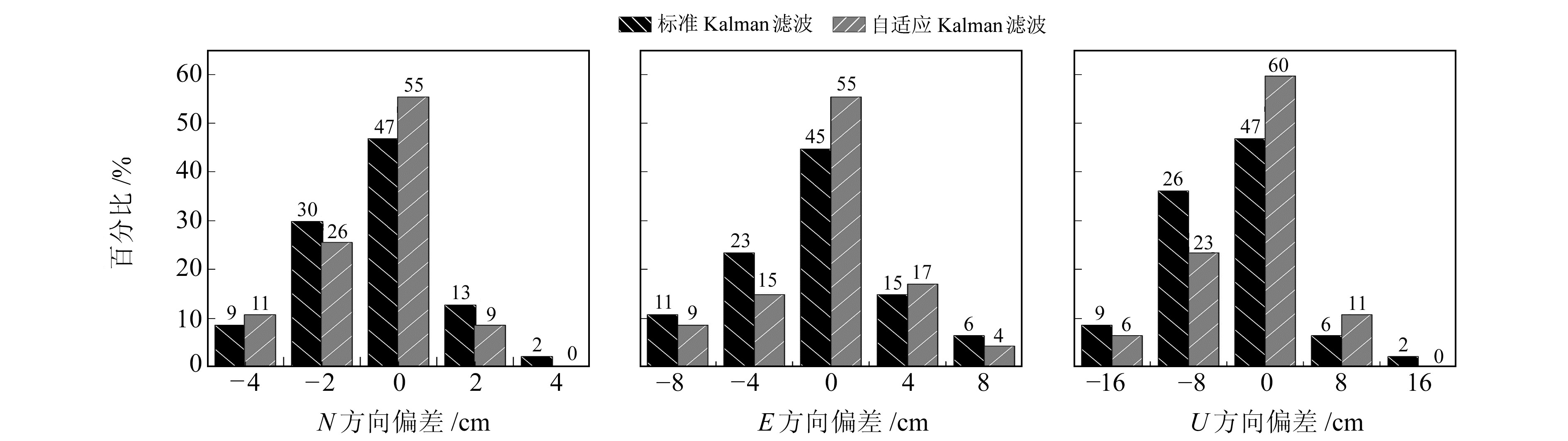
图 4 2种滤波情况下静态PPP解算N、E、U方向偏差统计 Fig. 4 Statistics of deviations of N, E and U directions of two filtering cases in static model |
从图 3可以看出,标准Kalman滤波的收敛时间有27.8%小于20 min,自适应Kalman滤波为57.4%,明显更优,进一步说明构建的自适应Kalman滤波能够加速PPP收敛。
从图 4可以看出,3个方向偏差均近似于正态分布。标准Kalman滤波PPP在N方向的定位精度有77%在2 cm内,自适应Kalman滤波为81%;在E方向,标准Kalman滤波有45%在2 cm内,自适应Kalman滤波为55%;在U方向,标准Kalman滤波有47%在4 cm内,79%在8 cm内,而自适应Kalman滤波有60%在4 cm内,94%在8 cm内。综上,静态模式下构建的自适应Kalman滤波在3个方向的定位精度都优于标准Kalman滤波。
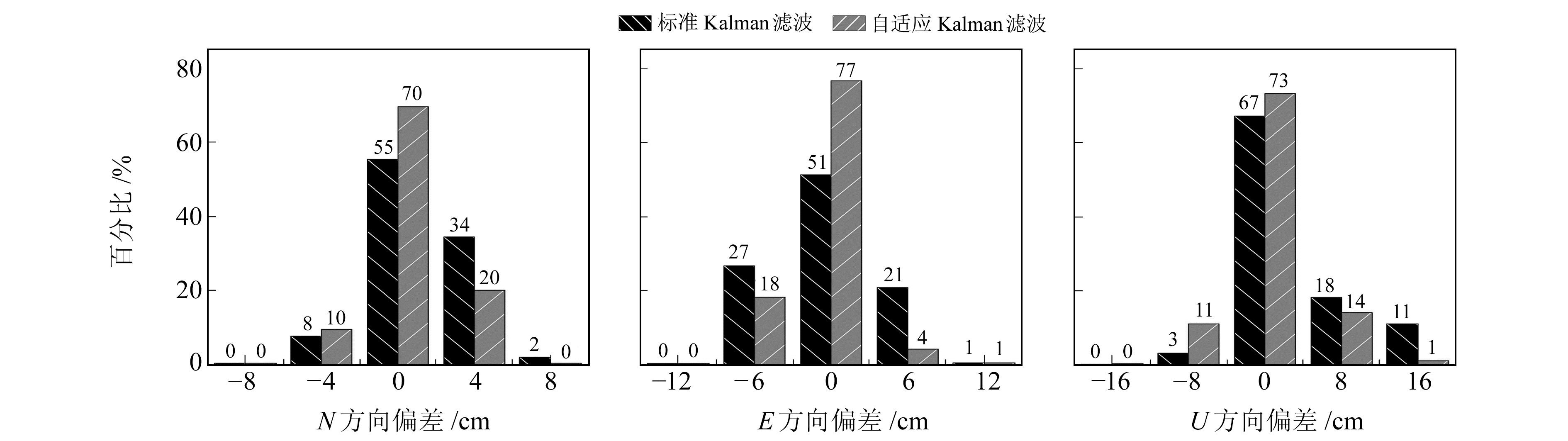
从图 5可以看出,动态模式下2种滤波3个方向偏差均近似于正态分布。在N方向的定位精度上,自适应Kalman有70%在2 cm,优于标准Kalamn滤波的55%;在E方向,自适应Kalman滤波有77%优于4 cm,优于标准Kalman滤波的51%;在U方向,自适应Kalman滤波有98%在10 cm以内,优于标准Kalman滤波的88%。综上,动态模式下构建的自适应Kalman滤波在3个方向上的定位精度都优于标准Kalman滤波。
|
图 5 2种滤波情况下动态PPP解算N、E、U方向偏差统计 Fig. 5 Statistics of deviations of N, E and U directions of two filtering cases in kinematic model |
表 1给出了2种滤波情况下进行静态PPP解算时3个方向偏差的RMS及平均收敛时间。可以看出,相较于标准Kalman滤波,构建的自适应Kalman滤波PPP解算的N、E、U方向偏差的RMS分别提高7%、14%、19%,且平均收敛时间从28.2 min缩减到19.4 min,减少31%。
|
|
表 1 2种滤波方法静态PPP解算性能的比较 Tab. 1 Comparison of two filtering methods for PPP estimating performance in static model |
表 2给出了2种滤波情况下进行动态PPP解算时3个方向偏差的RMS。可以看出,构建的自适应Kalman滤波动态PPP解算得到的N、E、U方向偏差的RMS值为2.7 cm、3.6 cm、6.3 cm,较标准Kalman滤波提高13%、28%、43%。
|
|
表 2 2种滤波方法动态PPP解算性能的比较 Tab. 2 Comparison of two filtering methods for PPP estimating performance in kinematic model |
在进行PPP参数解算时,由于对模型噪声方差矩阵和量测噪声方差矩阵理解不够准确,增益矩阵不足以修正滤波器,导致定位精度下降、收敛时间延长。本文以新息向量构造异常判别统计量,考虑到各参数对于动力学模型的可靠性不同,以位置相关为条件确定分类自适应因子,采用两段函数模型构建自适应Kalman滤波器。实验结果表明,在进行PPP解算时,该自适应Kalman滤波方法能够通过分类自适应因子修正状态预测协方差波动,加速状态预测协方差收敛。相较于标准Kalman滤波,自适应Kalman滤波在N、E、U方向上的定位精度分别提高7%、14%、19%;在收敛时间方面,自适应Kalman滤波平均收敛时间为19.4 min,减少31%。由仿动态PPP解算结果可知,构建的自适应Kalman滤波能够提高定位精度,相较于标准Kalman滤波在N、E、U方向上分别提高13%、28%、43%。
| [1] |
Guo Y F, Chai S C, Cui L G. GNSS Precise Point Positioning Based on Dynamic Kalman Filter with Attenuation Factor[C]. The 37th Chinese Control Conference, Beijing, 2018
(  0) 0) |
| [2] |
Guo F, Zhang X H. Adaptive Robust Kalman Filtering for Precise Point Positioning[J]. Measurement Science and Technology, 2014, 25(10)
(  0) 0) |
| [3] |
许阿裴, 归庆明, 韩松辉. 卡尔曼滤波模型误差的影响分析[J]. 大地测量与地球动力学, 2008, 28(1): 101-104 (Xu Apei, Gui Qingming, Han Songhui. Analysis of Model Error Effect on Kalman Filtering[J]. Journal of Geodesy and Geodynamics, 2008, 28(1): 101-104)
(  0) 0) |
| [4] |
高为广, 张晓东. 基于Kalman滤波的动力学模型误差估计算法[J]. 测绘科学, 2011, 36(2): 56-58 (Gao Weiguang, Zhang Xiaodong. An Algorithm Based on Kalman Filtering for Estimating Kinematic Model Errors[J]. Science of Surveying and Mapping, 2011, 36(2): 56-58)
(  0) 0) |
| [5] |
陈泉余, 隋立芬, 刘乾坤, 等. 一种适用于精密单点定位的抗差自适应滤波[J]. 大地测量与地球动力学, 2016, 36(8): 732-736 (Chen Quanyu, Sui Lifen, Liu Qiankun, et al. Robust Adaptive Filtering for Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(8): 732-736)
(  0) 0) |
| [6] |
杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报:信息科学版, 2003, 28(6): 714-718 (Yang Yuanxi, Xu Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714-718)
(  0) 0) |
| [7] |
Yang Y X, He H, Xu G C. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109-116 DOI:10.1007/s001900000157
(  0) 0) |
| [8] |
杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J]. 测绘学报, 2002, 31(2): 95-99 (Yang Yuanxi, Song Lijie, Xu Tianhe. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 95-99 DOI:10.3321/j.issn:1001-1595.2002.02.001)
(  0) 0) |
| [9] |
Yang Y X, Cui X Q, Gao W G. Adaptive Integrated Navigation for Multi-Sensor Adjustment Outputs[J]. Journal of Navigation, 2004, 57(2): 287-295 DOI:10.1017/S0373463304002711
(  0) 0) |
| [10] |
欧吉坤, 柴艳菊, 袁运斌.自适应选权滤波[C].大地测量与地球动力学进展, 武汉, 2004 (Ou Jikun, Chai Yanju, Yuan Yunbin.Adaptive Selective Filtering[C].Progress of Geodesy and Geodynamics, Wuhan, 2004)
(  0) 0) |
| [11] |
郝明, 欧吉坤, 郭建锋, 等. 一种加速精密单点定位收敛的新方法[J]. 武汉大学学报:信息科学版, 2007, 32(10): 902-905 (Hao Ming, Ou Jikun, Guo Jianfeng, et al. A New Method for Improvement of Convergence in Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2007, 32(10): 902-905)
(  0) 0) |
| [12] |
郭斐. GPS精密单点定位质量控制与分析的相关理论和方法研究[D].武汉: 武汉大学, 2013 (Guo Fei. Theory and Methodology of Quality Control and Quality Analysis for GPS Precise Point Positioning[D]. Wuhan: Wuhan University, 2013)
(  0) 0) |
| [13] |
徐宗秋, 徐爱功, 高扬, 等. 精密单点定位中对流层延迟参数的相关性研究[J]. 测绘科学, 2013, 38(5): 8-10 (Xu Zongqiu, Xu Aigong, Gao Yang, et al. Correlation of Troposphere Delay Parameters in Precise Point Positioning[J]. Science of Surveying and Mapping, 2013, 38(5): 8-10)
(  0) 0) |
| [14] |
Yang Y X, Gao W G. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177-183
(  0) 0) |
2. 2 Key Laboratory of Aviation-Aerospace-Ground Cooperative Monitoring and Early Warning of Coal Mining-induced Disasters of Anhui Higher Education Institutes, 168 Taifeng Street, Huainan 232001, China;
3. 3 Coal Industry Engineering Research Center of Collaborative Monitoring of Mining Area's Environment and Disasters, 168 Taifeng Street, Huainan 232001, China;
4. 4 Beijing Piesat Information Technology Co Ltd, 65 Xingshikou Road, Beijing 100195, China
 2020, Vol. 40
2020, Vol. 40

