高精度定位广泛应用于地壳形变分析、板块速度场监测和地震研究等领域[1],提取和重构基线时间序列季节项是开展GNSS坐标和基线时间序列相关研究的重要环节。本文运用EMD、EEMD和CEEMD 3种模态分解方法对TXLR-TXLI基线时间序列进行分解,提取和重构时间序列季节项,通过比较3种方法对应的重构季节项与原始基线时间序列的功率谱图,确定最佳提取和重构方法。
1 模态分解方法 1.1 经验模态分解(EMD)EMD方法可将一维的复杂信号转化为时频域下的多维信号,并将信号频率从高到低进行排序,分解成不同频率的IMF。EMD算法分解流程如下。
1) 找出数据极大值点和极小值点,利用三次样条法进行插值,求解新的连续序列的数据均值mi(t):
| $ {{m}_{i}}\left( t \right)=\frac{{{u}_{\text{max}}}\left( t \right)+{{v}_{\text{min}}}\left( t \right)}{2} $ | (1) |
2) 求解数据信号与均值序列的差值hi(t):
| $ {{h}_{i}}\left( t \right)={{x}_{i}}-{{m}_{i}}\left( t \right) $ | (2) |
式中,umax(t)为信号序列极大值,vmin(t)为信号序列极小值,xi为原始数据序列。如果hi(t)满足IMF性质则可作为其分量,否则将hi(t)作为x时间序列继续迭代获得各个IMF分量,直到下一个IMF分量为常数分量或单调函数即可。
1.2 集合经验模态分解(EEMD)EMD方法会出现模态混叠的问题,而EEMD方法可削弱模式混叠现象的影响,为一种噪声辅助的数据分析方法。分解前在原始序列信号中加入高斯白噪声生成新的待分解信号,然后将信号分解为不同频率尺度的IMF分量[2]。EEMD方法的实现过程如下。
1) 在原始时间序列中加入白噪声以获取新的时间序列,对新时间序列进行分解得到分量Cim(i=1, 2, …, n)和残差序列rm。
2) 计算各个Cim和rm均值,并将计算结果作为原始时间序列,通过EEMD分解得到第i个IMF分量和趋势项:
| $ \overline {{c_i}} = \frac{1}{N}\mathop {\mathop \sum \limits^N }\limits_{m = 1} {\kern 1pt} {c_{im}},\bar r = \frac{1}{N}\sum\limits_{m = 1}^n {{r_m}} $ | (3) |
当m=n时分解结束,原始序列x(t)结果为:
| $ x\left( t \right)=\underset{i=1}{\overset{n}{\mathop \sum }}\, \overline{{{c}_{i}}}+\bar{r} $ | (4) |
式中,Ci为第i个IMF分量,r为趋势项。
1.3 完备总体经验模态分解(CEEMD)CEEMD方法是在时间序列中加入正、负噪声,可克服EMD分解模态混叠的问题,又可完全削弱时间序列中的噪声,极大地提高了运算效率[3]。CEEMD实现流程如下。
1) 在原始基线时间序列中加入固定长度的白噪声,并对其进行EMD分解得到IMF1分量,再从原始信号中减去IMF1分量。公式如下:
| $ \text{IM}{{\text{F}}_{\text{1}}}=\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\, E\left[ x+\varepsilon {{\omega }_{i}} \right], {{r}_{1}}=x-\text{IM}{{\text{F}}_{1}} $ | (5) |
2) 进行n次迭代后可得到rn=rn-1-IMFn,然后求取各分量的平均值IMFn+1分量,当残差的极值个数小于等于2时则停止迭代:
| $ {\rm{IM}}{{\rm{F}}_{n + 1}} = \frac{1}{N}\mathop {\mathop \sum \limits^N }\limits_{i = 1} {\kern 1pt} {E_i}\left[ {{r_n} + {\rm{\varepsilon }}{\omega _i}} \right] $ | (6) |
| $ R = x - \mathop {\mathop \sum \limits^N }\limits_{i = 1} {\kern 1pt} {\rm{IM}}{{\rm{F}}_n} $ | (7) |
3) 原始时间序列信号可用公式表示为:
| $ x\left( t \right) = \mathop {\mathop \sum \limits^N }\limits_{i = 1} {\kern 1pt} {\rm{IM}}{{\rm{F}}_n} + R $ | (8) |
式(6)~(8)中,N为运算次数,ωi为加入的白噪声,ε为不同强度的白噪声,R为残差项。
2 功率谱分析法功率谱分析法可表现单位频带内信号功率随频率的变化,若某个信号具有周期特性,则其周期运动所对应的功率在全部功率中占有较大比重,在功率谱图上表现为峰值[4]。
1) 地球物理现象的功率谱分析公式为[5]:
| $ {{P}_{x}}={{P}_{0}}{{f}^{\theta }}~ $ | (9) |
2) 在均匀采样条件下进行傅里叶变换(FFT)并绘制功率谱密度图,确定季节项周期特性:
| $ P\left( {{f_0}} \right) = \frac{1}{N}\left[ {{{\left( {\mathop {\mathop \sum \limits^N }\limits_{i = 1} {\kern 1pt} {x_i}{\rm{cos}}2{\rm{ }}\pi {\rm{ }}i{f_n}} \right)}^2} + {{\left( {\mathop {\mathop \sum \limits^N }\limits_{i = 1} {\kern 1pt} {x_i}{\rm{sin}}2{\rm{ }}\pi {\rm{ }}i{f_n}} \right)}^2}} \right] $ | (10) |
3) 在非均匀采样条件下,利用Lomb周期图计算序列的功率谱:
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {{P_x}\left( f \right) = \frac{1}{2}\left\{ {\frac{{{{\left[ {\mathop \sum \limits_{j = 1}^N {x_j}{\rm{cos}}\varphi \left( {{t_j} - \tau } \right)} \right]}^2}}}{{\mathop \sum \limits_{j = 1}^N {\rm{co}}{{\rm{s}}^2}\varphi \left( {1 - \tau } \right)}} + \frac{{{{\left[ {\mathop \sum \limits_{j = 1}^N {x_j}{\rm{sin}}\varphi \left( {{t_j} - \tau } \right)} \right]}^2}}}{{\mathop \sum \limits_{j = 1}^N {\rm{co}}{{\rm{s}}^2}\varphi \left( {{t_j} - \tau } \right)}}} \right\}}\\ {\tan \left( {2\varphi t} \right) = \frac{{\sum\limits_{i = 1}^N {\sin \left( {2{\varphi _i}} \right)} }}{{\sum\limits_{i = 1}^N {\cos \left( {2{\varphi _i}} \right)} }}} \end{array}} \right.\\ \end{array} $ | (11) |
式中,N为运算次数,Px(f)为功率谱密度,P0为常态功率系数,θ为谱指数,fn=n/T为采样频率,T为采样总长度,xi为坐标时间序列,ti为所取观测天数。
3 实验与结果分析实验数据包含美国CORS网站中TXLR和TXLI基准站的观测数据及从IGS下载的导航文件(*.n)和精密星历文件(*.sp3)。
3.1 原始基线时间序列获取利用GAMIT/GLOBK软件求解CORS的单天解,并批量提取2次解向量中第2次基线解算结果作为原始时间序列解算数据。季节项主要体现在U方向上,其原始基线时间序列见图 1。
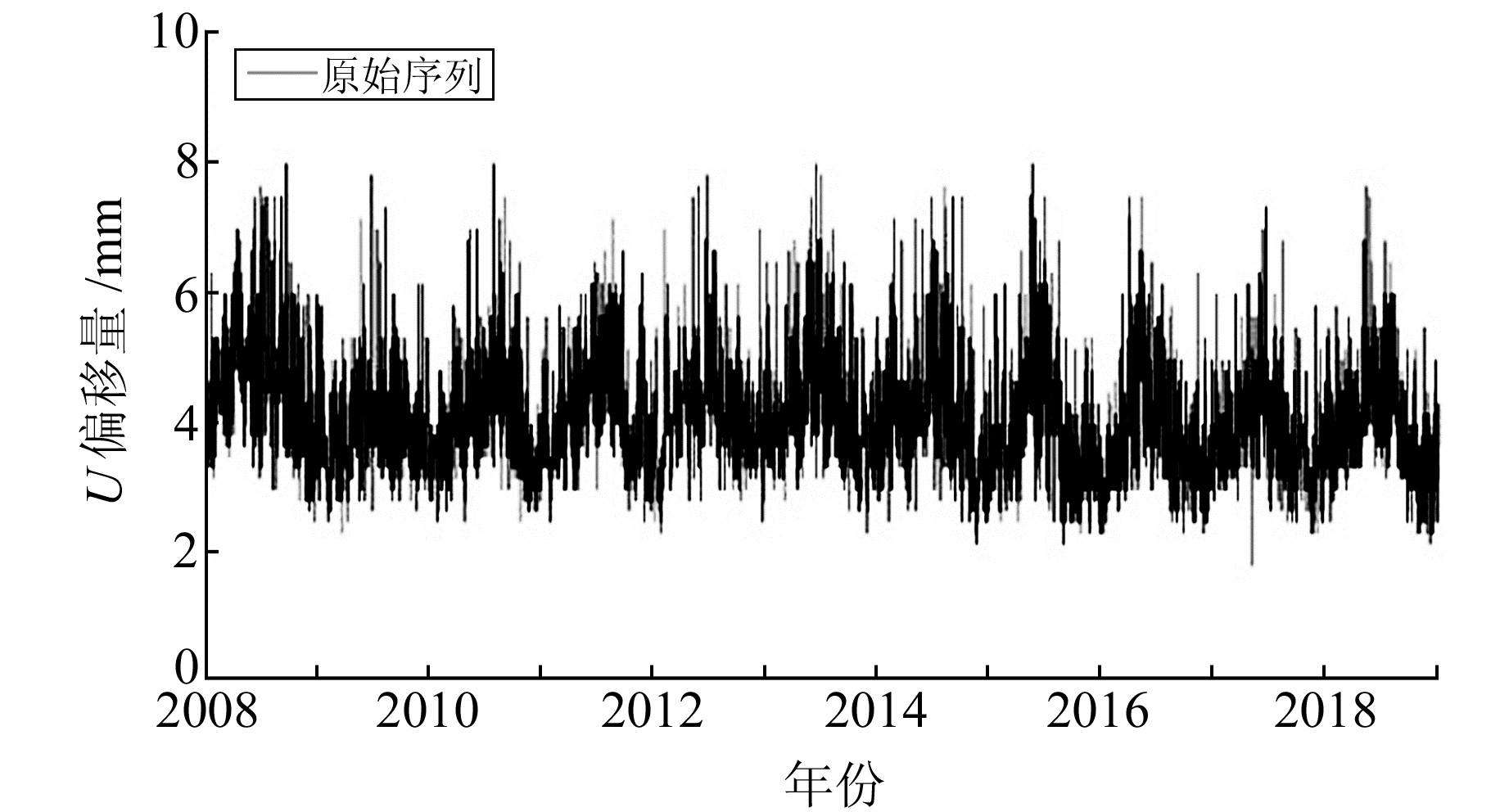
|
图 1 TXLR-TXLI基线时间序列 Fig. 1 Time series of TXLR-TXLI baseline |
1) 季节项提取。利用3种方法对TXLR-TXLI基线时间序列进行自适应分解,并求出各分解方法的IMF分量,结果见图 2。
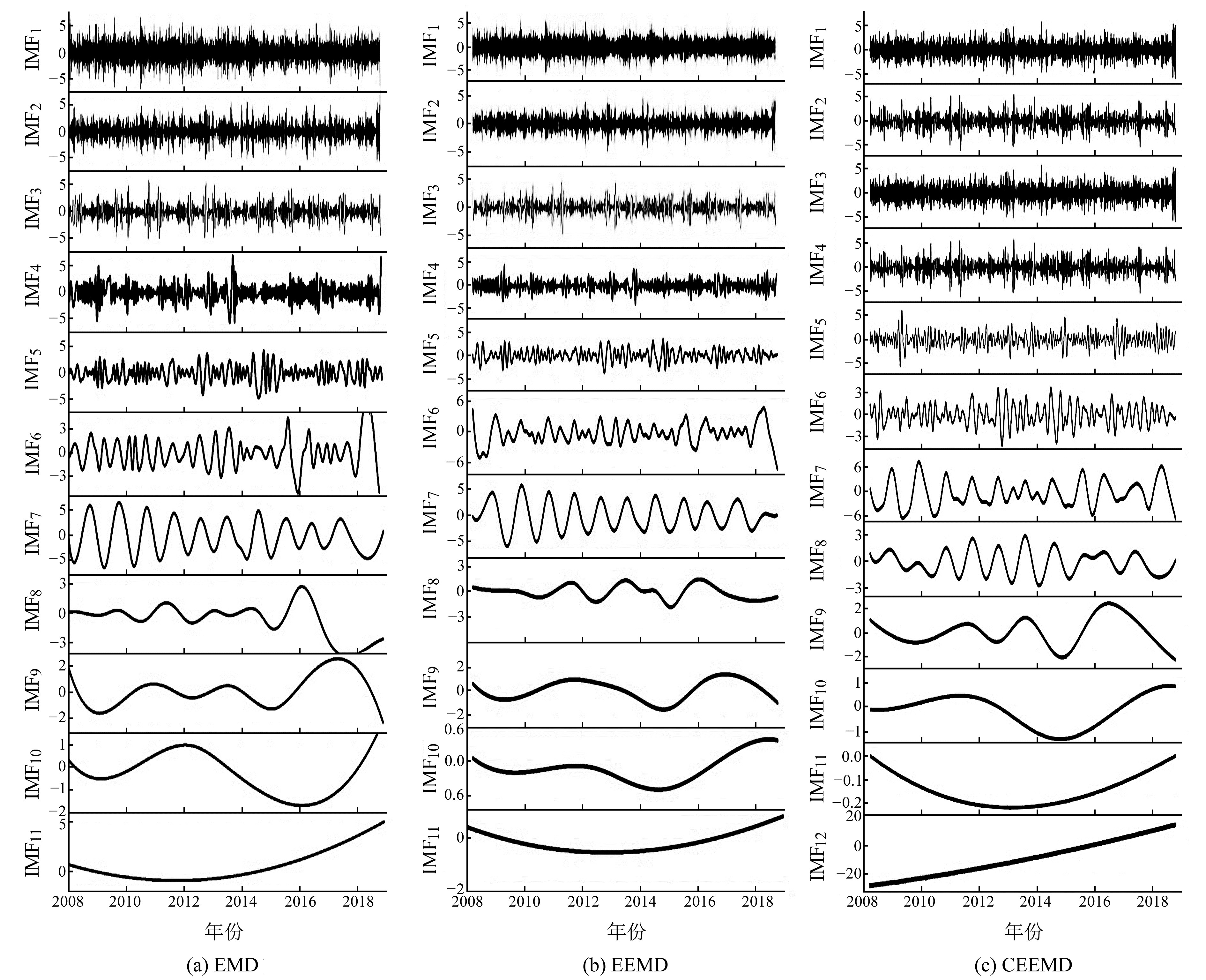
|
图 2 TXLR-TXLI基线时间序列U方向分解结果 Fig. 2 U-direction decomposition of time series of TXLR-TXLI baseline |
图 2中季节项与残差项的分界点可根据分量谱指数确定,与趋势项的区别可根据周期性强度进行判断。在上述分量中,趋势项的周期性波动趋势接近线性。研究表明,趋势项会对季节项造成干扰,为防止趋势项对季节项提取的影响,在原始时间序列基础上减去趋势项对应的偏移量可得到去趋势项的基线时间序列。图 3中去趋势项后U方向基线时间序列与图 1原始基线时间序列相比,表现出相对明显的周期特性。根据去趋势项后IMF分量与原始信号的相关系数制作能量谱指数表(表 1)。
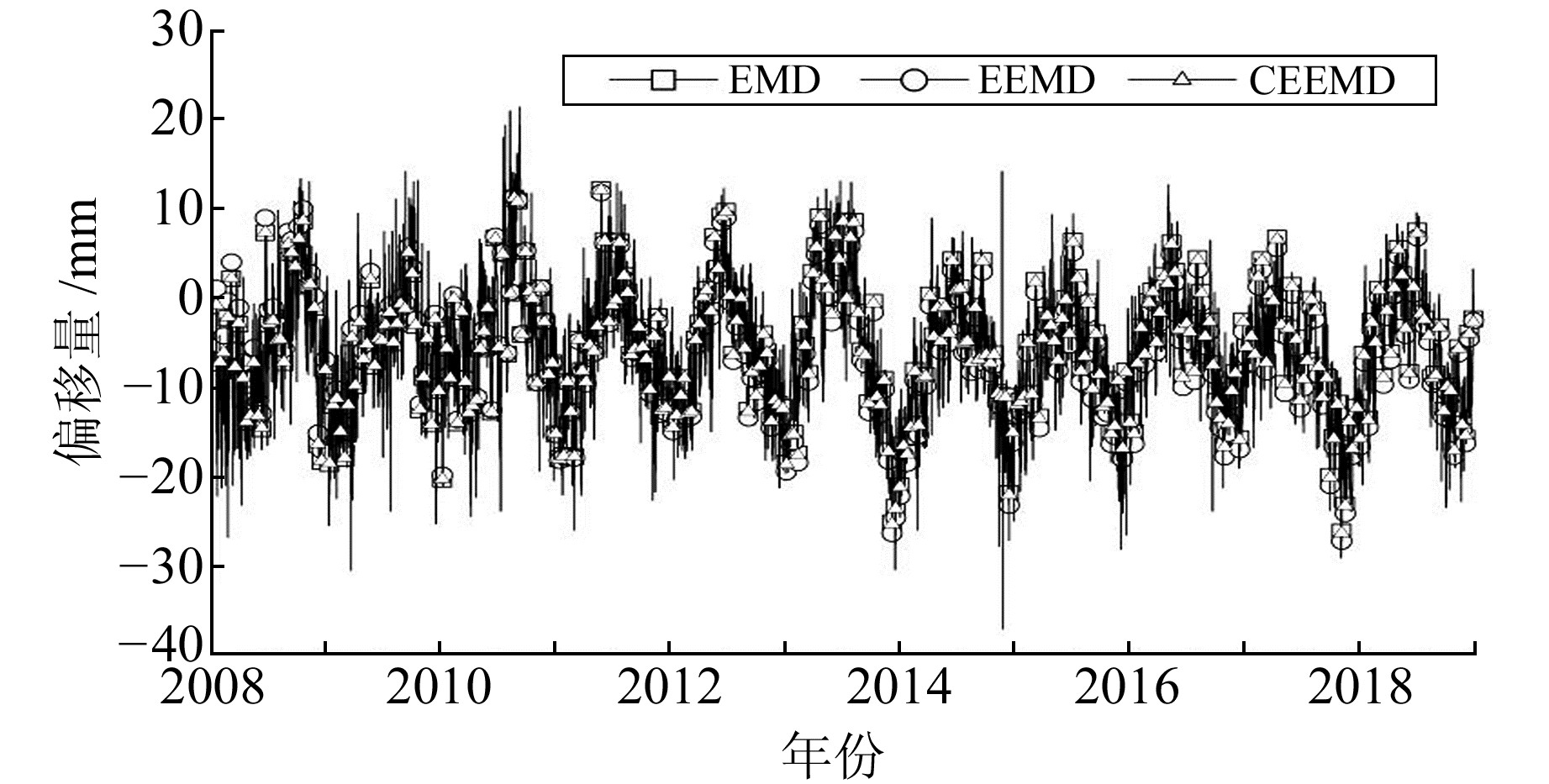
|
图 3 去趋势项后的TXLR-TXLI基线时间序列 Fig. 3 Time series eliminated trend item of TXLR-TXLI baseline |
|
|
表 1 能量谱指数 Tab. 1 Energy spectrum index |
每组能量谱指数的第1个极小值点为残差项与季节项分界点[6],第1个极小值点之前的分量为残差项部分。在TXLR-TXLI基线时间序列中,EMD结果中IMF3之前部分为残差项,而在EEMD和CEEMD结果中IMF5之前部分为残差项,即IMF1~IMF3为EMD方法提取的残差时间序列,IMF1~IMF5为EEMD与CEEMD方法提取的基线残差时间序列。
2) 季节项重构。取EMD结果中IMF4~IMF9分量和EEMD与CEEMD结果中IMF6~IMF10分量重构季节项,结果见图 4。
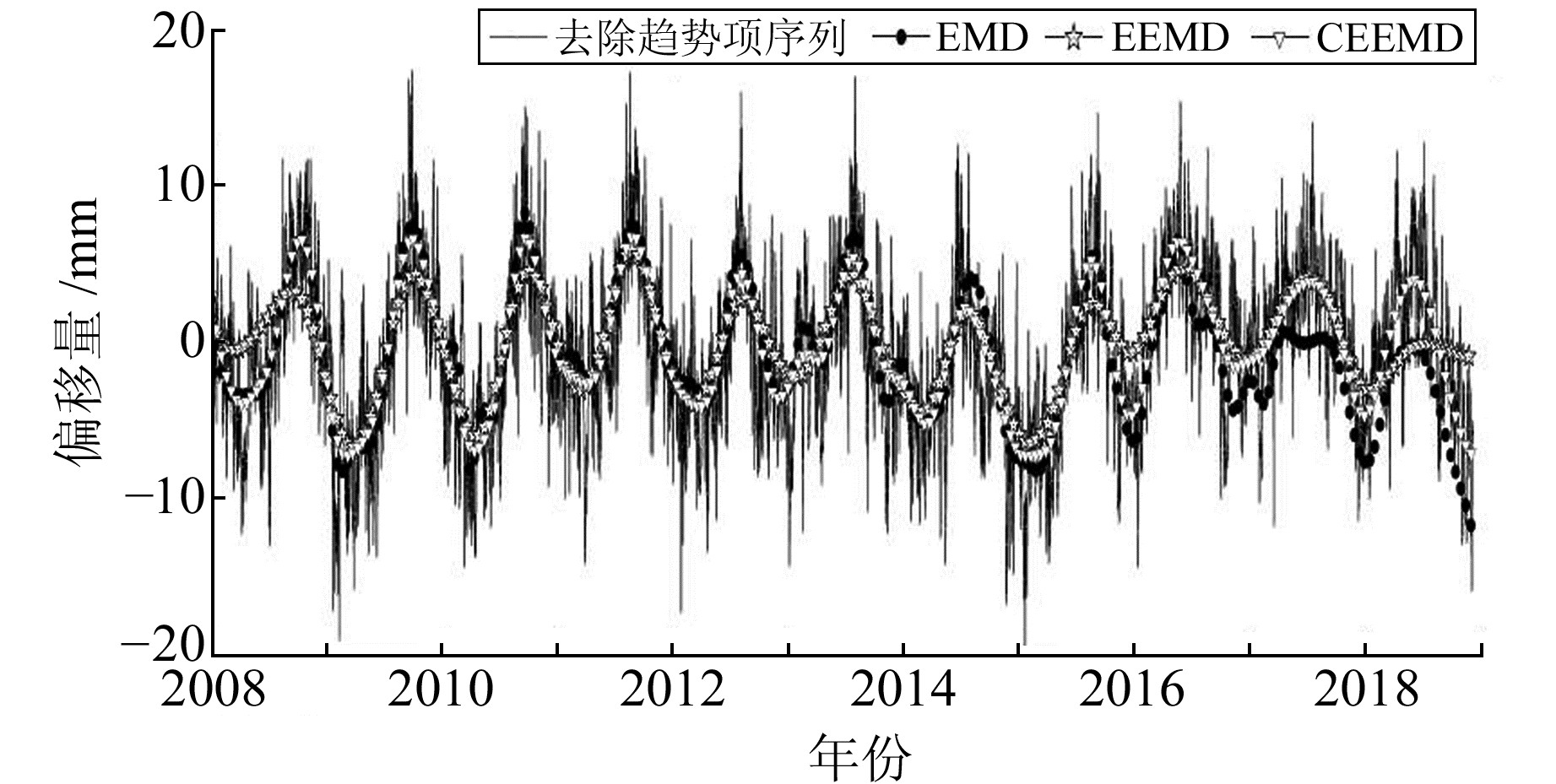
|
图 4 TXLR-TXLI基线U方向季节项重构图 Fig. 4 Season item reconstruction of U-direction of TXLR-TXLI baseline |
从图 4中可以看出,3种分解方法均可实现季节项重构,但随着时间的推移,EMD和EEMD方法重构曲线的运动趋势与原始时间曲线存在明显偏差,而CEEMD方法重构的效果较好。
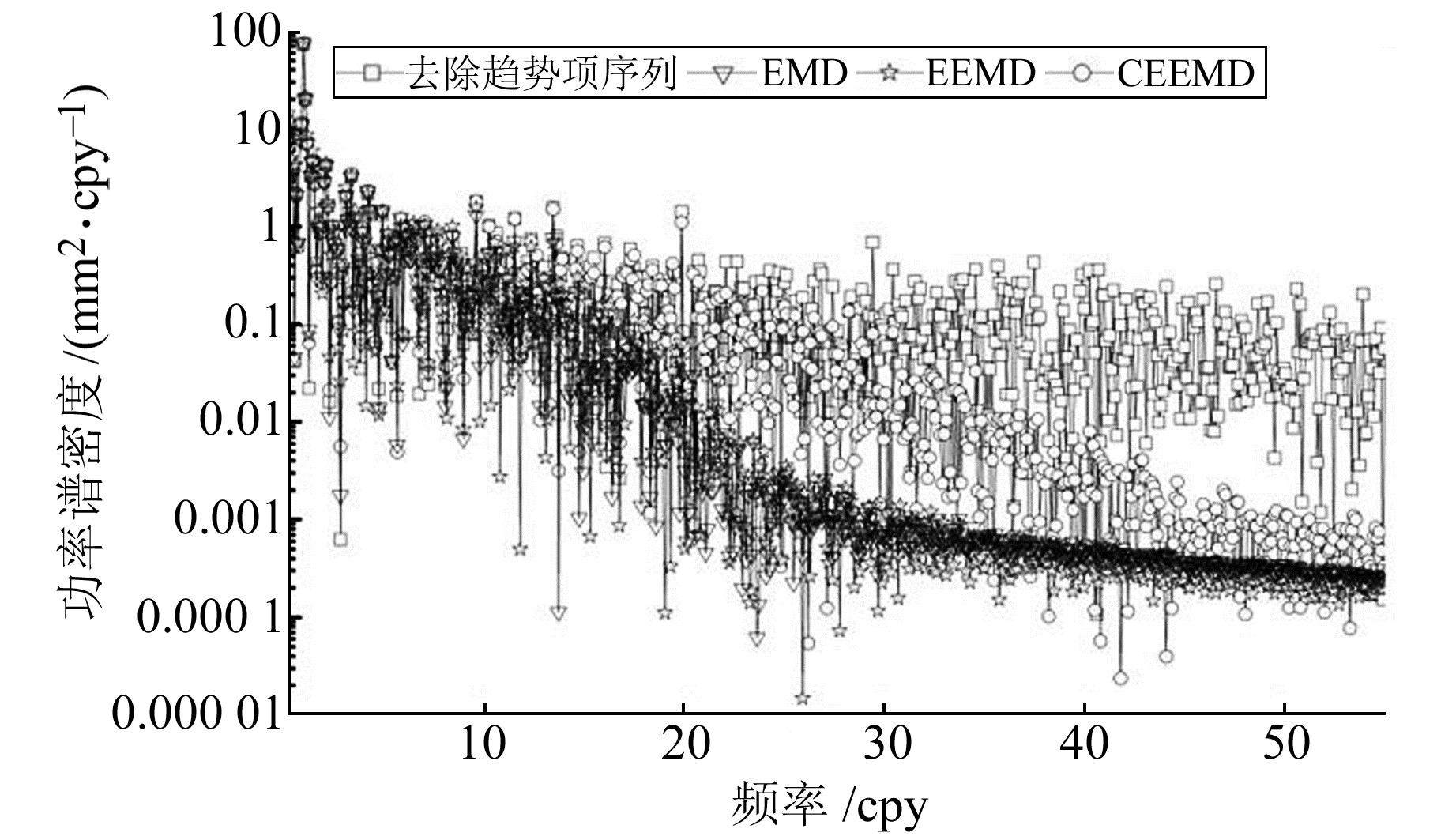
3) 模态分解方法优选。通过比较3种分解方法所提取的季节项与原始基线时间序列信号的叠加功率谱图确定最佳模态分解方法,图 5为3种方法对应的功率谱图。
|
图 5 TXLR-TXLI基线叠加功率谱 Fig. 5 Superposition power spectrum of TXLR-TXLI baseline |
当重构季节项功率谱图与原始序列功率谱图越接近时,表明重构的季节项能够保留更多的原始序列信息成分,提取和重构季节项效果更好。从图 5中可以看出,3种分解方式重构的季节项功率谱图与原始基线时间序列功率谱图均存在偏差,但CEEMD方法所重构的季节项功率谱图在全频段内与原始时间序列功率谱图最为接近,即能更好地提取和重构季节项,尤其在高频部分优势更明显。
4 结语1) 3种分解方法可得到不同频率的IMF分量,通过谱指数第1个极小值点和对比周期性强度可区分残差项、季节项与趋势项分量,从而提取季节项分量。
2) 将季节项分量部分进行重构,相比于EMD和EEMD方法,经CEEMD方法重构的季节项与原始序列波动趋势更相似。
3) EMD和EEMD功率谱图在中频部分出现突变下降,而CEEMD功率谱图匀速下降且无突变,同时下降速度慢于前2种方法。因此CEEMD方法为最佳模态分解方法,能更多地保留原始时间序列中的信息成分。
| [1] |
徐爱功, 李娜, 张涛. 时间序列分析在地铁沉降观测中的应用[J]. 测绘科学, 2013, 38(5): 57-60 (Xu Aigong, Li Na, Zhang Tao. Application of Time Series Analysis in Subway Settlement Observation[J]. Science of Surveying and Mapping, 2013, 38(5): 57-60)
(  0) 0) |
| [2] |
Wu Z H, Huang N. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41
(  0) 0) |
| [3] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition:A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156
(  0) 0) |
| [4] |
李蕾, 葛悉佑, 王静涛. 南极IGS基准站时间序列极大似然法分析[J]. 测绘科学, 2016, 41(7): 173-180 (Li Lei, Ge Xiyou, Wang Jingtao. Analysis of Coordinate Time Series of IGS Stations in Antarctic Based on Maximum Likelihood Estimation[J]. Science of Surveying and Mapping, 2016, 41(7): 173-180)
(  0) 0) |
| [5] |
韩英, 符养. GPS高程数据时间序列分析[J]. 武汉大学学报:信息科学版, 2003, 28(4): 425-428 (Han Ying, Fu Yang. Analysis of GPS Time Series of Height Component[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 425-428)
(  0) 0) |
| [6] |
Davis J L, Wernicke B P, Tamisiea M E. On Seasonal Signals in Geodetic Time Series[J]. Journal of Geophysical Research Atmospheres, 2012, 117: B01403
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


