基于信噪比(signal-to-noise ratio, SNR)的GNSS干涉测量(GNSS-IR)技术可对土壤湿度、雪深、潮汐等参数进行反演[1-4]。GNSS-IR反演潮位是基于一种静态假设,即卫星运行时反射面不变,但潮位时刻发生变化,因此在反演潮位时存在高度变化引起的误差。国内学者[5-8]对GNSS-IR海潮监测进行过大量研究,但关于潮位高度变化引起的误差的研究较少。目前潮位改正的方法有经典改正法和最小二乘改正法[3, 9-10],这2种方法均能实现误差改正,但缺乏关于这2种动态改正方法的观测环境和要求的研究。本文对GNSS-IR反演潮位理论和潮位偏差改正进行深入研究,针对静态假设引起的海面高度误差,利用海平面日涨落幅度较大的PBAY站点数据和伴有风暴潮特殊环境的HKQT站点数据进行实验,对比分析经典改正法和最小二乘改正法的改正效果,探讨2种方法的适用情况。
1 GNSS-IR反演及潮位动态改正的原理 1.1 GNSS-IR潮位监测原理多路径误差的产生与测站周围环境密切相关,若将GNSS测站置于海边,接收机在海域方位会接收到卫星直射与经海水表面反射后产生干涉的合成信号[11]。令θ为直射信号与瞬时潮位面的夹角,同时也可用来表示天线相位中心处的卫星高度角,h为瞬时潮位面到天线相位中心的垂直反射距离,则直射信号和反射信号之间的相位差为[12]:
| $ \varphi =\frac{2\pi \delta }{\lambda }=\frac{4\pi h\sin \theta }{\lambda } $ | (1) |
式中,δ为反射信号与直射信号的路程差,θ为卫星高度角,h为垂直反射距离,λ为信号波长。
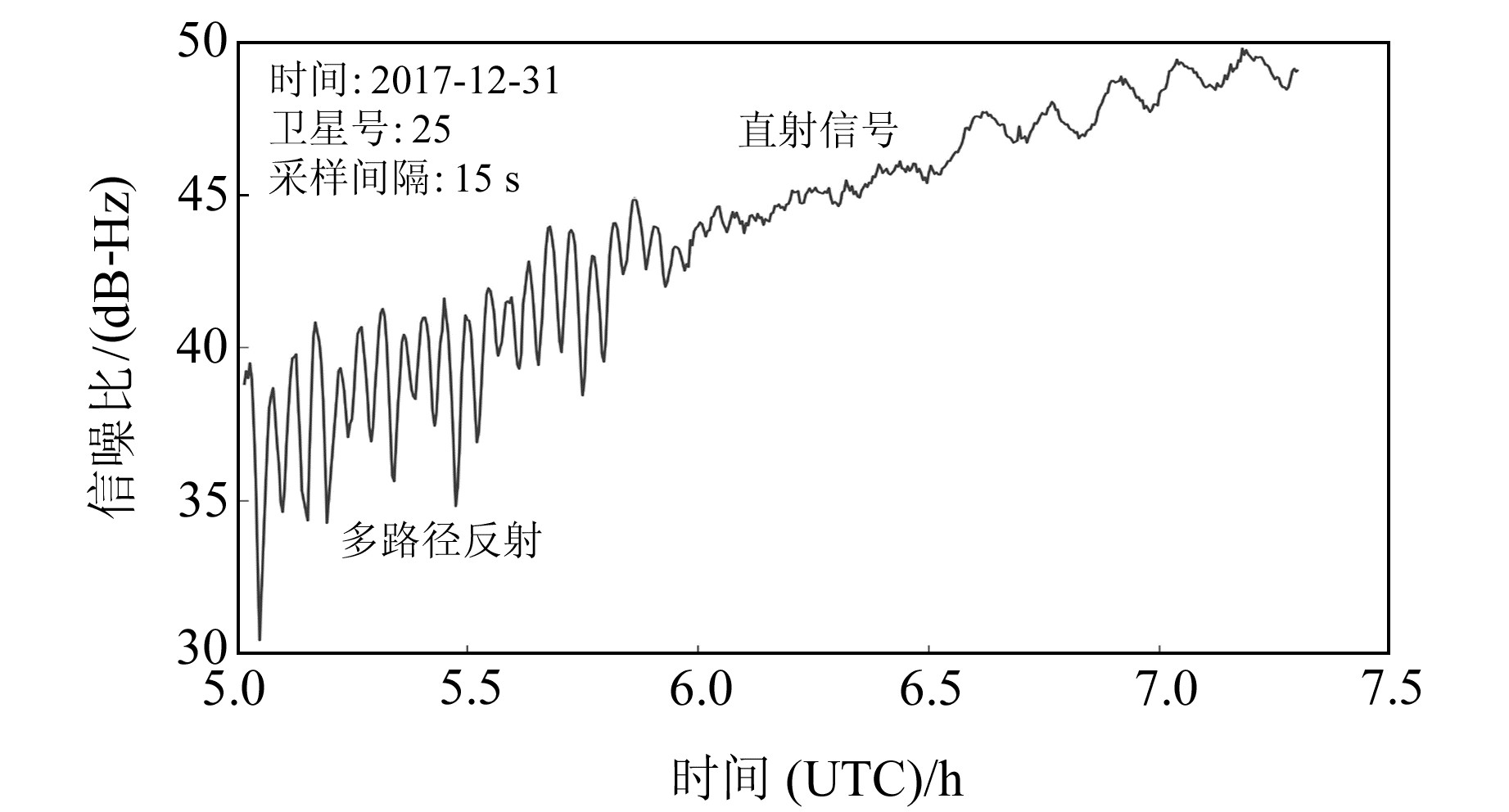
图 1为岸边测站2017-12-31 GPS卫星的SNR时序图,采样间隔为15 s。可以看出,SNR值在低高度角时振荡明显,随着卫星上升趋于稳定,这种变化主要受卫星信号发射功率、天线增益和多路径效应等因素的影响[13]。通过2阶多项式拟合SNR可去除信号中直射信号的影响,得到反射信号的SNR残差序列,从而可提取地表环境参数。
|
图 1 GPS 25号卫星信噪比时序图 Fig. 1 Time sequence of signal-to-noise ratio of GPS 25 satellite |
受多路径影响的SNR残差序列振幅可以表示为[14]:
| $ {{\rm{A}}_m}{\rm{ = Acos}}\left( {\frac{{4{\rm{ \mathsf{ π} }}h}}{{\rm{ \mathsf{ λ} }}}\sin \theta + \varphi } \right) $ | (2) |
式中,Am为反射信号振幅,A为振幅,φ为相位差。SNR残差序列中包含的频率信息为[9]:
| $ {{\omega }_{\varphi }}=2\pi f=\frac{\text{d}\varphi }{\text{d}\left( \sin \theta \right)}=\frac{4\pi h}{\lambda } $ | (3) |
式中,f为信号频率。令t=sinθ,f=2h/ λ,式(2)可简化为标准余弦函数。对SNR残差序列进行L-S频谱(lomb-scargle)分析[9, 12]可确定频率f和垂直反射距离h。
1.2 潮位动态改正原理及方法经典潮位反演中一般采用L-S频谱分析法进行信号处理,该方法可解决散点采样时间间隔不均匀的问题,同时可在一定程度上减弱时域序列不均匀所产生的虚假信号,克服数据缺失、序列长度不足等问题[15-16]。考虑到海面动态变化的特性,本文引入由卫星移动导致的高度角变化率
| $ \bar{h}=\frac{\tan \theta }{{\dot{\theta }}}\dot{h}+h $ | (4) |
式中,h为静态假设下的垂直反射距离,h为动态情况下的垂直反射距离。基于上述潮位动态改正原理,本文对2种动态改正算法进行说明。
1.2.1 经典改正法原理Larson等[17]提出一种基于h序列拟合潮波曲线的改正方法,具体的曲线拟合方法可借鉴潮波参数的求解公式:
| $ \bar{h}=\sum\limits_{i=1}^{N}{{{C}_{i}}{{f}_{i}}\cos \left( {{\omega }_{i}}t+{{\nu }_{i}} \right)+{{S}_{i}}{{f}_{i}}\sin \left( {{\omega }_{i}}t+{{\nu }_{i}} \right)} $ | (5) |
式中,(Si, Ci)为正弦和余弦因子,N为数据长度,ωi为海潮频率,νi为海潮相位,fi为调节振幅大小的因子。解算获取各参数后,再对该曲线进行求导可获得ḣ:
| $ \dot{h}\approx \bar{h}=-\sum\limits_{i=1}^{N}{{{\omega }_{i}}{{f}_{i}}\sin \left( {{\omega }_{i}}t+{{\nu }_{i}} \right)+{{\omega }_{i}}{{S}_{i}}{{f}_{i}}\cos \left( {{\omega }_{i}}t+{{\nu }_{i}} \right)} $ | (6) |
将h减去对应时刻的
Roussel等[3]提出动态SNR反演原理,用时间窗口截取SNR序列,对每个窗口中的弧段频谱进行分析,利用最小二乘方法求解动态垂直反射距离h(t)和变化率ḣ(t)。由于站点位置特殊,普通接收机干涉频率不能满足要求,因此时间窗口的选取具有不确定性。本文采用高度角窗口截取SNR序列,处理过程为:以高度角5°~20°的SNR序列为例,用长度为10°、增幅为2.5°将高度角窗口截取成[5°, 15°]、[7.5°, 17.5°]、[10°, 20°],将原先SNR长序列分解为3个SNR短序列,再分别进行L-S频谱分析求解3个反演结果。为减小相邻反演值求解的自相关性影响,可对h的时间序列进行加窗求解,窗口大小为对应时刻前后1 h。利用以上方法可建立观测方程:
| $ \mathit{\boldsymbol{\bar H}} = \left\{ {\begin{array}{*{20}{c}} {{{\bar h}_1}\left( t \right)}\\ {{{\bar h}_2}\left( t \right)}\\ {{{\bar h}_3}\left( t \right)}\\ \cdots \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{M_1}\mathit{\boldsymbol{\dot h}}\left( t \right) + \mathit{\boldsymbol{h}}\left( t \right)}\\ {{M_2}\mathit{\boldsymbol{\dot h}}\left( t \right) + \mathit{\boldsymbol{h}}\left( t \right)}\\ {{M_2}\mathit{\boldsymbol{\dot h}}\left( t \right) + \mathit{\boldsymbol{h}}\left( t \right)}\\ \cdots \end{array}} \right\} = {\rm{M}}\mathit{\boldsymbol{\dot h}}\left( t \right) + \mathit{\boldsymbol{h}}\left( t \right) = \mathit{\boldsymbol{AX}} $ | (7) |
式中,
| $ {M_i} = \frac{{\tan {\theta _i}}}{{\dot \theta }},\mathit{\boldsymbol{A}} = \left( {{M_1}} \right),\mathit{\boldsymbol{X}} = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot h}}\left( t \right)}\\ {\mathit{\boldsymbol{h}}\left( t \right)} \end{array}} \right),i = 1,2,3 \cdots $ | (8) |
每个窗口中的所有反演值均由同一种信号分析所得,因此各反演值精度相当。本文定义窗口中权重均为1,则根据最小二乘原理可知:
| $ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{\bar H}} $ | (9) |
改正前后差值V = h (t)-H,引入平差精度参数
| $ {\hat \sigma _0} = \sqrt {\frac{{{\mathit{\boldsymbol{V}}^T}\mathit{\boldsymbol{PV}}}}{r}} $ | (10) |
式中,r为自由度。潮位反演值等于特定常数(与站高、GNSS系统的框架基准和验潮站的高度基准有关)减去垂直反射距离,潮位的变化速率为-ḣ。
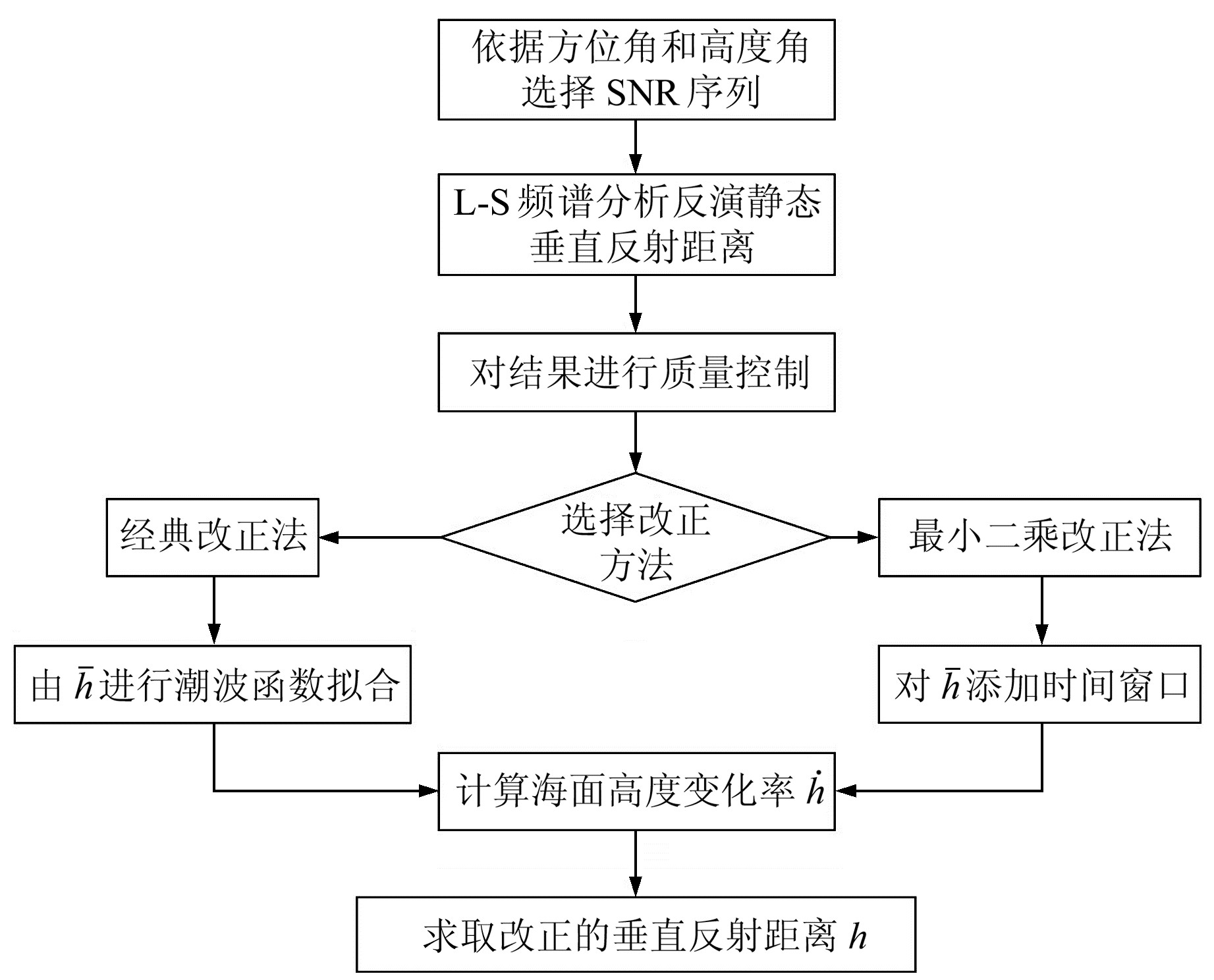
图 2为GNSS-IR反演潮位和动态改正的算法流程。
|
图 2 动态改正法流程 Fig. 2 The flow chart of dynamic correction method |
为分析经典改正法与最小二乘改正法的适用情况,选取美国PBAY站30 d的实测数据和香港HKQT站7 d的卫星观测数据进行实验,其中PBAY站海平面日涨落幅度较大,每日海潮潮位变化超过7 m[9],期间气象正常,HKQT站附近海域在实验期间受台风影响形成风暴潮。
2.1 站点介绍PBAY站(151.27°W,59.57°N)位于美国阿拉斯加Peterson湾,采样间隔为30 s。选用该站2017年年积日101~130的GPS L1波段数据进行实验,期间天气情况正常,无海啸、风暴潮等气象灾害。由于利用经典潮位反演原理监测潮位变化仅需接收从海面反射回的GPS卫星信号,因此提取高度角区间为5°~20°、方位角区间为100°~250°的GPS卫星数据。
HKQT站(114.21°E,22.29°N)属于香港卫星定位参考站网,采样间隔为1 s、5 s和30 s。选用2017年年积日232~238的GPS L1波段数据进行实验,采样间隔为5 s。由于该站点高度角大于9°的卫星信号会被遮挡,因此高度角区间选取4°~9°,海面相对于接收机的方位角选取-60°~105°[18]。
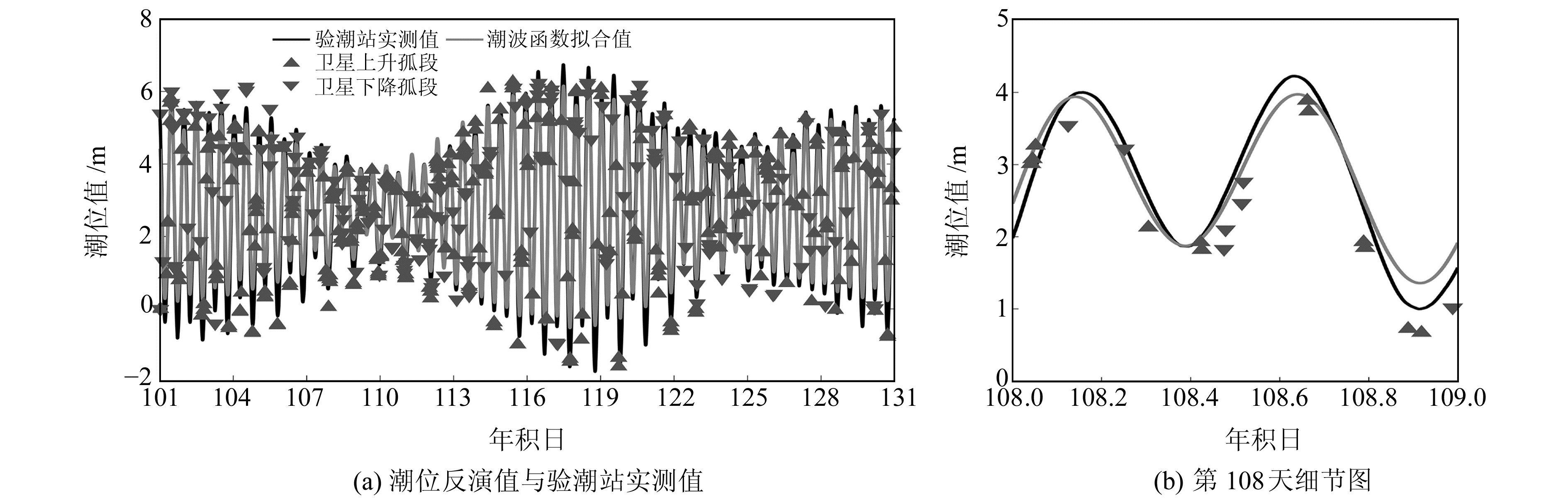
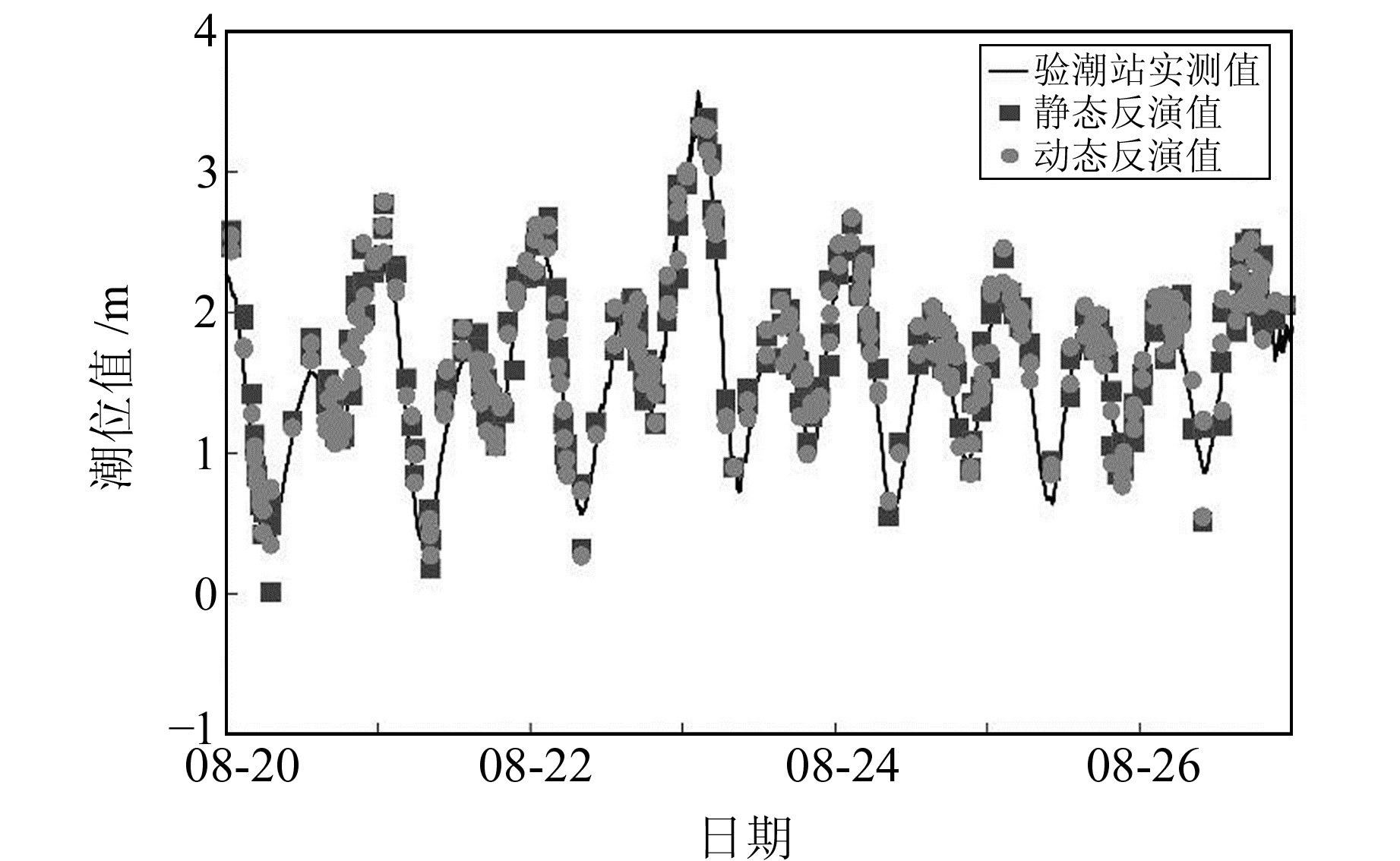
2.2 正常气象情况下的改正方法对比研究 2.2.1 经典改正法用长度为10°、步长为2.5°的滑动窗口截取PBAY站有效卫星弧段的SNR序列,在未作动态改正的静态假设下,图 3为利用经典潮位反演原理得到的结果。从图中可以看出,海潮波动会造成结果偏差,因此需要对其进行改正。使用经典改正算法拟合曲线可求解h,进一步改正
|
图 3 静态假设下的潮位反演值 Fig. 3 Inversion values of tidal level under static assumption |
|
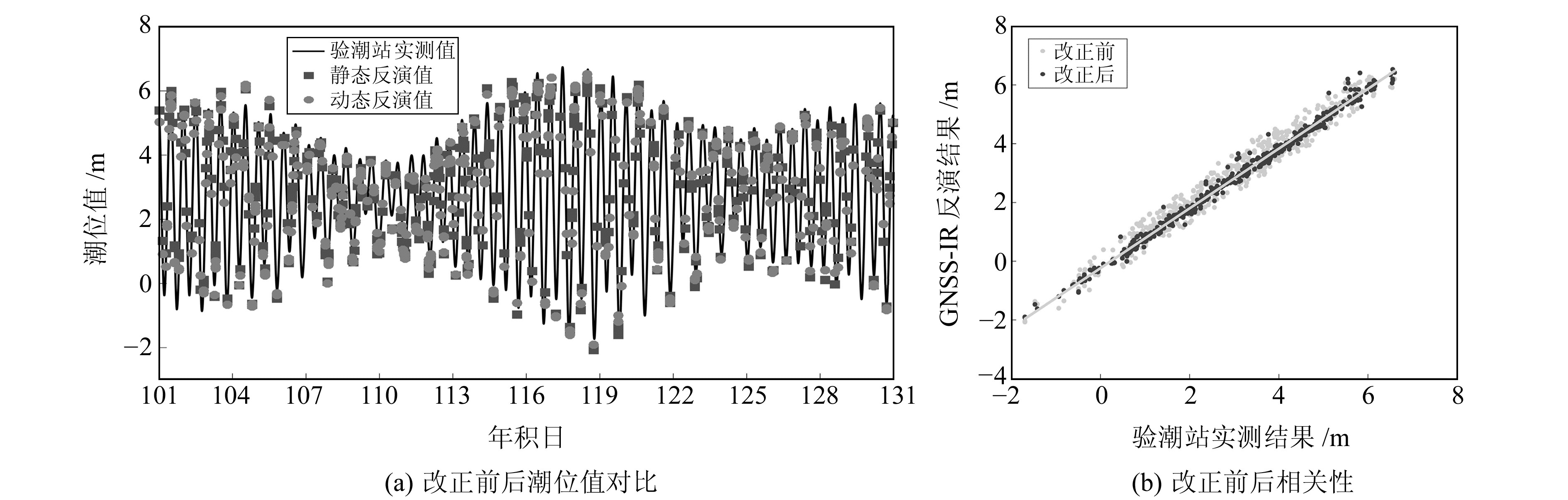
图 4 动态改正前后结果 Fig. 4 Results before and after dynamic correction |
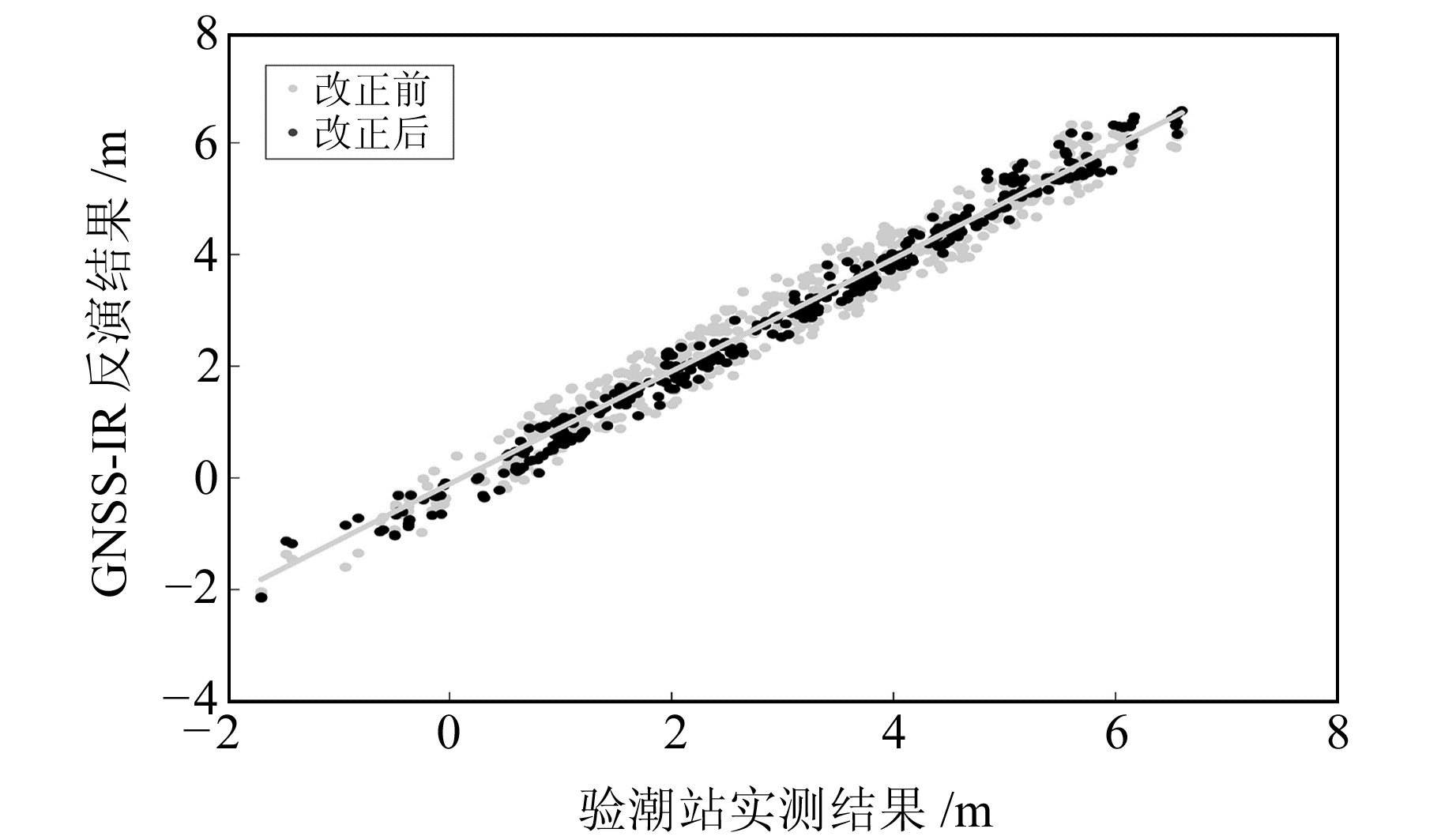
从图 4计算结果可知,静态反演值与实测值的相关系数为0.99,均方根误差为34.20 cm;动态改正后相关系数为0.98,均方根误差为16.64 cm。改正前后数据量均为477个,反演值时间分辨率不变但精度提高51.34%。相比于改正前对反演值进行Spline样条插值的拟合结果,改正后的插值拟合结果的振幅与验潮站一致性更好。
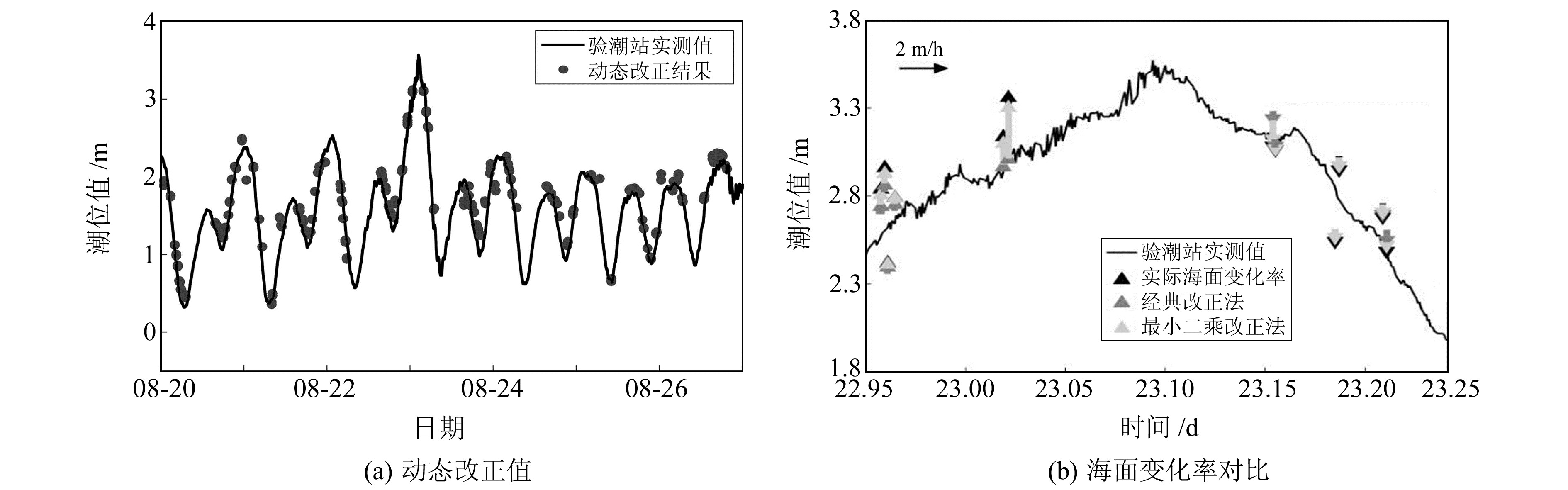
2.2.2 最小二乘改正法利用最小二乘改正法可同时求解改正后的潮位值和潮位变化率,解算滑动窗口处理后的组合方程可确定h和ḣ(图 5)。图 5(b)中黑色箭头为根据动态改正后的值计算的反演潮位变化率ḣ,箭头方向为潮位升降方向,箭头长度为潮位升降速率。动态改正后的反演潮位与验潮站实测潮位之间的均方根误差为22.39 cm,相关系数为0.96(图 6),改正前后数据量由477减少至365,精度提高34.53%。改正后的结果插值拟合情况与验潮站整体一致,但因部分潮位峰值数据缺失,拟合情况相比改正前稍差。

|
图 5 动态算法解算结果 Fig. 5 Solution results of dynamic algorithm |
|
图 6 改正结果与验潮站数据相关性 Fig. 6 Correlation between corrected results and tide gauge data |
对比2种方法的改正结果发现,在正常气象情况下,依赖潮波函数的经典改正法对海面变化拟合效果更好,可用潮波函数变化率近似代替海面实际变化率对静态假设下的潮位反演值进行改正。而最小二乘法改正效果比经典改正法差,并且由于改正后剔除了一部分数据,使得反演值时间分辨率降低,从而影响对潮位的实时监测能力。因此在正常气象情况下进行潮位动态改正时,应优先考虑经典改正法。
2.3 特殊气象情况下的改正方法对比研究 2.3.1 经典改正法经典改正法的改正效果依赖于潮波函数的整体拟合程度,暴风、飓风等自然气象会造成海面突变,由潮波函数确定的曲线无法拟合这种突变现象,从而会影响改正效果。图 7、8为HKQT站潮波函数拟合及潮位反演结果。2017-08-22~23台风形成风暴潮造成海面突变,潮波函数拟合效果较差,用经典改正法改正潮位的效果就会降低。动态改正前后的结果与实测值的相关性均为0.97,反演值数量由285减至283,均方根误差由17.83 cm降至16.97 cm,精度仅提高4.82%。对改正后的结果进行Spline样条插值,插值结果中振幅与验潮站数据相比和改正前几乎一致,这也说明经典改正法在风暴潮情况下改正效果不理想。

|
图 7 静态反演值拟合潮波曲线 Fig. 7 Tidal wave curve fitted by static inversion values |
|
图 8 动态改正前后潮位值对比 Fig. 8 Comparison of tidal level values before and after dynamic correction |
图 9为最小二乘方法改正潮位反演值的结果,改正后反演值数量为237个,与实测值相关性为0.93,均方根误差为13.14 cm,精度较改正前提高26.30%。对改正后的反演值进行样条插值可发现,整体振幅相比于验潮站数据要优于改正前,但在海面突变期间缺少峰值数据,插值后振幅要略低于改正前。图 9(b)为经典改正法与最小二乘改正法在风暴潮期间的海面变化率对比,图中黑色箭头方向为潮位升降方向,箭头长度为潮位变化速率大小。从图 9可以看出,最小二乘改正法的求解结果与实际值相当,并且改正效果优于经典改正法。根据平差精度参数对改正后的结果进行粗差剔除,有利于提高潮位监测精度,可用于特殊情况下的海面动态改正。
|
图 9 动态改正及海面变化率 Fig. 9 Dynamic correction and change rate of sea level |
表 1为经典改正法和最小二乘改正法在不同气象情况下的实验结果。从案例实验和表 1结果可知,对于气象情况正常的PBAY站,经典改正法和最小二乘改正法均能提高反演精度,但后者会对改正结果进行剔除,使原先反演值分辨率降低。对于HKQT站,在7 d内由于存在海面突变的情况,经典改正法改正效果不明显,而最小二乘改正法在特殊情况下改正效果良好,有利于提高潮位监测精度。
|
|
表 1 算例结果汇总 Tab. 1 Summary of example results |
经典改正法依赖于潮波函数的拟合程度,若可观测海域范围减小,则反演值数量减少,会对潮波曲线的拟合效果造成影响。最小二乘改正法中滑动窗口具有解算和粗差剔除功能,可观测海域范围减小会导致窗口中反演值数量减少,从而影响解算精度。以PBAY站年积日101~111的L1波段SNR序列为例进行分析,将方位角120°~160°作为小范围海域情况,100°~250°作为大范围海域情况,对比分析2种改正方法在不同情况下的改正效果。
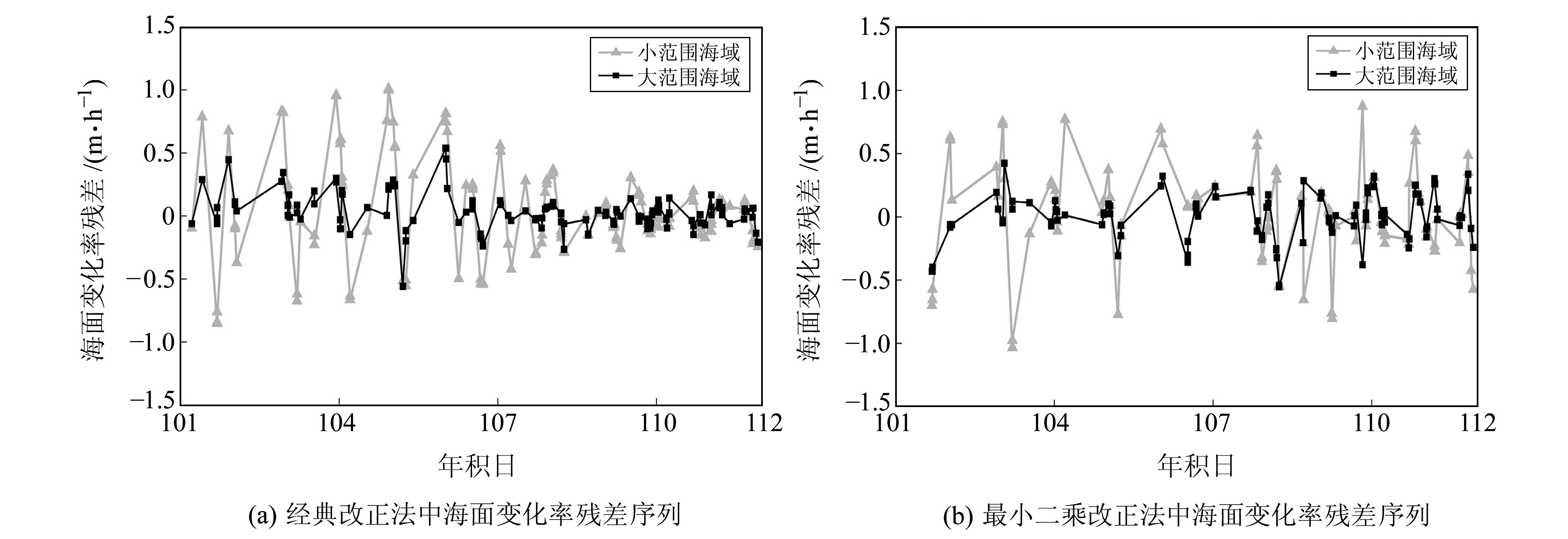
图 10为根据不同海域范围反演值拟合的潮波曲线。从图中可以看出,大范围海域潮波曲线拟合效果明显优于小范围海域,并且潮位涨落幅度越大,两者差异越明显。图 11为2种改正方法在不同范围海域下解算的海面变化率与实际海面变化率的残差序列。从图 11(a)可以看出,在大范围海域情况下,经典改正法求解的海面变化率与实际海面变化率残差在0处上下波动,表现效果优于小范围海域,并且两者差异随潮位涨落幅度增大而增大。图 11(b)中大范围海域情况下最小二乘改正效果同样优于小范围海域,但差异与潮位涨落幅度无明显相关性。

|
图 10 潮波函数 Fig. 10 Tidal wave function |
|
图 11 海面变化率残差序列 Fig. 11 Residual series of change rate of sea level |
对于最小二乘改正法,每个窗口中应至少存在2个静态假设下的反演值才能满足方程求解要求。当方位角较大时,窗口中反演值较多,观测条件增多使得解算结果更准确,且反演值个数不满足解算要求而被剔除的窗口也会减少。当方位角较小时,窗口中反演值数量减少,部分窗口中没有多余观测值而影响解算精度,同时不满足解算要求的窗口也会增多。
图 11(a)和11(b)分别为经典改正法和最小二乘改正法中不同方位角解算的海面变化率情况,灰色三角点为实际潮位变化率与小方位角情况下解算的海面变化率差值,黑色方点为实际潮位变化率与大方位角情况下解算的海面变化率差值,2条曲线均在0处上下波动。从图 11(a)可以看出,对于大方位角情况,海面变化率实际值与经典改正法解算值偏差整体较小;对于小方位角情况,由于受方位角限制,当潮位起伏较大时,潮波函数拟合效果较差而使解算的海面变化率与实际值偏差较大,随着潮位起伏变小,潮波函数拟合效果提高,解算的海面变化率与实际值偏差也随之变小。动态改正前精度为31.75 cm,小方位角时的改正精度为23.21 cm,大方位角时的改正精度为16.57 cm,2种情况下精度分别提高26.90%和47.81%,改正前后反演值数量均为143。
图 11(b)中大方位角情况下最小二乘解算的海面变化率结果整体优于小方位角情况。方位角较小时最小二乘改正后的精度为24.23 cm,方位角较大时最小二乘改正后的精度为19.32 cm,改正效果分别提高23.68%和39.15%,改正前后反演值数量由143减至120。
从结果来看,动态改正前反演精度为31.75 cm。随着可观测海域范围的减小,经典改正法的改正精度由16.57 cm下降为23.21 cm,精度降低40.07%;最小二乘改正法的改正精度由19.32 cm下降为24.23 cm,精度降低25.41%。实验结果表明,可观测海域范围对经典改正法和最小二乘改正法均具有一定影响,且经典改正法受影响更大。
3 结语基于GNSS-IR监测潮位原理,采用2种动态改正方法对静态假设下的潮位反演结果进行改正。对于气象情况正常的PBAY站,经典改正法与最小二乘改正法均能提高反演精度,但最小二乘法改正效果不及经典改正法,且改正后反演值时间分辨率降低。对于气象情况特殊的HKQT站,经典改正法改正效果不明显,最小二乘改正法能有效提高精度。可观测海域范围的大小会对2种改正方法的改正效果产生影响,当方位角较大时,反演值数量的增多有利于提高2种方法的改正效果;当方位角减小时,反演值数量也随之减少,2种方法求解海面变化率均受影响,改正效果降低。因此,对潮位反演结果进行改正时因根据测站环境和实际情况选择合适的改正方法,从而有利于提高潮位监测精度,更好地发挥GNSS网络在全球环境变化监测中的作用。
| [1] |
Larson K M, Small E E, Gutmann E D, et al. Using GPS Multipath to Measure Soil Moisture Fluctuations: Initial Results[J]. GPS Solutions, 2008, 12(3): 173-177 DOI:10.1007/s10291-007-0076-6
(  0) 0) |
| [2] |
Larson K M, Gutmann E D, Zavorotny V U, et al. Can We Measure Snow Depth with GPS Receivers?[J]. Geophysical Research Letters, 2009, 36(17)
(  0) 0) |
| [3] |
Roussel N, Ramillien G, Frappart F, et al. Sea Level Monitoring and Sea State Estimate Using a Single Geodetic Receiver[J]. Remote Sensing of Environment, 2015, 171: 261-277 DOI:10.1016/j.rse.2015.10.011
(  0) 0) |
| [4] |
Larson K M, Small E E. Estimation of Snow Depth Using L1 GPS Signal-to-Noise Ratio Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(10): 4 802-4 808 DOI:10.1109/JSTARS.2015.2508673
(  0) 0) |
| [5] |
南阳, 张双成, 张勤, 等. GNSS多径反射探测海平面变化初探[J]. 测绘科学, 2015, 40(12): 125-129 (Nan Yang, Zhang Shuangcheng, Zhang Qin, et al. Preliminary Results of Sea Level Change Monitoring with GNSS-MR[J]. Science of Surveying and Mapping, 2015, 40(12): 125-129)
(  0) 0) |
| [6] |
张双成, 南阳, 李振宇, 等. GNSS-MR技术用于潮位变化监测分析[J]. 测绘学报, 2016, 45(9): 1 042-1 049 (Zhang Shuangcheng, Nan Yang, Li Zhenyu, et al. Analysis of Tide Variation Monitored by GNSS-MR[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1 042-1 049)
(  0) 0) |
| [7] |
胡媛, 刘卫, 周悦, 等. 基于GNSS信号信噪比观测量的海平面高度变化研究[J]. 海洋预报, 2017, 34(3): 26-31 (Hu Yuan, Liu Wei, Zhou Yue, et al. Study on Sea Level Changes Based on the Observations of GPS Signal to Noise Ratio[J]. Marine Forecasts, 2017, 34(3): 26-31)
(  0) 0) |
| [8] |
刘立龙, 封海洋, 陈伟清, 等. 基于GPS信噪比反演海平面高度研究[J]. 桂林理工大学学报, 2017, 37(4): 629-634 (Liu Lilong, Feng Haiyang, Chen Weiqing, et al. Inversion of Sea Level Based on Signal-to-Noise Ratio of GPS[J]. Journal of Guilin University of Technology, 2017, 37(4): 629-634 DOI:10.3969/j.issn.1674-9057.2017.04.012)
(  0) 0) |
| [9] |
Larson K M, Ray R D, Nievinski F G, et al. The Accidental Tide Gauge: A GPS Reflection Case Study from Kachemak Bay, Alaska[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1 200-1 204 DOI:10.1109/LGRS.2012.2236075
(  0) 0) |
| [10] |
Löfgren J S, Haas R, Scherneck H G, et al. Three Months of Local Sea Level Derived from Reflected GNSS Signals[J]. Radio Science, 2011, 46(6): RS0C05
(  0) 0) |
| [11] |
Song M F, Xiao R Y, He X F, et al. Water Level Measurements Using Multi-Station and Dual-System GNSS-MR——A Case of Shuangwangcheng Reservoir[C]. China Satellite Navigation Conference, Beijing, 2019
(  0) 0) |
| [12] |
Larson K M, Löfgren J S, Haas R, et al. Coastal Sea Level Measurements Using a Single Geodetic GPS Receiver[J]. Advances in Space Research, 2013, 51(8): 1 301-1 310 DOI:10.1016/j.asr.2012.04.017
(  0) 0) |
| [13] |
Bilich A, Larson K M, Axelrad P. Observations of Signal-to-Noise Ratio(SNR) at Geodetic GPS Site CASA: Implications for Phase Multipath[J]. Proceedings of the Centre for European Geodynamics and Seismology, 2004, 23: 77-83
(  0) 0) |
| [14] |
Larson K M, Small E E, Gutmann E D, et al. Use of GPS Receivers as a Soil Moisture Network for Water Cycle Studies[J]. Geophysical Research Letters, 2008, 35(24)
(  0) 0) |
| [15] |
徐斌, 杨涛, 谭保华, 等. 基于Lomb-Scargle算法的周期信号探测的模拟研究[J]. 核电子学与探测技术, 2011, 31(6): 702-705 (Xu Bin, Yang Tao, Tan Baohua, et al. The Simulate Study of Signal Detection Based on Lomb-Scargle Algorithm[J]. Nuclear Electronics and Detection Technology, 2011, 31(6): 702-705 DOI:10.3969/j.issn.0258-0934.2011.06.026)
(  0) 0) |
| [16] |
任超, 彭家頔, 佘娣, 等. 低高度角卫星信号对提高对流层估计精度的影响分析[J]. 大地测量与地球动力学, 2011, 31(6): 124-127 (Ren Chao, Peng Jiadi, She Di, et al. Effects of Low GPS Satellite Elevation Mask Angle on Estimation of Tropospheric Delay[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 124-127)
(  0) 0) |
| [17] |
Larson K M, Ray R D, Williams S D P. A 10-Year Comparison of Water Levels Measured with a Geodetic GPS Receiver versus a Conventional Tide Gauge[J]. Journal of Atmospheric and Oceanic Technology, 2017, 34(2): 295-307 DOI:10.1175/JTECH-D-16-0101.1
(  0) 0) |
| [18] |
Peng D J, Hill E M, Li L L, et al. Application of GNSS Interferometric Reflectometry for Detecting Storm Surges[J]. GPS Solutions, 2019, 23(2): 47 DOI:10.1007/s10291-019-0838-y
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

