2. 华东交通大学土木工程国家实验教学示范中心,南昌市双港东大街808号,330013
电离层总电子含量(total electric content, TEC)是描述电离层特征的一个重要参量,对其精准预测有助于更好地认知近地空间环境。由于电离层具有时空变化特性,使得建立高精度电离层模型较为困难。为探求高精度的电离层TEC预报模型,国内外学者开展了广泛的研究并取得一些成果。文献[1-6]利用时间序列模型进行预测,在短期TEC值的预测上,时间序列模型结构简单且预测精度有所提高。文献[7-10]利用BP神经网络模型对TEC进行预测建模,与时间序列相比,BP神经网络模型的预测精度及运算速度均有显著提高。越来越多的研究表明,传统BP神经网络模型是基于梯度下降函数(gradient descent)的原理进行数据计算。在数据训练过程中,这种方法极易使模型陷入局部最小值的死循环中,从而错过真正的最优值。另一方面,BP神经网络在结构设置上为输入层-隐含层-输出层,虽然隐含层在训练过程中与输入、输出层有联系,但每一个隐含层所包含的单一神经元之间却相互独立,没有在神经元之间形成信息的反馈。这种层内信息反馈的缺乏进一步降低了网络结构的数据处理能力。
基于上述原因,为建立高精度的电离层TEC预报模型,充分考虑TEC值序列的非线性、非平稳性等特征,对传统神经网络算法进行优化,使其更适用于TEC序列的预报与应用,本文利用基于贝叶斯正则化的Elman神经网络模型对电离层TEC进行建模研究,并将得到的预报结果与实际TEC值进行对比。
1 模型算法原理 1.1 基于贝叶斯正则化的Elman神经网络Elman神经网络增加了连接隐含层的承接层,提高了模型的数据处理能力。其主要作用是用于层内或层间的反馈联结,使其能够表达输入与输出之间在时间上的延迟,可以看作是一个延时因子,因此需要用动态方程描述,而前馈神经网络仅仅只能实现非线性映射。为了解决网络结构复杂化的弊端,对梯度下降的传统训练函数进行优化,本文提出使用贝叶斯正则化方法对神经网络作优化。正则化是在神经网络的训练性能函数中加入一个“惩罚项”,使网络的权值结构得到简化,从而进一步提高网络泛化能力的方法。在一般神经网络的训练函数中,训练过程的目标是使模型输出值与实际观测值的均方误差函数达到最小,可表示为:
| $ {E_D} = \frac{1}{2}\sum\limits_{i = 1}^N {{{({\rm{TEC}}_{{\rm{obs}}}^i - {\rm{TE}}{{\rm{C}}^i})}^2}} $ | (1) |
式中,N为训练样本总数,TECobsi、TECi分别为实际值、预测值。
在正则化方法中,添加“惩罚项”后的目标函数变为:
| $ \left\{ \begin{align} & J(w)=\alpha {{E}_{W}}+\beta {{E}_{D}} \\ & {{E}_{W}}=\frac{1}{2}\sum\limits_{i}^{{{N}_{w}}}{w_{i}^{2}} \\ \end{align} \right. $ | (2) |
式中,α、β为正则化参数,EW为权值衰减项,即神经网络各个权值的平方和,wi为第i个权值。正则化参数α、β控制着其他参数(权值及阈值)的分布形式,其大小决定着神经网络的训练目标。因此,在正则化方法中,确定参数的值至关重要。本文采用贝叶斯方法确定α、β具体数值。
MacKay[11]首次提出将贝叶斯方法应用于神经网络建模过程,之后又对网络训练过程中后验概率计算问题提出基于高斯逼近方法计算Hessian矩阵。在贝叶斯规则中,通过一系列数值计算得到新的后验概率密度函数,具体推导过程可参考文献[12-13]。
设J(w)取最小值时所对应的权值(包含阈值)为wMP,将J(w)在点wMP附近利用泰勒级数展开,忽略高次项后得到:
| $ {{Z}_{J}}\approx {{(2\pi )}^{{{N}_{w}}/2}}{{(\det ({{({{\nabla }^{2}}J({{w}_{MP}}))}^{-1}}))}^{1/2}}*\exp (-J({{w}_{MP}})) $ | (3) |
式中,▽2J(wMP)=β▽2ED+▽2EW是J(w)在wMP点的Hessian矩阵。但是由于Hessian矩阵的计算量很大,故利用高斯-牛顿逼近法进行简化,得到:
| $ H={{\nabla }^{2}}J(w)\approx 2\beta {{J}^{T}}J+2\alpha {{I}_{N}} $ | (4) |
式中,J是训练误差的Jacobi矩阵。最终得到α、β的表达式为:
| $ \left\{ \begin{align} & \alpha =\gamma /(2{{E}_{W}}) \\ &338; \beta =(N-\gamma )/(2{{E}_{D}}) \\ \end{align} \right. $ | (5) |
式中,γ=Nw-2αtr(H)-1,称为有效权值个数,在网络中表示有多少参数在减少总误差函数方面起作用。
综上所述,贝叶斯正则化在Elman神经网络的具体迭代步骤为:1)确定网络结构,初始正则化参数α、β,一般设定为α=0、β=1;2)进行1个回合的误差反向传导,用最速下降法调整权值以减小函数J(w),使其达到最小;3)利用高斯牛顿逼近法求Hessian矩阵,并计算有效权值γ;4)重新计算α、β值,得到新的估计值;5)重复步骤1)~3),当误差达到0.001时,迭代终止。
1.2 模型参数及处理电离层TEC的分布主要受太阳活动、地磁活动、行星波、引力波、地磁风暴等的影响。总体来看,电离层总是随纬度、经度呈现复杂的空间变化,并且具有昼夜、季节、年积日等因素导致的非线性、非平稳性的变化特征。地磁指数Dst由地球水平磁场变化确定,有助于对磁暴机制的认识[14]。Gonzalez等[15]根据Dst指数的变化,将磁暴分为3类:强磁暴(Dst≤-100 nT)、中等磁暴(Dst≤ -50 nT)和弱磁暴(Dst ≤ -30 nT)。本文建立的电离层预测模型的输入参数包括TEC的时变化(HR)、日变化(doy)、地磁活动指数(赤道环电流指数,Dst)和TEC,其中网络训练样本选取前20 d的TEC值序列及对应年积日各参数作为网络输入层,后5 d的TEC值序列及对应年积日各参数作为输出层进行网络的训练(样本数量N=2 880)。在进行数据训练前,将TEC值序列及地磁指数Dst通过归一化函数进行处理,将值控制在(-1, 1)的范围内,方便神经网络数据训练。为了使输入参数合理化,HR、doy用式(6)进行处理:
| $ \left\{ \begin{array}{l} {\rm{DNS}} = \sin (\frac{{{\rm{2\pi doy}}}}{{{\rm{365}}}})\begin{array}{*{20}{c}} ,&{}&{{\rm{DNC}} = \cos (\frac{{{\rm{2\pi doy}}}}{{{\rm{365}}}})} \end{array}\\ {\rm{HRS}} = \sin (\frac{{{\rm{2\pi HR}}}}{{{\rm{24}}}})\begin{array}{*{20}{c}} ,&{{\rm{HRC}} = \cos (\frac{{{\rm{2\pi HR}}}}{{{\rm{24}}}})} \end{array} \end{array} \right. $ | (6) |
基于TEC、地磁活动指数,利用所建立的基于贝叶斯正则化的Elman神经网络模型对平静期与扰动期的TEC分别进行建模及预测,并分析模型预报精度。
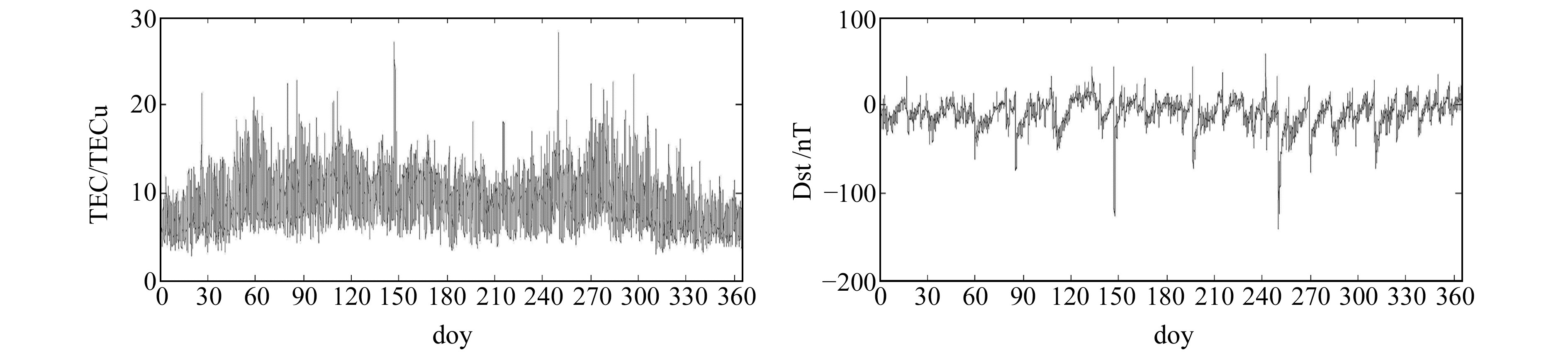
2 实验结果与讨论采用IGS中心提供的2017年(5°N, 120°E)、(40°N, 120°E)处的全年TEC值进行实验分析。图 1所示为TEC值以及地磁活动指数Dst的数据。由图可见,在地磁活动指数发生扰动时,对应的TEC值也产生明显的波动,地磁活动指数值为-125 nT时对应的TEC值接近30 TECu。本文将其分为平静期与扰动期进行对比研究,其中平静期区段为doy150~174、doy200~224等,该时期Dst为-24~34 nT,其Dst > -30 nT,较为平静;扰动期区段为doy64~88、doy175~199等,该时期Dst < -100 nT,发生强磁暴。
|
图 1 2017年电离层TEC值及地磁活动指数(Dst)值 Fig. 1 Number of ionospheric TEC and Dst index in 2017 |
为了分析本文所建立模型与对比模型预测结果的精度,采用均方根误差(RMSE)、残差(Δ)以及相关系数(ρ)进行精度评估,计算公式如下:
| $ \left\{ \begin{matrix} \text{RMSE}=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{{{(f_{i}^{p}-f_{i}^{0})}^{2}}}}\text{ } \\ \rho =\frac{\sum\limits_{i=1}^{n}{(f_{i}^{p}-\overline{f_{i}^{p}})(f_{i}^{0}-\overline{f_{i}^{0}})}}{\sqrt{\sum\limits_{i=1}^{n}{{{(f_{i}^{p}-\overline{f_{i}^{p}})}^{2}}}}\sqrt{\sum\limits_{i=1}^{n}{{{(f_{i}^{0}-\overline{f_{i}^{0}})}^{2}}}}} \\ \Delta =\left| f_{i}^{p}-f_{i}^{0} \right|\text{ } \\ \end{matrix} \right. $ | (7) |
式中,fip、fi0分别为TEC预测值、实际值,f ip、fi0分别为TEC预测值及实际值的平均值,n为所选样本的数量。
本文建立基于贝叶斯正则化的Elman神经网络模型(BR-Elman),选取基于贝叶斯正则化的BP神经网络模型(BR-BP)以及BP神经网络模型(BP)作为对比模型,并进行精度比较分析。受篇幅限制,以下仅分别展示平静期与扰动期为期5 d的预报结果及模型精度评定指标对比。
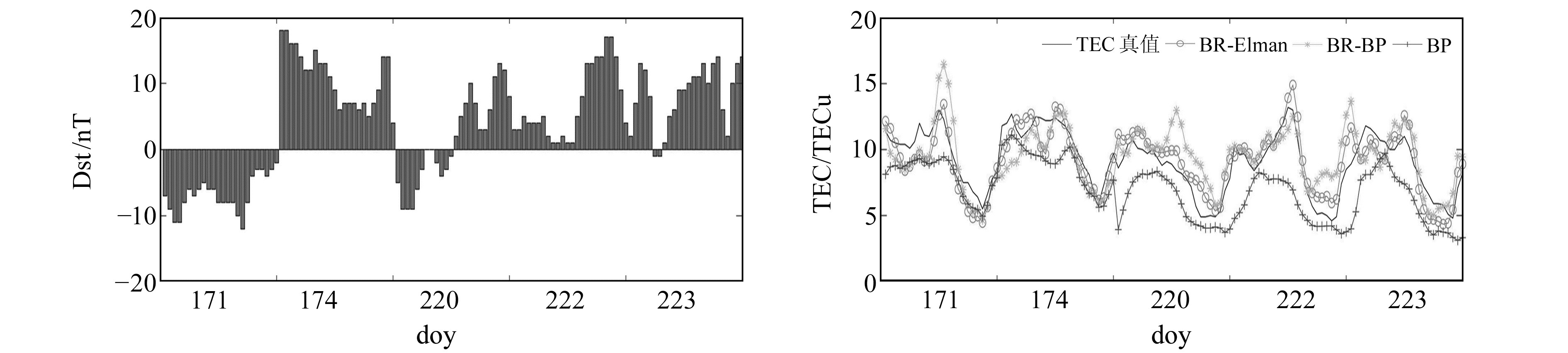
2.1 磁静日图 2为年积日171、174、220、222、223的平静期Dst指数和不同模型TEC值预报结果图。由图可见,Dst指数的数值变化维持在-10 ~15 nT,整体变化趋势较为平缓且不存在变化峰值,故可将其归为平静区段。本文所建立的BR-Elman模型在预报精度上能较好地与TEC实际值吻合。BR-BP模型较BR-Elman模型在整体TEC值预测精度上基本保持一致,但是在个别值突变处的预测上,BR-BP模型的精度有较为明显的降低。单一BP模型的预测精度是3个模型中最低的,虽然整体数值变化趋势与TEC实际值保持一致,但是预测曲线上存在较多的极端误差值,并且整体的误差至少在3~4 TECu,个别预测值的误差甚至更大。因此,在平静期TEC值的预测上,BR-Elman的整体预报精度是3个模型中最高的。
|
图 2 磁静日Dst指数及TEC预测模型结果对比 Fig. 2 The Dst index and the comparison of different prediction models in quiet period |
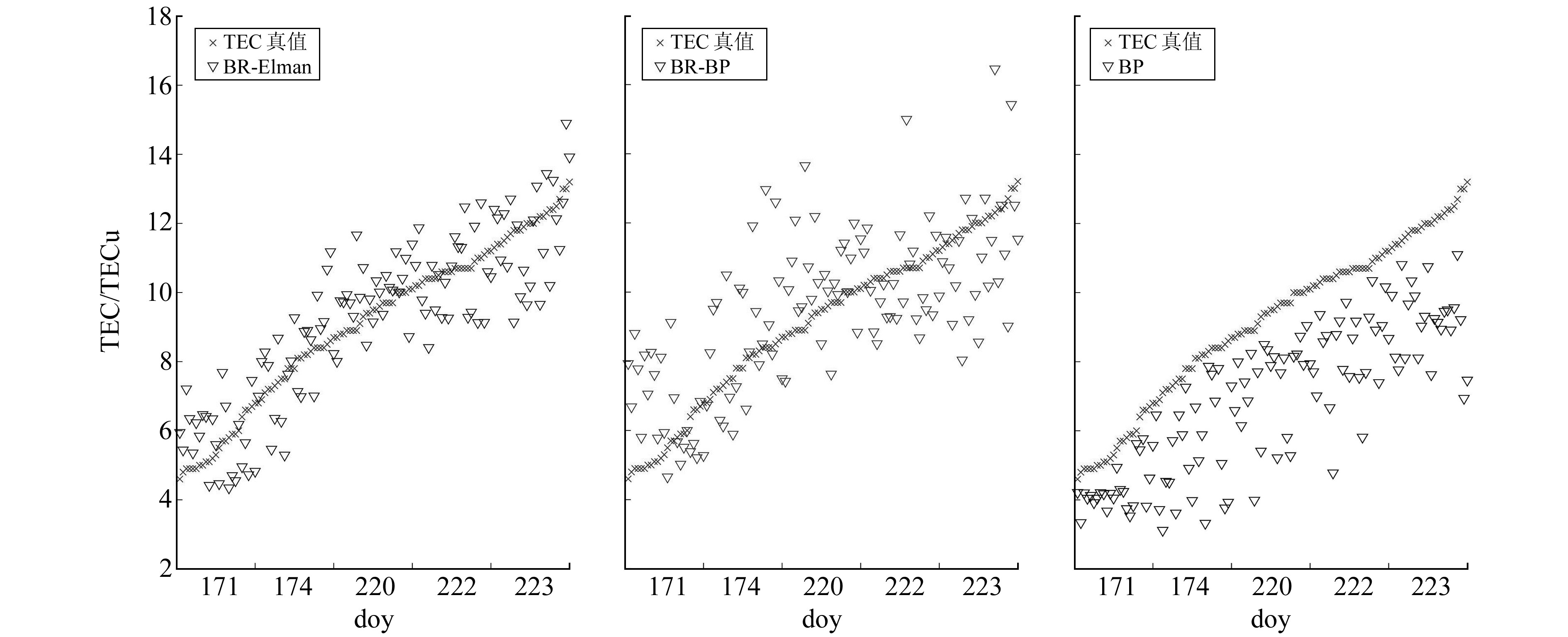
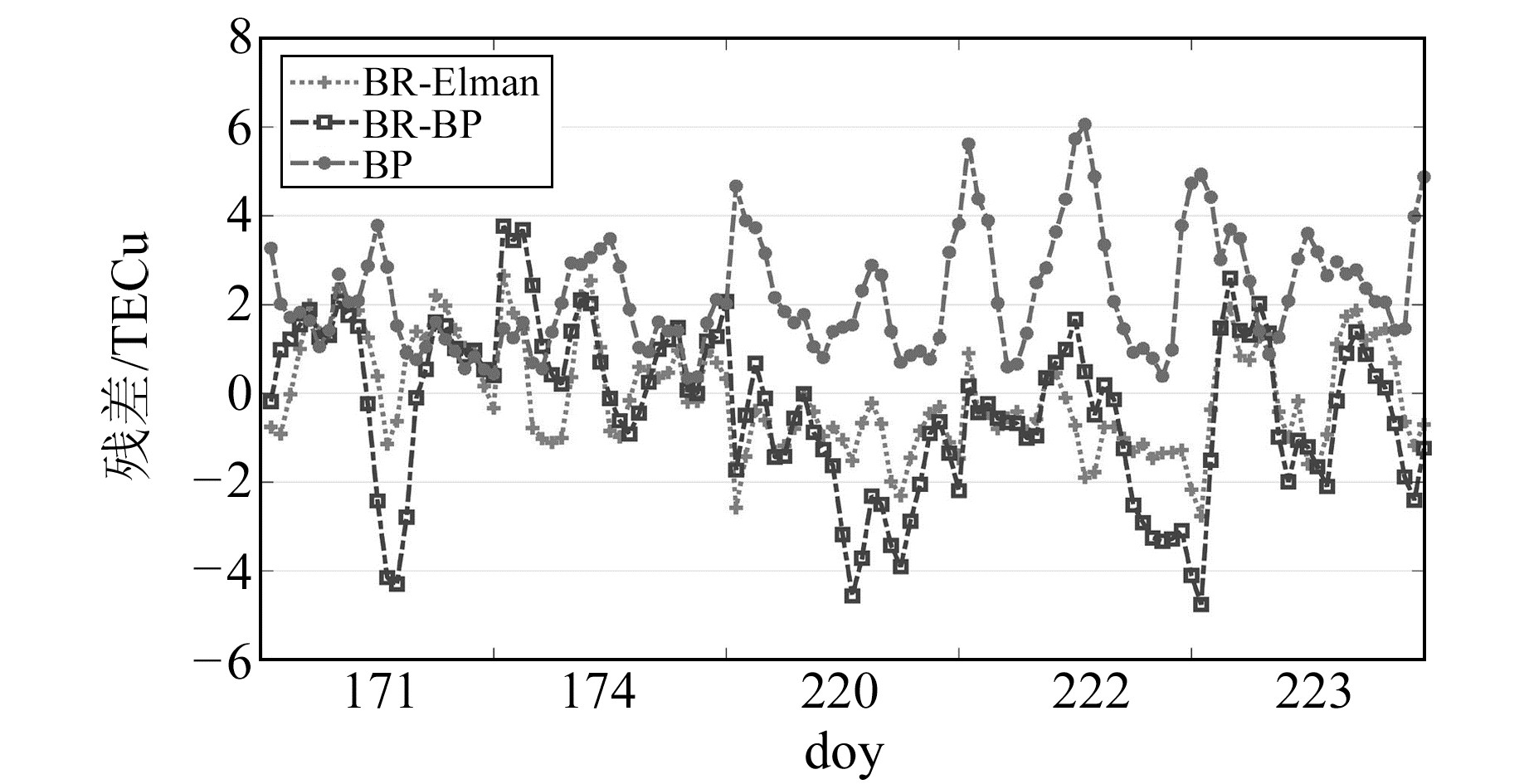
图 3、4为平静期5 d的3个模型预测值与实际值的散点图以及残差图。在散点图的绘制上,为直观分析预测值与实际值的相关性,将TEC实际值按照升序依次排列,3个模型的预测值同时按照相对应的TEC实际值同步排列。图 4的残差图即为不同模型的预测值与TEC实际值之间的差值。由图 3可以看出,BR-Elman模型的预测值分布更为紧凑,与TEC实际值的吻合度更高,并且相对均匀地分布在TEC实际值曲线的两侧。BR-BP模型与BR-Elman模型相比,少数几个预测值存在较大的误差,预测值的整体分布较为离散,大部分数值偏向TEC实际值曲线的上侧。单一BP模型的预测值均分布在TEC实际值曲线的下侧,并且是3个模型中预测值分布最为离散的。由图 4可以看出,BR-Elman模型的残差值均小于2 TECu,大部分数值维持在1 TECu左右,同时数值变化趋势相对较为平稳。BR-BP模型的残差值在2~4 TECu范围内波动,与BR-Elman模型相比,预测精度偏低。BP模型的残差值大部分在2~6 TECu的范围内,是3个模型中残差值最大也是数值趋势变化最不稳定的。因此,从散点图和残差图可以进一步看出,BR-Elman模型是3个模型中最优的。
|
图 3 磁静日5 d的3个模型预测值与实际值散点图 Fig. 3 The scatter diagram of predicted TEC and original TEC by three models for 5 days in quiet period |
|
图 4 磁静日5 d的3个模型预测值与实际值的残差 Fig. 4 The residual error of predicted TEC and original TEC by three models for 5 days in quiet period |
从表 1中可以看出,在平静期5 d的TEC值预报上,BR-Elman模型的RMSE为1.19 TECu,残差(Δ)为1.03 TECu,相关系数(ρ)最优可以达到0.93。BR-BP模型的RMSE为1.87 TECu,残差(Δ)为1.50 TECu,相关系数(ρ)最优可以达到0.79。单一BP模型的RMSE为2.51 TECu,残差(Δ)为2.22 TECu,相关系数(ρ)最优可以达到0.84。从以上具体的数值指标可以看出,在平静期TEC值的预报精度上,BR-Elman模型在均方根误差、残差及相关系数3个指标上均优于其他两个模型。
|
|
表 1 磁静日3个模型在不同评定指标下的精度对比 Tab. 1 The comparison of different evaluation indicators by three models in quiet period |
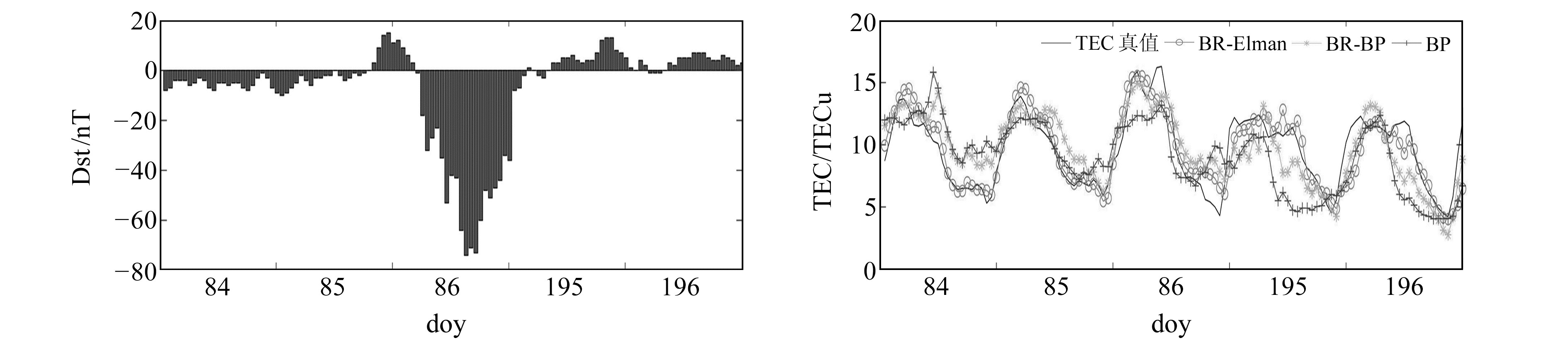
图 5为年积日84、85、86、195、196的扰动期Dst指数以及3个模型预测值与实际值的对比。由图可见,Dst指数数值在-80 ~20 nT之间变化,与平静期相比,扰动期的Dst指数有明显的波动趋势并且正负峰值相差较大。在扰动期下,BR-Elman模型预测值与TEC实际值吻合最佳,未出现预测极端值。相比其他2个模型,BR-BP模型在整体预报精度上与BR-Elman模型较为接近,但是在每日TEC数值连续变化处的峰值预报上精度较低,并且部分预测值与实际值的误差较大,吻合度低于BR-Elman模型。单一BP模型是3个模型中预报精度最低的,其整体误差均大于其他2个模型。
|
图 5 磁暴日Dst指数及3个模型预测值与实际值的对比 Fig. 5 The Dst index and the comparison of prediction values of three models in disturbed period |
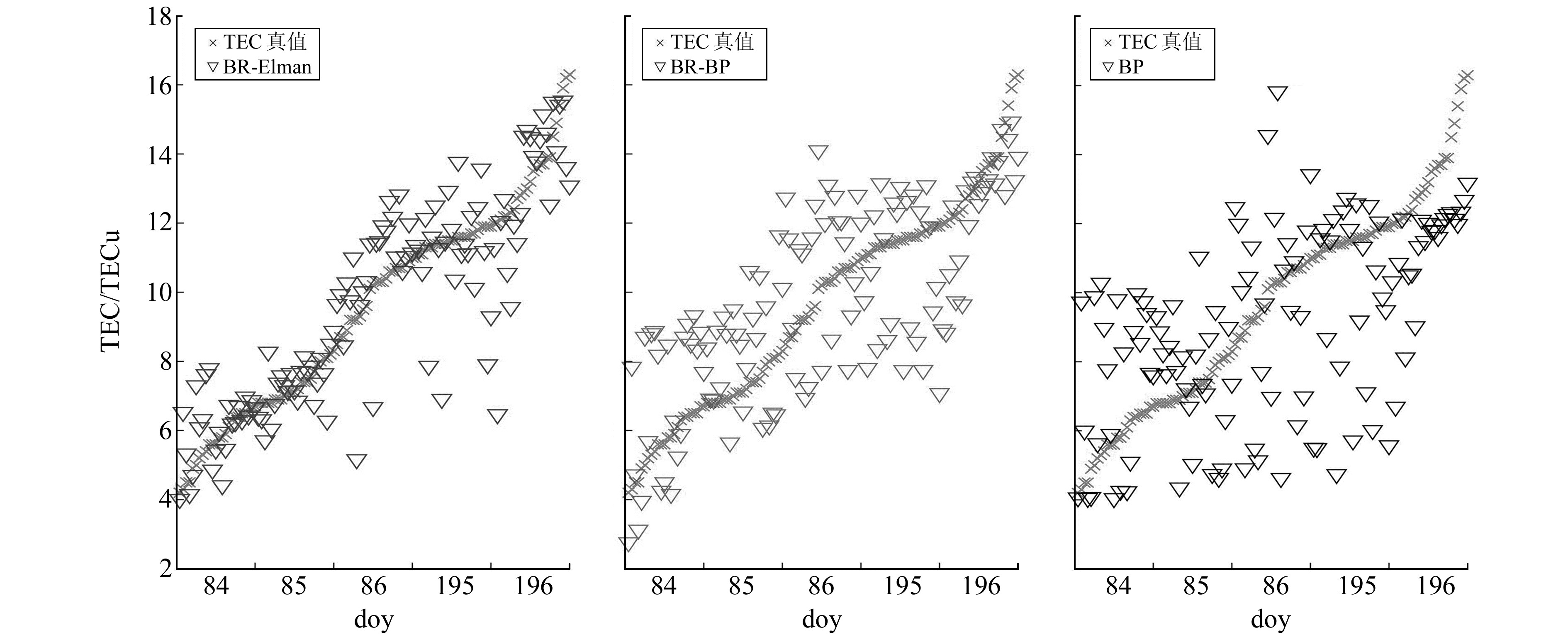
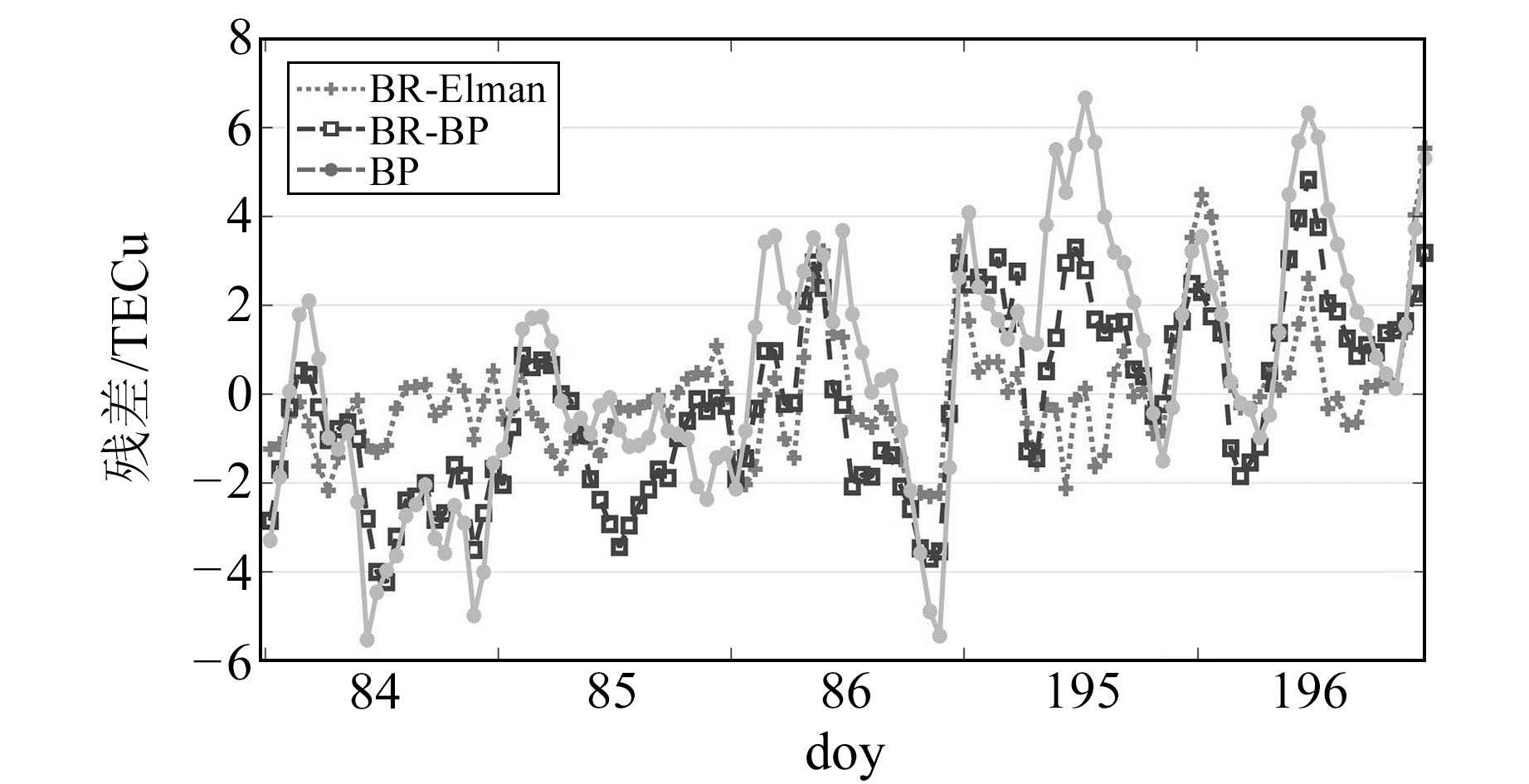
图 6、7为扰动期5 d的3个模型预测值与实际值的散点图以及残差图。由图 6可见,BR-Elman模型的预测值大部分紧凑地分布在TEC实际值曲线的两侧,吻合度为3个模型中最高的;BR-BP模型的预测值偏离TEC实际值曲线更大,分布范围更广,精度较低;单一BP模型的预测值大部分集中在TEC实际值曲线的下侧,存在较多的极大误差值,是3个模型中最为离散的。由图 7可见,BR-Elman模型的预测值与实际值的残差值基本上小于等于2 TECu,并且残差变化较为平稳;BR-BP模型的预测残差值在2~4 TECu范围内变化,误差较BR-Elman模型有所降低;单一BP模型的预测残差值在2~6 TECu范围内变化,并且大于等于4 TECu的残差值数量占比较大,是3个模型中残差值最大的。
|
图 6 磁暴日5 d的3个模型预测值与实际值散点图 Fig. 6 The scatter diagram of predicted TEC and original TEC by three models for 5 days in disturbed period |
|
图 7 磁暴日5 d的3个模型预测值与实际值的残差 Fig. 7 The residual error of predicted TEC and original TEC by three models for 5 days in disturbed period |
表 2为扰动期3个模型5 d的预报效果在均方根误差(RMSE)、残差(Δ)、相关系数(ρ)等评定指标下的具体数值对比。由表可见,在扰动期5 d的TEC值预报上,BR-Elman模型的RMSE为1.34 TECu,残差(Δ)为1.01 TECu,相关系数(ρ)最优达到0.91;BR-BP模型的RMSE为2.03 TECu,残差(Δ)为1.73 TECu,相关系数(ρ)最优达到0.87;单一BP模型的RMSE为2.66 TECu,残差(Δ)为2.25 TECu,相关系数(ρ)最优达到0.75。从以上3个指标的对比可以看出,在扰动期的TEC值预测上,BR-Elman模型的预测精度为3个模型中最高的,3项指标均优于其他2个模型。
|
|
表 2 磁暴日3个模型在不同评定指标下的精度对比 Tab. 2 The comparison of different evaluation indicators by three models in disturbed period |
为了更好地验证本文提出的模型在不同纬度预测值的可靠性,利用IGS中心提供的2017年5°N,120°E处的TEC值进行建模预报,将得到的预测TEC值与欧洲定轨中心(CODE)发布的相同位置及时段的TEC值进行对比分析。表 3为模型预测值与CODE中心发布的实际值在磁静日与磁暴日下不同评定指标的精度对比,图 8为模型预测值与CODE中心发布的实际值在磁静日与磁暴日的残差图。可以看出,本文提出的模型在低纬度得到的预测值与CODE中心发布的TEC实际值相比,磁静日时段的RMSE平均为1.57 TECu、残差平均为1.23 TECu,磁暴日时段的RMSE平均为3.09 TECu、残差为2.66 TECu,磁静日的整体预报精度较磁暴日更优,符合前文在中纬度地区预报的精度趋势。对比分析可知,本文所提出的BR-Elman模型可以有效地对中低纬度地区的TEC值进行预报,并且预测值精度较高。
|
|
表 3 5°N,120°E处磁静日与磁暴日的预测值与CODE实际值的评定指标对比 Tab. 3 The evaluation indicators comparison of predicted TEC and TEC from CODE at 5°N, 120°E |
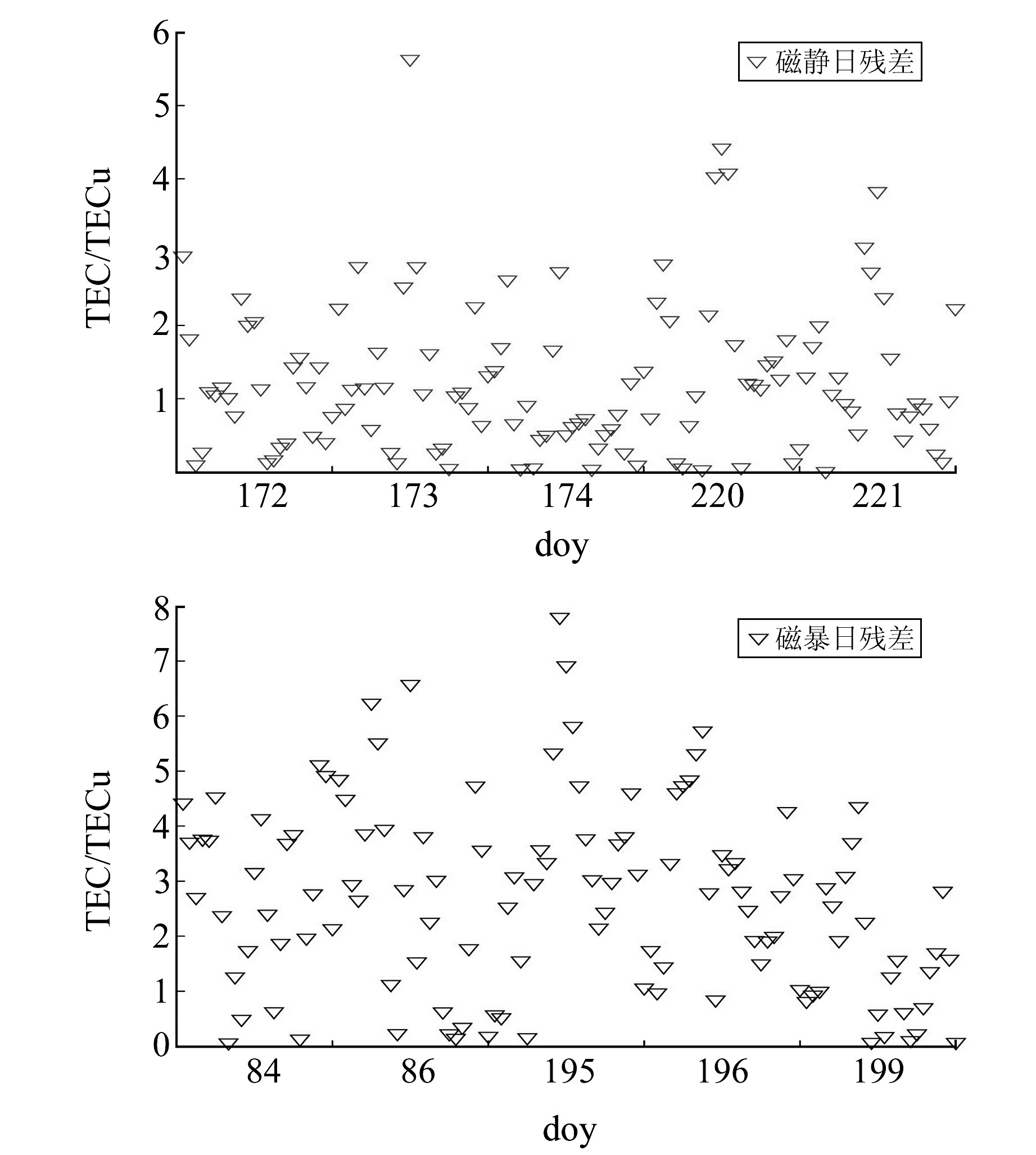
|
图 8 5°N,120°E处磁静日与磁暴日的预测值与CODE中心实际值的残差 Fig. 8 The residual error of predicted TEC and TEC from CODE at 5°N, 120°N in quiet and disturbed period |
利用贝叶斯正则化的Elman神经网络对电离层TEC进行预测,该模型利用TEC、Dst、doy等参数观测数据作为输入。实验结果表明,本文建立的贝叶斯正则化的Elman和BP神经网络模型均能有效预测电离TEC,Elman神经网络比传统BP神经网络更加精确,在保证平静电离层预报精度的同时,提高了扰动电离层的预报精度。贝叶斯正则化的Elman神经网络是一种较好的预测电离层TEC的方法,其对电离层TEC的预报能力在平静期和扰动期均优于其他2个模型。然而,由于本文进行连续5 d的TEC预报,在实际预报中存在个别时段预测结果精度下降的问题,有待进一步提高预报模型的精度。
| [1] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报:信息科学版, 2011, 36(3): 267-270 (Chen Peng, Yao Yibin, Wu Han. TEC Prediction of Ionosphere Based on Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 267-270)
(  0) 0) |
| [2] |
盛峥. 电离层电子总含量不同时间尺度的预报模型研究[J]. 物理学报, 2012, 61(21): 562-568 (Sheng Zheng. Research on Different Time-Scale Prediction Models for the Total Electron Content[J]. Acta Physica Sinica, 2012, 61(21): 562-568)
(  0) 0) |
| [3] |
张小红, 任晓东, 吴风波, 等. 自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报, 2014, 43(2): 118-124 (Zhang Xiaohong, Ren Xiaodong, Wu Fengbo, et al. Short-Term TEC Prediction of Ionosphere Based on ARIMA Model[J]. Acta Deodaetica et Cartographica Sinica, 2014, 43(2): 118-124)
(  0) 0) |
| [4] |
李志刚, 程宗颐, 冯初刚, 等. 电离层预报模型研究[J]. 地球物理学报, 2007, 50(2): 327-337 (Li Zhigang, Cheng Zongyi, Feng Chugang, et al. A Study of Prediction Models for Ionosphere[J]. Chinese Journal of Geophysics, 2007, 50(2): 327-337 DOI:10.3321/j.issn:0001-5733.2007.02.001)
(  0) 0) |
| [5] |
张小红, 任晓东, 吴风波, 等. 震前电离层TEC异常探测新方法[J]. 地球物理学报, 2013, 56(2): 441-449 (Zhang Xiaohong, Ren Xiaodong, Wu Fengbo, et al. A New Method for Detection of Pre-Earthquake Ionospheric Anomalies[J]. Chinese Journal of Geophysics, 2013, 56(2): 441-449)
(  0) 0) |
| [6] |
安家春, 宁新国, 王泽民, 等. 利用球冠谐函数和时间序列分析预报南极地区电离层[J]. 武汉大学学报:信息科学版, 2015, 40(5): 677-681 (An Jiachun, Ning Xinguo, Wang Zemin, et al. Antarctic Ionospheric Prediction Based on Spherical Cap Harmonic Analysis and Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 677-681)
(  0) 0) |
| [7] |
陈春, 吴振森, 孙树计, 等. 集合卡尔曼滤波在电离层短期预报中的应用[J]. 空间科学学报, 2010, 30(2): 148-153 (Chen Chun, Wu Zhensen, Sun Shuji, et al. Application of the Ensemble Kalman Filter in Short-Term Ionospheric Forecast[J]. Chinese Journal of Space Science, 2010, 30(2): 148-153)
(  0) 0) |
| [8] |
翁利斌, 方涵先, 缪子青, 等. 利用人工神经网络提前1 h预报电离层TEC[J]. 空间科学学报, 2012, 32(2): 204-208 (Weng Libin, Fang Hanxian, Miao Ziqing, et al. Forecasting of Ionospheric TEC One Hour in Advance by Artificial Neural Network[J]. Chinese Journal of Space Science, 2012, 32(2): 204-208)
(  0) 0) |
| [9] |
李淑慧, 彭军还, 徐伟超, 等. 利用神经网络预报短期电离层TEC变化[J]. 测绘科学, 2013, 38(1): 8-9 (Li Shuhui, Peng Junhuan, Xu Weichao, et al. Short-Term Ionospheric TEC Change Prediction by Neural Network[J]. Science of Surveying and Mapping, 2013, 38(1): 8-9)
(  0) 0) |
| [10] |
陆建华, 王斌, 胡伍生. 利用BP神经网络改进电离层短期预报模型[J]. 测绘科学技术学报, 2017, 34(1): 1-4 (Lu Jianhua, Wang Bin, Hu Wusheng. Improved Prediction Models of Ionospheric TEC by BP Neural Network[J]. Journal of Geomatics Science and Technology, 2017, 34(1): 1-4)
(  0) 0) |
| [11] |
MacKay D J C. A Practical Bayesian Framework for Backpropagation Networks[J]. Neural Computation, 1992, 4(3): 448-472
(  0) 0) |
| [12] |
杨海深, 傅红卓. 基于贝叶斯正则化BP神经网络的股票指数预测[J]. 科学技术与工程, 2009, 9(12): 3 306-3 310 (Yang Haishen, Fu Hongzhuo. Stock Index Forecast Based on Bayesian Regularization BP Neural Network[J]. Science Technology and Engineering, 2009, 9(12): 3 306-3 310)
(  0) 0) |
| [13] |
祝树金, 赖明勇. 基于贝叶斯正则化的TDBPNN模型在中国外贸预报中的应用及评估[J]. 中国管理科学, 2005(1): 2-9 (Zhu Shujin, Lai Mingyong. An Application of the TDBPNN Model Based on Bayes' Regularization to Forecasting China's Foreign Trade and Evaluation[J]. Chinese Journal of Management Science, 2005(1): 2-9)
(  0) 0) |
| [14] |
徐文耀. 地磁活动指数的过去、现在和未来[J]. 地球物理学进展, 2009, 24(3): 830-841 (Xu Wenyao. Yesterday, Today and Tomorrow of Geomagnetic Indices[J]. Progress in Geophys, 2009, 24(3): 830-841 DOI:10.3969/j.issn.1004-2903.2009.03.002)
(  0) 0) |
| [15] |
Gonzalez W D, Joselyn J A, Kamide Y, et al. What is a Geomagnetic Storm?[J]. Journal of Geophysical Research, 1994, 99(A4): 5771-5792 DOI:10.1029/93JA02867
(  0) 0) |
2. National Experimental Teaching Demonstration Center of Civil Engineering, East China Jiaotong University, 808 East-Shuanggang Street, Nanchang 330013, China
 2020, Vol. 40
2020, Vol. 40

