2. 中国科学院精密测量科学与技术创新研究院,武汉市徐东大街340号,430077;
3. 大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
海潮负荷对重力测量影响很大[1-2],尤其是在沿海与岛屿区域。因此,在我国沿海和岛屿区域构建高精度的重力海潮负荷改正模型对提高观测点的重力测量精度具有重要意义。很多学者对海潮负荷进行了相关研究[3-7],其计算理论已日趋成熟。海潮负荷与负荷格林函数及海潮模型有关[8],负荷格林函数可由地球模型确定,海潮模型可通过计算点附近的验潮站观测资料进行约束[9-11]。海陆边界对沿海地区的海潮负荷计算影响较大[12-13],但目前海潮负荷计算软件中采用的海陆边界资料精度较低。由航天飞机雷达地形测绘任务(shuttle radar topography mission, SRTM)获得的数字高程模型可提供较高精度的海陆边界资料,能有效提高沿海地区海潮负荷的计算精度。本文以马祖岛为例,利用NAO99b全球海潮模型、NAO99Jb区域海潮模型、SRTM地形模型和PREM地球模型,采用积分格林函数方法构建该岛的重力海潮负荷改正模型,并采用绝对重力测量数据对该模型的可靠性进行分析。
1 海潮负荷计算理论重力海潮负荷的计算公式可表示为[3]:
| $ \Delta g\left( \theta ,\varphi ,t \right)={{R}^{2}}\rho \int_{0}^{2\pi }{\int_{0}^{\pi }{H\left( \psi ,A,t \right)G\left( \psi \right)}}\sin \psi d\psi dA $ | (1) |
式中,Δg为重力海潮负荷;θ、φ和t分别为计算点的余纬、经度和计算时刻;R为地球半径,通常取6 371 km;ρ为海水密度,通常取1.025 kg/m3;ψ和A分别为计算点到负荷点的球面角距离和方位角;H为海潮的瞬时潮高,由海潮模型确定;G为格林函数,由所采用的地球模型确定。当采用积分格林函数方法时,式(1)可表示为:
| $ \Delta g\left( {\theta ,\phi ,t} \right) = \rho \sum\nolimits_{i = 1}^N {{F_i}} \int_0^{2\pi } H \left( {{\psi _i},A,t} \right){\rm{d}}A = {R^2}\rho \sum\nolimits_{i = 1}^N {{F_i}} \sum\nolimits_{j = 1}^M {{H_{ij}}} \Delta A $ | (2) |
式中,
| $ {F_i} = {R^2}\int_{{\psi _i} - \delta {\rm{/}}2}^{{\psi _i} + \delta {\rm{/}}2} {G\left( \psi \right)} \sin \psi {\rm{d}}\psi $ | (3) |
称为积分格林函数[3],其中δ和ΔA分别为角距和方位角的网格大小,N和M的乘积为网格总数。
当采用近海模型时,需用近海模型替换全球模型的相应空间区域,因此式(1)可转化为:
| $ \Delta g\left( \theta ,\phi ,t \right)={{R}^{2}}\rho \iint_{{{S}_{G-L}}}{H\left( \psi ,A,t \right)G\left( \psi \right)\text{d}S}+{{R}^{2}}\rho \iint_{{{S}_{L}}}{H\left( \psi ,A,t \right)G\left( \psi \right)\text{d}S} $ | (4) |
式中,SL和SG-L分别为近海区域及去除近海区域的全球区域。
当采用计算点附近的验潮站观测资料时,式(4)可表示为:
| $ \begin{align} & \Delta g\left( \theta ,\phi ,t \right)={{R}^{2}}\rho \iint_{{{S}_{G-L}}}{H\left( \psi ,A,t \right)G\left( \psi \right)\text{d}S} \\ & +{{R}^{2}}\rho \iint_{{{S}_{L}}-I}{H\left( \psi ,A,t \right)G\left( \psi \right)\text{d}S}+C\times h(t) \\ \end{align} $ | (5) |
式中,I为积分区域,即以计算点为中心、半径为0.02°(约为2 km)的球冠区域。
| $ C={{R}^{2}}\rho \int_{0}^{2\pi }{\int_{0}^{{{0.02}^{{}^\circ }}}{\vartheta \left( \psi ,A \right)G\left( \psi \right)}}\sin \psi \text{d}\psi \text{d}A $ | (6) |
本文认为海潮的潮高值相等且与验潮站观测的潮高h(t)一致。式(6)中,ϑ为海洋函数,当积分面元(负荷点)在海洋时,函数值为1,在陆地时为0,该函数由海陆边界确定。在上述公式中,海洋函数隐含在海潮的潮高中,即海洋函数的空间分辨率与海潮模型的空间分辨率一致。因此,高分辨率的海陆边界会直接影响实际计算中潮高的数值,进而对最终的负荷结果产生影响。
2 数据来源 2.1 海潮模型本文采用的海潮模型为NAO99b全球模型及近海部分NAO99Jb区域模型[14],空间分辨率分别为0.5°和5′。该模型中短周期潮波可通过将5 a的T/P卫星测高数据同化到水动力学模型中计算获得,而长周期潮波仅为水动力学模型结果。NAO99Jb区域模型除了采用测高数据,还使用了219个验潮站的资料。该模型包含23个潮波,其中7个长周期潮波(Sa、Ssa、Msm、Mm、Msf、Mf、Mtm)、7个周日潮波(Q1、O1、M1、P1、K1、J1和OO1)和9个半日潮波(2N2、μ2、N2、ν2、M2、L2、T2、S2和K2),近海模型不包含长周期潮波。
2.2 数字高程模型本文采用的数字高程模型SRTM版本为Ⅴ4.1,空间分辨率约为90 m(相当于3′)。该模型提供的高程为正高,因此获得的海陆边界高程为正的地方表示陆地,其他地方为海洋。同时,在计算海潮负荷时,计算点的高程也取自该模型。
2.3 实测资料本文所用实测资料来源于文献[2]。2005-01-26在马祖岛用FG5型绝对重力仪进行连续的绝对重力测量和验潮观测,绝对重力测量每半小时1组,1组约100次落体,每组获得1个平均的重力值,共连续观测24 h左右(2005-01-26 01:08:08~2005-01-27 00:38:07),获得由48个重力值组成的采样率为半小时的时间序列。在此过程中,依据规范进行数据处理并扣除固体潮、气压、极移等影响,认为最终的残差主要包含海潮负荷的影响。同时,相应地选取马祖岛验潮站同时间段测量资料的平均值。
3 数值计算与讨论使用通过PREM地球模型获得的负荷Love数计算积分格林函数。采用NAO99b模型,在积分格林函数及SRTM地形数据基础上分析海潮负荷对沿海地区和岛屿重力测量的影响。本文以马祖岛为例,给出具体的计算方法和数值结果,并用实测的绝对重力资料对模型的可靠性进行验证。
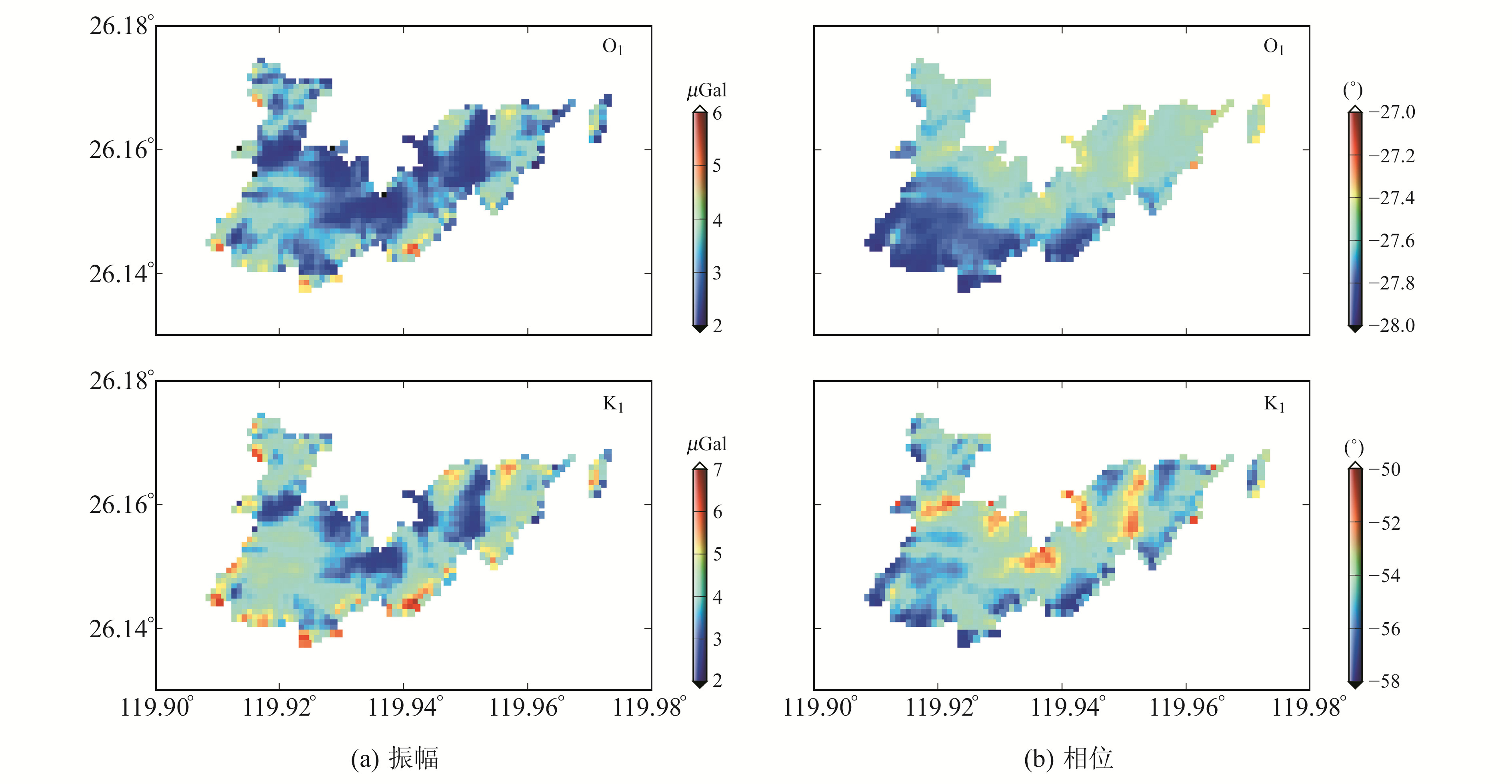
3.1 模型计算将马祖岛划分成大小为3′的网格,网格点上的高程值由SRTM数据确定。沿海台站的重力海潮负荷主要来源于随海潮涨落的海水质量引力的垂向分量,而高程的差异会直接影响海水质量对观测点引力线与垂线的夹角,从而影响重力值。因此,高程的准确性对沿海台站海潮负荷重力的计算尤为重要。图 1、2分别为振幅相对较大的2个周日潮波(O1、K1)和2个半日潮波(M2、S2)的振幅和相位结果。沿海或岛屿的验潮站分布比较零散,许多地区缺少验潮数据。因此,图 1、2中所示结果未考虑站点附近的真实潮高,仅采用了海潮模型计算的结果。由于马祖岛范围较小,为更好地显示负荷大小在全岛的分布差异,本文采用不同的色标来表示负荷大小,即每个网格采用相同的颜色。
|
图 1 马祖岛周日波重力海潮负荷结果 Fig. 1 Amplitude and phase of OTL gravity for diurnal tides at Matzu island |
|
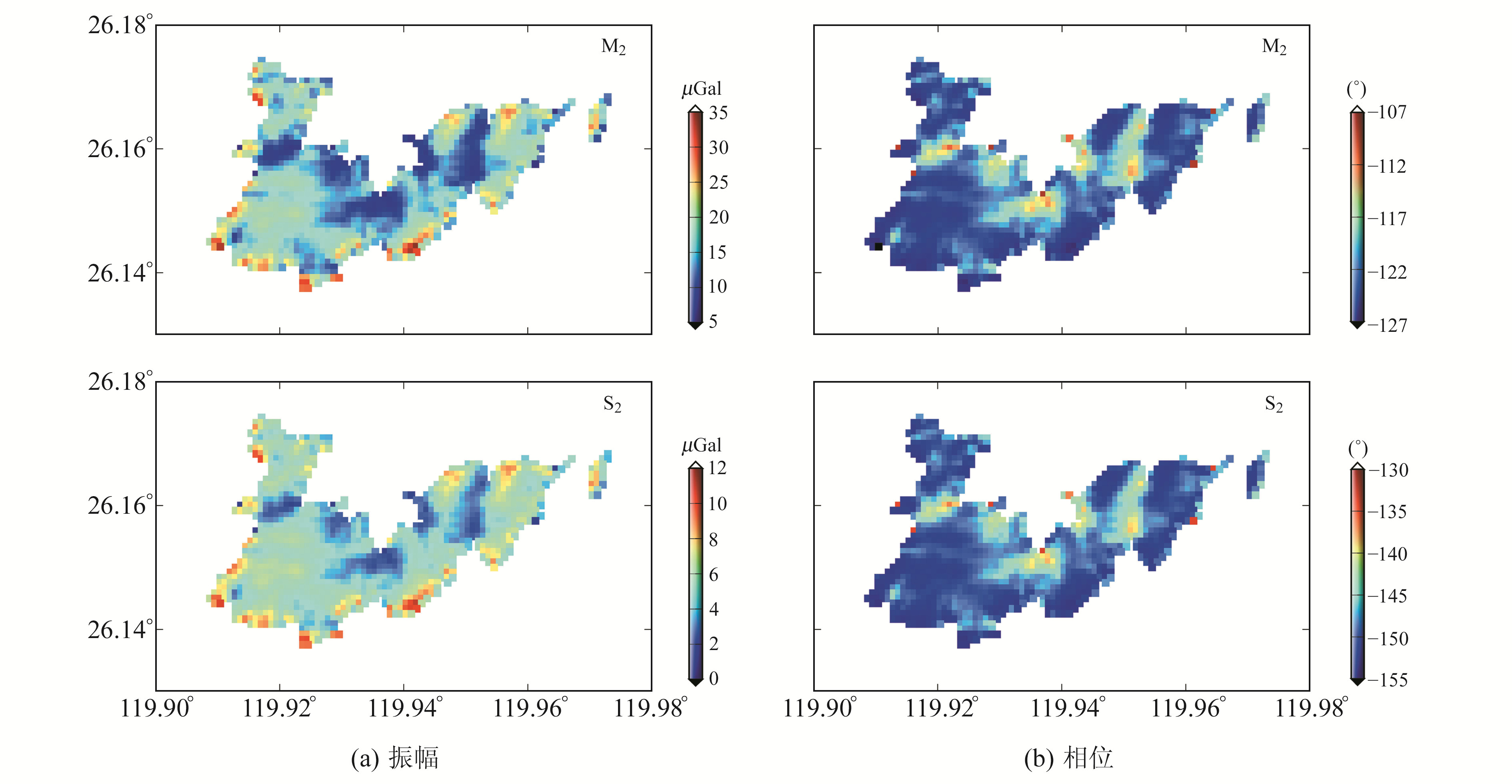
图 2 马祖岛半日波重力海潮负荷结果 Fig. 2 Amplitude and phase of OTL gravity for semi-diurnal tides at Matzu island |
从图 1、2可以看出,马祖岛重力海潮负荷的振幅具有较大的水平梯度,这也是沿海地区的典型特征。从总体上看,半日波的振幅要比周日波大,岛内腹地振幅最小,振幅最大值出现在海陆边界附近。因此,高精度的海陆边界在计算沿海地区的重力海潮负荷时尤为重要。在图 2中的海陆边界处,相邻的网格点上的重力海潮负荷相差非常大,故在沿海地区实施重力测量时,需要准确记录仪器所在位置的三维坐标。
图 1、2中右半部分为相应的相位分布,相位的变化较小,O1波相位相差在1°以内。这是因为海潮的波长比较长,所以在很小的范围内海潮应该是同相的。从图中还可以看出,相位差异较大的地区,其海潮负荷的振幅较小。对于海潮负荷振幅较大的地区,附近海域的负荷贡献较大,远洋区的负荷贡献相对非常小;而振幅较小的地区,附近海域的负荷贡献相对较小,远洋区的负荷贡献相对较大,因此在相位上会存在很大差异。
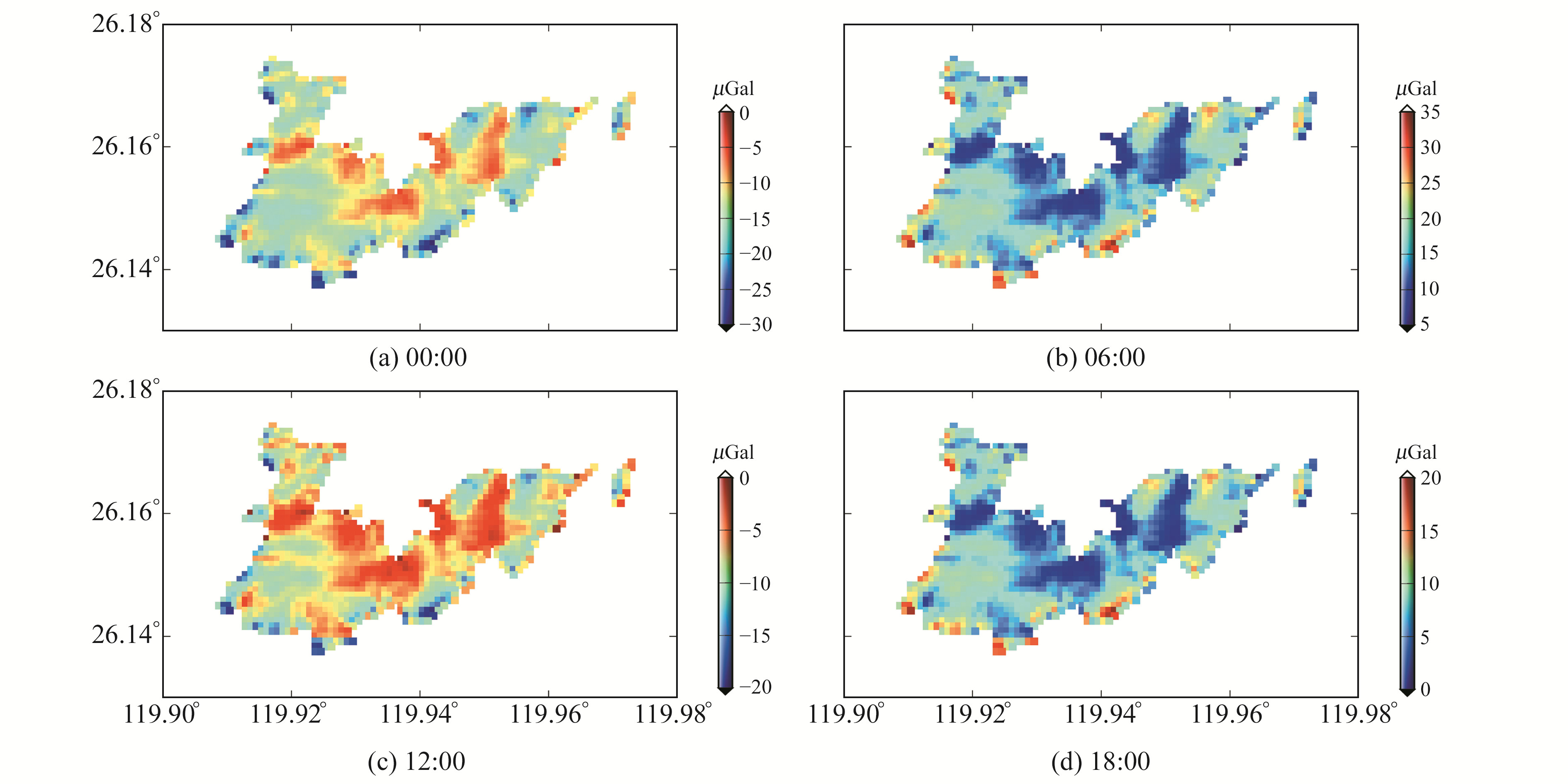
从图 3可以看出,马祖岛的重力海潮负荷变化的最大幅度为-30~35 μGal,变化幅度大小的分布与图 1、2中振幅大小的分布具有很好的一致性。
|
图 3 马祖岛重力海潮负荷(2017-01-01) Fig. 3 OTL gravity at Matzu island on Jan 1, 2017 |
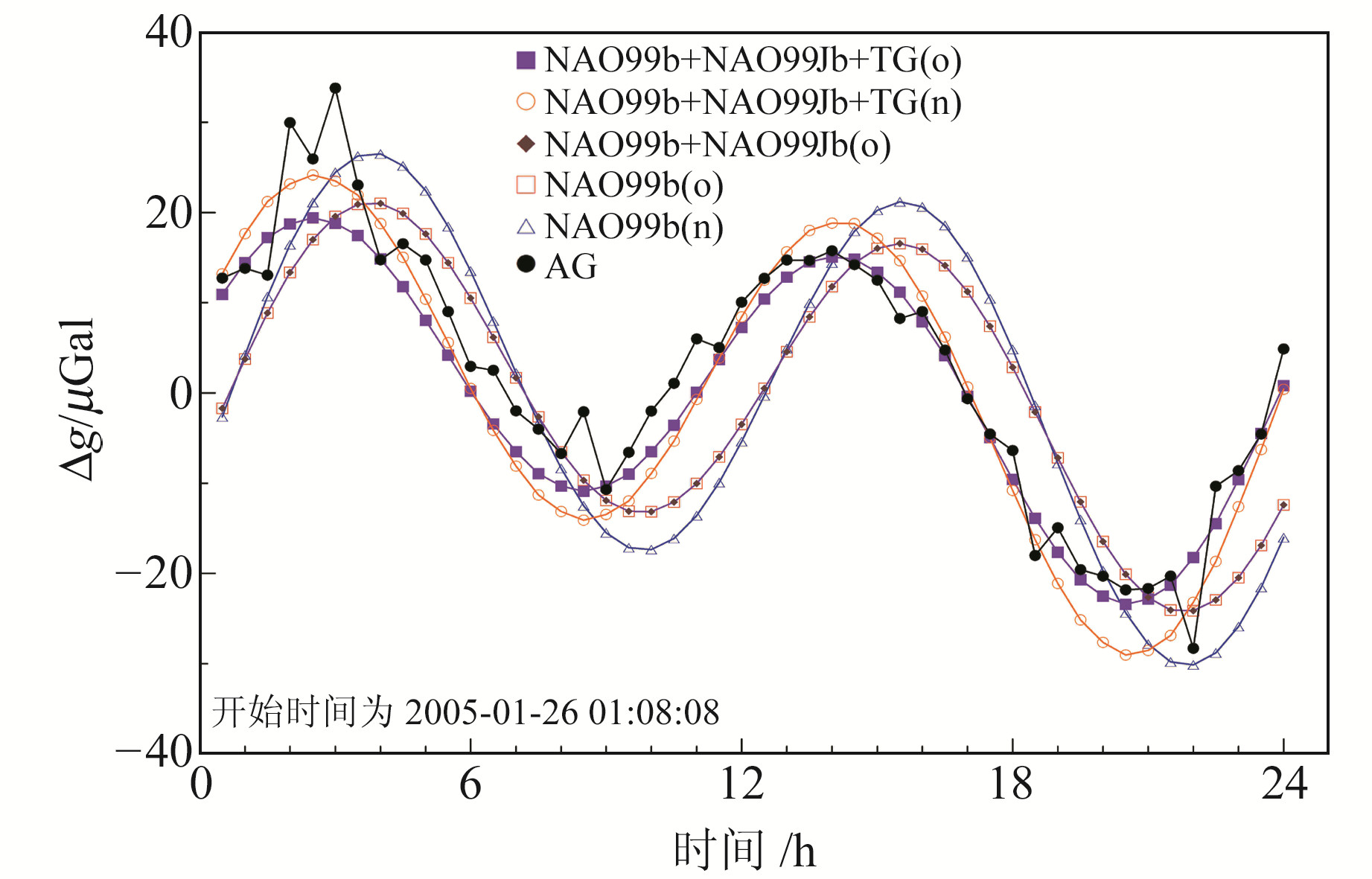
构建海潮负荷模型的目的是对观测资料进行海潮负荷改正,为评估模型的准确性,需要对实际观测资料的改正效果进行评价。运用上述重力海潮负荷模型构建与绝对重力测量时间段相同的重力海潮负荷时间序列,并与实际观测序列进行对比,结果见图 4。
|
TG表示采用验潮站观测资料; o表示采用旧版本SRTM资料; n表示采用新版本SRTM资料; AG表示实际观测资料 图 4 马祖台重力海潮负荷与观测值比较 Fig. 4 Comparison between modeled OTL gravity and AG observation at Matzu station |
比较发现,考虑近海潮汐模型及验潮站观测资料构建的重力海潮负荷序列与实际的观测值一致。考虑近海潮汐模型NAO99Jb对结果几乎无影响,表明NAO99Jb区域模型在马祖岛附近对NAO99b全球模型的改善作用并不明显。因此,在构建该地区的负荷模型时,可以不采用NAO99Jb区域模型而仅采用NAO99b全球模型。从图 4可以发现,不考虑验潮资料对计算结果的影响非常大,变化幅度比采用验潮站资料结果稍大,且相位偏移特别明显,这是因为真实潮高与由模型获得的潮高之间存在差异。在近海地区,重力海潮负荷的贡献主要来自于沿海海潮的直接引力,因此重力海潮负荷主要受近区的海潮变化特征所控制。同时,海潮的波长比较长,尽管近区的地理环境复杂,但是不足以明显改变海潮的振幅,而主要是改变海潮的相位。地理环境的影响会改变海水的运动特征,从而产生一些非线性的浅水潮波,但这些浅水潮波的频率与海潮的主要潮波的频率有所不同。
为评估未采用验潮资料时构建的海潮负荷模型的改正效果,分别计算重力观测时间序列的均方差以及进行海潮负荷改正后的序列的均方差。均方差可反映时间序列的波动幅度,即海潮负荷信号的强度。重力观测序列的均方差为14.5 μGal,采用验潮站资料的模型改正后的均方差为4.0 μGal,未采用验潮站资料的模型改正后的均方差为9.0 μGal,改正效果明显变差,但在缺乏验潮资料时,该模型仍具有一定的改正效果。
比较最新版本(Ⅴ4.1)和旧版本(Ⅴ2.1)的SRTM数据计算结果发现,两者之间存在明显差异,新版本结果的振幅稍大,但相位保持一致。新版本结果的均方差为11.0 μGal,改正效果变差。用新、旧版本的SRTM数据计算的式(5)中系数C分别为6.13 μGal/m和4.14 μGal/m,该差异可能与测点下方的基础设施建设和部分海域被填埋有关。平均海平面的变化、海浪的冲刷、港口的建设等都会引起海陆边界发生明显变化,因此在计算海潮负荷时,除了验潮站观测与重力观测需同步外,海陆边界资料也必须是同步的。在对以前的观测数据进行处理时,需要采用以前的边界资料,否则会因测区的海陆边界变化而对结果产生不利影响。
4 结语本文提出一种在沿海地区和岛屿构建高精度重力海潮负荷改正模型的方法,该方法采用NAO99b全球海潮模型和NAO99Jb区域海潮模型,结合由SRTM地形模型确定的高空间分辨率的高程信息和海陆边界信息,计算23个潮波的海潮负荷对沿海和岛屿重力测量的影响。
以马祖岛为例,给出重力海潮负荷改正模型的数值结果。该结果与马祖岛实测结果的比较说明,使用验潮站观测资料构建的模型能够达到较高的精度,而未使用验潮站资料的模型的改正效果稍差,这主要是由相位不一致导致的,振幅的差异相对较小。同时,加入验潮站观测资料能够有效改正相位的差异。这表明,如果能够确定某一地区全球模型与实际在验潮站测得的潮汐相位之差,就可对相位进行改正,从而提高在缺乏同步验潮站观测资料时海潮负荷模型的改正精度,比如可通过已有的潮汐观测或通过临时的、简易的连续验潮观测进行调和分析以确定主要潮波的潮汐参数,并与全球模型进行比较获得相位差异。
| [1] |
周江存, 孙和平. 中国及邻区重力合成潮汐参数[J]. 地震学报, 2007, 29(6): 618-624 (Zhou Jiangcun, Sun Heping. Synthetic Tidal Parameters for Gravity over China and Its Neighbor Area[J]. Acta Seismologica Sinica, 2007, 29(6): 618-624)
(  0) 0) |
| [2] |
Zhou J C, Hwang C, Sun H P, et al. Precise Determination of Ocean Tide Loading Gravity Effect for Absolute Gravity Stations in Coastal Area of China: Effects of Land-Sea Boundary and Station Coordinate[J]. Journal of Geodynamics, 2013, 68: 29-36
(  0) 0) |
| [3] |
Goad C C. Gravimetric Tidal Loading Computed from Integrated Green's Function[J]. Journal of Geophysical Research, 1980, 85(B5): 2679-2683
(  0) 0) |
| [4] |
陈宪冬. GPS精密定位中的海潮负荷改正[J]. 西南交通大学学报, 2006, 41(4): 429-432 (Chen Xiandong. Ocean Tide Loading Correction in GPS Precise Positioning[J]. Journal of Southwest Jiaotong University, 2006, 41(4): 429-432)
(  0) 0) |
| [5] |
周江存, 孙和平, 李正媛. 佘山台倾斜固体潮观测的海潮负荷改正[J]. 测绘学报, 2006, 35(1): 4-8 (Zhou Jiangcun, Sun Heping, Li Zhengyuan. Ocean Tidal Loading Correction to Tilt Observations at Sheshan Station[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 4-8)
(  0) 0) |
| [6] |
周江存, 徐建桥, 孙和平. 中国大陆精密重力潮汐改正模型[J]. 地球物理学报, 2009, 52(6): 1474-1482 (Zhou Jiangcun, Xu Jianqiao, Sun Heping. Accurate Correction Models of Gravity in Chinese Continent[J]. Chinese Journal of Geophysics, 2009, 52(6): 1474-1482)
(  0) 0) |
| [7] |
刘经南, 张化疑, 刘焱雄, 等. GNSS研究海潮负荷效应进展[J]. 武汉大学学报:信息科学版, 2016, 41(1): 9-14 (Liu Jingnan, Zhang Huayi, Liu Yanxiong, et al. Progress of Ocean Tide Loading Inversion Based on GNSS[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 9-14)
(  0) 0) |
| [8] |
Pagiatakis S D. The Response of a Realistic Earth to Ocean Tide Loading[J]. Geophysical Journal International, 1990, 103(2): 541-560
(  0) 0) |
| [9] |
Fang G H, Kwok Y K, Yu K J, et al. Numerical Simulation of Principal Tidal Constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand[J]. Continental Shelf Research, 1999, 19(7): 845-869
(  0) 0) |
| [10] |
Neumeyer J, Pino J, Dierks O, et al. Improvement of Ocean Loading Correction on Gravity Data with Additional Tide Gauge Measurements[J]. Journal of Geodynamics, 2005, 40(1): 104-111
(  0) 0) |
| [11] |
Lysaker D I, Breili K, Pettersen B R. The Gravitational Effect of Ocean Tide Loading at High Latitude Coastal Stations in Norway[J]. Journal of Geodesy, 2008, 82(9): 569-583
(  0) 0) |
| [12] |
Bos M S, Baker T F, Røthing K, et al. Testing Ocean Tide Models in the Nordic Seas with Tidal Gravity Observations[J]. Geophysical Journal International, 2002, 150(3): 687-694
(  0) 0) |
| [13] |
Bos M S, Baker T F. An Estimate of the Errors in Gravity Ocean Tide Loading Computation[J]. Journal of Geodesy, 2005, 79(1-3): 50-63
(  0) 0) |
| [14] |
Matsumoto K, Ooe M, Sato T, et al. Ocean Tide Model Obtained from TOPEX/POSEIDON Altimetry Data[J]. Journal of Geophysical Research, 1995, 100(C12): 25319-25330
(  0) 0) |
2. Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China;
3. State Key Laboratory of Geodesy and Earth's Dynamics, 340 Xudong Street, Wuhan 430077, China
 2020, Vol. 40
2020, Vol. 40

