受轨道精度、多路径效应及各类观测误差的影响,北斗二号系统(BDS-2)和北斗三号系统(BDS-3)组成的北斗混合系统中地球静止轨道卫星(GEO)、倾斜地球同步轨道卫星(IGSO)和地球中圆轨道卫星(MEO)的观测值精度存在较大差异。相比于BDS-2,BDS-3在轨道、预报钟差等精度上具有很大提高[1-5],且观测值不含明显随卫星高度角变化的系统偏差[6-7]。因此,在定位时若对BDS-2、BDS-3及不同轨道卫星的观测值赋以不合理的权重,将会导致构造权阵不准确和定位精度较低。大量学者[8-10]对北斗系统定位进行过研究,且北斗区域系统单点定位技术已相对成熟,但对适用于全球范围的单点定位的研究较少,现有的研究未考虑北斗混合系统中不同轨道类型及BDS-2/BDS-3卫星观测值的差异对定位的影响。随着北斗系统的完善与服务范围的拓展,亟需一种适用于混合系统在全球范围内的定位方法,这对提高我国北斗系统在全球的导航定位能力具有重要意义。本文充分考虑北斗混合系统中不同轨道类型及BDS-2/BDS-3卫星观测值的差异,对定位的随机模型进行优化,并与采用等权模型、普通Helmert方差分量估计模型的定位结果进行对比分析。
1 BDS伪距单点定位原理伪距单点定位函数模型与随机模型可表示为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{V = B\hat X - L}}\\ \mathit{\boldsymbol{\hat X}} = {({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}})^{ - 1}}({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}}) \end{array} \right. $ | (1) |
式中,V为改正数,B为设计矩阵,L为常数项,为待估计的接收机坐标分量与钟差,P为权阵,通常可由等权模型、卫星高度角模型和方差分量估计法等确定:
| $ \begin{array}{l} \mathit{\boldsymbol{P}} = {{\rm{diag}}}({P_1}, {P_2}, \cdots , {P_n}) = \\ \;\;\;\;\;\;{{\rm{diag}}}(\frac{{\sigma _0^2}}{{\sigma _1^2}}, \frac{{\sigma _0^2}}{{\sigma _2^2}}, \cdots , \frac{{\sigma _0^2}}{{\sigma _n^2}}) \end{array} $ | (2) |
式中,n为观测值总数,σ02为单位权方差,一般取σi2中某一值,σi2为观测值误差方差。由式(1)和式(2)可知,观测值误差方差的取值不合理会影响定位精度。
2 北斗混合系统单点定位随机模型优化观测值误差方差的取值会影响最终的定位结果,为避免因方差值选择不合理而造成定位精度较低,可利用Helmert方差分量估计对先验权进行迭代更新,得到观测值误差方差的最优估值,进而确定最佳权阵和待求参数的最优估值。因此,本文提出基于北斗UERE(user equivalent range error,用户等效测距误差)的Helmert方差分量估计法对北斗混合系统定位的随机模型进行优化。
2.1 基于北斗UERE的先验定权定位中常用的随机模型有等权模型、卫星高度角模型等[11-12]。等权模型虽然计算简单,但精度较差;卫星高度角模型虽能反映观测值的误差趋势,但该模型并不完全适用于北斗混合系统,混合系统情况更加复杂。北斗混合系统由3种轨道卫星组成,不同轨道卫星的轨道高度及轨道精度存在差异。受多路径效应及其他观测误差的影响,BDS-2/BDS-3卫星观测值的精度不同。考虑到观测值受诸多误差因素的影响,采用UERE来表示混合系统的观测值精度。
UERE包括用户测距误差、电离层延迟、对流层延迟、接收机噪声及多路径影响等[13],具体表达式为[14]:
| $\sigma _{i,{\rm{UERE}}}^2 = \sigma _{i,{\rm{URA}}}^2 + \sigma _{i,{\rm{ion}}}^2 + \sigma _{i,{\rm{trop}}}^2 + \sigma _{i,{\rm{mp}}}^2 + \sigma _{i,{\rm{re}}}^2$ | (3) |
式中,i为观测值序号;σi, URA2为用户测距精度;σi, ion2、σi, trop2为电离层、对流层延迟引起的测距误差,可分别由广播星历电离层延迟模型和Saastamoinen模型确定;σi, mp2、σi, re2为多路径效应与接收机噪声引起的测距误差。σi, URA2可由广播星历播发的URAI(user range accuracy index,用户测距精度指标)确定[15],北斗系统的URAI对于不同卫星均相同[16],因此无法反映混合系统中不同轨道类型、BDS-2/BDS-3卫星的空间测距精度。本文根据现有的相关研究,采用北斗混合系统中不同轨道、不同系统卫星长期的URE(user range error,用户测距误差)的均值来代替常用的URA值,从而更合理地反映北斗混合系统中各卫星的空间测距精度。
多路径效应与接收机噪声等引起的测距误差可由卫星高度角函数确定:
| $ \sigma _{i,{\rm{mp}}}^2 + \sigma _{i,{\rm{re}}}^2 \approx {m^2} + {n^2}/{\rm{si}}{{\rm{n}}^2}(el) $ | (4) |
式中,m、n为模型经验值,一般取4 mm和3 mm,el为卫星高度角。则基于北斗UERE的先验权阵可表示为:
| $ \mathit{\boldsymbol{P}} = {\rm{diag}}(\frac{{\sigma _0^2}}{{\sigma _{1, {\rm{UERE}}}^2}}, \frac{{\sigma _0^2}}{{\sigma _{2, {\rm{UERE}}}^2}}, \cdots , \frac{{\sigma _0^2}}{{\sigma _{n, {\rm{UERE}}}^2}}) $ | (5) |
采用北斗UERE获取的先验信息能够较好地反映观测误差的趋势,但这种先验信息具有一定的局限性,因此可采用验后估计的方法对各类观测值的方差进行重新估计。本文采用Helmert方差分量估计法,将BDS-2 GEO卫星的观测值分为第1类,BDS-2 IGSO/MEO卫星的观测值分为第2类,BDS-3 MEO卫星的观测值分为第3类进行估计。
将式(1)按不同观测值类型分为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}{\bf{ = }}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{L}}_1}}\\ {{\mathit{\boldsymbol{V}}_2}{\bf{ = }}{\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{L}}_2}}\\ {{\mathit{\boldsymbol{V}}_3}{\bf{ = }}{\mathit{\boldsymbol{B}}_3}\mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{L}}_3}} \end{array}} \right. $ | (6) |
根据式(5)确定各类观测值的先验权阵,分别设为P1、P2、P3。利用Helmert方差分量估计近似公式确定各类观测值方差分量的估计值,具体公式为[17]:
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \sigma } _{0i}^2 = \frac{{\mathit{\boldsymbol{V}}_i^{\rm{T}}{\mathit{\boldsymbol{P}}_{\bf{i}}}{\mathit{\boldsymbol{V}}_i}}}{{{n_i} - tr({\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_{\bf{i}}})}} $ | (7) |
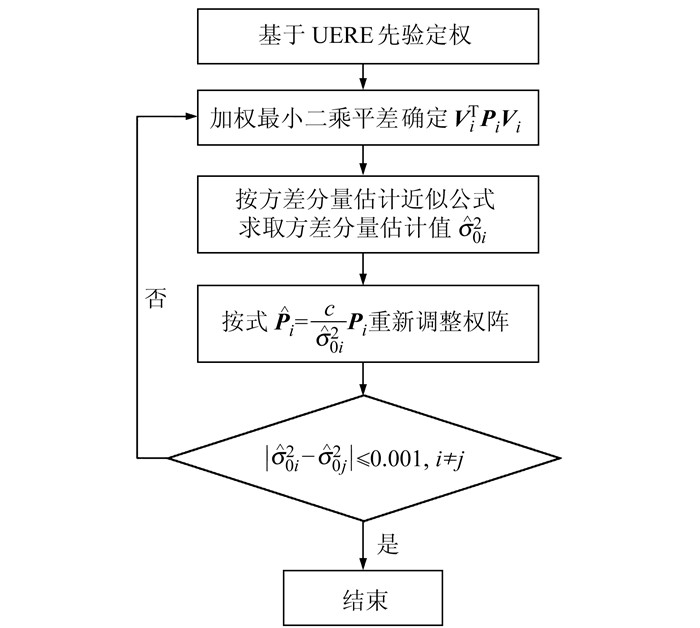
式中,ni为观测值个数,Ni= BiTPi B i,N = N1+ N2+ N3。具体计算步骤见图 1。
|
图 1 方差分量估计流程 Fig. 1 The flow chart of variance component estimation |
为验证本文提出的优化模型的有效性,采用MGEX全球范围内6个测站在2019-01-01~2019-01-07的实测数据进行测试,并从可见卫星数(NSAT)、定位精度、定位成功率等方面对采用等权模型、普通Helmert方差分量估计模型、基于北斗UERE的Helmert方差分量估计模型的定位性能进行对比分析。本文所选测站的坐标真值均采用RTKLIB中RTKPOST模块,通过GPS双频精密单点定位解算得到。
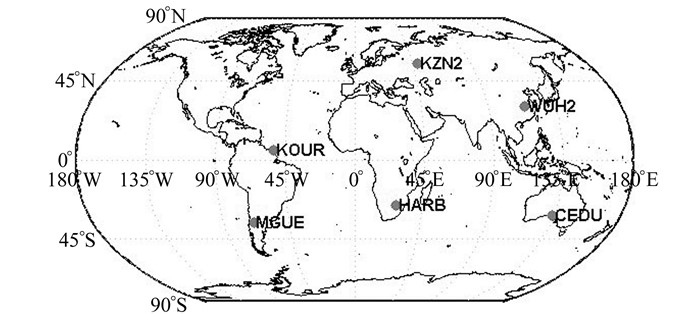
3.1 可见卫星数分析可见卫星数(NSAT)与卫星星座空间几何构型的强弱都会影响最终的定位精度。混合系统中BDS-2与BDS-3的覆盖范围不同,各测站的可见卫星数与PDOP值也会存在差异。图 2为各测站分布图,表 1为各测站连续7 d的可见卫星数与PDOP值,其中max、min、mean分别为连续7 d的PDOP值的最大值、最小值与平均值。
|
图 2 各测站分布 Fig. 2 Distribution of sites |
|
|
表 1 各测站7 d的可见卫星数与PDOP值 Tab. 1 The NSAT and PDOP values of each site for 7 days |
从表 1可以看出,所有测站在解算时段内均满足定位所需最少卫星个数的要求,BDS-2与BDS-3覆盖范围不同,因此各测站观测到BDS-2与BDS-3的卫星个数存在差异。WUH2测站与CEDU测站位于亚太地区,能够观测到绝大部分混合系统中的卫星,从PDOP值可以看出,其星座的空间几何构型最强;KZN2测站与HARB测站能够观测到小部分BDS-2与BDS-3卫星,其PDOP值次之;KOUR测站与MGUE测站位于南美洲,无法观测到BDS-2 GEO卫星,可观测到大部分BDS-3卫星,由于可见卫星总数较少,其PDOP值较大,星座的空间几何构型最弱。
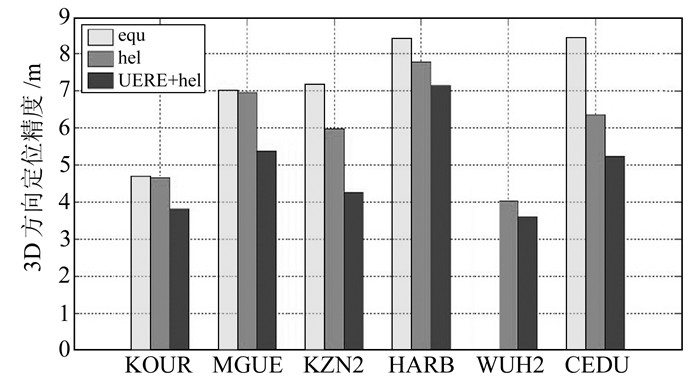
3.2 定位精度分析分别采用等权模型(equ)、普通Helmert方差分量估计模型(hel)和基于北斗UERE的Helmert方差分量估计模型(UERE+hel)对各测站连续7 d的观测数据进行解算。表 2为3种定权模型E、N、U方向误差的RMS值及本文提出的优化模型的定位结果较其他2种模型的提高率。图 3为各测站7 d的3D方向RMS值。
|
|
表 2 3种定权模型定位结果中各方向RMS值 Tab. 2 RMS values in different directions of positioning result of three weighted models |
|
图 3 各测站3D方向7 d定位精度 Fig. 3 The 3D direction positioning accuracy of each site for 7 days |
从表 2和图 3可以看出,相比于其他2种定权模型,本文提出的优化模型的定位结果精度更高,在E、N、U方向上比等权模型分别提高14%~53%、17%~48%、10%~43%,比普通Helmert方差分量估计模型分别提高6%~28%、8%~31%、7%~30%。本文提出的优化模型所采用的先验信息较普通Helmert方差分量估计模型的先验信息更为合理,能够更好地反映出北斗不同轨道类型、BDS-2/BDS-3卫星观测值之间的差异,合理的先验信息能够加快收敛方差分量估计,提高定位精度。由于各测站所处的地理环境和观测到的BDS-2/BDS-3卫星个数不同,使得各方向定位精度提升的幅度存在一定差异。从表 1和图 3可知,在测站KOUR和MGUE中,由于可见卫星总数较少,PDOP值较大,卫星星座的空间几何构型强度较弱;普通Helmert方差分量估计模型较等权模型定位结果的精度提高幅度较小,但使用本文提出的优化模型可使精度提高1~3 m。这是因为在该测站3类可见卫星中,BDS-3的可见卫星数较多且能够提供更多高质量的观测值,普通Helmert方差分量估计模型无法充分发挥该优势,本文提出的优化算法可充分发挥BDS-3的优势,能显著减少因卫星星座空间几何构型较差而导致定位精度较低的情况。
3.3 定位成功率分析定位时存在粗差会严重影响定位结果,本文对3种定权模型的定位结果进行统一输出质量控制,即去除3D方向定位误差超过20 m的历元。利用式(8)计算各测站7 d的定位成功率,表 3为满足条件的解算结果:
| $ 定位成功率{\rm{ = }}\frac{满足条件的解算历元个数}{理论历元总数} \times 100\% $ | (8) |
|
|
表 3 3种定权模型的定位成功率 Tab. 3 Positioning success rate of three weighted models |
由表 3可知,在同样输出质量控制下,本文提出的优化模型的定位成功率较其他2种方法均有提高。结合表 1与表 3可知,在测站KOUR与MGUE中,普通Helmert方差分量估计模型的定位成功率较等权模型更低,这也说明普通Helmert方差分量估计模型在卫星星座几何构型较差时不能充分发挥BDS-3的优势,导致成功解算历元的个数较少,而本文提出的优化模型在定位成功率上比等权模型高0.8%~4.5%。因此,本文提出的优化模型能够有效避免粗差对定位结果的影响,在保证整体定位精度的同时可提高定位成功率,这对提高实时导航定位的连续性与准确性具有较好的借鉴意义。
4 结语本文充分考虑北斗混合系统间不同轨道类型、BDS-2/BDS-3卫星间观测值的差异,对随机模型进行优化,并与等权模型、普通Helmert方差分量估计模型的定位精度与定位成功率进行对比分析,得到以下结论:
1) 本文提出的优化模型具有更合理的先验信息,能够充分发挥BDS-3的优势,通过迭代对权阵进行动态更新获取最优权阵。优化模型能够显著提高定位精度,可有效减少因卫星星座空间几何构型较差而导致定位精度较低的情况。
2) 在同样输出质量控制下,本文提出的优化模型能有效避免粗差对定位结果的影响,提高定位成功率,同时可保证定位的连续性与准确性。
| [1] |
谢慧, 宋淑丽, 焦国强, 等. 北斗卫星导航系统SISURE初步评估[J]. 天文学报, 2019, 60(3): 94-104 (Xie Hui, Song Shuli, Jiao Guoqiang, et al. Preliminary Evaluation of SISURE of Beidou Satellite Navigation System[J]. Acta Astronomica Sinica, 2019, 60(3): 94-104)
(  0) 0) |
| [2] |
刘万科, 任杰, 曾琪, 等. 2013-2015年BDS空间信号测距误差的精度评估[J]. 国防科技大学学报, 2016, 38(3): 1-6 (Liu Wanke, Ren Jie, Zeng Qi, et al. Accuracy Assessment of BDS Signal-in-Space Range Errors in 2013-2015[J]. Journal of National University of Defense Technology, 2016, 38(3): 1-6)
(  0) 0) |
| [3] |
马下平, 鲁尚强, 李秦政, 等. 北斗卫星导航系统的空间信号精度评估[J]. 测绘科学, 2019, 44(1): 90-97 (Ma Xiaping, Lu Shangqiang, Li Qinzheng, et al. Evaluation of Signal in Space Accuracy for Beidou Navigation Satellite System[J]. Science of Surveying and Mapping, 2019, 44(1): 90-97)
(  0) 0) |
| [4] |
张清华, 隋立芬, 贾小林, 等. 北斗卫星导航系统空间信号误差统计分析[J]. 武汉大学学报:信息科学版, 2014, 39(3): 271-274 (Zhang Qinghua, Sui Lifen, Jia Xiaolin, et al. SIS Error Statistical Analysis of Beidou Satellite Navigation System[J]. Geomatics and Information Science of Wuhan University, 2014, 39(3): 271-274)
(  0) 0) |
| [5] |
毛亚, 王潜心, 胡超, 等. 北斗三号试验卫星的钟差评估及预报[J]. 天文学报, 2018, 59(1): 56-69 (Mao Ya, Wang Qianxin, Hu Chao, et al. Performance Analysis and Prediction of Clock Offsets for the BDS-3 Test Satellites[J]. Acta Astronomica Sinica, 2018, 59(1): 56-69)
(  0) 0) |
| [6] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测——试验验证数据分析[J]. 中国科学:地球科学, 2018, 48(5): 584-594 (Yang Yuanxi, Xu Yangyin, Li Jinlong, et al. Progress and Performance Evaluation of Beidou Global Navigation Satellite System: Data Analysis Based on BDS-3 Demonstration System[J]. Science China:Earth Science, 2018, 48(5): 584-594)
(  0) 0) |
| [7] |
李昕, 张小红. BDS-2和BDS-3卫星伪距多路径偏差特性比较[J]. 大地测量与地球动力学, 2018, 38(2): 191-194 (Li Xin, Zhang Xiaohong. Comparison of Satellite-Induced Code Bias between BDS-2 and BDS-3 Satellites[J]. Journal of Geodesy and Geodynamics, 2018, 38(2): 191-194)
(  0) 0) |
| [8] |
Cai C S, Pan L, Gao Y. A Precise Weighting Approach with Application to Combined L1/B1 GPS/BDS Positioning[J]. Journal of Navigation, 2014, 67(5): 911-925
(  0) 0) |
| [9] |
刘永建, 江勇. 北斗GEO/IGSO/MEO卫星观测值精度分析及随机模型精化[J]. 全球定位系统, 2018, 43(1): 1-6 (Liu Yongjian, Jiang Yong. Precision Analysis of the BDS GEO/IGSO/MEO Observables and Stochastic Model Refining[J]. GNSS World of China, 2018, 43(1): 1-6)
(  0) 0) |
| [10] |
刘天骏, 王坚, 韩厚增, 等. GPS/BDS分类组合定位的指数加权Helmert方差分量估计法[J]. 大地测量与地球动力学, 2018, 38(7): 684-688 (Liu Tianjun, Wang Jian, Han Houzeng. Exponential Weighted Helmert Variance Component Estimation for GPS/BDS Combined Positioning with Satellite Classification[J]. Journal of Geodesy and Geodynamics, 2018, 38(7): 684-688)
(  0) 0) |
| [11] |
周锋.多系统GNSS非差非组合精密单点定位相关理论和方法研究[D].上海: 华东师范大学, 2018 (Zhou Feng.Theory and Methodology of Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[D].Shanghai: East China Normal University, 2018) https://www.ixueshu.com/document/91c3f56eaf3c7f548e12486c331329e0318947a18e7f9386.html
(  0) 0) |
| [12] |
戴吾蛟, 丁晓利, 朱建军. 基于观测值质量指标的GPS观测量随机模型分析[J]. 武汉大学学报:信息科学版, 2008, 33(7): 718-722 (Dai Wujiao, Ding Xiaoli, Zhu Jianjun. Comparing GPS Stochastic Models Based on Observation Quality Indices[J]. Geomatics and Information Science of Wuhan University, 2008, 33(7): 718-722)
(  0) 0) |
| [13] |
胡志刚.北斗卫星导航系统性能评估理论与试验验证[D].武汉: 武汉大学, 2013 (Hu Zhigang.Beidou Navigation Satellite System Performance Assessment Theory and Experiment Verification[D].Wuhan: Wuhan University, 2013) http://cdmd.cnki.com.cn/Article/CDMD-10486-1014136513.htm
(  0) 0) |
| [14] |
Delgado N B, Nunes F D.Satellite Selection Based on WDOP Concept and Convex Geometry[C].5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing, Netherlands, 2010
(  0) 0) |
| [15] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2005)
(  0) 0) |
| [16] |
Ouyang C H, Shi J B, Shen Y R, et al. Six-Year BDS-2 Broadcast Navigation Message Analysis from 2013 to 2018: Availability, Anomaly, and SIS UREs Assessment[J]. Sensors, 2019, 19(12): 2767
(  0) 0) |
| [17] |
崔希璋. 广义测量平差[M]. 武汉: 武汉大学出版社, 2009 (Cui Xizhang. Generalized Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


