2. 中国科学院国家授时中心,西安市书院东路3号,710600;
3. 中国科学院大学,北京市玉泉路19号甲,100049;
4. 中国科学院精密导航定位与定时技术重点实验室,西安市书院东路3号,710600
随着全球卫星导航系统(global navigation satellite system,GNSS)在越来越多的学科领域发挥重要作用,许多国家和地区建立了大量连续运行参考站(continuously operating reference system,CORS),致使GNSS数据量呈几何倍数增长。GNSS数据量的增长有助于提高产品的解算精度,但也会增加模型的复杂度和计算时间。为了提高大规模GNSS系统的数据处理效率,国内部分学者提出OpenMP(open multi-processing)并行计算、MPI(message-passing-interface)并行计算、分布式计算、子网划分等技术[1-11]。Bernese GNSS software Version 5.2是GNSS数据处理领域的主流软件之一[12],包括国际GNSS服务(international GNSS service,IGS)分析中心在内的多家科研单位都使用该软件进行科学研究、生产测量等工作。为了满足科学、工程及金融等领域的科学计算需求,英特尔公司专门开发了一套经过高度优化和广泛线程化的数学例程,称为数学核心函数库(math kernel library,MKL)。由于英特尔MKL在Bernese GNSS software数据处理中的研究较少,本文将主要分析英特尔MKL在Bernese GNSS software数据处理中的应用,重点分析其矩阵求逆函数对数据处理效率的影响。
1 矩阵求逆算法 1.1 Bernese GNSS softwareBernese GNSS software Version 5.2软件可调用子程序syminvg对法方程系数矩阵进行求逆,其基本思想为[13]:1)对对称矩阵进行一系列初等变换,将其转换为对角阵;2)对对角矩阵的对角线元素取倒数;3)对转换后的新对角矩阵按照上述初等变换的逆顺序进行初等变换,得到矩阵的逆矩阵。其基本原理如下。
假定A1为n×n的对称矩阵,Ai+1、Ai为对矩阵A1进行i次、i-1次初等变换后的矩阵,可表示为:
| $ {\mathit{\boldsymbol{A}}_{i + 1}} = {\mathit{\boldsymbol{Q}}_i}^{\text{T}}{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{Q}}_i} $ | (1) |
式中,矩阵Qi为第i次初等变换对应的n×n阶初等矩阵,其取值为:当k≤i时取值为克罗内克函数,当j=i, k>i时取值为-Ai; i, k/Ai; i, i。
使用上述变换后,Ai+1中第i行与第i列的非对角线元素均为0。为了提高数值稳定性,需要在对角线元素中选取主元。以Ai选取主元为例,假定Ai; l, l为对角线元素的最大值,将第i行与第j行以及第i列与第j列进行交换,即可将最大元素Ai; l, l和Ai; i, i进行互换,用矩阵表示为:
| $ \mathit{\boldsymbol{A}}_i'= {\mathit{\boldsymbol{X}}_i}{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{X}}_i} $ | (2) |
| $ {\mathit{\boldsymbol{X}}_i} = \left\{ {\begin{array}{*{20}{c}} {{X_{i;j, k}} = {\delta _{jk}}}\\ {{X_{i;i, l}} = {X_{i;l, i}} = 1}\\ {{X_{i;i, i}} = {X_{i;l = l}} = 0} \end{array}} \right. $ | (3) |
经过n次选取主元和相似变换后,矩阵An可表示为:
| $ {\mathit{\boldsymbol{A}}_n} = \mathit{\boldsymbol{Q}}_{n - 1}^{\rm{T}} \cdots \mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{X}}_1}{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{X}}_1}{\mathit{\boldsymbol{Q}}_1} \cdots {\mathit{\boldsymbol{Q}}_{n - 1}} $ | (4) |
对矩阵An的对角线元素取倒数,即可得到矩阵An-1,然后对矩阵An-1按照相反的顺序进行一系列初等变换,可得到矩阵A1-1的表达式为:
| $ {\mathit{\boldsymbol{A}}_1}^{ - 1} = {\mathit{\boldsymbol{X}}_1}{\mathit{\boldsymbol{Q}}_1} \cdots {\mathit{\boldsymbol{Q}}_{n - 1}}\mathit{\boldsymbol{A}}_n^{ - 1}\mathit{\boldsymbol{Q}}_{n - 1}^{\rm{T}} \cdots \mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{X}}_1} $ | (5) |
Bernese软件中syminvg子程序采用上述算法对对称矩阵进行求逆。为节省存储空间,选取主元后程序不再进行行列交换[14-15],且不再对n×n阶变换矩阵Qi进行存储,该算法时间复杂度为O(n3)。
1.2 Intel MKL英特尔MKL是一套经过高度优化和广泛线程化的数学例程,核心数学函数包括BLAS、LAPACK、ScaLAPACK1、稀疏矩阵解算器、快速傅立叶转换、矢量数学及其他函数。针对不同的存储方式和不同类型的矩阵,英特尔MKL均可提供相应的求逆函数,且不同的求逆函数具有不同的性能。矩阵类型包括一般矩阵、对称矩阵、三角矩阵,存储方式包括全存储、带状存储、压缩存储、矩形全压缩存储4种。本文矩阵类型为法方程系数矩阵,一般为对称正定矩阵,表 1为Intel MKL相关的矩阵求逆函数,从表中可以看出,对于对称正定矩阵的全存储和压缩存储2种不同的存储方式,英特尔MKL可提供多个矩阵求逆函数,其中“?”表示数据类型,共包括4种:s(实数单精度浮点型)、d(实数双精度浮点型)、c(复数单精度浮点型)、z(复数双精度浮点型)。
|
|
表 1 Intel MKL矩阵求逆函数列表 Tab. 1 Matrix inversion functions from Intel MKL |
本文以dgetri为例介绍Intel MKL求逆函数算法。使用dgetri函数对矩阵进行求逆之前,需要调用dgetrf函数对矩阵进行分解,该函数使用列主元素法对矩阵A进行LU分解, 分解后的矩阵A可表示为:
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{P}} * \mathit{\boldsymbol{L}} * \mathit{\boldsymbol{U}} $ | (6) |
式中,矩阵 P为置换矩阵,L为单位下三角矩阵,U为上三角矩阵。
对矩阵An×n进行分解后,调用dgetri函数求逆矩阵,即求解方程Ax = I,基本算法为:
for i= 1:n
使用前向回代法计算Ly = ei
使用后向回代法计算Uxi = y
end
其中,ei为n×n阶单位矩阵的列向量。
与dgetri函数类似,dpotri和dpptri函数在进行求逆前也需要调用相应的分解函数。dpotrf函数在进行Cholesky分解时与dgetrf函数不同,具体算法参考文献[10-11]。dgetrf、dpotrf、dpptrf函数浮点数运算次数分别为2n3/3、n3/3、n3/3,dgetri、dpotri、dpptri函数浮点数运算次数分别为4n3/3、2n3/3、2n3/3,因此使用Intel MKL求逆函数的时间复杂度均为O(n3),时间复杂度与Bernese软件syminvg函数一致。但英特尔MKL已使用以下技术对算法进行优化:循环展开技术(减小循环管理成本)、数据块技术(提高数据重用机会)、缓存管理技术、数据预加载技术(削弱内存延迟)、多处理器并行技术等。
以dpotri为例介绍英特尔MKL库函数的使用方法。在使用dpotri对法方程系数矩阵进行求逆之前,需要使用dpotrf进行Cholesky分解,其方法为:
| $ {\rm{call}}\;\;\;{\rm{dpotrf}}\;{\rm{(uplo, n}}, \mathit{\boldsymbol{a}}, {\rm{lda, info)}} $ | (7) |
式中,uplo为字符变量,取值为‘U’或‘L’,其中‘U’表示仅存储对称矩阵上三角部分元素,‘L’表示仅存储对称矩阵下三角部分元素;n为整型变量,表示方阵a的阶数;a为双精度浮点型二维数组变量,存储求逆的原始矩阵,其维度为(lda, *),函数运行后其上三角部分和下三角部分分别存储Cholesky分解后得到的U和L矩阵;lda为整型变量,表示矩阵a的第一维度;info为整型变量,表示子程序执行结果的变量,info=0表示子程序运行成功,info=-i表示第i个参数为非法值,info=i表示矩阵a的i阶方阵为非正定矩阵,无法进行Cholesky分解。
使用dpotri进行矩阵求逆的方法为:
| $ {\rm{call}}\;\;\;{\rm{dpotri}}\;{\rm{(uplo, n}}, \mathit{\boldsymbol{a}}, {\rm{lda, info)}} $ | (8) |
式中,uplo、n、a、lda、info参数类型与dpotrf函数一致,参数执行后若info=0表示子程序运行成功,逆矩阵存储在矩阵a中;info=-i表示第i个参数为非法值,info=i表示矩阵a的第i个对角线元素为0,矩阵求逆失败。
2 数值实验本文以精密轨道产品生成为例,分析Intel MKL求逆函数对Bernese数据处理性能的影响。事后最终精密轨道为IGS、国际GNSS监测评估系统(international GNSS monitoring and assessment system, iGMAS)等提供的核心精密产品之一。本文采用以下流程计算最终轨道产品:1)使用全球300多个测站的单天观测数据进行精密定轨数据处理,并保留其法方程;2)对连续3 d法方程进行叠加,将中间1 d的叠加结果作为最终轨道产品。本文实验平台为单台服务器,其配置信息为:操作系统为64位Red Hat Enterprise Linux Server Release 6.2;CPU型号为Intel(R) Xeon(R) CPU E5-2609 @2.40 GHz,逻辑CPU个数为8;系统内存为64 G;服务器上安装有Composer_xe_2011版本Intel MKL。
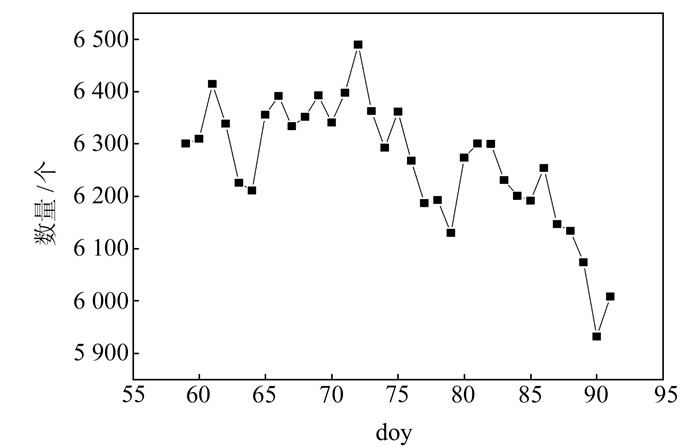
本文使用中国科学院国家授时中心iGMAS分析中心2019年年积日59~91共33个单天法方程进行分析。单天法方程中包括以下几种未知参数:测站坐标、卫星轨道参数(包括卫星轨道根数、虚拟随机脉冲)、对流层延迟、差分码偏差、地球自转参数、高阶电离层延迟参数,其中全局参数为测站坐标、卫星轨道根数、差分码偏差参数。图 1为2019年年积日59~91共33个单天法方程未知参数个数。从图中可以看出,单天法方程未知参数个数约为6 000,最大值为6 490,最小值为5 932。将连续3 d法方程进行叠加,3 d法方程的未知参数个数约为12 000,即需要对维度为(12 000,12 000)的法方程系数矩阵进行求逆运算。
|
图 1 单天法方程参数个数统计 Fig. 1 Statistics of parameters number in single-day normal equation |
参数预消除和回代求解是Bernese软件常用的一种数据处理策略。通过参数预消除可减小法方程维度,同时不影响数值解算结果。其具体算法如下:假设p1为法方程矩阵中卫星轨道、测站坐标参数,p2为法方程矩阵中对流层延迟参数、电离层延迟参数、差分码偏差、地球自转参数等需要消除的参数,则法方程可表示为:
| $ \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{N}}_{11}}}&{\mathit{\boldsymbol{N}}_{21}^{\rm{T}}}\\ {{\mathit{\boldsymbol{N}}_{21}}}&{{\mathit{\boldsymbol{N}}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{p_1}}\\ {{p_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{b_1}}\\ {{b_2}} \end{array}} \right] $ | (9) |
式中,b1、b2为法方程矩阵对应参数p1、p2的常数项,N11、N22、N12、N21为未知参数分类后法方程系数矩阵分块形成的分块矩阵。
利用式(9)中第2个方程可求得:
| $ {p_2} = \mathit{\boldsymbol{N}}_{22}^{ - 1}\left( {{b_2} - {\mathit{\boldsymbol{N}}_{21}}{p_1}} \right) $ | (10) |
将式(10)代入式(9)中第1个方程可得:
| $ \left( {{\mathit{\boldsymbol{N}}_{11}} - \mathit{\boldsymbol{N}}_{21}^{\rm{T}}\mathit{\boldsymbol{N}}_{22}^{ - 1}{\mathit{\boldsymbol{N}}_{21}}} \right) \cdot {p_1} = \left( {{b_1} - \mathit{\boldsymbol{N}}_{21}^{\rm{T}}\mathit{\boldsymbol{N}}_{22}^{ - 1}{b_2}} \right) $ | (11) |
从上述过程可以看出,经过参数预消除后,法方程仅保留需要解算的参数,可减小法方程矩阵的维度。
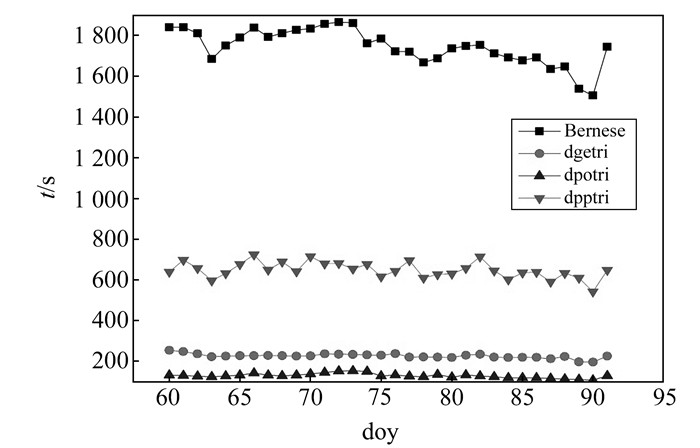
本文首先分析在未采用参数预消除策略情况下,英特尔MKL对Bernese精密定轨数据处理的影响,对比分析syminvg、dpptri、dgetri、dpotri四个函数的矩阵求逆效率。由于部分英特尔数学库函数具有并行运算功能,因此将3个Intel MKL函数设置为单线程模式,并且预先不消除任何参数。图 2为4个矩阵求逆函数执行时间,从图中可以看出,syminvg函数执行时间最长,随着参数个数的变化,执行时间约为1 500~1 800 s;dpptri函数执行时间为600~700 s;dgetri函数执行时间在200~300 s;dpotri函数执行时间为110~155 s。表 2(单位s)为4个矩阵求逆函数执行时间的最大值、最小值和平均值,从表中可以看出,syminvg、dpptri、dgetri、dpotri执行时间平均值分别为1 745.88 s、649.96 s、228.15 s、131.33 s。综合上述分析可知,相比Bernese自带syminvg函数,使用英特尔MKL可明显缩短矩阵求逆时间,提高数据处理效率。与syminvg函数相比,dpotri函数性能最优,计算速度可提高13倍。
|
图 2 矩阵求逆执行时间 Fig. 2 Computing time of matrix inversion |
|
|
表 2 矩阵求逆执行时间统计 Tab. 2 Statistic of computing time of matrix inversion |
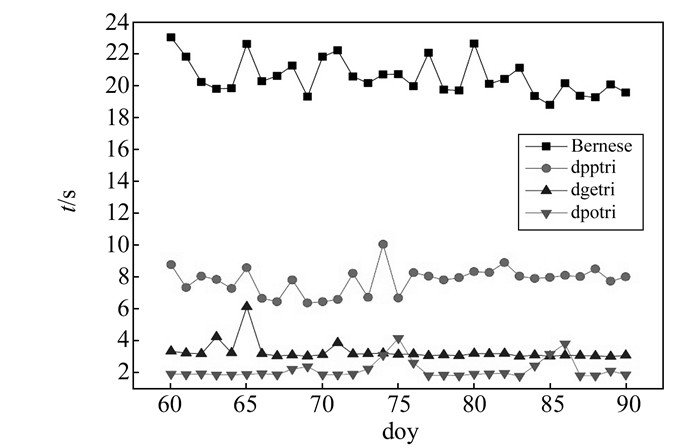
进一步分析使用预消除策略后英特尔MKL对Bernese软件数据处理的影响。对连续3 d法方程进行叠加,仅保留卫星轨道相关参数、测站坐标参数,预消除对流层参数、电离层相关参数、地球自转参数。参数预消除后,3 d法方程叠加时需对维度为(2 800,2 800)的法方程系数矩阵进行求逆运算。图 3为预消除参数后矩阵求逆时间序列,从图中可以看出,对于2 800×2 800维度的法方程系数矩阵,使用英特尔MKL时矩阵求逆计算速度相比Bernese原有算法仍具有较大提高;与图 2相比可知,经过参数预消除后,法方程系数矩阵维度由12 000减小为2 800,syminvg、dpptri、dgetri、dpotri四个矩阵求逆函数执行时间缩短为20 s、8 s、4 s、2 s,矩阵求逆时间明显缩短,但参数预消除过程会花费很长时间。图 4为参数预消除过程所用时间,从图中可以看出,虽然参数预消除可减小法方程系数矩阵维度,大大缩短矩阵求逆使用时间,但参数预消除过程会增加1 400~1 700 s的额外计算时间。
|
图 3 预消除参数后矩阵求逆执行时间 Fig. 3 Computing time of matrix inversion after parameter pre-elimination |

|
图 4 参数预消除执行时间 Fig. 4 Computing time of parameter pre-elimination |
综上分析可知,取消参数预消除,使用英特尔dpotri函数代替syminvg子程序可明显缩短矩阵求逆时间,提高Bernese软件GNSS精密轨道确定的计算效率。
3 结语本文首先详细介绍Bernese GNSS software和英特尔MKL矩阵求逆函数的求逆算法,然后对比分析syminvg、dpptri、dgetri、dpotri函数对Bernese软件精密定轨数据处理效率的影响。实测数据分析表明,在未进行参数预消除情况下,相比Bernese原有syminvg函数,英特尔MKL函数可显著缩短矩阵求逆时间,其中dpotri函数效率最高,矩阵求逆时间为133 s,相比syminvg函数计算速度可提高约13倍;在采用参数预消除策略情况下,矩阵求逆时间明显减少,但参数预消除过程会额外增加1 400~1 700 s的计算时间。另外,本文仅分析单线程模式下英特尔矩阵求逆效率,下一步将对多线程模式下英特尔MKL求逆函数性能进行分析研究。
致谢: 感谢iGMAS、IGS提供GNSS全球跟踪站观测数据,感谢中国科学院国家授时中心iGMAS分析中心提供软硬件测试平台。
| [1] |
宋力杰, 欧阳桂崇. 超大规模大地网分区平差快速解算方法[J]. 测绘学报, 2003, 32(3): 204-207 (Song Lijie, Ouyang Guichong. A Fast Method of Solving Partitioned Adjustment for Super Large-Scale Geodetic Network[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 204-207 DOI:10.3321/j.issn:1001-1595.2003.03.004)
(  0) 0) |
| [2] |
姜卫平, 赵倩, 刘鸿飞, 等. 子网划分在大规模GNSS基准站网数据处理中的应用[J]. 武汉大学学报:信息科学版, 2011, 36(4): 389-391 (Jiang Weiping, Zhao Qian, Liu Hongfei, et al. Application of the Sub-Network Division in Large Scale GNSS Reference Station Network[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 389-391)
(  0) 0) |
| [3] |
邹贤才, 李建成, 汪海洪, 等. OpenMP并行计算在卫星重力数据处理中的应用[J]. 测绘学报, 2010, 39(6): 636-641 (Zou Xiancai, Li Jiancheng, Wang Haihong, et al. Application of Parallel Computing with OpenMp in Data Processing for Satellite Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 636-641)
(  0) 0) |
| [4] |
陈秋杰, 沈云中, 张兴福. MKL和OpenMP多核并行算法解算高阶地球重力场的效率分析[J]. 大地测量与地球动力学, 2012, 32(5): 118-123 (Chen Qiujie, Shen Yunzhong, Zhang Xingfu. Analysis of Efficiency of Applying MKL and OpenMP Polynuclear Parallel Algorithms to Recovery of High Degree Earth's Gravity Field[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 118-123)
(  0) 0) |
| [5] |
陈正生, 吕志平, 崔阳, 等. 基于BPE的GNSS数据并行快速解算[J]. 大地测量与地球动力学, 2013, 33(5): 79-82 (Chen Zhengsheng, Lü Zhiping, Cui Yang, et al. Parallel Computing of GNSS Data Based on Bernese Processing Engine[J]. Journal of Geodesy and Geodynamics, 2013, 33(5): 79-82)
(  0) 0) |
| [6] |
崔阳, 吕志平, 陈正生, 等. 多核环境下的GNSS网平差数据并行处理研究[J]. 测绘学报, 2013, 42(5): 661-667 (Cui Yang, Lü Zhiping, Chen Zhengsheng, et al. Research of Parallel Data Processing for GNSS Network Adjustment under Multi-Core Environment[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 661-667)
(  0) 0) |
| [7] |
陈正生, 吕志平, 崔阳, 等. 大规模GNSS数据的分布式处理与实现[J]. 武汉大学学报:信息科学版, 2015, 40(3): 384-389 (Chen Zhengsheng, Lü Zhiping, Cui Yang, et al. Implementation of Distributed Computing with Large-Scale GNSS Data[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 384-389)
(  0) 0) |
| [8] |
周浩, 罗志才, 钟波, 等. 利用最小二乘直接法反演卫星重力场模型的MPI并行算法[J]. 测绘学报, 2015, 44(8): 833-839 (Zhou Hao, Luo Zhicai, Zhong Bo, et al. MPI Parallel Algorithm in Satellite Gravity Field Model Inversion on the Basis of Least Square Method[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 833-839)
(  0) 0) |
| [9] |
施闯, 王成, 张涛. 基于超算的全球电离层模型快速并行解算[J]. 武汉大学学报:信息科学版, 2018, 43(12): 2093-2098 (Shi Chuang, Wang Cheng, Zhang Tao. Rapid Parallel Estimation of Global Ionospheric Model Based on Supercomputer[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2093-2098)
(  0) 0) |
| [10] |
张强, 赵齐乐. OpenMP并行计算在全球电离层反演中的应用[J]. 武汉大学学报:信息科学版, 2018, 43(2): 227-233 (Zhang Qiang, Zhao Qile. Application of Parallel Computing with OpenMP in Global Ionosphere Mapping[J]. Geomatics and Information Science of Wuhan University, 2018, 43(2): 227-233)
(  0) 0) |
| [11] |
王成, 毛大智, 施闯, 等. 全球电离层模型的分布式并行解算[J]. 武汉大学学报:信息科学版, 2018, 43(8): 1207-1213 (Wang Cheng, Mao Dazhi, Shi Chuang, et al. Distributed Parallel Estimation for Global Ionospheric Modeling[J]. Geomatics and Information Science of Wuhan University, 2018, 43(8): 1207-1213)
(  0) 0) |
| [12] |
Dach R, Lutz S, Walser P, et al. Bernese GNSS Software Version 5.2[J]. Bern: Astronomical Institute, University of Bern, 2015
(  0) 0) |
| [13] |
Busing W R, Levy H A. A Procedure for Inverting Large Symmetric Matrices[J]. Communications of the ACM, 1962, 5(8): 445-446 DOI:10.1145/368637.368760
(  0) 0) |
| [14] |
Rutishauser H. Algorithm 150: Syminv2[J]. Communications of the ACM, 1963, 6(2): 67-68
(  0) 0) |
| [15] |
Rutishauser H. Remark on Algorithm 150: Syminv2[J]. Communications of the ACM, 1963, 6(7): 390
(  0) 0) |
2. National Time Service Center, CAS, 3 East-Shuyuan Road, Xi'an 710600, China;
3. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
4. Key Laboratory of Precision Navigation and Timing Technology, CAS, 3 East-Shuyuan Road, Xi'an 710600, China
 2020, Vol. 40
2020, Vol. 40

