空间插值是在地面离散点测量数据的基础上,通过数学模型建立地面连续的插值曲面来预测未知点的高程[1]。当数据中含有短程变异时,局部多项式插值法生成的曲面能较好地描述这种短程变异,同时运用以每一个内插点为中心的邻近区域的点建立多项式来表达曲面模型[2-4]。在一定区域内不同采样点对内插点的影响不同,因此在计算多项式时各点的权重也存在差异[5-6],通常情况下邻近区域内采样点的权重会随内插点与采样点之间距离的增加而减小[7]。反距离权重法和局部距离比是使用最广泛的对样本点进行加权的地理信息系统插值方法,但对于存在粗差的数据,这2种方法不能很好地减弱粗差对结果的影响。因此在实际测量中引入稳健估计来处理粗差问题,即事先不确定观测数据中有效或有害信息及其所占的比例[8-12]。在估计过程中充分利用观测数据中的有效数据,排除有害信息,利用选权迭代法对不同采样点的权重进行迭代计算,避免粗差对结果的影响[13-16]。本文对具有粗差的数据进行局部多项式插值,采用选权迭代法对采样点进行赋权,并对比3种方法的结果,通过拟合优度检验对插值结果进行验证,获得准确性和可靠性更高的结果。
1 曲面模型建立原理 1.1 采样点选取方法本文基于三维模型,提出动态球半径选点法,即从采样点的平均密度出发,对总体数据构建三维模型,以内插点为球心,R为半径,选取各内插点周围可用来计算的采样点(图 1)。半径R可通过构造函数来确定:
| $\pi {R^2} = n \times \frac{A}{N}$ | (1) |

|
图 1 动态球半径选点法原理示意图 Fig. 1 Schematic diagram of dynamic sphere radius point selection method |
式中,N为总采样点数,A为研究区面积,n为规定的球内的数据点数。
采样点与内插点距离的计算公式为:
| ${d_i} = \sqrt {{{(X - {x_i})}^2} + {{(Y - {y_i})}^2} + {{(Z - {z_i})}^2}} $ | (2) |
式中,X、Y、Z分别为内插点坐标,X、Y、Z分别为采样点坐标。
1.2 建立局部多项式插值方程为建立某一区域的插值曲面,需要在已知点的基础上建立方程式对插值曲面进行表达。设选取的采样点坐标为(xi, yi)(i=1, 2, …, n)、内插点N的坐标为(XN, YN),将(xi, yi)运用到以N为原点的局部坐标系中,即
| $\left\{ \begin{array}{l} {{\tilde x}_i} = {x_i} - {X_N}\\ {{\tilde y}_i} = {y_i} - {Y_N} \end{array} \right.$ | (3) |
本文采用二次插值,由n个采样点的值可得到以下方程组:
| $\begin{array}{l} {v_i} = {a_1} + {a_2}{{\tilde x}_i} + {a_3}{{\tilde y}_i} + {a_4}{{\tilde x}_i}{{\tilde y}_i} + \\ \;\;\;{a_5}{{\tilde x}_i}^2 + {a_6}{{\tilde y}_i}^2 - {z_i}, i = 1, 2, \cdots , n \end{array}$ | (4) |
矩阵表示形式为:
| $ \begin{array}{l} {\bf{Z}} = \left[ \begin{array}{c} {z_1}\\ {z_2}\\ \vdots \\ {z_n} \end{array} \right], {\bf{X}} = \left[ \begin{array}{c} {a_1}\\ {a_2}\\ \vdots \\ {a_6} \end{array} \right], {\bf{V}} = \left[ \begin{array}{c} {\varepsilon _1}\\ {\varepsilon _2}\\ \vdots \\ {\varepsilon _n} \end{array} \right], \\ {\bf{B}} = \left[ {\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}}&{{x_1}{y_1}}&{x_1^2}&{y_1^2}\\ 1&{{x_2}}&{{y_2}}&{{x_2}{y_2}}&{x_2^2}&{y_2^2}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1&{{x_n}}&{{y_n}}&{{x_n}{y_n}}&{x_n^2}&{y_n^2} \end{array}} \right] \end{array} $ | (5) |
改正数求解的矩阵形式为:
| $\mathit{\boldsymbol{V = BX - Z}}$ | (6) |
通过最小二乘求解多项式系数X为:
| $\mathit{\boldsymbol{X}} = {({\mathit{\boldsymbol{B}}^{\text{T}}}\mathit{\boldsymbol{PB}})^{ - 1}}({\mathit{\boldsymbol{B}}^{\text{T}}}\mathit{\boldsymbol{PV}})$ | (7) |
式中,P为每个采样点通过函数确定的权重,由此可求解系数ai(i=1, 2, …, 6)和所对应的曲面方程,进而得到所求内插点的值。
1.3 采样点权重确定不同采样点与内插点的距离不同,可通过权函数来反映该点与内插点的相关程度。对每个采样点进行赋权,权重Pi确定的原则与该数据点到内插点的距离di有关,di越小,数据点对内插点的影响越大,权重Pi也越大。可采用以下3种方法来确定权函数[17]:
1) 以动态球选点法的半径R为标准,以该数据点到圆周的距离R-di与该点到圆点的距离di之比的平方为权,表达式为:
| ${P_i} = |\frac{{R - {d_i}}}{{{d_i}}}{|^2}$ | (8) |
2)以距离平方的反比为权,表达式为:
| ${P_i} = \frac{1}{{{d_i}^2}}$ | (9) |
式中,R为选取点的半径,di为内插点到采样点的距离。
上述2种方法为通常情况下局部多项式的选权方法,都是以距离远近为定权的标准。
3) 以选权迭代法定权。该方法以内插点到采样点的距离为自变量,内插点的值为因变量,计算每个采样点的权重,ρ函数选用Huber函数[18]。对各采样点构造新权重
| $ \rho (u) = \left\{ \begin{array}{l} \frac{1}{2}{u^2}, \begin{array}{*{20}{c}} {}&{}&{\left| u \right| \le k} \end{array}\\ k\left| u \right| - \frac{1}{2}{k^2}\begin{array}{*{20}{c}} , &{\left| u \right| > k} \end{array} \end{array} \right. $ | (10) |
| $ \varphi (u) = \left\{ \begin{array}{l} u\begin{array}{*{20}{c}} , &{\left| u \right| \le k}&{}&{} \end{array}\\ k{\text{sign}}(u)\begin{array}{*{20}{c}} , &{\left| u \right| > k} \end{array} \end{array} \right. $ | (11) |
| $ \omega (u) = \left\{ \begin{array}{l} 1\begin{array}{*{20}{c}} , &{|u| \le k}&{} \end{array}\\ \frac{k}{{|u|}}\begin{array}{*{20}{c}} , &{|u| > k} \end{array} \end{array} \right. $ | (12) |
式中,u为采样点残差,k为限差。
2 拟合精度检验通过拟合优度R-squared可验证曲面插值后模型的拟合程度,拟合优度r公式为:
| $r = 1 - \sqrt {\frac{{\sum {{{(h - \hat h)}^2}} }}{{\sum {{h^2}} }}} $ | (13) |
当R越趋近于1时,表明拟合程度越好。实际应用中数据往往具有粗差,为验证本文所引用方法的有效性,以无粗差时拟合优度最高的曲面为参考标准,对存在粗差的曲面选用均方根误差进行验证,其公式为:
| ${\text{RMSE}} = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{(h - \hat h)}^2}} } $ | (14) |
式中,m为插值点个数,h为无粗差时拟合的高程值,为存在粗差时拟合的高程值,RMSE为拟合精度。
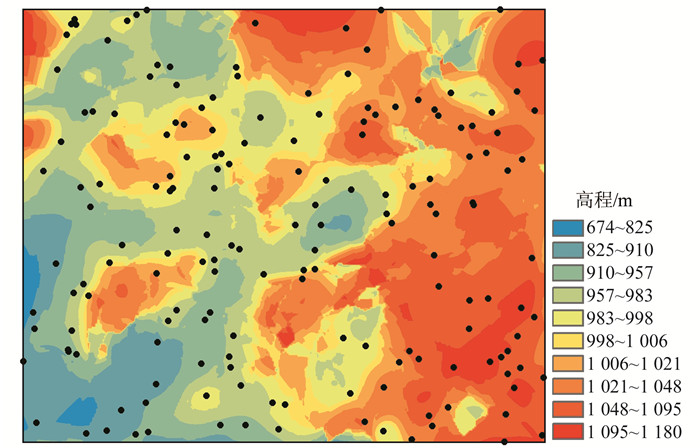
3 案例分析本次共选用170个采样点数据[19],采样点高程分布均匀,且高程起伏度明显。为建立曲面拟合多项式及分析不同权函数对曲面的拟合效果,将全部采样点通过ArcGIS软件以空间分布的形式进行表示(图 2),表 1为部分采样点数据。
|
图 2 采样点分布 Fig. 2 Distribution of sample points |
|
|
表 1 部分采样点坐标及高程 Tab. 1 Coordinate and elevation of some sample points |
根据样本点分布特征及研究区大小将研究区划分为18×22个以内插点为原点的矩形区域,每个矩形区域的大小约为500 m×500 m。通常情况下,动态球覆盖的区域内约含4~7个样本点,通过公式可计算出动态球半径选点法中半径R约为2 000 m。本文研究中含396个内插点,可建立396个二次曲面拟合多项式来拟合研究区。
3.1 无粗差情况下不同权函数结果对比在无粗差情况下,选取采样点建立多项式,运用上述3种不同的权函数对各采样点进行定权并计算多项式,采用MATLAB软件将曲面插值结果在三维空间中显示(图 3)。

|
图 3 无粗差情况下3种权函数结果对比 Fig. 3 Comparison of three weight functions without gross error |
从图 3可以看出,3种方法建立的曲面插值结果的整体效果相当,但仍存在一些细微差别。局部距离比定权插值的曲面在限定半径内,在视觉上保留高程变异明显的效果,在数据上遵从原数据的特征;反距离权重拟合的曲面与周围高程保持一致,变化较平缓;选权迭代法拟合的曲面相比于前两者较为平滑,这是因为权因子的迭代使其相对于相邻区域的高程值变化较为平缓。
为进一步验证曲面拟合程度,对多项式进行拟合优度检验,评判标准为每个多项式拟合优度r的均值,结果见表 2。
|
|
表 2 无粗差时拟合优度对比 Tab. 2 Comparison of goodness-of-fit without gross error |
地面高程测量的结果中往往存在粗差,为验证稳健估计中选权迭代法对含有粗差数据的抗差性,在数据中随机加入3组粗差。将存在粗差的数据代入模型中进行曲面拟合,图 4为3种不同权函数拟合的结果。
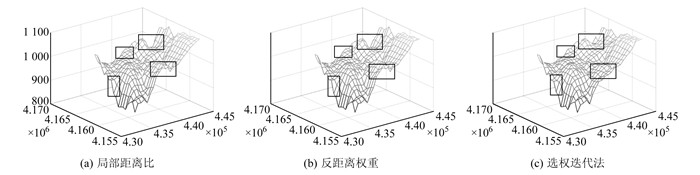
|
图 4 存在粗差情况下3种权函数结果对比 Fig. 4 Comparison of three weight functions with gross error |
从图 4可以看出,选权迭代法的效果最接近无粗差数据时的结果,图中标注的部分为插值曲面中效果明显的区域。由于稳健估计具有抗差性,运用选权迭代法将稳健估计思想运用到局部多项式插值中,通过在平差过程中改变权函数来实现参数估计的稳健性。依据计算误差的大小,利用公式对权因子进行修正得到新权重。对于含有粗差的数据,对选中数据点的权重进行多次迭代,减小误差大的数据的权重,增加计算结果的可信度。前2种定权方法的结果相似,均不能有效地避免粗差的影响。
对上述3种方法进行拟合优度检验并将结果进行对比,由于加入粗差后缺少标准来检验实验数据是否准确,因此以无粗差时拟合优度最高的反距离权重的结果为检验标准,表 3为拟合检验结果。
|
|
表 3 存在粗差时拟合优度对比 Tab. 3 Comparison of goodness-of-fit with gross error |
针对无粗差的高程数据,反距离权重法为最优的定权方法,插值的结果与原数据的拟合度和准确度较高,在插值效果图上完全遵循原数据的特征;局部距离比拟合效果次之,选权迭代法的插值结果在三维显示中较其他两者更为平滑。加入粗差数据后,由于反距离权重法及局部距离比的结果都遵循原始数据的特征,因此在构建曲面模型时会引入粗差,使结果偏离准确值,这2种方法具有一定风险性;而通过稳健估计的选权迭代法的插值结果在视觉效果上与无粗差插值的结果相差较小,且拟合优度更高,其原因是基于稳健估计的选权迭代法具有良好的抗差性,结果更真实可靠。本文利用局部多项式插值与稳健估计思想相结合的方法来处理含有粗差的数据,能有效减弱粗差对插值结果的影响,提高插值精度,为局部多项式插值曲面的建立提供保证。
| [1] |
汪俊, 高金耀, 吴招才, 等. 局部多项式插值方法在多源海底沉积厚度数据融合中的应用[J]. 海洋科学, 2009, 33(4): 25-28 (Wang Jun, Gao Jinyao, Wu Zhaocai, et al. The Local Polynomials Fitting Methods on Geospatial Data Merging: An Application to the Multi-Resources Marine Sediment Thickness Data[J]. Marine Sciences, 2009, 33(4): 25-28)
(  0) 0) |
| [2] |
宋向阳, 吴发启. 几种插值方法在微DEM构建中的应用[J]. 水土保持研究, 2010, 17(5): 45-50 (Song Xiangyang, Wu Faqi. Application of the Spatial Interpolation Methods to the Study on Micro-DEM[J]. Research of Soil and Water Conservation, 2010, 17(5): 45-50)
(  0) 0) |
| [3] |
肖城龙. 基于ArcGIS的空间数据插值方法的研究与实验[J]. 城市勘测, 2017(6): 71-73 (Xiao Chenglong. The Study and Experiment of Spatial Data Interpolation Based on ArcGIS[J]. Urban Geotechnical Investigation and Surveying, 2017(6): 71-73 DOI:10.3969/j.issn.1672-8262.2017.06.018)
(  0) 0) |
| [4] |
Das R K, Samanta S, Jana S K, et al. Polynomial Interpolation Methods in Development of Local Geoid Model[J]. The Egyptian Journal of Remote Sensing and Space Science, 2018, 21(3): 265-271 DOI:10.1016/j.ejrs.2017.03.002
(  0) 0) |
| [5] |
卢月明, 王亮, 仇阿根, 等. 局部加权线性回归模型的PM2.5空间插值方法[J]. 测绘科学, 2018, 43(11): 79-84 (Lu Yueming, Wang Liang, Qiu Agen, et al. PM2.5 Spatial Interpolation Method Based on Local Weighted Linear Regression Model[J]. Science of Surveying and Mappin, 2018, 43(11): 79-84)
(  0) 0) |
| [6] |
李杰, 翟亮, 桑会勇, 等. PM2.5浓度插值中不同空间插值方法对比[J]. 测绘科学, 2016, 41(4): 50-54 (Li Jie, Zhai Liang, Sang Huiyong, et al. Comparison of Different Spatial Interpolation Methods for PM2.5[J]. Science of Surveying and Mapping, 2016, 41(4): 50-54)
(  0) 0) |
| [7] |
樊子德, 李佳霖, 邓敏. 顾及多因素影响的自适应反距离加权插值方法[J]. 武汉大学学报:信息科学版, 2016, 41(6): 1-6 (Fan Zide, Li Jialin, Deng Min. An Adaptive Inverse-Distance Weighting Spatial Interpolation Method with the Consideration of Multiple Factors[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 1-6)
(  0) 0) |
| [8] |
高彦林, 胡斌, 张瑞天, 等. 基于局部曲面加权的曲面插值方法[J]. 石油地球物理勘探, 2009, 44(5): 587-589 (Gao Yanlin, Hu Bin, Zhang Ruitian, et al. Surface Interpolation Technique Based on Local Surface Weighting Method[J]. Oil Geophysical Prospecting, 2009, 44(5): 587-589 DOI:10.3321/j.issn:1000-7210.2009.05.013)
(  0) 0) |
| [9] |
周秋生. 建立数字地面模型的算法研究[J]. 测绘工程, 2001, 10(1): 14-18 (Zhou Qiusheng. Research on the Algorithm of Construction of Digital Terrian Model[J]. Engineering of Surveying and Mapping, 2001, 10(1): 14-18 DOI:10.3969/j.issn.1006-7949.2001.01.004)
(  0) 0) |
| [10] |
Bhunia G S, Shit P K, Maiti R. Comparison of GIS-Based Interpolation Methods for Spatial Distribution of Soil Organic Carbon(SOC)[J]. Journal of the Saudi Society of Agricultural Sciences, 2018, 17(2): 114-126 DOI:10.1016/j.jssas.2016.02.001
(  0) 0) |
| [11] |
魏继德.空间插值方法的比较与优化[D].福州: 福州大学, 2010 (Wei Jide. The Comparison and Optimization of Spatial Interpolation Approaches[D]. Fuzhou: Fuzhou University, 2010) http://cdmd.cnki.com.cn/Article/CDMD-10386-1015022905.htm
(  0) 0) |
| [12] |
张锦明, 郭丽萍, 张小丹. 反距离加权插值算法中插值参数对DEM插值误差的影响[J]. 测绘科学技术学报, 2012, 29(1): 51-56 (Zhang Jinming, Guo Liping, Zhang Xiaodan. Effects of Interpolation Parameters in Inverse Distance Weighted Method on DEM Accuracy[J]. Journal of Geomatics Science and Technology, 2012, 29(1): 51-56 DOI:10.3969/j.issn.1673-6338.2012.01.013)
(  0) 0) |
| [13] |
张志伟, 暴景阳, 肖付民. 抗差估计的多波束测深数据内插方法[J]. 测绘科学, 2016, 41(10): 14-18 (Zhang Zhiwei, Bao Jingyang, Xiao Fumin. An Interpolation Method of Multibeam Data Based on Robust Estimation[J]. Science of Surveying and Mapping, 2016, 41(10): 14-18)
(  0) 0) |
| [14] |
杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993 (Yang Yuanxi. Robust Estimation Theory and Its Application[M]. Beijing: Bayi Press, 1993)
(  0) 0) |
| [15] |
杨勇喜, 贾东振, 何秀凤. 基于选权迭代法的抗差整体最小二乘及其应用[J]. 测绘工程, 2014, 23(12): 56-59 (Yang Yongxi, Jia Dongzhen, He Xiufeng. Robust Total Least-Squares Based on Selecting Weight Iteration Method and Its Application[J]. Engineering of Surveying and Mapping, 2014, 23(12): 56-59 DOI:10.3969/j.issn.1006-7949.2014.12.014)
(  0) 0) |
| [16] |
肖明.抗差估计等价权函数的优化及其抗差效果评价[D].淮南: 安徽理工大学, 2018 (Xiao Ming. Optimizations for Equivalent Weight Function in Robust Estimation and Evaluation of Its Robustness[D]. Huainan: Anhui University of Science and Technology, 2018) http://cdmd.cnki.com.cn/Article/CDMD-10361-1018180967.htm
(  0) 0) |
| [17] |
王建民, 谢锋珠. MATLAB与测绘数据处理[M]. 武汉: 武汉大学出版社, 2015 (Wang Jianmin, Xie Fengzhu. MATLAB and Surveying Data Processing[M]. Wuhan: Wuhan University Press, 2015)
(  0) 0) |
| [18] |
邱卫宁. 测量数据处理理论与方法[M]. 武汉: 武汉大学出版社, 2008 (Qiu Weining. The Theory and Method of Surveying Data Processing[M]. Wuhan: Wuhan University Press, 2008)
(  0) 0) |
| [19] |
汤国安, 杨昕. ArcGIS地理信息系统空间分析实验教程[M]. 北京: 科学出版社, 2006 (Tang Guoan, Yang Xin. Spatial Analysis Experiment Course of Geographic Information System[M]. Beijing: Science Press, 2006)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


