2020, Vol. 40
基于普通克里金外推的迭代维纳滤波法向下延拓
1. 中国地质大学(北京)土地科学技术学院，北京市学院路29号，100083;
2. 中国地震局第一监测中心，天津市耐火路7号，300180;
3. 青海省自然资源遥感中心，西宁市黄河路13号，810001;
4. 青海省有色第一地质勘查院，西宁市金和路36号，810007
2. 中国地震局第一监测中心，天津市耐火路7号，300180;
3. 青海省自然资源遥感中心，西宁市黄河路13号，810001;
4. 青海省有色第一地质勘查院，西宁市金和路36号，810007
摘要：在利用普通克里金方法外推的基础上，通过频域径向平均功率谱估算噪声方差，采用迭代维纳滤波法获取较为稳定的重力场向下延拓结果，并分别利用模拟算例和实际数据进行实验。对于模拟算例，外推后的均方根误差由6.72 μGal下降到1.89 μGal，相对误差由9.26%下降到4.44%。对于实际数据，外推后延拓结果不仅可避免边缘失真现象，而且能更好地反映浅源高频异常特征信息。
关键词：重磁位场；解析延拓；普通克里金；径向平均功率谱；维纳滤波；快速傅里叶变换
重力研究对于开展地震预测、地球勘探、地质构造以及其他领域的研究具有重要意义[1-6]。借助重力手段进行向下延拓计算，可以获取更为清晰的浅源重力场信息，但下延计算极不稳定。频域维纳滤波法是常用的解决方法之一[7-9]，但如果未进行边界外推，下延结果常会出现边界失真的现象。最小曲率方法是进行外推的常用方法之一[10]，但在进行外推时需要考虑待解算结点与约束点之间的关系，算法效率相对低下，且必须指定外推边界值。本文优选普通克里金方法进行外推，无需指定外推边界，在此基础上利用频域迭代维纳滤波法进行下延计算，下延结果可较好地凸显浅源高频信息特征，同时可避免解算边界失真。
1 方法原理假定三维笛卡尔坐标系中z垂直向下，在z=0和z=h(h>0)平面上的位场分别为g(x, y, 0)和g(ξ, η, h)，g(x, y, 0)已知，g(ξ, η, h)为待求位场。则有：
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g(x, y, 0) = \\ \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {k(\xi - x, \eta - y)g(\xi , \eta , h){\rm{d}}\xi {\rm{d}}\eta } } \end{array} $ | (1) |
| $ \begin{array}{l} {\rm{其中}}{\kern 1pt} {\kern 1pt} , {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k(\xi - x, \eta - y) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{2\pi }}\frac{h}{{{{[{{(\xi - x)}^2} + {{(\eta - y)}^2} + {h^2}]}^{3/2}}}} \end{array} $ |
式(1)为卷积形式，可进一步简化为：
| $ {G_2} = K*{G_1} $ | (2) |
式中，G2=F[g(x, y, 0)]，K=F[(ξ－x, η－y)]，G1=F[g(x, y, h)]。F[·]为Fourier变换，*为卷积。
进一步推导出频域迭代维纳滤波表达式[9]：
| $ {G_1}^{n + 1} = \frac{{{K^*}}}{{K{K^*} + N/{G_1}^{(n)}}}{G_2} $ | (3) |
式中，K*为K共轭，N为噪声频谱，n=1, 2, 3, …，为迭代次数。初次迭代时令G1=G2，N值可利用Parseval定理估算得到[9]。
在进行迭代维纳滤波前，首先需对位场数据进行克里金外推。克里金插值方法是建立在变异函数理论及结构分析基础上，在有限的局部区域内对区域化变量进行线性无偏最优估计。利用任意两点之间的协方差函数以及任意点与待求点的协方差函数，求解相应点值的权重系数λ为克里金方法的关键，其表达式为：
| $ \left\{ \begin{array}{l} \sum\limits_{j = 1}^n {{\lambda _i}C({x_i}, {x_j}) - u = C({x_i}, {x_0})} , i = 1, 2, ..., n\\ \sum\limits_{i = 1}^n {{\lambda _i}} - 1 = 0 \end{array} \right. $ | (4) |
式中，C(xi, xj)为任意两点之间的协方差，u为常数。λ一旦求出，待插点也随之确定。本文计算选用普通克里金方法，该方法假设随机函数二阶平稳，较为稳健灵活。
2 算例分析 2.1 模拟算例以球体模型组合作为模拟算例(数据见表 1)，从z=0 m向z=10 m延拓。首先采用普通克里金外推方法，再进行向下延拓对比分析，其中加入的白噪声均值为0，方差为0.1 μGal。图 1(c)和1(e)分别为未经外推的维纳滤波下延结果以及误差分布情况，图 1(d)和1(f)分别为外推后的维纳滤波下延结果以及误差分布情况。从图中可以看出，外推前后结果的主要区别集中在边缘处。图 1(g)和1(h)为外推前后的均方根误差和相对误差计算结果对比，外推后向下延拓结果的均方根误差为1.89 μGal，相对误差为4.44%；而未经外推的向下延拓结果的均方根误差为6.72 μGal，相对误差为9.26%，表明外推后的维纳滤波向下延拓结果优于未经外推的重力场向下延拓结果。
|
表 1 模拟算例 Tab. 1 Simulation example |
|
图 1 模拟算例对比 Fig. 1 Comparison of simulation example |
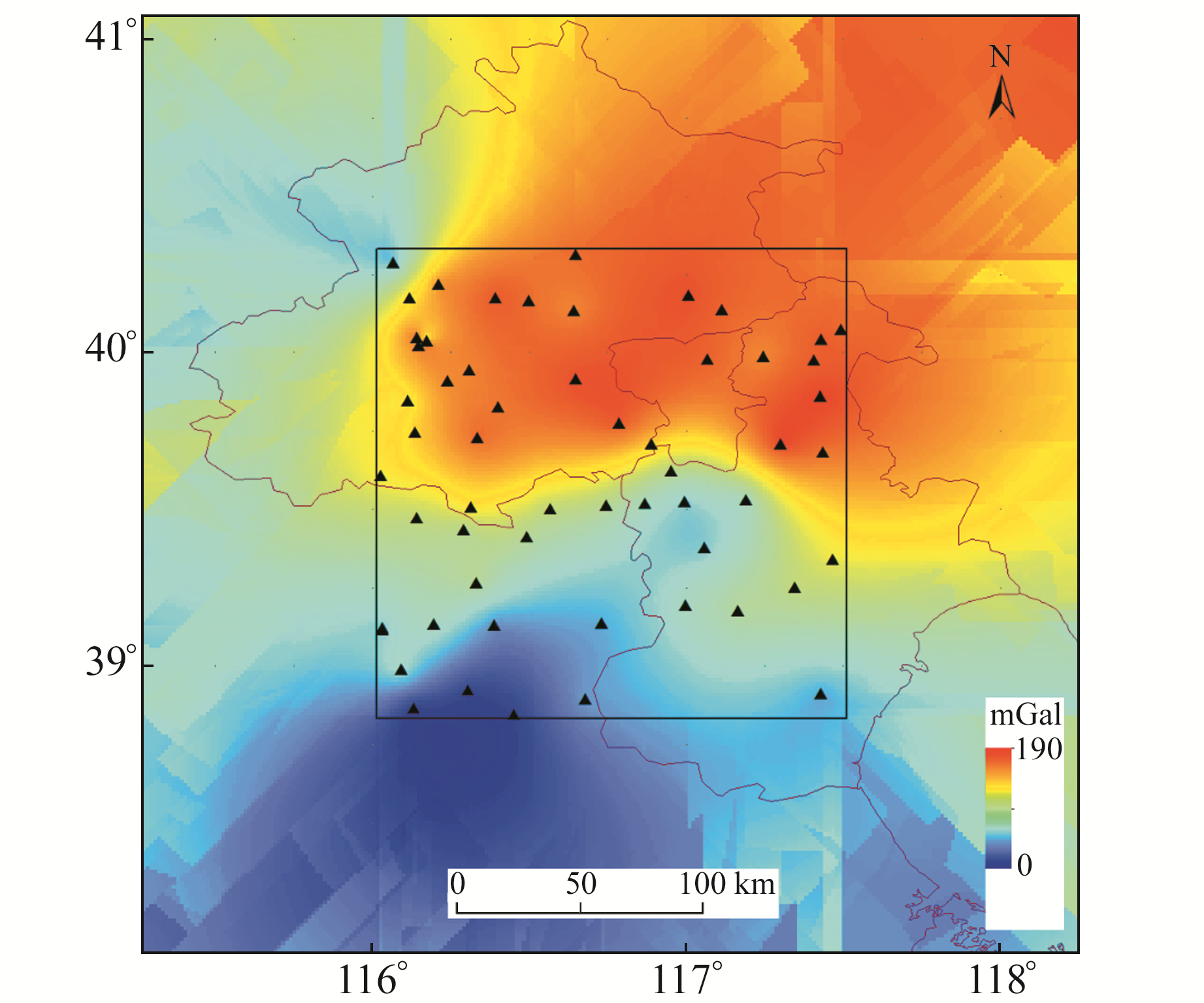
如图 2所示，黑色矩形框为研究区，位于北京、天津、河北交界处(38.8°~40.3°N，116.0°~117.5°E)，数据来自2014年流动重力观测结果，黑色矩形框外为外推区域(38.0°~41.1°E，115.2°~118.2°N)。首先利用普通克里金方法进行插值处理，同时进行内插和外推处理，然后分别利用外推前后的流动重力场数据进行重力异常下延计算，延拓距离为1 000 m。
|
图 2 研究区重力位场及外推结果 Fig. 2 Gravity potential field and extrapolation result of study area |
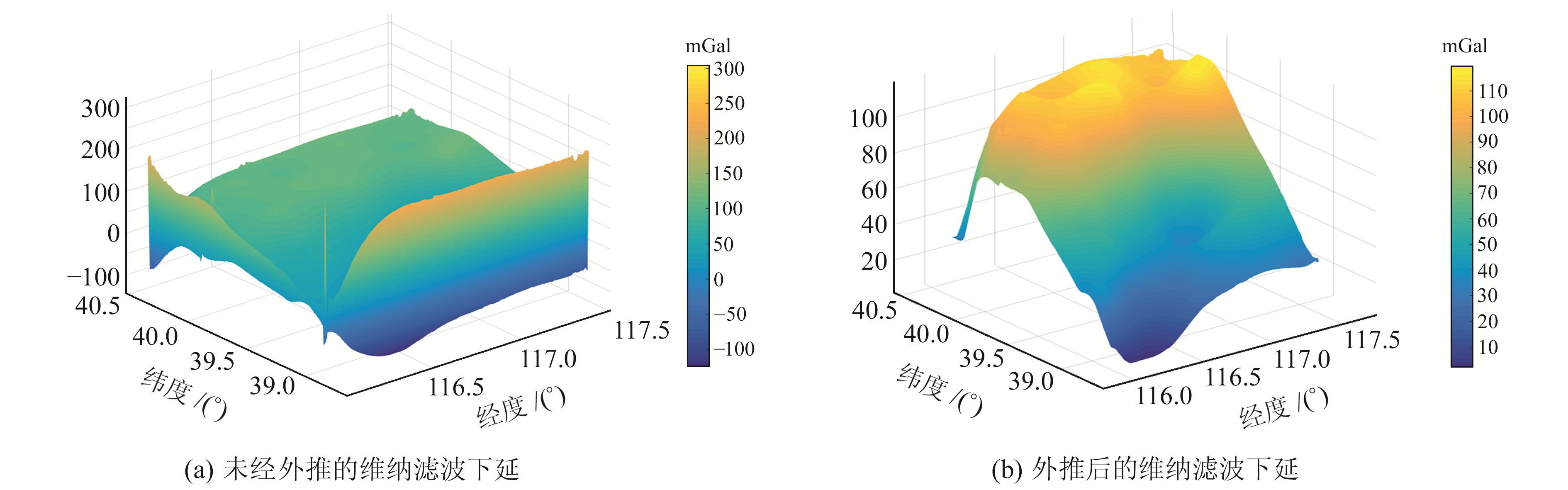
为了更好地显示延拓效果，使用三维形式展示延拓解算结果。如图 3(a)所示，解算结果虽在一定程度上仍能反映延拓前原始重力异常的轮廓信息，但在解算区两侧边缘的狭长范围内会出现计算结果失真的现象。如图 3(b)所示，延拓结果不仅可避免边缘失真现象，同时能更好地反映浅源高频特征信息。
|
图 3 实测数据延拓结果对比 Fig. 3 Comparison of continuation result of actual data |
向下延拓有利于提取地壳浅表层高频信息，对于识别浅源地震的重力变化特征具有重要意义，但下延计算的不稳定性会约束该方法的广泛使用。本文利用普通克里金方法对数据进行外推处理，然后利用迭代维纳滤波法进行重力位场向下延拓解算，可有效避免出现边缘失真的现象，得到更为稳定的延拓解。
参考文献
| [1] |
祝意青, 梁伟锋, 赵云峰, 等. 2017年四川九寨沟MS7.0地震前区域重力场变化[J]. 地球物理学报, 2017, 60(10): 4 124-4 131 (Zhu Yiqing, Liang Weifeng, Zhao Yunfeng, et al. Gravity Changes before the Jiuzhaigou, Sichuan, MS7.0 Earthquake of 2017[J]. Chinese Journal of Geophysics, 2017, 60(10): 4 124-4 131)
(  0) |
| [2] |
申重阳, 杨光亮, 谈洪波, 等. 维西-贵阳剖面重力异常与地壳密度结构特征[J]. 地球物理学报, 2015, 58(11): 3 952-3 964 (Shen Chongyang, Yang Guangliang, Tan Hongbo, et al. Gravity Anomalies and Crustal Density Structure Characteristics of Profile[J]. Chinese Journal of Geophysics, 2015, 58(11): 3 952-3 964)
( 0) |
| [3] |
陈石, 郑秋月, 徐伟民. 南北地震带南段地壳厚度重震联合最优化反演[J]. 地球物理学报, 2015, 58(11): 3 941-3 951 (Chen Shi, Zheng Qiuyue, Xu Weimin. Joint Optimal Inversion of Gravity and Seismic Data to Estimate Crustal Thickness of the Southern Section of the North-South Seismic Belt[J]. Chinese Journal of Geophysics, 2015, 58(11): 3 941-3 951)
( 0) |
| [4] |
胡敏章, 郝洪涛, 宋浩, 等. 弱地震活动背景地区流动重力变化探析[J]. 大地测量与地球动力学, 2019, 39(4): 339-343 (Hu Minzhang, Hao Hongtao, Song Hao, et al. Analysis of Gravity Changes in Areas of Weak Seismic Activity Background[J]. Journal of Geodesy and Geodynamics, 2019, 39(4): 339-343)
( 0) |
| [5] |
王同庆, 陈石, 梁伟锋, 等. 2016年门源MS6.4地震前的区域重力场变化与定量参数分析[J]. 地震地质, 2018, 40(2): 349-360 (Wang Tongqing, Chen Shi, Liang Weifeng, et al. Variations of the Gravity Field and Quantitative Parameter Analysis before the 2016 Menyuan MS6.4 Earthquake[J]. Seismology and Geology, 2018, 40(2): 349-360 DOI:10.3969/j.issn.0253-4967.2018.02.005)
( 0) |
| [6] |
朱文武, 秦昆, 王同庆, 等. 内蒙古阿拉善左旗MS5.8震源区及周边重力布格异常的计算与分析[J]. 大地测量与地球动力学, 2016, 36(10): 851-853 (Zhu Wenwu, Qin Kun, Wang Tongqing, et al. Calculation and Analysis of Bouguer Anomaly in Alxa Left Banner MS5.8 Epicenter and Sourrounding Regions of Inner-Mongolia[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 851-853)
( 0) |
| [7] |
Clarke G K C. Optimum Second-Derivative and Downward Continuation Filters[J]. Geophysics, 1969, 34(3): 424-437 DOI:10.1190/1.1440020
( 0) |
| [8] |
Pawlowski R S. Preferential Continuation for Potential-Field Anomaly Enhancement[J]. Geophysics, 1995, 60(2): 390-398
( 0) |
| [9] |
曾小牛, 刘代志, 李夕海, 等. 位场向下延拓的改进迭代维纳滤波法[J]. 地球物理学报, 2014, 57(6): 1 958-1 967 (Zeng Xiaoniu, Liu Daizhi, Li Xihai, et al. An Improved Iterative Wiener Filter for Downward Continuation of Potential Fields[J]. Chinese Journal of Geophysics, 2014, 57(6): 1 958-1 967)
( 0) |
| [10] |
王万银, 邱之云, 刘金兰, 等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009, 24(4): 1 327-1 338 (Wang Wanyin, Qiu Zhiyun, Liu Jinlan, et al. The Research to the Extending Edge and Interpolation Based on the Minimum Curvature Method in Potential Field Data Processing[J]. Progress in Geophysics, 2009, 24(4): 1 327-1 338)
( 0) |
Iterative Wiener Filter Based on Ordinary Kriging Extrapolation for Downward Continuation
1. School of Land Science and Technology, China University of Geosciences, 29 Xueyuan Road, Beijing 100083, China;
2. The First Monitoring and Application Center, CEA, 7 Naihuo Road, Tianjin 300180, China;
3. Qinghai Natural Resources Remote Sensing Center, 13 Huanghe Road, Xining 810001, China;
4. Qinghai Nonferrous First Geological Survey Institute, 36 Jinhe Road, Xining 810007, China
2. The First Monitoring and Application Center, CEA, 7 Naihuo Road, Tianjin 300180, China;
3. Qinghai Natural Resources Remote Sensing Center, 13 Huanghe Road, Xining 810001, China;
4. Qinghai Nonferrous First Geological Survey Institute, 36 Jinhe Road, Xining 810007, China
Abstract: Based on ordinary Kriging extrapolation method, the noise variance is estimated by frequency radially averaged power spectrum, and then the downward continuation of stable gravity field is calculated by the iterative Wiener filter. The simulation example and actual data are separately used to do experiments. The accuracy of simulation example is significantly improved after extrapolation, the mean square error decreases from 6.72 μGal to 1.89 μGal, and the relative error decreases from 9.26% to 4.44%. The continuation result of actual data after extrapolation reflects the shallower anomaly information with high frequency better and avoids obtaining false values in the boundary.
Key words:
gravity and magnetic field; analytic continuation; ordinary Kriging; radially averaged power spectrum; Wiener filter; fast Fourier transformation