地震会对发震断层周边区域的构造应力场产生影响,造成的库仑应力变化会触发后续地震或延缓地震的发生[1]。库仑应力变化被广泛应用于大地震后断层周围余震活动的时空分布特征及其触发机制研究[2-5],但仍有许多问题有待更深入分析,如源断层模型参数、接收断层几何参数(走向、倾角和滑动角)、摩擦系数、Skempton系数等对库仑应力变化可靠性的影响。近年来,国内外学者相继对上述参数进行研究,并探讨各参数对库仑应力变化的影响[5-10]。目前已有很多文献对汶川MW7.9地震库仑应力变化的不确定性及库仑应力变化与余震的关系进行研究[10-13],但仍缺乏相关参数对库仑应力变化可靠性影响的系统和定量研究,而可靠的库仑应力变化对研究余震分布和地震危险性评估具有重要意义。本文采用精细的同震滑动分布模型,研究汶川地震接收断层走向、倾角、滑动角、摩擦系数、Skempton系数对库仑应力变化的影响,并利用变化系数评估库仑应力变化的可靠性,分析可靠库仑应力变化与余震分布之间的关系。
1 数据和参数选取 1.1 余震数据和源断层模型汶川MW7.9地震震源深度为14~19 km,地震发生在龙门山中央断裂和前山断裂上。截至2008-08-27,汶川震区内共记录到余震25 797次,其中5.0~5.9级余震55次,6级以上余震8次。由于同震破裂深度范围约为0~22 km[14],本文选取近似平均深度10 km作为研究深度,计算10 km深度面的库仑应力变化。考虑到余震定位误差的影响,选取震源深度为10±0.5 km的余震数据。
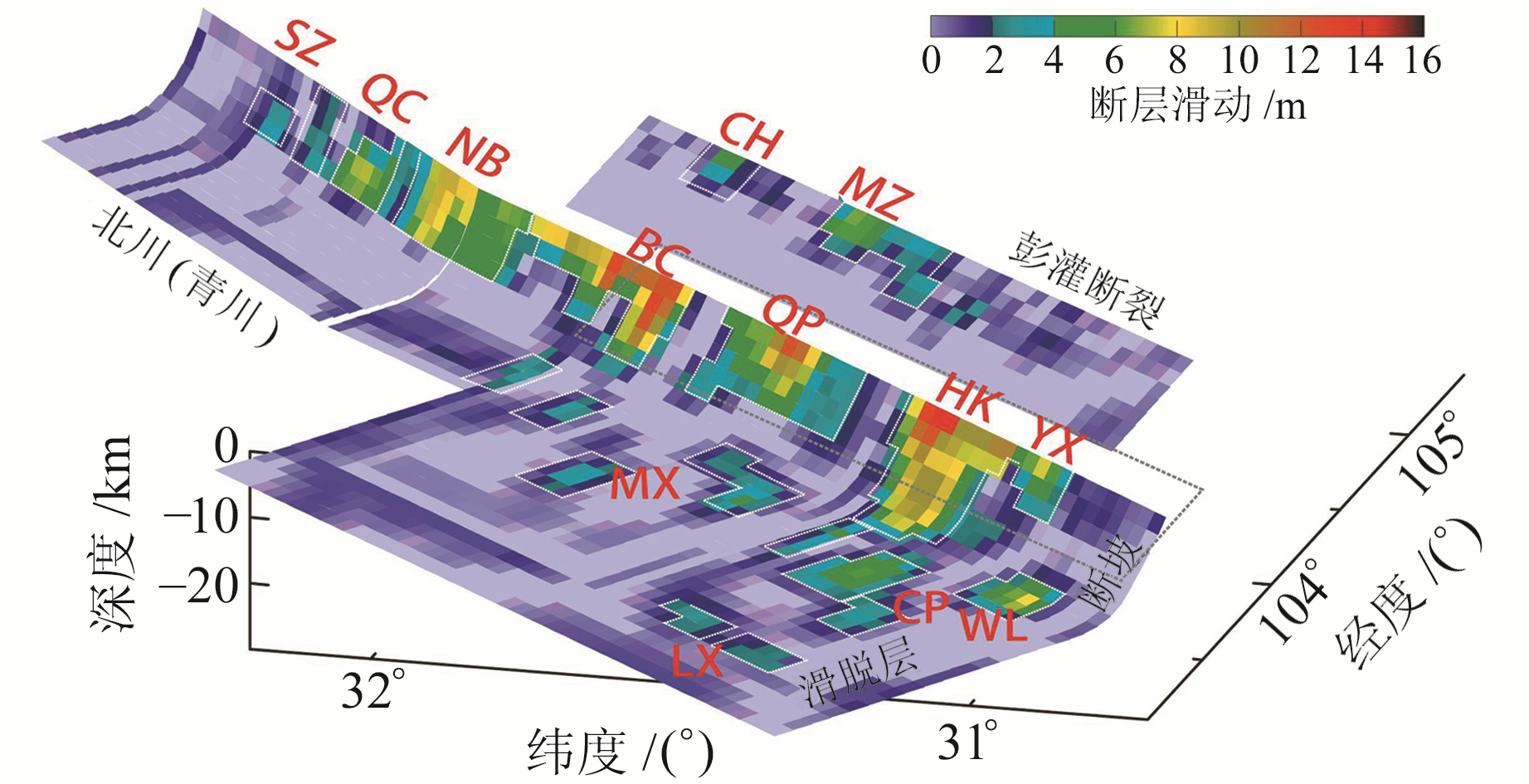
国内外学者在汶川地震后相继提出多种同震滑动分布模型[14-17],本文选取Wang等[14]的同震滑动分布模型作为计算库仑应力变化的源断层模型(图 1)。该模型采用更为密集的大地测量数据,根据InSAR、GPS、水准网及三角网观测数据证实汶川地震映秀至北川段深部滑脱断层的存在,得到的同震滑动分布模型更为可靠、精细。
|
图 1 汶川地震同震滑动分布模型(改绘自Wang等[14]) Fig. 1 Coseismic slip distribution model of Wenchuan earthquake |
在研究影响库仑应力变化的参数时,通常是参考其他文献直接对接收断层走向、倾角、滑动角及其不确定性进行预定义,摩擦系数和Skempton系数则一般使用经验值。本文在计算汶川地震源断层周围水平网格点的库仑应力变化时,主要研究接收断层走向、倾角、滑动角、摩擦系数及Skempton系数对库仑应力变化可靠性的影响及可靠库仑应力变化与近场余震触发的关系,近场余震参数一般与主震参数接近,故假设网格点各参数均与主震断层参数一致。表 1为上述参数在本文中所采用的均值和标准差[10],其中接收断层走向、倾角、滑动角的均值和标准差为2008年汶川地震多个震源机制解的均值和标准差,摩擦系数和Skempton系数的均值和标准差则根据经验值直接假设得到。
|
|
表 1 各参数均值和标准差 Tab. 1 Mean and standard deviation of parameters |
库仑破裂准则表明,当岩石内部某点在截面上的剪应力大于该点的抗剪强度时,岩石将沿该截面发生破裂。库仑应力为剪应力与抗剪强度之差,可表征岩石沿截面趋于破裂的程度。岩石内部应力状态较难获取,所以通常研究库仑应力变化[2]。断层面上的库仑应力变化计算公式为[3]:
| $ \Delta {\rm{CFS}} = \Delta \tau + \mu (\Delta {\sigma _n} + \Delta P) $ | (1) |
式中,Δτ为剪应力变化,μ为摩擦系数,Δσn为正应力变化(拉伸为正),ΔP为孔隙压力变化。孔隙压力减小摩擦系数的效应可用μ′=μ(1-B)表示,其中B为Skempton系数,其范围为0~1。故式(1)可转化为:
| $ \Delta {\rm{CFS}} = \Delta \tau + {\mu ^\prime}\Delta {\sigma _n} $ | (2) |
采用Coulomb 3.3软件在库仑破裂准则下基于弹性半空间位错理论[18]计算地震引起的库仑应力变化。
2.2 变化系数本文采用变化系数(coefficient of variation, CV)来评价库仑应力变化的可靠性,库仑应力变化的可靠性随着CV值的增大而降低,其计算公式为[3, 8]:
| $ {\rm{CV}} = \frac{{\sigma (\Delta {\rm{CFS}})}}{{\left| {{\rm{mean}}(\Delta {\rm{CFS}})} \right|}} $ | (3) |
式中,σ(ΔCFS)为库仑应力变化标准差,|mean(ΔCFS)|为库仑应力变化均值的绝对值。本文参考前人研究将可靠阈值设置为0.5[8],即当|mean(ΔCFS)|超过σ(ΔCFS)两倍(CV≤0.5)时,库仑应力变化值被认为是可靠的。
本文以表 1中走向φ、倾角δ、滑动角λ、摩擦系数μ和Skempton系数B的均值P=[φ, δ, λ, μ, B]为参考值,根据各参数的参考值计算得到整体的库仑应力变化参考值。根据表 1中各参数的均值和标准差,利用正态分布生成各参数的随机数据集SPi(i=1, 2, …, 5),各数据集中分别包含1 000个元素。当分析上述某一参数,如接收断层走向时,接收断层走向分别采用随机数据集Sφ中的1 000个元素,其他参数均采用参考值[δ, λ, μ, B],计算得到网格点库仑应力变化值ΔCFSφ.j, k(j为其中一个网格点,k=1, 2, …, 1 000),然后计算得到网格点1 000个库仑应力变化值的均值为:
| $ {\rm{mean}}(\Delta {\rm{CF}}{{\rm{S}}_{\varphi , j}}) = \frac{1}{{{\rm{1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{000}}}}\sum\limits_{k = 1}^{{\rm{1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{000}}} {\Delta {\rm{CF}}{{\rm{S}}_{\varphi , j, k}}} $ | (4) |
库仑应力变化值的标准差为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta (\Delta {\rm{CF}}{{\rm{S}}_{\varphi , j}}) = \\ \sqrt {\frac{1}{{{\rm{1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{000}}}}\sum\limits_{k = 1}^{{\rm{1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{000}}} {{{[\Delta {\rm{CF}}{{\rm{S}}_{\varphi , j, k}} - {\rm{mean}}(\Delta {\rm{CF}}{{\rm{S}}_{\varphi , j}})]}^2}} } \end{array} $ | (5) |
网格点库仑应力变化的变化系数为:
| $ {\rm{C}}{{\rm{V}}_{\varphi , j}} = \frac{{\sigma (\Delta {\rm{CF}}{{\rm{S}}_{\varphi , j}})}}{{\left| {{\rm{mean}}(\Delta {\rm{CF}}{{\rm{S}}_{\varphi , j}})} \right|}} $ | (6) |
通过上述方法可得到受接收断层走向影响的整体的库仑应力变化均值(以下称为受接收断层走向影响的库仑应力变化值)和变化系数,采用同样方法可分析其他参数对库仑应力变化的影响。
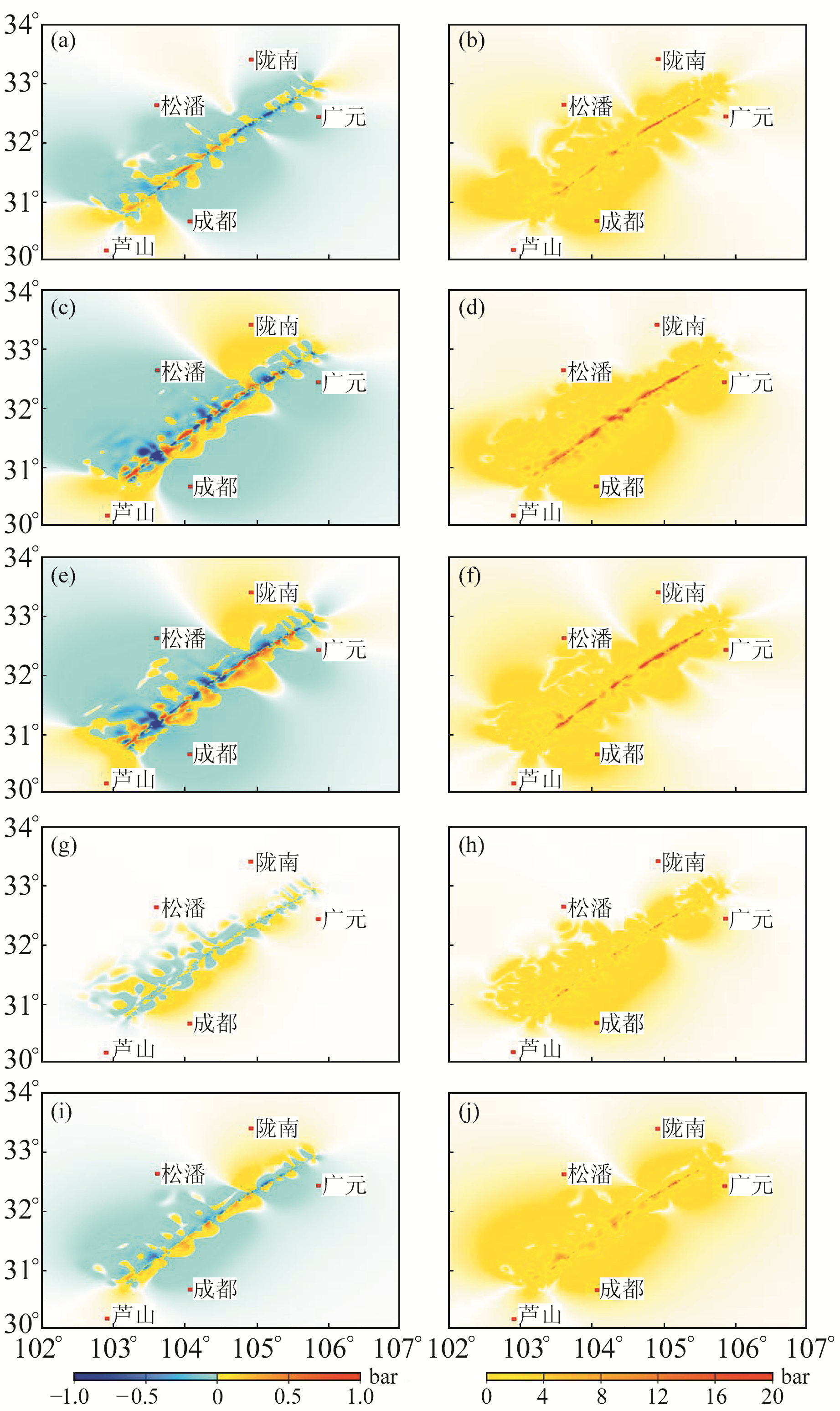
3 计算结果与分析 3.1 库仑应力变化的可靠性从图 2(a)、2(c)、2(e)、2(g)和2(i)中可知,受各参数影响的库仑应力变化值与库仑应力变化参考值的偏差基本小于1 bar,主要集中在靠近源断层的两侧区域。从整体来看,相对于接收断层几何参数,受摩擦系数和Skempton系数影响的库仑应力变化值与库仑应力变化参考值的偏差更小,特别是摩擦系数,几乎可忽略不计。由图 2(b)、2(d)、2(f)、2(h)和2(j)可知,受各参数影响的库仑应力变化标准差在源断层两侧附近普遍偏大,表明该区域库仑应力变化较离散,不确定性高。
|
(a)、(c)、(e)、(g)、(i)分别为受接收断层走向、倾角、滑动角、摩擦系数、Skempton系数影响的库仑应力变化值与库仑应力变化参考值的偏差; (b)、(d)、(f)、(h)、(j)分别为受接收断层走向、倾角、滑动角、摩擦系数、Skempton系数影响的库仑应力变化标准差 图 2 库仑应力变化偏差和标准差 Fig. 2 Deviation and standard deviation of Coulomb stress change |
本文采用CV评价库仑应力变化可靠性,CV值越大表明库仑应力变化可靠性越低。从图 3可以看出,CV在库仑应力变化正值区或负值区内部较小,普遍小于0.1,可靠性高;在接近正负值交界处,CV逐渐增大,且越靠近源断层CV变化率越大,表明越靠近库仑应力变化正负值交界处,库仑应力变化的可靠性越低,且越靠近源断层降低趋势会更明显。本文认为当CV>0.5时表示库仑应力变化不可靠,图 3 CV掩膜分布中红色区域为满足CV≤0.5的可靠库仑应力变化分布区域。从CV掩膜分布图可知,不可靠库仑应力变化主要分布在库仑应力变化正负值交界处附近。

|
(a)、(c)、(e)、(g)、(i)分别为受接收断层走向、倾角、滑动角、摩擦系数、Skempton系数影响的库仑应力变化的变化系数; (b)、(d)、(f)、(h)、(j)分别为受接收断层走向、倾角、滑动角、摩擦系数、Skempton系数影响的可靠库仑应力变化分布掩膜(红色区域为满足CV≤0.5的可靠库仑应力变化分布区域) 图 3 CV和CV掩膜 Fig. 3 CV and mask of CV |
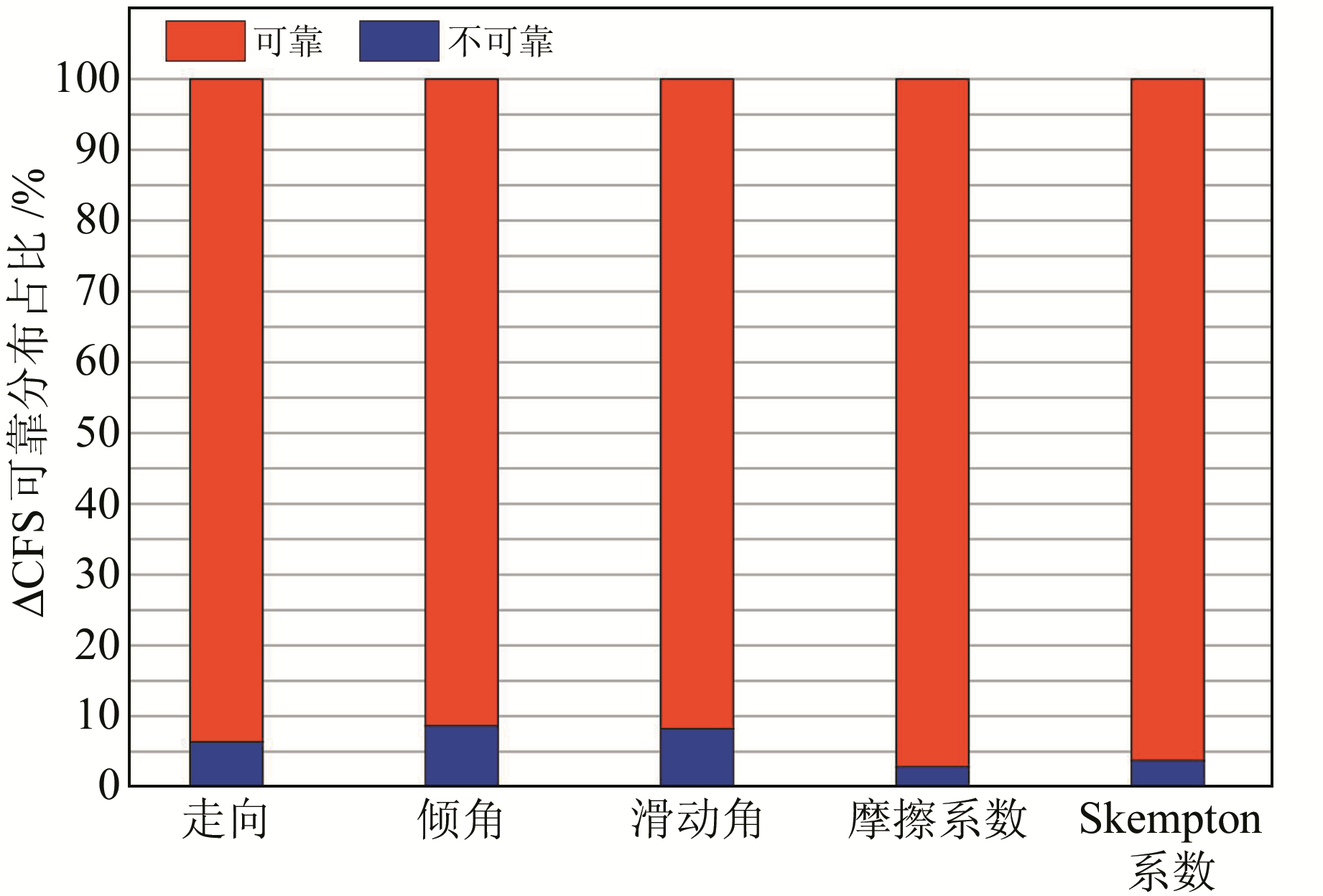
图 4为受各参数影响的可靠与不可靠库仑应力变化分布区域占比。从图 3、4可知,受接收断层走向、倾角、滑动角影响的不可靠库仑应力变化分布区域相对较小。受倾角影响的不可靠库仑应力变化分布区域主要集中在近场区域;受走向和滑动角影响的不可靠库仑应力变化分布区域主要集中在垂直于源断层方向并远离源断层的区域;受摩擦系数和Skempton系数影响的可靠库仑应力变化分布区域较大,占比均超过95%。以上结果表明,在本文所考虑的5个参数中,接收断层几何参数对库仑应力变化可靠性的影响较大,其中倾角影响最大。
|
图 4 可靠与不可靠库仑应力变化分布区域占比 Fig. 4 The proportion of distribution area of reliable and unreliable Coulomb stress change |
图 5为库仑应力变化参考分布、余震分布及剔除不可靠库仑应力变化后的参考分布。地震引起的断层滑动会释放断层累积的能量,并对断层周围的库仑应力产生影响。从图 5 (a)可知,汶川地震同震滑动引起断层周围区域的库仑应力发生变化,断层两端库仑应力变化为正;垂直于走向的近场区域的库仑应力变化正负值相互交错且变化量较大,远场区域主要为负值且变化量小。结合余震分布可知,汶川地震同震滑动会延缓块体内部地震的发生,而在错动块体附近和断层两端的广大区域则会促进地震发生。

|
(a)库仑应力变化参考分布, 黑点为震源深度10±0.5 km的余震; (b) ~ (f)分别为剔除受接收断层走向、倾角、滑动角、摩擦系数、Skempon系数影响的不可靠库仑应力变化的参考分布, 灰色区域为不可靠库仑应力变化分布区域 图 5 可靠库仑应力变化分布 Fig. 5 Distribution of reliable Coulomb stress change |
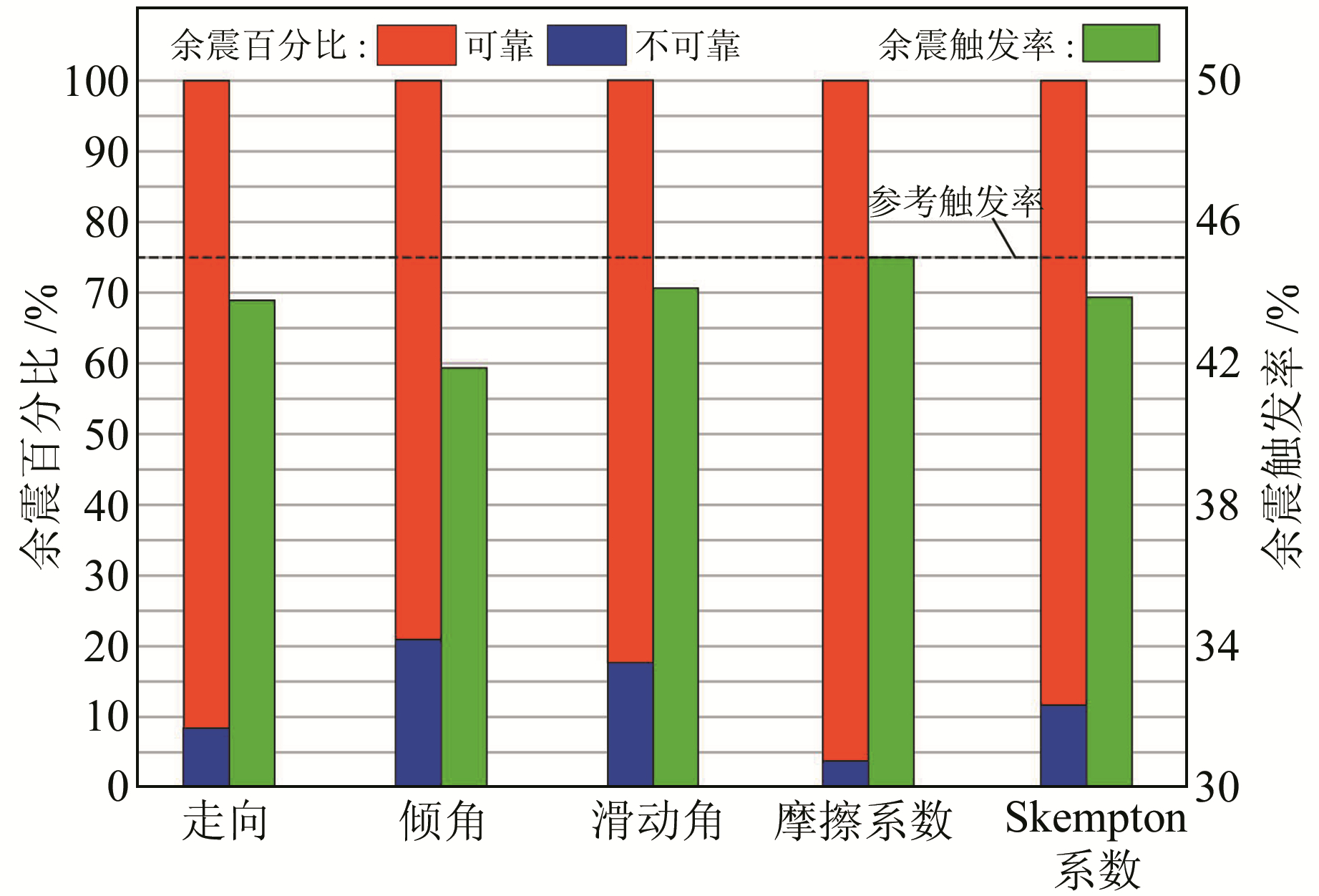
可靠的库仑应力变化在余震时空分布和触发机制研究中具有重要意义。图 6为余震位于受各参数影响的库仑应力变化分布中可靠和不可靠分布区域的占比及可靠库仑应力变化分布区域的余震触发率[19],其中余震触发率为余震位于库仑应力变化正值区的占比,参考触发率为余震位于库仑应力变化参考分布正值区的占比。在受各参数影响的库仑应力变化分布中,余震位于可靠分布区域占比均大于不可靠分布区域占比。受接收断层倾角影响的库仑应力变化分布中余震位于不可靠分布区域的占比最大,超过20.0%,表明接收断层倾角造成的库仑应力变化可靠性差异对余震分布的影响最大;受摩擦系数影响的库仑应力变化分布中余震位于不可靠分布区域的占比最小,低于5.0%。剔除不可靠库仑应力变化和不可靠库仑应力变化分布区域内的余震后,余震触发率有所下降,其中受接收断层倾角影响的库仑应力变化分布中余震触发率下降最大,从参考触发率45.0%降至41.9%;受摩擦系数影响的库仑应力变化分布中余震触发率与参考触发率相当,表明摩擦系数对余震触发率无影响。从整体上看,接收断层几何参数和Skempton系数对余震触发率的影响均大于摩擦系数。
|
红蓝色柱分别为余震位于可靠和不可靠库仑应力变化分布区域占比; 绿色柱为余震触发率; 虚线为余震参考触发率 图 6 余震百分比和余震触发率 Fig. 6 The percentage of aftershock and aftershock triggering rate |
本文采用变化系数评估接收断层走向、倾角、滑动角、摩擦系数及Skempton系数对源断层周围库仑应力变化可靠性的影响,分析库仑应力变化可靠性与余震分布的关系。结果表明,库仑应力变化正值区或负值区内部CV值较小,可靠性高,越接近正值与负值交界处CV值迅速增大,可靠性急剧下降。在本文所研究的参数中,接收断层倾角对库仑应力变化可靠性的影响最大,可靠库仑应力变化分布区域占比91.4%,9.3%的余震位于可靠库仑应力变化分布区域,剔除不可靠库仑应力变化和不可靠库仑应力变化分布区域内的余震后,余震触发率下降3.1%。接收断层走向、滑动角及Skempton系数对库仑应力变化可靠性和余震触发率的影响小于接收断层倾角,但仍不可忽视;摩擦系数对库仑应力变化可靠性影响很小,对余震触发率无影响。通过对汶川地震可靠库仑应力变化的分析发现,汶川地震会促进断层附近及断层两端延伸方向区域地震的发生,而对垂直于走向方向的远场区域有延缓地震发生的作用。
| [1] |
李琦.龙门山至小江断裂滑动与应力变化研究[D].武汉: 中国地震局地震研究所, 2017 (Li Qi. Study on Slip and Stress Variation of Longmenshan to Xiaojiang Fault[D]. Wuhan: Institude of Seismology, CEA, 2017) https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&filename=1017181015.nh
(  0) 0) |
| [2] |
Harris R A, Simpson R W. Changes in Static Stress on Southern California Faults after the 1992 Landers Earthquake[J]. Nature, 1992, 360(6 401): 251-254
(  0) 0) |
| [3] |
缪淼, 朱守彪. 2013年芦山MS7.0地震产生的静态库仑应力变化及其对余震空间分布的影响[J]. 地震学报, 2013, 35(5): 619-631 (Miao Miao, Zhu Shoubiao. The Static Coulomb Stress Change of the 2013 Lushan MS7.0 Earthquake and Its Impact on the Spatial Distribution of Aftershocks[J]. Acta Seismologica Sinica, 2013, 35(5): 619-631 DOI:10.3969/j.issn.0253-3782.2013.05.001)
(  0) 0) |
| [4] |
黄禄渊, 张贝, 瞿武林, 等. 2010智利Maule特大地震的同震效应[J]. 地球物理学报, 2017, 60(3): 972-984 (Huang Luyuan, Zhang Bei, Qu Wulin, et al. The Co-Seismic Effects of 2010 Maule Earthquake[J]. Chinese Journal of Geophysics, 2017, 60(3): 972-984)
(  0) 0) |
| [5] |
Hainzl S, Enescu B, Cocco M, et al. Aftershock Modeling Based on Uncertain Stress Calculations[J]. Journal of Geophysical Research, 2009, 114(B5)
(  0) 0) |
| [6] |
Mildon Z K, Toda S, Walker J P, et al. Evaluating Models of Coulomb Stress Transfer: Is Variable Fault Geometry Important?[J]. Geophysical Research Letters, 2016, 43(24): 12 407-12 414 DOI:10.1002/2016GL071128
(  0) 0) |
| [7] |
Zhan Z W, Jin B K, Wei S J, et al. Coulomb Stress Change Sensitivity Due to Variability in Mainshock Source Models and Receiving Fault Parameters: A Case Study of the 2010-2011 Christchurch, New Zealand, Earthquakes[J]. Seismological Research Letters, 2011, 82(6): 800-814 DOI:10.1785/gssrl.82.6.800
(  0) 0) |
| [8] |
Woessner J, Jónsson S, Sudhaus H, et al. Reliability of Coulomb Stress Changes Inferred from Correlated Uncertainties of Finite-Fault Source Models[J]. Journal of Geophysical Research, 2012, 117(B7)
(  0) 0) |
| [9] |
熊维, 谭凯, 刘刚, 等. 2015年尼泊尔MW7.9地震对青藏高原活动断裂同震、震后应力影响[J]. 地球物理学报, 2015, 58(11): 4 305-4 316 (Xiong Wei, Tan Kai, Liu Gang, et al. Coseismic and Postseismic Coulomb Stress Changes on Surrounding Major Faults Caused by the 2015 Nepal MW7.9 Earthquake[J]. Chinese Journal of Geophysics, 2015, 58(11): 4 305-4 316)
(  0) 0) |
| [10] |
Wang J J, Xu C J, Freymueller J T, et al. Sensitivity of Coulomb Stress Change to the Parameters of the Coulomb Failure Model: A Case Study Using the 2008 MW7.9 Wenchuan Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(4): 3 371-3 392 DOI:10.1002/2012JB009860
(  0) 0) |
| [11] |
熊维, 谭凯, 刘刚, 等. 汶川地震对周边断层的库仑应力和发震概率影响的定量研究[J]. 大地测量与地球动力学, 2014, 34(5): 6-10 (Xiong Wei, Tan Kai, Liu Gang, et al. Quantitative Study on Influence of Wenchuan Earthquake on Fault Coulomb Stress and Earthquake Probability of the Faults Around[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 6-10)
(  0) 0) |
| [12] |
Nalbant S S, Mccloskey J. Stress Evolution before and after the 2008 Wenchuan, China Earthquake[J]. Earth and Planetary Science Letters, 2011, 307(1-2): 222-232 DOI:10.1016/j.epsl.2011.04.039
(  0) 0) |
| [13] |
石耀霖, 曹建玲. 库仑应力计算及应用过程中若干问题的讨论——以汶川地震为例[J]. 地球物理学报, 2010, 53(1): 102-110 (Shi Yaolin, Cao Jianling. Some Aspects in Static Stress Change Calculation——Case Study on Wenchuan Earthquake[J]. Chinese Journal of Geophysics, 2010, 53(1): 102-110 DOI:10.3969/j.issn.0001-5733.2010.01.011)
(  0) 0) |
| [14] |
Wang Q, Qiao X J, Lan Q G, et al. Rupture of Deep Faults in the 2008 Wenchuan Earthquake and Uplift of the Longmen Shan[J]. Nature Geoscience, 2011, 4(9): 634-640 DOI:10.1038/ngeo1210
(  0) 0) |
| [15] |
Shen Z K, Sun J B, Zhang P Z, et al. Slip Maxima at Fault Junctions and Rupturing of Barriers during the 2008 Wenchuan Earthquake[J]. Nature Geoscience, 2009, 2(10): 718-724 DOI:10.1038/ngeo636
(  0) 0) |
| [16] |
Feng G C, Hetland E A, Ding X L, et al. Coseismic Fault Slip of the 2008 MW7.9 Wenchuan Earthquake Estimated from InSAR and GPS Measurements[J]. Geophysical Research Letters, 2010, 37(1): L01302
(  0) 0) |
| [17] |
Tong X P, Sandwell D T, Fialko Y. Coseismic Slip Model of the 2008 Wenchuan Earthquake Derived from Joint Inversion of Interferometric Synthetic Aperture Radar, GPS and Field Data[J]. Journal of Geophysical Research, 2010, 115(B4)
(  0) 0) |
| [18] |
Okada Y. Internal Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1992, 82(2): 1 018-1 040
(  0) 0) |
| [19] |
Hardebeck J L, Nazareth J J, Hauksson E. The Static Stress Change Triggering Model: Constraints from Two Southern California Aftershock Sequences[J]. Journal of Geophysical Research, 1998, 103(B10): 24 427-24 437 DOI:10.1029/98JB00573
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


