2. 安徽省地震局郯庐断裂带中南段重点研究室,合肥市长江西路558号,230031
2009-06中国地震局在武汉及江西九江庐山基线场进行了10台CG-5型相对重力仪的测试工作,认为该型仪器漂移率大,但短期内线性程度好[1]。张松堂等[2]利用CG-5型重力仪的长期观测数据,分析了弹簧应力松弛效应对CG-5型重力仪的零点漂移、弹簧弹性滞后效应对观测精度及弹簧蠕变特性对仪器寿命的影响。沈博等[3]基于多台CG-5型重力仪数年来积累的漂移数据,分析阐述了仪器的主要漂移特征,并结合有关数据对使用寿命进行了推测。汪健等[4]基于实验数据,从时空角度对CG-5型重力仪静、动态漂移的特性进行系统分析,得到漂移幅值随时间变化逐渐减小、最终趋于稳定,以及随空间纬度(重力值读数段)增大而减小的认识。郝洪涛等[5]讨论了重力仪漂移率和格值系数长时间内的稳定性,并利用分测线漂移改正方法,对云南重力测区数据进行精细处理。
仪器厂家提供的漂移参数、参考寿命较粗略,对仪器之间技术指标的显著差异没有给予必要的阐述,会在一定程度上对使用者产生误导。前人在CG-5型重力仪的漂移特性上进行了很多研究工作,取得了一定成果,但对仪器的长期漂移特性和漂移规律的普适性认识等方面研究较少。同时,对于重力数据处理而言,能否有效改正仪器漂移的影响,直接关系到后期重力网平差分析的效果及对异常的识别。只有对重力仪的漂移特性进行深入研究,才能更好地有针对性地确定漂移改正方法,对重力数据处理质量提高、地球重力场变化分析及地震预报等方面具有十分重要的意义。本文利用多年CG-5型重力仪的检测、标定资料及安徽测网流动重力测量数据,在分析CG-5型重力仪静、动态漂移特性的基础上提出分时段的平差处理方法。
1 静态漂移特性 1.1 静态测试及数据处理重力仪的静态漂移测试是将重力仪静置于某一稳定、无外界噪声干扰的环境中,漂移率趋于稳定后进行至少24 h的连续观测,将观测值经固体潮改正后绘出仪器的静态漂移曲线,计算平均静态漂移率以检测静态漂移曲线的线性度。
表 1为2018-05对4台CG-5型重力仪的静态测试结果。仪器均放置于淮北地震台重力观测室,该观测室位于地震台山洞内,距洞口约60 m,有4套密封舱门,外界干扰小,洞内温度约15.5 ℃,日温差小于0.05 ℃,年温差小于0.1 ℃。重力仪读数周期均设置为60 s,采样时间设置为55 s,读数为采样时间内的均值。
|
|
表 1 2018-05 CG-5型重力仪静态测试结果 Tab. 1 Static test results of CG-5 gravimeter in May 2018 |
2018-05重力仪静态测试结果显示,4台重力仪经理论固体潮改正后均呈很好的线性上升趋势,拟合成直线的相关系数接近1,4台仪器静态漂移率在30~44 μGal/h之间。漂移残差由固体潮改正后的仪器观测数据与线性拟合值相减获得,结果显示,4台仪器的漂移残差均较小。
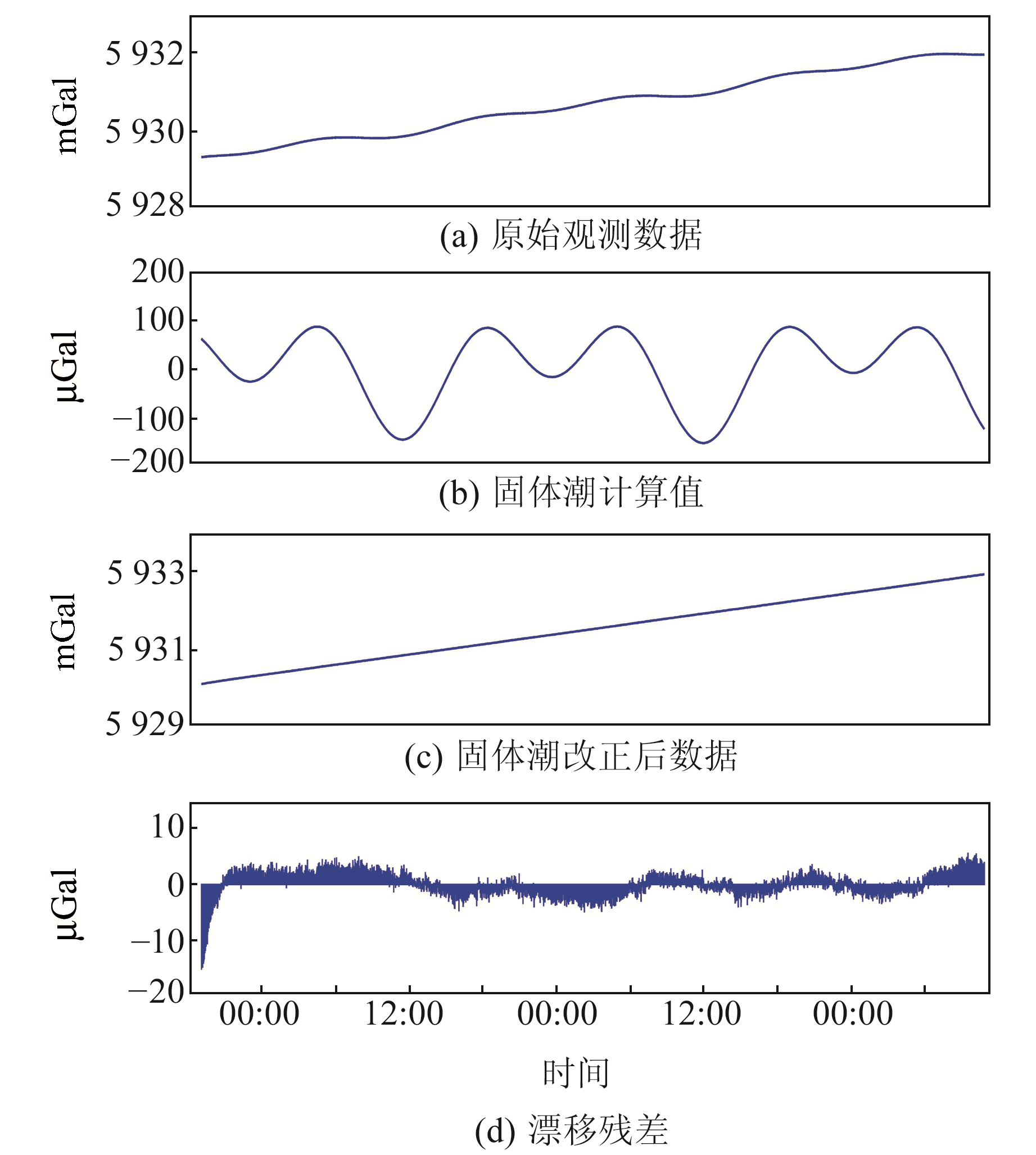
以2018-05-27~30 C114仪器为例,如图 1(a)和1(c)所示,该仪器原始观测数据为呈上升趋势的微小波浪型曲线,观测数据经理论固体潮改正后线性程度高,平均静态漂移率为43.63 μGal/h。图 1(d)中,静态观测的前2 h,由于仪器刚从运动状态转为静止状态,存在漂移残差较大的现象,2 h后仪器逐渐稳定,漂移残差减小,呈正负相间型变化,变化幅度为±5 μGal。
|
图 1 C114重力仪静态处理结果 Fig. 1 Static drift curve of C114 gravimeter |
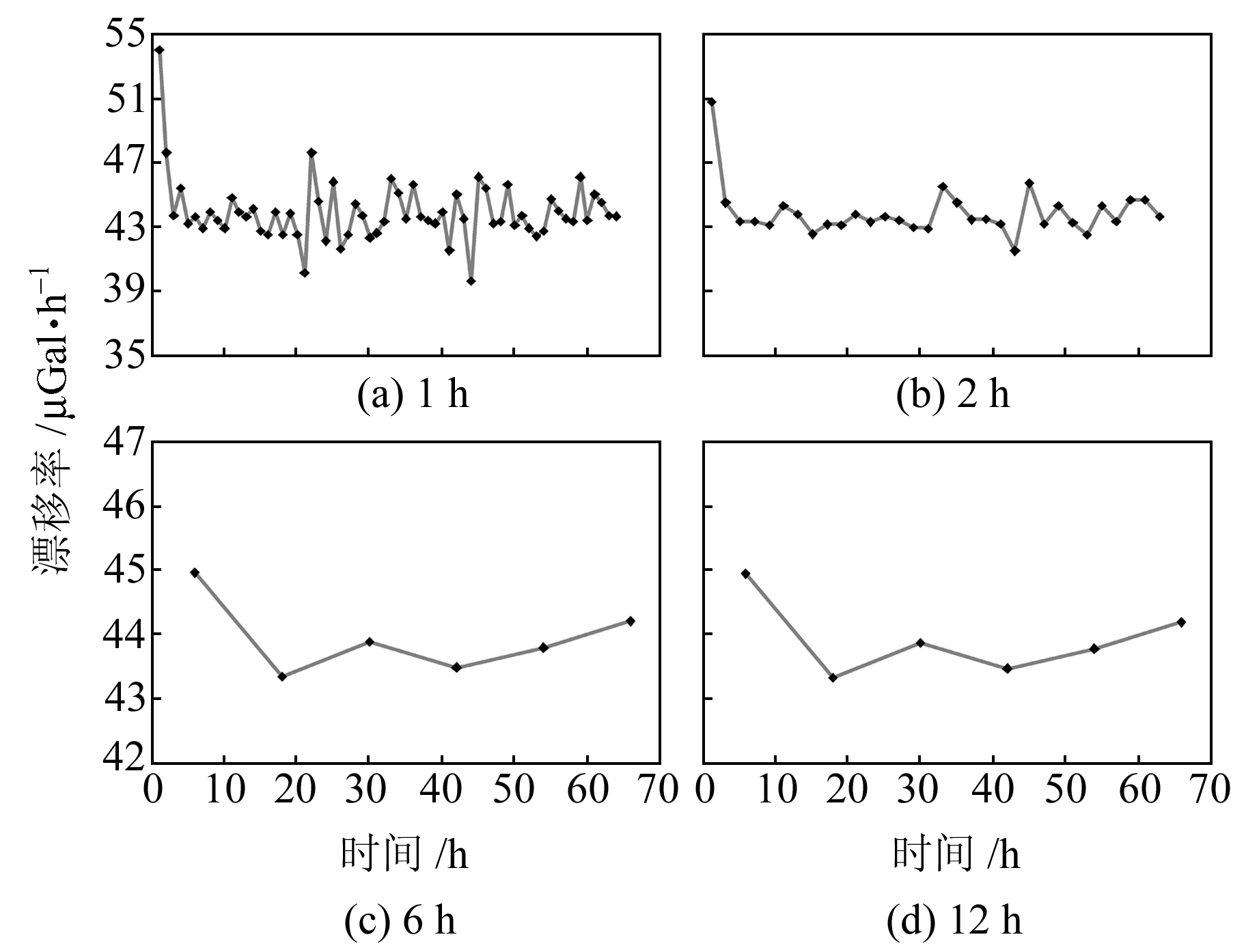
在流动重力测量过程中,重力测线均采用A → B → C…C→ B → A的方式进行往返闭合观测,单条测线一般当天闭合(约12 h),测点间的单程观测时间一般较短。因此,为了研究短时间内漂移率随时间的变化特性,本文区分了不同时间尺度,将整个静态测试过程划分成不同的时间段,计算在各时间段内仪器的静态漂移率。例如本次C114重力仪静态测试共进行66 h,1 h尺度就是把整个静态测试过程划分成以1 h为单元的66段,拟合计算每个时间段内仪器的平均静态漂移率。图 2分别为1 h、2 h、6 h和12 h尺度的静态漂移率变化,由图可知,静态测试前期,由于刚开始测量,仪器存在不稳定的情况,漂移率较大,随后逐渐稳定,在一定区间内震荡,均值为44 μGal/h。从不同时间尺度来看,1 h尺度仪器漂移率震荡幅度较大,静态观测开始2 h后的最大、最小漂移率之差仍达8 μGal/h; 随着时间尺度的增大,漂移率震荡幅度逐渐减小,12 h尺度仪器漂移率震荡幅度较小,最大与最小漂移率之差为1.7 μGal/h。本文认为漂移率的变化主要是由仪器本身的系统误差造成的,时间尺度越小,系统误差对计算出的漂移率影响越大,也正是因为系统误差的存在,在静态测试中改正后的漂移数据拟合成直线会出现漂移残差的现象。
|
图 2 C114重力仪不同时间尺度静态漂移率 Fig. 2 Static drift rate of C114 gravimeter with different time scales |
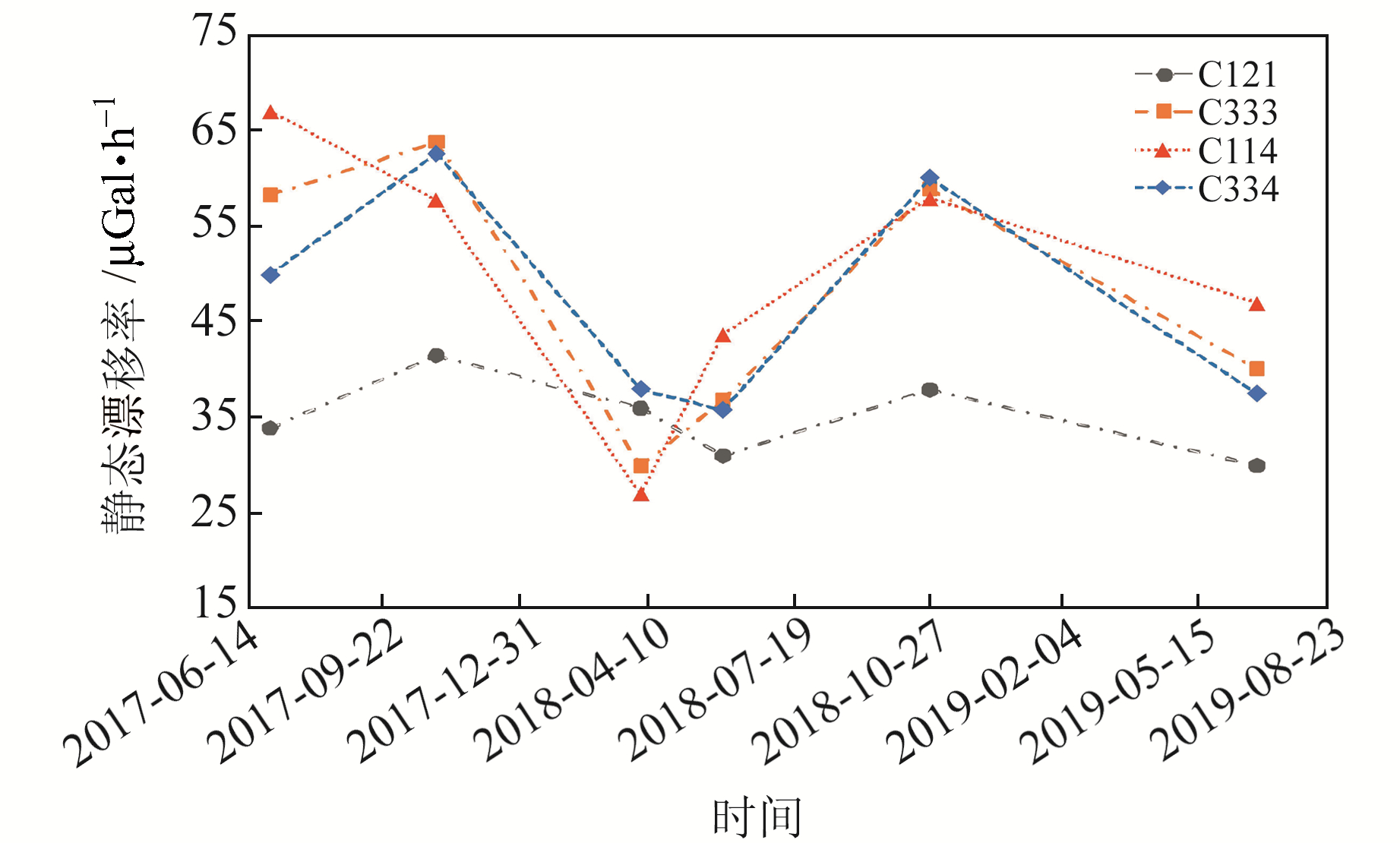
为分析CG-5型重力仪在长时间情况下的静态漂移特性,统计4台重力仪在2017~2019年共6期的静态漂移率计算结果,每期观测中4台仪器均放置在淮北地震台山洞重力观测室的固定位置。如图 3所示,4台重力仪的漂移率均呈不同程度的变化特征,C121仪器漂移率相对变化较小,变化范围在15 μGal/h左右,C114仪器变化幅度最大,达40 μGal/h。4台重力仪的变化趋势基本一致,2017-10~2018-04呈下降趋势,2018-06~2018-11呈上升趋势,2019-07四台仪器静态漂移率相对于上期结果均有所减小,除C121仪器漂移率较为稳定外,其余3台重力仪的漂移率变化均较为剧烈。以C114仪器为例,仪器静态漂移率从2017-07的66 μGal/h下降到2018-04的26 μGal/h,再上升到2018-10的57 μGal/h,2019-07又下降为49 μGal/h,平均每月的漂移率变化量可达4.5 μGal/h。对于流动重力测量及数据处理来说,一般单个测网单期的观测时间约2~5个月,若在数据平差处理中采用单一的漂移率计算,可能会造成一定的处理误差。
|
图 3 静态漂移率随时间变化 Fig. 3 Change curve of static drift rate with time |
CG-5型重力仪的动态漂移是指重力仪在运输与野外测量过程中,经过一段时间连续观测,待漂移率趋于稳定并进行固体潮改正后得到的重力仪平均动态漂移情况。
各条测线的漂移率一般通过式(1)计算:
| $ K = \frac{{\sum {\rm{d}} {R_i} \times {\rm{d}}{t_i}}}{{\sum {\rm{d}} {t_i} \times {\rm{d}}{t_i}}} $ | (1) |
式中,K为测线拟合漂移率;dRi为第i点经固体潮改正后的往返观测重力值之差;dti为往返观测时间。
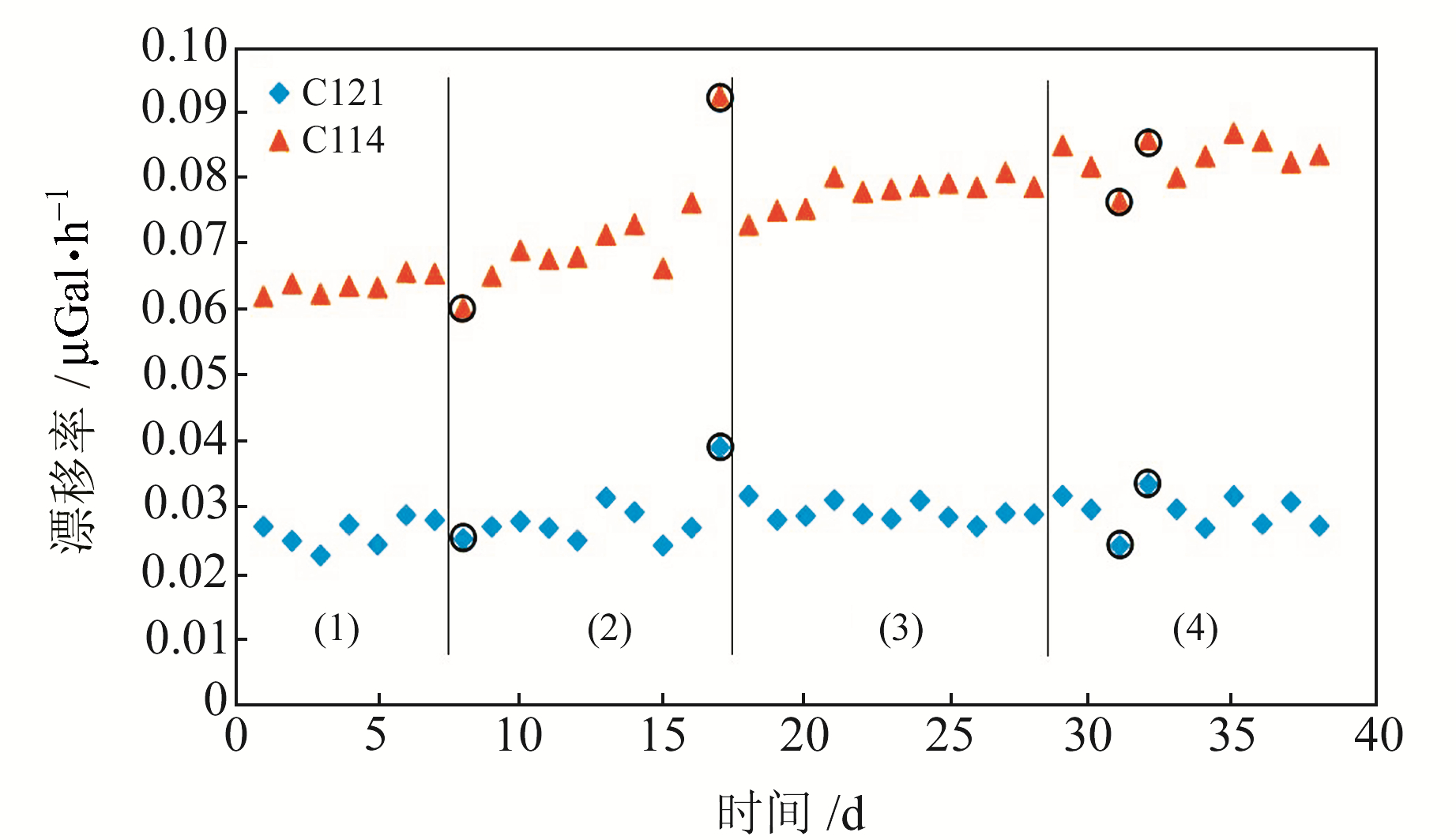
本文以2014-04期流动重力观测资料为例,该期流动重力观测采用C114和C121组合测量。图 4为整个测量周期以测量时间为顺序每条测线的仪器动态漂移率结果,可以看出,整个测量周期中2台重力仪的动态漂移率均在一定区间内震荡,C114的动态漂移率大于C121,呈较弱的上升趋势。如图 4中黑色圆圈所示,2台仪器动态漂移率的变化趋势具有一定的一致性,在某几天中2台仪器都出现漂移率向上或向下的突跳现象。分析发现,漂移率的突跳现象一般发生在2种情况下:1)野外测量环境不稳定和人为因素造成较大的读数误差,从数据质量的角度出发,出现这种情况可考虑对当天测线进行返工测量。2)漂移率突跳测线中测点较少且存在段差较小测段,由漂移率计算公式可知,测线漂移率的大小与第i点经固体潮改正后的往返观测重力值之差关系密切。当某一测段段差较小时,微小的系统或人为造成的误差就会对测线的漂移率计算值产生很大的影响,从而导致测线漂移率的突跳,进而造成单条测线平差时仪器段差的自差、互差较大。但将该测段数据放在区域网或几条测线整体平差时,其自差、互差明显减小。
|
图 4 2014-04期仪器各天的动态漂移率 Fig. 4 Dynamic drift rate of gravimeter on each day in 2014-04 |
在实际重力测量过程中经常遇见上山或下山的情形,上山过程中测点高程增加,重力仪重力值减小,下山过程则相反。本文在庐山国家重力基线场上选取段差为150 mGal的2个绝对重力测量点,对4台仪器进行5次来回检测(从山顶出发,4台仪器均放置在同一车辆的固定位置,每次上下山时间基本相同),从较短时间尺度分析CG-5型重力仪动态漂移率随空间的变化情况。同时,在第2次上山之后与第3次下山测量之间,在山顶的同一个测点进行相隔一段时间的2次测量,间隔期间仪器仍处于运动状态,获得在无重力变化情况下的动态漂移率。表 2和图 5为此次动态漂移率测试结果。
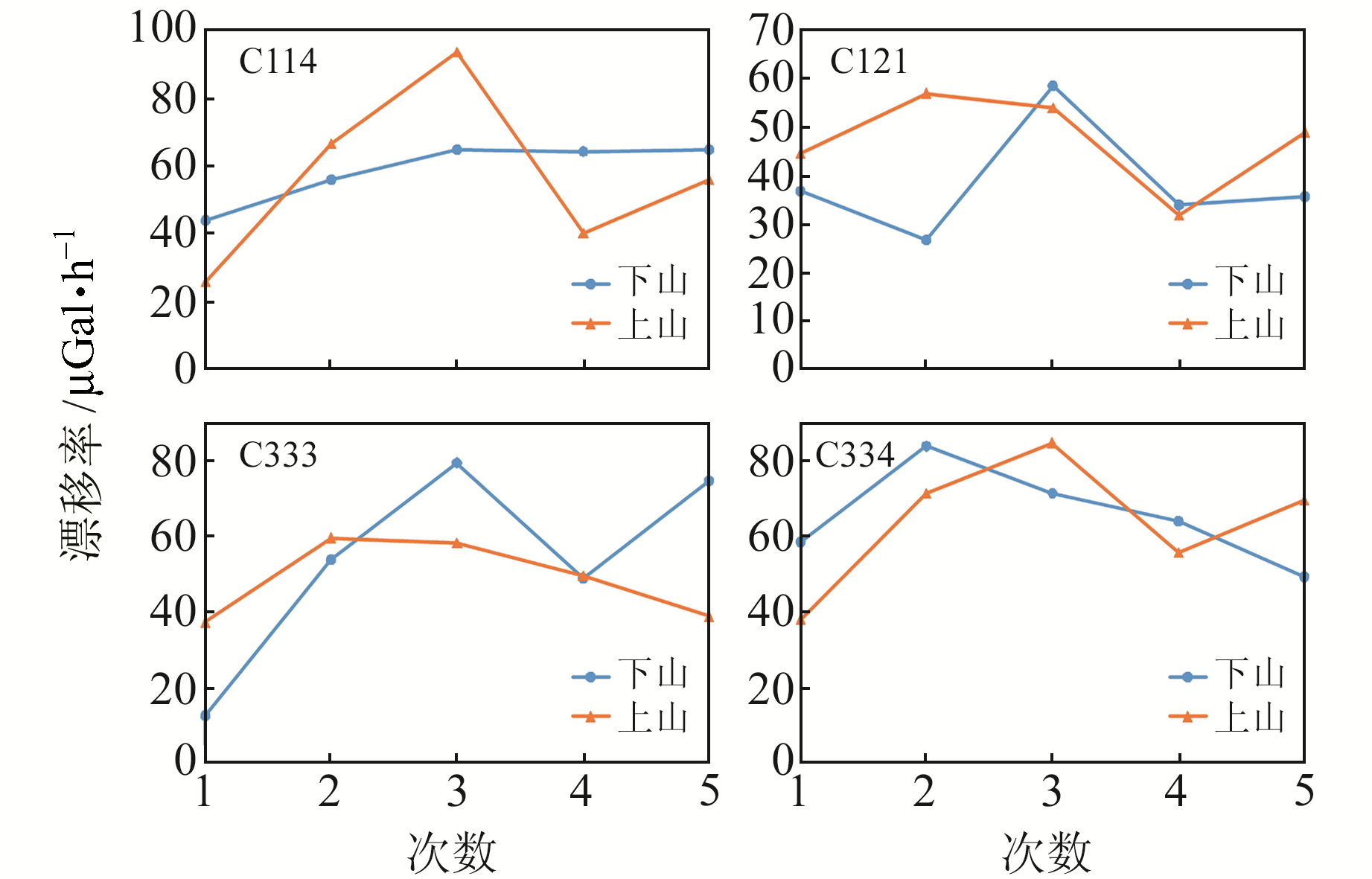
由表 2可知,4台仪器同点测量的动态漂移率与上山、下山的情况相比,其值均出现在5次上山、下山时动态漂移率的最大或最小值附近,且没有必然联系。由图 5可知,4台仪器的动态漂移率与仪器空间变化关系不密切,均在一定的幅度内震荡变化,但不论上山下山,4台仪器的漂移率变化趋势的一致性较好,基本呈现出先增大后减小再增大的变化过程。
|
|
表 2 重力仪上、下山过程动态漂移率变化情况 Tab. 2 Variation of dynamic drift rate in gravimeter during ascending and descending process |
|
图 5 重力仪上、下山过程动态漂移率变化情况 Fig. 5 Dynamic drift rate change of gravimeter in the process of ascending and descending |
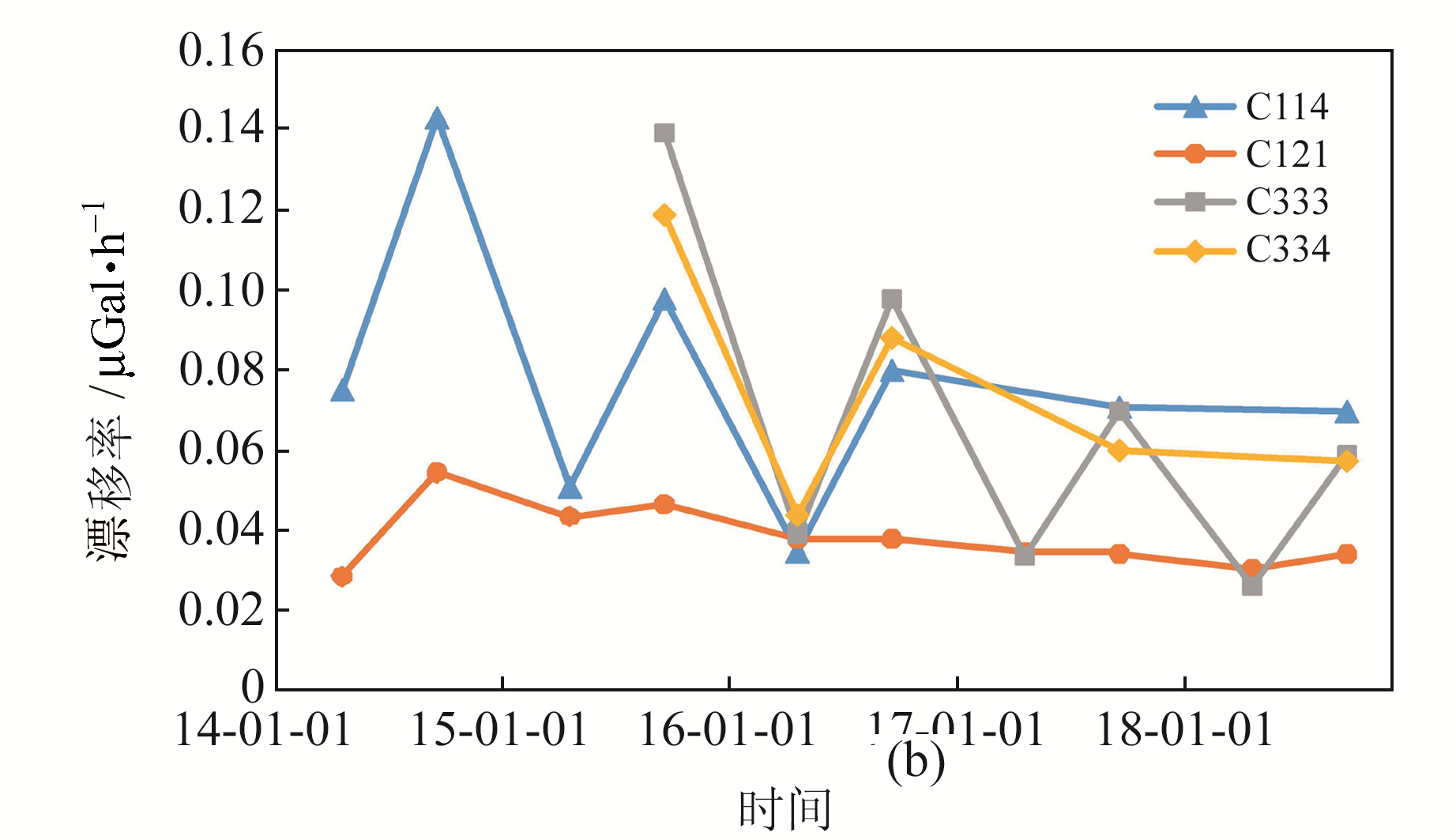
在地震重力观测数据处理中,重力仪漂移率通常是作为仪器参数,通过平差计算与测点重力值同时求解获得,也称为全网最或然漂移率,图 6为2013~2018年平差处理获得的各期全网最或然漂移率。
|
图 6 不同期全网最或然漂移率 Fig. 6 The most probable drift rate of the whole network in different measuring periods |
C114和C121仪器于2014年上半年投入测量,C333和C334仪器于2015年下半年投入测量,4台仪器在刚投入测量的一段时间内仪器漂移率变化较大,随着时间变化漂移率幅值逐渐减小,均在一定区间内震荡。
不同批次的重力仪出厂后的静态漂移率差异较大,同一批次出厂的重力仪个体之间静态漂移率也不尽相同,这与重力仪内部零长弹簧系统的状态有关。随着使用时间的增长,重力仪静态漂移率会在某一稳定值附近震荡,而这也是评价仪器稳定性、观测数据可靠性的指标之一。只有在重力仪的漂移率稳定、漂移曲线线性较好时,才可以用一定的数据处理方法将漂移的影响尽可能地模拟并消除,得到所需的重力观测值。
3.2 平差漂移改正CG-5型重力仪漂移率及随时空持续变化的漂移特征对重力数据处理有较大影响。如果动、静态漂移率变化过大,则证明仪器状态不稳定,在数据处理时不宜采用单一的漂移率进行改正。现有的重力数据处理过程中,为减小漂移的影响,一般假定重力仪漂移率为线性并进行线性漂移改正。此方法对漂移率线性度好,且动、静态漂移率差距小的仪器改正效果明显,若线性度差,且动、静态漂移率差值大,则改正效果不佳。从前文结果来看,该型重力仪在单次的静态测试中漂移率变化较小,但从单期测量乃至整个使用周期来看,漂移率变化较为明显,均在一定范围中震荡。因此,为尽可能减小仪器漂移率变化产生的数据处理精度误差,本文在平差计算中采用分时间段平差的方法进行解算。该方法首先将观测数据按照每条测线的闭合观测时间进行分段,并逐段进行平差,计算得到不同仪器各时间段的漂移率,再根据各数据段漂移率的计算结果,用式(2)对观测数据进行漂移改正。
| $ \Delta {D^i} = D \times ({t^i} - {t^0})/E $ | (2) |
式中,ΔDi为漂移改正值;D为分时段解算出的仪器平均漂移率;t0、ti分别为单个测段数据中的初始点和漂移改正点的观测时间;E为平差计算采用的仪器格值系数。
具体的分时段方式根据仪器的漂移特性而定。以2014-04期流动资料为例,本文将整个流动重力观测期分为4个时段,如图 4所示,第1时段与第3时段中2台仪器的动态漂移率较为平稳,变化幅度较小;第2时段中2台仪器均呈现出一定的上升趋势;第4时段中,仪器的漂移率虽均值变化较小,但震荡幅度较大。
2014-04期和2014-09期的安徽地区流动重力观测均采用C114和C121仪器进行同步数据观测,以此2期数据为基础,对漂移改正前和改正后的观测数据分别进行整体平差计算,对比改正前后的精度指标,结果见表 3(单位μGal)。
|
|
表 3 漂移改正前后平差联测精度 Tab. 3 Combined measurement accuracy before and after drift correction |
由表 3可知,观测数据进行漂移改正后联测精度指标均有所提高,C114仪器自差减小非常明显,2014-04期2台仪器整体计算的联测点值精度由7.46 μGal提高至4.83 μGal;2014-09期2台仪器整体计算的联测点值精度由7.9 μGal提高至5.31 μGal。
CG-5型重力仪于2014年上半年投入安徽测网的测量工作,2013-09期安徽测网重力数据采用Lacoste重力仪测量。2014-04期皖西南地区流动重力观测于2014-03底完成,2014-04-20霍山发生MS4.3地震。对2013-09期和2014-03期安徽测网流动重力数据进行平差处理分析,对比分段漂移改正前后2013-09~2014-03安徽西南地区地球物理重力场变化情况,如图 7所示。

|
图 7 漂移改正前后重力场变化 Fig. 7 Gravity field changes before and after drift correction |
由图 7可以看出,2013-09~2014-03安徽西南地区地球物理重力场(图中红色圆圈为霍山MS4.3地震)在大别山地区出现重力异常梯度带,幅度约80 μGal。分段漂移改正前后的安徽西南地区重力场变化形态基本一致,变化幅度不是特别明显,赋值最大达15 μGal;但漂移改正后,大别山地区重力变化零值线稍向南移动,在霍山震中附近,2期重力场差值由-19 μGal减小为-10 μGal,震中位置更加靠近零值线。由于2013-09期采用Lacoste重力仪测量,该仪器零漂较小[6],2013-09~2014-03地球物理重力场在分段漂移改正前后的变化主要是2014-03期重力数据采用分时段漂移改正的结果。
4 结语1) 单次静态观测过程中,CG-5型重力仪经固体潮改正后的观测值呈很好的线性上升趋势,但划分不同时间尺度,每个时间段内的仪器漂移率仍存在一定差异;静态漂移率的长期变化中,不同时间段CG-5型重力仪的静态漂移率变化幅度较大,但4台重力仪整体变化趋势一致。
2) 单期流动重力测量过程中,CG-5型重力仪的动态漂移率存在一定变化,均在一定区间内震荡,4台仪器的动态漂移率与仪器空间变化关系不密切,但仪器间的漂移特性在上下山的动态实验和各测线的动态漂移率变化中都表现出较为一致的变化趋势。
3) 全网最或然漂移率结果显示,刚投入使用时,CG-5型重力仪的漂移率变化幅度较大,随着时间的变化其幅度逐渐减小,最终在一定区间内震荡。本文采用分时段平差方法对观测数据进行分段漂移改正,改正后各台仪器的联测精度指标均有所提高,资料分析更加可靠。
值得注意的是,4台仪器不论是静态漂移率的长期变化还是单条测线的动态漂移率,都表现出较为一致的变化趋势,静态漂移率的长期变化趋势是否跟季节、温度有着一定的联系,单条测线的动态漂移率趋势一致性是否跟车辆的运行状况有关,值得深入研究。
| [1] |
邢乐林, 李辉, 夏正超, 等. CG-5重力仪零漂特性研究[J]. 地震学报, 2010, 32: 369-373 (Xing Lelin, Li Hui, Xia Zhengchao, et al. Study on Zero Drift Characteristics of CG-5 Gravimeter[J]. Acta Seismologica Sinica, 2010, 32(3): 369-373 DOI:10.3969/j.issn.0253-3782.2010.03.013)
(  0) 0) |
| [2] |
张松堂, 陆银龙, 王应建. CG-5重力仪弹簧形变对测量的影响[J]. 测绘科学与工程, 2014, 34(6): 18-21 (Zhang Songtang, Lu Yinlong, Wang Yingjian. Effect of Spring Deformation on Measurement of CG-5 Gravity Instrument[J]. Science and Mapping Science and Engineering, 2014, 34(6): 18-21)
(  0) 0) |
| [3] |
沈博, 袁尚武, 马玄龙, 等. CG-5重力仪的漂移与寿命[J]. 物探与化探, 2015, 39(2): 383-386 (Shen Bo, Yuan Shangwu, Ma Xuanlong, et al. Zero Drift of CG-5 Gravimeter and Its Service Life Time[J]. Geophysical and Geochemical Exploration, 2015, 39(2): 383-386)
(  0) 0) |
| [4] |
汪健, 孙少安, 邢乐林, 等. CG-5重力仪的漂移特征[J]. 大地测量与地球动力学, 2016, 36(6): 556-560 (Wang Jian, Sun Shao'an, Xing Lelin, et al. Drift Characteristics of CG-5 Gravimeter[J]. Journal of Geodesy and Geodynamics, 2016, 36(6): 556-560)
(  0) 0) |
| [5] |
郝洪涛, 李辉, 孙和平, 等. CG-5重力仪零漂改正及格值系数检测应用研究[J]. 武汉大学学报:信息科学版, 2016, 41(9): 1 265-1 271 (Hao Hongtao, Li Hui, Sun Heping, et al. Application of Zero Drift Correct and Detection of Scale Parameters of CG-5 Gravimeter[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1 265-1 271)
(  0) 0) |
| [6] |
孙中苗, 李迎春, 翟振和. LaCoste and Romberg航空重力仪的零点漂移[J]. 测绘通报, 2009(11): 24-26 (Sun Zhongmiao, Li Yingchun, Zhai Zhenhe. Zero Drift of the LaCoste and Romberg Airborne Gravimeter[J]. Bulletin of Surveying and Mapping, 2009(11): 24-26)
(  0) 0) |
2. Key Laboratory of Research on the South Section of the Tan-Lu Fault Zone, Anhui Earthquake Agency, 558 West-Changjiang Road, Hefei 230031, China
 2020, Vol. 40
2020, Vol. 40

