活动断层是诱发地震的主要原因,也是破坏城市建筑设施的重要因素[1]。当前活动断层探测主要采用小道距反射地震法[2-3],但反射波常被直达波、声波、面波等干扰波干扰,资料信噪比较低[4],同时浅层反射波受动校正拉伸切除影响,有效覆盖次数和叠加剖面浅层分辨率较低,不利于活动断层上断点的识别[5]。浅层折射波具有能量强、信噪比高、频带宽、易于识别等特点[6],常用于野外低降速带调查和反射地震资料野外静校正量计算[7]。共中心点域折射波叠加方法虽然可以粗略显示折射界面总体构造形态,但该方法存在叠加剖面横向分辨率较低、断层断点模糊不清等缺点,不适用于活动断层上断点的识别。本文基于折射波传播理论,在共检波点域采用折射波叠加方法探测浅层断点。模型模拟和实际资料应用表明,该方法可有效提高成像剖面的横向分辨率,对活动断层上断点的探测具有可行性。
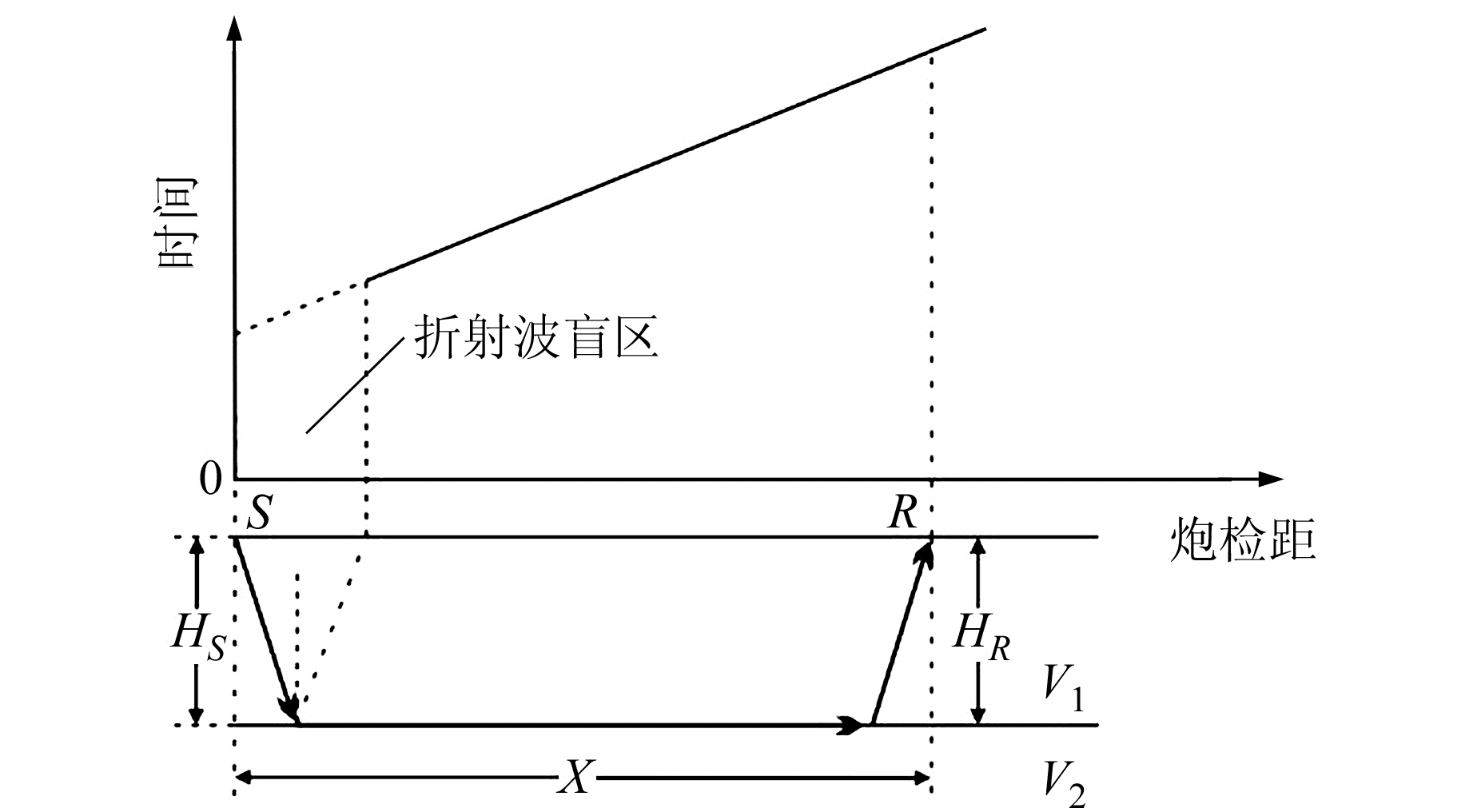
1 方法原理 1.1 折射波时距曲线地震波在传播过程中遇到波阻抗界面会产生反射波和透射波,当地震波入射角等于临界角时,透射波会沿着低速层与高速层的分界面传播形成滑行波,此时在折射波盲区之外可以接收到折射波[8]。图 1为二层速度结构折射波传播路径及时距曲线示意图,当地表和折射界面水平时,折射波时距曲线如式(1)所示[9]:
|
图 1 二层速度结构折射波路径及时距曲线 Fig. 1 Refraction path and time-distance curve of 2 layers velocity structure |
| $ T(X) = \frac{X}{{{V_2}}} + \frac{{{H_S}{\rm{cos}}{\theta _C}}}{{{V_1}}} + \frac{{{H_R}{\rm{cos}}{\theta _C}}}{{{V_1}}} $ | (1) |
式中,T(X)为折射波初至时间,X为炮检距,V1为低速层速度,V2为折射波滑行速度,θC为临界角,HS、HR分别为炮点和接收点下方低速层厚度。当折射界面倾角较小时,HS和HR可视为常数。由式(1)可知,在共检波点道集中,折射波初至时间与炮检距呈线性关系。采用类似反射波动校正处理方法,将式(1)右端前两项消去,消除同一接收点因炮检距及炮点延迟时间不同产生的影响,即可在共检波点域将折射波校正成一条水平线,通过叠加处理可增强折射波信噪比。式(1)中炮检距X可直接由野外测量资料获取,因此折射波滑行速度V2和各炮点延迟时间的求取是问题的关键。
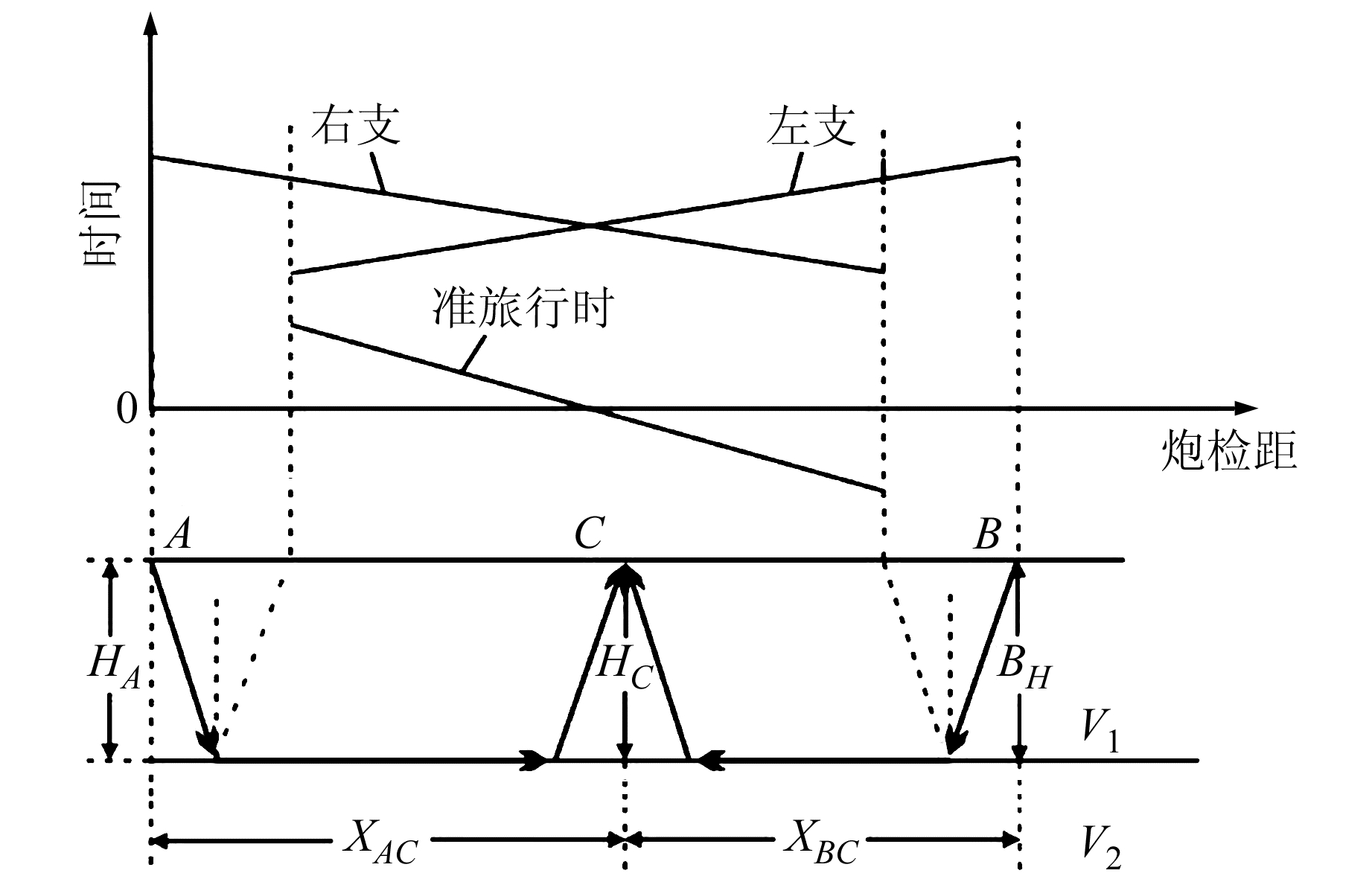
1.2 折射波滑行速度求取对于多次观测数据,可采用差数时间法计算折射界面速度[10],计算原理类似于相遇折射中高速层速度的求取方法。图 2为相遇折射法观测系统示意图,图中A、B分别为左右支炮点,在C点处左右支折射波旅行时间分别为:
|
图 2 差数时间法计算折射层速度 Fig. 2 Refraction layer velocity calculated by difference time method |
| $ {{T_A}({X_{AC}}) = \frac{{{X_{AC}}}}{{{V_2}}} + \frac{{{H_A}{\rm{cos}}{\theta _C}}}{{{V_1}}} + \frac{{{H_C}{\rm{cos}}{\theta _C}}}{{{V_1}}}} $ | (2) |
| $ {{T_B}({X_{BC}}) = \frac{{{X_{BC}}}}{{{V_2}}} + \frac{{{H_B}{\rm{cos}}{\theta _C}}}{{{V_1}}} + \frac{{{H_C}{\rm{cos}}{\theta _C}}}{{{V_1}}}} $ | (3) |
式中,XAC、XBC分别为左右支炮点A、B到接收点C的水平距离,HA、HB、HC分别为A、B、C三点的低速层厚度。将式(2)和式(3)等号两侧同时作差可得:
| $ \begin{array}{*{20}{c}} {{T_A}({X_{AC}}) - {T_B}({X_{BC}}) = }\\ {\frac{{{X_{AC}} - {X_{BC}}}}{{{V_2}}} + \frac{{({H_A} - {H_B}){\rm{cos}}{\theta _C}}}{{{V_1}}}} \end{array} $ | (4) |
式中,HA、HB为常数,准旅行时T′(XC)=TA(XAC)-TB(XBC),对式(4)两侧同时微分:
| $ {\rm{d}}{T^\prime }({X_C}) = \frac{{{\rm{d}}{X_{AC}} - {\rm{d}}{X_{BC}}}}{{{V_2}}} $ | (5) |
因为XAC+XBC=XAB为常数,故dXBC=-dXAC,结合式(5)可得C点处折射层速度为:
| $ {V_2} = 2\frac{{{\rm{d}}{X_{AC}}}}{{{\rm{d}}{T^\prime }({X_C})}} $ | (6) |
由式(6)可知,应用差数时间法计算的结果与测线处地形及低速层速度分布无关,式(6)中XAC、T′(XC)可从野外观测数据中直接或间接获得。对于实际数据,由于存在初至拾取误差和测量误差,会对计算结果产生一定影响,可采用滤波器对计算结果进行平滑处理,提高计算结果的稳定性。
1.3 炮点延迟时间求取在获取折射界面速度后,由于T(X)、X/V2两项参数均已求出,因此式(1)可转化为:
| $ T_0^S + T_0^R = T(X) - \frac{X}{{{V_2}}} $ | (7) |
式中,
将式(1)右端前两项校正后,应用共检波点域折射波叠加方法即可获得折射波叠加剖面,该剖面时间轴为检波点处T0时间,而非双程旅行时间:
| $ {T_0}(x) = \frac{{{H_R}(X){\rm{cos}}{\theta _C}}}{{{V_1}}} $ | (8) |
由式(8)可得折射界面深度表达式为:
| $ {H_R}(X) = \frac{{{T_0}(X){V_1}}}{{{\rm{cos}}{\theta _C}}} = \frac{{{T_0}(X){V_1}{V_2}}}{{\sqrt {V_2^2 - V_1^2} }} $ | (9) |
在近炮点处可接收到较丰富的浅层直达波信息,对直达波初至时间作线性拟合即可求得低速层速度,再结合折射波速度和检波点延迟时间,利用式(9)即可估算出折射界面的深度。
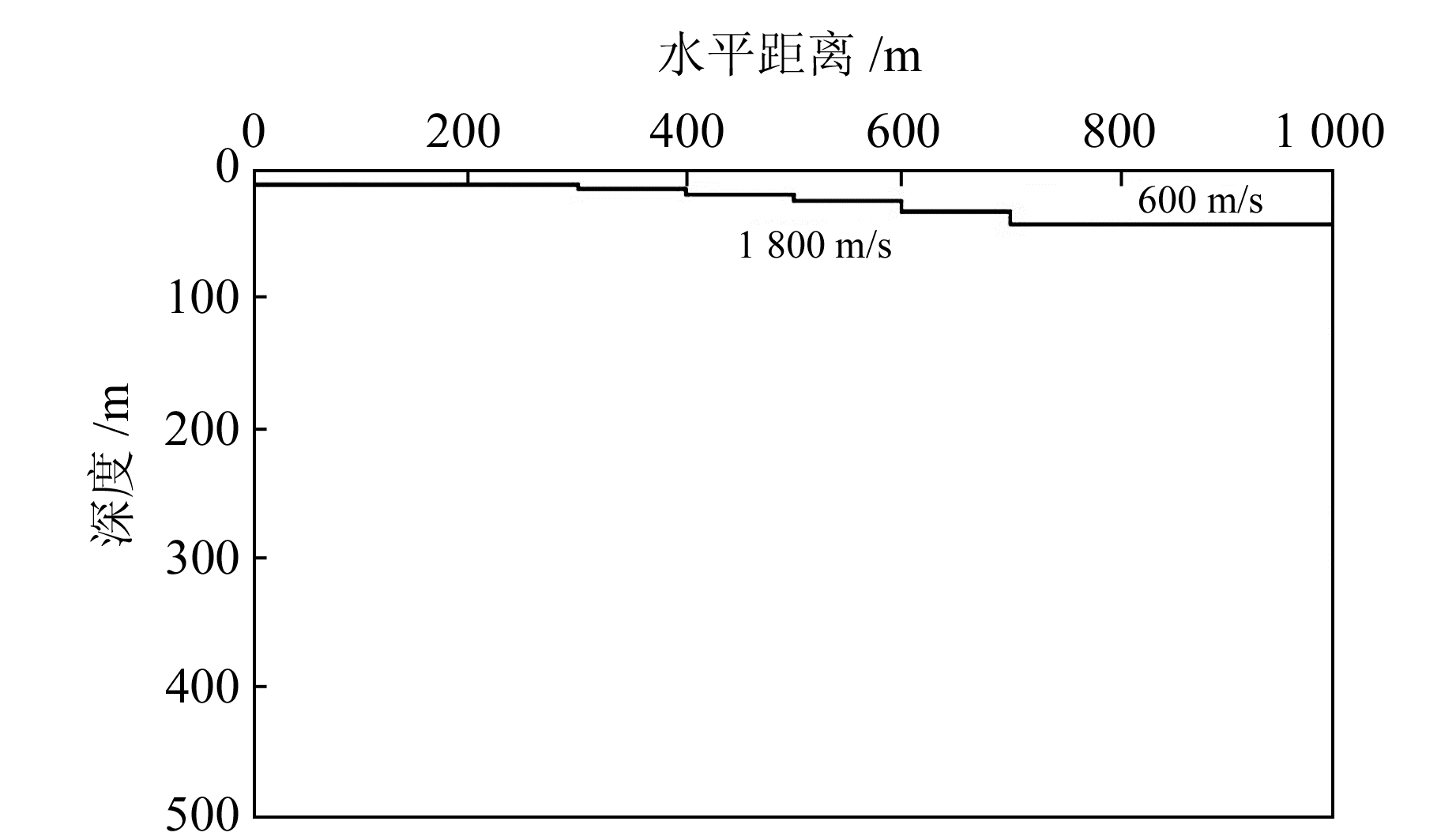
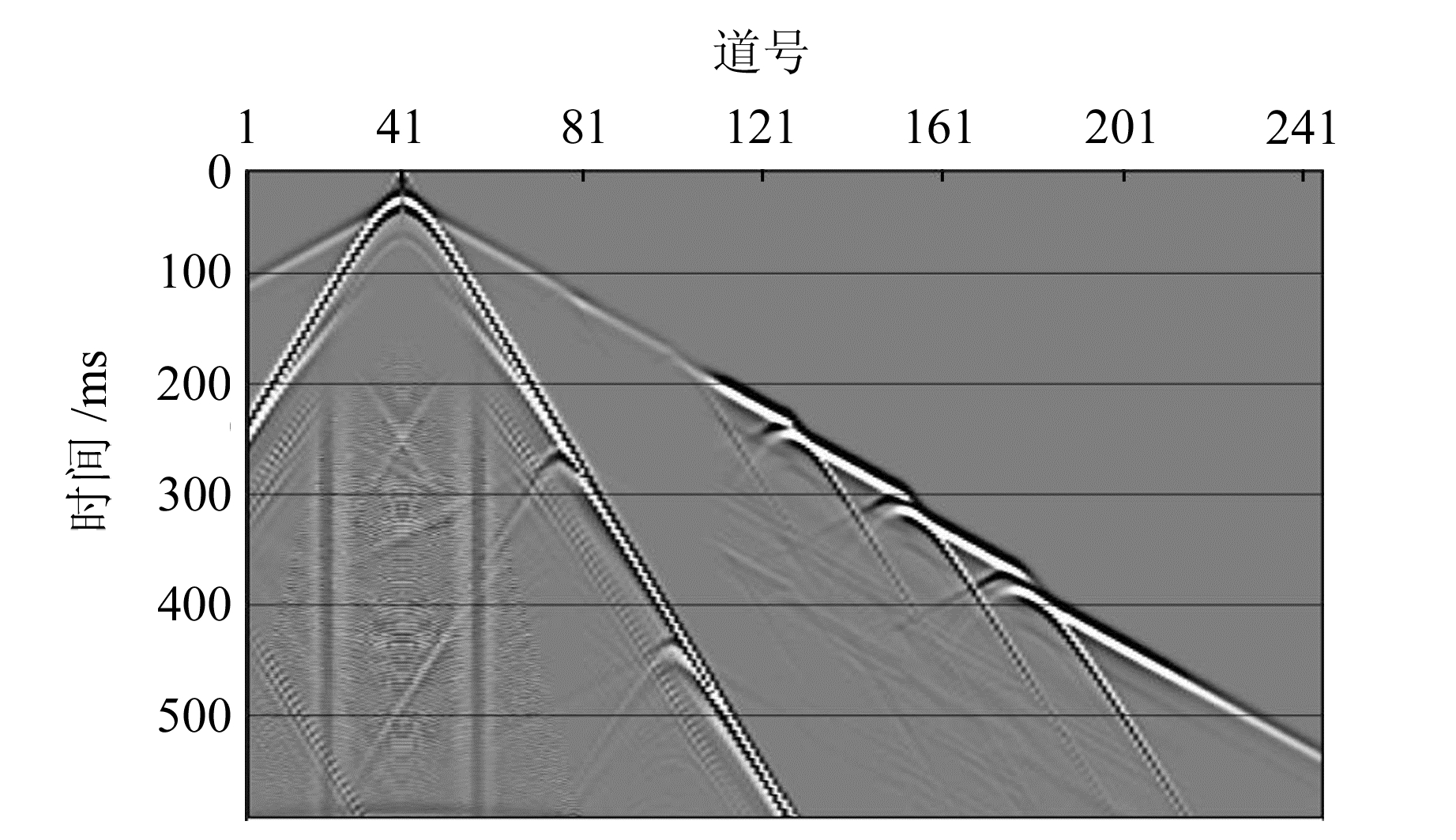
2 模型研究为验证本文方法的可行性,建立如图 3所示的二维地质模型。该模型长1 000 m,深500 m,浅部低速层速度为600 m/s,下伏基岩速度为1 800 m/s,模型左端低速层厚度为10 m,在模型横向300 m、400 m、500 m、600 m、700 m处分别发育有断距为2 m、4 m、6 m、8 m、10 m的断层,在断点以外位置,基岩顶界面呈水平阶梯状分布。采用表 1所示的观测系统模拟63张单炮记录,图 4为一典型单炮记录。从图中可以看出,该单炮记录中折射波较发育,在断点处折射波明显错断,且发育断点绕射波。
|
图 3 断层速度模型 Fig. 3 Fault velocity model |
|
|
表 1 观测系统参数 Tab. 1 Observation system parameters |
|
图 4 速度模型的典型单炮记录 Fig. 4 Typical shot record of velocity model |
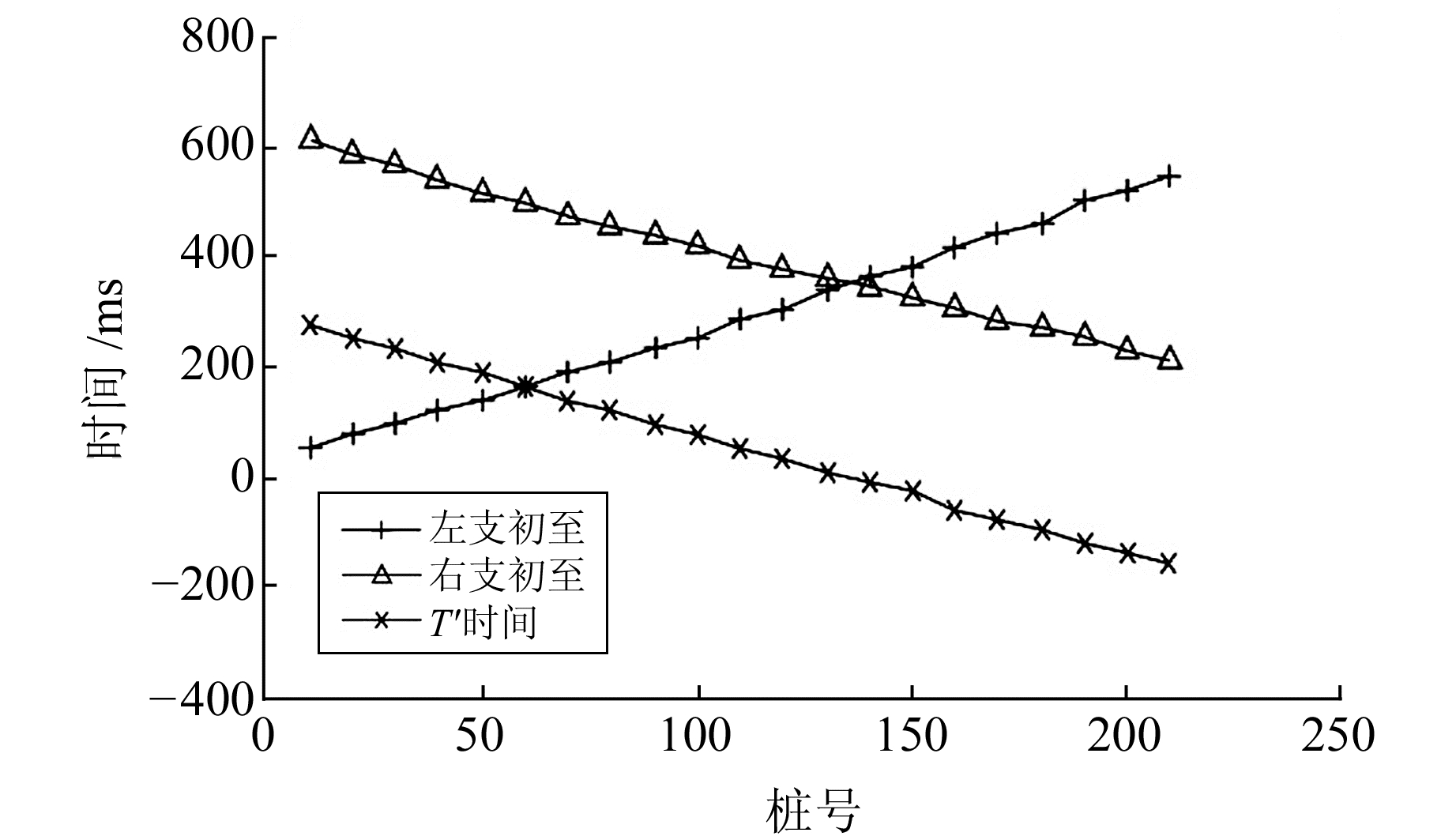
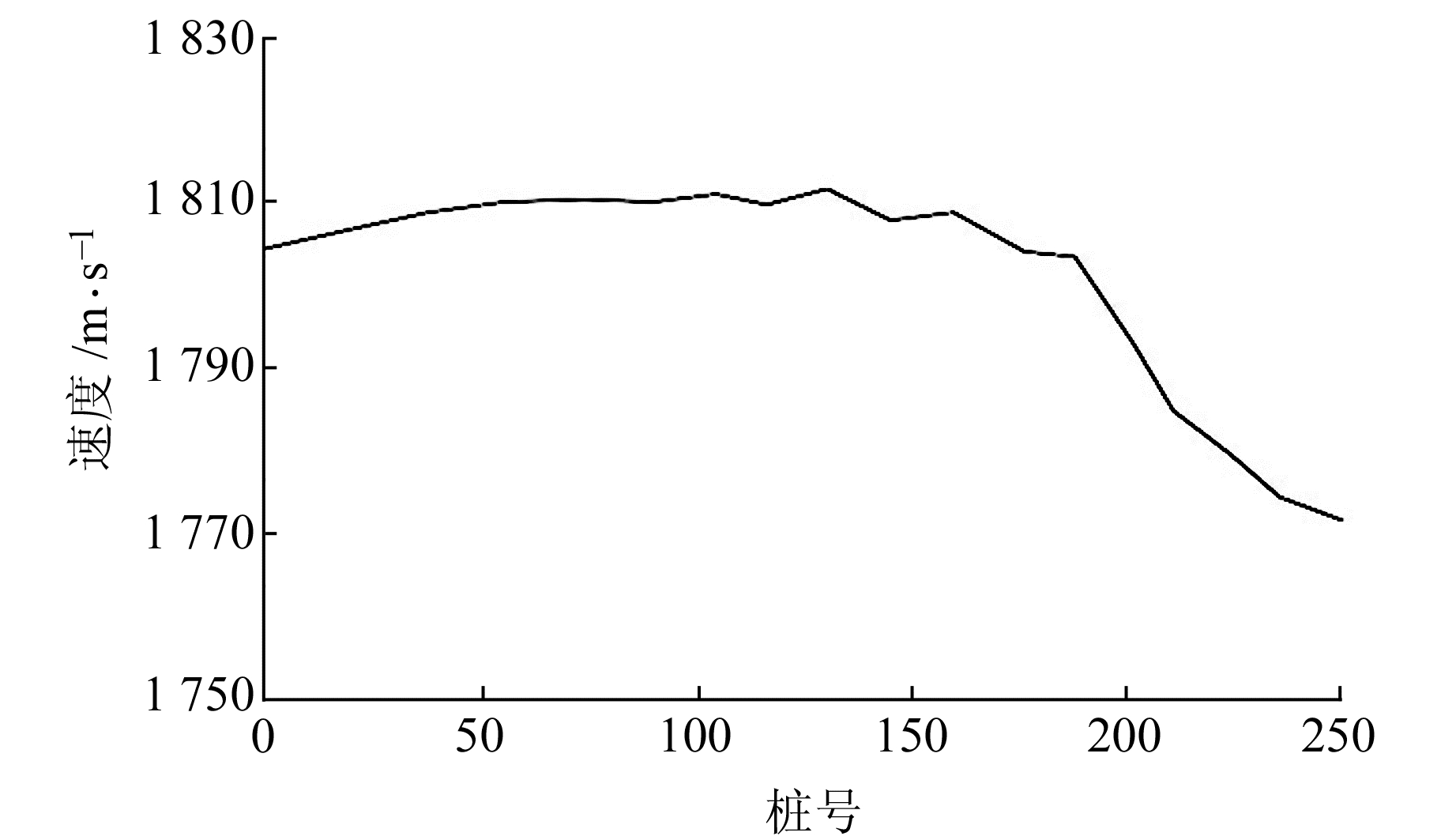
分别拾取左端和右端两单炮的折射波初至时间,采用差数时间法分析折射界面速度在水平方向的变化趋势,将同一接收点左支及右支初至时间作差后,得到准旅行时曲线(图 5),利用式(6)计算各接收点下方折射层速度。为提高计算结果的稳定性,在计算前对准旅行时曲线进行平滑处理,求得折射层速度沿横向的弯化曲线(图 6)。折射界面速度在1 770~1 810 m/s之间,绝对误差在30 m/s以内。
|
图 5 差数时间法分析折射层速度 Fig. 5 Refraction layer velocity analyzed by differential time method |
|
图 6 折射层速度在水平方向的变化 Fig. 6 Variation of refractive layer velocity in horizontal direction |
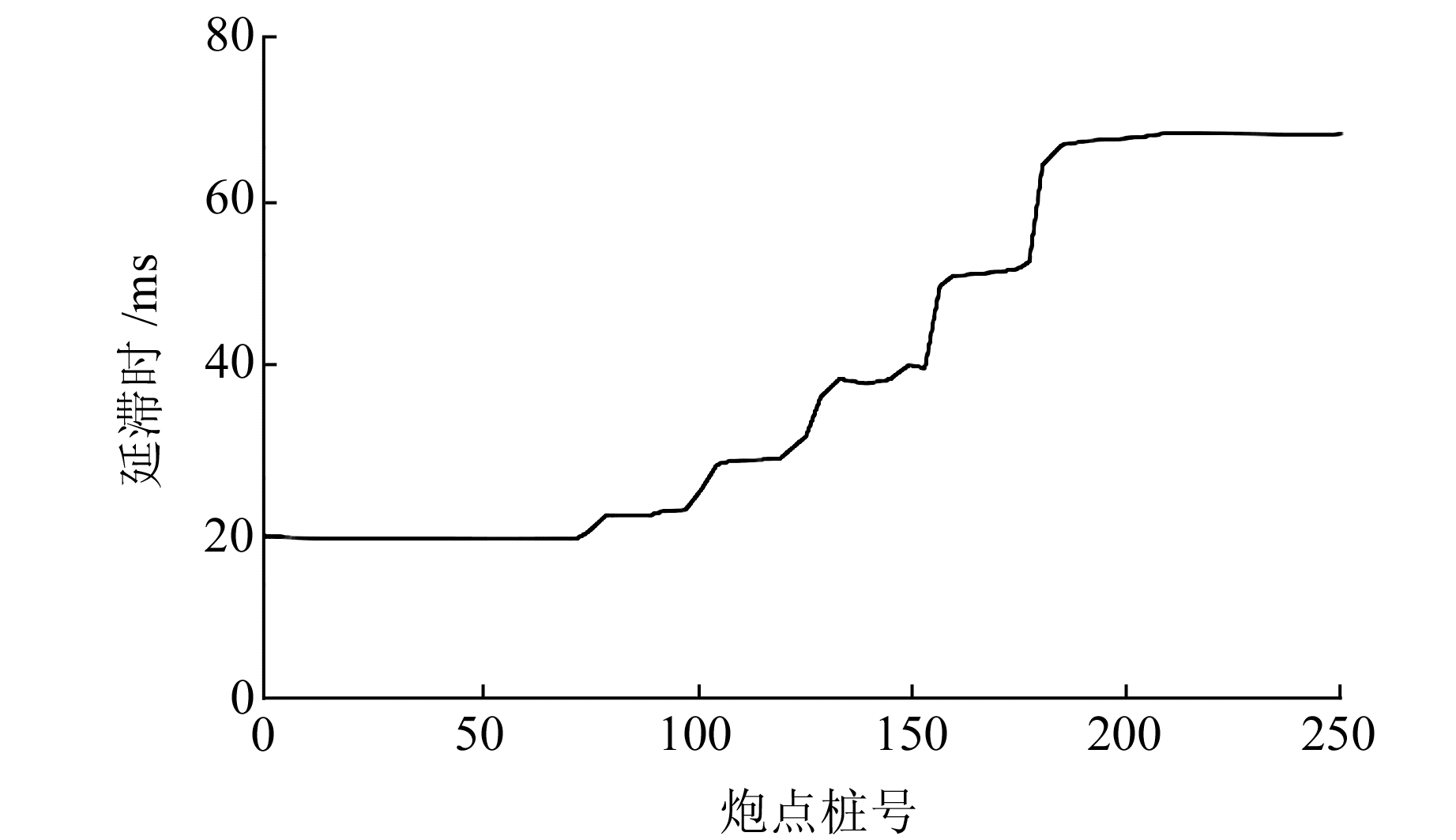
应用式(7)计算得到炮点延迟时间曲线(图 7),从图中可以看出,炮点延迟时间曲线在一定程度上也反映了高速层界面的大致形态。在得到炮点延迟时间和高速层速度后,分别在共中心点域和共检波点域对线性动校正后的初至折射波进行叠加(图 8)。在共中心点域叠加剖面上,模型中几个断点位置显示不清,同相轴连续性较差,存在严重串相位现象,不能用于上断点的解释;在共检波点叠加剖面上,折射波同相轴频率较高、连续性较好,断点处绕射波形态清晰,模型中5个断点识别度较高,断层断距从左到右逐渐变大的特征明显。
|
图 7 炮点延迟时间曲线 Fig. 7 Delay time curve of shot point |

|
图 8 共中心点与共检波点域折射波叠加剖面 Fig. 8 Refractive wave stack profiles in common mid-point domain and common-receiver domain |
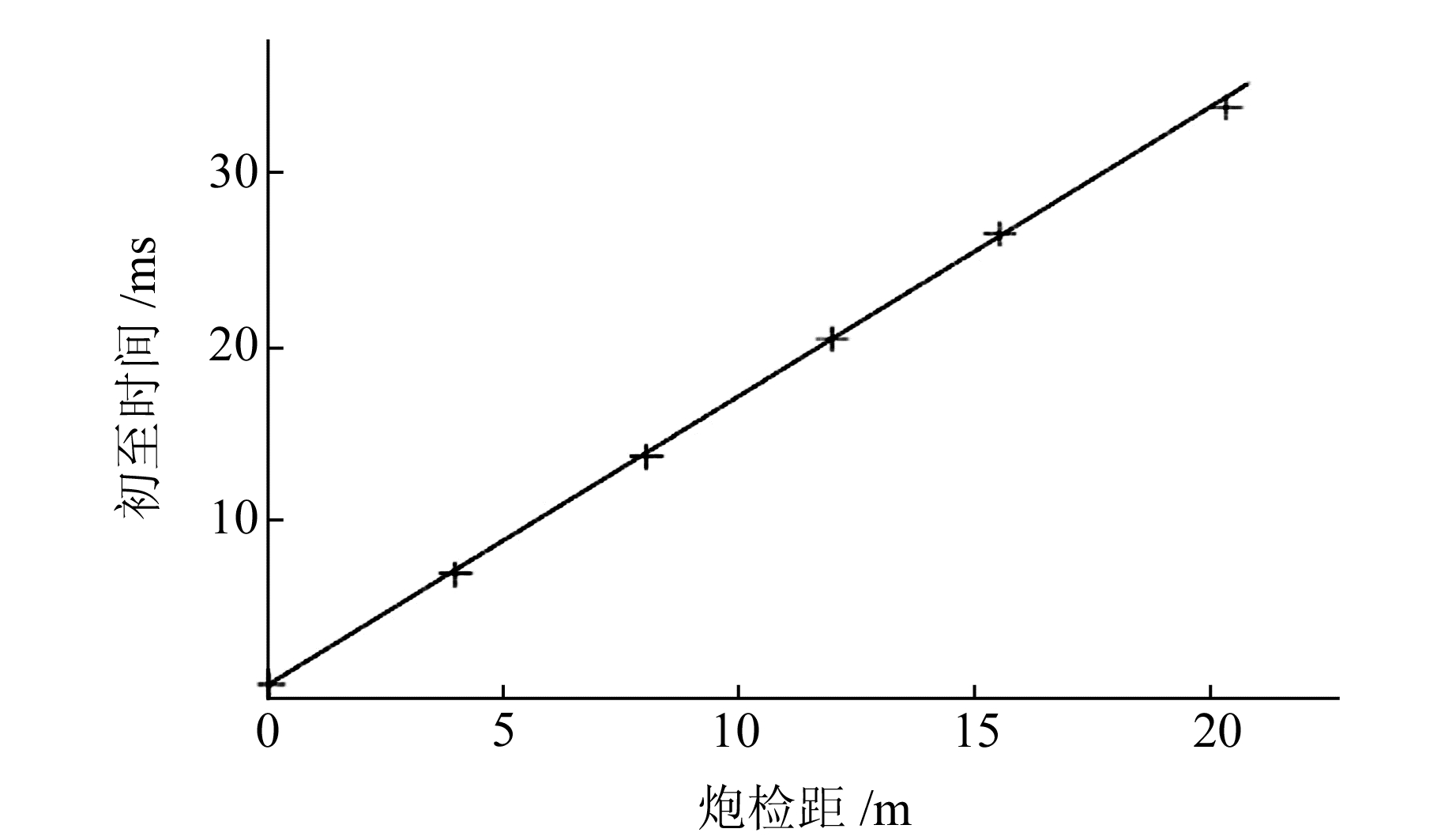
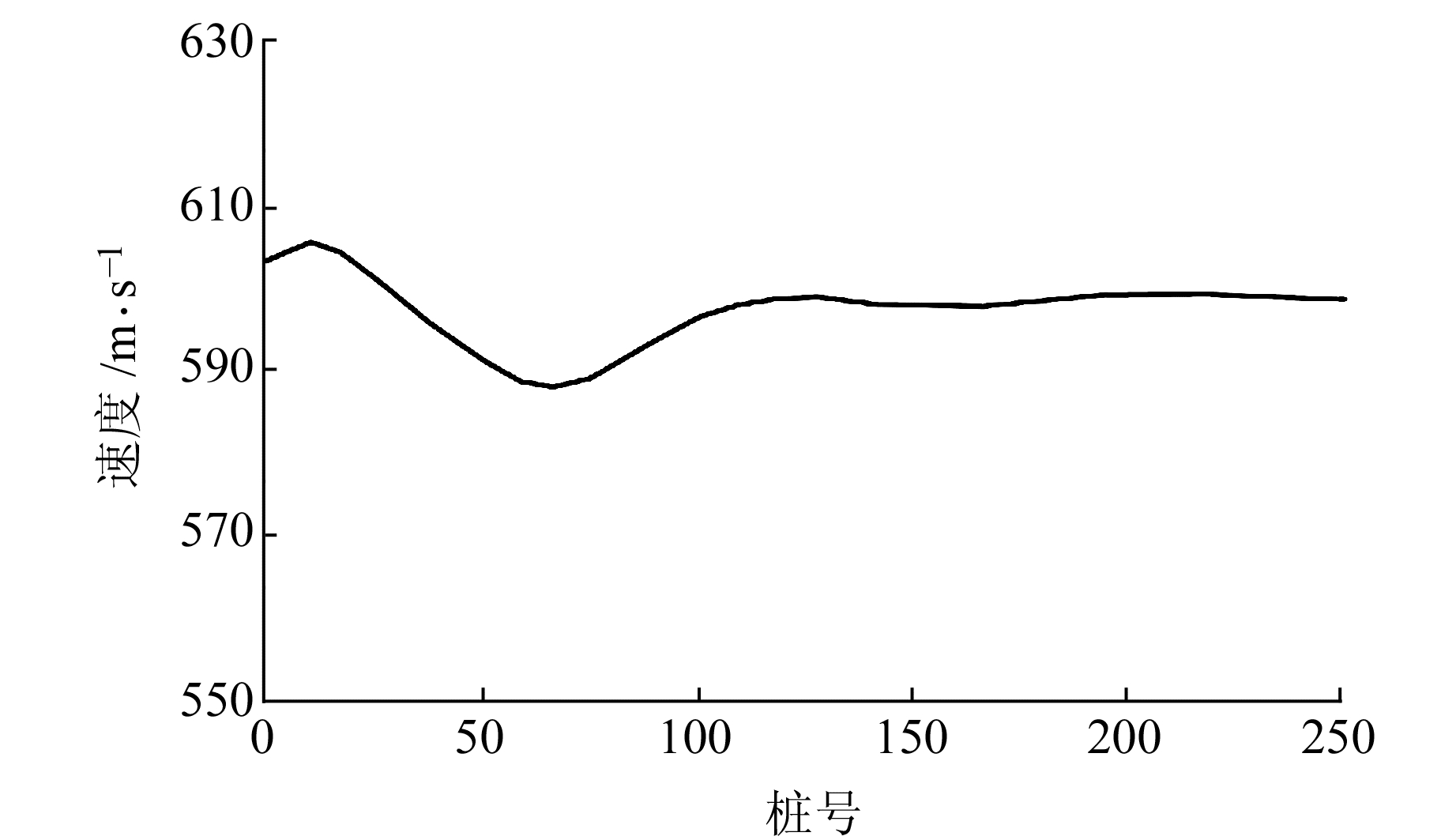
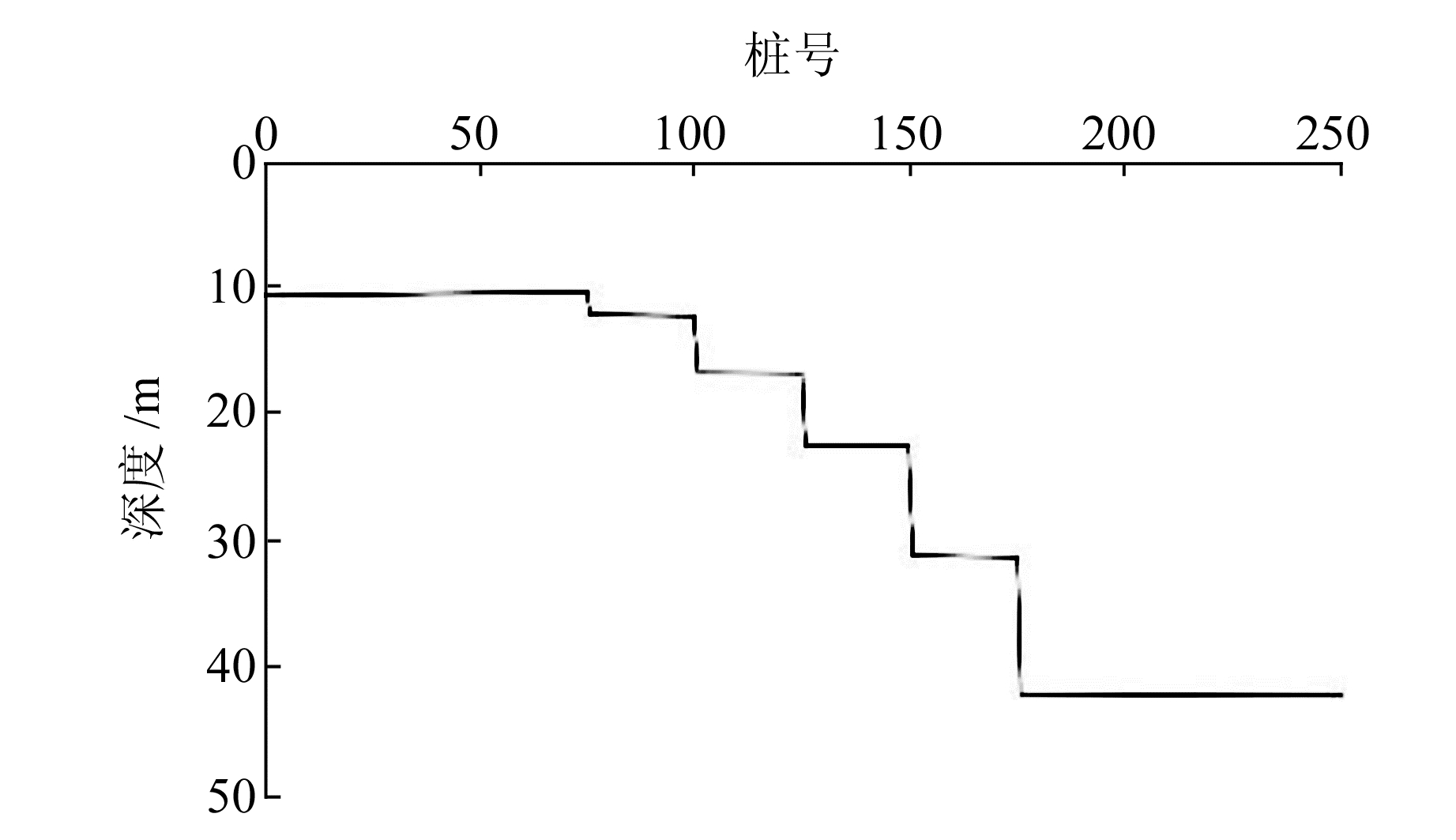
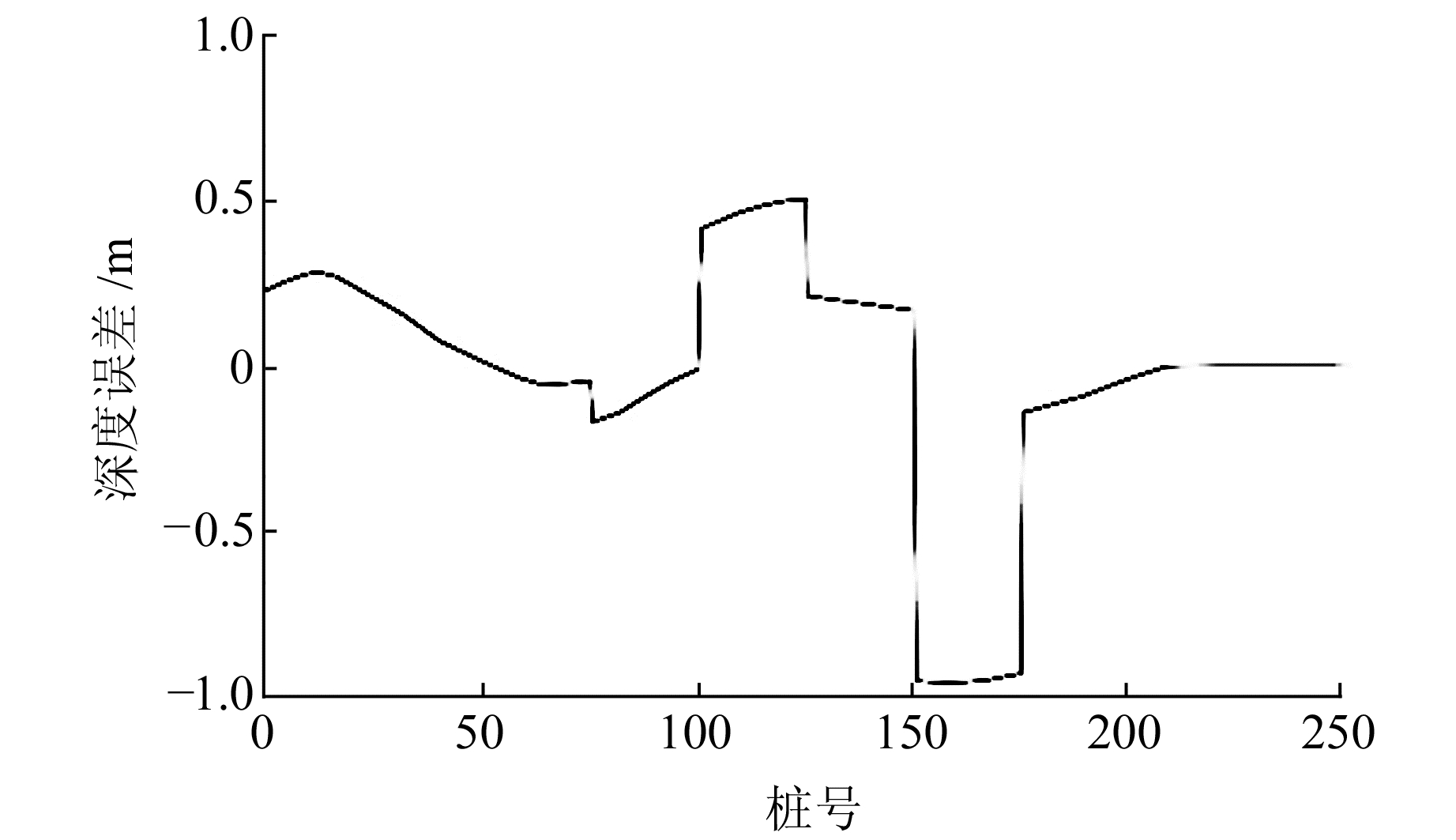
图 9为某一单炮记录近炮点直达波初至时间随偏移距变化的散点图。通过对该散点图进行线性拟合得到近炮点处低速层速度,利用该方法每隔5个炮点取一个速度分析点,得到离散的低速层速度后,通过空间插值平滑的方法得到低速层速度沿水平方向的弯化趋势(图 10)。在桩号1~100之间,由于低速层厚度较小,近炮点附近直达波数据较少,计算误差相对较大;桩号100之后随着直达波数据的增多,计算结果相对较稳定。基于共接收点叠加剖面上同相轴时间,应用式(9)计算得到基岩深度曲线(图 11)及其误差(图 12),从结果可以看出,反演结果与模型的一致性较好,绝对深度误差在±1 m以内。
|
图 9 利用近炮点初至时间计算低速层速度 Fig. 9 Velocity calculation of low velocity layer based on near shotpoint arrival time |
|
图 10 低速层速度曲线 Fig. 10 Velocity curve of low velocity layer |
|
图 11 时深转换获得基岩深度曲线 Fig. 11 Bedrock depth curve obtained by time-depth conversion |
|
图 12 时深转换的深度误差 Fig. 12 Depth error of time-depth conversion |
应用共检波点域折射波叠加方法对位于河西走廊戈壁砾石区的二维地震测线资料进行处理,该测线浅部发育全新统残、坡积物及更新统湖积物,压实度较低,对震源激发不利。图 13为该测线的一张典型单炮记录,该记录中面波及多次折射波比较发育,近炮点处反射波信噪比较差,在280道附近可见明显折射波错断现象,并发育断点绕射波。采用共中心点反射波叠加法、共中心点折射波叠加法及共检波点折射波叠加法进行资料处理,得到叠加剖面(图 14和15)。反射波叠加剖面中,100~300 ms时间段反射波同相轴信噪比较高,在CDP440、475、540附近,反射波同相轴发生错断,断点较明显;在100 ms以内,反射波信噪比较低,无法辨别该断层的浅部断点位置。对于共中心点折射波叠加剖面,100 ms以上同相轴连续性较好,但仍不能分辨上断点的确切位置。在共检波点折射波叠加剖面上,100 ms以内同相轴连续性较好,剖面左右两侧频率特征差异较大,在桩号275附近出现同相轴错断现象,并发育有断点绕射波,由此可判定该处存在断点。

|
图 13 测线上的典型单炮记录 Fig. 13 Typical shot record on the line |

|
图 14 二维测线共中心点反射波叠加剖面 Fig. 14 Reflection wave stacking profile of 2D line in common midpoint domain |

|
图 15 二维测线共中心点与共接收点折射波叠加剖面 Fig. 15 Refractive wave stacking profiles of 2D line in commonmidpoint domain and common-receiver domain |
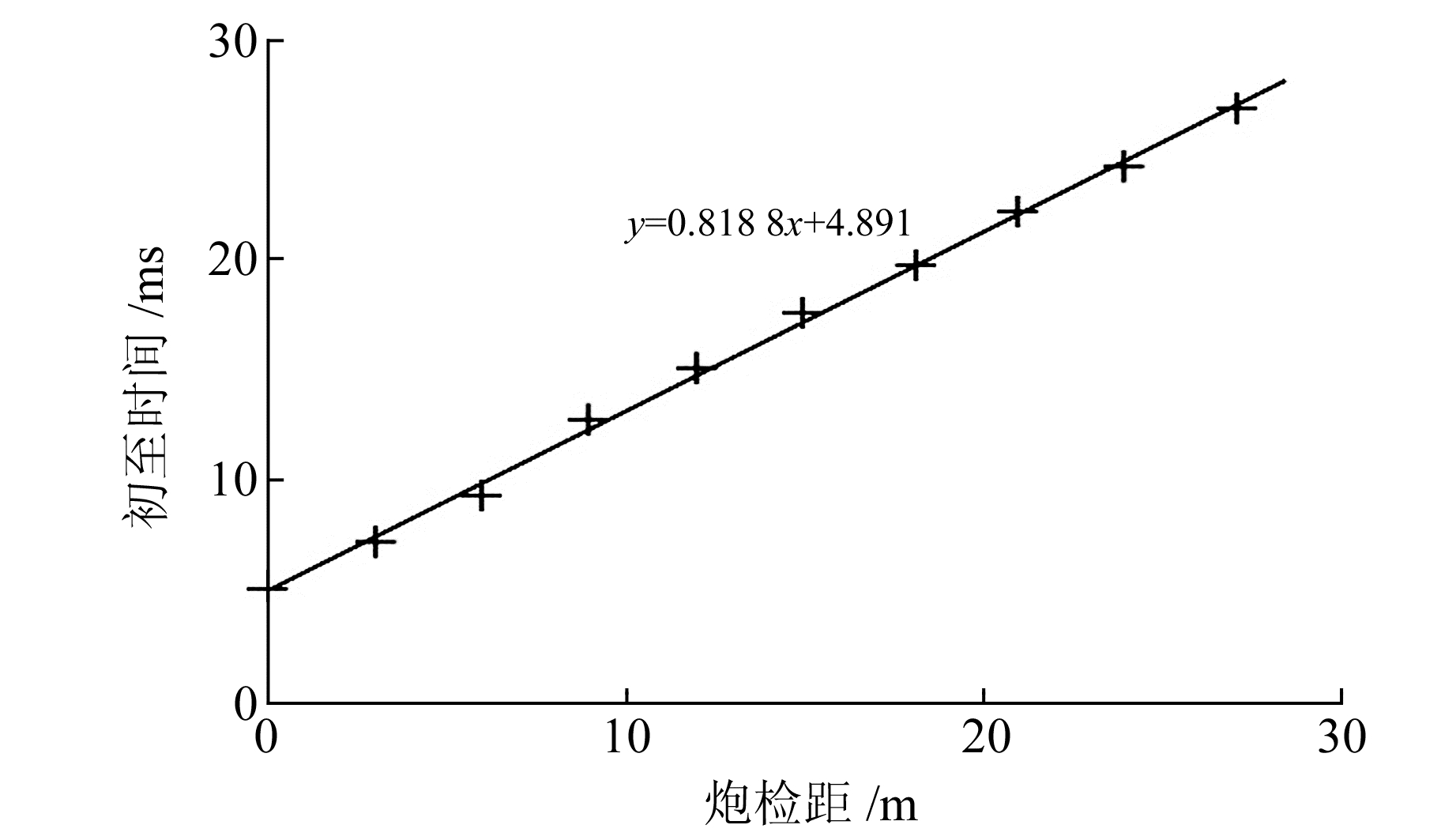
图 16为该测线钻孔联合剖面对应的工程地质剖面,ZK1、ZK3、ZK4、ZK2等4个钻孔中相邻钻孔间距依次为23.0 m、8.5 m、8.5 m,剖面总长度为40.0 m,钻孔深度分别为60 m、68 m、56 m、48 m。由钻孔资料可知,该测线浅层覆盖物主要为第四系砂卵石层(Q3a1+p1),下伏地层为白垩系砂泥岩。钻孔ZK1揭露地层均为砂卵石层,未见白垩系砂泥岩层;ZK3、ZK4、ZK2分别在45 m、51 m、66 m深处揭露白垩系砂泥岩。该排钻孔验证了断层F5-1浅部断点的存在,结合叠加剖面(图 15)与钻孔资料(图 16)可以判定该断层为逆断层,断距约为10 m,倾向为测线小号方向。图 17为该测线一单炮记录近炮点直达波初至时间与炮检距散点图,经线性拟合,其斜率为0.818 8 ms/m,估算该点低速层速度约为1 200 m/s,共接收点域折射波叠加剖面中浅部断点的旅行时间约为50 ms。利用式(9)估算其埋深约为60 m,该结果与图 16钻孔资料揭露的断层深度相当,误差约为4 m,断点横向位于桩号275附近(CDP514)。由共中心点叠加速度分析测得该断点附近130 ms处叠加速度约为2 700 m/s,由此可估算反射叠加剖面上所反映的断点深度约为175 m,位于CDP475附近。结合深部断点和浅部断点的空间位置估算该断层倾角约为60°。

|
图 16 二维剖面对应的工程地质剖面 Fig. 16 Engineering geological profile corresponding to 2D profile |
|
图 17 二维测线低速层速度求取 Fig. 17 Velocity calculation of low velocity layer of 2D line |
本文基于折射波时距曲线方程,讨论了共检波点折射波叠加成像方法的原理,并应用该方法和共中心点域折射波叠加技术对二维模型及实际地震资料进行叠加处理,经过对比分析叠加剖面,得到以下结论:
1) 在共接收点域,可以应用消除炮检距及炮点延迟时间的方法将折射波及断点绕射波校正到同一时间,通过叠加技术可进一步提高折射波及断点绕射波信噪比。
2) 差数时间法不依赖于测线地形和低速层速度,可以获得较准确的折射波速度;采用直达波初至时间线性拟合方法可以得到较准确的低速层速度,应用该速度作时深转换精度较高。
3) 共检波点折射波叠加方法可以得到横向分辨率和信噪比较高的叠加剖面,剖面上折射波和断点绕射波形态清晰,可以较可靠地反映埋深较浅的活动断层上断点的空间位置,结合反射地震剖面及钻孔资料可以较准确地判定活动断层的浅部形态。
| [1] |
邓起东, 卢造勋, 杨主恩. 城市活动断层探测和断层活动性评价问题[J]. 地震地质, 2007, 29(2): 189-200 (Deng Qidong, Lu Zaoxun, Yang Zhu'en. Remarks on Urban Active Faults Exploration and Associated Activity Assessment[J]. Seismology and Geology, 2007, 29(2): 189-200 DOI:10.3969/j.issn.0253-4967.2007.02.001)
(  0) 0) |
| [2] |
田一鸣, 刘保金, 石金虎, 等. 南阳盆地朱阳关-夏馆断裂的浅部特征及活动[J]. 地震地质, 2018, 40(1): 87-96 (Tian Yiming, Liu Baojin, Shi Jinhu, et al. Shallow Structure and Activity Characteristics of the Zhuyangguan-Xiaguan Fault in the Nanyang Basin[J]. Seismology and Geology, 2018, 40(1): 87-96 DOI:10.3969/j.issn.0253-4967.2018.01.007)
(  0) 0) |
| [3] |
杨晓平, 袁洪克, 宋新初, 等. 浙江宁波育王山山前隐伏断层勘探和新活动时代[J]. 地球科学——中国地质大学学报, 2011, 36(6): 967-976 (Yang Xiaoping, Yuan Hongke, Song Xinchu, et al. Exploration of the Buried Fault in Front of Yuwang Mountain and Its Neomovement's Epoch in Ningbo, Zhejiang Province[J]. Earth Science——Journal of China University of Geosciences, 2011, 36(6): 967-976)
(  0) 0) |
| [4] |
何正勤, 潘华, 胡刚, 等. 核电厂址隐伏断裂探测中的地震勘探方法研究[J]. 地球物理学报, 2010, 53(2): 326-334 (He Zhengqin, Pan Hua, Hu Gang, et al. Study on the Seismic Exploration Method to Detect Buried Fault in the Site of Nuclear Power Plant[J]. Chinese Journal of Geophysics, 2010, 53(2): 326-334 DOI:10.3969/j.issn.0001-5733.2010.02.010)
(  0) 0) |
| [5] |
高景华, 徐明才. 地震方法确定活动断裂上断点的影响因素分析[J]. 地震地质, 2012, 34(2): 338-347 (Gao Jinghua, Xu Mingcai. Analysis of Influencing Factors in Determining the Upper Offset Point of Active Faults Using Seismic Method[J]. Seismology and Geology, 2012, 34(2): 338-347 DOI:10.3969/j.issn.0253-4967.2012.02.012)
(  0) 0) |
| [6] |
单娜琳, 程志平, 刘云祯. 工程地震勘探[M]. 北京: 冶金工业出版社, 2006 (Shan Nalin, Cheng Zhiping, Liu Yunzhen. Engineering Seismic Exploration[M]. Beijing: Metallurgical Industry Press, 2006)
(  0) 0) |
| [7] |
梁运基, 万应明, 高峻, 等. 低降速带资料解释新方法及其可视化研究[J]. 江汉石油学院学报, 2004, 26(2): 67-70 (Liang Yunji, Wan Yingming, Gao Jun, et al. A New Method of Data Interpretation in Low Deceleration Zone and Its Visulization[J]. Journal of Jianghan Petroleum Institute, 2004, 26(2): 67-70 DOI:10.3969/j.issn.1000-9752.2004.02.026)
(  0) 0) |
| [8] |
冯太林, 张学工, 李衍达, 等. 折射波地震记录叠加成像方法研究[J]. 地球物理学报, 2001, 44(1): 129-134 (Feng Tailin, Zhang Xuegong, Li Yanda, et al. Research on Methodology of Stack Image of Refraction Seismic Recording[J]. Chinese Journal of Geophysics, 2001, 44(1): 129-134 DOI:10.3321/j.issn:0001-5733.2001.01.015)
(  0) 0) |
| [9] |
王克斌.复杂地表条件下初至折射波静校正方法研究[D].成都: 成都理工大学, 2003 (Wang Kebin. Refratcion First-Break Statics Method under Complex Near-surface Conditions[D]. Chengdu: Chengdu University of Technology, 2003) http://cdmd.cnki.com.cn/Article/CDMD-10616-2004085855.htm
(  0) 0) |
| [10] |
熊翥. 地震数据处理应用技术[M]. 北京: 石油工业出版社, 2008 (Xiong Zhu. The Applying Techniques of Seismic Data Processing[M]. Beijing: Petroleum Industry Press, 2008)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

