2. 中国科学院测量与地球物理研究所,武汉市徐东大街340号,430077;
3. 中国科学院大学,北京市玉泉路19号甲,100049
目前,基于LEO(low earth orbit)星座的GNSS增强技术是国内外的研究热点。GNSS联合LEO星座通信系统,可明显增强GNSS的抗干扰能力[1],有利于快速解算GNSS载波相位的整周模糊度[2],提高GNSS的导航性能和故障检测能力[3],还可依靠LEO星座发展建设GNSS信号天基全球监测体系[4]。同时,有学者将LEO星座卫星用于导航的轨道预报[5]、星历参数设计[6]及LEO星座与GNSS时钟同步[7]等相关领域,为LEO星座增强GNSS的应用提供了很多有价值的基础研究。
LEO星座增强GNSS的导航应用中,由于卫星视向运行速度快,星座几何结构变化快,有利于载波相位模糊度的快速解算。综合考虑LEO星座卫星轨道高度低、信号强的特点,其在GNSS增强中的作用较其他系统优势明显,同时全球覆盖的LEO星座有望实现全球范围内的高精度快速GNSS导航。本文结合用户高精度快速定位的应用及LEO星座在GNSS中的优势,初步分析了Iridium增强GPS的精密单点定位(PPP)性能,得到具有参考价值的结论,并基于GPS星座和Iridium星座及其轨道数据,仿真BJFS站GPS和Iridium系统的双频观测数据,在此基础上进行PPP实验,从可视卫星数、DOP值、PPP滤波矩阵的病态性、PPP定位精度和收敛时间及模糊度首次固定成功所需的时间等方面,初步分析在PPP中LEO星座对GNSS的增强作用。
1 星座及轨道仿真Iridium系统采用Walker星座结构[8],共有66颗卫星,分布在6条轨道上,每条轨道上部署11颗在轨卫星,同向运动的卫星轨道面之间间隔31.6°,反向运动的卫星轨道面之间间隔22°,卫星的轨道高度约为781 km,轨道倾角为86.4°,卫星的运行周期为100 min左右。近极轨道的Iridium星座易于建立星间链路,能够覆盖全球,增加高纬度地区的可视卫星数,改善高纬度地区的导航能力,Iridium星座的轨道数据由卫星数据库导出。GPS星座的32颗卫星分布在6个轨道面上,高度约为20 200 km,轨道数据从IGS网站中下载。
2 地面测站的观测数据仿真及PPP数据处理仿真地面测站的观测数据涉及的误差项有卫星钟差、电离层延迟、对流层延迟、地球自转效应、相对论效应、接收机钟差及观测噪声,为简化后续PPP处理及分析,暂不考虑卫星轨道误差、卫星天线相位中心、接收机天线相位中心、硬件延迟、海潮及固体潮等误差项。为简化实验,本文认为Iridium与GPS播发相同的导航信号(信号包含双频伪距P1、P2及载波L1、L2等测距信息),依此仿真观测数据,并仿真了BJFS站GPS单系统和GPS+Iridium双系统的双频伪距观测值和载波相位观测值。
实验采用GPSTK2.9软件进行消电离层组合的伪动态PPP数据处理,在GPSTK2.9默认设置下,利用Kalman滤波解算坐标改正数、接收机钟差、对流层延迟天顶湿分量和LC模糊度,具体的数学模型及参数设置详见文献[9]。本文对GPSTK2.9软件进行以下改进:1)使GPSTK2.9软件兼容处理地面测站对Iridium的观测数据;2)PPP处理的坐标初值由首历元P1伪距观测值的标准单点定位得出;3)PPP浮点解处理后采用星间单差的MW方法进行模糊度固定(仿真数据不考虑硬件延迟)。改进后的GPSTK2.9软件进行PPP数据处理的流程如图 1所示。

|
图 1 PPP数据处理流程 Fig. 1 PPP data processing flow chart |
实验中BJFS站观测数据的仿真时间为2015年年积日为248的00 :00 :00~23 :59 :59,采样间隔为5 s,将24 h平均分成48个时段,对每个时段(0.5 h)的数据单独进行PPP数据处理。为对比分析GPS+Iridium双系统与GPS单系统PPP的优劣,根据历元对48个时段的平均可视卫星数、精度因子(DOP)平均值、PPP滤波矩阵条件数、三维定位和U、E、N方向的定位RMS、PPP浮点解收敛时间及模糊度首次固定成功时间等进行统计。
3.1 可视卫星数及DOP分析精度因子是评估卫星导航定位性能的重要指标之一,反映了导航定位结果的质量和导航星座几何分布的均匀程度,可作为基于空间布局结构的导航性能增强的分析手段[10]。在卫星星座几何构型已经确定的情况下,可视卫星数成为影响DOP的主要因素,随着可视卫星数的增加,DOP将逐渐降低,DOP值越小则导航性能越优。
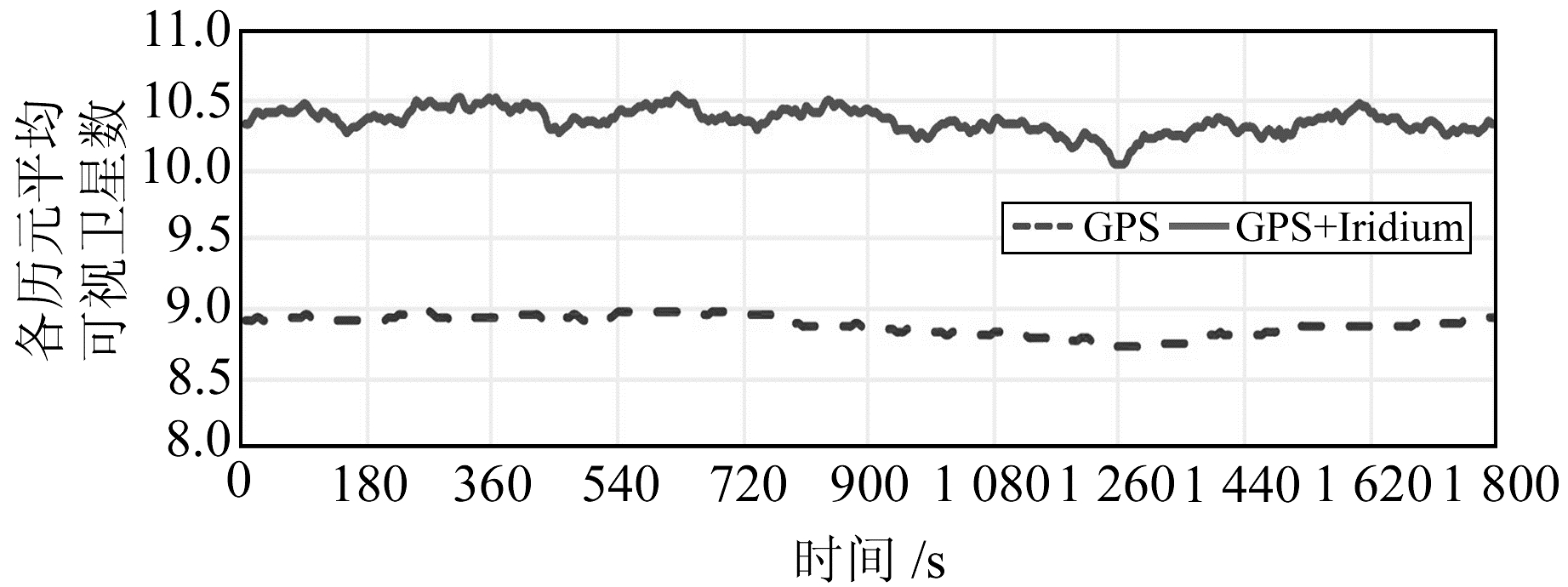
GPS与GPS+Iridium的平均可视卫星数随时间的变化如图 2所示,GPS+Iridium与GPS相比,每个历元平均增加1.5颗可视卫星。GPS与GPS+Iridium的GDOP、PDOP、HDOP、VDOP的平均值随时间的变化如图 3所示,由图可知,GPS+Iridium与GPS相比,每个历元的GDOP平均值从2.17降至1.9,平均降低0.27;PDOP平均值从1.9降至1.68,平均降低0.22;每个历元的HDOP平均值从1.04降至0.92,平均降低0.12;每个历元的VDOP平均值从1.58降至1.40,平均降低0.18。当Iridium星座增强GPS时,增加了可视卫星数,降低了精度因子,与水平精度因子相比,垂直精度因子降低的效果更为明显。
|
图 2 GPS与GPS+Iridium的平均可视卫星数随时间的变化 Fig. 2 The visual satellite averages of GPS and GPS+Iridium change over time |

|
图 3 GPS与GPS+Iridium的GDOP、PDOP、HDOP、VDOP的平均值随时间的变化 Fig. 3 GDOP, PDOP, HDOP and VDOP values of GPS and GPS+Iridium change over time |
本文PPP采用Kalman滤波解算,Kalman滤波的状态方程和观测方程为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{k + 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1, k}}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_k}}\\ {{\mathit{\boldsymbol{L}}_{k + 1}} = {\mathit{\boldsymbol{B}}_{k + 1}}{\mathit{\boldsymbol{X}}_{k + 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_{k + 1}}} \end{array}} \right. $ | (1) |
式中,X k、X k+1分别为k和k+1时刻的状态向量,Φ k+1, k为状态转移矩阵,Ω k为动态噪声(干扰)向量,L k+1为观测向量,B k+1为测量矩阵,Δ k+1为观测噪声。解算主要分为2步。
1) 预测:
| $ {\mathit{\boldsymbol{X}}_{k + 1, k}} = {{\rm{\Phi }}_{k + 1, k}}{\mathit{\boldsymbol{X}}_k} $ | (2) |
| $ {\mathit{\boldsymbol{D}}_X}_{_{k + 1, k}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1, k}}{\mathit{\boldsymbol{D}}_X}_{_k}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1, k}^{\rm{T}} + {\mathit{\boldsymbol{D}}_{\rm{\varOmega }}}_{_k} $ | (3) |
2) 修正:
| $ {\mathit{\boldsymbol{D}}_X}_{_{k + 1}} = {\left( {\mathit{\boldsymbol{D}}_{{X_{k + 1, k}}}^{ - 1} + \mathit{\boldsymbol{B}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{D}}_{{\Delta _{k + 1}}}^{ - 1}{\mathit{\boldsymbol{B}}_{k + 1}}} \right)^{ - 1}} $ | (4) |
| $ {\mathit{\boldsymbol{X}}_{k + 1}} = {\mathit{\boldsymbol{D}}_{{X_{k + 1}}}}(\mathit{\boldsymbol{D}}_{{X_{k + 1,k}}}^{ - 1}{\mathit{\boldsymbol{X}}_{k + 1,k}} + \mathit{\boldsymbol{B}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{D}}_{{\Delta _{k + 1}}}^{ - 1}{\mathit{\boldsymbol{L}}_{k + 1}}) $ | (5) |
式中,
采用Kalman滤波解算的PPP中,PPP滤波矩阵的病态性指标可以由矩阵
| $ {\rm{cond}}\left( \mathit{\boldsymbol{N}} \right) = \left\| {{\mathit{\boldsymbol{N}}^{ - 1}}} \right\| \cdot \left\| \mathit{\boldsymbol{N}} \right\| = \frac{{{\lambda _{{\rm{max}}}}}}{{{\lambda _{{\rm{min}}}}}} $ | (6) |
式中,λmax和λmin分别为矩阵N的最大特征值和最小特征值。该矩阵的条件数反映了参数之间的相关性,也反映了该矩阵的病态性和求逆稳定性。
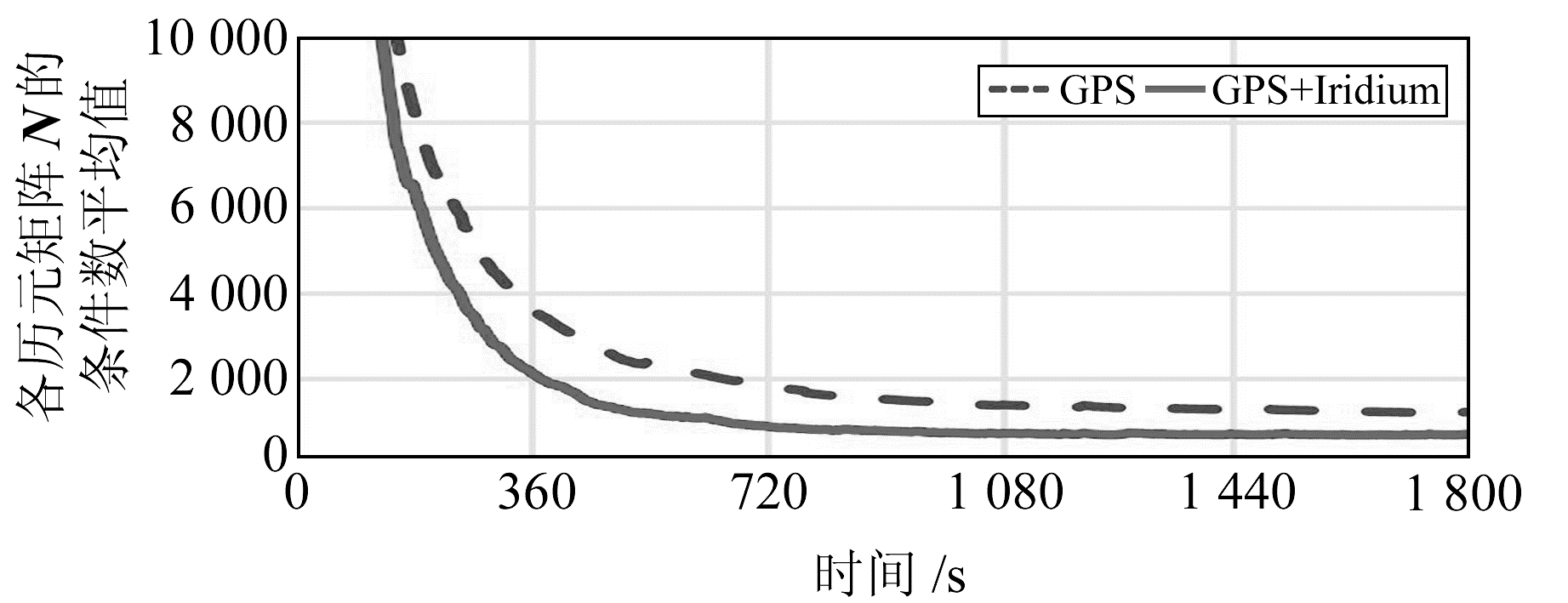
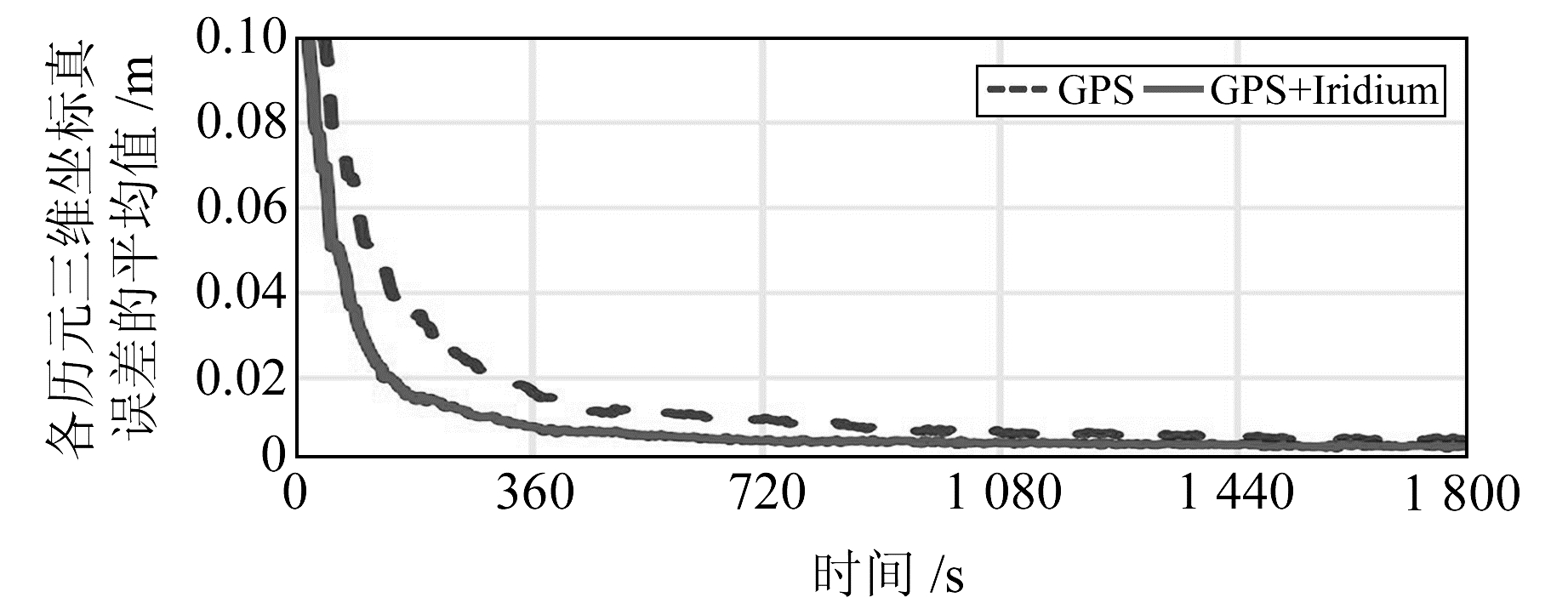
在PPP数据处理中,GPS与GPS+Iridium滤波矩阵N的条件数平均值随时间的变化如图 4所示。GPS单系统PPP处理时,滤波矩阵N的条件数在185 s时小于8 000,在335 s时小于4 000,在640 s小于2 000,最终收敛于1 150左右;GPS+Iridium双系统滤波矩阵N的条件数在150 s时小于8 000,在250 s时小于4 000,在370 s时小于2 000,最终收敛于630左右,与GPS单系统相比降低了45%。各历元的GPS与GPS+Iridium三维坐标真误差(PPP解算坐标与坐标仿真值的差)的平均值随时间的变化如图 5所示,可以看出,GPS+Iridium双系统的坐标真误差在收敛前明显小于GPS单系统。以滤波矩阵N的条件数为指标,可以认为Iridium系统增强GPS定位,削弱了Kalman滤波解算中滤波矩阵N的病态性,减小了解算坐标的真误差。
|
图 4 GPS与GPS+Iridium滤波矩阵N的条件数平均值随时间的变化 Fig. 4 The mean value of the conditional number of the filtration matrix N of GPS and GPS+Iridium change over time |
|
图 5 GPS与GPS+Iridium三维坐标真误差的平均值随时间的变化 Fig. 5 The mean value of three-dimensional coordinate true error of GPS and GPS+Iridium change over time |
PPP收敛时间过长则无法快速定位,影响PPP的作业效率。PPP收敛时间受观测数据质量、卫星轨道与钟差、测站纬度、电离层与对流层等误差模型、待估参数个数、卫星空间几何构型等因素的影响[11],其中对流层模型和卫星空间几何构型GDOP对PPP收敛时间的影响非常明显。GPS+Iridium双系统与GPS单系统相比,在其他因素不变的情况下,Iridium星座使卫星空间几何构型发生了重大变化。
本文采用均方根误差(RMSE)来进行PPP结果的精度评估,GPS与GPS+Iridium定位结果的3D-RMS、U-RMS、E-RMS、N-RMS随时间的变化如图 6所示。从图中可以看出,GPS+Iridium双系统与GPS单系统相比,3D-RMS和U-RMS的改善非常显著,E-RMS几乎没有改善,N-RMS的改善较为明显。对比图 6(a)和6(b)发现,GPS+Iridium双系统的U-RMS与3D-RMS的变化趋势一致(GPS单系统类似),可认为Iridium在PPP定位中对于天顶U方向的精度增强作用最为显著。

|
图 6 GPS与GPS+Iridium定位结果随时间的变化 Fig. 6 The positioning results of GPS and GPS+Iridium changes over time |
PPP处理结果中,GPS单系统的3D-RMS在55 s时小于0.1 m,在145 s时小于0.05 m,在245 s时小于0.03 m,最终收敛在0.006 m左右;GPS+Iridium双系统的3D-RMS在30 s时小于0.1 m,在80 s时小于0.05 m,在120 s时小于0.03 m,最终收敛在0.004 m左右,与GPS相比收敛时间分别缩短了45%、45%、51%,收敛后精度提高了33%。GPS单系统的U-RMS在140 s时小于0.05 m,在210 s时小于0.03 m,在425 s时小于0.01 m;GPS+Iridium双系统的U-RMS在80 s时小于0.05 m,在105 s时小于0.03 m,在280 s时小于0.01 m,与GPS相比收敛时间分别缩短了43%、50%、34%。对于N方向,在收敛前GPS+Iridium双系统的RMS比GPS单系统降低了0.01 m左右。
3.4 PPP模糊度首次固定成功的时间在实际处理中,PPP开始前一段时间内,消电离层组合的浮点解模糊度受Kalman滤波收敛的影响,无法固定成功,因此模糊度首次固定成功的时间决定了PPP固定解的定位效率。本文采用单差的MW方法固定模糊度[12],并用Ratio值检验法判定模糊度是否固定成功。GPS+Iridium双系统与GPS单系统在Ratio=1.5、3、5为指标时及PPP固定的模糊度与仿真的模糊度(真值)对比的模糊度首次固定成功所需要的时间标准差、平均值见表 1。从表中可以看出,GPS+Iridium双系统与GPS单系统相比,PPP固定的模糊度在Ratio=1.5、3、5时及与模糊度仿真值对比的首次固定成功所需要的时间平均分别缩短了50%、46%、42%及47%。
|
|
表 1 GPS+Iridium与GPS的模糊度首次固定成功所需时间的统计 Tab. 1 The statistics of the time required for the first fixed success of ambiguity of GPS+Iridium and GPS |
本文以BJFS站为例,从可视卫星数、DOP值、滤波矩阵的病态性、PPP收敛时间、浮点解的定位精度和模糊度固定所需的时间等方面初步分析了GPS+Iridium双系统和GPS单系统的PPP性能。通过对PPP处理结果进行对比分析,得出以下结论:1)极轨道的Iridium增强GNSS定位中,增加了可视卫星数,降低了DOP值;2)GPS+Iridium双系统利用载波相位进行PPP时,与GPS单系统相比,降低了PPP滤波矩阵的病态性;3)Iridium增强GPS的PPP浮点解,E方向的精度改善不明显,N方向的精度得到一定的改善,U方向的精度改善非常显著,收敛时间明显缩短,决定了三维精度得到显著提高,明显缩短PPP收敛时间,有利于GNSS快速甚至实时精密定位的应用;4)GPS+Iridium双系统与GPS单系统相比,PPP模糊度首次固定成功的时间明显缩短。
本文基于同等的仿真条件,比较了GPS+LEO双系统与GPS单系统在PPP时的差异,讨论了LEO星座对PPP性能的提升,但在仿真实验中,对于Iridium与GPS采用相同的观测数据误差模型和PPP处理策略(如导航信号频率、观测值权重等),没有考虑二者的不同。另外,卫星轨道误差对PPP的影响并未考虑,且本文的仿真条件过于理想化,使得单GPS的PPP收敛时间与现实存在一定差异,但这并不影响本文的研究结论。在下一步研究中将对这些问题加以考虑,同时将深入探讨LEO星座卫星对BDS精密单点定位的增强作用。
| [1] |
邓琳, 李广侠, 田世伟, 等. 基于LEO增强的COMPASS导航系统抗干扰能力研究[J]. 军事通信技术, 2012, 33(2): 65-59 (Deng Lin, Li Guangxia, Tian Shiwei, et al. Capabilities of LEO Enhanced COMPASS Navigation System for Anti-jamming[J]. Journal of Military Communications Technology, 2012, 33(2): 65-59)
(  0) 0) |
| [2] |
Tian S W, Dai W H, Liu R F, et al. System Using Hybrid LEO-GPS Satellites for Rapid Resolution of Integer Cycle Ambiguities[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 1 774-1 785 DOI:10.1109/TAES.2014.120662
(  0) 0) |
| [3] |
赵金峰, 于笑, 冯少栋, 等. 基于LEO增强的COMPASS系统设计及性能分析[J]. 电讯技术, 2013, 53(2): 131-135 (Zhao Jinfeng, Yu Xiao, Feng Shaodong, et al. Design and Performance Analysis of LEO Satellites Enhanced COMPASS System[J]. Telecommunication Engineering, 2013, 53(2): 131-135)
(  0) 0) |
| [4] |
俞能杰, 方晖, 王盾, 等.基于低轨星座的GNSS信号全球监测约束条件初步分析[C].第六届中国卫星导航学术年会, 西安, 2015 (Yu Nengjie, Fang Hui, Wang Dun, et al. The Preliminary Constraints Analysis of GNSS Signals Global Monitoring Based on LEO Constellation[C]. The Sixth China Satellite Navigation Conference, Xi'an, 2015) https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=IPFD&filename=WXDH201505005007
(  0) 0) |
| [5] |
王亚菲, 钟世明, 王海涛, 等. LEO卫星轨道预报精度分析[J]. 测绘学报, 2016, 45(9): 1 035-1 041 (Wang Yafei, Zhong Shiming, Wang Haitao, et al. Precision Analysis of LEO Satellite Orbit Prediction[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1 035-1 041)
(  0) 0) |
| [6] |
方善传, 杜兰, 周佩元, 等. 低轨导航增强卫星的轨道状态型星历参数设计[J]. 测绘学报, 2016, 45(8): 904-910 (Fang Shanchuan, Du Lan, Zhou Peiyuan, et al. Oribital List Ephemerides Design of LEO Navigation Augmentation Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 904-910)
(  0) 0) |
| [7] |
Pratt J, Axelrad P, Larson K M, et al. Satellite Clock Bias Estimation for iGPS[J]. GPS Solutions, 2013, 17(3): 381-389 DOI:10.1007/s10291-012-0286-4
(  0) 0) |
| [8] |
Fossa C E, Raines R A, Gunsch G H, et al. An Overview of the IRIDIUM(R) Low Earth Orbit(LEO) Satellite System[C]. Proceeding of the IEEE 1998 National Aerospace and Electronics Conference, Dayton, 1998 https://www.researchgate.net/publication/3766499_An_Overview_of_the_Iridium_Low_Earth_Orbit_LEO_Satellite_System
(  0) 0) |
| [9] |
Salazar D, Hernandez-Pajares M, Juan J M, et al. GNSS Data Management and Processing with the GPSTk[J]. GPS Solutions, 2009, 14(3): 293-299
(  0) 0) |
| [10] |
李建文, 李作虎, 周巍, 等. 卫星导航中几何精度衰减因子最小值分析及应用[J]. 测绘学报, 2011, 40(增1): 85-88 (Li Jianwen, Li Zuohu, Zhou Wei, et al. Study on the Minimum of GDOP in Satellite Navigation and Its Applications[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 85-88)
(  0) 0) |
| [11] |
曹相, 高成发. GPS精密单点定位(静态)影响收敛速度的因素分析[J]. 现代测绘, 2007, 30(1): 19-21 (Cao Xiang, Gao Chengfa. Factors Analyze of the Convergence Rate for GPS Precise Point Positioning[J]. Modern Surveying and Mapping, 2007, 30(1): 19-21 DOI:10.3969/j.issn.1672-4097.2007.01.006)
(  0) 0) |
| [12] |
赵兴旺, 王胜利, 刘超. GNSS精密单点定位理论与方法[M]. 合肥: 中国科学技术大学出版社, 2015 (Zhao Xingwang, Wang Shengli, Liu Chao. Theory and Method of GNSS Precise Point Positioning[M]. Hefei: University of Science and Technology of China Press, 2015)
(  0) 0) |
2. Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China;
3. University of Chinese Academy of Science, A19 Yuquan Road, Beijing 100049, China
 2020, Vol. 40
2020, Vol. 40

