卫星导航定位已经进入多系统时代,现存的全球四大导航系统分别为GPS、GLONASS、Galileo、BDS,多系统的出现也使得联合定轨成为现代导航的热点。多系统联合定轨极大地增加了多余观测量,优化了解算过程中法方程的结构,提高了定轨精度[1]。在多系统定轨过程中,公共参数包括测站坐标参数、对流层参数、接收机钟差参数;非公共参数包括卫星初始轨道参数和卫星钟差参数等。
目前北斗全球卫星导航系统(简称北斗三号系统,BDS-3)正处于建设阶段,虽已具备全球导航定位能力,但测站数量较少且BDS-3卫星星座不完整,可观测到的BDS-3卫星数较少[2-3],BDS-3单独导航定位功能差,所以本文仍然针对已经完善的、可独立运转的BDS-2进行轨道精度评价。李敏等[4]利用实测多模观测数据实现统一框架下的多导航系统卫星精密轨道及钟差确定,验证了基于非差模型的多模GNSS卫星融合精密定轨理论与方法的可行性;刘伟平等[5]给出一种基于模糊度固定的北斗卫星系统融合非差精密定轨方法,得出BDS轨道径向精度优于10 cm的结论;王乐等[6]分析了不同策略下获得BDS卫星轨道的差异,得到利用区域监测站进行BDS卫星定轨的优选方案。但上述方法仅在处理策略、解算模型等方面对GPS/BDS联合定轨进行了改进,并未详细分析公共参数的精度及贡献。
本文采用非差模式进行数据处理,首先给出多系统联合定轨的观测方程、动力学模型及处理策略;然后解析无电离层组合中公共测站坐标、对流层和接收机钟差参数对多系统联合定轨的贡献量;最后将各系统单独解算与联合解算的定轨结果进行对比,给出GPS系统加入后联合求解的公共参数对轨道精度的贡献量。
1 联合定轨理论与方法 1.1 多GNSS数据处理观测方程GNSS观测值中一般采用2种最基本的观测量, 即伪距和载波相位观测值。与单系统不同的是,多系统融合过程中由于各系统的观测值在卫星端与接收机端的延迟量不同,在融合过程中需要顾及系统间的信号延迟量,对于非GLONASS卫星此信号延迟量即系统间偏差,对于GLONASS卫星此信号延迟量为系统间偏差与接收机端频率偏差的统称[4]。通常卫星端的系统间偏差可以被卫星钟差吸收,接收机端相位的系统间偏差可以被模糊度参数吸收,而接收机端伪距的系统间偏差则需要估计[7]。
GPS无论是在卫星星座、测站数量、测站覆盖范围还是系统稳定度、处理策略、产品类型多样化及产品精度方面,始终保持绝对的领先状态。因此多系统融合中,考虑各系统信号延迟问题时,仍然以GPS系统作为基准,将各系统间的不同信号延迟量均归算至相对于GPS的信号延迟量。需要说明的是,此时对多GNSS系统间的信号延迟量有一定的约束条件:1)所有接收机对于GPS的偏差值为0;2)所有接收机端对同一系统的偏差值和为0;3)所有接收机端对同一GLONASS频率的偏差值和为0[8]。本文采用无电离层组合,则伪距和载波相位非差观测方程可描述为:
| $ \left\{ \begin{array}{l} {\rm{PC}} = \rho + c({\rm{d}}{t_{\rm{r}}} - {\rm{d}}{t_{\rm{s}}}) + {d_{{\rm{ion}}}} + {d_{{\rm{trop}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} c{\delta _{{\rm{tg}}}} + {\varepsilon _p}\\ {\rm{LC}} = \rho + c({\rm{d}}{t_{\rm{r}}} - {\rm{d}}{t_{\rm{s}}}) - {d_{{\rm{ion}}}} + {d_{{\rm{trop}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} c{\delta _{{\rm{tg}}}} + N\lambda + {\varepsilon _\varPhi } \end{array} \right. $ | (1) |
式中,PC与LC分别为伪距和载波相位观测值,ρ为卫星和测站之间的几何距离,c为光速,dtr与dts分别为接收机和卫星端的钟差,dion为电离层延迟,dtrop为对流层延迟,δtg为多模GNSS系统间的信号延迟量,N为整周模糊度,λ为相应的载波波长,εP、εΦ分别为伪距与载波相位未能模型化的剩余误差。
1.2 动力学模型与处理策略本文采用融合了几何观测信息与动力学信息的简化动力学定轨方式,充分利用几何观测信息与运动学信息[5],观测信息见§1.1,运动学信息如下述。卫星的运动方程可表示为:
| $ \bar a = {\bar a_{\rm{g}}} + {\bar a_{{\rm{ng}}}} + {\bar a_{{\rm{emp}}}} $ | (2) |
式中,ag 为卫星所受的由保守力引起的加速度,包括地球中心引力、地球非球形引力摄动加速度、N体引力摄动加速度、潮汐效应引起的摄动加速度、广义相对论摄动力加速度;ang为卫星所受的非保守力加速度,包括太阳辐射、地球反照辐射和热辐射摄动力加速度、大气阻力摄动加速度;aemp为经验加速度,不具有实际物理意义,由摄动力模型误差和未模型化的摄动力引起。
多GNSS联合精密定轨的观测模型与GPS系统精密定轨模型并无太大差别,仅需要注意多GNSS联合精密定轨时需要考虑各系统之间的时间基准、坐标基准的统一及各系统之间不同信号的偏差量。表 1和2为具体处理策略与动力学模型,其中卫星及接收机天线相位中心改正采用文献[9]中的解算参数。
|
|
表 1 多GNSS联合定轨处理策略 Tab. 1 Multi-GNSS joint orbit determination model |
|
|
表 2 多GNSS联合定轨动力学模型 Tab. 2 Multi-GNSS joint orbit determination dynamics model |
单系统定轨时观测方程可以表示为:
| $ {\mathit{\boldsymbol{V}}_1} = {\mathit{\boldsymbol{L}}_1} - \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}_1}}&{{\mathit{\boldsymbol{B}}_1}} \end{array}} \right]{\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_1}}\\ \mathit{\boldsymbol{X}} \end{array}} \right]^{\rm{T}}} $ | (3) |
式中,V 1为残差向量,L 1为各种误差的观测值常数项,A 1、B 1分别为X 1、X的系数矩阵,X 1为非公共参数,X为各系统公共参数。式中参数X的观测方程可等价表示为:
| $ {\mathit{\boldsymbol{U}}_1} = {\mathit{\boldsymbol{L}}_1} - (\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{J}}_1}){\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{X}} $ | (4) |
其中,矩阵J 1可表示为:
| $ {\mathit{\boldsymbol{J}}_1} = {\mathit{\boldsymbol{A}}_1}{(\mathit{\boldsymbol{A}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{A}}_1})^{ - 1}}\mathit{\boldsymbol{A}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1} $ | (5) |
式中,U 1为残差向量,I为单位矩阵,P1为各单系统观测值权阵。设C 1=(I - J 1) B 1,此时单系统公共参数的最小二乘解为:
| $ \mathit{\boldsymbol{\hat X}} = {(\mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{C}}_1})^{ - 1}}(\mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{L}}_1}) $ | (6) |
各单系统与GPS系统联合定轨时,采取分别建立观测方程、约化整理部分参数后再合并观测方程的方法,则联合定轨时公共参数的观测方程可表示为:
| $ \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{U}}_1}}\\ {{\mathit{\boldsymbol{U}}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{L}}_1}}\\ {{\mathit{\boldsymbol{L}}_2}} \end{array}} \right] - \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{C}}_1}}\\ {{\mathit{\boldsymbol{C}}_2}} \end{array}} \right]{\mathit{\boldsymbol{X}}^\prime } $ | (7) |
式中,下标为2的向量均表示GPS系统,各参数代表意义及方程形式均与各单系统相同;X′为联合定轨公共参数。此时公共参数的最小二乘解为:
| $ {\mathit{\boldsymbol{\hat X}}^\prime } = {(\mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{C}}_1} + \mathit{\boldsymbol{C}}_2^{\rm{T}}{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{C}}_2})^{ - 1}}(\mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{L}}_1} + \mathit{\boldsymbol{C}}_2^{\rm{T}}{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{L}}_2}) $ | (8) |
式中,P 2为GPS系统观测值的权阵。
由式(7)与式(8)可知,加入GPS系统对于公共参数解的贡献为:
| $ {\rm{d}}\mathit{\boldsymbol{\hat X}} = {\mathit{\boldsymbol{\hat X}}^\prime } - \mathit{\boldsymbol{\hat X}} $ | (9) |
联合定轨相对于单系统定轨,极大地增加了观测方程的多余观测数。多余观测数的增加使得定轨结果的单位权中误差更加接近无偏,多系统间的公共参数精度也会相应提高[10]。通过最小二乘配置的循环迭代过程,仅与单系统有关的非公共参数精度也会得到一定程度的提高,最终使得各系统的定轨精度得到提高。
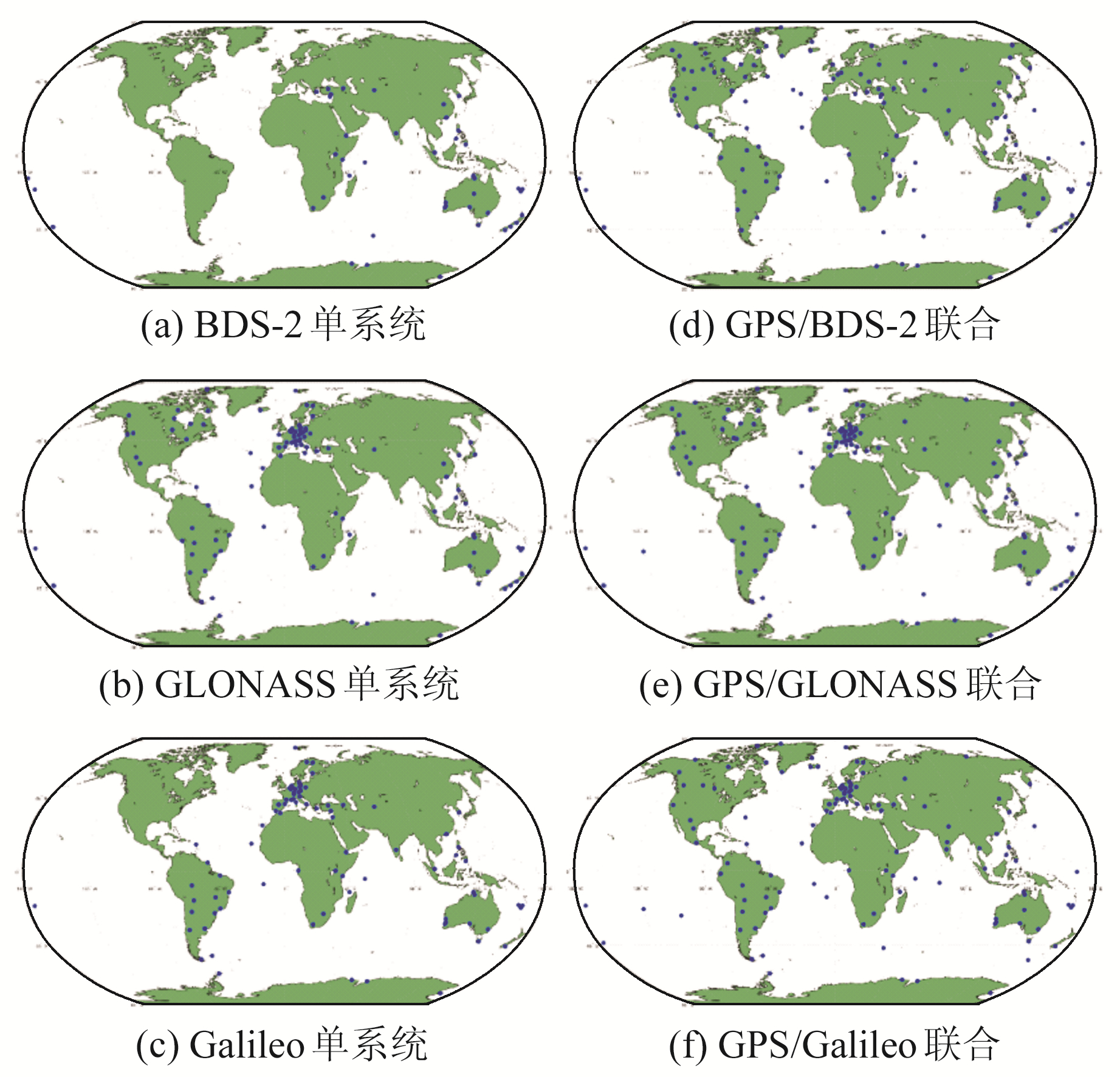
2 实验及结果分析 2.1 测站选择实验采用2018年年积日为182~188共7 d的观测数据,在全球IGS与MGEX站中选取测站。为强调GPS解算的公共参数对于BDS-2、GLONASS、Galileo单系统定轨精度的影响,在进行3个系统的单系统定轨时,测站选取策略为:选取全球站中包含GPS卫星且该系统卫星每个历元卫星数均不少于5颗的所有测站,以保证单系统定轨能达到最高精度。联合定轨时,在保留单系统定轨测站的基础上,全球范围内均匀增加包含GPS卫星的测站,且使得最终3种联合定轨测站数相等。BDS-2、GLONASS、Galileo单系统定轨测站数量分别为52、117、96,GPS/BDS-2、GPS/GLONASS、GPS/Galileo联合定轨测站数量均为135,测站分布见图 1。
|
图 1 测站分布示意图 Fig. 1 Sketch of stations' distribution |
实现高精度导航定位的前提是有高精度的卫星轨道与钟差[11],而排除力学模型、定轨策略、数据处理方法对于轨道与钟差的影响,用于解算的测站选择对于轨道精度也有很大的影响[6]。测站选择主要包括测站数量及测站的分布,但除GPS在全球范围内有分布均匀的超过550个地面监测站外,其余3个系统的地面监测站数量相对较少且分布不均匀,其中BDS地面监测站情况最差,仅有50个左右。单系统进行卫星轨道确定时,地面跟踪站数量少、构型差将会导致公共参数精度差,在解算过程中参数精度差,其参数误差将会体现在最终的轨道精度上。而将各单系统与GPS联合定轨解算,公共参数将会在精度上有极大的提升,从而使各系统的定轨精度最终得到极大的提升。
2.2 实验结果分析本文采用GFZ与武汉大学提供的最终产品作为参考值,将解算的轨道与其进行对比(仅BDS-2定轨结果与武汉大学产品进行对比,其余系统均采用GFZ产品)[12-13],得到公共参数精度和轨道切向、法向、径向及三维平均精度。
图 2为接收机钟差RMS值,表 3为各天公共参数精度提升量,可以看出,联合GPS求解的接收机钟差参数精度均有所提升,其中相较于BDS-2提升量最高,均在50%以上,Galileo次之,GLONASS提升量最小。这是因为BDS-2与Galileo卫星星座不完整、地面监测站数量少,单系统解算时公共参数精度差,加入GPS后对其精度提升明显。

|
图 2 接收机钟差RMS Fig. 2 RMS of receiver clock error |
|
|
表 3 公共参数精度提升量 Tab. 3 Improvement of public parameters by GPS common parameters |
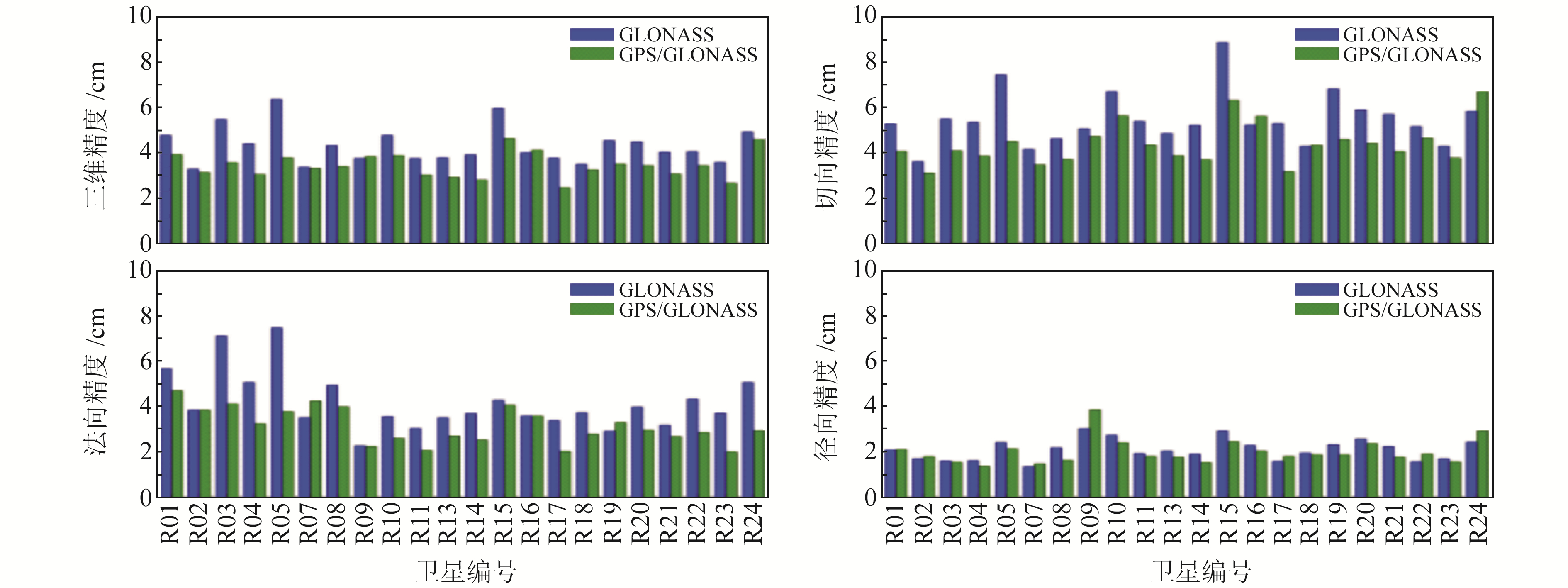
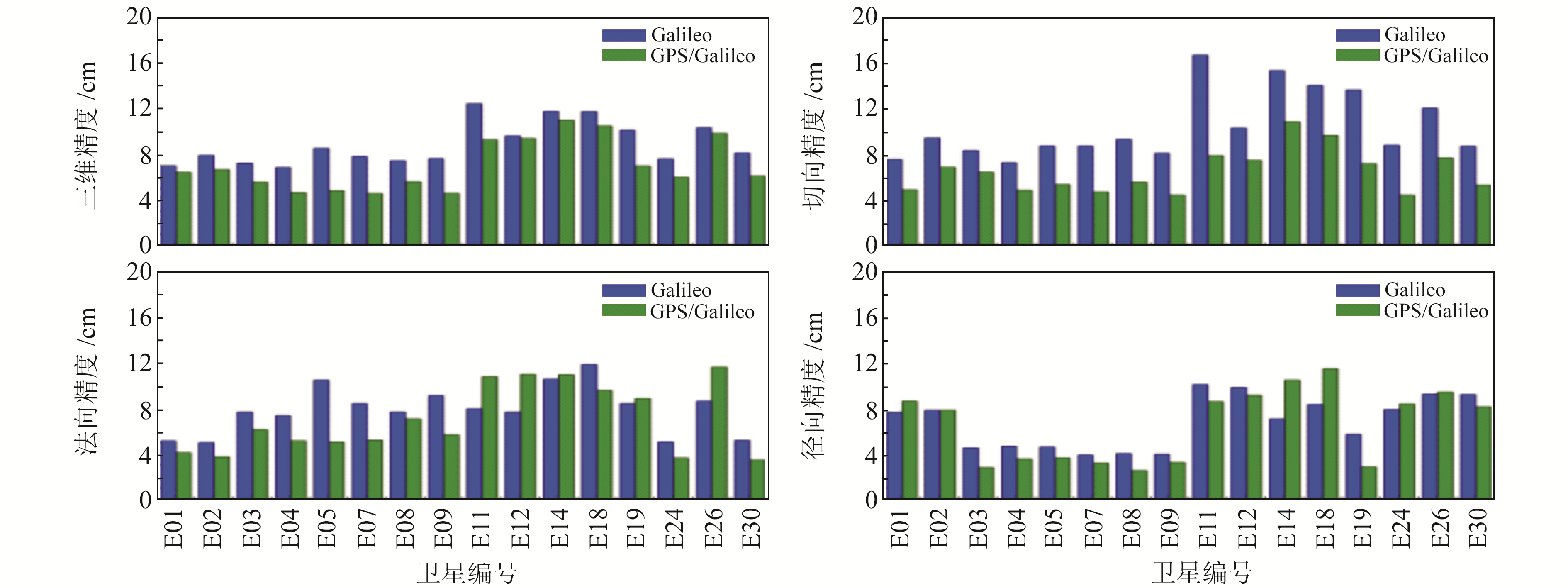
图 3~5分别为BDS-2、GLONASS、Galileo单系统与系统联合GPS定轨结果在三维平均、切向、法向、径向上的精度对比。可以看出,GLONASS与Galileo单系统三维平均定轨精度在4 cm、8 cm左右;BDS-2系统的GEO、IGSO、MEO卫星三维平均定轨精度分别优于1.5 m、0.4 m、0.2 m。GPS与BDS-2、GLONASS、Galileo联合定轨相对于各单系统定轨精度均有明显提高(除BDS-2的GEO卫星的切线方向),其中对BDS-2的IGSO、MEO分别提高5 cm、15 cm;对GLONASS与Galileo提高1 cm左右。

|
图 3 BDS-2与GPS/BDS-2定轨的三维平均、切向、法向、径向的精度对比 Fig. 3 Comparison of 3-D average, tangential, normal and radial accuracy of BDS-2 and GPS/BDS-2 orbit determination |
|
图 4 GLONASS与GPS/GLONASS定轨的三维平均、切向、法向、径向的精度对比 Fig. 4 Comparison of 3-D average, tangential, normal and radial accuracy of GLONASS and GPS/GLONASS orbit determination |
|
图 5 Galileo与GPS/Galileo定轨的三维平均、切向、法向、径向的精度对比 Fig. 5 Comparison of 3D average, tangential, normal and radial accuracy of Galileo and GPS/Galileo orbit determination |
图 6为各天GPS公共参数对单系统定轨精度的提升量,值为正表示提升,值为负表示降低。由于篇幅限制,图中仅给出三维平均轨道精度的提升量,其余各方向的提升量未给出。表 4为各天各方向轨道精度提升量的统计,由于GEO卫星切向精度提升量呈随机性,未给出该卫星的统计。由图 6及表 4可以看出,联合定轨中GPS公共参数对于BDS-2的IGSO、MEO和GLONASS、Galileo卫星的轨道精度在切向、法向、径向均有所提升;对于BDS-2的MEO卫星提升率可以达到62%以上,BDS-2的IGSO、GLONASS及Galileo的提升率均在20%左右。

|
图 6 GPS对各系统各天轨道三维平均精度的提升量 Fig. 6 GPS 3D average accuracy improvement of each system's orbits |
|
|
表 4 GPS公共参数对轨道精度的提升量/% Tab. 4 Improvement of orbit accuracy by GPS common parameters/% |
针对上述结果,有些情况需要特殊说明:
1) 由于BDS-2、GLONASS、Galileo单系统解算的公共参数精度不高,在进行与GPS联合定轨时,这3个系统对于公共参数的观测值数量越少,在进行法方程求解时对于解算公共参数的影响越小,联合定轨后相关的参数精度提升量越大。
2) GPS高精度公共参数对于BDS-2的GEO卫星在切向上的轨道精度无明显提升,法向与径向有所提高。在切向上,GEO卫星精度呈现一种随机性,即与联合定轨精度BDS-2单系统定轨精度相比较,部分卫星轨道精度有所提高(如C01、C02),部分卫星轨道精度有所下降(如C03、C05),部分卫星轨道精度基本不变(如C04)。其根本原因可能是由GEO卫星的轨道特性决定的,GEO卫星相对于各个地面跟踪站基本不变,轨道动力学模型精度差、几何观测信息差,导致其本身定轨精度差。
3 结语本文采用IGS与MGEX观测网数据,实现多系统联合定轨。将定轨结果与GFZ及武汉大学精密轨道产品进行比较,得出各方案的定轨精度,并将多系统定轨精度与各单系统定轨精度进行比较,得到GPS解算的公共参数对各单系统精度的提升量。实验结果分析与提升量统计均以单天解为前提,得到以下结论:
1) 对于BDS-2、GLONASS、Galileo等地面跟踪站数量少、分布不均匀或者卫星星座不完整的导航定位系统,加入GPS系统进行联合定轨可以改善公共参数的精度,最终体现为各系统卫星轨道精度的提高。
2) BDS-2由于其卫星轨道的特殊性,联合求解的公共参数对BDS-2卫星轨道精度的影响不可一概而论。联合求解后,仅GEO卫星的切向精度呈现随机性,但GEO卫星的法向与径向精度均有提升;IGSO、MEO卫星轨道精度也有提升,其中MEO卫星轨道精度提升量达到60%以上。
3) GLONASS与Galileo使用GPS解算的公共参数进行联合定轨,较其单系统定轨精度均有一定程度的提升,分别提升了19.80%、21.23%。由于GLONASS与Galileo单系统定轨精度较高,因此GPS公共参数对其提升无BDS-2明显。
| [1] |
杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505-510 (Yang Yuanxi. Concepts of Comprehensive PNT and Related Key Technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 505-510)
(  0) 0) |
| [2] |
杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72-81 (Yang Yuanxi, Li Jinlong, Wang Aibing., et al. Preliminary Assessment of the Navigation and Positioning Performance of Beidou Regional Navigation Satellite System[J]. Science China: Earth Sciences, 2014, 44(1): 72-81)
(  0) 0) |
| [3] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测——试验验证数据分析[J]. 中国科学:地球科学, 2018, 48(5): 584-594 (Yang Yuanxi, Xu Yangyin, Li Jinlong, et al. Progress and Performance Evaluation of Beidou Global Navigation Satellite System: Data Analysis Based on BDS-3 Demonstration System[J]. Science China: Earth Sciences, 2018, 48(5): 584-594)
(  0) 0) |
| [4] |
李敏, 施闯, 赵齐乐, 等. 多模全球导航卫星系统联合精密定轨[J]. 测绘学报, 2011, 40: 26-30 (Li Min, Shi Chuang, Zhao Qile., et al. Multi-GNSS Precision Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 26-30)
(  0) 0) |
| [5] |
刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1 132-1 138 (Liu Weiping, Hao Jinming, Li Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of Beidou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1 132-1 138)
(  0) 0) |
| [6] |
王乐, 黄观文, 张勤, 等. 基于区域监测站的BDS定轨策略分析[J]. 大地测量与地球动力学, 2018, 38(5): 497-509 (Wang Le, Huang Guanwen, Zhang Qin, et al. Analysis of Strategy of BDS Satellite Orbit Determination Using Regional Monitoring Statioin[J]. Journal of Geodesy and Geodynamics, 2018, 38(5): 497-509)
(  0) 0) |
| [7] |
党亚民, 张龙平, 陈俊勇. 多GNSS系统精密定轨ISB/IFB估计及特性分析[J]. 武汉大学学报:信息科学版, 2018, 43(12): 2 079-2 138 (Dang Yamin, Zhang Longping, Chen Junyong, et al. ISB/IFB Estimation and Characteristic Analysis with Multi-GNSS Precise Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 079-2 138)
(  0) 0) |
| [8] |
杨徐, 祝会忠, 徐爱功, 等. BDS/GPS联合精密定轨理论与精度分析[J]. 导航定位学报, 2018, 6(2): 87-92 (Yang Xu, Zhu Huizhong, Xu Aigong, et al. Analysis on Theory and Accuracy of BDS/GPS Precise Orbit Determination[J]. Journal of Navigation and Positioning, 2018, 6(2): 87-92)
(  0) 0) |
| [9] |
Guo J, Xu X L, Zhao Q L, et al. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison[J]. Cross Mark, 2016, 90: 143-159
(  0) 0) |
| [10] |
张睿, 杨元喜, 张勤, 等. BDS/GPS联合定轨的贡献分析[J]. 武汉大学学报:信息科学版, 2017, 42(5): 600-608 (Zhang Rui, Yang Yuanxi, Zhang Qin., et al. Contribution Analysis of BDS/GPS Combined Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 600-608)
(  0) 0) |
| [11] |
张龙平, 党亚民, 成英燕, 等. 北斗GEO/IGSO/MEO卫星定轨地面站构型影响分析及其优化[J]. 测绘学报, 2016, 45: 82-92 (Zhang Longping, Dang Yamin, Cheng Yingyan, et al. Analysis and Optimization on BDS GEO/IGSO/MEO Ground Monitoring Stations Configuration for Determining GNSS Orbit[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 82-92)
(  0) 0) |
| [12] |
计国锋, 杨志强, 贾小林. MGEX和IGMAS的多系统轨道和钟差产品精度分析[J]. 大地测量与地球动力学, 2019, 39(1): 13-19 (Ji Guofeng, Yang Zhiqiang, Jia Xiaolin, et al. Precise Orbit and Clock Products for Multi-GNSS System from MGEX and iGMAS[J]. Journal of Geodesy and Geodynamics, 2019, 39(1): 13-19)
(  0) 0) |
| [13] |
Zhang R, Tu R, Liu J H, et al. Performance of Galileo: Global Coverage, Precise Orbit Determination, and Precise Positioning[J]. Advance in Space Research, 2019, 42(3): 1-35
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

