2. 海军工程大学导航工程系, 武汉市解放大道717号,430033
随着星载GPS观测技术在TOPEX/Poseidon卫星上的成功应用,SST(satellite-to-satellite tracking)观测方式展现出巨大的潜力,逐步成为低轨卫星轨道确定的重要手段之一。特别是近年来各种观测任务的低轨卫星相继发射,如CHAMP、GRACE和SWARM等,其精密定轨精度均达到cm级[1-3]。在低轨卫星精密定轨中,地球重力变化、电离层延迟等可以通过精确的物理模型或观测值组合来消除或削弱,剩下的误差主要包括天线相位缠绕、天线相位中心误差和观测噪声等[4]。其中,天线相位中心误差虽然在卫星发射前会在地面进行标定,但由于低轨卫星在200~2 000 km高度高速飞行,所处的空间环境与地面差异较大,接收机天线易受到近场多路径、环境多路径等因素的影响,因此地面标定值与实际数值差异较大,无法满足精密定轨的要求[5]。
目前,LEO卫星接收机相位中心在轨改正主要使用直接法和残差法。直接法最早被用于改善JASON-1卫星的天线定轨精度[6],随后Jäggi等[2]对GRACE卫星使用直接法估计PCV模型,结果表明,虽然直接法不易受接收机钟差、模糊度等参数的影响,但其直接将PCV视为未知数,计算量大,对计算机性能要求较高。残差法最早由Haines等[7]提出,并被成功应用于JASON-1卫星,其主要思想就是对简化动力学定轨后的载波相位残差进行迭代计算,估计相应的PCV模型,由于此方法易于实现,被广泛应用于GOCE、GRACE、COMSMIC等LEO卫星的天线相位中心在轨标定[8-10]。
SWARM是ESA(European Space Agency)首个用于地球区域磁场信息探测的低轨卫星星座,该星座包含3颗卫星,其中SWARM-A和SWARM-C在高度为450 km的轨道面飞行(类似于GRACE卫星),而SWARM-B则在高度为530 km的轨道面飞行,由于其接收机相同且空间分布特殊,对其天线相位中心误差进行研究具有重要意义。
本文使用SWARM卫星星载双频GPS数据进行简化动力学定轨,估计接收机天线PCO,并基于所得到的载波相位残差对PCV误差进行建模,通过载波相位残差分析、与精密轨道比较和SLR检核3种手段来分析天线相位中心误差对轨道精度的影响,最后通过比较不同PCV格网模型的定轨精度,给出有益结论。
1 天线相位中心校正 1.1 载波相位残差表达式对于双频GPS载波相位观测值来说,其消电离层组合表达式为[2]:
| $ \begin{matrix} L_{\text{IF}}^{j}({{t}_{i}})=\frac{f_{1}^{2}}{f_{1}^{2}-f_{2}^{2}}L_{1}^{j}({{t}_{i}})-\frac{f_{2}^{2}}{f_{1}^{2}-f_{2}^{2}}L_{2}^{j}({{t}_{i}})= \\ {{\rho }^{j}}({{t}_{i}}, {{\tau }^{j}})+c\delta {{t}_{r}}({{t}_{i}})+{{\lambda }_{\text{IF}}}A_{\text{IF}}^{j}-c\delta \rho _{\text{clk}}^{j}({{t}_{i}}, {{\tau }^{j}})+ \\ \delta {{\rho }_{\text{rel}}}({{t}_{i}})+\delta \rho _{\text{GPS}}^{j}({{t}_{i}})+\delta {{\rho }_{\text{PCO, IF}}}({{\mathrm{e}}^{j}})+ \\ \delta {{\rho }_{\text{PCV, IF}}}({{\mathrm{e}}^{j}})+{{\varepsilon }^{j}}({{t}_{i}}) \\ \end{matrix} $ | (1) |
式中,LIF为消电离层组合相位观测值,ti为信号接收时间,上标j表示第j颗卫星,f1、f2为频率,L1、L2为不同频率的载波相位观测值,ρj(ti,τj)为LEO卫星与GPS卫星间的几何距离,c为光速,δtr为LEO卫星接收机钟差改正,λIF、AIFj为消电离层组合波长和模糊度,τj为信号路径延迟,cδρclkj为GPS卫星钟差改正,δρrel为相对论改正,δρGPSj为GPS卫星天线相位中心改正,δρLEO, IF为接收机天线消电离层组合PCO改正,δρPCV, IF为接收机天线消电离层组合PCV改正,εj为测量噪声。
如式(1)所示,在历元ti时刻加入各种误差改正(不考虑天线相位中心变化改正)的距离计算值为ZIFj(ti),则载波相位残差φ(e j)表达式为:
| $ \begin{matrix} \varphi ({{\mathrm{e}}^{j}})=L_{\text{IF}}^{j}({{t}_{i}})-Z_{\text{IF}}^{j}({{t}_{i}})= \\ \delta {{\rho }_{\text{PCV, IF}}}({{\mathrm{e}}^{j}})+{{\varepsilon }^{j}}({{t}_{i}}) \\ \end{matrix} $ | (2) |
SWARM卫星接收机天线相位中心改正所引起的等效距离误差Δρ(α, z)可表示为[5]:
| $ \Delta \rho (\alpha , z)=\Delta r\cdot \mathrm{e}+\text{PCV}(\alpha , z) $ | (3) |
式中,Δρ(α, z)为卫星与接收机间几何距离总的天线相位中心误差,α、z分别为星固坐标系下GPS卫星的方位角与天顶距,Δr (即PCO)定义为接收机天线参考点与平均天线相位中心(MAPC)之间的误差改正,e为GPS卫星与接收机间的单位方向向量,PCV(α, z)为MAPC与瞬时天线相位中心间的误差改正。
计算天线相位中心误差时,首先要求得天线相位中心偏差改正,将PCO作为未知参数引入观测方程中,与轨道等参数同时求解。根据最小二乘原理,求得多天PCO数值,取平均值作为PCO改正值:
| $ \int_{\alpha =0}^{2\pi }{\int_{z=0}^{{{z}_{\text{max}}}}{\Delta }}\rho (\alpha , z)\text{sin}z\partial z\partial \alpha =\text{min} $ | (4) |
式中,zmax为经验值[11]。
由于在不同观测历元下GPS卫星和LEO卫星间的方位角和天顶距是不相同的,所以载波相位残差φ(e j)与方位角和天顶距存在一一对应关系,可以表示为φ(α, z)。假设格网空间间隔为5°,以格网节点为中心,计算±2.5°矩形范围内所有相位残差的平均值作为该点的PCV模型值:
| $ \text{PCV} (\alpha ,z)=\frac{\sum\limits_{\alpha =2.5°}^{\alpha +2.5°}{\sum\limits_{z-2.5°}^{z+2.5°}{\varphi (\alpha ,z)}}}{n} $ | (5) |
式中,n为矩形范围内所有残差点的个数。
虽然PCV模型值并不完全等于真实的PCV值,如式(2)所示,差分后的载波相位残差φ(α, z)主要由接收机天线消电离层PCV改正和测量噪声组成,但实验证明,大部分的测量噪声会在长时间(如1个月)的PCV模型统计值中被平滑掉[9]。
2 定轨模型及策略 2.1 数据准备及定轨方案高精度的GPS卫星精密星历和卫星钟差是低轨卫星精密定轨的关键,本文采用CODE(Center for Orbit Determination in Europe)中心提供的精密星历、钟差和地球自转参数文件。GPS观测数据和卫星姿态由ESA(https://earth.esa.int)提供,时间为2017-04-25~08-12。由于SWARM卫星轨道高度在500 km左右,受电离层延迟和大气阻力影响较大,本文对双频星载GPS观测数据进行线性组合,消除电离层延迟的影响,并通过设置伪随机参数,削弱大气阻力和其他非保守力的影响。其余动力模型参数设置与其他LEO卫星相似,具体信息见表 1[12]。
|
|
表 1 SWARM卫星精密定轨所采用的标准模型 Tab. 1 Standard models of SWARM satellite precise orbit determination |
本文所使用的定轨平台为基于BERNESE 5.2的二次开发版本,针对天线相位中心误差研究设计3种定轨方案:1)方案1,不使用PCO和PCV改正,直接对星载GPS数据进行解算;2)方案2,仅使用天线PCO信息进行简化动力学定轨;3)方案3,同时使用载波相位残差解算得到的PCV模型和PCO信息进行轨道计算。最后,使用载波相位残差分析、事后科学轨道比较和SLR检核3种手段来比较3种方案对轨道精度的影响。
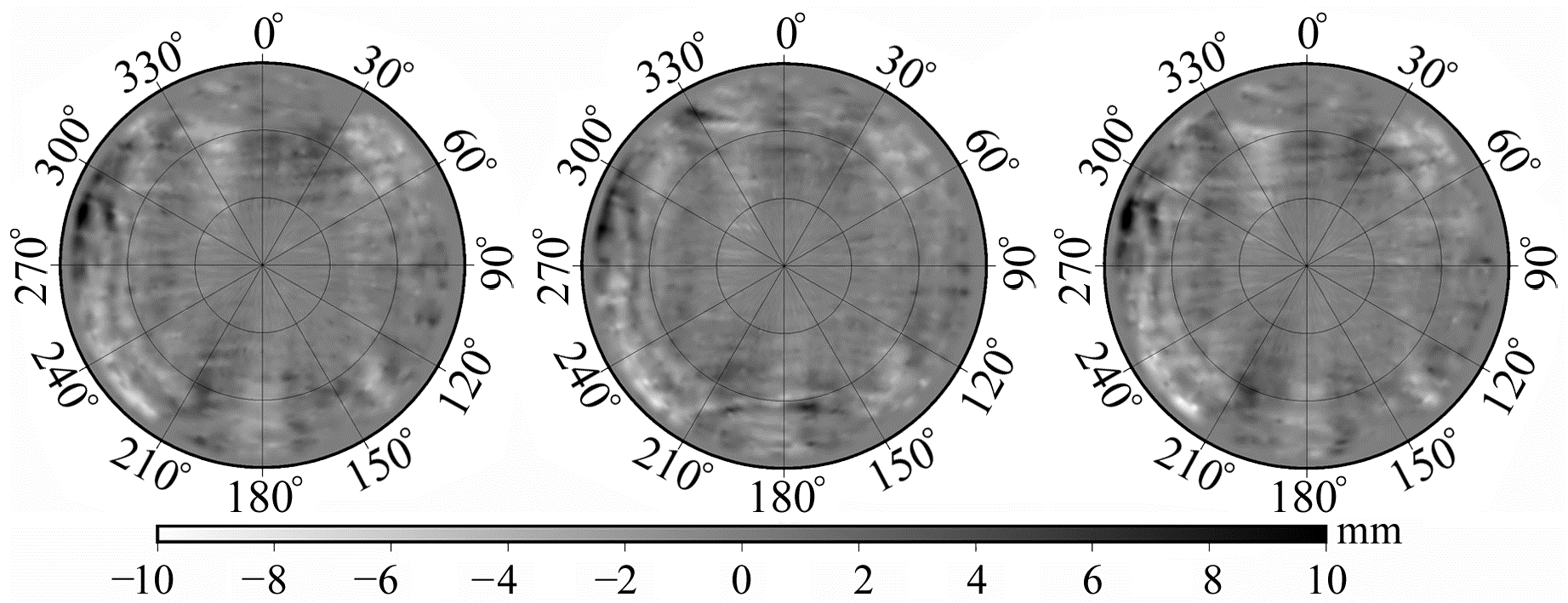
2.2 PCV模型将多天(本文取30 d)的PCO平均值作为SWARM卫星的PCO改正信息,然后将其引入到简化动力学定轨中,得到100 d的载波相位残差,最后利用残差法通过迭代得到5°×5°和1°×1°PCV格网模型,PCO和PCV均定义在天线固定参考系(AFS)。如图 1和2所示,3颗卫星的PCV模型差异很小,这是因为3颗卫星采用的是相同类型的GPS接收机,卫星构造也大致相同。并且数值较大的PCV主要集中在高度角较低的区域,因为高度角越低,观测数据质量越差,解算的载波相位残差也随之增大。随着分辨率的增加,估计的模型更加精细,计算效率也有所降低。
|
图 1 本文解算的SWARM-A、B、C卫星1°×1°PCV模型 Fig. 1 1°×1° PCV models of SWARM-A, B, C satellites in this paper |

|
图 2 本文解算的SWARM-A、B、C卫星5°×5°PCV模型 Fig. 2 5°×5° PCV models of SWARM-A, B, C satellites in this paper |
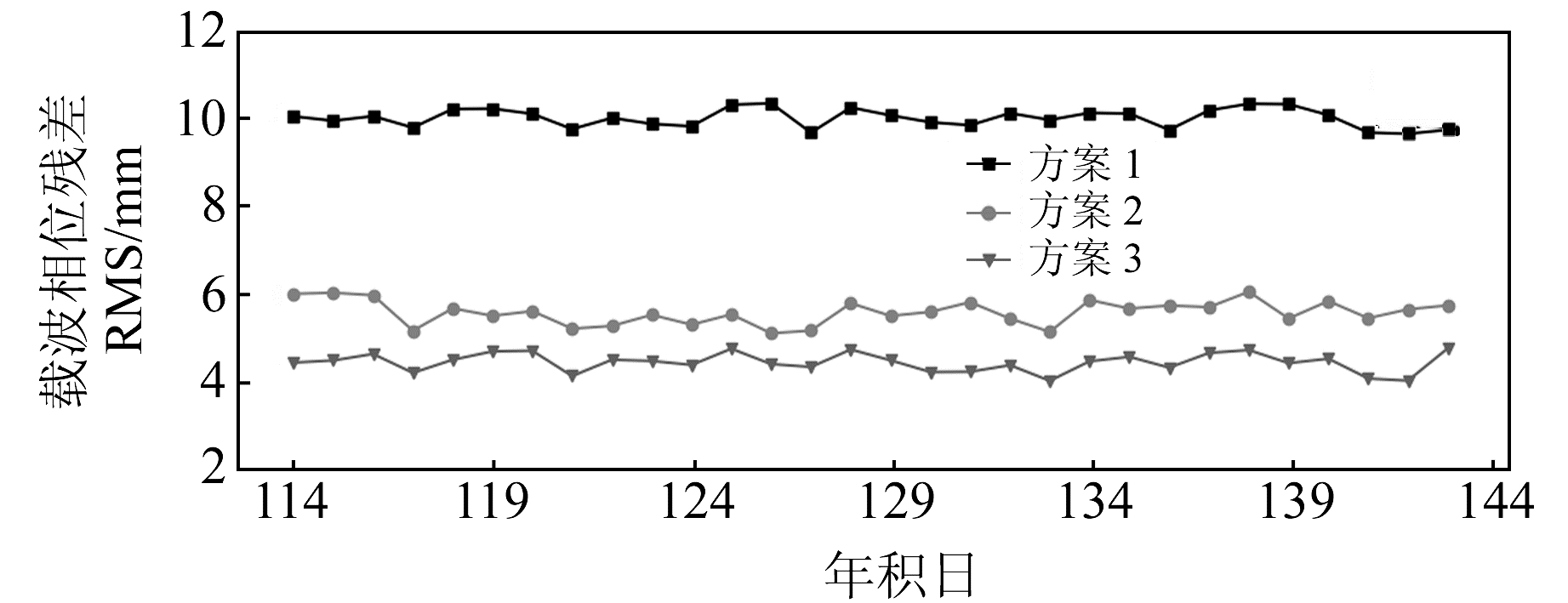
载波相位残差包含模型化的误差和未被模型化的误差,因此计算相位残差RMS是内符合精度评估的主要手段之一,所采用的力学模型与实际情况越符合,观测值残差RMS也就越小,载波相位残差就越接近噪声水平。对3种方案定轨后的载波相位残差进行分析,如图 3所示,当不进行天线相位中心误差改正时,SWARM三颗卫星平均载波相位残差RMS值为10.1 mm;当仅进行PCO改正时,残差RMS值为5.58 mm,减少了44.7%;当使用PCO信息和PCV模型时,残差RMS值为4.38 mm。对比3种方案可以看出,PCO改正对LEO精密定轨载波相位残差影响比较大,PCV改正影响略小,仅为1.2 mm。这一结论同样可以从后续的事后科学轨道和SLR检核中得到验证。
|
图 3 载波相位残差平均RMS值 Fig. 3 Average RMS of carrier phase residuals |
使用ESA提供的简化动力学轨道(定轨精度优于2 cm)作为参考轨道[3],将3种方案解算得到的100 d简化动力学轨道与其进行比较,以SWARM-A卫星为例,径向、切向和法向残差RMS如图 4所示,表 2(单位cm)列出SWARM三颗卫的星定轨结果统计值。

|
图 4 SWARM-A简化动力学精密定轨残差RMS Fig. 4 RMS of SWARM-A reduced-dynamic orbit residuals |
|
|
表 2 SWARM卫星定轨残差统计 Tab. 2 Residual statistics of SWARM satellite orbit determination |
1) PCO改正后,SWARM卫星3个方向平均RMS值分别提升47%、48%和66%,其中径向和切向的精度提升幅度较小,仅为8~12 mm,而法向精度改善最大,在27 mm左右。这是因为,法向的改正和太阳方向向量与卫星轨道面之间的夹角有关。Ijssel等[3]研究表明,在SWARM卫星精密定轨中,存在非重力模型误差,如果不进行天线相位中心改正,会对法向精度造成cm级的影响。
2) PCV改正后,SWARM三颗卫星各个方向的精度提升幅度明显减小,只有3~4 mm的改进。这是因为,大部分的天线相位改正误差都被PCO信息所吸收,可见PCO改正对SWARM卫星精密定轨影响更大。
3) 从整体上来看,3种方案中径向轨道残差RMS序列比较平滑,无较大的波动,而切向轨道RMS波动略微明显,这可能是因为切向上的大气阻力未能很好地模型化[4]。
3.3 SLR轨道检核SLR检核是目前国际上轨道验证最精确的手段,其核心思想就是利用星载GPS观测数据计算得到的轨道数据反算站心距,然后与激光测得的站心距进行对比,测距精度可达1 cm[13-14],相关数据可从CDDIS上下载(ftp://cddis.gsfc.nasa.gov/pub/slr/data/npt_crd/)。本文利用SWARM卫星100 d的SLR观测数据进行轨道检核,其中SWARM-A卫星共有17个测站10 096个NP(normal point)数据,SWARM-C有18个测站11 483个NP数据,而SWARM-B卫星则有19个测站25 916个NP数据。因为SWARM-A和SWARM-C在同一轨道面上飞行,而在瞬时观测历元同一SLR测站不能同时观测两颗卫星,所以在相同观测弧段内,SWARM-A和SWARM-C观测数据有明显差别。对于SWARM-B卫星来说,可能观测优先级比其他两颗卫星要高,所以观测数据个数是另外两颗卫星的2倍左右,相应的SLR测站坐标归算到ITRF2008框架下。
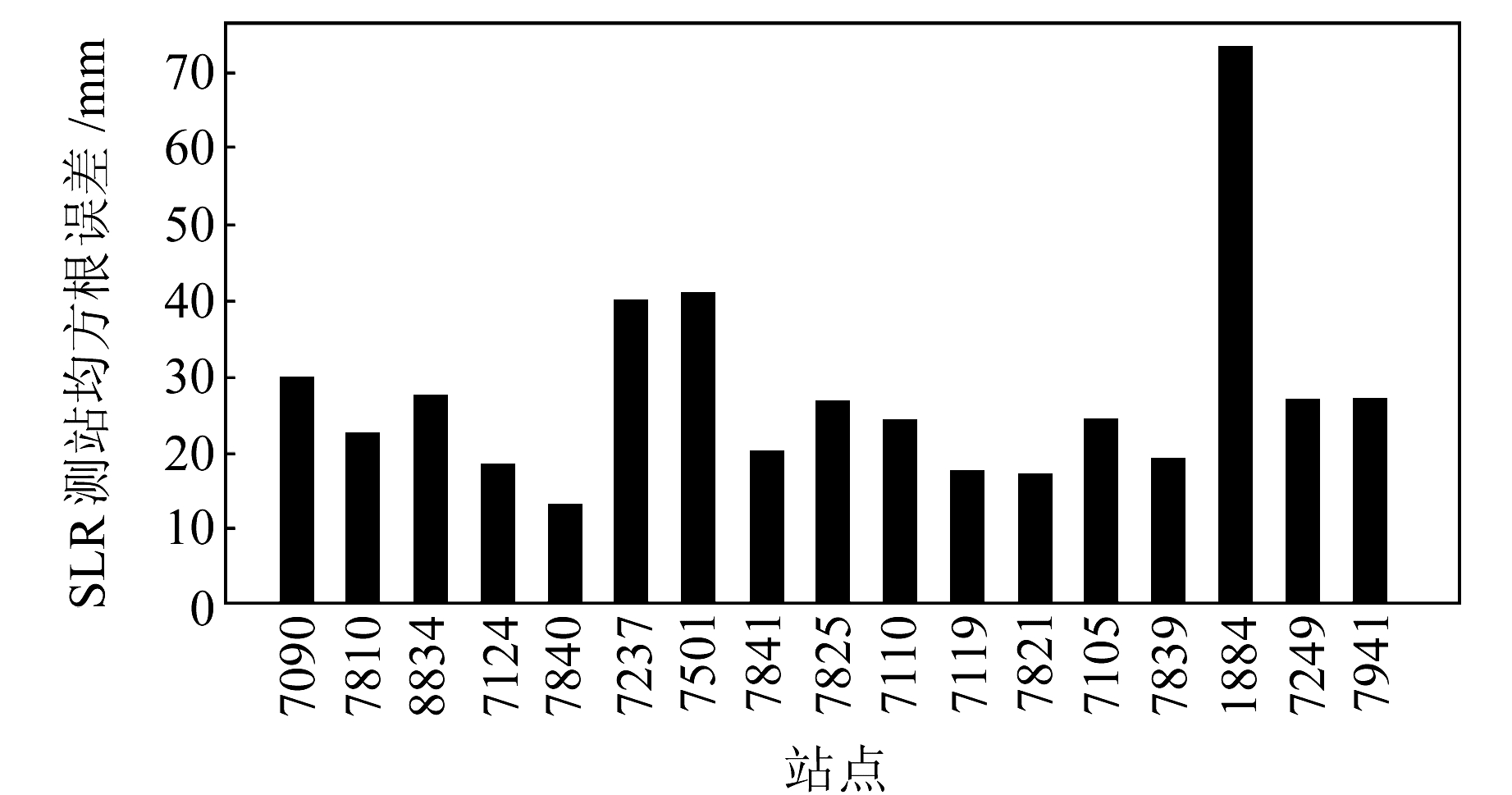
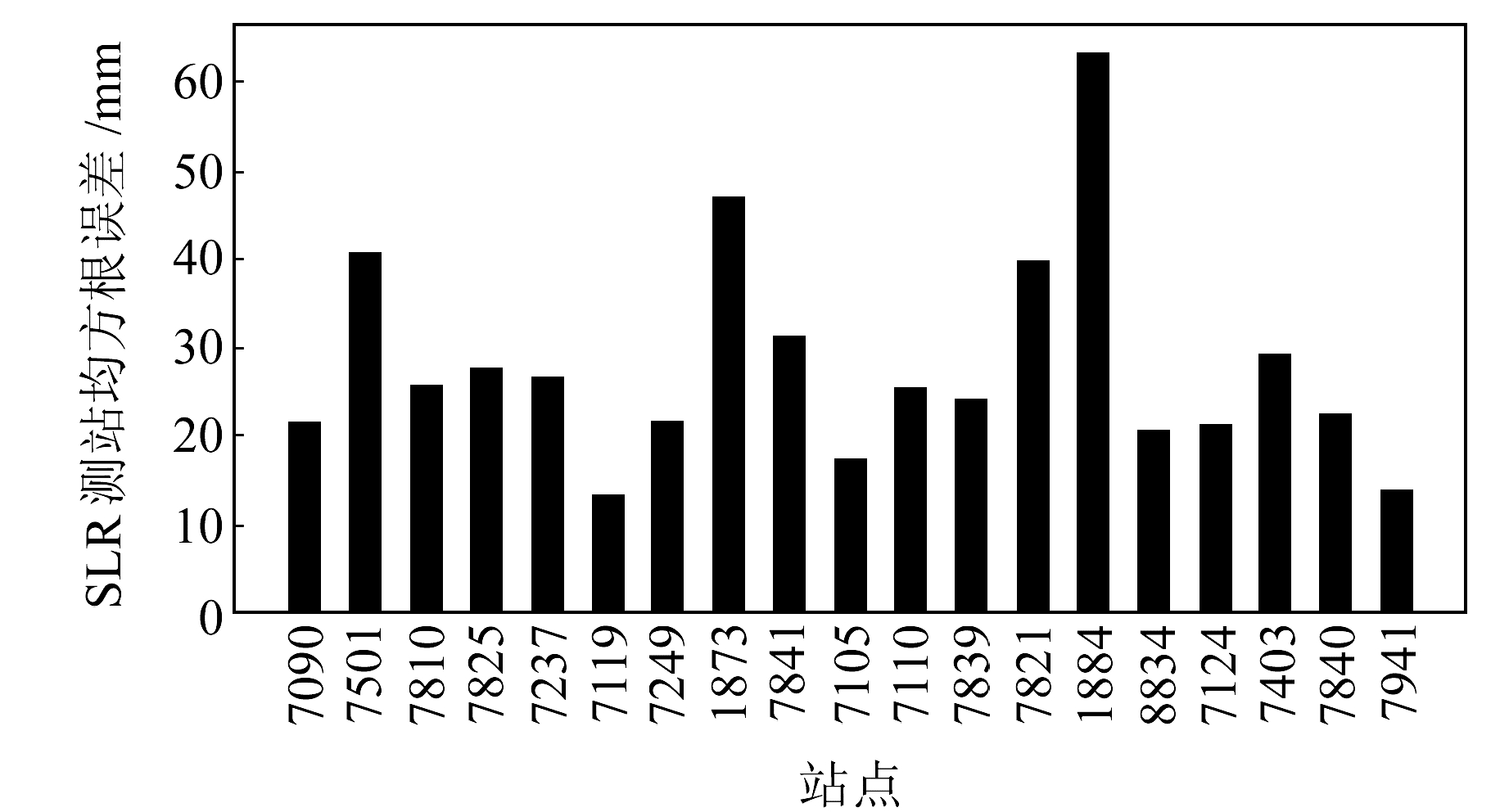
从表 3(单位cm)可以看出,当使用方案1时,SLR检核RMS平均值为4.97 cm,方案2较方案1精度提升49.9%,说明是否使用PCO信息对SWARM卫星精密定轨精度的影响很大。当使用方案3时,SWARM三颗卫星SLR检核RMS值精度提升2 mm左右。结合§3.2分析结果进一步说明,PCO信息在天线相位中心误差改正中占很大的权重。图 5~7展示了考虑PCO和PCV改正时各个SLR观测站的RMS值,其中7090站和7810站的观测数据最多。可以发现,对于SWARM三颗卫星,这两个SLR站检核结果稳定在20~30 mm。7119站虽然在100 d的观测时段内仅有不到70个数据,但综合分析各SLR测站结果,其检核精度最高,RMS值仅为13 mm。考虑PCO和PCV模型后SWARM简化动力学轨道定轨精度符合预期要求,且所有SLR测站RMS平均值(2.29 cm)与ESA发布的事后科学轨道精度(SLR检核优于2 cm)十分接近。
|
|
表 3 SWARM卫星SLR检核统计 Tab. 3 SLR residual statistics of SWARM satellite |
|
图 5 SWARM-A卫星考虑PCV模型SLR检核各测站RMS值 Fig. 5 RMS statistics considering PCV model of each SLR station for SWARM-A |
|
图 6 SWARM-B卫星考虑PCV模型SLR检核各测站RMS值 Fig. 6 RMS statistics considering PCV model of each SLR station for SWARM-B |
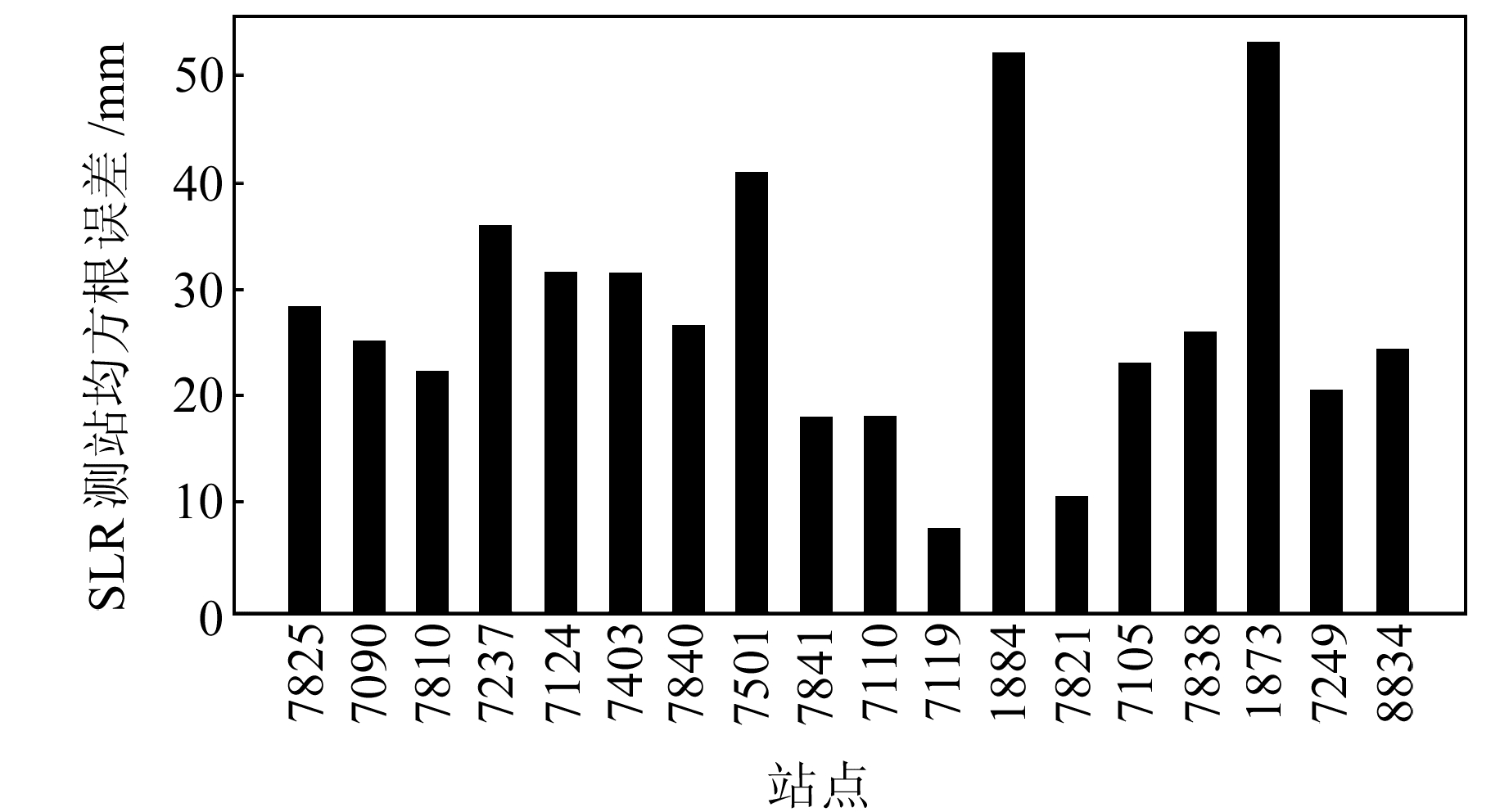
|
图 7 SWARM-C卫星考虑PCV模型SLR检核各测站RMS值 Fig. 7 RMS statistics considering PCV model of each SLR station for SWARM-C |
ESA发布的事后科学轨道是Delft大学利用GHOST软件计算得到,在考虑PCV模型的情况下,简化动力学轨道精度优于2 cm[3]。SWARM卫星接收机的改动从卫星发射算起,大约历时2 a才最终完成[15],而在卫星飞行期间其轨道高度是不断降低的,且SWARM-A和SWARM-C轨道高度下降速率较快,SWARM-B下降速率较慢,这就导致卫星所处的空间环境随时间发生改变,所以重新进行在轨PCV模型研究是必要的。
表 4(单位cm)列出了分别使用Delft大学发布的和本文估计的PCV模型下SWARM卫星简化动力学轨道的检核结果,可以发现,相对于Delft大学发布的PCV模型,本文使用的在轨PCV模型精度更高,但仅有1.1~1.5 mm提升,所以在实际轨道解算中,可以根据定轨精度的需要选择合适的PCV模型。对比1°×1°和5°×5°格网模型精度可以发现,随着模型的更加细化,轨道精度并没有明显提高,且更精细的模型意味着需要耗费更多的时间,这将降低星载GPS数据的解算效率,袁俊军等[16]通过对资源三号卫星进行研究给出了相同的结论。所以在SWARM卫星数据解算中,5°×5°PCV格网模型已能满足定轨工作需要,这也给后续的低轨卫星(如GRACE Follow-On)精密定轨研究提供了参考。
|
|
表 4 不同PCV模型下SWARM轨道SLR检核统计 Tab. 4 SLR RMS statistics of SWARM orbit with different PCV model |
本文基于SWARM卫星星载GPS数据,首先对低轨卫星GPS接收机天线相位模型和PCV估计方法进行了详细说明,并利用最小二乘原理计算PCO改正信息,使用载波相位残差估计在轨PCV模型;然后对天线相位中心误差进行简化动力学精密定轨实验;最后通过观测值残差分析、与事后科学轨道作差和SLR检核分析定轨结果,得到以下结论:
1) 通过观测值残差RMS可以看出,不进行天线相位中心误差改正时,SWARM三颗卫星的平均载波相位残差RMS值最大;仅进行PCO改正时,残差RMS减少了44.7%,对LEO精密定轨精度影响比较大;使用PCO信息和PCV模型时,定轨精度同样有小幅度的改善。
2) 通过与事后科学轨道进行对比可以看出,PCO信息在天线相位中心误差改正中占很大的权重,PCO改正后平均RMS值在3个方向分别提升47%、48%和66%,其中法向改正最大,因为非重力模型误差对法向影响最大;而PCV模型的应用对轨道精度的提升只在mm级,远小于PCO改正对轨道精度的影响。
3) 通过对不同PCV模型进行SLR检核结果表明,应根据实际工作需要选择合适的PCV模型,且5°×5°格网模型已经能满足高精度精密定轨需求,更高分辨率并不会带来明显的精度提升。
| [1] |
Reigber C, Lühr H, Schwintzer P. CHAMP Mission Status[J]. Advances in Space Research, 2002, 30(2): 129-134 DOI:10.1016/S0273-1177(02)00276-4
(  0) 0) |
| [2] |
Jäggi A, Dach R, Montenbruck U, et al. Phase Center Modeling for LEO GPS Receiver Antennas and Its Impact on Precise Orbit Determination[J]. Journal of Geodesy, 2009, 83(12): 1 145-1 162 DOI:10.1007/s00190-009-0333-2
(  0) 0) |
| [3] |
Ijssel J, Encarnação J, Doornbos E, et al. Precise Science Orbits for the SWARM Satellite Constellation[J]. Advances in Space Research, 2015, 56(6): 1 042-1 055 DOI:10.1016/j.asr.2015.06.002
(  0) 0) |
| [4] |
胡志刚, 赵齐乐, 郭靖, 等. GPS天线相位中心校正对低轨卫星精密定轨的影响研究[J]. 测绘学报, 2011, 40(增1): 34-38 (Hu Zhigang, Zhao Qile, Guo Jing, et al. Research on Impact of GPS Phase Center Variation on Precise Orbit Determination of Low Earth Orbit Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 34-38)
(  0) 0) |
| [5] |
田英国, 郝金明. Swarm卫星天线相位中心校正及其对精密定轨的影响[J]. 测绘学报, 2016, 45(12): 1 406-1 412 (Tian Yingguo, Hao Jinming. SWARM Satellite Antenna Phase Center Correction and Its Influence on the Precision Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1 406-1 412)
(  0) 0) |
| [6] |
Luthcke S B, Zelensky N P, Rowlands D D, et al. The 1-Centimeter Orbit: Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data[J]. Marine Geodesy, 2003, 26(3): 399-421
(  0) 0) |
| [7] |
Haines B, Bar-Sever Y, Bertiger W, et al. One-Centimeter Orbit Determination for Jason-1: New GPS-Based Strategies[J]. Marine Geodesy, 2004, 27(1-2): 299-318 DOI:10.1080/01490410490465300
(  0) 0) |
| [8] |
Bock H, Jäggi A, Meyer U, et al. Impact of GPS Antenna Phase Center Variations on Precise Orbits of the GOCE Satellite[J]. Advances on Space Research, 2011, 47: 1 885-1 893
(  0) 0) |
| [9] |
Montenbruck O, Garcia-Fernandez M, Yoon Y, et al. Antenna Phase Center Calibration for Precise Positioning of LEO Satellites[J]. GPS Solutions, 2009, 13(1): 23-25 DOI:10.1007/s10291-008-0094-z
(  0) 0) |
| [10] |
Hwang C, Tseng T P, Lin T, et al. Precise Orbit Determination for the FORMOSAT-3/COSMIC Satellite Mission Using GPS[J]. Journal of Geodesy, 2009, 83(5): 477-489 DOI:10.1007/s00190-008-0256-3
(  0) 0) |
| [11] |
Dach R, Hugentobler U, Fridez P, et al. Bernese GPS Software Version 5.2[Z]. Astronomical Institute, University of Bern, Switzerland, 2017 https://www.researchgate.net/publication/270793731_Bernese_GPS_software_version_50
(  0) 0) |
| [12] |
夏要伟, 郭金运, 刘路, 等. 基于运动学和简化动力学的SWARM卫星精密定轨研究[J]. 大地测量与地球动力学, 2019, 39(4): 392-398 (Xia Yaowei, Guo Jinyun, Liu Lu, et al. Precise Orbit Determination Research of SWARM Satellites Based on Kinematic and Reduced-Dynamic Methods[J]. Journal of Geodesy and Geodynamics, 2019, 39(4): 392-398)
(  0) 0) |
| [13] |
Guo J Y, Wang Y C, Shen Y, et al. Estimation of SLR Station Coordinates by Means of SLR Measurements to Kinematic Orbit of LEO Satellites[J]. Earth Planets and Space, 2018, 70(1)
(  0) 0) |
| [14] |
Kong Q L, Guo J Y, Sun Y, et al. Centimeter-Level Precise Orbit Determination for the HY-2A Satellite Using DORIS and SLR Tracking Data[J]. Acta Geophysica, 2017, 65(1): 1-12 DOI:10.1007/s11600-016-0001-x
(  0) 0) |
| [15] |
Ijssel J, Jose F, Montenbruck O. Impact of Swarm GPS Receiver Updates on POD Performance[J]. Earth, Planets and Space, 2016, 68(85): 1 103-1 120
(  0) 0) |
| [16] |
袁俊军, 赵春梅, 吴琼宝. 资源三号01星及02星星载GPS天线PCO、PCV在轨估计及对精密定轨的影响[J]. 测绘学报, 2018, 47(5): 672-682 (Yuan Junjun, Zhao Chunmei, Wu Qiongbao. Phase Center Offset and Phase Center Variations Estimation in-Flight for ZY-301 and ZY-302 Spaceborne GPS Antennas and the Influence on Precision Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(5): 672-682)
(  0) 0) |
2. Department of Navigation Engineering, Naval University of Engineering, 717 Jiefang Road, Wuhan 430033, China
 2020, Vol. 40
2020, Vol. 40


