二十世纪中叶以来，随着科学技术的发展和计算机应用的日益广泛和深入，四元数理论在计算机图形学、捷联惯性导航、机器与机构、多体系统力学、人造卫星姿态控制等领域已得到广泛应用^[1]。国内外学者^[2-4]对四元数的理论和应用进行了大量研究，本文在前人研究基础上，根据四元数运算法则所导出的向量的共轭、逆和范数(模)的概念，通过向量的格拉斯曼乘积来表示平面角、大圆弧和球面角所对应的四元数，推导球面三角形公式。

1 四元数的定义与性质

四元数为标量部与向量部的“和”，如：

$ \mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{p}}_0} + \mathit{\boldsymbol{p}}, \mathit{\boldsymbol{Q}} = {\mathit{\boldsymbol{q}}_0} + \mathit{\boldsymbol{q}} $

四元数乘积(用“$ \circ $”连接，称为格拉斯曼乘积)可表示为^[5]：

$ \mathit{\boldsymbol{P}} \circ \mathit{\boldsymbol{Q}} = ({\mathit{\boldsymbol{p}}_0}{\mathit{\boldsymbol{q}}_0} - \mathit{\boldsymbol{p}} \cdot \mathit{\boldsymbol{q}}) + ({\mathit{\boldsymbol{p}}_0}\mathit{\boldsymbol{q}} + {\mathit{\boldsymbol{q}}_0}\mathit{\boldsymbol{p}} + \mathit{\boldsymbol{p}} \times \mathit{\boldsymbol{q}}) $

(1)

定义四元数Q的共轭Q ^*、范数‖ Q ‖、模| Q |和逆Q ^－1分别为^[5]：

$ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Q}}^*} = {\mathit{\boldsymbol{q}}_0} - \mathit{\boldsymbol{q}}}\\ {\left\| \mathit{\boldsymbol{Q}} \right\| = |\mathit{\boldsymbol{Q}}{|^2} = \mathit{\boldsymbol{Q}} \circ {\mathit{\boldsymbol{Q}}^*} = {\mathit{\boldsymbol{Q}}^*} \circ \mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{q}}_0^2 + \mathit{\boldsymbol{q}} \cdot \mathit{\boldsymbol{q}}}\\ {{\mathit{\boldsymbol{Q}}^{ - 1}} = {{\left\| \mathit{\boldsymbol{Q}} \right\|}^{ - 1}}{\mathit{\boldsymbol{Q}}^*}} \end{array}} \right. $

(2)

显然存在$\mathit{\boldsymbol{Q }}\circ {{\mathit{\boldsymbol{Q }}}^{-1}}={{\mathit{\boldsymbol{Q }}}^{-1}}\circ \mathit{\boldsymbol{Q }}=1$，具体参见文献[5]。

2 单位四元数

单位四元数$\mathit{\boldsymbol{\hat Q}}$可表示为：

$ \mathit{\boldsymbol{\hat Q}} = {\rm{cos}}\theta + \mathit{\boldsymbol{\hat qsin}}\theta $

(3)

式中，$\mathit{\boldsymbol{\hat a}}$为单位向量。令单位向量$\mathit{\boldsymbol{\hat b}}$和$\mathit{\boldsymbol{\hat q}}$(夹角为θ)具有相同起点，即

$ \mathit{\boldsymbol{\hat a}} \cdot \mathit{\boldsymbol{\hat b}} = {\rm{cos}}\theta , \mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}} = \mathit{\boldsymbol{\hat q}}{\rm{sin}}\theta $

则单位四元数$\mathit{\boldsymbol{\hat Q}}$可表示为(令四元数标量部为0)：

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat Q}} = \mathit{\boldsymbol{\hat a}} \cdot \mathit{\boldsymbol{\hat b}} + \mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}} = }\\ { - \mathit{\boldsymbol{\hat b}} \circ \mathit{\boldsymbol{\hat a}} = \mathit{\boldsymbol{\hat b}} \circ {{\mathit{\boldsymbol{\hat a}}}^*} = \mathit{\boldsymbol{\hat b}} \circ {{\mathit{\boldsymbol{\hat a}}}^{ - 1}}} \end{array} $

(4)

3 球面三角形的四元数表示

根据式(4)可知，单位四元数可用2个单位向量的格拉斯曼乘积表示。将具有相同起点的2个单位向量$\mathit{\boldsymbol{\hat a}}$和$\mathit{\boldsymbol{\hat b}}$的端点连接起来，可构成单位圆上的大圆弧$\overset\frown{AB}$ (图 1)，单位四元数$\mathit{\boldsymbol{\hat Q}}$可对应大圆弧$\overset\frown{AB}$，即$\overset\frown{AB} \buildrel \wedge \over = \mathit{\boldsymbol{\hat Q}}$。基于此特性，本文将用单位四元数来表示球面上的大圆弧和球面角。

3.1 单位四元数在单位圆上的表示

如图 1所示，大圆弧$\overset\frown{AB}$的法向量方向为$\mathit{\boldsymbol{\hat q}}$，弧长取决于角θ的大小。大圆弧$\overset\frown{AB}$在大圆上的位置是任意的，即弧是滑动的(具有任意起算点)。本文约定角θ的度量方向与单位向量$\mathit{\boldsymbol{\hat q}}$的方向一致，由此可得：

$ \theta \mathit{\boldsymbol{\hat q}} = \overset\frown{AB} \buildrel \wedge \over = \mathit{\boldsymbol{\hat Q}} = {\rm{cos}}\theta + \mathit{\boldsymbol{\hat q}}{\rm{sin}}\theta = \mathit{\boldsymbol{\hat b}} \circ {{\mathit{\boldsymbol{\hat a}}}^{ - 1}} $

(5)

式(5)表明，平面角的单位四元数对应终边单位向量和始边单位向量逆的格拉斯曼乘积。

由式(3)可知，当θ=0或θ=π时，$\mathit{\boldsymbol{\hat Q}}$=1或$\mathit{\boldsymbol{\hat Q}}$=－1，向量$\mathit{\boldsymbol{\hat q}}$具有任意方向。该情况较为特殊，因为$\mathit{\boldsymbol{\hat Q}}$=1相当于球面上的任意一点，而$\mathit{\boldsymbol{\hat Q}}$=－1相当于大圆的任意一半，大圆的四分之一相当于单位向量$\mathit{\boldsymbol{\hat q}}$。如果$\overset\frown{AB}$对应单位四元数$\mathit{\boldsymbol{\hat Q}}$，则反向大圆弧$\overset\frown{BA}$对应逆单位四元数${{\mathit{\boldsymbol{\hat Q}}}^{ - 1}}$或共轭单位四元数${{\mathit{\boldsymbol{\hat Q}}}^*}$，即

$ \begin{array}{*{20}{c}} { - \theta \mathit{\boldsymbol{\hat q}} = \overset\frown{BA} \buildrel \wedge \over = {{\mathit{\boldsymbol{\hat Q}}}^{ - 1}} = {{\mathit{\boldsymbol{\hat Q}}}^*} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cos}}\theta - \mathit{\boldsymbol{\hat q}}{\rm{sin}}\theta = \mathit{\boldsymbol{\hat a}} \circ {{\mathit{\boldsymbol{\hat b}}}^{ - 1}}} \end{array} $

与四元数-$\mathit{\boldsymbol{\hat Q}}$对应的圆弧为：

$ \begin{array}{*{20}{c}} { - \mathit{\boldsymbol{\hat Q}} = - {\rm{cos}}\theta - \mathit{\boldsymbol{\hat q}}{\rm{sin}}\theta = - \mathit{\boldsymbol{\hat b}} \circ {{\mathit{\boldsymbol{\hat a}}}^{ - 1}} = }\\ {\mathit{\boldsymbol{\hat b}} \circ {{( - \mathit{\boldsymbol{\hat a}})}^{ - 1}} \buildrel \wedge \over = - (\pi - \theta )\mathit{\boldsymbol{\hat q}} = \overset\frown{A'B}} \end{array} $

即从径对称点A′到点B的大圆弧$\overset\frown{A′B}$ (图 1)。

3.2 球面三角形边和角的四元数表示

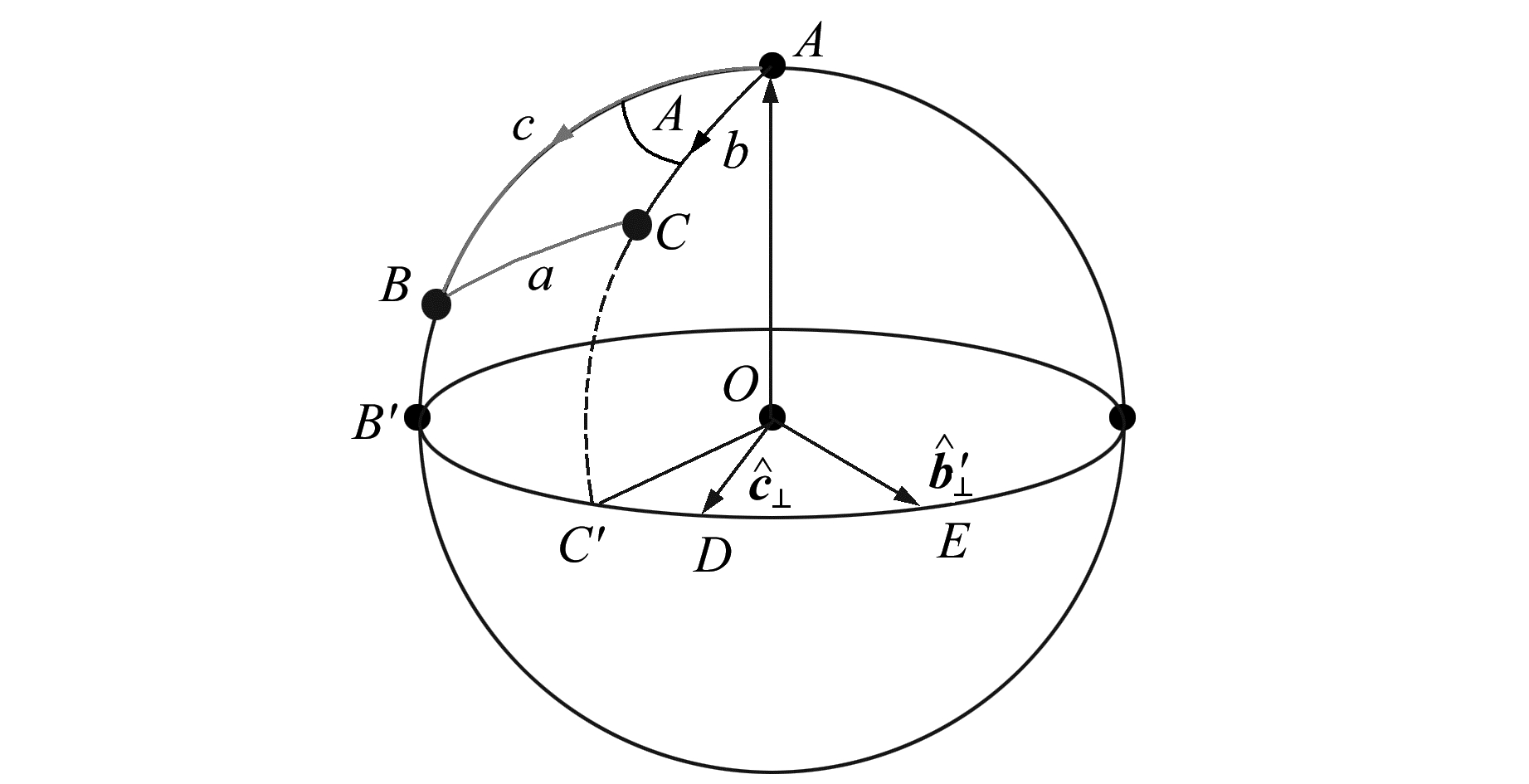
将球面上不在同一直径上的3个点A、B和C用3个大圆弧连接起来，所围成的图形为球面三角形，3个大圆弧为球面三角形的边，2个大圆弧相交所成的角为球面角。设大圆弧$\overset\frown{AB}$ (或其延长线)与以A点为极对应的大圆相交于B′点，$\overset\frown{AC}$ (或其延长线)与以A点为极对应的大圆相交于C′点，则以A点为极对应的大圆弧为$\overset\frown{B′C′DE}$。2个相交的大圆弧$\overset\frown{AB}$和$\overset\frown{AC}$所形成的球面角∠BAC可用平面AOB和AOC所构成的二面角来度量。OA垂直于平面OB′C′或大圆弧$\overset\frown{B′C′DE}$，因此也垂直于线段OB′和OC′，所以∠B′OC′为平面AOB和平面AOC所构成的二面角。令图 2所表示的球面为单位球面，并存在如下单位向量：

$ \begin{array}{*{20}{c}} {\overrightarrow {OA} = \mathit{\boldsymbol{\hat a}}, \overrightarrow {OB} = \mathit{\boldsymbol{\hat b}}, \overrightarrow {OC} = \mathit{\boldsymbol{\hat c}}}\\ {{{\mathit{\boldsymbol{\hat c}}}_ \bot } = \overrightarrow {OD} = \frac{{\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}}}{{|\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}|}} \bot \overset\frown{AB} = c, }\\ {{{\mathit{\boldsymbol{\hat b}}}^\prime }_ \bot = \overrightarrow {OE} = \frac{{\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}}}{{|\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}|}} \bot \overset\frown{AC} = b} \end{array} $

根据式(5)可知：

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} c{{\mathit{\boldsymbol{\hat c}}}_ \bot } = \overset\frown{AB} \buildrel \wedge \over = {\mathit{\boldsymbol{C}}_{{\rm{边}}}} = {\rm{cos}}c + {{\mathit{\boldsymbol{\hat c}}}_ \bot } {\rm{sin}}c = \mathit{\boldsymbol{\hat b}} \circ {{\mathit{\boldsymbol{\hat a}}}^{ - 1}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b\mathit{\boldsymbol{\hat b}}_ \bot ^\prime = \overset\frown{AC} \buildrel \wedge \over = {\mathit{\boldsymbol{B}}_{边}} = {\rm{cos}}b + \mathit{\boldsymbol{\hat b}}_ \bot ^\prime {\rm{sin}}b = \mathit{\boldsymbol{\hat c}} \circ {{\mathit{\boldsymbol{\hat a}}}^{ - 1}}\\ A\mathit{\boldsymbol{\hat a}} = \measuredangle BAC = \angle {B^\prime }O{C^\prime } = \overset\frown{B'C'} = \overset\frown{DE} \buildrel \wedge \over = {\mathit{\boldsymbol{A}}_{{\rm{角}}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cos}}A + \mathit{\boldsymbol{\hat a}}{\rm{sin}}A = \mathit{\boldsymbol{\hat b}}_ \bot ^\prime \circ \mathit{\boldsymbol{\hat c}}_ \bot ^{ - 1} \end{array} $

式中，C_边和B_边分别表示c边和b边的四元数，A_角表示A角的四元数。如果图 2中球面三角形b边沿相反方向(朝A点)度量，由于本文已约定角的度量方向与其所在平面的单位法向量方向一致，因此存在：

$ b{\mathit{\boldsymbol{\hat b}}_ \bot } = \overset\frown{CA} = {\mathit{\boldsymbol{B}}_{{\rm{123}}}} = {\rm{cos}}b + {\mathit{\boldsymbol{\hat b}}_ \bot }{\rm{sin}}b = \mathit{\boldsymbol{\hat a}} \circ {\mathit{\boldsymbol{\hat c}}^{ - 1}} $

(6)

$ \begin{array}{*{20}{c}} {A\mathit{\boldsymbol{\hat a}} = \overset\frown{DE} \buildrel \wedge \over = {\mathit{\boldsymbol{A}}_{{\rm{123}}}} = {{\mathit{\boldsymbol{\hat b}}}_ \bot } \circ \mathit{\boldsymbol{\hat c}}_ \bot ^{ - 1} = }\\ {{\rm{cos}}(\pi + A) + \mathit{\boldsymbol{\hat a}}{\rm{sin}}(\pi + A)} \end{array} $

(7)

式中，${\mathit{\boldsymbol{\hat b}}_ \bot } = - \mathit{\boldsymbol{\hat b}}_ \bot ^\prime $。

上述分析表明，球面三角形边长的四元数为球心指向边长终点的单位向量与球心指向边长始点的单位向量逆的格拉斯曼乘积。如果利用四元数表示球面三角形的二面角，按照球面角的度量方向(本文约定指向球面角顶点的方向为正)，角的四元数为终大圆弧(指向顶点)平面法向的单位向量与始大圆弧(背向顶点)平面法向的单位向量逆的格拉斯曼乘积，式(7)为其三角函数形式。

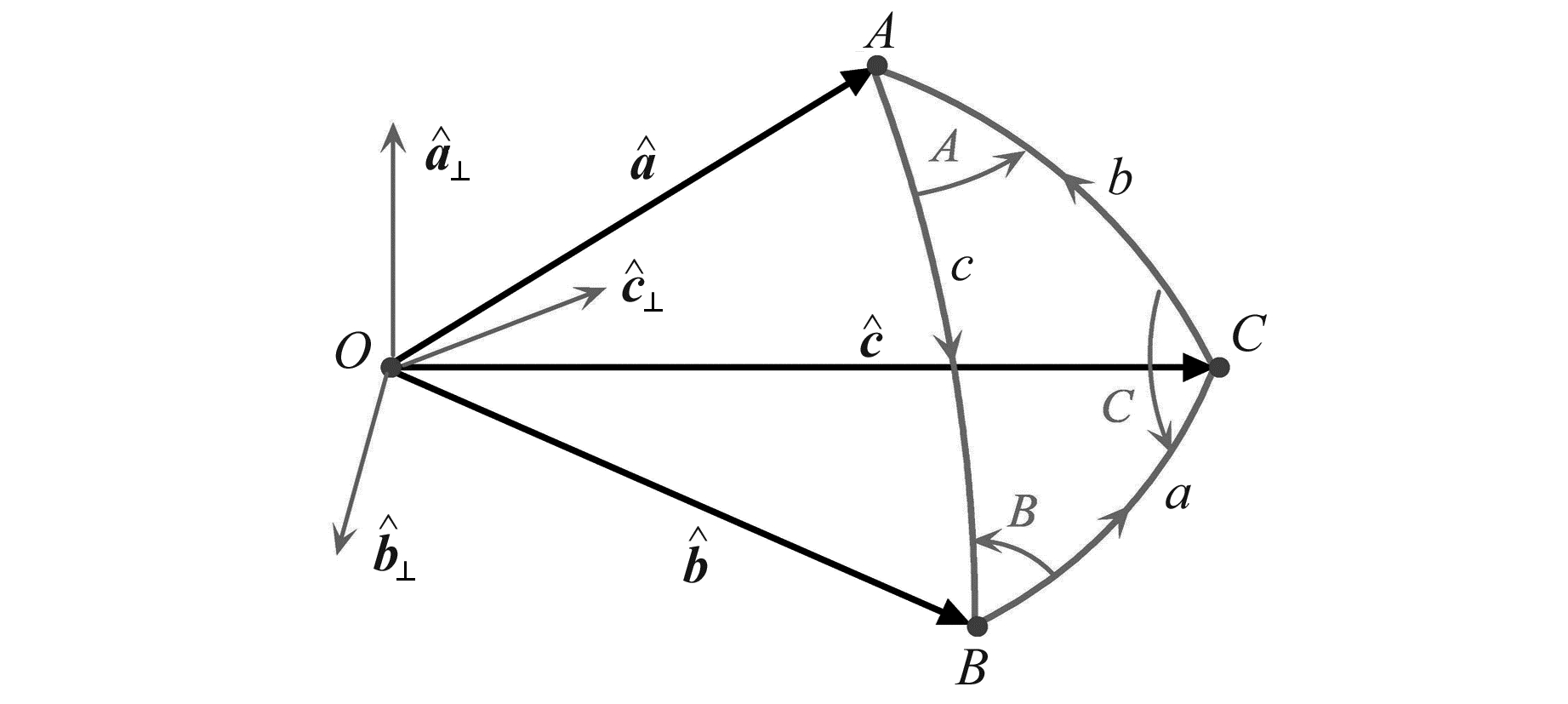
4 利用四元数推导球面三角形公式

本节将在3个角都小于90°的条件下推导球面三角形的有关公式，该结论适用于任何球面三角形。设存在球面三角形ABC，将各顶点与球心O连接，可得球心三面角O-ABC (图 3)。球心O指向A点、B点和C点的单位向量分别为$\mathit{\boldsymbol{\hat a}}、\mathit{\boldsymbol{\hat b}}$和$\mathit{\boldsymbol{\hat c}}, {\mathit{\boldsymbol{\hat a}}_ \bot }$垂直于由a边决定的平面，${{\mathit{\boldsymbol{\hat b}}}_ \bot }$垂直于由b边决定的平面，${{\mathit{\boldsymbol{\hat c}}}_ \bot }$垂直于由c边决定的平面。按照边约定的度量方向，存在以下关系式：

$ \begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\hat a}}}_ \bot } = \frac{{\mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}}}}{{\mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}}}} = \frac{{\mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}}}}{{{\rm{sin}}a}}, }\\ {{{\mathit{\boldsymbol{\hat b}}}_ \bot } = \frac{{\mathit{\boldsymbol{\hat c}} \times \mathit{\boldsymbol{\hat a}}}}{{|\mathit{\boldsymbol{\hat c}} \times \mathit{\boldsymbol{\hat a}}|}} = \frac{{\mathit{\boldsymbol{\hat c}} \times \mathit{\boldsymbol{\hat a}}}}{{{\rm{sin}}b}}, }\\ {{{\mathit{\boldsymbol{\hat c}}}_ \bot } = \frac{{\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}}}{{|\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}|}} = \frac{{\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}}}{{{\rm{sin}}c}}} \end{array} $

根据上节的讨论，可知球面三角形角的四元数为：

$ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {A\mathit{\boldsymbol{\hat a}} \buildrel \wedge \over = {\mathit{\boldsymbol{A}}_{{\rm{角}}}} = {{\mathit{\boldsymbol{\hat b}}}_ \bot } \circ \mathit{\boldsymbol{\hat c}}_ \bot ^{ - 1} = {\rm{cos}}(\pi + A) + }\\ {\mathit{\boldsymbol{\hat a}}{\rm{sin}}(\pi + A) = {{\mathit{\boldsymbol{\hat c}}}_ \bot } \cdot {{\mathit{\boldsymbol{\hat b}}}_ \bot } + {{\mathit{\boldsymbol{\hat c}}}_ \bot } \times {{\mathit{\boldsymbol{\hat b}}}_ \bot }} \end{array}\\ \begin{array}{*{20}{c}} {B\mathit{\boldsymbol{\hat b}} \buildrel \wedge \over = {\mathit{\boldsymbol{B}}_{{\rm{角}}}} = {{\mathit{\boldsymbol{\hat c}}}_ \bot } \circ \mathit{\boldsymbol{\hat a}}_ \bot ^{ - 1} = {\rm{cos}}(\pi + B)}\\ {\mathit{\boldsymbol{\hat b}}{\rm{sin}}(\pi + B) = {{\mathit{\boldsymbol{\hat a}}}_ \bot } \cdot {{\mathit{\boldsymbol{\hat c}}}_ \bot } + {{\mathit{\boldsymbol{\hat a}}}_ \bot } \times {{\mathit{\boldsymbol{\hat c}}}_ \bot }} \end{array}\\ \begin{array}{*{20}{c}} {C\mathit{\boldsymbol{\hat c}} \buildrel \wedge \over = {\mathit{\boldsymbol{C}}_{{\rm{角}}}} = {{\mathit{\boldsymbol{\hat a}}}_ \bot } \circ \mathit{\boldsymbol{\hat b}}_ \bot ^{ - 1} = {\rm{cos}}(\pi + C) + }\\ {\mathit{\boldsymbol{\hat c}}{\rm{sin}}(\pi + C) = {{\mathit{\boldsymbol{\hat b}}}_ \bot } \cdot {{\mathit{\boldsymbol{\hat a}}}_ \bot } + {{\mathit{\boldsymbol{\hat b}}}_ \bot } \times {{\mathit{\boldsymbol{\hat a}}}_ \bot }} \end{array} \end{array} \right. $

(8)

球面三角形边的四元数为：

$ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {a{{\mathit{\boldsymbol{\hat a}}}_ \bot } = \overset\frown {BC} \buildrel \wedge \over = {\mathit{\boldsymbol{a}}_{{\rm{边}}}} = \mathit{\boldsymbol{\hat c}} \circ {{\mathit{\boldsymbol{\hat b}}}^{ - 1}} = {\rm{cos}}a + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat a}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}a = \mathit{\boldsymbol{\hat b}} \cdot \mathit{\boldsymbol{\hat c}} + \mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}}} \end{array}\\ \begin{array}{*{20}{l}} {b{{\mathit{\boldsymbol{\hat b}}}_ \bot } = \overset\frown {CA} \buildrel \wedge \over = {\mathit{\boldsymbol{b}}_{{\rm{边}}}} = \mathit{\boldsymbol{\hat a}} \circ {{\mathit{\boldsymbol{\hat c}}}^{ - 1}} = {\rm{cos}}b + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat b}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}b = \mathit{\boldsymbol{\hat c}} \cdot \mathit{\boldsymbol{\hat a}} + \mathit{\boldsymbol{\hat c}} \times \mathit{\boldsymbol{\hat a}}} \end{array}\\ \begin{array}{*{20}{l}} {c{{\mathit{\boldsymbol{\hat c}}}_ \bot } = \overset\frown {AB} \buildrel \wedge \over = {\mathit{\boldsymbol{c}}_{{\rm{边}}}} = \mathit{\boldsymbol{\hat b}} \circ {{\mathit{\boldsymbol{\hat a}}}^{ - 1}} = {\rm{cos}}c + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat c}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}c = \mathit{\boldsymbol{\hat a}} \cdot \mathit{\boldsymbol{\hat b}} + \mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}} \end{array} \end{array} \right. $

(9)

4.1 边余弦公式、第一五元素公式和正弦公式推导

根据式(9)可得：

$ {\mathit{\boldsymbol{c}}_{{\rm{边}}}} \circ {\mathit{\boldsymbol{b}}_{{\rm{边}}}} = (\mathit{\boldsymbol{\hat b}} \circ {\mathit{\boldsymbol{\hat a}}^{ - 1}}) \circ (\mathit{\boldsymbol{\hat a}} \circ {\mathit{\boldsymbol{\hat c}}^{ - 1}}) = \mathit{\boldsymbol{\hat b}} \circ {\mathit{\boldsymbol{\hat c}}^{ - 1}} = \mathit{\boldsymbol{a}}_{{\rm{边}}}^{ - 1} $

将上式写成三角函数形式：

$ \begin{array}{*{20}{c}} {{\rm{cos}}a - {{\mathit{\boldsymbol{\hat a}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}a = }\\ {({\rm{cos}}c + {{\mathit{\boldsymbol{\hat c}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}c) \cdot ({\rm{cos}}b + {{\mathit{\boldsymbol{\hat b}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}b)} \end{array} $

(10)

按照式(1)进行乘法运算，使得式(10)等号两边的标量部分相等，则：

$ {\rm{cos}}a = {\rm{cos}}b{\rm{cos}}c - {\mathit{\boldsymbol{\hat c}}_ \bot } \cdot {\mathit{\boldsymbol{\hat b}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}b{\rm{sin}}c $

根据式(8)，可将式(10)写为：

$ {\rm{cos}}a = {\rm{cos}}b{\rm{cos}}c + {\rm{sin}}b{\rm{sin}}c{\rm{cos}}A $

(11)

式(11)即为球面三角形边余弦公式。

令式(10)等号两边的向量部分相等，则：

$ \begin{array}{*{20}{c}} { - {{\mathit{\boldsymbol{\hat a}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}a = {{\mathit{\boldsymbol{\hat c}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cos}}b{\rm{sin}}c + }\\ {{{\mathit{\boldsymbol{\hat b}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}b{\rm{cos}}c + {{\mathit{\boldsymbol{\hat c}}}_ \bot } \times {{\mathit{\boldsymbol{\hat b}}}_ \bot }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}b{\rm{sin}}c} \end{array} $

(12)

将式(12)等号两边分别点乘${{\mathit{\boldsymbol{\hat c}}}_ \bot }$和${{\mathit{\boldsymbol{\hat b}}}_ \bot }$，结合式(8)可得：

$ \left\{ {\begin{array}{*{20}{l}} {{\rm{sin}}a{\kern 1pt} {\rm{cos}}B = {\rm{cos}}b{\kern 1pt} {\rm{sin}}c - \sin b{\rm{cos}}c{\kern 1pt} {\rm{cos}}A}\\ {{\rm{sin}}a{\kern 1pt} {\rm{cos}}C = {\rm{cos}}c{\kern 1pt} {\rm{sin}}b - \sin c{\rm{cos}}b{\kern 1pt} {\rm{cos}}A} \end{array}} \right. $

(13)

式(13)为球面三角形的第一五元素公式。

另外，将式(12)等号两边点乘${\mathit{\boldsymbol{\hat a}}}$，结合式(8)和下列等式:

$ \mathit{\boldsymbol{\hat a}} \cdot {{\mathit{\boldsymbol{\hat b}}}_ \bot } = 0, \mathit{\boldsymbol{\hat a}} \cdot {{\mathit{\boldsymbol{\hat c}}}_ \bot } = 0, \mathit{\boldsymbol{\hat a}} \cdot {{\mathit{\boldsymbol{\hat a}}}_ \bot } = \frac{{\mathit{\boldsymbol{\hat a}} \cdot (\mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}})}}{{{\rm{sin}}a}} $

可得：

$ \frac{{{\rm{sin}}A}}{{{\rm{sin}}a}} = \frac{{\mathit{\boldsymbol{\hat a}} \cdot (\mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}})}}{{{\rm{sin}}a{\kern 1pt} {\rm{sin}}b{\kern 1pt} {\rm{sin}}c}} $

(14)

式(14)即为球面三角形正弦公式的另一种形式。

根据式(9)可得：

$ \begin{array}{l} {\mathit{\boldsymbol{a}}_{{\rm{边}}}} \circ {\mathit{\boldsymbol{c}}_{{\rm{边}}}} = (\mathit{\boldsymbol{\hat c}} \circ {{\mathit{\boldsymbol{\hat b}}}^{ - 1}}) \circ (\mathit{\boldsymbol{\hat b}} \circ {{\mathit{\boldsymbol{\hat a}}}^{ - 1}}) = \mathit{\boldsymbol{\hat c}} \circ {{\mathit{\boldsymbol{\hat a}}}^{ - 1}} = \mathit{\boldsymbol{b}}_{{\rm{边}}}^{ - 1}\\ {\mathit{\boldsymbol{b}}_{{\rm{边}}}} \circ {\mathit{\boldsymbol{a}}_{{\rm{边}}}} = (\mathit{\boldsymbol{\hat a}} \circ {{\mathit{\boldsymbol{\hat c}}}^{ - 1}}) \circ (\mathit{\boldsymbol{\hat c}} \circ {{\mathit{\boldsymbol{\hat b}}}^{ - 1}}) = \mathit{\boldsymbol{\hat a}} \circ {{\mathit{\boldsymbol{\hat b}}}^{ - 1}} = \mathit{\boldsymbol{c}}_{{\rm{边}}}^{ - 1} \end{array} $

采用类似的推导过程，可分别得到球面三角形边的余弦公式：

$ {{\rm{cos}}b = {\rm{cos}}c{\kern 1pt} {\rm{cos}}a + {\rm{sin}}c{\kern 1pt} {\rm{sin}}a{\kern 1pt} {\rm{cos}}B} $

(15)

$ {{\rm{cos}}c = {\rm{cos}}a{\kern 1pt} {\rm{cos}}b + {\rm{sin}}a{\kern 1pt} {\rm{sin}}b{\kern 1pt} {\rm{cos}}C} $

(16)

第一五元素公式为：

$ \left\{ {\begin{array}{*{20}{l}} {{\rm{sin}}b{\kern 1pt} {\rm{cos}}C = {\rm{cos}}c{\kern 1pt} {\rm{sin}}a - {\rm{sin}}c{\kern 1pt} {\rm{cos}}a{\kern 1pt} {\rm{cos}}B}\\ {{\rm{sin}}b{\kern 1pt} {\rm{cos}}A = {\rm{cos}}a{\kern 1pt} {\rm{sin}}c - {\rm{sin}}a{\kern 1pt} {\rm{cos}}c{\kern 1pt} {\rm{cos}}B} \end{array}} \right. $

(17)

$ \left\{ {\begin{array}{*{20}{l}} {{\rm{sin}}c{\kern 1pt} {\kern 1pt} {\rm{cos}}B = {\rm{cos}}b{\kern 1pt} {\rm{sin}}a - {\rm{sin}}b{\kern 1pt} {\rm{cos}}a{\kern 1pt} {\rm{cos}}C}\\ {{\rm{sin}}c{\kern 1pt} {\kern 1pt} {\rm{cos}}A = {\rm{cos}}a{\kern 1pt} {\rm{sin}}b - {\rm{sin}}a{\kern 1pt} {\rm{cos}}b{\kern 1pt} {\rm{cos}}C} \end{array}} \right. $

(18)

正弦公式为：

$ {\frac{{{\rm{sin}}B}}{{{\rm{sin}}b}} = \frac{{\mathit{\boldsymbol{\hat b}} \cdot (\mathit{\boldsymbol{\hat c}} \times \mathit{\boldsymbol{\hat a}})}}{{{\rm{sin}}a{\kern 1pt} {\rm{sin}}b{\kern 1pt} {\rm{sin}}c}}} $

(19)

$ {\frac{{{\rm{sin}}C}}{{{\rm{sin}}c}} = \frac{{\mathit{\boldsymbol{\hat c}} \cdot (\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}})}}{{{\rm{sin}}a{\kern 1pt} {\rm{sin}}b{\kern 1pt} {\rm{sin}}c}}} $

(20)

因为

$ \mathit{\boldsymbol{\hat a}} \cdot (\mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}}) = \mathit{\boldsymbol{\hat b}} \cdot (\mathit{\boldsymbol{\hat c}} \times \mathit{\boldsymbol{\hat a}}) = \mathit{\boldsymbol{\hat c}} \cdot (\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}) $

则：

$ \frac{{{\rm{sin}}A}}{{{\rm{sin}}a}} = \frac{{{\rm{sin}}B}}{{{\rm{sin}}b}} = \frac{{{\rm{sin}}C}}{{{\rm{sin}}c}} $

(21)

式(21)为通常情况下的球面三角形的正弦公式。

4.2 角余弦公式和第二五元素公式推导

根据式(8)可得：

$ \begin{array}{l} {\mathit{\boldsymbol{B}}_{{\rm{角}}}} \circ {\mathit{\boldsymbol{C}}_{{\rm{角}}}} = ({{\mathit{\boldsymbol{\hat c}}}_ \bot } \circ \mathit{\boldsymbol{\hat a}}_ \bot ^{ - 1}) \circ ({{\mathit{\boldsymbol{\hat a}}}_ \bot } \circ \mathit{\boldsymbol{\hat b}}_ \bot ^{ - 1}) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat c}}}_ \bot } \circ \mathit{\boldsymbol{\hat b}}_ \bot ^{ - 1} = \mathit{\boldsymbol{A}}_{{\rm{角}}}^{ - 1} \end{array} $

将上式写成三角函数形式：

$ \begin{array}{*{20}{l}} {{\rm{cos}}(\pi + A) - \mathit{\boldsymbol{\hat a}}{\rm{sin}}(\pi + A) = [{\rm{cos}}(\pi + B) + }\\ {\mathit{\boldsymbol{\hat b}}{\rm{sin}}(\pi + B)] \circ [{\rm{cos}}(\pi + C) + \mathit{\boldsymbol{\hat c}}{\rm{sin}}(\pi + C)]} \end{array} $

令等号两边的标量部分和向量部分分别相等，则：

$ \left\{ {\begin{array}{*{20}{l}} {{\rm{ - cos}}A = {\rm{cos}}B{\rm{cos}}C - \mathit{\boldsymbol{\hat c}} \cdot \mathit{\boldsymbol{\hat b}}{\rm{sin}}B{\rm{sin}}C}\\ {\mathit{\boldsymbol{\hat a}}{\rm{sin}}A = \mathit{\boldsymbol{\hat b}}{\rm{sin}}B{\rm{cos}}C + \mathit{\boldsymbol{\hat c}}{\rm{cos}}B{\rm{sin}}C + \mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}}{\rm{sin}}B{\rm{sin}}C} \end{array}} \right. $

(22)

根据式(22)的第1式和式(9)，可得球面三角形的角余弦公式为：

$ {\rm{cos}}A = - {\rm{cos}}B{\rm{cos}}C + {\rm{sin}}B{\rm{sin}}C{\rm{cos}}a $

(23)

将式(22)的第2式等号两边分别点乘${\mathit{\boldsymbol{\hat b}}}$和${\mathit{\boldsymbol{\hat c}}}$，结合式(9)可得第二五元素公式为：

$ \left\{ \begin{array}{l} {\rm{sin}}A{\rm{cos}}c = {\rm{cos}}C{\rm{sin}}B + {\rm{sin}}C{\rm{cos}}B{\rm{cos}}a\\ {\rm{sin}}A{\rm{cos}}b = {\rm{cos}}B{\rm{sin}}C + {\rm{sin}}B{\rm{cos}}C{\rm{cos}}a \end{array} \right. $

(24)

将式(22)的第2式等号两边点乘${{\mathit{\boldsymbol{\hat a}}}_ \bot }$，结合下式

$ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat b}} \cdot {{\mathit{\boldsymbol{\hat a}}}_ \bot } = \mathit{\boldsymbol{\hat c}} \cdot {{\mathit{\boldsymbol{\hat a}}}_ \bot } = 0, \mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}} = }\\ {{\rm{sin}}a{{\mathit{\boldsymbol{\hat a}}}_ \bot }, \mathit{\boldsymbol{\hat a}} \cdot {{\mathit{\boldsymbol{\hat a}}}_ \bot } = \frac{{\mathit{\boldsymbol{\hat a}} \cdot (\mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}})}}{{{\rm{sin}}a}}} \end{array} $

可得：    $\frac{{{\rm{si}}{{\rm{n}}^2}a{\kern 1pt} {\rm{sin}}B{\kern 1pt} {\rm{sin}}C}}{{{\rm{sin}}A}} = \mathit{\boldsymbol{\hat a}} \cdot (\mathit{\boldsymbol{\hat b}} \times \mathit{\boldsymbol{\hat c}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (25)$

同理，根据式(8)可得：

$ \begin{array}{l} \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{{\rm{角}}}} \circ {\mathit{\boldsymbol{A}}_{{\rm{角}}}} = ({{\mathit{\boldsymbol{\hat a}}}_ \bot } \circ \mathit{\boldsymbol{\hat b}}_ \bot ^{ - 1}) \circ ({{\mathit{\boldsymbol{\hat b}}}_ \bot } \circ \mathit{\boldsymbol{\hat c}}_ \bot ^{ - 1})}\\ {{{\mathit{\boldsymbol{\hat a}}}_ \bot } \circ \mathit{\boldsymbol{\hat c}}_ \bot ^{ - 1} = \mathit{\boldsymbol{B}}_{{\rm{角}}}^{ - 1}} \end{array}\\ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{{\rm{角}}}} \circ {\mathit{\boldsymbol{B}}_{{\rm{角}}}} = ({{\mathit{\boldsymbol{\hat b}}}_ \bot } \circ \mathit{\boldsymbol{\hat c}}_ \bot ^{ - 1}) \circ ({{\mathit{\boldsymbol{\hat c}}}_ \bot } \circ \mathit{\boldsymbol{\hat a}}_ \bot ^{ - 1}) = }\\ {{{\mathit{\boldsymbol{\hat b}}}_ \bot } \circ \mathit{\boldsymbol{\hat a}}_ \bot ^{ - 1} = \mathit{\boldsymbol{C}}_{{\rm{角}}}^{ - 1}} \end{array} \end{array} $

采用类似的推导过程，可分别得到球面三角形的角余弦公式为：

$ \left\{ {\begin{array}{*{20}{l}} {{\rm{cos}}B = - {\rm{cos}}C{\rm{cos}}A + {\rm{sin}}C{\rm{sin}}A{\rm{cos}}b}\\ {{\rm{cos}}C = - {\rm{cos}}A{\rm{cos}}B + {\rm{sin}}A{\rm{sin}}B{\rm{cos}}c} \end{array}} \right. $

(26)

第二五元素公式为：

$ \left\{ {\begin{array}{*{20}{l}} {{\rm{sin}}B{\rm{cos}}a = {\rm{cos}}A{\rm{sin}}C + {\rm{sin}}A{\rm{cos}}C{\rm{cos}}b}\\ {{\rm{sin}}B{\rm{cos}}c = {\rm{cos}}C{\rm{sin}}A + {\rm{sin}}C{\rm{cos}}A{\rm{cos}}b} \end{array}} \right. $

(27)

$ \left\{ {\begin{array}{*{20}{l}} {{\rm{sin}}C{\rm{cos}}b = {\rm{cos}}B{\rm{sin}}A + {\rm{sin}}B{\rm{cos}}A{\rm{cos}}c}\\ {{\rm{sin}}C{\rm{cos}}a = {\rm{cos}}A{\rm{sin}}B + {\rm{sin}}A{\rm{cos}}B{\rm{cos}}c} \end{array}} \right. $

(28)

及    $\frac{{{\rm{sin}}A{\rm{si}}{{\rm{n}}^2}b{\rm{sin}}C}}{{{\rm{sin}}B}} = \mathit{\boldsymbol{\hat b}} \cdot (\mathit{\boldsymbol{\hat c}} \times \mathit{\boldsymbol{\hat a}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (29)$

$ \frac{{{\rm{sin}}A{\rm{sin}}B{\rm{si}}{{\rm{n}}^2}c}}{{{\rm{sin}}C}} = \mathit{\boldsymbol{\hat c}} \cdot (\mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b}}){\kern 1pt} $

(30)

结合式(25)、式(29)和式(30)，可得到通常情况下的球面三角形的正弦公式(式(21))。

5 结语

实数单位四元数实际上为2个单位向量的格拉斯曼乘积。在向量理论中，引用四元数共轭和逆的概念可方便地表示角度，球面上的大圆弧对应的四元数为球心指向大圆弧终点的单位向量与球心指向大圆弧始点的单位向量逆的格拉斯曼乘积。

如果约定球面角的度量方向指向球面角的顶点，那么球面角对应的四元数只与构成球面角的2个大圆弧的法向矢量有关。球面角对应的四元数为终大圆弧(指向顶点)平面法向的单位向量与始大圆弧(背向顶点)平面法向的单位向量逆的格拉斯曼乘积。利用四元数运算法则可方便地推导球面三角形的边或角正弦和余弦公式及第一和第二五元素公式。