2. 台湾中央研究院地球科学研究所,台北市研究院路二段128号,11529
季节性水文负荷对地震活动性的调制作用是当前国际上的研究热点,但沿喜马拉雅板块边界的季节性非构造和构造变形之间的相互作用仍有争议[1]。在众多地表质量负荷中,陆地水文负荷已被证明是引起地壳形变呈季节性变化特征的主要因素[2],国内外学者对此也进行了相关研究。Zou等[3]联合GPS和GRACE数据研究了地表垂直和水平位移的变化;Dam等[4]研究了地表水文负荷引起的地壳形变特征;Larochelle等[5]利用独立成分分析并提取了地表载荷产生的季节性大地信号;熊福文等[6]研究了地表载荷与地表垂直位移之间的季节性关系;Birhanu等[7]得到季风降水与GPS站点垂直位移具有一致响应的结论;Kreemer等[8]指出季节性应变可能促进主震的发生,并导致地震震级的增大和余震数量的减少;Bettinelli等[9]和Bollinger等[10]研究了尼泊尔地区地壳季节性形变对地震活动性的调制作用,并推测夏季观测到的喜马拉雅地震活动性的抑制可能是地表水文负荷增加造成的。
目前对于尼泊尔地区季节性水文负荷对地震活动性调制作用的研究较少,且缺乏针对季节性地表位移和应力应变场变化特征的深入分析。本文利用最小二乘拟合方法提取尼泊尔境内GPS连续运行参考站时间序列中的季节信号,得到各测站季节性三维位移场信息及尼泊尔地区面应变与库仑应力的季节性变化特征,对比TRMM月降水数据和去震群之后的地震目录,讨论其变化的原因及季节性水文负荷变化对地震活动性的调制作用。
1 数据和方法 1.1 季节性信号提取尼泊尔境内所有GPS连续运行参考站的时间序列产品可在美国内华达大学大地测量实验室网站(http://geodesy.unr.edu/index.php)下载,本文选取了尼泊尔境内38个GPS站进行数据分析。利用最小二乘拟合方法,得到季节项信号,其模型表达式为:
| $ \begin{array}{l} y\left( {{t_i}} \right) = {y_0} + v{t_i} + A\sin \left( {2{\rm{ \mathsf{ π} }}{t_i}} \right) + B\cos \left( {2{\rm{ \mathsf{ π} }}{t_i}} \right) + \\ C\sin \left( {{\rm{4 \mathsf{ π} }}{t_i}} \right) + D\cos \left( {{\rm{4 \mathsf{ π} }}{t_i}} \right) + \sum\limits_{j = 1}^k {{O_j}H\left( {{t_i} - {t_{{O_j}}}} \right)} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^m {H\left( {{t_i} - {t_{{q_j}}}} \right)\left( {{c_j} + {p_j}\ln \left( {1 + \frac{{\left( {{t_i} - {t_{{q_j}}}} \right)}}{{\tau _j^{\log }}}} \right)} \right)} + {\varepsilon _i} \end{array} $ | (1) |
式中,ti为时间,v为线性趋势项, 反映长期构造运动,A、B、C、D分别为周年项和半周年项的正余弦函数振幅,O为由不同原因导致的点位突变,c、p、τ分别为同震阶跃项震后对数振幅松弛时间,k、m分别为非震和地震原因引起的阶跃个数,εi为误差项。
提取式(1)中的周年项正余弦函数振幅,可得到季节性位移模型:
| $ y\left( {{t_i}} \right) = {\rm{Amp}} \cdot \sin \left( {2{\rm{ \mathsf{ π} }}{t_i} + {\rm{Pha}}} \right) $ | (2) |
其中,
| $ {\rm{Amp}} = \sqrt {{A^2} + {B^2}} , {\rm{Pha}} = \arctan \left( {B/A} \right) $ |
式中,Amp和Pha为季节性位移模型的振幅和初相位,利用季节性位移模型可计算每个测站在周年内的季节性位移。对于时间ti,为便于进行变化趋势及变化区域的对比,本文将一个周年划分为上、下半年共24个时间区间,每个区间约为15 d,这样既能保证有足够的数据量反映每个月的位移情况,又能保证时间段之间有恰当的时间跨度。
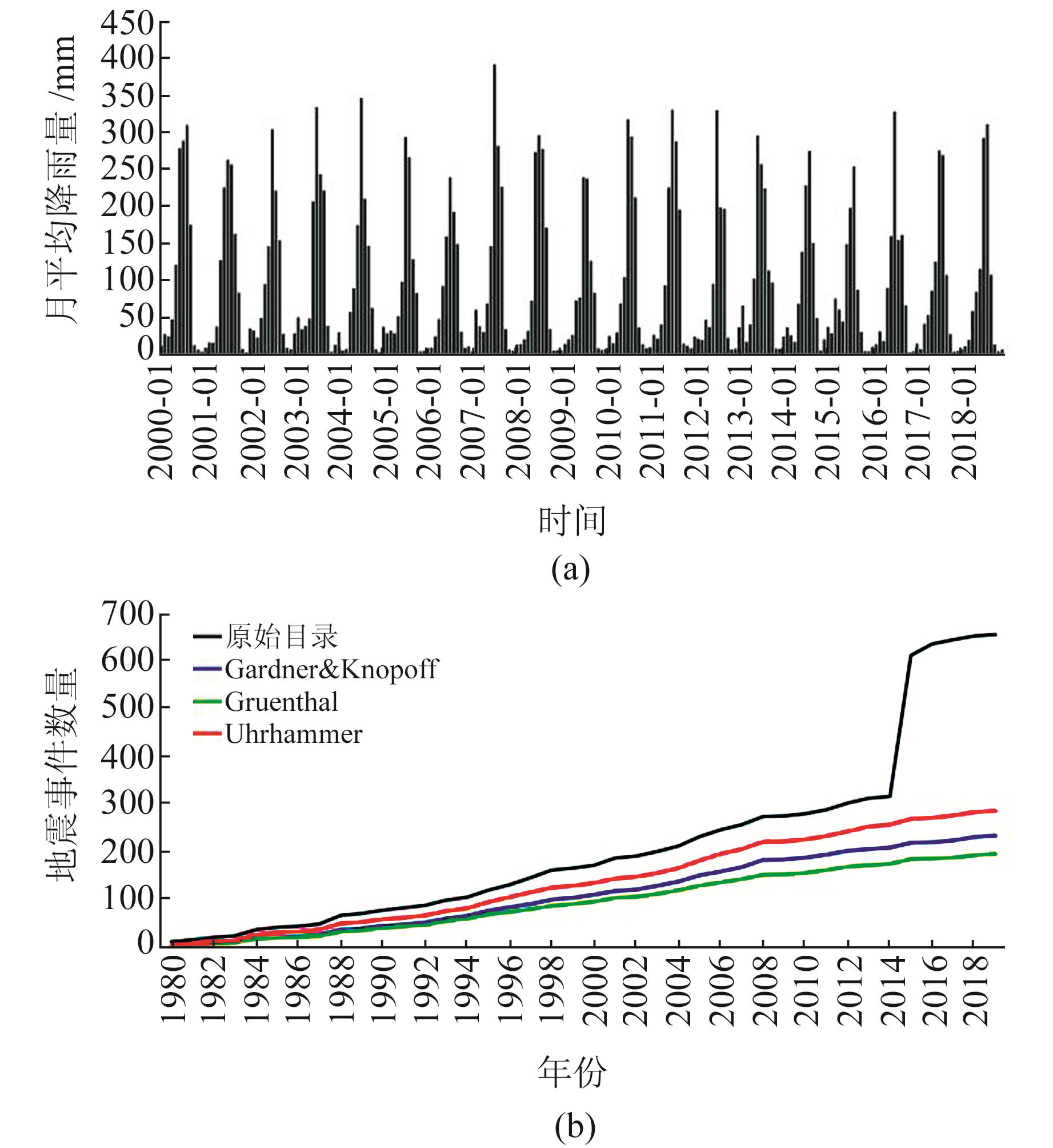
1.2 季节性降水和地震目录的去震群处理热带降雨测量任务(TRMM, tropical rainfall measuring mission)可以获取准全球的高时空分辨率降水数据[11]。本文使用时间分辨率为月、空间分辨率为0.25° ×0.25°、数据时段为2000~2018年的TRMM 3B43 V7数据作为尼泊尔地区月平均降水的数据来源,提取尼泊尔地区的格网范围并计算得到尼泊尔地区年周期内月降水量的变化特征(图 1(a))。Kansakar等[12]的研究结果表明,尼泊尔地区全年降水集中分布在6~9月的雨季,降水受季风影响显著,利用TRMM数据得到的月降水量变化和Kansakar等[12]的结论一致。
|
图 1 尼泊尔地区的月降水量时间序列及去震群算法处理结果对比 Fig. 1 Time series of monthly rainfall in Nepal, and comparison of processing results of the declustering algorithms |
尼泊尔地区的地震目录来自美国地质勘探局网站(https://earthquake.usgs.gov/),选取时间跨度为1980~2019年、震级大于2的地震事件,由于地震目录中一些余震群与大地震的发生有关,需要对地震目录进行去震群处理。为避免去震群算法结果的不确定性,本文利用Gardner&Knopoff、Uhrhammer和Gruenthal等3种去震群方法来抑制这些余震群对地震目录分析的影响[13],3种方法的结果对比见图 1(b)。这3种方法都是利用时空窗口来识别主震和余震,虽然计算窗口大小的算法不同,但效果基本一致,均能较好地去除与大地震相关的余震对分析结果的影响。
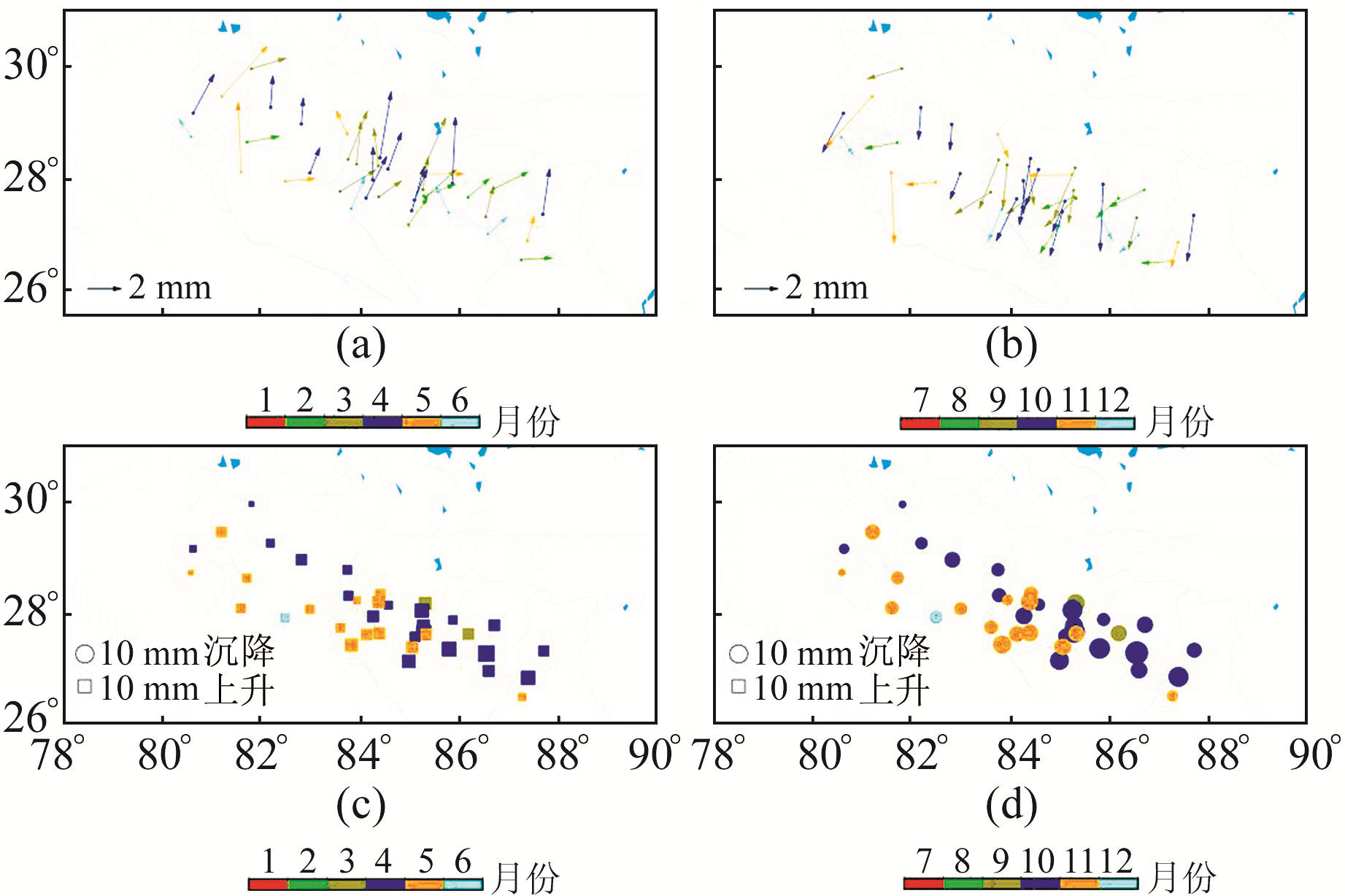
2 结果分析 2.1 季节性位移与降水的相关性利用季节性位移模型可计算得到每个GPS站24个时间区间端点上的水平和垂直位移情况。图 2(a)和2(b)分别为上半年和下半年最大水平位移出现的月份,颜色条对应月份,箭头指向代表位移的方向,长度代表最大水平位移大小;图 2(c)和2(d)分别为上半年和下半年最大垂直位移出现的月份,圆形代表沉降,方形代表上升,圆形和方形的尺寸代表最大垂直位移量大小。
|
图 2 1个年周期内测站最大季节性位移出现的月份 Fig. 2 The month in which the maximum seasonal displacement of the station occurs in an annual cycle |
对于图 2中测站最大位移出现时间,上半年最大水平位移出现在3~5月的测站数量占比达到70%,下半年大多数的测站出现最大水平位移时间在9~11月;垂直季节性位移出现最大值的时间更加集中,上半年90%的测站垂直位移出现最大值的时间集中于3月和4月,下半年则集中于10月和11月。对于测站最大位移的方向和大小,在上半年周期中,大多数GPS测站的水平季节性位移均朝向喜马拉雅山脉方向,水平位移最大值达到了4 mm;对于垂直季节性位移,所有的测站垂直位移都表现为上升,且垂直位移最大值达到13 mm。而在下半年周期中,最大水平和垂直位移的方向均与上半年相反,垂直位移大小的空间分布特征尤为明显,在尼泊尔东南部区域测站的垂直位移明显比尼泊尔西北部要大。
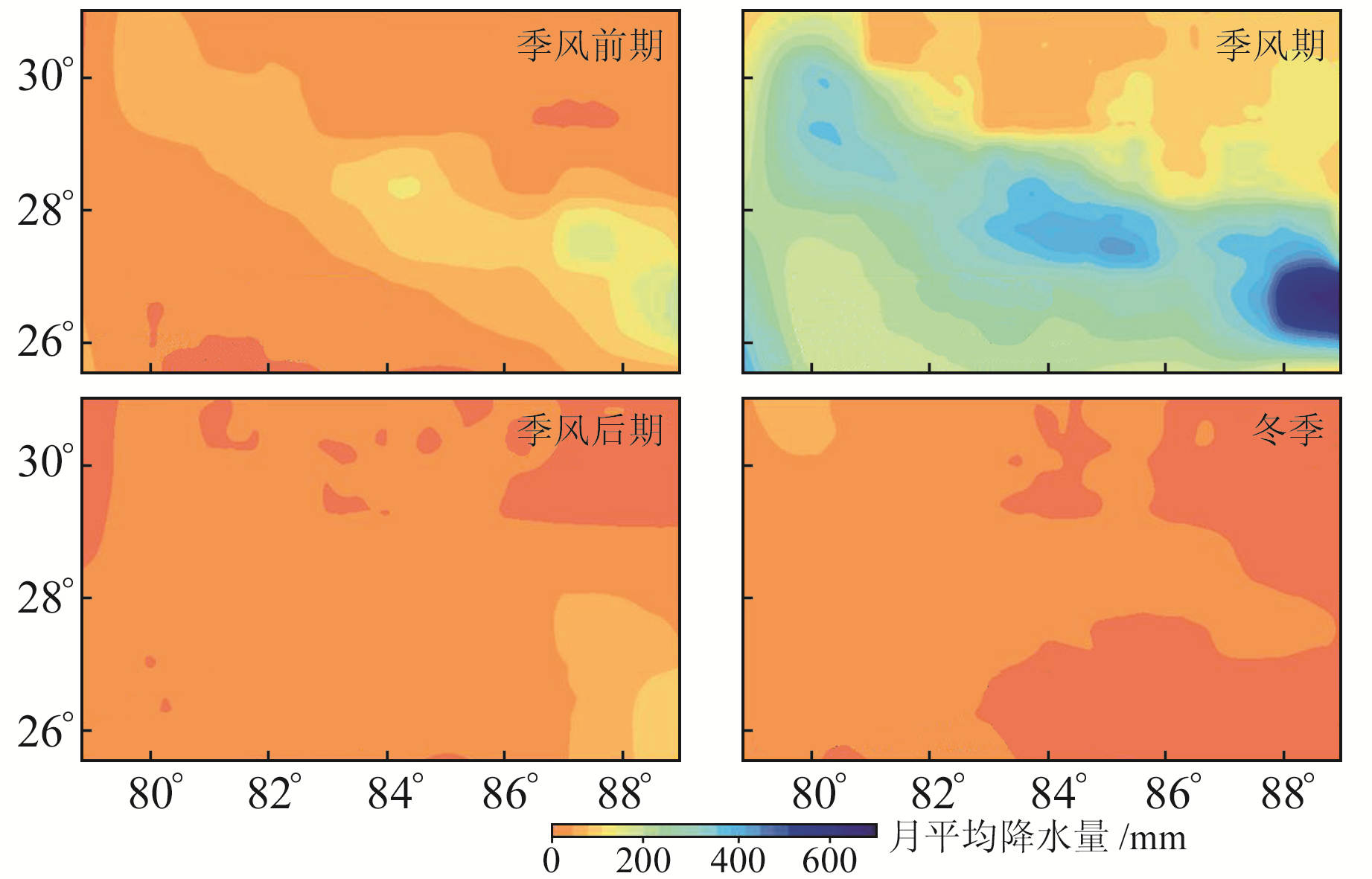
尼泊尔地区的年周期分为4个季节:季风前期(3~5月)、季风期(6~9月)、季风后期(10~11月)及冬季(12~2月)[12]。为更清楚地表达季节性位移与降水之间的关系,利用TRMM数据得到每个季节内的月平均降水分布(图 3)。在尼泊尔地区,季风前期气候干热,主要为尼泊尔东南部地区局部降水,月平均降水量在100 mm左右,而西北部只有约50 mm;季风期则是全国范围内的普遍降水,占全年总降水量的80%,尼泊尔首都及喜马拉雅山脉南部区域的月平均降水量甚至超过500 mm;季风后期最为干燥,表现为东南部降水较西北部多,东南部月平均降水量约为西北部的2倍;而在冬季,整个尼泊尔地区降水最少,月平均降水量不超过50 mm,详情见表 1(单位mm)。
|
图 3 尼泊尔地区4个季节内的月平均降水量 Fig. 3 Monthly average rainfall over the four seasons in Nepal |
|
|
表 1 尼泊尔西北部地区和东南部地区在4个季节中月平均降水量的对比 Tab. 1 Comparison of monthly mean rainfall in four seasons in northwestern and southeastern Nepal |
对比分析可以发现,在季风后期,垂直位移与月平均降水量较大的区域明显存在相关性,在月平均降水量较大的区域,测站的沉降量也出现较大值。图 4(a)和4(b)分别给出尼泊尔地区西北部和东南部月平均降水量及垂直位移平均值,结合表 1可以看出,在主要的降水期,西北部地区的月平均降水量低于东南部。在降水期结束的10月份,西北部地区各测站的平均沉降量约为6 mm,而在东南部地区这个值超过了8 mm;季风后期降水减少且呈局域性的分布,至4月份季风前期地表回弹也达到最值。众多研究表明,降水是陆地水载荷的主要来源之一,陆地水荷载的变化会导致地表垂直位移的变化[2, 4-5]。通过以上证据可以推测,尼泊尔地区的季节性降水可能是导致地表垂直位移出现季节性变化的主要原因。

|
图 4 尼泊尔地区月平均降水量及垂直位移变化 Fig. 4 The monthly average rainfall and the changes of vertical displacement in Nepal |
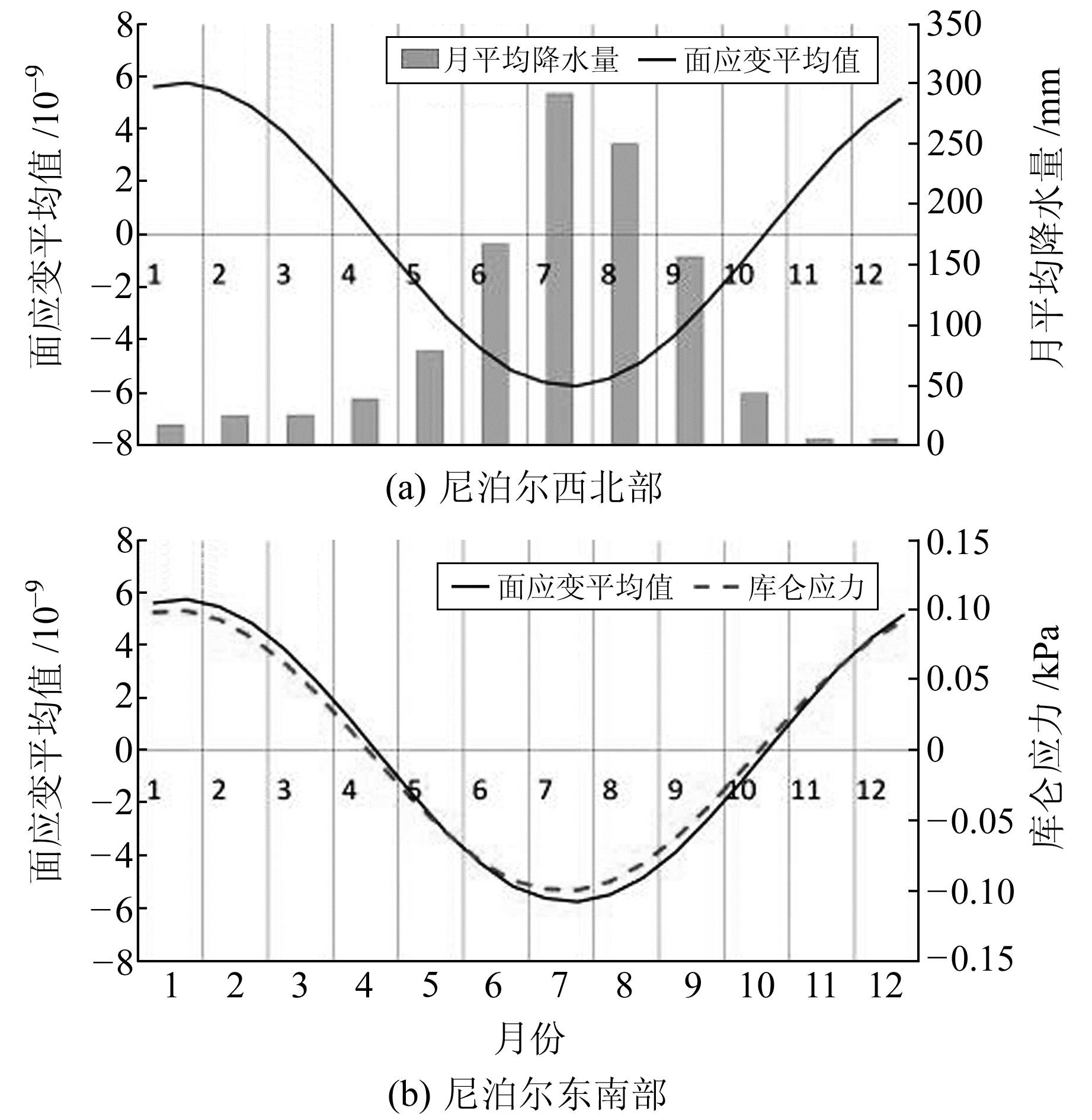
本文利用N和E方向的水平季节性位移,使用VISR程序[14]计算得到尼泊尔各月份的面应变平均值(图 5(a)),其中数值正负分别代表扩张和收缩。由图 5可见,在降水较少的月份,面应变均为扩张;随着降水的增多,面应变逐渐变为收缩,在月平均降水量最大的7月,面应变收缩量最大。面应变的季节性变化与季节性降水之间有较强的相关性,通过面应变分析进一步证明,尼泊尔地区季节性降水导致地表季节性形变,并从地表测站的位移反映出来。
地震触发机制通常根据库仑破坏准则来进行讨论,本文在走向与喜马拉雅主前缘断裂(MFT)平行的垂直断层上将季节性应变转换为库仑应力,转换过程中使用了40 GPa的杨氏模量和King等[15]的公式,其数学模型可简化为:
| $ \Delta {\rm{CFS}} = \Delta {\tau _S} + \mu '\Delta {\sigma _n} $ | (3) |
式中,ΔτS为沿断层滑动方向的剪切应力变化,Δσn为沿断层法线方向正应力的变化(以张应力为正),μ′为有效摩擦系数(本文取值0.4)。将尼泊尔地区各月份库仑应力的平均值与面应变平均值叠加显示在图 5(b),库仑应力正值代表应力聚集,岩石破裂的可能性增大;负值代表应力释放,岩石破裂的可能性减小。断层面上库仑应力的季节变化与面应变的相位和相对振幅非常接近,说明库仑应力的季节性变化受与断层走向正交的面应变控制。
|
图 5 尼泊尔地区月平均降水量、面应变和库仑应力的变化 Fig. 5 The monthly average rainfall and the changes of vertical displacement, surface strain and Coulomb stress in Nepal |
对于地震活动的季节性,将3种去震群方法得到的各月份结果按照不同震级地震数量进行统计(图 6),叠加显示的柱状图是尼泊尔地区月平均降水量。3种方法得到的结果略有差异,但整体趋势较为一致。由图 6可以看出,大于5级的地震由于数量少,变化趋势并不明显,但冬季1月份和季风期结束的9月份,大于3.5、4和4.5级的地震事件数量变化则非常显著,详细的事件数量统计见表 2。由表 2可以看出,经3种去震群方法处理后在1月份大于3.5、4和4.5级的地震数目大约是9月份的2倍。值得注意的是,大于3.5级地震的数量在1月份最多,恰好对应了冬季降水量少和库仑应力正值变化量最大的时期;9月份地震数量最少,对应了降水期结束和库仑应力负值累积量最大的时期,显示出地震数目的变化与季节性降水和库仑应力变化量之间存在着较强的相关性。

|
图 6 3种去震群方法在不同月份中地震事件的数量 Fig. 6 The number of earthquake events in different months by three declustering methods |
|
|
表 2 3种去震群方法1月和9月的不同震级地震事件数目统计 Tab. 2 Statistics of the number of earthquake events of different magnitudes in January and September of the three declustering methods |
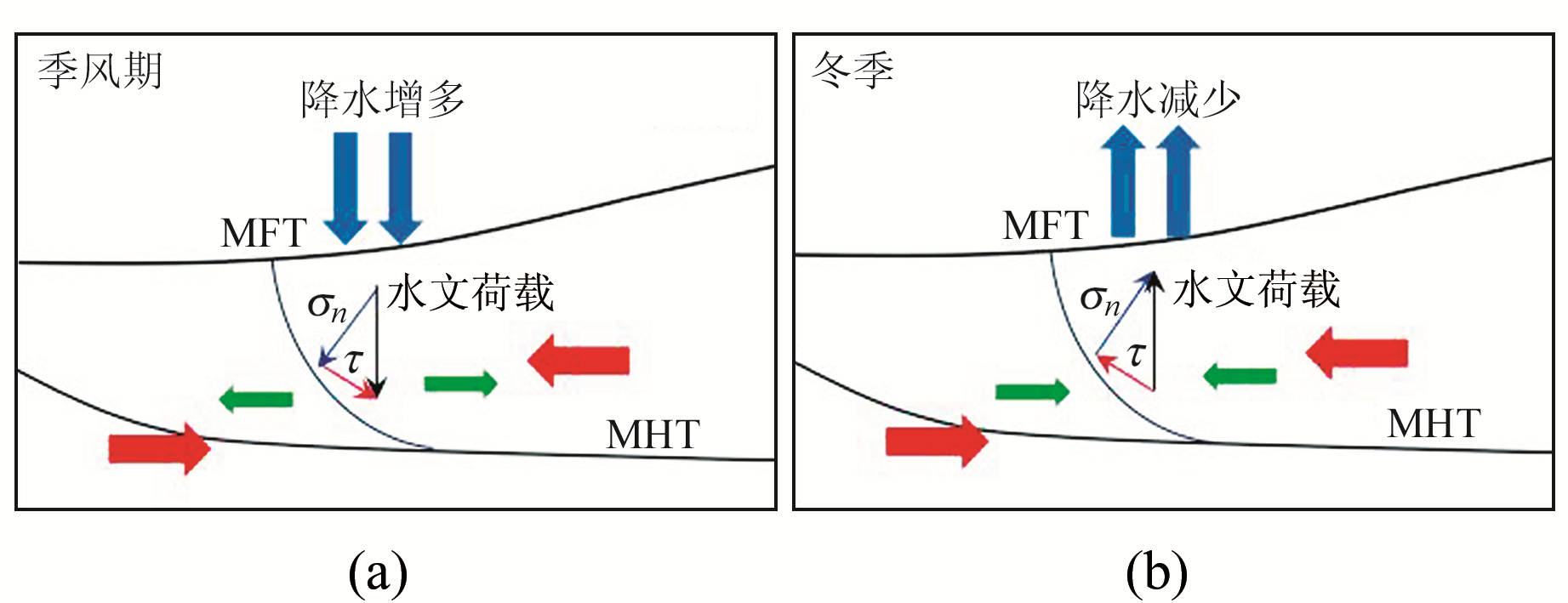
综上分析,季节性降水对计算断层面上的库仑应力产生了季节性的影响。图 7(a)和7(b)说明了这种影响的过程,其中τ为沿断层滑动方向的剪切应力,σn为沿断层法线方向的正应力,MHT为主喜马拉雅断裂,红色箭头代表断层的长期运动趋势,绿色箭头代表水文负荷对断层运动趋势的影响,蓝色箭头表示降水造成的水文荷载。季风期降水丰富导致地表水文负荷增大,地表出现压缩的弹性形变,沿断层的分力对断层的长期运动趋势产生一定程度的反向扰动,库仑应力得到一定程度的释放,岩石破裂的可能性减少;在冬季情况却相反,降水量减少,地表水文负荷得到卸载,对断层运动的反向扰动作用减少,库仑应力逐渐积聚,岩石破裂的可能性增加,这也能解释图 6中地震事件数量在冬季增多而在季风期减少的变化特征。Bollinger等[10]的研究中也排除了大气压力波动、雪荷载、温度变化和孔隙压力变化对尼泊尔地区应力变化造成的影响,因此本文推测,是尼泊尔地区季节性降水造成的水文负荷对断层的长期运动趋势产生一定程度的扰动,进而影响了地震发生的时间。
|
图 7 水文负荷对应变产生影响示意图 Fig. 7 Sketch map of the effect of hydrologic load on strain |
本文利用最小二乘拟合方法提取尼泊尔地区GPS时间序列的周期信号,反演得到由于负荷变化引起的季节性位移场和应力应变场模型。结合TRMM月降水数据和去震群之后的地震目录,进一步与季节性位移和应变进行对比分析,得出季节性降水造成的水文负荷对地震活动有一定调制作用的结论。结果表明:
1) 尼泊尔地区降水的季节性变化显著,垂直位移与季节性降水区域存在明显的时空相关性,季节性降水可能是导致地表垂直位移出现季节性变化的主要原因。
2) 面应变与水文负荷之间存在着相关性,在月平均降水量最大的7月,面应变收缩出现最大值,进而推断水文负荷是导致地表季节性形变的主要驱动因素。
3) 将应变转换为与喜马拉雅主前缘断裂(MFT)平行的垂直断层上的库仑应力,面应变和库仑应力在相位和相对振幅上存在一致性,库仑应力的季节性变化与水文负荷造成的地表形变有关。
4) 尼泊尔地区冬季地震的数量较夏季季风期多,结合库仑应力的变化推测,夏季季风期的降水对断层的长期运动趋势产生扰动,使库仑应力得到一定程度的释放,进而对地震活动产生抑制作用,影响了地震发生的时间。
致谢: 感谢日本统计数理研究所庄建仓教授和中国台湾中央研究院许雅儒研究员对本文给予的帮助,本文部分图片使用GMT软件绘制,在此一起表示感谢。
| [1] |
Panda D, Kundu B, Gahalaut V K, et al. Seasonal Modulation of Deep Slow-Slip and Earthquakes on the Main Himalayan Thrust[J]. Nature Communications, 2018, 9(1): 4140 DOI:10.1038/s41467-018-06371-2
(  0) 0) |
| [2] |
丁一航, 黄丁发, 师悦龄, 等. 利用GPS和GRACE分析四川地表垂向位移变化[J]. 地球物理学报, 2018, 61(12): 4774-4778 (Ding Yihang, Huang Dingfa, Shi Yueling, et al. Determination of Vertical Surface Displacements in Sichuan Using GPS and GRACE[J]. Chinese Journal of Geophysics, 2018, 61(12): 4774-4778)
(  0) 0) |
| [3] |
Zou R, Wang Q, Freymueller J T, et al. Seasonal Hydrological Loading in Southern Tibet Detected by Joint Analysis of GPS and GRACE[J]. Sensors, 2015, 15(12): 30525-30528 DOI:10.3390/s151229815
(  0) 0) |
| [4] |
Dam T V, Wahr J, Milly P C D, et al. Crustal Displacements due to Continental Water Loading[J]. Geophysical Research Letters, 2001, 28(4): 651-654 DOI:10.1029/2000GL012120
(  0) 0) |
| [5] |
Larochelle S, Gualandi A, Chanard K, et al. Identification and Extraction of Seasonal Geodetic Signals due to Surface Load Variations[J]. Journal of Geophysical Research: Solid Earth, 2018, 123: 11031-11047
(  0) 0) |
| [6] |
熊福文, 朱文耀. 长江三角洲地区地形变特征的GPS监测和分析[J]. 地球物理学报, 2007, 50(6): 1719-1730 (Xiong Fuwen, Zhu Wenyao. Land Deformation Monitoring by GPS in the Yangtze Delta and the Measurements Analysis[J]. Chinese Journal of Geophysics, 2007, 50(6): 1719-1730 DOI:10.3321/j.issn:0001-5733.2007.06.012)
(  0) 0) |
| [7] |
Birhanu Y, Bendick R. Monsoonal Loading in Ethiopia and Eritrea from Vertical GPS Displacement Time Series[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(10): 7231-7238 DOI:10.1002/2015JB012072
(  0) 0) |
| [8] |
Kreemer C, Zaliapin I. Spatio-Temporal Correlation Between Seasonal Variations in Seismicity and Horizontal Dilatational Strain in California[J]. Geophysical Research Letters, 2018, 45(1)
(  0) 0) |
| [9] |
Bettinelli P, Avouac J P, Flouzat M, et al. Seasonal Variations of Seismicity and Geodetic Strain in the Himalaya Induced by Surface Hydrology[J]. Earth and Planetary Science Letters, 2008, 266(3-4): 332-344 DOI:10.1016/j.epsl.2007.11.021
(  0) 0) |
| [10] |
Bollinger L, Perrier F, Avouac J P, et al. Seasonal Modulation of Seismicity in the Himalaya of Nepal[J]. Translated World Seismology, 2008, 34(8): 402-420
(  0) 0) |
| [11] |
孙晋东. TRMM卫星降雨数据在南流江流域径流模拟中的应用研究[D].南宁: 广西大学, 2018 (Sun Jindong. Research on Hydrologic Evaluation of TRMM Multi-Satellite Precipitation Analysis over Nanliujiang Basin[D]. Nanning: Guangxi University, 2018) http://cdmd.cnki.com.cn/Article/CDMD-10593-1018132833.htm
(  0) 0) |
| [12] |
Kansakar S R, Hannah D M, Gerrard J, et al. Spatial Pattern in the Precipitation Regime of Nepal[J]. International Journal of Climatology, 2004, 24(13): 1645-1659 DOI:10.1002/joc.1098
(  0) 0) |
| [13] |
Stiphout T, Zhuang J, Marsan D. Seismicity Declustering[J]. Community Online Resource for Statistical Seismicity Analysis, 2012(10): 1-25
(  0) 0) |
| [14] |
Shen Z K, Wang M, Zeng Y H, et al. Optimal Interpolation of Spatially Discretized Geodetic Data[J]. Bulletin of the Seismological Society of America, 2015, 105(4): 2117-2127 DOI:10.1785/0120140247
(  0) 0) |
| [15] |
King G C P, Stein R S, Lin J. Static Stress Changes and the Triggering of Earthquakes[J]. Bulletin of the Seismological Society of America, 1994, 84(3)
(  0) 0) |
2. Institute of Earth Sciences, Academia Sinica, 128 Section 2 of Yanjiuyuan Road, Taipei 11529, China
 2020, Vol. 40
2020, Vol. 40


