2. 中国测绘科学研究院,北京市莲花池西路28号,100830;
3. 浙江省测绘科学技术研究院,杭州市文二西路,310000
根据弹性地球负荷响应理论,地球上的大气负荷会对地面产生压力,使地面点发生形变,并且会使地面重力发生变化[1],但这种影响相较于其他的影响较弱,在很长一段时间内没有被考虑。近年来,随着大地测量技术及物理观测技术的快速发展[2],超导重力仪的观测精度及SLR、GPS等基线的解算精度得到大幅度提升,大气对于地面观测的影响逐渐显露出来,由大气压引起的地面垂直形变可达±2.5 cm,对地面重力的影响达到±10 μGal。因此,如果想要获得高精度的大地测量结果,大气负荷的影响不可忽略。
目前,已有学者针对大气负荷进行深入研究,其中最常用的计算大气负荷的方法为负荷格林函数法和球谐函数法[3-4]。Rabbel等[5]根据负荷理论得到大气影响的具体数值,大气负荷对垂直形变的影响高达±2.5 cm,对水平位移的影响为±2.5 mm;孙和平等[6]提出褶积分区方案,指出重力观测中约90%为台站周围50 km区域贡献的;王伟等[7]采用移去-恢复法结合全球大气模型及气象站数据,计算出大气负荷对三峡地区地壳形变及重力场的影响。
本文利用浙江及周边地区气象站数据及全球大气负荷模型,基于负荷理论,采用移去-恢复法计算浙江地区大气负荷对形变场及重力场的影响。
1 理论方法 1.1 负荷形变理论和公式地表环境质量变化产生的负荷变化可用等效水高hw表示,其规格化负荷球谐展开式为[7-9]:
| $ \begin{array}{l} {h_w}\left( {\varphi , \lambda } \right) = R\sum\limits_{n = 1}^N {\sum\limits_{m = 0}^n {\left[ {\Delta C_{nm}^q\cos m\lambda } \right.} } + \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta S_{nm}^q\sin m\lambda } \right]{{\bar P}_{nm}}\left( {\sin \lambda } \right) \end{array} $ | (1) |
式中,(φ, λ)为地面点的纬经度,ΔCnmq、ΔSnmq为n阶m次规格化负荷球谐系数,Pnm(t)为n阶m次规格化缔合Legendre函数。
地面大地高变化可表示为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}\Delta r\left( {\varphi , \lambda } \right) = 3\frac{{{\rho _w}}}{{{\rho _e}}}\frac{{GM}}{{\gamma R}}\sum\limits_{n = 1}^N {{{h'}_{2n + 1}}} \cdot \\ \sum\limits_{m = 0}^n {\left( {\Delta C_{nm}^q\cos m\lambda + {\kern 1pt} \Delta S_{nm}^q\sin m\lambda } \right)} {{\bar P}_{nm}}\left( {\sin \varphi } \right) \end{array} $ | (2) |
由地球重力理论可知,地面重力位变化gt(φ, λ)也可用引力位系数表示为:
| $ \begin{array}{l} {g_t}\left( {\varphi , \lambda } \right) = - 3\frac{{{\rho _w}}}{{{\rho _e}}}\sum\limits_{n = 1}^N {\frac{{n + 2{{h'}_n} - \left( {n + 1} \right){{k'}_n}}}{{2n + 1}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}\sum\limits_{m = 0}^n {\left( {\Delta C_{nm}^q\cos m\lambda + {\kern 1pt} \Delta S_{nm}^q\sin m\lambda } \right)} {{\bar P}_{nm}}\left( {\sin \varphi } \right) \end{array} $ | (3) |
大气负荷对垂线偏差的影响分为2个分量,即NS分量ξ(θ, λ)和EW分量η(θ, λ),其表达式为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}\zeta \left( {\theta , \lambda } \right) = 3\frac{{GM}}{{\gamma {R^2}}}\frac{{{\rho _w}}}{{{\rho _e}}}\sum\limits_{n = 1}^N {\frac{{1 + 2{{k'}_n} - {{h'}_n}}}{{2n + 1}}} \cdot \\ \sum\limits_{m = 0}^n {\left( {\Delta C_{nm}\cos m\lambda + {\kern 1pt} \Delta S_{nm}^{}\sin m\lambda } \right)} \frac{{\partial {{\bar P}_{nm}}\left( {\cos \theta } \right)}}{{\partial \theta }} \end{array} $ | (4) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}n\left( {\theta , \lambda } \right) = 3\frac{{GM}}{{\gamma {R^2}\sin \theta }}\frac{{{\rho _w}}}{{{\rho _e}}}\sum\limits_{n = 1}^N {\frac{{1 + 2{{k'}_n} - {{h'}_n}}}{{2n + 1}}} \cdot \\ \sum\limits_{m = 0}^n {\left( {\Delta C_{nm}^{}\cos m\lambda + {\kern 1pt} \Delta S_{nm}^{}\sin m\lambda } \right)} {{\bar P}_{nm}}\left( {\cos \theta } \right) \end{array} $ | (5) |
大气负荷对水平形变的影响也分为2个分量,即EW分量e(θ, λ)和NS分量n(θ, λ),其表达式为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}e\left( {\theta , \lambda } \right) = 3\frac{{GM}}{{\gamma {R^{}}\sin \theta }}\frac{{{\rho _w}}}{{{\rho _e}}}\sum\limits_{n = 1}^N {\frac{{{{l'}_n}}}{{2n + 1}}} \cdot \\ \sum\limits_{m = 0}^n {m\left( {\Delta C_{nm}^{}\cos m\lambda - {\kern 1pt} \Delta S_{nm}^{}\sin m\lambda } \right)} {{\bar P}_{nm}}\left( {\cos \theta } \right)\\ \end{array} $ | (6) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}n\left( {\theta , \lambda } \right) = 3\frac{{GM}}{{\gamma {R^{}}\sin \theta }}\frac{{{\rho _w}}}{{{\rho _e}}}\sum\limits_{n = 1}^N {\frac{{{{l'}_n}}}{{2n + 1}}} \cdot \\ \sum\limits_{m = 0}^n {m\left( {\Delta C_{nm}^{}\cos m\lambda + {\kern 1pt} \Delta S_{nm}^{}\sin m\lambda } \right)} {{\bar P}_{nm}}\left( {\cos \theta } \right) \end{array} $ | (7) |
式(2)~式(7)中,h′n、l′n和k′n为负荷Love数,ρw≈103 kg·m-3为水的密度,ρe≈5.5×103 kg·m-3为固体地球的平均密度,G为万有引力常数,M为地球总质量,γ为地面平均重力。
等效水高变化引起的地面站点位置或地面重力参数变化ΔΘ(φ, λ)还可采用负荷格林函数积分表示为通用形式[8]:
| $ \Delta \Theta \left( {\varphi , \lambda } \right) = G{\rho _w}\int {\int_S^{} {\frac{{{h_w}\left( {\varphi ', \lambda '} \right)}}{L}} } G\left( \psi \right){\rm{d}}S $ | (8) |
式中,(φ′, λ′)为地面积分流动点,dS为地面流动积分面元,L为地面或地球外部计算点与地面流动点间的空间距离,ψ为球面角距,G(ψ)为通用的负荷格林函数。
1.2 移去-恢复法移去-恢复法经常被应用于重力场及大地水准面拟合的研究[10],利用移去-恢复法计算大气负荷的影响能够充分利用区域高精度大气压数据,减小单独使用全球模型计算时的误差,更准确地表现出大气负荷对区域影响的变化特征。在进行移去-恢复法计算中需要将积分区域分成近区S0与远区S-S0这2个部分,近区被积等效水高参数的积分形式可表示为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt}\Delta \Theta \left( {\varphi , \lambda } \right)\left| {_{{S_0}}} \right. = G{\rho _w}\int {\int_S^{} {\frac{{{h_w}\left( {\varphi ', \lambda '} \right)}}{L}} } G\left( \psi \right){\rm{d}}S + \\ \int {\int_{{S_0}}^{} {\left[ {\Delta {h_w}\left( {\varphi ', \lambda '} \right) - \Delta {h_{wM}}\left( {\varphi ', \lambda '} \right)} \right]} } G\left( {{\psi _0}} \right){\rm{d}}S + {\varepsilon _M} \end{array} $ | (9) |
其中, Δhw(φ ', λ')对应的简化形式为:
| $ \begin{array}{l} \Delta \Theta \left( {\varphi , \lambda } \right)\left| {_{{S_0}}} \right. = \Delta {\Theta _M}\left( {\varphi , \lambda } \right)\left| {_{{S_0}}} \right. + \\ \int {\int_{{S_0}}^{} {{\rm{d}}{h_w}\left( {\varphi ', \lambda '} \right)G\left( {{\psi _0}} \right){\rm{d}}S + {\varepsilon _M}} } \end{array} $ | (10) |
式中,Δhw(φ′, λ′)为区域等效水高,ΔhwM(φ′, λ′)为全球大气模型等效水高,hw(φ′, λ′)=Δhw(φ′, λ′)-ΔhwM(φ′, λ′)为残差等效水高。
利用浙江及周边地区气象站数据,结合全球大气负荷模型计算高精度区域负荷的步骤为:
1) 将全球大气压变化数据模型扣除基准值,构建全球等效水高变化格网数字模型,利用球谐函数对其进行计算,得到全球等效水高规格化球谐系数模型。
2) 将各气象站数据扣除基准值后,利用全球等效水高规格化球谐系数模型计算等效水高模型值。从区域等效水高变化格网中移去等效水高模型值,得到区域剩余等效水高格网模型,再采用克里金插值法将站点残差等效水高格网化,利用负荷格林函数积分法确定大气压引起的区域剩余负荷地壳形变场及重力场变化格网的时间序列。
3) 将区域剩余负荷影响格网与全球负荷影响模型值格网相加,得到区域高精度非潮汐负荷影响格网数字模型,包括各种类型的大气负荷形变场与重力场变化格网的数字模型,得到大气负荷的间接影响。
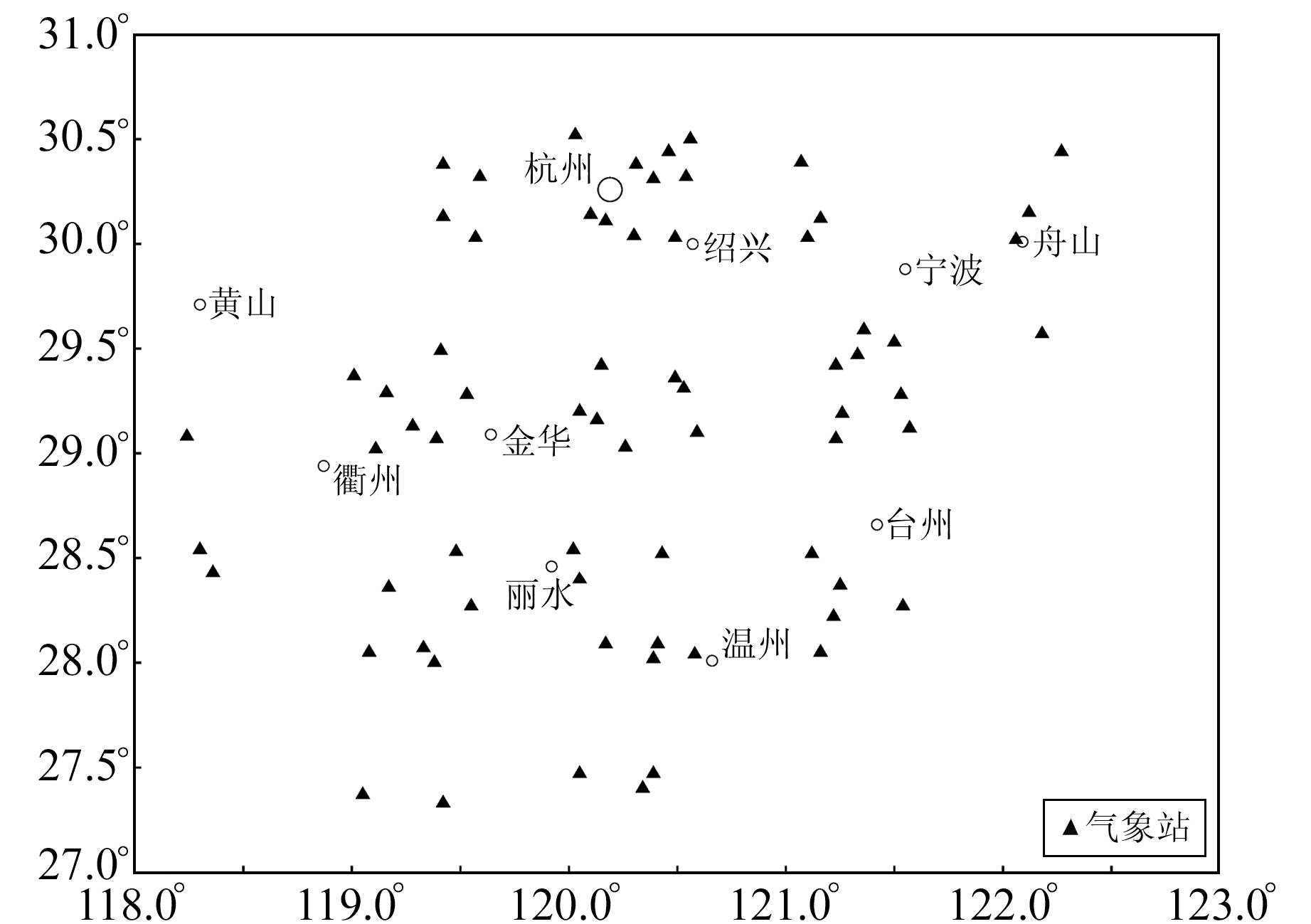
2 数据获取及处理 2.1 研究范围本文的研究范围为118°~123°E、27°~31°N,研究区内气象站分布见图 1。
|
图 1 气象站分布 Fig. 1 Meteorological station distribution |
1) 全球大气压模型。从欧洲中期天气预报中心下载2015-01~2017-12分辨率为0.25°的全球大气压月变化格网模型[11],将数据扣除基准之后按照1 hPa=10.2 mm的换算关系将大气压数据转换为等效水高。根据式(1)进行球谐展开,得到等效水高球谐系数,根据研究区内气象站点坐标求得每月等效水高作为模型值。
2) 气象站资料。从国家气象信息中心下载浙江丽水、温州地区周边98个气象站的中国地面气候资料月值数据,将其扣除基准之后转化为等效水高,再扣除第1)步中求得的模型值,得到残差等效水高,并利用克里金插值法生成2015-01~2017-12大气压变化格网时间序列。
3 大气负荷形变场计算与分析 3.1 大气负荷对地壳形变影响为方便计算,选择2015-01~03的平均值作为基准值扣除,将格林函数计算的区域剩余大气负荷影响格网与利用球谐系数计算出的全球大气负荷影响模型值格网相加,得到大气负荷对区域地壳形变的总影响。本文计算时间跨度为2015-01~2017-12、空间分辨率为1′×1′的大气负荷影响。
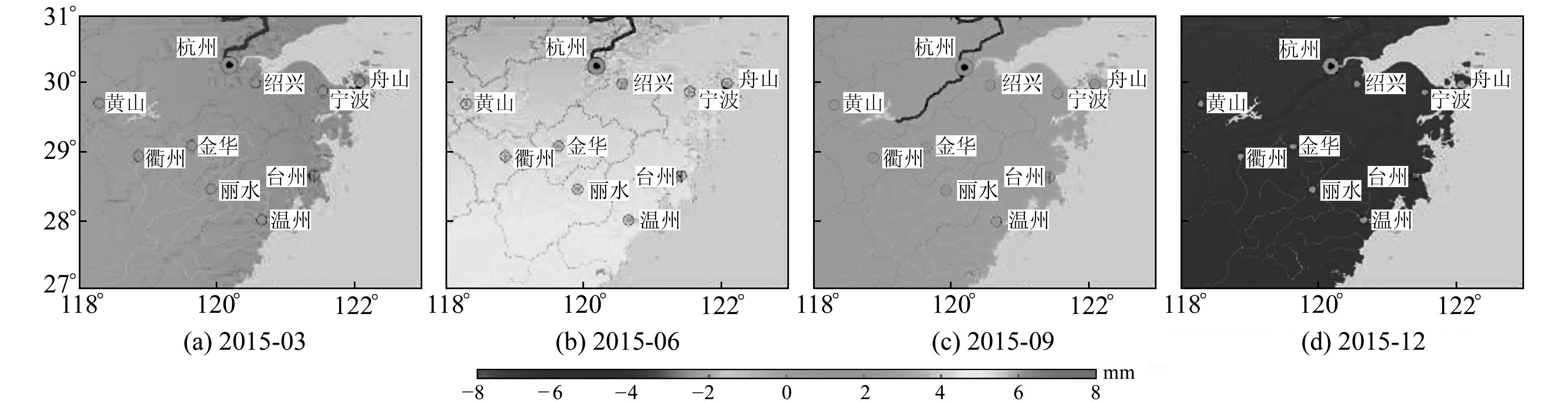
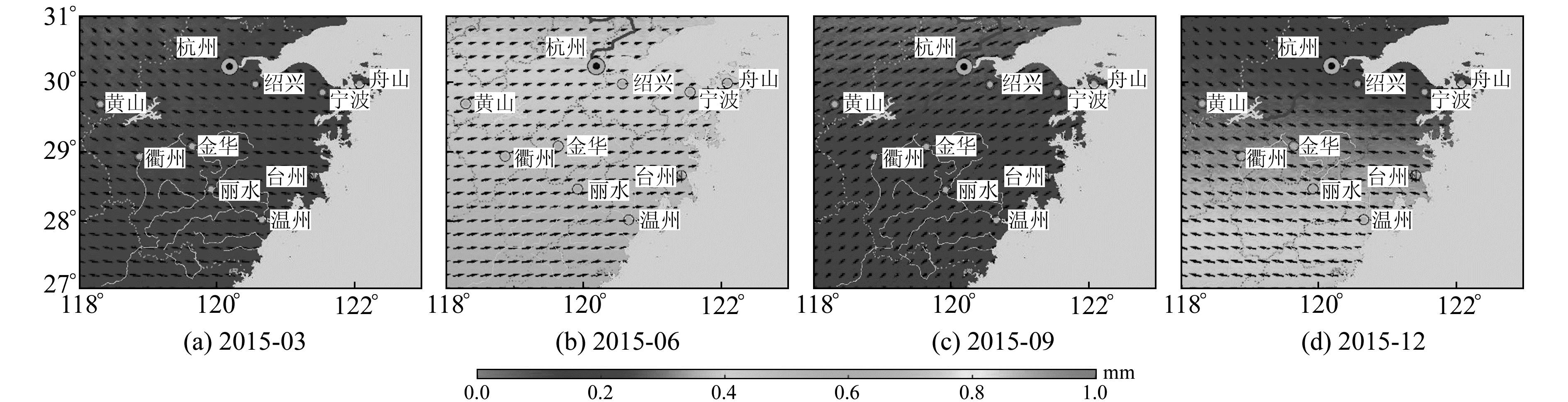
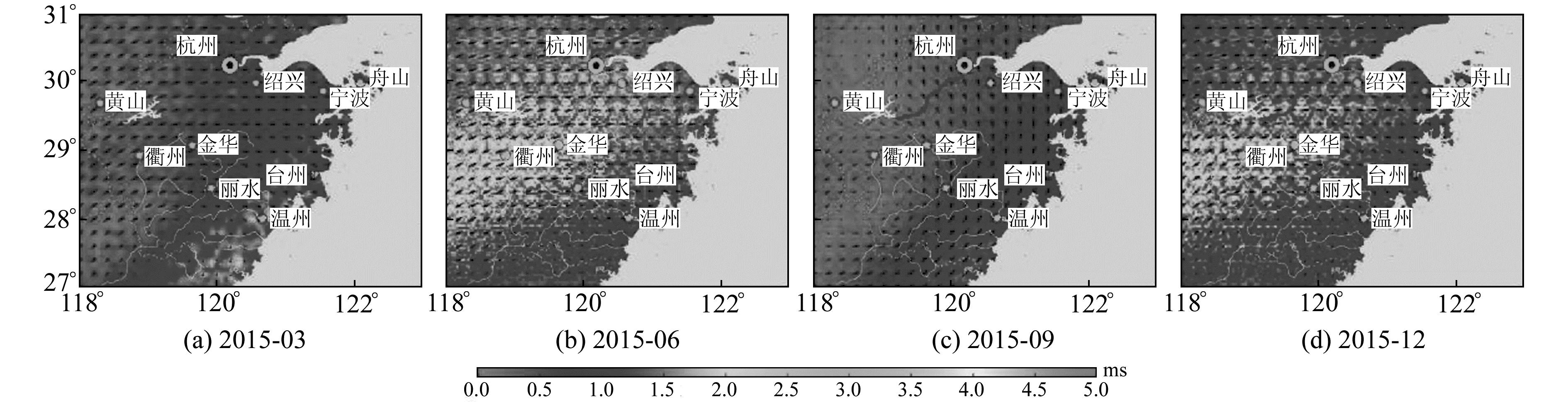
由于大气压的变化与季节降雨等有明显的相关性,本文选取2015-03、06、09、12等4个月的大气负荷对形变场影响的空间分布进行分析。图 2为大气负荷引起的浙江区域地壳垂直形变变化,由图可知,大气负荷引起的地壳垂直形变的年变化幅度超过15 mm。图 3为大气负荷引起的水平形变变化,可以看出,水平形变相较于垂直形变变化较小,年变化幅度为1 mm左右,仅为垂直形变的1/10。图 4为大气负荷对垂线偏差的影响,可以看出,大气负荷对垂线偏差的影响较小,年变化幅度为5 ms。总体而言,大气负荷对形变场的影响具有明显的周期性。
|
图 2 2015年大气负荷引起的垂直形变的变化 Fig. 2 Change of vertical deformation caused by atmospheric load in 2015 |
|
图 3 2015年大气负荷引起的水平形变的变化 Fig. 3 Changes of horizontal deformation caused by atmospheric load in 2015 |
|
图 4 2015年大气负荷引起的垂线偏差变化 Fig. 4 Variation of vertical deviationcaused byatmosphericloadin 2015 |
计算大气负荷对地面重力的影响需要分为2个部分进行:1)通过大气导纳方法计算出大气负荷的直接影响[11];2)采用移去-恢复法计算出大气负荷对地面重力的间接影响。将两者结果相加,即得到大气负荷对地面重力的总影响。
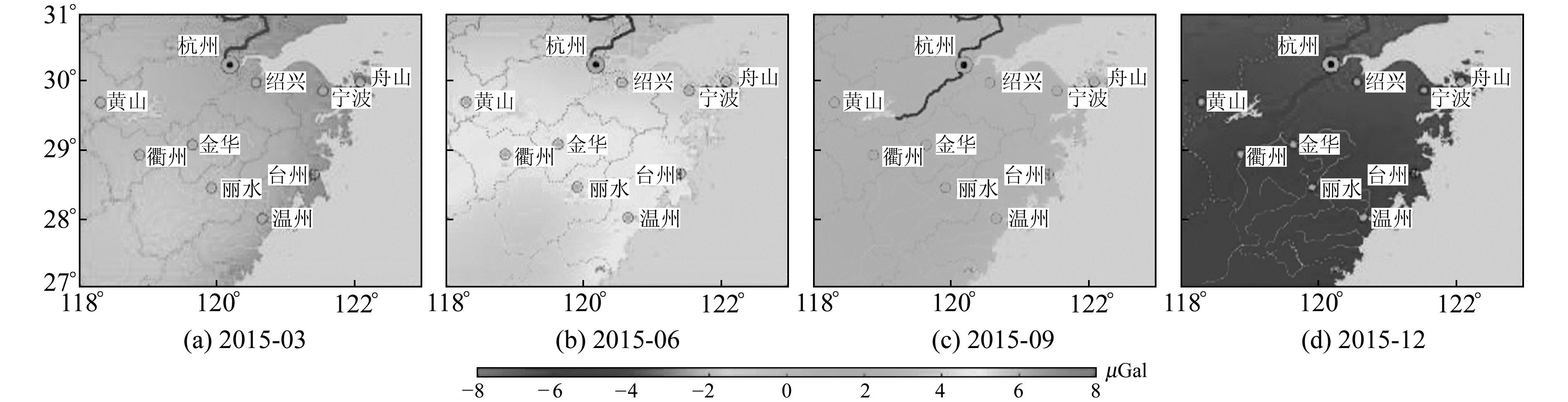
图 5为大气负荷对重力场的影响,由图可知,大气负荷对地面重力影响的年变化幅度可达12 μGal,其变化趋势与形变及大气压的变化相反,即地面重力会随着大气压的增大而减小。
|
图 5 2015年大气负荷引起的浙江区域地面重力变化 Fig. 5 Thechange ofregional gravityin Zhejiang cansed byatmosphericloadin 2015 |
表 1统计了浙江地区大气负荷形变场、重力场的标准差及年变化幅度等信息,可以看出,大气负荷对地壳形变及地面重力变化影响存在明显的年周期性,在长周期占优势的信号中,仅统计其标准差不足以看出其变化特征,因此本文对年变化幅度也进行了统计,年变化幅度大约为准周期振幅的2倍。由此可知,大气负荷对垂直形变的影响较大,对水平形变及垂线偏差变化的影响较小,对地面重力的影响最小为6.82 μGal,最大为-7.13 μGal。
|
|
表 1 2015~2017年浙江区域大气负荷形变场及重力场影响统计 Tab. 1 Statistics of the influence of atmospheric load deformation field and gravity field in Zhejiang province from 2015 to 2017 |
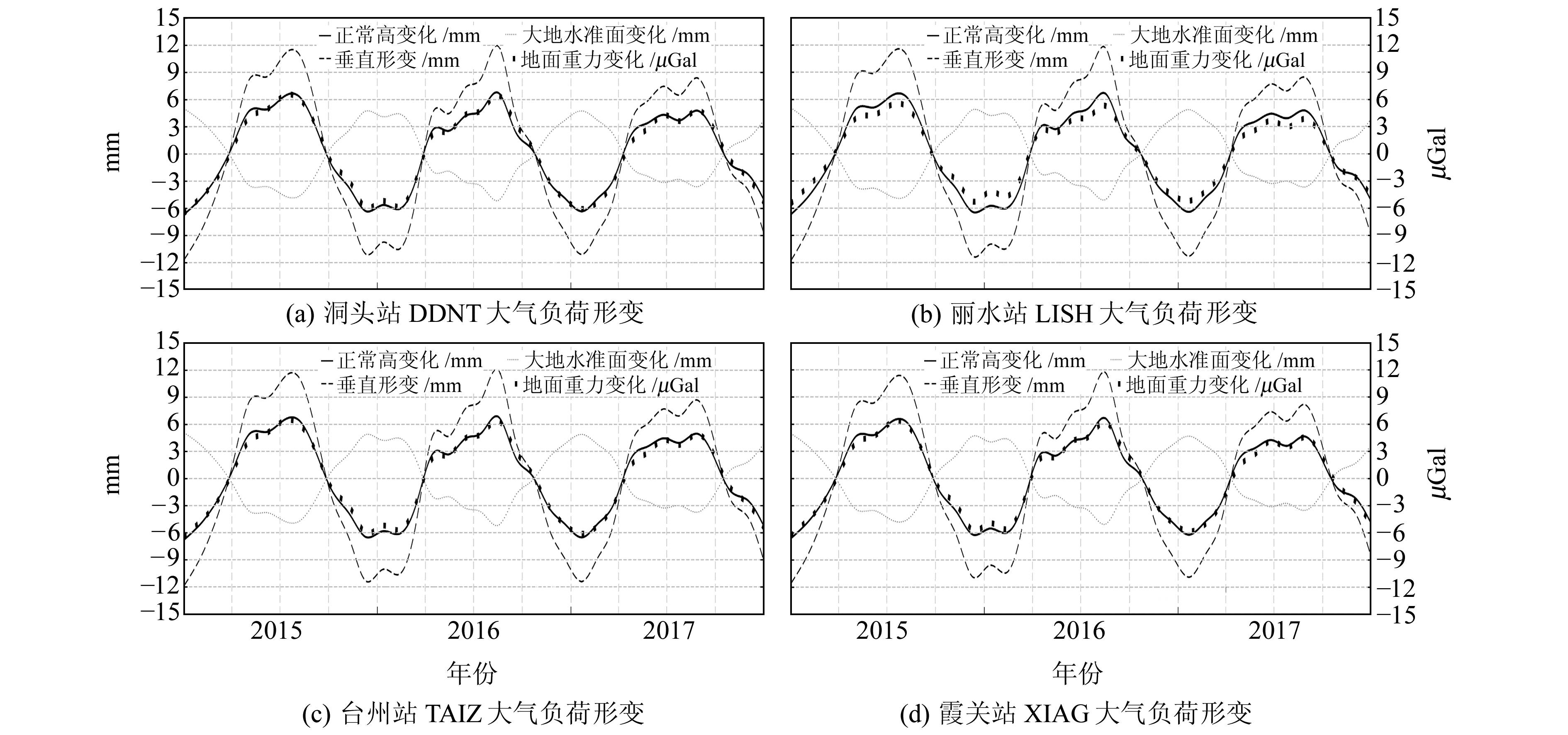
选取研究区内台州(TAIZ)、霞关(XIAG)、洞头(DONT)、丽水(LISH)4个连续运行参考站(CORS),采用球面克里金插值法将大气负荷对各种形变的影响插值到选取的CORS站点,结果见图 6。从图 6可以看出,大气负荷的影响具有年周期性和季节性特征。从季节性角度来看,大气负荷对形变的影响在每年的夏季最大、冬季最小,与中国大陆地区的气候特征有明显的联系,同时与浙江地区夏季降雨丰富、气温高等地理特征相匹配。
|
图 6 CORS站处大气负荷对各种形变的影响 Fig. 6 Effect of CORS outgoing atmospheric load on various deformations |
为精确计算大气负荷对浙江地区地壳垂直形变及地面重力的影响,本文以浙江地区的实测气象站数据为研究对象,采用负荷格林函数积分公式,基于全球大气负荷球谐系数模型的移去-恢复法,计算了浙江地区大气负荷形变场及重力场格网。结果表明,大气负荷具有明显的周期性特征,其对地壳垂直形变的影响较大,对水平形变及垂线偏差的影响较小,均呈正相关性;大气负荷对地面重力的影响与形变相反,呈负相关性。
| [1] |
许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010 (Xu Houze. Solid Earth Tides[M]. Wuhan: Hubei Science and Technology Press, 2010)
(  0) 0) |
| [2] |
罗少聪, 孙和平, 徐建桥. 大气负荷引起的重力与位移变化理论计算的精度估计[J]. 测绘学报, 2001, 30(4): 309-315 (Luo Shaocong, Sun Heping, Xu Jianqiao. Theoretical Computation in the Precision Estimation of the Change in Gravity and Displacements due to Atmospheric Loading[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 309-315 DOI:10.3321/j.issn:1001-1595.2001.04.007)
(  0) 0) |
| [3] |
Longman I M. A Green's Function for Determining the Deformation of the Earth under Surface Mass Loads: 2. Computations and Numerical Results[J]. Journal of Geophysical Research, 1963, 68(2): 485-496 DOI:10.1029/JZ068i002p00485
(  0) 0) |
| [4] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797
(  0) 0) |
| [5] |
Rabbel W, Zschau J. Static Deformations and Gravity Changes at the Earth's Surface due to Atmospheric Loading[J]. Journal of Geophysics: Zeitschrift fuer Geophysik, 1985, 56: 81-89
(  0) 0) |
| [6] |
孙和平, 罗少聪. 大气重力信号的理论计算及其检测[J]. 地球物理学报, 1998, 41(5): 634-641 (Sun Heping, Luo Shaocong. Theoretical Computation and Detection of the Atmospheric Gravity Signals[J]. Acta Geophysica Sinica, 1998, 41(5): 634-641 DOI:10.3321/j.issn:0001-5733.1998.05.006)
(  0) 0) |
| [7] |
王伟, 章传银, 杨强, 等. 大气负荷对区域地壳形变和重力变化的影响分析[J]. 武汉大学学报:信息科学版, 2018, 43(9): 1302-1308 (Wang Wei, Zhang Chuanyin, Yang Qiang, et al. Impact of Atmospheric Pressure Loading on Regional Crustal Deformation and Gravity Change[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1302-1308)
(  0) 0) |
| [8] |
王海涛, 王斌, 王伟, 等. 大气负荷对新疆地区地壳形变和地面重力变化的影响[J]. 大地测量与地球动力学, 2019, 39(2): 189-194 (Wang Haitao, Wang Bin, Wang Wei, et al. Research on the Effect of Atmospheric Pressure Load on Crust Deformation and Gravity Change in Xinjiang Redion[J]. Journal of Geodesy and Geodynamics, 2019, 39(2): 189-194)
(  0) 0) |
| [9] |
党亚民, 章传银, 陈俊勇, 等. 现代大地测量基准[M]. 北京: 测绘出版社, 2015 (Dang Yamin, Zhang Chuanyin, Chen Junyong, et al. Modern Geodetic Datum[M]. Beijing: Surveying and Mapping Press, 2015)
(  0) 0) |
| [10] |
郭春喜, 宁津生, 陈俊勇, 等. 珠峰地区似大地水准面精化与珠峰顶正高的确定[J]. 地球物理学报, 2008, 51(1): 101-107 (Guo Chunxi, Ning Jinsheng, Chen Junyong, et al. Improvement of Regional Quasi-Geoid in Qomolangma(Mt. Everest) and Determination of Orthometric Elevation[J]. Chinese Journal of Geophysics, 2008, 51(1): 101-107 DOI:10.3321/j.issn:0001-5733.2008.01.013)
(  0) 0) |
| [11] |
Ray R D, Ponte R M. Barometric Tides from ECMWF Operational Analyses[J]. Annales Geophysicae, 2003, 21(8): 1897-1910 DOI:10.5194/angeo-21-1897-2003
(  0) 0) |
| [12] |
孙和平, 罗少聪. 中国及其邻区地表气象数据预处理和网格化数值结果分析[J]. 地壳形变与地震, 1998, 18(3): 51-56 (Sun Heping, Luo Shaocong. Preprocessing of the Surface Meteorological Data in China and Its Neighbor Area and Analysis of the Gridding Numerical Results[J]. Crustal Deformation and Earthquake, 1998, 18(3): 51-56)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China;
3. Zhejiang Institute of Surveying and Mapping Science and Technology, West-Wen'er Road, Hangzhou 310000, China
 2020, Vol. 40
2020, Vol. 40


