2. 河海大学地球科学与工程学院,南京市佛城西路8号,211100
建立高精度的边坡变形预测模型具有重大的理论和实际意义[1]。目前边坡位移预测模型主要有回归分析、灰色理论、神经网络等[2-5],但由于边坡变形受到多种因素的影响[6],监测到的位移时间序列具有高度复杂性和非线性的特征,传统预测模型的预测精度受到一定限制。神经网络模型的应用使得预测精度在一定程度上有所提高,但神经网络模型容易陷入局部最优,同时模型参数难以确定[7]。支持向量机(support vector machine, SVM)基于统计原理,以结构最小化为原则,能够较好地解决非线性、小样本和高维度的边坡位移预测问题[8]。但支持向量机模型的预测精度受到核函数的影响,常用的径向基核函数并不能高精度地拟合任意函数。而小波核函数基于小波理论构造,具有局部化和多层次的优点,且有更强的函数逼近能力[9],目前已在许多领域有不错的应用[10-11]。考虑到边坡变形数据的非线性特征,单时间序列并不能充分地描述数据信息,而相空间重构(phase space reconstruction, PSR)理论[12]能够将边坡位移时间序列扩展到高维空间,从而充分显示时间序列中蕴藏的信息。
基于此,本文首先通过相空间重构理论中的C-C方法确定延迟时间和嵌入维数,重构原始边坡位移时间序列,同时构造符合核函数条件的小波核函数,以改进传统支持向量机模型,将重构后的多维数据作为小波支持向量机(waveletsupport vector machine, WSVM)的输入数据,最终建立PSR-WSVM模型,并将模型应用到边坡位移预测中, 对模型的有效性进行评价。
1 PSR-WSVM模型 1.1 相空间重构理论(PSR)当嵌入维数m≥2d+1(d为动力系统维数)时,相空间与原系统在拓扑意义上是等价的。对于具体的边坡位移时间序列{xi, i=1, 2, …, n},时间延迟τ和嵌入维数m确定后重构的相空间为:
| $ \begin{array}{l} X\left\{ {{X_i}\left| {{Xi} = \left[ {{x_i}, {x_{i + \tau }} \cdots , {x_{i + \left( {m - 1} \right)\tau }}} \right]} \right.} \right., \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {i = 1, 2, \cdots M} \right\} \end{array} $ | (1) |
式中,m为嵌入维数, τ为时间延迟, M=N-(m-1)τ为相空间中相点个数,N为边坡位移时间序列长度。
从式(1)可以看出,相空间重构的关键步骤为时间延迟τ和嵌入维数m的确定,目前关于两者的确定主要有2种观点:一种认为时间延迟τ和嵌入维数m的确定是独立的,不具有任何相关性,比如确定时间延迟τ的自相关法和互信息法等及确定嵌入维数m的G-P算法和虚假最邻近法等;另一种认为时间延迟τ和嵌入维数m的确定是相互影响的,比如时间窗口法和C-C法。本文选取C-C法确定时间延迟τ和嵌入维数m。
1.2 支持向量机支持向量机(SVM)基于统计原理,以结构最小化为原则,可以很好地解决小样本、非线性和高维度的问题,通过引入核函数将输入数据映射到高维特征空间,从而将非线性问题转化为线性问题,并且通过核函数避免了高维特征空间中的点积运算。SVM的目标函数为:
| $ f\left( x \right) = \mathit{\boldsymbol{w}} \cdot \phi \left( x \right) + b $ | (2) |
式中,w为权向量; b为偏置常数。考虑到拟合误差,引入回归损失函数理念避免过拟合的问题,通过解算最终可得拟合函数为:
| $ f\left( x \right) = \sum\limits_{i = 1}^n {\left( {{\alpha _i} - {\alpha _i}^*} \right)} K\left( {{x_i}, x} \right) + b $ | (3) |
式中,αi和αi*为拉格朗日乘子;K(xi, x)为核函数。支持向量机常用的核函数为径向基核函数,其具有良好的映射性能,但当使用径向基核函数去逼近某些复杂函数时,结果通常并不令人满意。小波核函数继承了小波分析对信号逐步细化分析的特征,能够以较高精度拟合复杂函数,而传统核函数并不具备该特征。为了提升支持向量机的泛化能力,本文采用基于Morlet小波构造的小波核函数(式(4))作为SVM模型的核函数[13],构造小波核函数支持向量机(WSVM):
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K\left( {{x_i}, x} \right) = \\ \prod\limits_{i = 1}^d {\cos } \left( {\frac{{1.75\left( {{x_i} - x} \right)}}{\sigma }} \right)\exp \left( { - \frac{{{{\left( {{x_i} - x} \right)}^2}}}{{2{\sigma ^2}}}} \right) \end{array} $ | (4) |
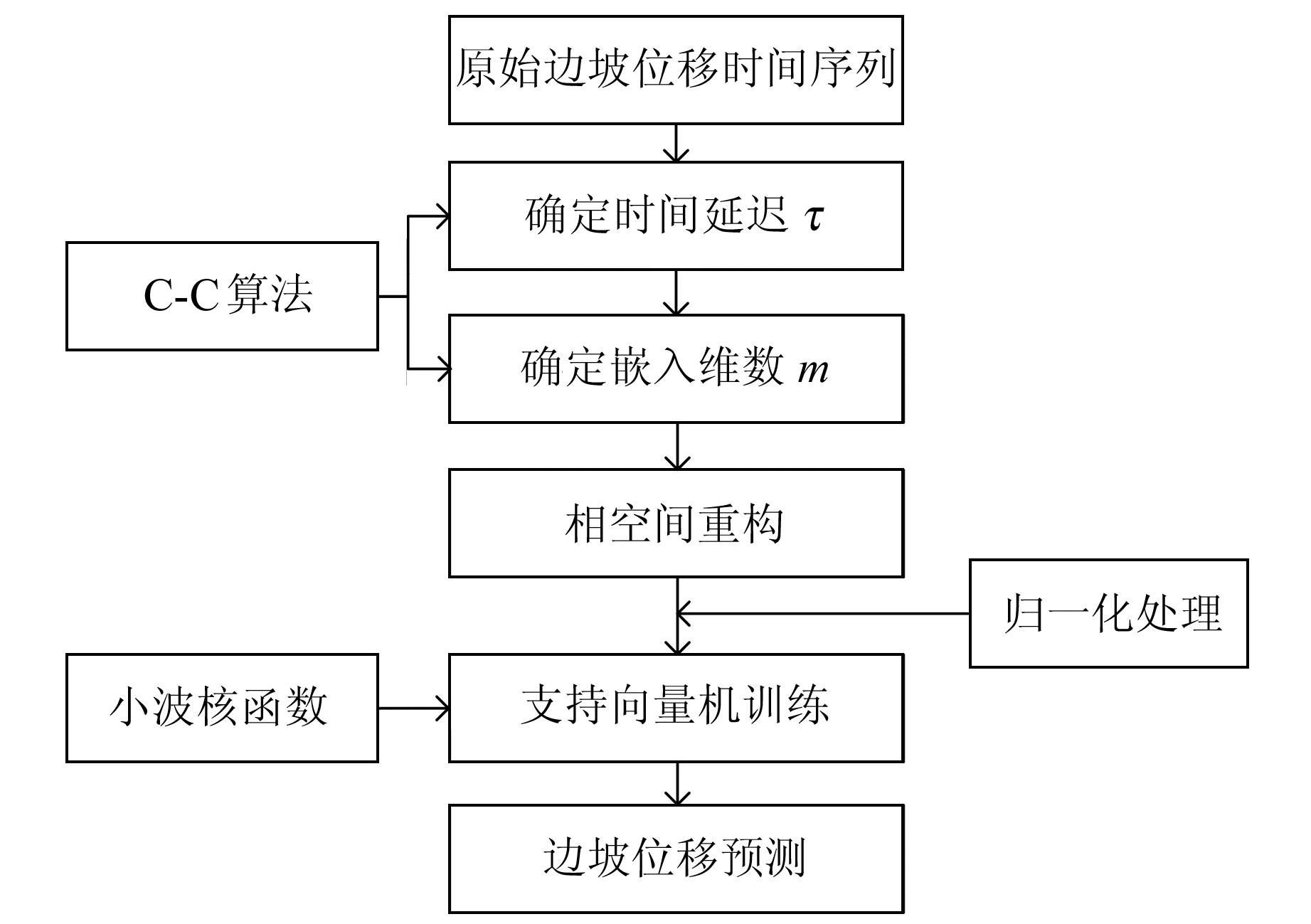
设原始边坡位移时间序列为{xi, i=1, 2, …, n},首先通过C-C算法确定时间延迟τ和嵌入维数m,然后重构原始边坡位移时间序列,同时构造符合核函数条件的Morlet小波核函数作为支持向量机模型的核函数,建立小波核函数支持向量机(WSVM)模型。经过相空间重构之后,边坡位移时间序列由一维形式转换成多维形式,将多维形式数据经过归一化后作为小波核函数支持向量机的输入数据,最终建立PSR-WSVM模型。PSR-WSVM模型流程如图 1所示。
|
图 1 PSR-WSVM模型流程 Fig. 1 PSR-WSVM model flow chart |
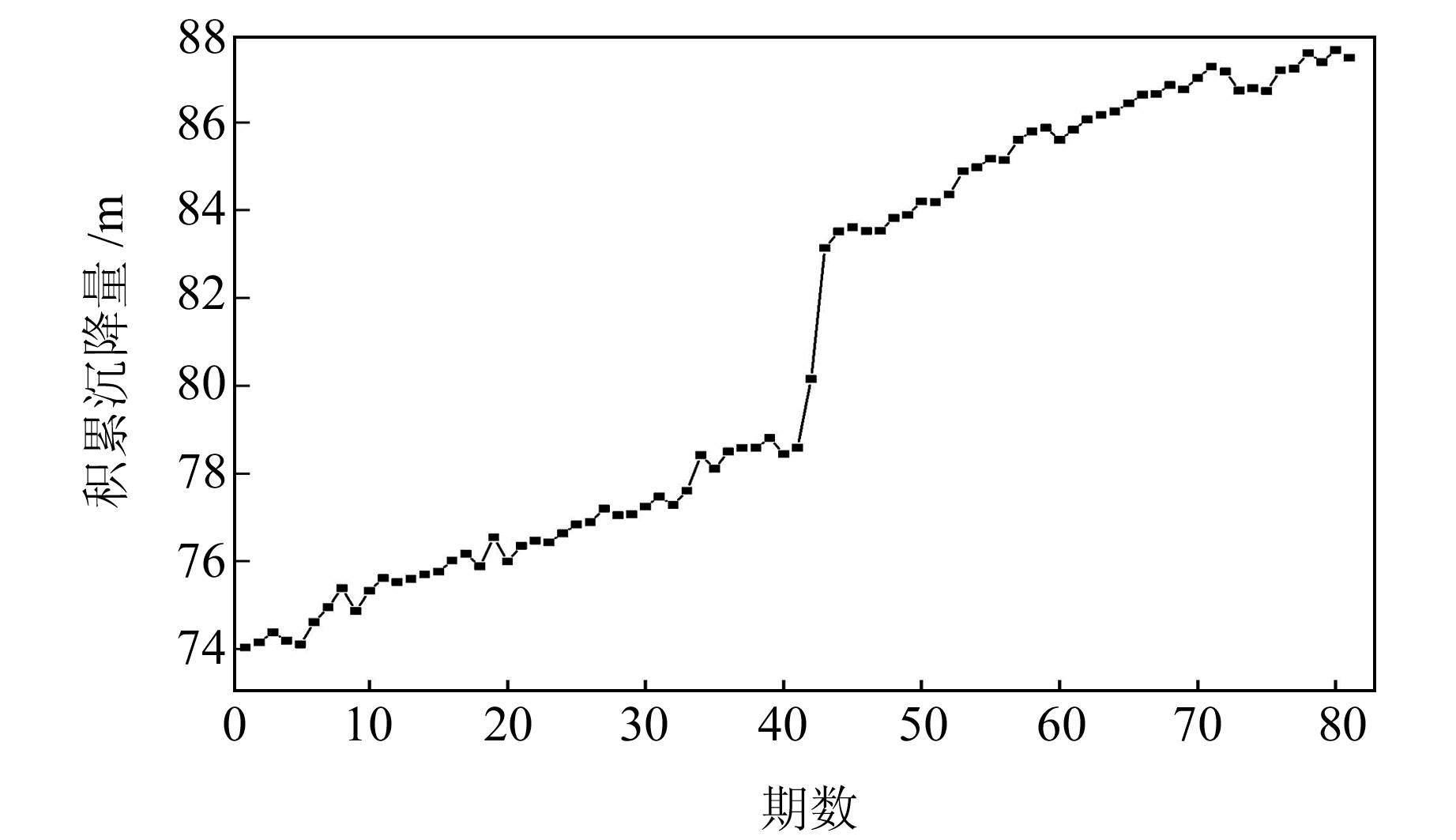
以江西某钨矿边坡监测数据为例,收集边坡8号监测点2014-04-01~06-20的81期沉降监测数据,数据间隔为1 d,监测点累积沉降变化曲线见图 2。以前76期数据作为训练数据,后5期数据作为测试数据,验证模型边坡位移预测的有效性。
|
图 2 监测点累积沉降变化曲线 Fig. 2 Cumulative settlement curve of monitoring point |
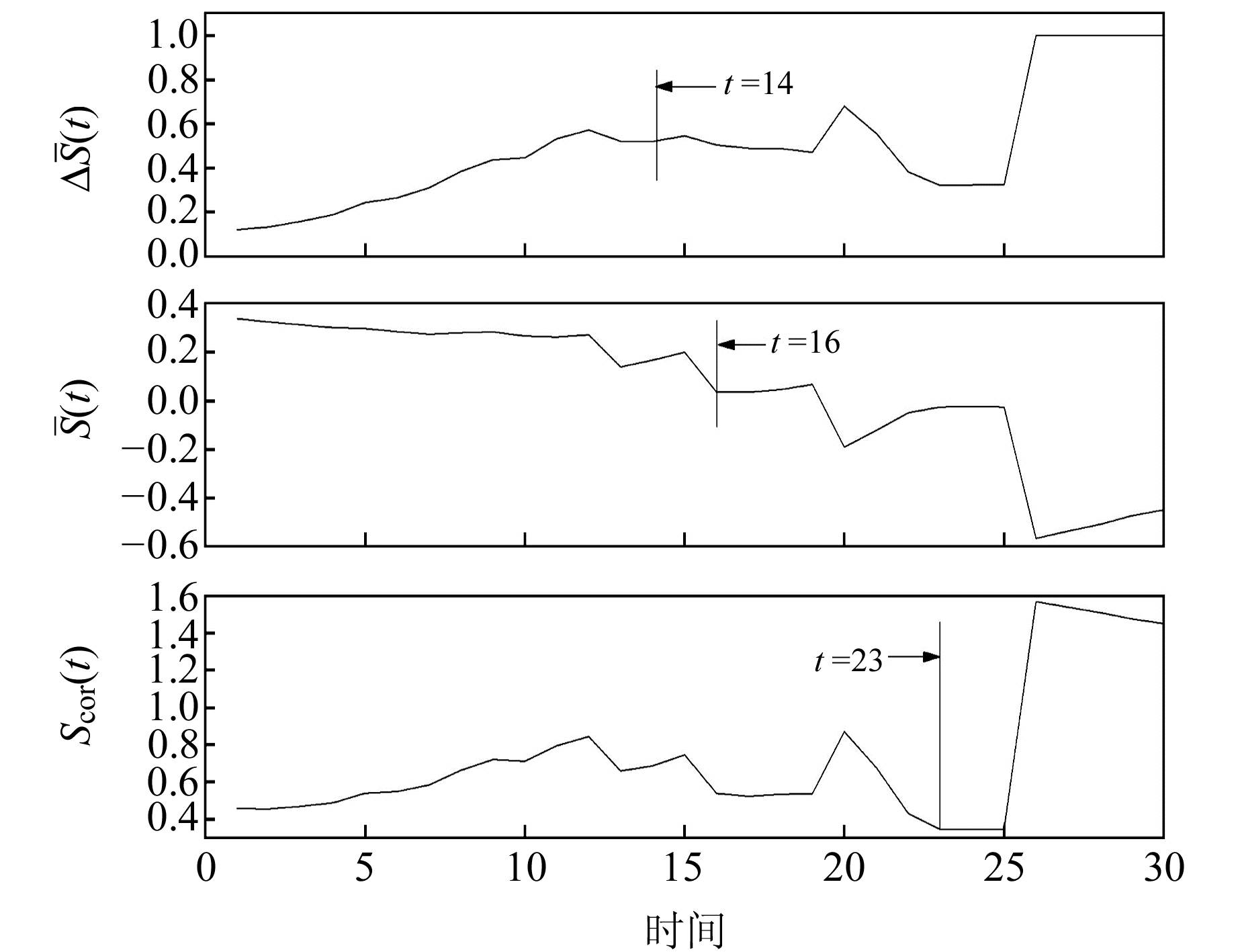
C-C算法可以同时确定时间延迟τ和嵌入维数m的原因在于tw=(m-1)t, tw为时间窗口,也就意味着只要确定了时间延迟τ和时间窗口tw,嵌入维数m也随之确定。算法运行过程中计算3个统计量(ΔS(t)、S(t)和Scor(t))随时间的变化情况,具体计算过程见文献[14]。通常选择ΔS(t)的第1个局部极小值点和S(t)的第1个零点中的较小值作为时间延迟τ,Scor(t)的全局最小值作为时间窗口tw。本文C-C算法统计量计算结果见图 3,由图可知,时间延迟τ取14较为合适,时间窗口tw取23,根据三者的关系可确定嵌入维数m取3较为合适。
|
图 3 C-C算法统计量计算结果 Fig. 3 Statistical calculation results of C-C algorithm |
根据所确定的时间延迟τ和嵌入维数m对原始边坡位移时间序列进行相空间重构,并将其作为WSVM模型的输入对边坡位移进行预测。为验证本文PSR-WSVM模型的有效性,将预测结果与传统支持向量机(SVM)模型、小波核函数支持向量机(WSVM)模型和基于相空间重构的支持向量机(PSR-SVM)模型的预测结果进行对比,其中SVM模型和PSR-SVM模型的核函数采用的是径向基核函数,具体结果见表 1。采用平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error, MAPE)和均方根误差(root mean square error, RMSE)作为模型预测结果的评价指标,具体评价结果见表 1。
|
|
表 1 模型预测结果及评价指标 Tab. 1 Model prediction results and evaluation indicators |
由表 1可知,PSR-WSVM模型预测结果的各项精度评价指标均优于其他3种模型(SVM、WSVM和PSR-SVM),相较于传统SVM模型,各项精度评价指标均有明显的提升,MAE、MAPE和RMSE都提升了70%以上。因此可以证实,本文建立的PSR-WSVM模型具有较高的边坡位移预测精度,一定程度上也表明通过相空间重构确实能够充分挖掘出原始边坡位移时间序列的隐藏信息,而小波核函数能通过平移产生一组平方可积空间内的完备正交基,进而实现对复杂非线性函数的高精度拟合。
3 结语将相空间重构理论、小波核函数和支持向量机理论进行有机结合,建立用于边坡位移预测的PSR-WSVM模型,并通过工程实例对模型的可行性进行评价,得到以下结论:
1) 将相空间重构理论应用于边坡位移时间序列,通过C-C算法确定时间延迟τ和嵌入维数m,将一维数据形式转换为高维形式,能够充分挖掘出边坡位移时间序列的隐藏信息,为边坡位移预测奠定基础。
2) 构造小波核函数作为支持向量机的核函数,通过工程实例验证了小波核函数具有较高的函数逼近能力,能够提高支持向量机模型的泛化能力和预测精度。
3) 工程实例测试结果显示,PSR-WSVM模型的预测精度优于SVM模型、WSVM模型和PSR-SVM模型,因此PSR-WSVM模型在边坡预测领域具有一定的应用前景,能够为边坡位移预测提供参考。
| [1] |
刘小生, 秦志强. 基于相空间重构的GA-SVR组合模型边坡位移预测研究[J]. 大地测量与地球动力学, 2017, 37(10): 1024-1028 (Liu Xiaosheng, Qin Zhiqiang. GA-SVR Combined Model for Forecasting Landside Displacement: Study on Based on Phase-Space Reconstruction[J]. Journal of Geodesy and Geodynamics, 2017, 37(10): 1024-1028)
(  0) 0) |
| [2] |
张安兵, 高井祥, 刘新侠, 等. 边坡变形时序非线性判定及混沌预测研究[J]. 中国安全科学学报, 2008, 18(4): 55-60 (Zhang Anbing, Gao Jingxiang, Liu Xinxia, et al. Nonlinear Test and Chaotic Prediction of Slope Deformation Sequences[J]. China Safety Science Journal, 2008, 18(4): 55-60 DOI:10.3969/j.issn.1003-3033.2008.04.008)
(  0) 0) |
| [3] |
李胜, 韩永亮. 基于MFOA-SVR露天矿边坡变形量预测研究[J]. 中国安全生产科学技术, 2015, 11(1): 11-16 (Li Sheng, Han Yongliang. Research on Forecasting of Slope Deformation in Open-Pit Mine Based on MFOA-SVR[J]. Journal of Safety Science and Technology, 2015, 11(1): 11-16)
(  0) 0) |
| [4] |
冯腾飞, 刘小生, 钟钰, 等. 基于IABC优化LSSVR的变形预测研究[J]. 大地测量与地球动力学, 2019, 39(1): 98-102 (Feng Tengfei, Liu Xiaosheng, Zhong Yu, et al. Research on Deformation Prediction Based on LSSVR Optimized by IABC[J]. Journal of Geodesy and Geodynamics, 2019, 39(1): 98-102)
(  0) 0) |
| [5] |
刘文生, 张燕凤, 张贺然, 等. 灰色系统模型在露天矿边坡沉降预测中的应用[J]. 辽宁工程技术大学学报:自然科学版, 2014, 33(12): 1608-1612 (Liu Wensheng, Zhang Yanfeng, Zhang Heran, et al. Application of Grey System Model in the Deformation Prediction of the Open-Pit Mine Slope[J]. Journal of Liaoning Technical University:Natural Science, 2014, 33(12): 1608-1612)
(  0) 0) |
| [6] |
罗亦泳, 姚宜斌, 王亚. 基于MRVM的多输出边坡变形预测模型[J]. 大地测量与地球动力学, 2017, 37(12): 1239-1242 (Luo Yiyong, Yao Yibin, Wang Ya. Multi Output Slope Deformation Model Based on Multi-output Relevance Vector Machine[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1239-1242)
(  0) 0) |
| [7] |
罗亦泳, 张立亭, 鲁铁定, 等. 露天矿边坡变形预测的协同进化多核相关向量机模型[J]. 中国安全科学学报, 2016, 26(11): 110-114 (Luo Yiyong, Zhang Liting, Lu Tieding, et al. Forecasting of Slope Deformation in Open-Pit Mine Based on CEPSO-MK-RVM[J]. China Safety Science Journal, 2016, 26(11): 110-114)
(  0) 0) |
| [8] |
Vapnik V N. The Nature of Statistical Learning Theory[M]. New York: Springer, 1995
(  0) 0) |
| [9] |
高春钦.基于PSO优化小波支持向量机的岩土力学参数反演[D].昆明: 昆明理工大学, 2018 (Gao Chunqin. Inversion of Rock and Soil Mechanics Parameters Based on PSO Optimization Wavelet Support Vector Machine[D].Kunming: Kunming University of Science and Technology, 2018) http://cdmd.cnki.com.cn/Article/CDMD-10674-1018715707.htm
(  0) 0) |
| [10] |
李春祥, 殷潇. 基于小波支持向量机的非高斯空间风压内外插预测[J]. 上海交通大学学报, 2018, 52(11): 1516-1523 (Li Chunxiang, Yin xiao. Interpolation Prediction and Extrapolation Prediction of Non-Gaussian Spatial Wind Pressure Using LSSVM with Wavelet Kernel Function[J]. Journal of Shanghai Jiaotong University, 2018, 52(11): 1516-1523)
(  0) 0) |
| [11] |
迟恩楠, 李春祥, 郑晓芬. 基于小波和乘法混合核函数LSSVM的顺风向非高斯空间风压预测[J]. 振动与冲击, 2017, 36(9): 116-121 (Chi Ennan, Li Chunxiang, Zheng Xiaofen. Forecasting Non-Gaussian Spatial Along-Wind Pressure Using Wavelet Kernel and Multiplicative Mixed Kernel Functions Based LSSVM[J]. Journal of Vibration and Shock, 2017, 36(9): 116-121)
(  0) 0) |
| [12] |
Niu M F, Gan K, Sun S L, et al. Application of Decomposition-Ensemble Learning Paradigm with Phase Space Reconstruction for Day-Ahead PM2.5 Concentration Forecasting[J]. Journal of Environmental Management, 2017, 196: 110-118
(  0) 0) |
| [13] |
Yang J, Tian J W, Liu J, et al. SVM Algorithm Based on Wavelet Kernel Function for Medical Image Segmentation[C]. International Symposium on Multispectral Image Processing and Pattern Recognition. International Society for Optics and Photonics, Yichang, 2009
(  0) 0) |
| [14] |
陆振波, 蔡志明, 姜可宇. 基于改进的C-C方法的相空间重构参数选择[J]. 系统仿真学报, 2007, 19(11): 2527-2529 (Lu Zhenbo, Cai Zhiming, Jiang Keyu. Determination of Embedding Parameters for Phase Space Reconstruction Based on Improved C-C Method[J]. Journal of System Simulation, 2007, 19(11): 2527-2529 DOI:10.3969/j.issn.1004-731X.2007.11.036)
(  0) 0) |
2. School of Earth Sciences and Engineering, Hohai University, 8 West-Focheng Road, Nanjing 211100, China
 2020, Vol. 40
2020, Vol. 40


