2011-03-11日本本州岛东海岸附近海域发生MW9.0地震,美国宇航局ARIA团队利用日本的GEONET网络GPS观测数据迅速给出地震近场-中场的同震位移。随后,国内学者利用“中国地壳运动观测网络”(简称网络工程)项目一期(CMONOCⅠ)和二期(CMONOCⅡ)的GPS连续站观测资料解算并获取了地震在中国大陆东部产生的同震位移场[1-3],结果表明,中国华北和东北地区向E移动了mm至cm级,尤其东北地区产生了最大35 mm的水平形变量。以近场-中场同震位移为约束可以反演断层破裂的空间分布,中国境内的远场同震位移同样有助于认识地震的发震构造与滑动分布。有学者利用震后1~2 a的GPS观测资料揭示日本岛存在非常明显的E向运动的震后变形,并分析认为震后变形的动力学机制为上地幔粘弹性松弛或应力变化驱动的余滑,抑或是两者的综合作用[4-6]。Shao等[7]对中国境内的网络工程项目二期11个GPS连续站震后1.5 a的位移时间序列进行分析,发现地震在中国东北地区也产生了较为明显的震后变形。中国大陆的远场震后位移有助于区分此次地震震后变形的物理机制,对了解地震后地壳应力、应变及余震演化具有重要意义,但目前对中国东部地区的同震和震后变形研究中GPS台站的空间分布较稀疏,震后观测累积时间较短。
本文利用收集到的空间分布较密的网络工程项目一、二期及中国气象局(CMA)的GPS站观测数据,获取日本东北大地震在中国东部地区产生的同震位移场,并利用网络工程1999~2017年GPS连续站和流动站观测资料建立震后松弛模型,构建一个半动态参考基准模型,即线性趋势运动速率、同震位移和震后松弛形变模型,以修正地震对地壳运动变形的影响,对维护高精度的区域连续运行参考站(CORS)坐标系统和区域现代大地基准具有重要意义。另外,震后形变位移场的时空变化可用来约束反演岩石圈及上地幔介质的流变性质。
1 数据来源及处理方法本文收集了1999~2017年网络工程项目一、二期共280个GPS连续站和2 000余个GPS流动站的观测数据及中国气象局290个GPS连续站在地震前后各4 d的观测数据。对于地震发生当天的GPS观测数据,只使用UTC 06:00之后的观测值(地震发生于UTC 05:46),GPS站分布见图 1。

|
图 1 中国东部GPS连续站和流动站分布 Fig. 1 Continuous and campaign mode GPS stations in eastern China |
数据处理采用双差模式,由GAMIT/GLOBK软件完成。首先由GAMIT获得GPS站的位置参数及其方差-协方差矩阵的单日松弛解,采用双频消电离层组合消除电离层1阶影响,用FES2004模型改正海洋潮汐负荷影响(以地球质心(CM)为中心)。再采用GPT模型对对流层天顶延迟进行改正,每个测站1 h估计1个天顶方向对流层延迟参数,映射函数采用VMF1模型,同时由GAMIT采用相同策略解算全球均匀分布的近100个ITRF框架点的GPS观测数据。最后利用GLOBK将区域站和全球ITRF站的所有单日松弛解组合在一起,用7参数转换方法获取GPS站在ITRF2008参考框架下的位移时间序列。
GPS站3个分量的坐标时间序列均可表示为[8]:
| $ \begin{array}{l} y\left( {{t_i}} \right) = a + b{t_i} + c\sin \left( {2{\rm{ \mathsf{ π} }}{t_i}} \right) + d\cos \left( {2{\rm{ \mathsf{ π} }}{t_i}} \right) + \\ e\sin \left( {{\rm{4 \mathsf{ π} }}{t_i}} \right) + f\cos \left( {{\rm{4 \mathsf{ π} }}{t_i}} \right) + \sum\limits_{j = 1}^{{n_g}} {{g_j}H\left( {{y_i} - {t_{{\rm{eq}}}}} \right)} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^{{n_k}} {{k_j}\log } \left( {1 + \frac{{{t_i} - {t_{{\rm{eq}}}}}}{\tau }} \right)H\left( {{t_i} - {t_{{\rm{eq}}}}} \right) + v \end{array} $ | (1) |
式中,a为初始位置,b为长期运动速率,c、d、e和f分别为年周期和半年周期项系数,gj为同震位移变化,kj为震后对数松弛振幅,τ为震后对数松弛时间,ti为观测时刻,teq为地震发生时刻,H为阶梯函数,v为误差。如果没有地震发生,GPS站的坐标时间序列仅用式(1)中的前6项表示,发生地震后就需考虑式中第7和第8项的同震及震后变形影响。
2 线性趋势运动对GPS连续站位移时间序列,利用式(1)中前6项基于最小二乘方法估计线性速率、年周期及半年周期项参数和中误差,对不定期观测的GPS流动站位移时间序列,无法拟合出准确的周期项参数,只估计线性速率及中误差。网络工程项目一期的GPS站于1999年开始观测,二期的GPS流动站于2009年实施第1期观测,GPS连续站则于2010年开始观测。对网络工程项目二期的GPS观测数据,仅利用2011年日本东北大地震震前的资料来估计线性运动速率是不可靠的,因此先利用一期1999~2010年的GPS观测数据估计线性运动速率,再利用球面小波基多尺度分解方法[9]进行内插,得出二期GPS站的长期运动速率。
值得注意的是,研究区的GPS站1999~2010年的观测数据受2004年印尼苏门答腊9.1级地震和2008年四川汶川8.0级地震的影响。对于苏门答腊地震,本文采用Chlieh等[10]提供的同震破裂模型基于球体位错理论[11]计算同震变形,结果表明,苏门答腊地震在华南地区产生的同震位移为4~10 mm,需从GPS位移时间序列中进行改正,本文忽略该地震震后变形的影响。汶川地震影响了龙门山断裂带以东600 km范围内的地壳变形[12],所以对受汶川地震影响的台站采用1999~2007年的位移时间序列拟合线性运动速率,其余则利用1999~2010年的GPS位移时间序列拟合。图 2为研究区的GPS水平运动速度场(相对ITRF2008)。
|
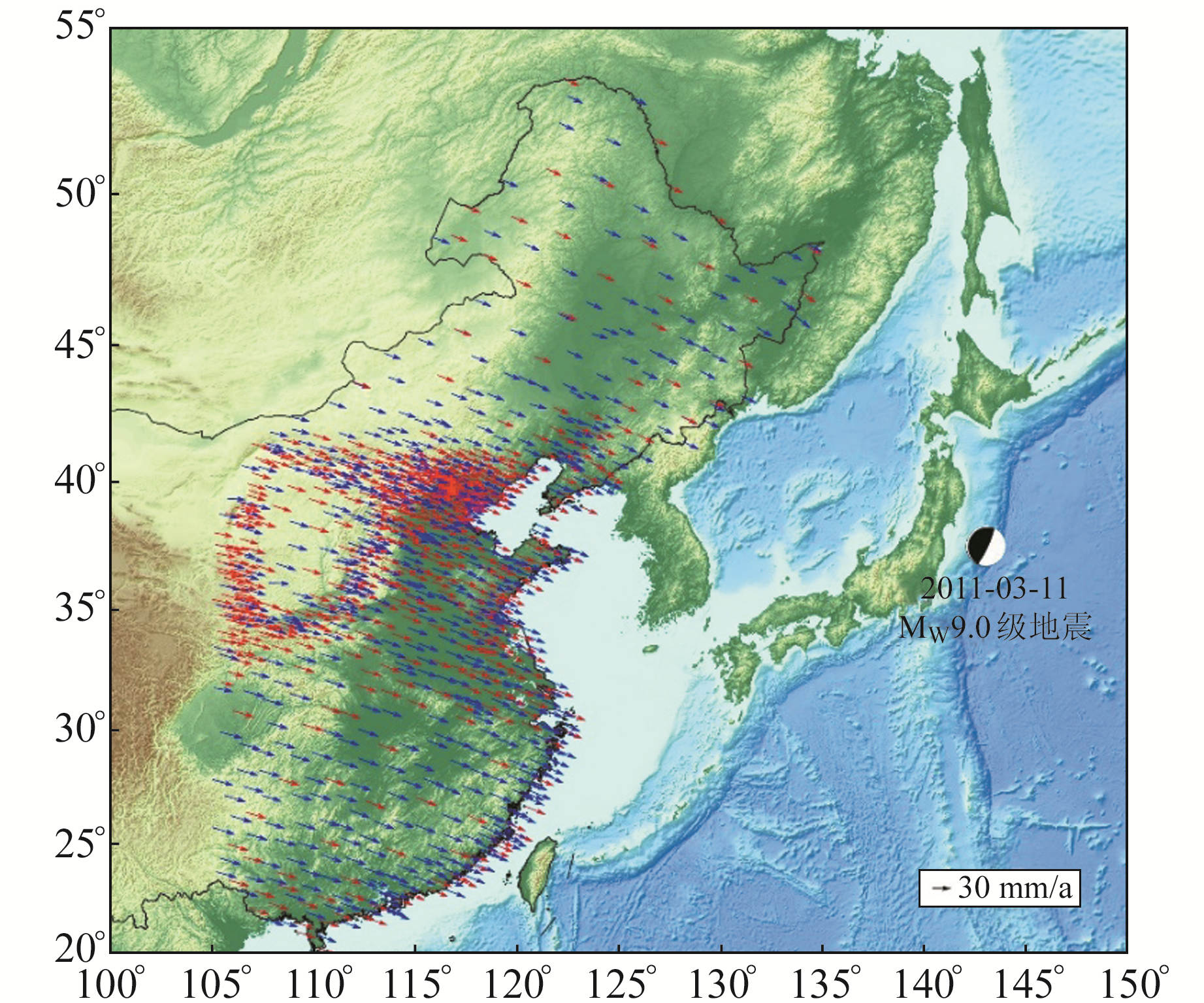
红色为网络工程项目一期 GPS 速率, 蓝色为内插出的网络工程项目二期 GPS 速率 图 2 中国东部地区GPS水平运动速度场 Fig. 2 GPS velocity field within eastern China |
假设GPS站点的线性运动速率在地震前后保持不变,取地震后4 d(含地震当天)的E向位移加权平均值,减去地震前4 d的E向位移加权平均值,即得到地震在远场产生的E向同震位移场,同样的方法可得N向同震位移场。图 3给出估算的同震位移大于3 mm的结果,可以看出,日本东北大地震使得中国大陆向东运动,产生的远场同震位移往西至鄂尔多斯地块西缘一带,除东北和华北地区存在明显的同震变形外,华南地块也有约5 mm的E向运动。
|
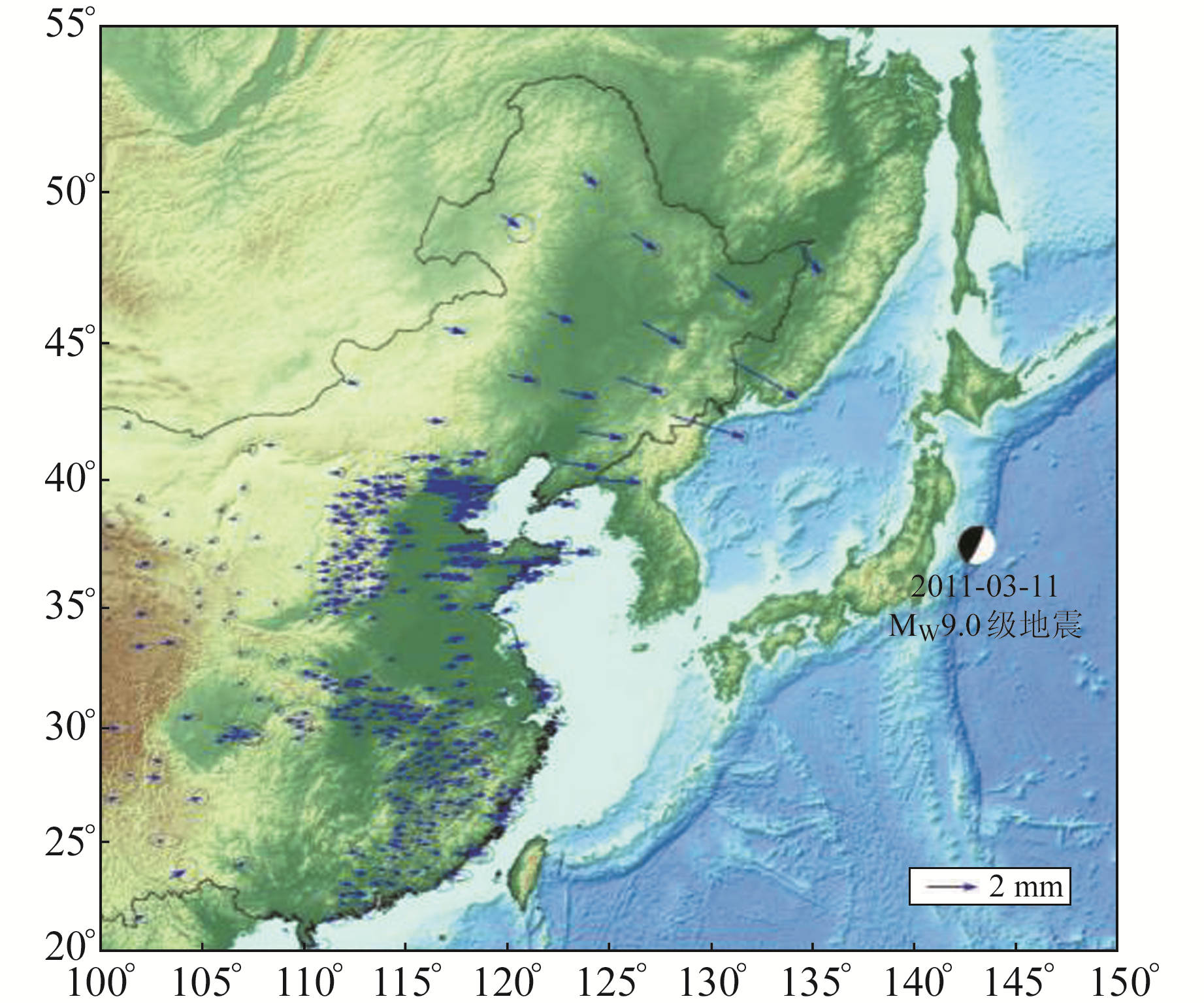
误差椭圆代表95%置信水平 图 3 2011年日本东北大地震在中国东部产生的同震位移场 Fig. 3 Coseismic displacements within eastern China following the 2011 Tohoku-Oki earthquake, Japan |
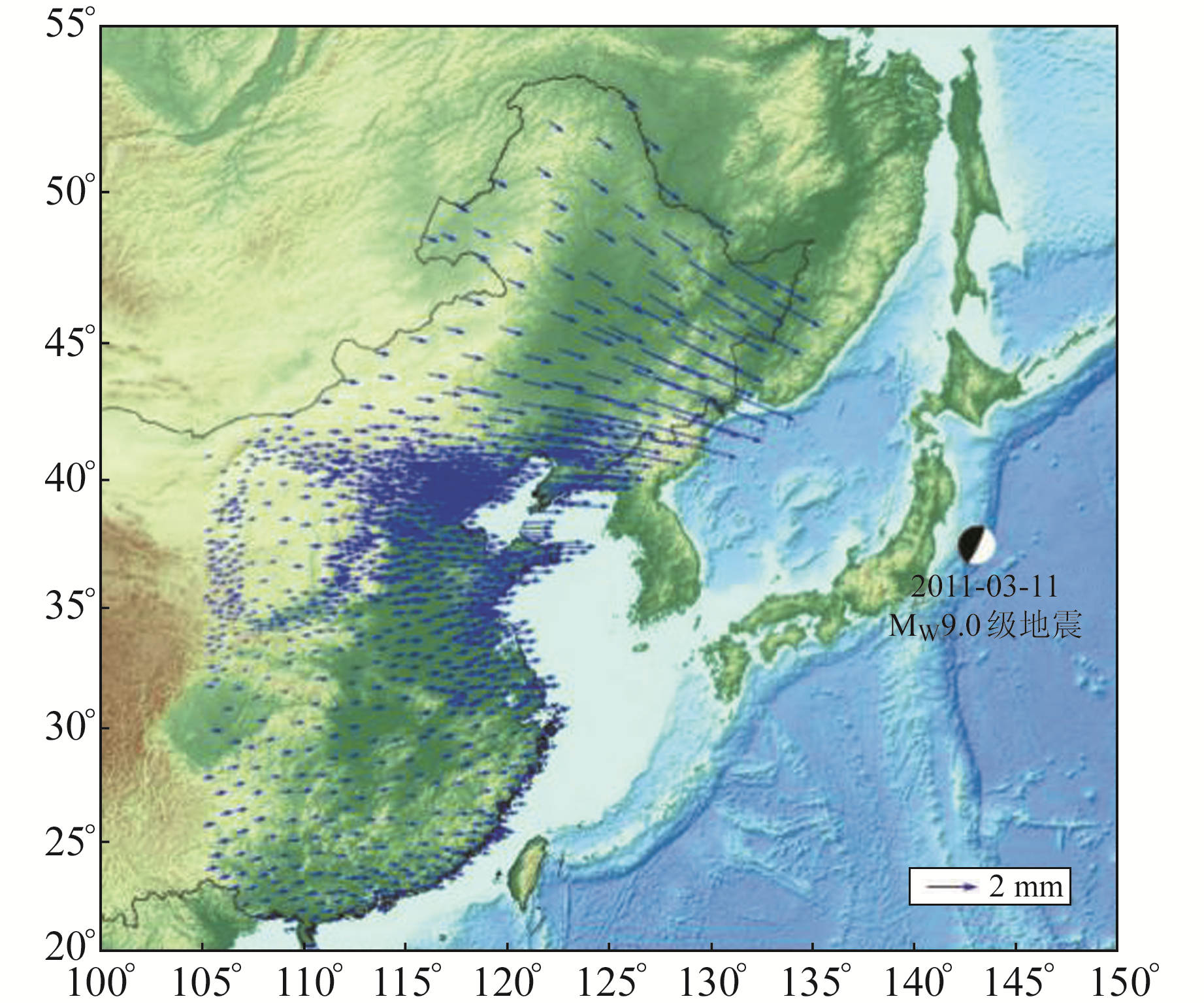
对空间分布不均匀的GPS同震位移结果采用球面小波分解方法[9]进行内插,得到研究区内任意点的同震形变量,从而改正日本东北大地震对高精度区域参考系统的影响。以网络工程项目一期和二期GPS流动站为例,图 4给出该地震在这些GPS站产生的同震位移场,可以看出,日本东北大地震主要对我国105°E以东区域产生同震变形影响。
|
图 4 中国东部GPS流动站的同震位移场内插结果 Fig. 4 Interpolated coseismic displacements of campaign GPS stations within eastern China |
强震发生后数年内,利用大地测量技术可在震区观测到地表位移随时间的对数(或指数)型衰减过程。式(1)表明,若要获取震后变形,需从原始GPS位移时间序列中扣除震前线性趋势运动、年周期和半年周期位移变化。限于篇幅,以距离震中较近的网络工程项目一期GPS连续站SUIY站和CHUN站为例,给出去线性项、年周期和半年周期项之后的震后位移时间序列(图 5),并用对数函数进行拟合。由于震后变形属于非线性过程,本文采用对数模型的振幅作为震后变形的运动位移场,图 5表明,SUIY站和CHUN站的位移在地震后呈明显的随时间衰减趋势,式(1)中的对数松弛时间τ分别为3.4 a和5 a,松弛振幅分别为36.4 mm和32.3 mm,尤其是地震之后E向运动显著。需要说明的是,此处的松弛时间τ是一种简单的函数模型结果,不代表震后长期变形的粘弹性松弛时间。

|
虚线为地震发生时刻, 红线为对数模型拟合结果,k 为 SUIY 站和 CHUN 站 NS 分量和 EW 分量的震后松弛振幅 图 5 典型GPS台站的震后位移时间序列 Fig. 5 Typical postseismic displacements following the great earthquake |
图 6为中国东部地区震后变形的松弛振幅,由图可知,日本东北大地震震后的影响范围比同震影响范围小,主要集中在中国东北和山东半岛区域,但GPS站的震后松弛振幅要比相应的同震位移大,对数松弛时间为1~11 a。其中,SUIY站的震后松弛振幅最大为36.4 mm,大于同震位移32.7 mm。Shestako等[13]也发现,国后岛(库纳施尔岛)的GPS站震后1 a产生的形变量已是相应同震变形的2倍多,与同震位移场(图 4)相比,山东半岛震后运动方向由同震的近E向偏转为NE向。

|
红色矢量为 GPS 连续站松弛振幅, 蓝色矢量为 GPS 流动站松弛振幅, 误差椭圆代表95%置信水平 图 6 2011年日本东北大地震在中国东部产生的震后松弛振幅 Fig. 6 The amplitudes of postseismic displacements within eastern China following the 2011 Tohoku-Oki earthquake |
本文利用空间分布密集的GPS连续站和流动站1999~2017年观测资料,处理分析2011年日本东北大地震对中国东部地壳运动形变产生的影响,得出以下结论:
1) 同震位移场结果表明,地震的远场同震效应向西最远可到105°E,包括东北、华北、华南等地区及鄂尔多斯地块,最大同震位移主要集中在东北地区。
2) 震后位移场揭示,地震的远场震后效应影响区域明显比同震影响区域小,仅包括中国东北地区的东南部和山东半岛等区域,但震后松弛振幅要比相应的同震位移大,震后松弛时间为1~11 a。
3) 利用本文构建的半动态参考基准模型,包括线性趋势项、同震及震后形变模型,可修正2011年日本东北大地震对区域现代大地基准的影响,为高精度CORS坐标系统的维护与更新提供了一个解决方案,本文得到的震后变形可用来约束估计区域岩石圈和上地幔粘滞性质。
| [1] |
Wang Min, Li Qiang, Wang Fan, et al. Far-Field Coseismic Displacements Associated with the 2011 Tohoku-Oki Earthquake in Japan Observed by Global Positioning System[J]. Chinese Science Bulletin, 2011, 56(23): 1593-1596
(  0) 0) |
| [2] |
杨少敏, 聂兆生, 贾志革, 等. GPS解算的日本MW9.0级地震的远场同震地表位移[J]. 武汉大学学报:信息科学版, 2011, 36(11): 1336-1339 (Yang Shaomin, Nie Zhaosheng, Jia Zhige, et al. Far-Field Coseismic Surface Displacement Caused by the MW9.0 Tohoku Earthquake[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11): 1336-1339)
(  0) 0) |
| [3] |
蔡华, 孙汉荣, 赵齐乐, 等. GPS测定的2011年日本9.0级地震的中国大陆地区同震位移场[J]. 武汉大学学报:信息科学版, 2012, 37(8): 953-955 (Cai Hua, Sun Hanrong, Zhao Qile, et al. Coseismic Displacement Field of Continental Area of China Associated with the MW9.0 Japan Earthquake in 2011 by GPS[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 953-955)
(  0) 0) |
| [4] |
Diao F Q, Xiong X, Wang R J, et al. Overlapping Post-Seismic Deformation Processes: Afterslip and Viscoelastic Relaxation Following the 2011 MW9.0 Tohoku(Japan) Earthquake[J]. Geophysical Journal International, 2014, 196(1): 218-229 DOI:10.1093/gji/ggt376
(  0) 0) |
| [5] |
Yamagiwa S, Miyazaki S, Hirahara K, et al. Afterslip and Viscoelastic Relaxation Following the 2011 Tohoku-Oki Earthquake(MW9.0) Inferred from Inland GPS and Seafloor GPS/Acoustic Data[J]. Geophysical Research Letters, 2015, 42(1): 66-73 DOI:10.1002/2014GL061735
(  0) 0) |
| [6] |
Sun T H Z, Wang K L, Iinuma T, et al. Prevalence of Viscoelastic Relaxation after the 2011 Tohoku-Oki Earthquake[J]. Nature, 2014, 514(7520): 84-87 DOI:10.1038/nature13778
(  0) 0) |
| [7] |
Shao Z G, Zhan W, Zhang L P, et al. Analysis of the Far-Field Co-Seismic and Post-Seismic Responses Caused by the 2011 MW9.0 Tohoku-Oki Earthquake[J]. Pure and Applied Geophysics, 2016, 173(3): 411-424
(  0) 0) |
| [8] |
田云锋, 沈正康. GPS坐标时间序列中非构造噪声的剔除方法研究进展[J]. 地震学报, 2009, 31(1): 68-81 (Tian Yunfeng, Shen Zhengkang. Progress on Reduction of Non-Tectonic Noise in GPS Position Time Series[J]. Acta Seismologica Sinica, 2009, 31(1): 68-81 DOI:10.3321/j.issn:0253-3782.2009.01.008)
(  0) 0) |
| [9] |
Tape C, Musé P, Simons M, et al. Multiscale Estimation of GPS Velocity Fields[J]. Geophysical Journal International, 2009, 179(2): 945-971 DOI:10.1111/j.1365-246X.2009.04337.x
(  0) 0) |
| [10] |
Chlieh M, Avouac J P, Hjorleifsdottir V, et al. Coseismic Slip and Afterslip of the Great MW9.15 Sumatra–Andaman Earthquake of 2004[J]. Bulletin of the Seismological Society of America, 2007, 97(1A): 152-173 DOI:10.1785/0120050631
(  0) 0) |
| [11] |
付广裕, 孙文科. 球体位错理论计算程序的总体设计与具体实现[J]. 地震, 2012, 32(2): 73-87 (Fu Guangyu, Sun Wenke. Overall Design and Specific Structures of the Computing Codes for Coseismic Deformations on a Layered Spherical Earth[J]. Earthquake, 2012, 32(2): 73-87)
(  0) 0) |
| [12] |
杨少敏, 兰启贵, 聂兆生, 等. 用多种数据构建2008年汶川特大地震同震位移场[J]. 地球物理学报, 2012, 55(8): 2575-2588 (Yang Shaomin, Lan Qigui, Nie Zhaosheng, et al. Coseismic Displacement Caused by the 2008 Great Wenchuan Earthquake Derived from Various Types of Geodetic Data[J]. Chinese Journal of Geophysics, 2012, 55(8): 2575-2588)
(  0) 0) |
| [13] |
Shestako N, Ohzono M, Takahashi H. Upper Mantle Rheology of Sea of Japan Inferred from Postseismic Displacements of the Tohoku Earthquake[C]. Japan Geoscience Union Meeting, Chiba Prefecture, 2013
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

