当观测值中不含粗差且观测误差服从正态分布时,传统最小二乘法能求得最优无偏估值。但实际观测中难以避免粗差,因此最小二乘估值不再是最优无偏的,粗差观测值将严重影响参数的估计结果[1-6]。观测粗差的处理一直是测量学者研究的重点问题之一,其解决方法主要分为粗差探测和抗差估计。粗差探测是将粗差归入函数模型,通过统计检验剔除后,再处理不含粗差的观测值[7-11];抗差估计是将粗差归入随机模型,通过增大含有粗差的观测值方差,使其对参数估值的影响降低[12],其关键是构造合适的等价权模型。基于Hubert等价权函数概念[13],我国著名大地测量学家周江文和杨元喜[14-16]提出IGG Ⅰ、IGG Ⅱ和IGG Ⅲ抗差估计方案。为了在构建等价权后保持观测值相关性不变,刘经南等[17]提出等价协方差矩阵法。杨元喜[18-19]提出双因子抗差估计方法,通过方差膨胀函数和权因子收缩函数构建双因子等价权,不仅保持了等价权阵和协方差阵的对称性,而且保持了原协方差矩阵的相关特性,是目前较为常用的相关观测值抗差估计方法。
等价权抗差估计法根据每个观测值的标准化残差计算等价权,但一个观测值的粗差会影响多个观测值的残差估值,导致不含粗差的观测值被错误降权,这将损害参数估值的精度。为减轻错误降权的影响,提升估值的抗差性,文献[20]使用中位数法计算初值,再用等价权抗差估计法计算最终参数估值;文献[21]利用中位数残差计算残差置信区间,构造等价权函数自适应临界值,均取得一定成效。本文针对相关观测中错误降权的问题,改进双因子抗差估计法降权的过程,在含有足够明显的粗差时仅对标准化残差最大的观测值降权,避免正常观测值被错误降权;并通过模拟实验验证本方法的优点,含有明显粗差时参数估值的精度优于双因子法,粗差不明显或个数较少时计算效率高于双因子法。
1 双因子抗差估计法利用n维相关观测向量l估计m(m<n)维未知参数向量x的误差方程为:
| $ \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{l}} $ | (1) |
式中,A为m×n维系数矩阵,v为残差向量。相关观测值的方差-协方差阵D和权阵P=(D/ σ02)-1是对称正定的非对角阵,其中σ02为方差因子。双因子抗差估计是通过构建等价权矩阵进行抗差估计,其参数估值为:
| $ \mathit{\boldsymbol{\hat x}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\bar PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\bar Pl}} $ | (2) |
参数估值的验后方差-协方差阵近似表示为[22]:
| $ {\mathit{\boldsymbol{D}}_{\hat x}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\bar PA}}} \right)^{ - 1}}\hat \sigma _0^2 $ | (3) |
其中方差因子的估值为:
| $ \hat \sigma _0^2 = {{{v^{\rm{T}}}\mathit{\boldsymbol{\bar Pv}}} \over r} $ | (4) |
式中,r=n-m为冗余观测数。其双因子等价权矩阵为:
| $ \eqalign{ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\bar P}} = \left\{ {{{\bar p}_{ij}}} \right\} = \left\{ {{p_{ij}}{\gamma _{ij}}} \right\} = \cr & \left[ {\matrix{ {\matrix{ {{p_{11}}{\gamma _{11}}} & {{p_{12}}{\gamma _{12}}} \cr {{p_{21}}{\gamma _{21}}} & {{p_{22}}{\gamma _{22}}} \cr } } & \cdots & {\matrix{ {{p_{1n}}{\gamma _{1n}}} \cr {{p_{2n}}{\gamma _{2n}}} \cr } } \cr \vdots & \ddots & \vdots \cr {\matrix{ {{p_{n1}}{\gamma _{n1}}} & {{p_{n2}}{\gamma _{n2}}} \cr } } & \cdots & {{p_{nn}}{\gamma _{nn}}} \cr } } \right] \cr} $ | (5) |
式中,pij和P ij分别为权阵P和等价权P的第i行j列的权元素,
| $ {\gamma _{ij}} = \sqrt {{\gamma _{ii}}{\gamma _{jj}}} $ | (6) |
式中,γii和γjj为自适应降权因子,可采用Huber函数或Hampel函数等,本文使用IGGⅢ降权因子[16,18]:
| $ $$\eqalign{ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\gamma _{ii}} = \cr & \left\{ \matrix{ 1, \left| {{v_i}/{\sigma _i}} \right| \le {k_{\matrix{ 0 \cr } }} \hfill \cr {{{k_0}} \over {\left| {{v_i}/{\sigma _i}} \right|}}{\left( {{{{k_1} - \left| {{v_i}/{\sigma _i}} \right|} \over {{k_1} - {k_0}}}} \right)^2}, {k_0} < \left| {{v_i}/{\sigma _i}} \right| \le {k_{\matrix{ 1 \cr } }} \hfill \cr 0, \left| {{v_i}/{\sigma _i}} \right| > {k_1} \hfill \cr} \right. \cr} $$ $ | (7) |
式中,vi/σi为第i个观测值的标准化残差;k0和k1为相应的临界值,通常k0取2.0~3.0,k1取4.5~8.5,需根据问题的客观需求来具体确定[19]。
实际计算时,式(7)可按如下步骤迭代解算,终止条件为前后两次估值的变化小于阈值:
| $ $${{\mathit{\boldsymbol{\hat x}}}^{k + 1}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\bar P}}}^k}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\bar P}}}^k}\mathit{\boldsymbol{l}}$$ $ | (8) |
| $ $${\mathit{\boldsymbol{v}}^{k + 1}} = \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat x}}}^{k + 1}} - \mathit{\boldsymbol{l}}$$ $ | (9) |
| $ $${{\mathit{\boldsymbol{\bar P}}}^{k + 1}} = \left\{ {{{\bar p}_{ij}}^{k + 1}} \right\} = \left\{ {{p_{ij}}^k{\gamma _{ij}}^{k + 1}} \right\}$$ $ | (10) |
式中,γijk+1由式(6)和式(7)根据v k+1求得。
2 双因子等价权的改进算法由于一个观测值的粗差会影响多个观测值的残差估值,同时构建所有观测值的等价权会导致不含粗差的观测值被错误降权,降低参数估值的精度,因此,本文根据最大标准化残差的检验结果确定是否为粗差或明显可疑的粗差,并将算法作如下改进:每次迭代时,计算各观测值的标准化残差,选取最大值max(vi/σi)=vt/σt,对其进行检验。
1) 当|vt/σt|>k1时,认为该观测值含有粗差,对其降权因子赋值为零,其余观测值的权不变;
2) 当kt<|vt/σt|≤k1时,认为该观测值含有明显可疑的粗差,只计算其降权因子,其余观测值的权不变;
3) 当k0<|vt/σt|≤kt时,认为观测值中不含明显可疑的粗差,所有观测值按式(7)构建等价权,计算参数估值;
4) 当|vt/σt|≤k0时,等价权与参数估值不再改变。
每次迭代后,若与前一次参数估值之差小于阈值,则停止迭代。
临界值kt∈(k0, k1),其性质与k0、k1相同,可根据问题的需求确定取值,本文取kt= k0+k1 2来说明对明显粗差单独降权的优点。注意:若kt取值过大,则单独降权的观测数较少,估值精度变化不明显;若kt取值过小,则单独降权的观测数较多,计算效率低下,故应兼顾估值精度与计算效率,选取相对平衡适中的kt临界值。
在1)、2)两种情况下,每次迭代选取标准化残差最大的观测值,与其相关的等价权元素即为该观测值对应权所在行和列的各元素,故只需计算这些元素的等价权,其余元素权不变,无需计算。针对该特征,可简化等价权的构建方法和计算步骤。具体过程可如下进行。
先对第t列的权进行调整:
| $ $${{\bar P}_{it}} = {P_{it}}\sqrt {{d_t}} $$ $ | (11) |
再对第t行的权进行调整:
| $ $${{\bar P}_{tj}} = {P_{tj}}\sqrt {{d_t}} $$ $ | (12) |
式中,dt∈[0, 1]为最大标准化残差对应的降权因子:
| $ \eqalign{ & {d_t} = \left\{ \matrix{ 1, \left| {{v_t}/{\sigma _t}} \right| \le k \hfill \cr {{{k_0}} \over {\left| {{v_t}/{\sigma _t}} \right|}}{\left( {{{{k_1} - \left| {{v_t}/{\sigma _t}} \right|} \over {{k_1} - {k_0}}}} \right)^2} \hfill \cr} \right. \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{{k_{\matrix{ 0 \cr } }} + {k_{\matrix{ 1 \cr } }}} \over 2} < \left| {{v_t}/{\sigma _t}} \right| \le {k_{\matrix{ 1 \cr } }} \cr} $ | (13) |
经过步骤1)、2)的单独降权后,如果最大标准化残差|vt/σt|(k0+k1)/2,则说明观测值中已不存在明显可疑的粗差,按步骤3)、4)进行计算时,通常迭代一次就能收敛,并在保证参数估值精度的基础上,减少迭代次数,提高计算效率。
若第一次迭代时最大标准化残差k0|vt/σt|(k0+k1)/2,即观测值不含明显的可疑粗差,此时本文算法与双因子法降权过程一致,估值结果相同,计算代价略小,在算例分析部分将结合实验详细说明。
若第一次迭代时最大标准化残差|vt/σt|≤k0,即观测值不含粗差,本文算法与双因子法将按最小二乘平差计算参数估值,但需注意实际使用中k0的选取将影响对粗差的判别。理想状态下两种方法的结果与最小二乘结果相同,但实际使用中若出于保守考虑,选取的k0较小,则可能将不含粗差的观测值判别为可疑粗差,对其进行降权,则此时本文算法与双因子法结果相同,而与最小二乘结果不同。
综上,本文的改进算法在观测值明显含有粗差时,只对粗差观测值降权;在观测值不含明显的粗差时,对所有观测值同时降权。因此,本文改进后的双因子算法,有望求得更高的参数估值精度,并减少计算时间。
3 算例分析选取一个GPS网进行模拟实验,该GPS网中有8个坐标点,其中1号点和8号点坐标已知,其余6个点坐标未知;测得基线向量16条,各观测基线向量互相独立,同一基线各方向分量相关。其网型如图 1所示,各基线向量观测值及其协方差,以及已知点坐标可参考文献[23]。
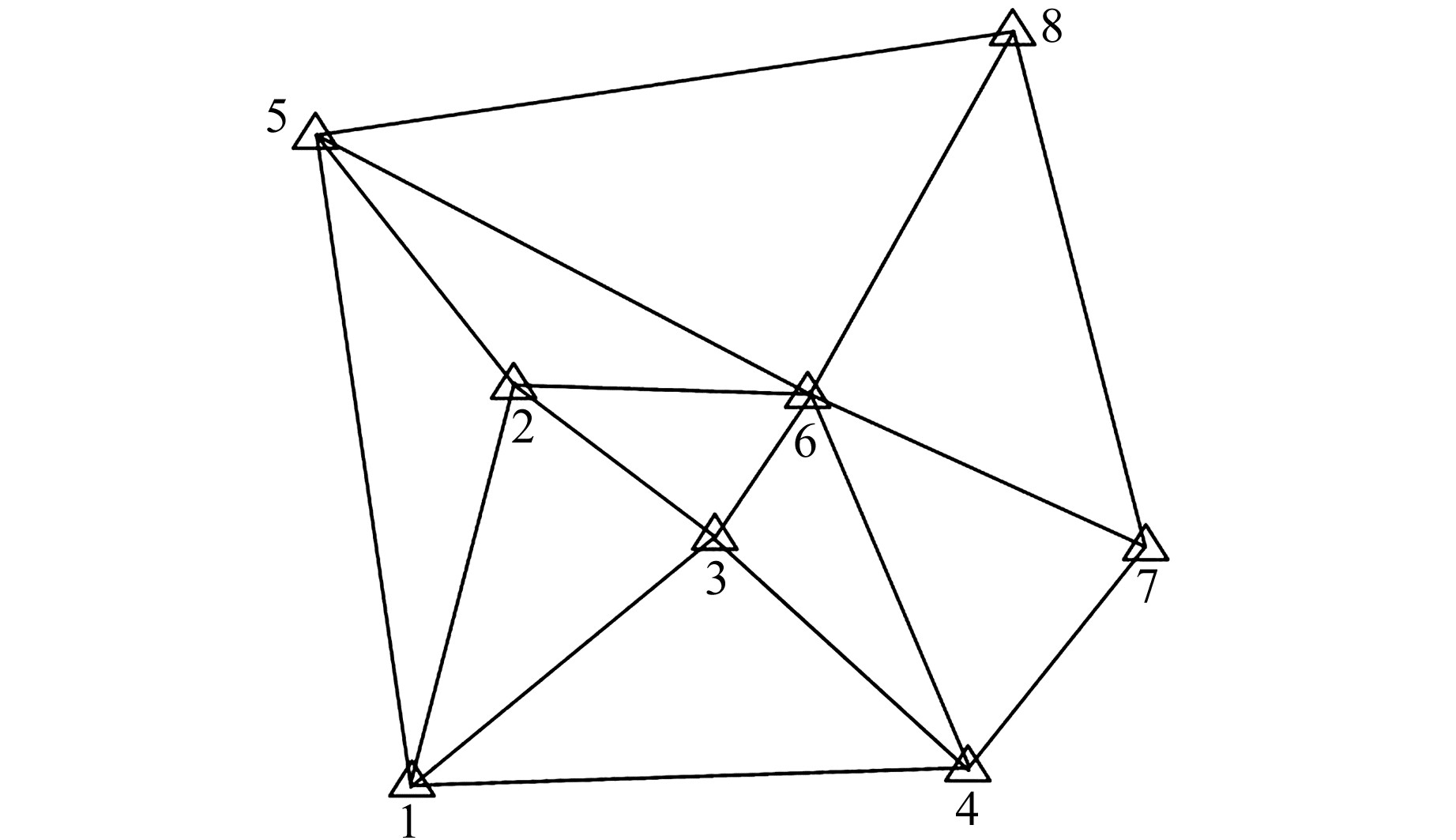
|
图 1 GPS网 Fig. 1 GPS network |
模拟实验通过如下步骤生成观测数据[19]:
1) 使用原始基线向量进行最小二乘平差,根据已知点坐标计算的坐标参数估值作为坐标真值,残差改正后的基线观测值作为真值y。
2) 通过Monte-Carlo模拟生成标准正态分布的随机误差向量ε′~N(0, 1)。
3) 对基线向量观测值的协方差矩阵D进行Cholesky分解得D = FF T,其中F为下三角矩阵。将随机误差向量ε′转换成相关观测误差向量ε = Fε′。
4) 将观测误差向量ε添加到基线向量真值y上,得到模拟的基线向量观测值y = y + ε。
5) 在y中随机挑选观测值添加粗差,添加粗差时应注意避免挑选到同一基线或相邻基线。
分别使用双因子法和本文改进算法估计坐标参数,每种情况各进行200次实验,计算平均点位的均方根误差(RMSE)和运算时间,比较两种方法的参数精度和计算效率。本实验中k0取3.0,k1取5.0。
1) 添加5~10倍中误差,并比较在含有粗差情况下本文算法和双因子法的效果,结果如表 1所示。
|
|
表 1 含有粗差时两种方法的效果对比 Tab. 1 Comparison of RMSE and calculation efficiency with outlier |
在含有1个、2个、3个粗差时,本文算法的点位RMSE分别比双因子法提高了1.43%、6.02%和11.2%。由于粗差通常会被除权,此时影响估值精度的主要是正常观测值的错误降权。随着粗差个数的增加,本文算法精度降低幅度较小,而双因子法精度降低幅度较大,说明本文算法可较好地将粗差观测值单独除权或降权,受粗差污染的影响较小,而双因子法则影响较大,错误降权情况较多,导致精度下降。由于本文算法迭代次数与粗差个数有关,而双因子法迭代次数则相对固定,本文算法仅在含有1个粗差时计算效率较高。
2) 添加4~5倍中误差,比较在含有明显可疑粗差时两种算法的效果,结果如表 2所示。
|
|
表 2 含有明显可疑粗差时两种方法的效果对比 Tab. 2 Comparison of RMSE and calculation efficiency with obvious outlier |
在含有1个、2个、3个明显可疑粗差时,本文算法的点位RMSE分别比双因子法提高0.15%、0.28%和0.39%。由于明显可疑粗差只会被降权,不会被除权,故这些粗差的残留是导致估值精度降低的主要原因。本文算法避免了部分正常观测值的错误降权,但相较于粗差观测值残留带来的误差,其影响非常微弱。本文算法仅在含有1个明显可疑粗差时计算效率较高。
3) 添加3~4倍中误差,在不含明显可疑粗差时,本文算法不再单独降权,与双因子法经过一致的降权过程得到相同的结果。
4) 不含粗差时,本文算法和双因子法均按最小二乘平差计算参数估值,此时3种方法结果相同。
在3)、4)两种情况下两种方法的效果对比如表 3所示。
|
|
表 3 不含明显可疑粗差和不含粗差时 Tab. 3 Comparison of RMSE and calculation efficiency without outlier/obvious outlier |
在求得相同结果的情况下,虽然两种方法的降权和参数估计过程一致,计算时间差异很小,但本文算法计算代价稍小。本文算法在第一次迭代时需选取最大的标准化残差,依次与k1、(k0+k1)/2、k0比较后,确定不含粗差或明显可疑粗差,可同时降权,此后每个观测值的标准化残差只需与k0比较一次即可确定降权因子;而双因子法不选取最大的标准化残差,但每个观测值的标准化残差都需与k1、k0比较两次才能确定降权因子。故总体而言,在估值结果相同时,本文算法计算代价较双因子法稍小,计算效率稍高。将每次实验中本文算法用时减去双因子法用时,计算每次实验的计算用时之差,结果如图 2、图 3所示。
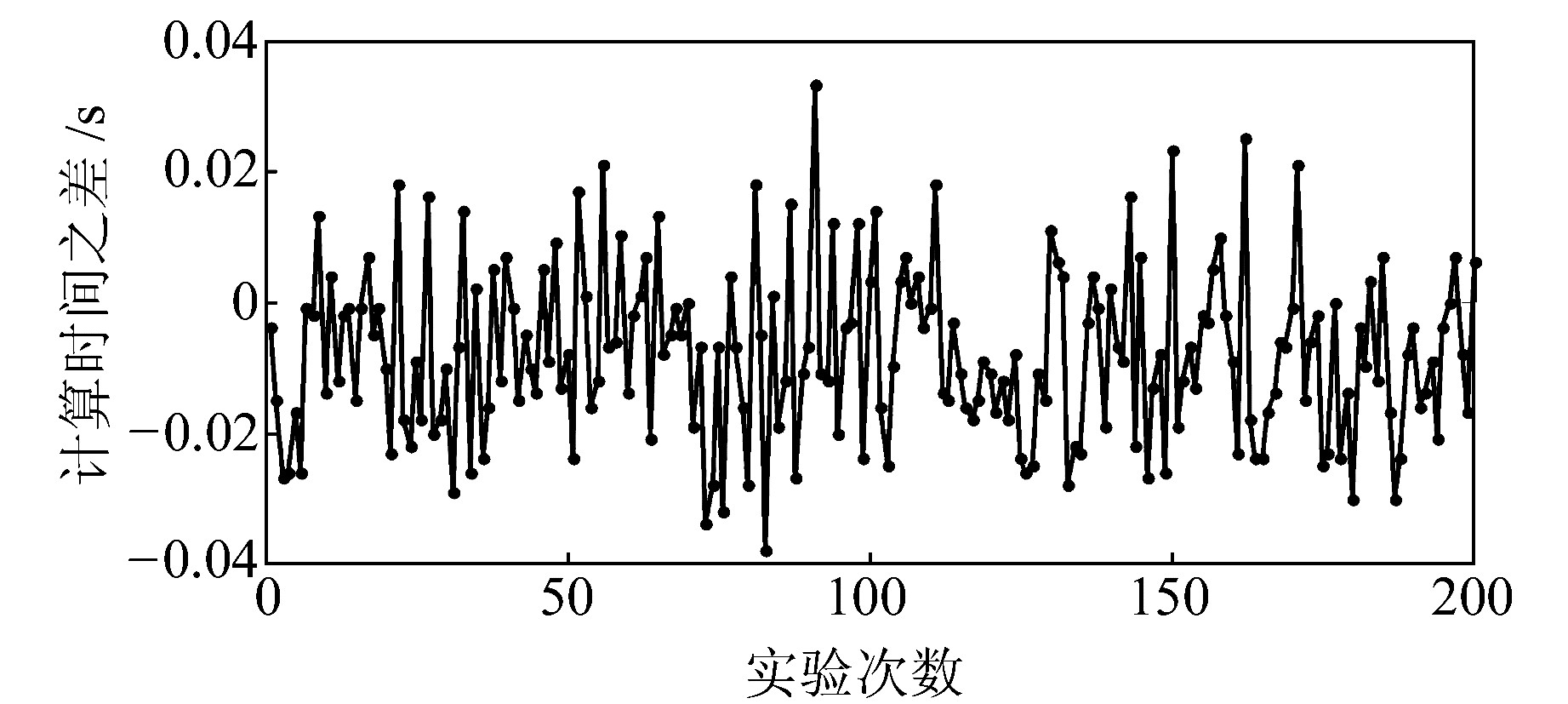
|
图 2 不含明显可疑粗差时两种方法计算用时之差 Fig. 2 Difference of calculation efficiency without obvious outlier |
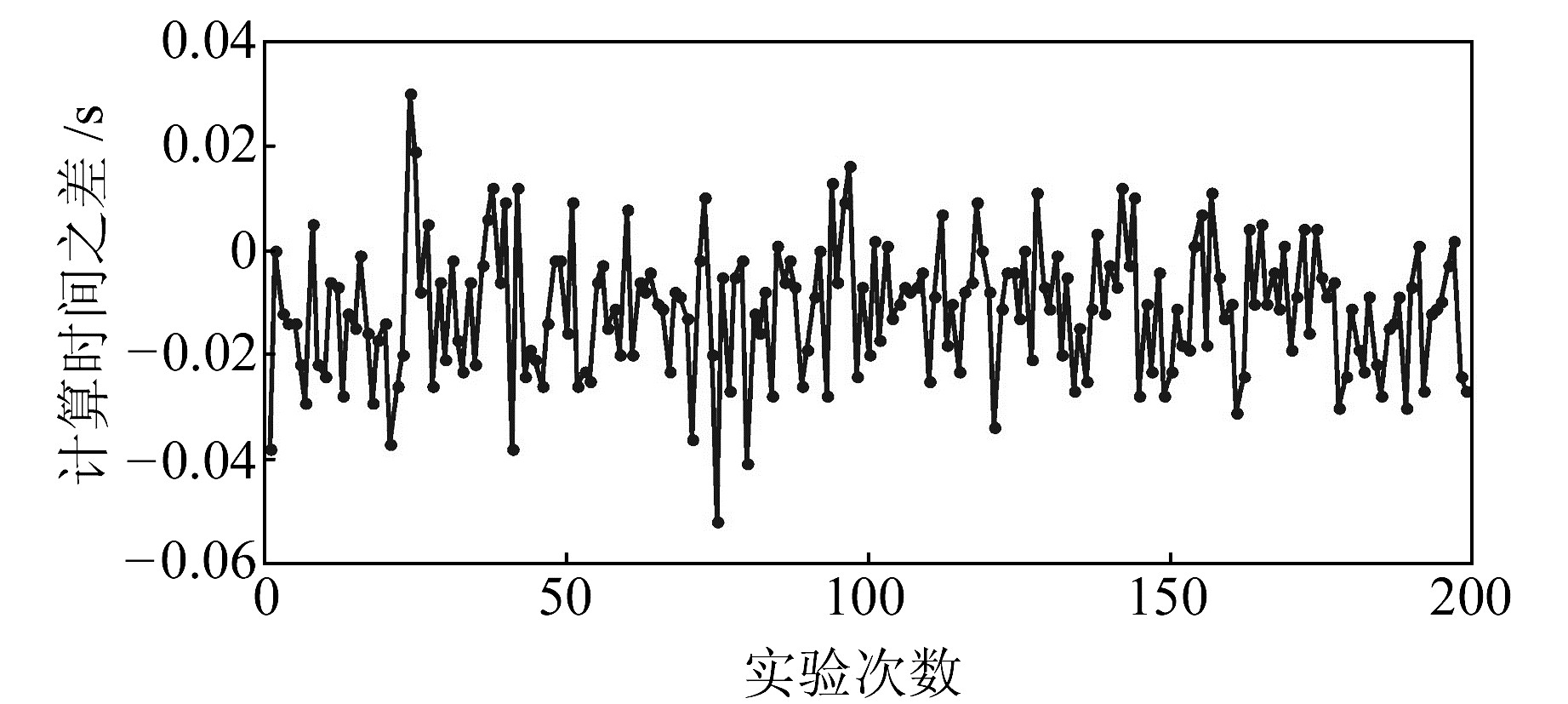
|
图 3 不含粗差时两种方法计算用时之差 Fig. 3 Difference of calculation efficiency without outlier |
本文算法的计算用时基本低于双因子法的计算用时,考虑到每次计时由计算机引起的误差,认为本文算法计算效率高于双因子法。
4 结语由于一个观测值的粗差会影响多个观测值的残差估值,当观测值含有粗差或明显的可疑粗差时,若采用双因子抗差估计,同时构建所有观测值的等价权,会导致不含粗差的观测值被错误降权,损害参数估值的精度。对此,本文改进了双因子抗差估计的降权方法,当检验发现存在粗差或明显可疑粗差时,只对粗差或可疑粗差进行双因子降权;只有当可疑粗差不明显时,才根据标准化残差量对所有观测值进行降权处理。实验证明,本文的改进算法在含有明显粗差时可提高参数估值的精度;在粗差不明显或个数较少时,可在保持参数估计精度的基础上提高计算效率。
| [1] |
Huber P J. Robust Statistics[M]. New York: John Wiley and Sons, 1981
(  0) 0) |
| [2] |
Amiri-simkooei A. Formulation of L1 Norm Minimization in Gauss-Markov Models[J]. Journal of Surveying Engineering, 2003, 129(1): 37-43 DOI:10.1061/(ASCE)0733-9453(2003)129:1(37)
(  0) 0) |
| [3] |
彭军还, 李淑慧, 师芸, 等. 不等式约束M估计的均方误差矩阵和解的改善条件[J]. 测绘学报, 2010, 39(2): 129-134 (Peng Junhuan, Li Shuhui, Shi Yun, et al. The Mean Squares Error Matrix of Inequality Constrained M Estimate and the Conditions for Improving Solutions[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 129-134)
(  0) 0) |
| [4] |
欧吉坤. 一种三步抗差方案的设计[J]. 测绘学报, 1996, 25(3): 173-179 (Ou Jikun. Design of a New Scheme of Robust Estimation by Three Steps[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 173-179 DOI:10.3321/j.issn:1001-1595.1996.03.003)
(  0) 0) |
| [5] |
Guo J F, Ou J K, Wang H T. Robust Estimation for Correlated Observations: Two Local Sensitivity based Down weighting Strategies[J]. Journal of Geodesy, 2010, 84(4): 243-250 DOI:10.1007/s00190-009-0361-y
(  0) 0) |
| [6] |
王新洲, 陶本藻, 邱卫宁, 等. 高等测量平差[M]. 北京: 测绘出版社, 2006 (Wang Xinzhou, Tao Benzao, Qiu Weining, et al. Advanced Surveying Adjustment[M]. Beijing: Surveying and Mapping Press, 2006)
(  0) 0) |
| [7] |
沈云中, 赵财福. 虚拟误差方程及其在粗差探测中的应用[J]. 同济大学学报, 1994, 22(1): 59-62 (Shen Yunzhong, Zhao Caifu. Fictitious Observation Equation and Its Application in Outlier Detecting[J]. Journal of Tongji University, 1994, 22(1): 59-62)
(  0) 0) |
| [8] |
宋力杰, 杨元喜. 论粗差修正与粗差剔除[J]. 测绘通报, 1999(6): 5-6 (Song Lijie, Yang Yuanxi. Discuss of Gross Error Correction and Elimination[J]. Bulletin of Surveying and Mapping, 1999(6): 5-6 DOI:10.3969/j.issn.0494-0911.1999.06.002)
(  0) 0) |
| [9] |
李博峰, 沈云中. 基于等效残差积探测粗差的方差-协方差分量估计[J]. 测绘学报, 2011, 40(1): 10-14 (Li Bofeng, Shen Yunzhong. Equivalent Residual Product Based Outlier Detection for Variance and Covariance Component Estimation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 10-14)
(  0) 0) |
| [10] |
欧吉坤. 粗差的拟准检定法(QUAD法)[J]. 测绘学报, 1999, 28(1): 15-20 (Ou Jikun. Quasi-Accurate Detection of Gross Errors (QUAD)[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 15-20 DOI:10.3321/j.issn:1001-1595.1999.01.004)
(  0) 0) |
| [11] |
沈云中, 陶本藻. 实用测量数据处理方法(2版)[M]. 北京: 测绘出版社, 2012 (Shen Yunzhong, Tao Benzao. Pratical Methods for Surveying Data Processing(2nd ed)[M]. Beijing: Surveying and Mapping Press, 2012)
(  0) 0) |
| [12] |
Krarup T, Juhl J, Kubik K. Gotterdammerung over Least Squares Adjustment[C]. 14th Congress of International Archives of Photogrammetry, Hamburg, 1980 https://www.researchgate.net/publication/307509686_Gotterdammerung_over_least_squares_adjustment
(  0) 0) |
| [13] |
刘大杰, 陶本藻. 实用测量数据处理方法[M]. 北京: 测绘出版社, 2000 (Liu Dajie, Tao Benzao. Practical Measurement Data Processing Method[M]. Beijing: Surveying and Mapping Press, 2000)
(  0) 0) |
| [14] |
周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115-120 (Zhou Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(2): 115-120 DOI:10.3321/j.issn:1001-1595.1989.02.005)
(  0) 0) |
| [15] |
周江文, 黄幼才, 杨元喜. 抗差最小二乘法[M]. 武汉: 华中理工大学出版社, 1997 (Zhou Jiangwen, Huang Youcai, Yang Yuanxi. Robust Least-Square Regression[M]. Wuhan: Huazhong University of Science and Technology Press, 1997)
(  0) 0) |
| [16] |
杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993 (Yang Yuanxi. Robust Estimation and Application[M]. Beijing: Bayi Press, 1993)
(  0) 0) |
| [17] |
刘经南, 姚宜斌, 施闯. 基于等价方差-协方差阵的稳健最小二乘估计理论研究[J]. 测绘科学, 2000, 25(3): 1-5 (Liu Jingnan, Yao Yibin, Shi Chuang. Theory Research on Robustified Least Squares Estimator Based on Equivalent Variance-Covariance[J]. Science of Surveying and Mapping, 2000, 25(3): 1-5 DOI:10.3771/j.issn.1009-2307.2000.03.001)
(  0) 0) |
| [18] |
杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J]. 测绘学报, 2002, 31(2): 95-99 (Yang Yuanxi, Song Lijie, Xu Tianhe. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 95-99 DOI:10.3321/j.issn:1001-1595.2002.02.001)
(  0) 0) |
| [19] |
Yang Y, Song L, Xu T. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6-7): 353-358 DOI:10.1007/s00190-002-0256-7
(  0) 0) |
| [20] |
杨玲, 沈云中, 楼立志. 基于中位参数初值的等价权抗差估计方法[J]. 测绘学报, 2011, 40(1): 28-32 (Yang Ling, Shen Yunzhong, Lou Lizhi. Equivalent Weight Robust Estimation Method Based on Median Parameter Estimates[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 28-32)
(  0) 0) |
| [21] |
蒋晨, 张书毕, 张秋昭. 自适应临界值的等价权函数及抗差估计方法[J]. 中国矿业大学学报, 2017, 46(4): 911-916 (Jiang Chen, Zhang Shubi, Zhang Qiuzhao. Equivalent Weight Function and Robust Estimation Method with Adaptive Criterion[J]. Journal of China University of Mining & Technology, 2017, 46(4): 911-916)
(  0) 0) |
| [22] |
Yang Y X. Estimators of Covariance Matrix at Robust Estimation Based on Influence Functions[J]. ZfV, 1997, 122(4): 166-174
(  0) 0) |
| [23] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础(第二版)[M]. 武汉: 武汉大学出版社, 2009 (Subject Group of Surveying Adjustment, School of Geodesy and Geomatics, Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

