2. 许昌学院城乡规划与园林学院,河南省许昌市八一路88号,461000
数学史学家们把四元数的诞生称之为“代数学的革命”。四元数是建立在复数基础之上的,复数的概念是在16世纪由Cardano首先引入,但在很长的时间里它仍然给人们以模棱两可的感觉。直到18世纪,才由Wessel、Argand以及Gauss等数学家们给出它的几何解释,并使得复数的意义明确起来[1]。1843年Hamilton引入的四元数是复数和向量在四维空间的扩展。起初,四元数在实际工程技术中并没有得到普遍的应用。直到19世纪中叶之后,四元数才在天文学、物理学、力学、数字图像和信号处理等领域得到广泛应用。美国数学家Derbyshire的著作《代数的历史》[2]、Crowe的著作《向量分析的历史》[3]以及美国数学史学家Kline的著作《古今数学思想》(第四册)[4]等,都对哈密顿的生平以及四元数的概念和意义进行了阐述。在中国,张祖贵[5]和孙自行[6]分别对四元数产生的背景和影响,以及代数学中的数系扩充进行介绍。李迪[7]和吴文俊[8]在其著作中都详细论述了四元数的发展历史等相关内容。另外,李文林[9-10]、张顺燕[11]和梁宗巨[12]也在各自的著作中分别把四元数作为一个重要内容进行阐述。孙庆华的博士论文《向量理论历史研究》[13]详细介绍了复数和四元数的发现和发展历程。四元数在某些科学研究和工程技术应用方面所具有的一些独特优势,使得目前仍然有很多学者热衷于对它的研究。Goldman [14]在对四元数的基本理论研究之后,给出四元数在计算机图形学中的应用原理。Pujol [15]在哈密顿最初研究的基础上,对四元数的基本概念及理论进行进一步的推导。近年来,中国大地测量学和地球动力学领域的很多青年学者也对四元数的应用作了大量工作。戚宪东等[16]为减少由于陀螺仪漂移带来的航向误差,基于四元数提出一种新的航向修正算法。马涛峰等[17]利用对偶四元数能同时描述旋转矩阵和平移向量的优势,提出一种适用于大角度的三维空间坐标转换参数求解模型。张德先等[18]为消除磁场观测量对四元数中横滚角和俯仰角分量的影响,通过对四元数进行分解,构造了观测噪声和观测量自适应补偿算法。伏家杰等[19]针对当前常用一阶互补滤波算法中阻带衰减速率慢和陀螺仪常值漂移产生的稳态误差问题,设计了一种基于四元数的二阶互补滤波算法,有效地减少了姿态解算的累积误差。鲁丹丹等[20]为解决标准DR算法中采用欧拉角法进行姿态角外推计算量大等问题,提出一种基于四元数的DR姿态角外推算法。
向量(矢量)代数和向量分析来源于四元数,并在较长的时间内取代了四元数。当前,四元数在空间定位与导航、数字图像处理等领域得到了非常广泛的应用。因此,利用成熟的向量理论再来理解四元数是有意义的。本文通过向量(两个相互平行或垂直的向量)的相关性质引出四元数的概念及其运算法则,证明所有四元数都等价于两个向量的格拉斯曼积,以及可以利用单位四元数的正交变换来表示向量旋转的欧拉公式(1776年)[21]。
1 两个相互平行或垂直向量之间的一个不可交换积定义本文所讨论的是遵循平行四边形定则(三角形定则)的自由向量。当两个向量a和b相互平行或垂直时,定义其一个不可交换积为:
| $ $$\mathit{\boldsymbol{a}} \circ \mathit{\boldsymbol{b}} = \left\{ {\matrix{ \hfill { - (\mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{b}})} \cr \hfill {\mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}}} \cr } \matrix{ {\matrix{ , \hfill \cr } \mathit{\boldsymbol{a}}\parallel \mathit{\boldsymbol{b}}} \hfill \cr {\matrix{ , \hfill \cr } \mathit{\boldsymbol{a}} \bot \mathit{\boldsymbol{b}}} \hfill \cr } } \right.$$ $ | (1) |
式(1)的意义是:当两个向量a和b相互平行时,a°b返回的是一个标量,其数值等于a和b内积或点积的负值;当两个向量a和b相互垂直时,a °b返回的是一个向量,此向量就是a和b的叉积或外积,且按a、b和a × b这个次序构成右手系。式(1)称为格拉斯曼乘积。
如果λ和β为标量,则定义
| $ $$\lambda \circ \mathit{\boldsymbol{b}}{\rm{ = }}\lambda \mathit{\boldsymbol{b,a}}\circ \beta {\rm{ = }}\beta \mathit{\boldsymbol{a}},\lambda \circ \beta {\rm{ = }}\lambda \beta $$ $ | (2) |
也就是说,标量与标量(或向量)之间的格拉斯曼积等于标量与标量(或向量)的数乘。
如果e1、e2和e3是空间直角坐标系的坐标基,根据式(1)的定义可得:
| $ {\boldsymbol{e}_i} \circ {\boldsymbol{e}_j} = \left\{ {\begin{array}{*{20}{l}} { - 1},&{i = j}\\ {{\varepsilon _{ijk}}{e_k}},&{i \ne j \ne k} \end{array}} \right. $ | (3) |
式中,εijk为顺序符号,其约定为:
| $ {\varepsilon _{ijk}} = \left\{ {\begin{array}{*{20}{c}} {1, i, j, k = 123, 231, 312}\\ { - 1, i, j, k = 213, 321, 132} \end{array}} \right. $ | (4) |
坐标基的格拉斯曼乘积既表示出单位向量的性质,同时也表现出虚数单位的性质。
2 任意两个向量之间的格拉斯曼乘积如图 1所示,设有任意两个向量a和b,向量b在沿着向量a方向上的投影是向量b1,在垂直于向量a方向上的投影是向量b2,显然有:

|
图 1 向量分解 Fig. 1 Vector decomposition |
| $ $$\mathit{\boldsymbol{b}}{\rm{ = }}{\mathit{\boldsymbol{b}}_1}{\rm{ + }}{\mathit{\boldsymbol{b}}_2}$$ $ | (5) |
如果式(5)成立,则令下式也成立:
| $ $$\mathit{\boldsymbol{a}}\circ \mathit{\boldsymbol{b}} = \mathit{\boldsymbol{a}}\circ {\mathit{\boldsymbol{b}}_1} + \mathit{\boldsymbol{a}}\circ {\mathit{\boldsymbol{b}}_2}$$ $ | (6) |
也就是规定向量的格拉斯曼积满足分配律。因为a‖b1,a⊥b2,根据式(1)有:
| $ $$\eqalign{ & \mathit{\boldsymbol{a}} \circ {\mathit{\boldsymbol{b}}_1} = - \mathit{\boldsymbol{a}} \cdot {\mathit{\boldsymbol{b}}_1} = - \left( {\mathit{\boldsymbol{a}} \cdot {\mathit{\boldsymbol{b}}_1} + \mathit{\boldsymbol{a}} \cdot {\mathit{\boldsymbol{b}}_2}} \right) = \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \mathit{\boldsymbol{a}} \cdot \left( {{\mathit{\boldsymbol{b}}_1} + {\mathit{\boldsymbol{b}}_2}} \right) = - \mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{b}} \cr} $$ $ | (7) |
| $ \begin{array}{l} \boldsymbol{a}\circ {\boldsymbol{b}_2} = \boldsymbol{a} \times {\boldsymbol{b}_2} = \boldsymbol{a} \times {\boldsymbol{b}_1} + \boldsymbol{a} \times {\boldsymbol{b}_2} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \boldsymbol{a} \times ({\boldsymbol{b}_1} + {\boldsymbol{b}_2}) = \boldsymbol{a} \times \boldsymbol{b} \end{array} $ | (8) |
这样,式(6)就可写为:
| $ \boldsymbol{a} \circ \boldsymbol{b} = - \boldsymbol{a} \cdot \boldsymbol{b} + \boldsymbol{a} \times \boldsymbol{b} $ | (9) |
这表明,任意两个向量之间的格拉斯曼乘积等于这两个向量的叉积减去其内积。
由于以下3个等式成立:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\boldsymbol{a} \times \boldsymbol{b}) \times \boldsymbol{c} = (\boldsymbol{a} \cdot \boldsymbol{c})\boldsymbol{b} - \boldsymbol{a}(\boldsymbol{b} \cdot \boldsymbol{c})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \boldsymbol{a} \times (\boldsymbol{b} \times \boldsymbol{c}) = (\boldsymbol{a} \cdot \boldsymbol{c})\boldsymbol{b} - (\boldsymbol{a} \cdot \boldsymbol{b})\boldsymbol{c}\\ \boldsymbol{a} \cdot (\boldsymbol{b} \times \boldsymbol{c}) = (\boldsymbol{c} \times \boldsymbol{a}) \cdot \boldsymbol{b} = (\boldsymbol{a} \times \boldsymbol{b}) \cdot \boldsymbol{c} \end{array} $ |
以及向量的格拉斯曼积满足分配律,那么根据式(9)有:
| $ $$\eqalign{ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\mathit{\boldsymbol{a}} \circ \mathit{\boldsymbol{b}}) \circ \mathit{\boldsymbol{c}} = ( - \mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{b}}) \circ \mathit{\boldsymbol{c}} + (\mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}}) \circ \mathit{\boldsymbol{c}} = \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - (\mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{b}})\mathit{\boldsymbol{c}} - (\mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}}) \cdot \mathit{\boldsymbol{c}} + (\mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}}) \times c = \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - (\mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{b}})\mathit{\boldsymbol{c}} - (\mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}}) \cdot \mathit{\boldsymbol{c}} + \mathit{\boldsymbol{a}} \times (\mathit{\boldsymbol{b}} \times \mathit{\boldsymbol{c}}) + \cr & (\mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{b}})\mathit{\boldsymbol{c}} - \mathit{\boldsymbol{a}}(\mathit{\boldsymbol{b}} \cdot \mathit{\boldsymbol{c}}) = - \mathit{\boldsymbol{a}}(\mathit{\boldsymbol{b}} \cdot \mathit{\boldsymbol{c}}) - (\mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}}) \cdot \mathit{\boldsymbol{c}} + \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{a}} \times (\mathit{\boldsymbol{b}} \times \mathit{\boldsymbol{c}}) = - (\mathit{\boldsymbol{b}} \cdot \mathit{\boldsymbol{c}})\mathit{\boldsymbol{a}} - \mathit{\boldsymbol{a}} \cdot (\mathit{\boldsymbol{b}} \times \mathit{\boldsymbol{c}}) + \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{a}} \times (\mathit{\boldsymbol{b}} \times \mathit{\boldsymbol{c}}) = \mathit{\boldsymbol{a}} \circ ( - \mathit{\boldsymbol{b}} \cdot \mathit{\boldsymbol{c}}) + \mathit{\boldsymbol{a}} \circ (\mathit{\boldsymbol{b}} \times \mathit{\boldsymbol{c}}) = \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{a}} \circ (\mathit{\boldsymbol{b}} \circ \mathit{\boldsymbol{c}}) \cr} $$ $ |
也就是说,向量的格拉斯曼积满足结合律。当然也可证明:
| $ (\lambda \circ \boldsymbol{b}) \circ \boldsymbol{c} = \lambda \circ (\boldsymbol{b} \circ \boldsymbol{c}) = \lambda (\boldsymbol{b} \circ \boldsymbol{c}) $ |
式中,λ为标量。
向量a的共轭a、范数‖ a ‖、绝对值| a |和逆a -1分别定义为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{a}^ * } = - \boldsymbol{a}}\\ {\left\| \boldsymbol{a} \right\| = {{\left| \boldsymbol{a} \right|}^2} = \boldsymbol{a} \circ {\boldsymbol{a}^ * } = {\boldsymbol{a}^ * } \circ \boldsymbol{a} = \boldsymbol{a} \cdot a}\\ {{\boldsymbol{a}^{ - 1}} = {{(\boldsymbol{a} \cdot \boldsymbol{a})}^{ - 1}}{\boldsymbol{a}^ * } = - {{(\boldsymbol{a} \cdot \boldsymbol{a})}^{ - 1}}\boldsymbol{a}} \end{array}} \right. $ | (10) |
因此,向量a与其共轭a和逆a -1的方向相反。当a是单位向量时,有a = a -1。
3 四元数的定义与其运算法则任意两个向量之间的格拉斯曼乘积给出了一个新的数学概念,即四元数。四元数就是标量与向量的组合,即
| $ $$\mathit{\boldsymbol{Q}} \equiv {q_0} + \mathit{\boldsymbol{q}}$$ $ | (11) |
式中,Q称为四元数,它由标量部q0和向量部q组合而成。定义四元数Q的共轭值为:
| $ $$\mathit{\boldsymbol{Q}}* \equiv {q_0} - \mathit{\boldsymbol{q}}$$ $ | (12) |
四元数Q的绝对值定义为:
| $ $${\left| \mathit{\boldsymbol{Q}} \right|^2} = {({q_0})^2} + \mathit{\boldsymbol{q}} \cdot \mathit{\boldsymbol{q}}$$ $ | (13) |
四元数的绝对值应该是非负实数。
设有两个四元数:
| $ $$\mathit{\boldsymbol{P}} = {p_0} + \mathit{\boldsymbol{p}},\mathit{\boldsymbol{Q}} = {q_0} + \mathit{\boldsymbol{q}}$$ $ |
定义其加减法为:
| $ $$\mathit{\boldsymbol{P}} \pm \mathit{\boldsymbol{Q}} \equiv ({p_0} \pm {q_0}) + (\mathit{\boldsymbol{p}} \pm \mathit{\boldsymbol{q}})$$ $ | (14) |
显然,四元数满足加减法的交换律和结合律。
根据式(2)和式(9)可知,两个四元数的格拉斯曼乘积为:
| $ $$\matrix{ {\mathit{\boldsymbol{P}}\circ \mathit{\boldsymbol{Q}} \equiv ({p_0} + \mathit{\boldsymbol{p}})\circ ({q_0} + \mathit{\boldsymbol{q}})} \cr { = {p_0}\circ {q_0} + {p_0}\circ \mathit{\boldsymbol{q}} + \mathit{\boldsymbol{p}}\circ {q_0} + \mathit{\boldsymbol{p}}\circ \mathit{\boldsymbol{q}}} \cr { = ({p_0}{q_0} - \mathit{\boldsymbol{p}} \cdot \mathit{\boldsymbol{q}}) + ({p_0}\mathit{\boldsymbol{q}} + {q_0}\mathit{\boldsymbol{p}} + \mathit{\boldsymbol{p}} \times \mathit{\boldsymbol{q}})} \cr } $$ $ | (15) |
显然,两个四元数之间的格拉斯曼积不满足交换律,但是满足分配率和结合律,即
| $ $$\eqalign{ & \mathit{\boldsymbol{G}} \circ (\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{Q}}) = (\mathit{\boldsymbol{G}} \circ \mathit{\boldsymbol{P}}) + (\mathit{\boldsymbol{G}} \circ \mathit{\boldsymbol{Q}}) \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{G}} \circ (\mathit{\boldsymbol{P}} \circ \mathit{\boldsymbol{Q}}) = (\mathit{\boldsymbol{G}} \circ \mathit{\boldsymbol{P}}) \circ \mathit{\boldsymbol{Q}} \cr} $$ $ |
这里,四元数G =g0+g,证明从略。根据四元数的共轭值可得:
| $ $$\matrix{ {(\mathit{\boldsymbol{P}}\circ \mathit{\boldsymbol{Q}})^*} = ({p_0}{q_0} - \mathit{\boldsymbol{p}} \cdot \mathit{\boldsymbol{q}}) - ({q_0}\mathit{\boldsymbol{p}} + {p_0}\mathit{\boldsymbol{q}} + \hfill \cr \mathit{\boldsymbol{p}} \times \mathit{\boldsymbol{q}}) = ({q_0} - \mathit{\boldsymbol{q}})\circ ({p_0} - \mathit{\boldsymbol{p}}) = \mathit{\boldsymbol{Q}}^*\circ \mathit{\boldsymbol{P}}^* \hfill \cr} $$ $ |
当然,也可证明:
| $ $$\left( {\mathit{\boldsymbol{G}}\circ \mathit{\boldsymbol{P}}\circ \mathit{\boldsymbol{Q}}} \right)^* = \mathit{\boldsymbol{Q}}^*\circ \mathit{\boldsymbol{P}}^*\circ \mathit{\boldsymbol{G}}^*$$ $ |
上式可扩展到任意多个四元数格拉斯曼乘积的情况。同时,可证明:
| $ $${\left| \mathit{\boldsymbol{Q}} \right|^2} = \mathit{\boldsymbol{Q}}\circ \mathit{\boldsymbol{Q}}^* = \mathit{\boldsymbol{Q}}^*\circ \mathit{\boldsymbol{Q}}$$ $ | (16) |
也就是说,四元数Q的绝对值的平方等于其与共轭值的格拉斯曼积。
4 所有四元数都等价于两个向量的格拉斯曼积任何四元数都可以表示为两个向量a和b之间的格拉斯曼积,即
| $ $$\mathit{\boldsymbol{Q}} \equiv {q_0} + \mathit{\boldsymbol{q}} \equiv \mathit{\boldsymbol{a}}\circ \mathit{\boldsymbol{b}} \equiv - \mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{b}} + \mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}}$$ $ | (17) |
证明:令
| $ $${\left| \mathit{\boldsymbol{Q}} \right|^2} = {({q_0})^2} + {\left| \mathit{\boldsymbol{q}} \right|^2} = {({q_0})^2} + \mathit{\boldsymbol{q}} \cdot \mathit{\boldsymbol{q}}$$ $ |
再令
| $ $${q_0} = \left| \mathit{\boldsymbol{Q}} \right|\cos \theta ,\mathit{\boldsymbol{q}} = \left| \mathit{\boldsymbol{q}} \right|\mathit{\boldsymbol{\hat q}} = \mathit{\boldsymbol{\hat q}}\left| \mathit{\boldsymbol{Q}} \right|\sin \theta $$ $ |
那么式(17)可化为:
| $ $$\matrix{ \mathit{\boldsymbol{Q}} \equiv {q_0} + \mathit{\boldsymbol{q}} = \left| \mathit{\boldsymbol{Q}} \right|\left( {\cos \theta + \mathit{\boldsymbol{\hat q}}\sin \theta } \right) = \hfill \cr - \left| \mathit{\boldsymbol{Q}} \right|\cos \left( {\pi - \theta } \right) + \left| \mathit{\boldsymbol{Q}} \right|\mathit{\boldsymbol{\hat q}}\sin \left( {\pi - \theta } \right) \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - \mathit{\boldsymbol{a}} \cdot \mathit{\boldsymbol{b}} + \mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}} \hfill \cr} $$ $ |
式中,约定| a || b |=| Q |,两个向量a和b之间的夹角是(π-θ)。式(17)证毕。
5 向量旋转公式如图 2所示,向量
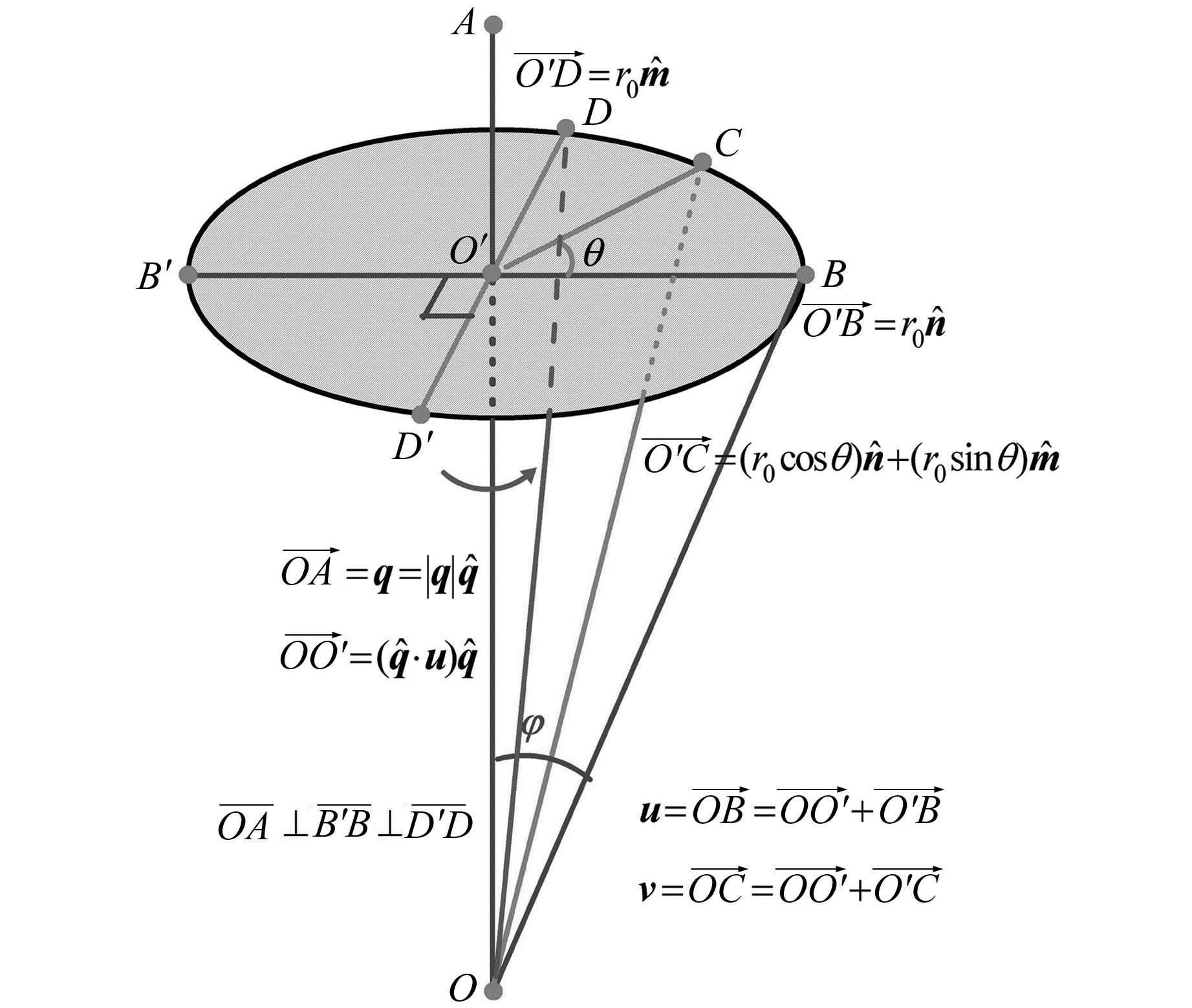
|
图 2 向量旋转示意图 Fig. 2 Vector rotation |
| $ $$\eqalign{ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\hat n}} = {{\overrightarrow {{{O'B}}} } \over {\left| {\overrightarrow {{{O'B}}} } \right|}} = {{\mathit{\boldsymbol{u}} - \overrightarrow {{{OO'}}} } \over {\left| {{\\\mathit{\boldsymbol{u}}} - \overrightarrow {{{OO'}}} } \right|}} \cr & \mathit{\boldsymbol{\hat m}} = {{\overrightarrow {{{O'D}}} } \over {\left| {\overrightarrow {{{O'D}}} } \right|}} = {{\mathit{\boldsymbol{\hat q}} \times \overrightarrow {{{O'B}}} } \over {\left| {\mathit{\boldsymbol{\hat q}} \times \overrightarrow {{{O'B}}} } \right|}} = {{\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}}} \over {\left| {\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}}} \right|}} \cr} $$ $ |
假设
| $ $$\matrix{ {{r_0} = \left| {\overrightarrow {{{O'B}}} } \right| = \left| {\mathit{\boldsymbol{u}} - \overrightarrow {{{OO'}}} } \right| = \left| {\overrightarrow {{{OO'}}} } \right| = } \hfill \cr {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {\mathit{\boldsymbol{\hat q}} \times \overrightarrow {{{O'B}}} } \right| = \left| {\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}}} \right|} \hfill \cr } $$ $ |
由于
| $ $$\matrix{ {\overrightarrow {{{O'C}}} = {r_0}\cos \theta \mathit{\boldsymbol{\hat n}} + {r_0}\sin \theta \mathit{\boldsymbol{\hat m}}} \cr { = (\mathit{\boldsymbol{u}} - \overrightarrow {{{OO'}}} )\cos \theta + (\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}})\sin \theta } \cr } $$ $ |
另外,向量
| $ $$\overrightarrow {{{OO'}}} = (\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}}$$ $ |
这样向量v就可表示为:
| $ $$\matrix{ \matrix{ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{v}} = \overrightarrow {{{OO'}}} + \overrightarrow {{{O'C}}} = \overrightarrow {{{OO'}}} + (\mathit{\boldsymbol{u}} - \overrightarrow {{{OO'}}} )\cos \theta + \hfill \cr (\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}})\sin \theta = (\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}} + \left[ {\mathit{\boldsymbol{u}} - (\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}}} \right]\cos \theta + \hfill \cr (\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}})\sin \theta = \mathit{\boldsymbol{u}}\cos \theta + (\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}}(1 - \cos \theta ) + \hfill \cr} \cr {(\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}})\sin \theta } } $$ $ | (18) |
式(18)就是著名的向量旋转的欧拉公式[21]。
利用四元数的定义与运算法则,可把式(18)写为:
| $ $$\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{\hat Q}}\circ \mathit{\boldsymbol{u}}\circ \mathit{\boldsymbol{\hat Q}}^*$$ $ | (19) |
其中,
| $ $$\eqalign{ & \mathit{\boldsymbol{\hat Q}} = - \mathit{\boldsymbol{\hat a}} \cdot \mathit{\boldsymbol{\hat b}} + \mathit{\boldsymbol{\hat a}} \times \mathit{\boldsymbol{\hat b = }} \cr & \left( {\cos {\theta \over 2} + \mathit{\boldsymbol{\hat q}}\sin {\theta \over 2}} \right) \cr} $$ $ | (20) |
式中,â和
考虑到任意两个向量的格拉斯曼乘积的表述(式(9)),那么有:
| $ $$\eqalign{ & \mathit{\boldsymbol{\hat q}}\circ \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{u}}\circ \mathit{\boldsymbol{\hat q}} = 2(\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}}) \cr & \mathit{\boldsymbol{\hat q}}\circ \mathit{\boldsymbol{u}}\circ \mathit{\boldsymbol{\hat q}} = \mathit{\boldsymbol{u}} - 2(\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}} \cr} $$ $ |
由此,式(18)可进一步改写为:
| $ $$\matrix{ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{u}}\cos \theta + (\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}}(1 - \cos \theta ) + } \hfill \cr {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}})\sin \theta = \left( {1 - 2{{\sin }^2}{\theta \over 2}} \right)\mathit{\boldsymbol{u}} + } \hfill \cr {2{{\sin }^2}{\theta \over 2}(\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}} + 2\sin {\theta \over 2}\cos {\theta \over 2}(\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}}) = } \hfill \cr {\left( {1 - {{\sin }^2}{\theta \over 2}} \right)\mathit{\boldsymbol{u}} - {{\sin }^2}{\theta \over 2}\left[ {\mathit{\boldsymbol{u}} - 2(\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}}} \right] + } \hfill \cr {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin {\theta \over 2}\cos {\theta \over 2}\left[ {2(\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}})} \right] = {{\cos }^2}{\theta \over 2}\mathit{\boldsymbol{u}} + } \hfill \cr {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin {\theta \over 2}\cos {\theta \over 2}\left[ {2(\mathit{\boldsymbol{\hat q}} \times \mathit{\boldsymbol{u}})} \right] - } \hfill \cr {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\sin }^2}{\theta \over 2}\left[ {\mathit{\boldsymbol{u}} - 2(\mathit{\boldsymbol{\hat q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{\hat q}}} \right] = {{\cos }^2}{\theta \over 2}\mathit{\boldsymbol{u}} + } \hfill \cr {\sin {\theta \over 2}\cos {\theta \over 2}\left[ {\mathit{\boldsymbol{\hat q}}^\circ \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{u}}^\circ \mathit{\boldsymbol{\hat q}}} \right] - {{\sin }^2}{\theta \over 2}\mathit{\boldsymbol{\hat q}}^\circ \mathit{\boldsymbol{u}}^\circ \mathit{\boldsymbol{\hat q}} = } \hfill \cr {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\cos {\theta \over 2} + \mathit{\boldsymbol{\hat q}}\sin {\theta \over 2}} \right)^\circ \mathit{\boldsymbol{u}}^\circ \left( {\cos {\theta \over 2} - \mathit{\boldsymbol{\hat q}}\sin {\theta \over 2}} \right)} \hfill \cr } $$ $ | (21) |
这样,式(19)证毕。
5.2 式(19)的证明方法之二:直接导出法由于
| $ $$\mathit{\boldsymbol{\hat q}}\circ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{\hat q}}\circ \overrightarrow {{{OO'}}} + \mathit{\boldsymbol{\hat q}}\circ \overrightarrow {{{O'B}}} $$ $ |
| $ $$\mathit{\boldsymbol{u}}\circ \mathit{\boldsymbol{\hat q}} = \overrightarrow {{{OO'}}} \circ \mathit{\boldsymbol{\hat q}} + \overrightarrow {{{O'B}}} \circ \mathit{\boldsymbol{\hat q}} = \mathit{\boldsymbol{\hat q}}\circ \overrightarrow {{{OO'}}} - \mathit{\boldsymbol{\hat q}}\circ \overrightarrow {{{O'B}}} $$ $ |
进而可得:
| $ $$\mathit{\boldsymbol{\hat q}}\circ \overrightarrow {{{OO'}}} = {1 \over 2}\left( {\mathit{\boldsymbol{\hat q}}\circ \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{u}}\circ \mathit{\boldsymbol{\hat q}}} \right)$$ $ |
| $ $$\mathit{\boldsymbol{\hat q}}\circ \overrightarrow {{{O'B}}} = {1 \over 2}\left( {\mathit{\boldsymbol{\hat q}}\circ \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{u}}\circ \mathit{\boldsymbol{\hat q}}} \right)$$ $ |
以上两式的两边作格拉斯曼左积
| $ $$\overrightarrow {{{OO'}}} = {1 \over 2}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{\hat q}}\circ \mathit{\boldsymbol{u}}^\circ \mathit{\boldsymbol{\hat q}}} \right)$$ $ |
| $ \overrightarrow {O'B} = {1 \over 2}\left( {\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{\hat q}}\circ \mathit{\boldsymbol{u}}\circ \mathit{\boldsymbol{\hat q}}} \right) $ |
由于
| $ \eqalign{ & \overrightarrow {O'C} = {r_0}\cos \theta {{\overrightarrow {O'B} } \over {\left| {\overrightarrow {O'B} } \right|}} + {r_0}\sin \theta {{\mathit{\boldsymbol{\hat q}}\circ \overrightarrow {O'B} } \over {\left| {\overrightarrow {O'D} } \right|}} = \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos \theta \overrightarrow {O'B} + \sin \theta \mathit{\boldsymbol{\hat q}}\circ \overrightarrow {O'B} \cr} $ |
因此,可把向量v表示为:
| $ $$\eqalign{ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{v}} = \overrightarrow {{{OO'}}} + \overrightarrow {{{O'C}}} = \overrightarrow {{{OO'}}} + \cos \theta \overrightarrow {{{O'B}}} + \cr & \sin \theta \mathit{\boldsymbol{\hat q}} \circ \overrightarrow {{{O'B}}} = {1 \over 2}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{\hat q}} \circ \mathit{\boldsymbol{u}} \circ \mathit{\boldsymbol{\hat q}}} \right) + \cos \theta {1 \over 2}\left( {\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{\hat q}} \circ \mathit{\boldsymbol{u}} \circ \mathit{\boldsymbol{\hat q}}} \right) \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \sin \theta \mathit{\boldsymbol{\hat q}} \circ {1 \over 2}\left( {\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{\hat q}} \circ \mathit{\boldsymbol{u}} \circ \mathit{\boldsymbol{\hat q}}} \right) = {\cos ^2}{\theta \over 2}\mathit{\boldsymbol{u}} - \cr & {\sin ^2}{\theta \over 2}\left( {\mathit{\boldsymbol{\hat q}} \circ \mathit{\boldsymbol{u}} \circ \mathit{\boldsymbol{\hat q}}} \right) + \sin {\theta \over 2}\cos {\theta \over 2}\left( {\mathit{\boldsymbol{\hat q}} \circ \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{u}} \circ \mathit{\boldsymbol{\hat q}}} \right) = \cr & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\cos {\theta \over 2} + \mathit{\boldsymbol{\hat q}}\sin {\theta \over 2}} \right) \circ \mathit{\boldsymbol{u}} \circ \left( {\cos {\theta \over 2} - \mathit{\boldsymbol{\hat q}}\sin {\theta \over 2}} \right) \cr} $$ $ | (22) |
这也从另一方面证明式(19)成立。
6 讨论与分析如果令四元数
| $ $$\mathit{\boldsymbol{U}} = {u_0} + \mathit{\boldsymbol{u}},\mathit{\boldsymbol{V}} = {v_0} + \mathit{\boldsymbol{v}},\mathit{\boldsymbol{Q}} = {q_0} + \mathit{\boldsymbol{q}}$$ $ |
使得它们之间满足下面的函数关系:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{Q}}\circ \mathit{\boldsymbol{U}}\circ \mathit{\boldsymbol{Q}}^* $ | (23) |
利用式(15)给出的四元数格拉斯曼积,可把式(23)表示为:
| $ $$\left\{ {\matrix{ {{v_0} = \left[ {{{({q_0})}^2} + \mathit{\boldsymbol{q}} \cdot \mathit{\boldsymbol{q}}} \right]{u_0} = {{\left| \mathit{\boldsymbol{Q}} \right|}^2}{u_0}} \hfill \cr {\mathit{\boldsymbol{v}} = \left[ {{{({q_0})}^2} - \mathit{\boldsymbol{q}} \cdot \mathit{\boldsymbol{q}}} \right]\mathit{\boldsymbol{u}} + 2(\mathit{\boldsymbol{q}} \cdot \mathit{\boldsymbol{u}})\mathit{\boldsymbol{q}} + 2{q_0}\mathit{\boldsymbol{q}} \times \mathit{\boldsymbol{u}}} \hfill \cr } } \right.$$ $ | (24) |
当Q是单位四元数时(例如式(20)),式(24)的第一式变为v0=u0,式(24)的第二式就可化为式(18)。由于四元数的格拉斯曼积满足结合律,当| Q |=1时,利用式(23)可得:
| $ $$\mathit{\boldsymbol{U}} = \mathit{\boldsymbol{Q}}^*\circ \mathit{\boldsymbol{V}}\circ \mathit{\boldsymbol{Q}}$$ $ | (25) |
因此,式(23)称为四元数的正交变换,式(25)称为其反变换。可见,利用单位四元数对向量进行正交变换时,就等价于该向量绕某个确定轴(构成单位四元数的向量方向)逆时针旋转一定角度后的新向量,这就是四元数正交变换的几何意义。
| [1] |
焦俊萍.四元数的发现及其意义[D].临汾: 山西师范大学, 2012 (Jiao Junping. Quaternions Discovery and Its Significance[D].Linfen: Shanxi Normal University, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10118-1012340600.htm
(  0) 0) |
| [2] |
德比希. 代数的历史:人类对未知量的不舍之追踪[M]. 北京: 人民邮电出版社, 2010 (Derbyshire J. Unknown Quantity: A Real and Imaginary History of Algebra[M]. Beijing: Post and Telecom Press, 2010)
(  0) 0) |
| [3] |
Crowe M J. A History of Vector Analysis[M]. New York: Dover Publications, 1985
(  0) 0) |
| [4] |
克莱因. 古今数学思想(第四册)[M]. 上海: 上海科学技术出版社, 2006 (Kline M. Mathematical Thought from Ancient to Modern Times(The Fourth Volumes)[M]. Shanghai: Shanghai Scientific and Technical Publishers, 2006)
(  0) 0) |
| [5] |
张祖贵. 四元数与代数学的变革[J]. 自然辩证法研究, 1987, 3(5): 49-56 (Zhang Zugui. The Reform of Quaternion and Algebra[J]. Studies in Dialectics of Nature, 1987, 3(5): 49-56)
(  0) 0) |
| [6] |
孙自行. 复数以后——我们能走多远[J]. 自然杂志, 1992, 15(8): 615-619 (Sun Zixing. How Far Can We Go after the Plural[J]. Chinese Journal of Nature, 1992, 15(8): 615-619)
(  0) 0) |
| [7] |
李迪. 中国科学技术史论文集[M]. 呼和浩特: 内蒙古教育出版社, 1991 (Li Di. A Collection of Papers on the History of Science and Technology in China[M]. Hohhot: Inner Mongolia Education Press, 1991)
(  0) 0) |
| [8] |
吴文俊. 世界著名科学家传记[M]. 北京: 科学出版社, 1995 (Wu Wenjun. Biographies of the World Famous Scientists[M]. Beijing: Science Press, 1995)
(  0) 0) |
| [9] |
李文林. 数学珍宝[M]. 北京: 科学出版社, 1998 (Li Wenlin. Mathematics Treasure[M]. Beijing: Science Press, 1998)
(  0) 0) |
| [10] |
李文林. 数学史概论[M]. 北京: 高等教育出版社, 2002 (Li Wenlin. A History of Mathematics[M]. Beijing: Higher Education Press, 2002)
(  0) 0) |
| [11] |
张顺燕. 数学的源与流[M]. 北京: 高等教育出版社, 2000 (Zhang Shunyan. The Origin and Flow of Mathematics[M]. Beijing: Higher Education Press, 2000)
(  0) 0) |
| [12] |
梁宗巨, 王青建, 孙宏安. 世界数学通史(上册)[M]. 沈阳: 辽宁教育出版社, 2004 (Liang Zongju, Wang Qingjian, Sun Hongan. General History of World Mathematics[M]. Shenyang: Liaoning Education Press, 2004)
(  0) 0) |
| [13] |
孙庆华.向量理论历史研究[D].西安: 西北大学, 2006 (Sun Qinghua. A Research of the History of the Vector Theory[D].Xi'an: Northwest University, 2006) http://d.wanfangdata.com.cn/Thesis/Y894250
(  0) 0) |
| [14] |
Goldman R. Understanding Quaternions[J]. Graphical Models, 2011, 73: 21-49 DOI:10.1016/j.gmod.2010.10.004
(  0) 0) |
| [15] |
Pujol J. On Hamilton's Nearly-Forgotten Early Work on the Relation between Rotations and Quaternions and on the Composition of Rotations[J]. American Mathematical Monthly, 2014, 121(6): 515-522 DOI:10.4169/amer.math.monthly.121.06.515
(  0) 0) |
| [16] |
戚宪东, 郭英, 孙玉曦, 等. 基于四元数法的航向修正算法分析[J]. 全球定位系统, 2018, 43(2): 7-11 (Qi Xiandong, Guo Ying, Sun Yuxi, et al. Analysis of Heading Correction Algorithm Based on Quaternion Method[J]. GNSS World of China, 2018, 43(2): 7-11)
(  0) 0) |
| [17] |
马涛峰, 卢小平, 禄丰年. 基于对偶四元数的三维空间坐标转换直接解法[J]. 大地测量与地球动力学, 2017, 37(12): 1276-1280 (Ma Taofeng, Lu Xiaoping, Lu Fengnian. A Direct Solution of Three-Dimensional Space Coordinate Transformation Based on Dual Quaternion[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1276-1280)
(  0) 0) |
| [18] |
张德先, 聂桂根. 基于分解四元数的自适应姿态四元数卡尔曼滤波[J]. 控制理论与应用, 2018, 35(3): 367-374 (Zhang Dexian, Nie Guigen. Adaptive Attitude Quaternion Kalman Filter Based on Factored Quaternions[J]. Control Theory and Applications, 2018, 35(3): 367-374)
(  0) 0) |
| [19] |
伏家杰, 周翟和, 尹辉, 等. 基于四元数二阶互补滤波的四旋翼姿态解算[J]. 机械制造与自动化, 2019, 48(2): 169-172 (Fu Jiajie, Zhou Zhaihe, Yin Hui, et al. Attitude Estimation of Quadrotor Based on Quaternion Second Order Complementary Filter Algorithm[J]. Machine Building & Automation, 2019, 48(2): 169-172)
(  0) 0) |
| [20] |
鲁丹丹, 翟永翠, 周玉芳. 基于四元数的DR技术[J]. 指挥控制与仿真, 2019, 41(2): 98-103 (Lu Dandan, Zhai Yongcui, Zhou Yufang. DR Technology Based on Quaternion[J]. Command Control and Simulation, 2019, 41(2): 98-103 DOI:10.3969/j.issn.1673-3819.2019.02.019)
(  0) 0) |
| [21] |
Euler L. Nova Methodus Motum Corporum Rigidorum Determinandi[J]. Novi Commentari Academiae Imperialis Petropolitanae, 1776, 20: 208-238
(  0) 0) |
2. School of Urban Planning and Landscape Architecture, Xuchang University, 88 Bayi Road, Xuchang 461000, China
 2020, Vol. 40
2020, Vol. 40

