2. 贵州大学林学院,贵阳市甲秀南路西,550025;
3. 贵州省第一测绘院,贵阳市花溪大道南段1268号,550025
全球卫星导航系统反演大气水汽技术是20世纪90年代发展起来的一种全新的大气探测手段,具有精度高、成本低、时间分辨率高、全球覆盖和全天候观测等优点,可作为传统大气探测手段的有力补充[1-2]。地基GNSS水汽反演是通过对流层天顶湿延迟(zenith total delay,ZWD)乘以水汽转换系数(Π)得到PWV,而Π的精度主要取决于Tm的质量,故Tm是地基GNSS反演PWV的关键参数之一[3]。
Tm的计算主要依赖于探测站上空的绝对温度和水汽压等气象元素,而这些气象元素往往不易获取。依据Tm与地表温度Ts的线性关系,Bevis等[4]基于美国的探空资料率先建立了适用于中纬度地区的经验Tm模型(下称“Bevis模型”)。但由于对流层存在区域差异性,Bevis模型应用于其他地区势必会产生较大偏差[5]。为实现Tm模型的本地化,基于Bevis的研究思路,学者们采用区域气象资料,建立了大量适用于区域的Tm模型[6-12]。贵州位于云贵高原斜坡上,全省大部分地区气候温和湿润,但在山地、河谷的气候垂直变化却特别明显。建立贵州局地Tm模型,开展PWV的反演研究,对于贵州区域气候变化监测、降水预报具有重要意义。为此,本文首先基于贵阳、威宁两个探空站2014~2016年的气象观测资料,采用数值积分法计算出Tm,并对Tm和Ts进行相关性分析;然后顾及对流层的区域差异性和季节差异性,分别建立贵州整体模型(Tm-GZ)、贵阳局地模型(Tm-GY)、威宁局地模型(Tm-WN),以及春(Tm-Spr)、夏(Tm-Sum)、秋(Tm-Fal)、冬(Tm-Win)4个季节模型;最后通过与现有模型的Tm计算值进行比较,分析局地模型反演所得PWV与实际降水的关系,并对贵州局地Tm模型的精度进行验证。
1 数据处理方法 1.1 数据来源本文使用的探空数据来自怀俄明州立大学网站(http://weather.uwyo.edu/upperair/sounding),时间为2014~2017年(该时间段内探空数据无缺失),探空站具体情况见表 1。降水与地表温度数据来源于中国气象数据网(http://data.cma.cn/data)。
|
|
表 1 探空站信息 Tab. 1 Information of radiosonde stations |
由GNSS反演PWV的表达式为:
| $ {\rm{PWV}} = \mathit{\Pi} *{\rm{ZWD}} $ | (1) |
式中,Π为水汽转换系数,其计算式为:
| $ \mathit{\Pi} = \frac{{{{10}^6}}}{{{\rho _w}{R_v}({{k'}_2} + {k_3}/{T_m})}} $ | (2) |
式中,ρw为液态水的密度(一般取1×103 kg/m3),Rv为水汽的气体常数(取值为461.495 J/(kg·K)),k′2和k3为大气折射常数(k′2=22.13±2.2 K/hPa、k3=(3.739±0.012)×105 K/hPa),Tm可由测站上空水汽压和绝对气温沿天顶方向通过数值积分解求[13]。
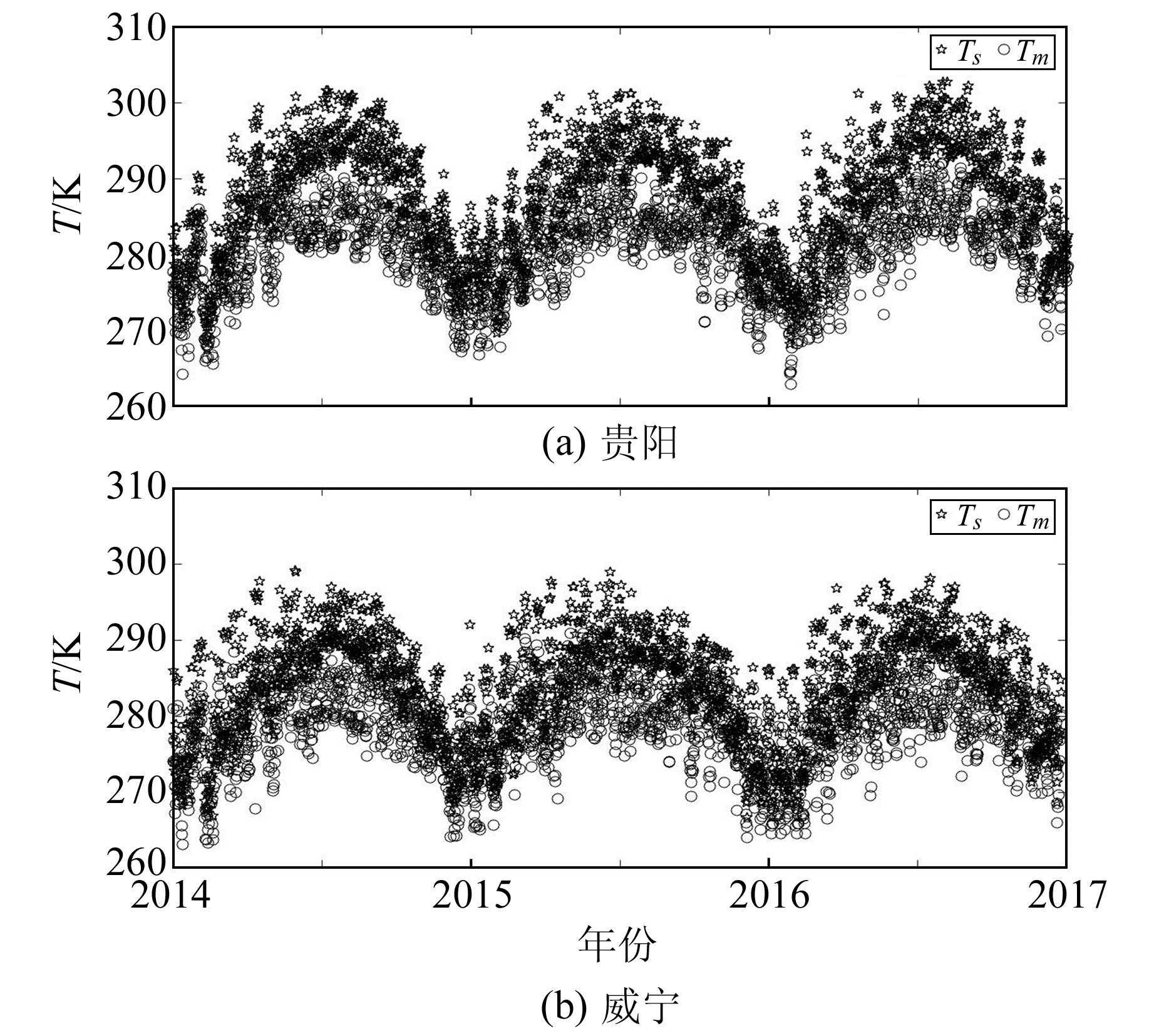
2 贵州局地大气加权平均温度模型的建立由于探空站分布稀疏,且探空数据时间分辨率较低,导致Tm值的计算受到一定的限制。学者们往往采用统计分析的方法建立Tm与Ts的关系式,进而依据关系式基于Ts解求Tm。为分析贵州局地Tm与Ts的变化特征,绘制出贵阳、威宁地区2014~2016年Tm与Ts的散点图(图 1)。
|
图 1 Tm与Ts散点图 Fig. 1 Scatter plot of Tm and Ts |
由图 1可看出,贵阳、威宁两地的Tm和Ts均具有一致的变化趋势,且Ts数值整体大于Tm。贵阳地区Tm的年均值为280.84 K,威宁地区Tm的年均值为285.11 K,两地Tm年均值相差4.27 K,Tm在地理位置上呈现出西高东低的特点。两地Tm出现较大差值可能与两地的海拔相差较大(高差为1 014 m),经度相差2.4°,年平均气温相差6 ℃,以及贵州在山地、河谷的气候垂直变化较大等因素有关。此外,Tm、Ts还呈现出明显的季节性变化特征,1~8月份逐渐增大,至7~8月达到峰值;9~12月逐渐减小,秋冬季节与春夏季节的Tm最大相差达35 K。上述分析表明,贵州地区Tm在空间和时间上均具有鲜明的特点。
为进一步分析Tm与Ts之间的函数关系,绘制贵州地区的Tm-Ts相关关系图(图 2)。由图可知,随着Ts的升高Tm也随之升高,Tm与Ts之间存在较好的线性正相关关系。

|
图 2 Tm与Ts相关关系 Fig. 2 Correlation between Tm and Ts |
因此,本文利用2014~2016年Tm和Ts数据,采用一元线性拟合方法,在空间上建立贵州整体大气加权平均温度模型(Tm-GZ)、以贵阳地区为代表的贵州中东部局地大气加权平均温度模型(Tm-GY)、以威宁地区为代表的贵州西部局地大气加权平均温度模型(Tm-WN),在时间上建立春、夏、秋、冬模型(Tm-Spr、Tm-Sum、Tm-Fal、Tm-Win)。设一元线性方程为:
| $ {T_m} = a + b{T_s} $ | (3) |
其误差方程为:
| $ \boldsymbol{V} = \left[ {\begin{array}{*{20}{c}} {\rm{1}}&{{T_s}} \end{array}} \right]\;\;\left[ {\begin{array}{*{20}{c}} a\\ b \end{array}} \right] - {T_m} $ | (4) |
基于最小二乘原理即可解求出系数a、b。由2014~2016年探空数据得到贵州局地Tm模型(表 2)。
|
|
表 2 贵州局地Tm模型 Tab. 2 Tm model in Guizhou |
由表 2可知,所有Tm模型中,Tm与Ts之间的相关系数均大于0.7,在统计学上表现为显著相关。此外,Tm-Sum模型中Tm与Ts之间的相关系数较低,这可能是由于夏季降水事件较多,导致Tm与Ts之间存在较大差异所致。
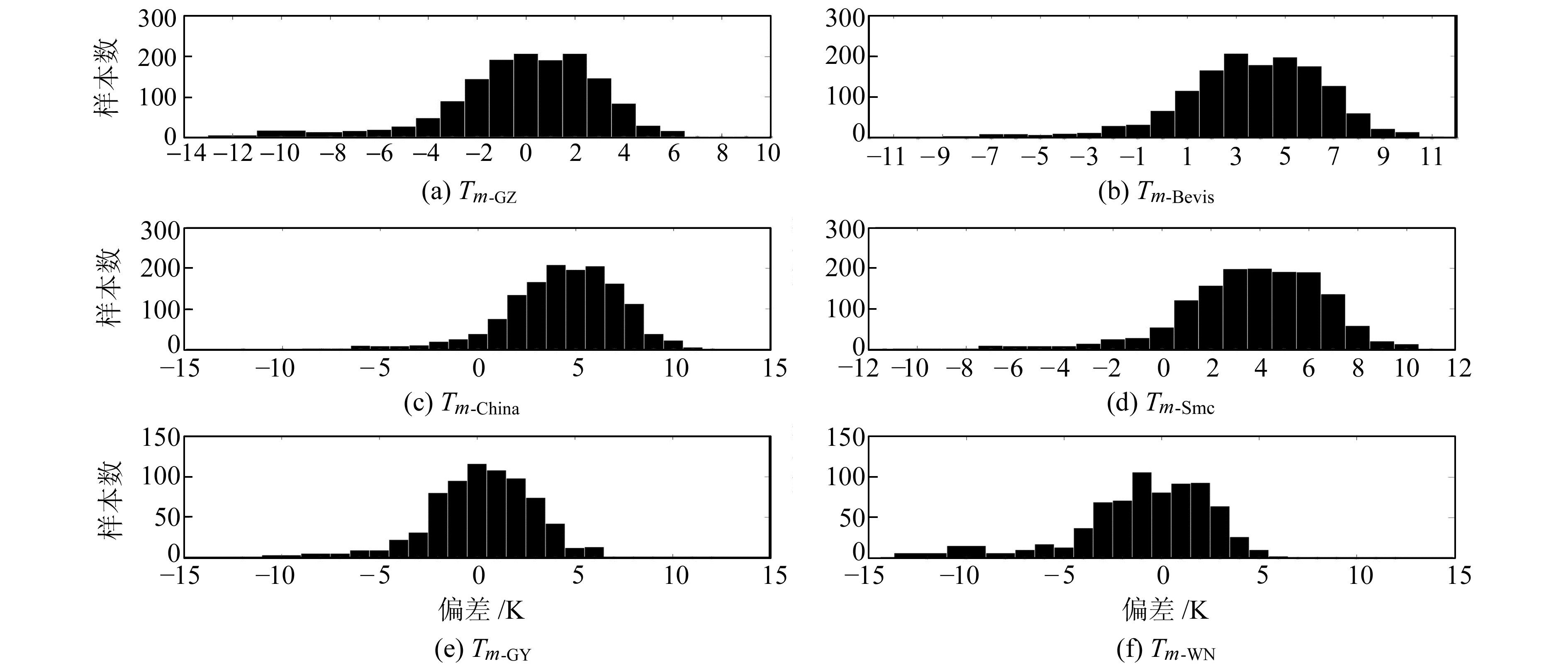
3 贵州局地Tm模型精度分析 3.1 贵州局地Tm模型与现有模型的比较将Tm-GZ、Tm-GY、Tm-WN、Bevis模型(Tm-Bevis=0.72Ts+70.20)、龚绍琦建立的全国模型(Tm-China=0.594Ts+105.450)和亚热带季风气候模型(Tm-Smc=0.650Ts+90.100)计算的2017年Tm值与基于探空资料计算的Tm(计算方法详见文献[13])参考值进行比较,绘制图 3所示的偏差直方图。由图可见,Tm-GZ、Tm-GY、Tm-WN的偏差在-4~4 K之间,Tm-Bevis的偏差在-1~8 K之间,Tm-China与Tm-Smc的偏差在0~8 K之间。相较于Tm-WN模型,Tm-GY模型的偏差分布更加集中,这主要得益于贵阳探空站测量的分层探空数据比威宁探空数据密集,获取的Tm数据质量较好,且威宁地区气候变化较贵阳地区更加突出。
|
图 3 Tm模型偏差直方图 Fig. 3 Tm model deviation histogram |
Tm模型的精度如表 3、表 4所示。由表 3可以看出,Tm-GZ模型的平均偏差、标准差、均方根误差均小于Tm-Bevis、Tm-China和Tm-Smc模型的结果。
|
|
表 3 Tm-GZ模型与其他模型的精度对比 Tab. 3 Comparison of different Tm model accuracy |
|
|
表 4 局地Tm模型的精度对比 Tab. 4 Comparison of local Tm model accuracy |
由表 4可以看出,Tm-GZ、Tm-GY、Tm-WN模型的平均偏差与标准差基本相同,而Tm-GY和Tm-WN模型的均方根误差均小于Tm-GZ模型的结果。因此局地模型较整体模型的精度有所提高,可以利用Tm-GY、Tm-WN获得更高精度的Tm值。
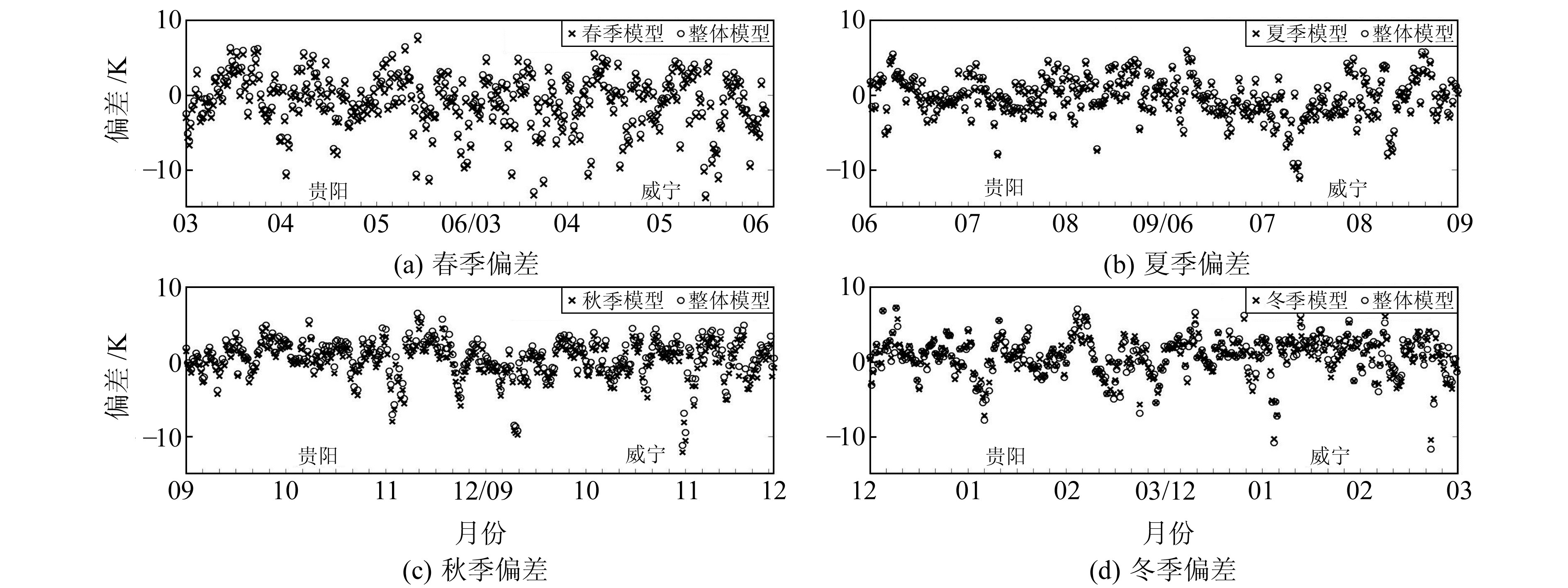
由Tm-GZ、Tm-Spr、Tm-Sum、Tm-Fal、Tm-Win模型分别计算出2017年对应季节各自的Tm值,并以基于探空资料计算的Tm值作为参考值,计算各模型的Tm偏差,得到图 4所示的整体模型和季节模型的Tm偏差情况。
|
图 4 整体与季节模型的Tm偏差 Fig. 4 Tm deviation of overall and season models |
通过图 4可看出,相较于Tm-Spr模型, Tm-Sum、Tm-Fal、Tm-Win等3个模型的预测值更接近真值,Tm-Spr、Tm-Sum、Tm-Fal等3个模型在贵阳地区的偏差比威宁地区更加集中,而冬季Tm模型在威宁地区的偏差更加集中。产生这种现象的原因可能为:贵州地区夏半年受副热带高压控制,导致威宁地区在春、夏、秋季的降水更加频繁;冬半年由于受秦巴山阻挡,南下冷空气在西部形成静止锋,而中东部地区正好处于锋后,导致贵阳地区在冬季多阴雨天气[14]。Tm-GZ与Tm-Spr、Tm-Sum、Tm-Fal、Tm-Win的精度对比如表 5所示。由表 5可以看出,季节模型在夏、秋季的平均偏差、标准差、均方根误差比整体模型小,而在春、冬季的平均偏差、标准差、均方根误差比整体Tm模型略大。因此,在夏、秋季使用季节模型计算Tm值精度会有所提高。
|
|
表 5 季节Tm模型的精度对比 Tab. 5 Comparison of season Tm model accuracy |
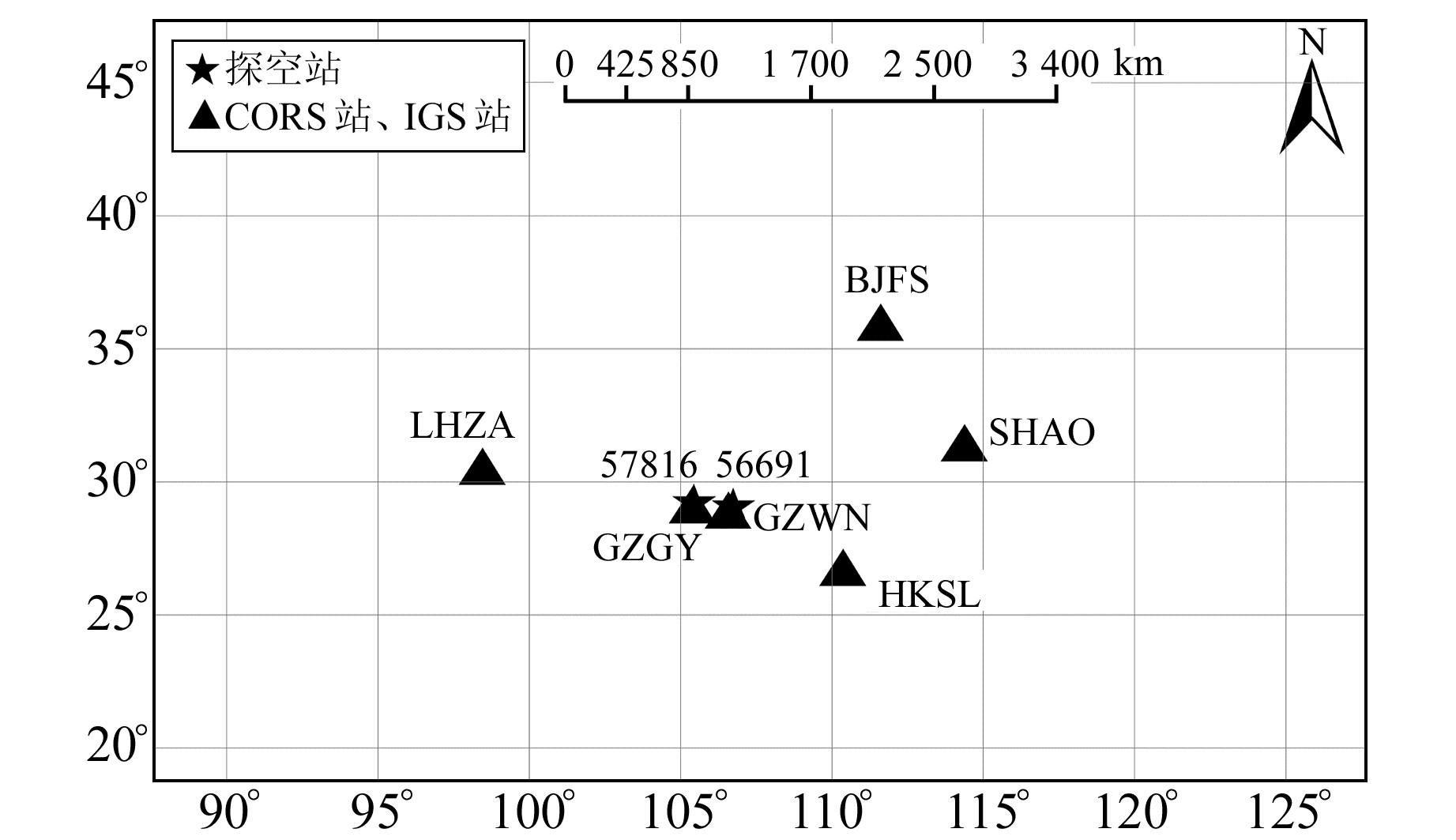
为进一步验证贵州局地Tm模型反演PWV的精度,选用2017-09-01~09-30贵阳、威宁CORS数据进行实验。为减少对流层延迟相关性,引入LHZA、HKSL、BJFS、SHAO等4个IGS站数据进行联合解算。CORS、IGS站、探空站的位置如图 5所示。
|
图 5 CORS、IGS站、探空站的分布 Fig. 5 Distribution of CORS, IGS and radiosonde stations |
基于表 6解算策略及参数设置,采用GAMIT软件分别解算出北京时间08:00和20:00贵阳、威宁的ZWD,具体的数据解算流程如图 6所示。
|
|
表 6 解算策略及参数设置 Tab. 6 Solution strategy and parameter settings |
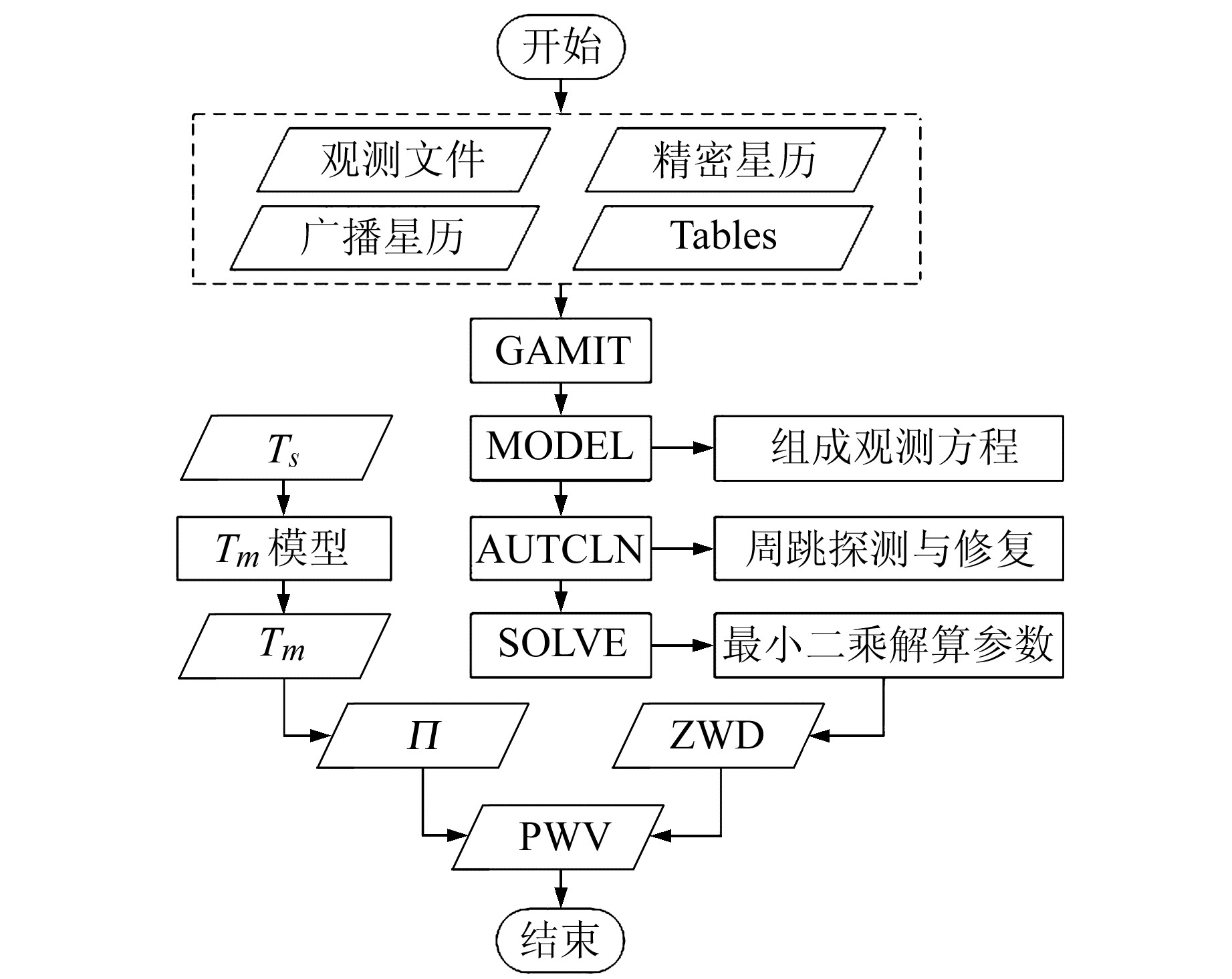
|
图 6 数据处理流程 Fig. 6 Data processing flow chart |
根据式(1)式和文献[2]的方法分别计算出探空可降水量(RS/PWV)、GY/PWV、WN/PWV,并将解算结果与实际降水量进行对比,结果如图 7所示。
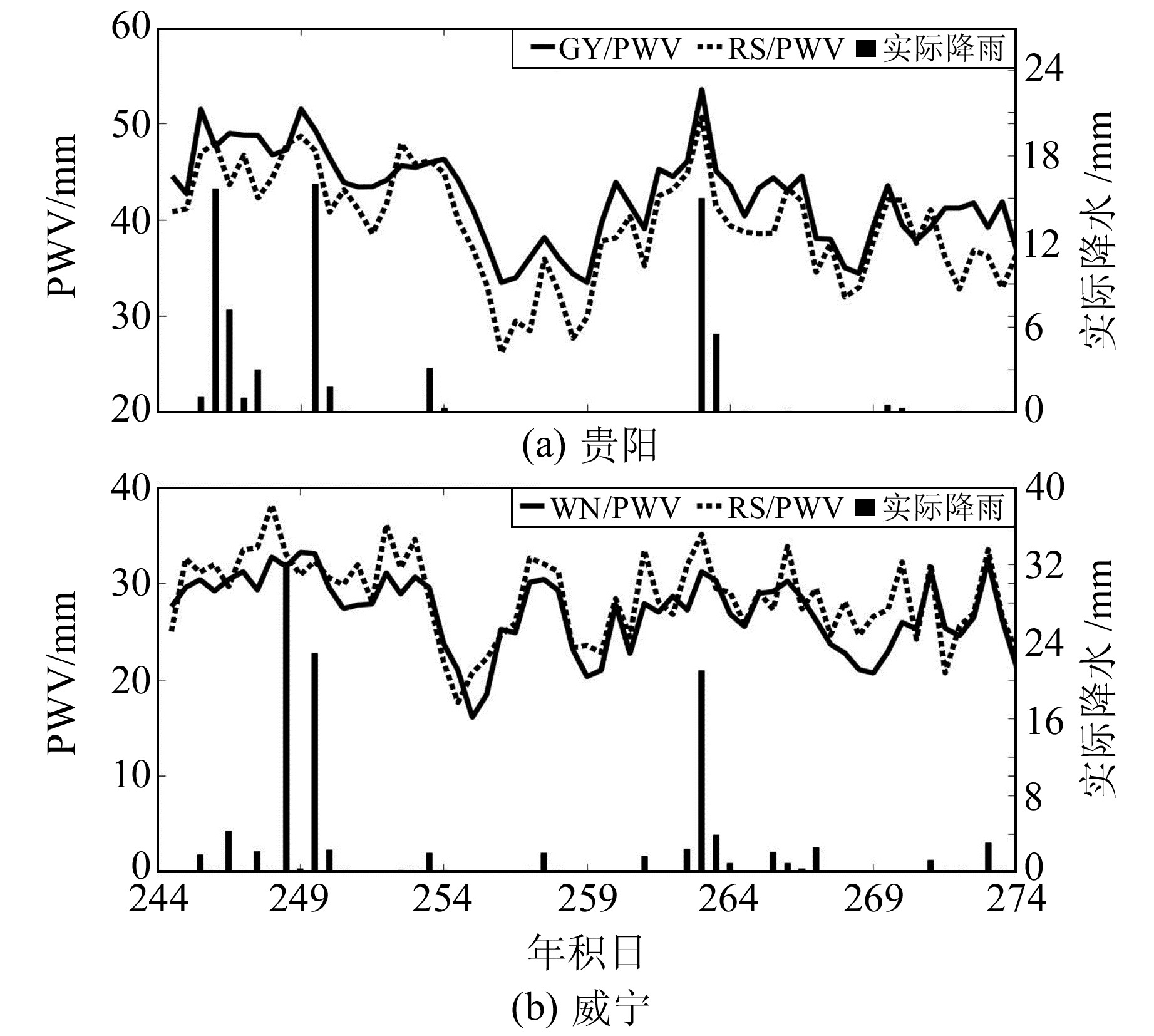
|
图 7 PWV与实际降水的关系 Fig. 7 Relationship between PWV and actual precipitation |
通过图 7可看出,RS/PWV与GY/PWV、WN/PWV的变化趋势基本一致;PWV在降水发生前连续增长,当其达到峰值时常伴有降水发生,PWV可以为降水预报提供有力依据。GY/PWV、WN/PWV、Bevis/PWV的精度对比如表 7所示。
|
|
表 7 PWV精度对比 Tab. 7 Comparison of PWV accuracy |
表 7中,GY/PWV的平均偏差、标准差、均方根误差较Bevis/PWV分别降低0.05 mm、0.06 mm、0.09 mm,WN/PWV分别降低0.07 mm、0.09 mm、0.14 mm,说明本地模型比Bevis模型精度高,更加有利于局地PWV的反演。
4 结语本文利用2014~2016年贵阳、威宁探空数据建立了贵州整体、局地、季节Tm模型,并对模型的精度进行分析,得到以下结论:1)贵州本地Tm模型精度高于Bevis模型、全国模型、亚热带季风气候模型;2)建立的贵阳、威宁局地Tm模型较贵州整体模型精度有所提高,季节模型在夏、秋季的精度高于整体模型;3)采用贵州局地Tm模型反演的PWV与RS/PWV变化趋势一致,很好地刻画了实际降水趋势,可为降水预报提供有力依据。此外,与Bevis/PWV相比,GY/PWV、WN/PWV的平均偏差、标准差、均方根误差均有所降低,说明贵州局地Tm模型具有较高的精度。
致谢: 感谢贵州省国土资源厅支持的贵州省北斗卫星导航定位基准站网(GZCORS)项目及贵州省第一测绘院(贵州省北斗导航位置服务中心)对本研究提供基准站数据;感谢国家信息中心提供气象数据;感谢怀俄明州立大学提供探空站数据。
| [1] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报:信息科学版, 2011, 36(4): 412-416 (Wang Xiaoying, Dai Ziqiang, Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-416)
(  0) 0) |
| [2] |
李剑锋, 王永前, 胡伍生. 地基GPS水汽反演中区域大气加权平均温度模型[J]. 测绘科学技术学报, 2015, 32(1): 13-17 (Li Jianfeng, Wang Yongqian, Hu Wusheng. Regional Weighted Average Atmospheric Temperature Model of Ground-Based GPS Water Vapor Retrieval[J]. Journal of Geomatics Science and Technology, 2015, 32(1): 13-17 DOI:10.3969/j.issn.1673-6338.2015.01.003)
(  0) 0) |
| [3] |
姚宜斌, 刘劲宏, 张豹, 等. 地表温度与加权平均温度的非线性关系[J]. 武汉大学学报:信息科学版, 2015, 40(1): 112-116 (Yao Yibin, Liu Jinhong, Zhang Bao, et al. Nonlinear Relationships between the Surface Temperature and the Weighted Mean Temperature[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 112-116)
(  0) 0) |
| [4] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15801 DOI:10.1029/92JD01517
(  0) 0) |
| [5] |
李国翠, 李国平, 杜成华, 等. 华北地区地基GPS水汽反演中加权平均温度模型研究[J]. 南京气象学院学报, 2009, 32(1): 80-86 (Li Guocui, Li Guoping, Du Chenghua, et al. Weighted Mean Temperature Models for Mapping Zenith Wet Delays on to Precipitable Water in North China[J]. Journal of Nanjing Institute of Meteorology, 2009, 32(1): 80-86 DOI:10.3969/j.issn.1674-7097.2009.01.010)
(  0) 0) |
| [6] |
龚绍琦. 中国区域大气加权平均温度的时空变化及模型[J]. 应用气象学报, 2013, 24(3): 332-341 (Gong Shaoqi. The Spatial and Temporal Variations of Weighted Mean Atmospheric Temperature and Its Models in China[J]. Journal of Applied Meteorological Science, 2013, 24(3): 332-341 DOI:10.3969/j.issn.1001-7313.2013.03.009)
(  0) 0) |
| [7] |
Isioye O A, Combrinck L, Botai J. Modeting Weighted Mean Temperature in the West African Region: Implications for GNSS Meteorology[J]. Meteorological Applications, 2016, 23(4): 614-632 DOI:10.1002/met.1584
(  0) 0) |
| [8] |
Mekik C, Deniz I. Modeting and Validation of the Weighted Mean Temperature for Turkey[J]. Meteorological Applications, 2017, 24(1): 92-100
(  0) 0) |
| [9] |
谢劭峰, 黎峻宇, 刘立龙, 等. 新疆地区GGOS Atmosphere加权平均温度的精化[J]. 大地测量与地球动力学, 2017, 37(5): 472-477 (Xie Shaofeng, Li Junyu, Liu Lilong, et al. Refinement of GGOS Atmosphere Weighted Mean Temperature in Xinjiang[J]. Journal of Geodesy and Geodynamics, 2017, 37(5): 472-477)
(  0) 0) |
| [10] |
张洛恺, 杨力, 王艳玲, 等. 郑州地区大气加权平均温度模型确定[J]. 测绘科学技术学报, 2014, 31(6): 566-569 (Zhang Luokai, Yang Li, Wang Yanling, et al. Modeling of Atmosphere Weighted Mean Temperature of Zhengzhou Region[J]. Journal of Geomatics Science and Technology, 2014, 31(6): 566-569 DOI:10.3969/j.issn.1673-6338.2014.06.004)
(  0) 0) |
| [11] |
陈发德, 刘立龙, 黄良珂, 等. 小波去噪的广西加权平均温度插值研究[J]. 测绘科学, 2018, 43(4): 24-29 (Chen Fade, Liu Lilong, Huang Liangke, et al. Study of Weighted Mean Temperature Interpolation of the Atmosphere Grid Date Based on Wavelet Denoising in Guangxi[J]. Science of Surveying and Mapping, 2018, 43(4): 24-29)
(  0) 0) |
| [12] |
李黎, 田莹, 谢威, 等. 基于探空资料的湖南地区加权平均温度本地化模型研究[J]. 大地测量与地球动力学, 2017, 37(3): 282-286 (Li Li, Tian Ying, Xie Wei, et al. Localization Model Research of Weighted Average Temperature in Hunan Area Based on Radiosonde Date[J]. Journal of Geodesy and Geodynamics, 2017, 37(3): 282-286)
(  0) 0) |
| [13] |
罗宇, 罗林艳, 吕冠儒. 加权平均温度模型对GPS水汽反演的影响[J]. 测绘科学, 2018, 43(9): 6-9 (Luo Yu, Luo Lin-yan, Lü Guanru. Impact Analysis on Localization of Tm Model in GPS Precipitable Water Vapor Retrieval[J]. Science of Surveying and Mapping, 2018, 43(9): 6-9)
(  0) 0) |
| [14] |
赵志龙, 罗娅, 余军林, 等. 贵州高原1960~2016年降水变化特征及重心转移分析[J]. 地球信息科学学报, 2018, 20(10): 1432-1442 (Zhao Zhilong, Luo Ya, Yu Junlin, et al. Analysis of Precipitation Variation Characteristics and Barycenter Shift in Guizhou Plateau during 1960-2016[J]. Journal of Geo-Information Science, 2018, 20(10): 1432-1442 DOI:10.12082/dqxxkx.2018.180215)
(  0) 0) |
2. College of Forestry, Guizhou University, West-Jiaxiunan Road, Guiyang 550025, China;
3. Guizhou Provincial First Insitute of Surveying and Mapping, 1268 South-Huaxi Road, Guiyang 550025, China
 2020, Vol. 40
2020, Vol. 40


