2. 空中交通管理系统与技术国家重点实验室,南京市永智路1号,210014
如何快速、准确地检测电离层异常是GBAS电离层监测的重要研究方向之一[1]。目前GBAS地面站用来监测电离层异常现象的方法主要有3种。Pullen等[2]提出通过监测载波平滑码相位测量更新(CSC Inno)判断电离层是否异常,该方法延时较大。Jiang等[3]根据卫星信号载波相位测量值计算其加速-斜坡-步长(ARS),以监测电离层风暴,该方法能够快速检测较大梯度电离层延时,但是对于电离层慢变斜坡故障的检测效果不佳。Xie[4]提出通过计算卫星信号伪码-载波偏离度(CCD)以监测电离层异常,并采用一阶线性时不变(LTI)低通滤波器抑制伪距测量噪声、多路径误差等,但由于LTI低通滤波器时间常数固定,因此该方法无法同时兼顾滤波器估计精度和响应时间两项指标。Kim等[5]提出一种基于广义最小二乘法的电离层梯度估计方法,该方法假设电离层梯度在几十分钟内是常数。然而,由于载波相位模糊度不确定,该方法响应时间长,无法实时估计电离层梯度。为了实时估计电离层梯度大小,Ouzeau等[6]提出一种基于Kalman滤波器的电离层延时与载波相位整周模糊度估计方法,虽然该方法满足系统实时性需求,但是当模型与实际情形不匹配时,滤波估计精度会受到影响。此外,通过精确位置点也能估计电离层延时,但不能满足系统实时性需求,且卫星姿态异常容易影响估计精度[7-8]。Simili等[9]在Xie等[4]的研究基础上提出采用二级LTI低通滤波器抑制高频噪声,该方法既提高了异常估计精度,又减小了异常响应时间,然而在固定滤波常数下,二阶LTI低通滤波器与一阶LTI低通滤波器存在同样的缺陷。
针对上述问题,本文首先开展LMS自适应滤波算法的研究;然后提出一种基于LMS自适应滤波的卫星信号CCD高频噪声抑制方法,通过对输入卫星信号的CMC差分值进行自适应滤波以获得较为准确的电离层延时变化率;最后利用实验室研制的GBAS平台进行电离层检测验证实验,实验结果验证了本文方法的有效性。
1 单通道变步长LMS自适应滤波 1.1 单通道LMS自适应滤波算法标准LMS自适应滤波器有两个信号输入通道,如图 1所示,其中主通道为被检测信号,副通道为参考噪声[10],但是在本文中只涉及一路被检测信号,没有参考噪声信号可以利用,因此无法直接使用标准双通道LMS算法。
|
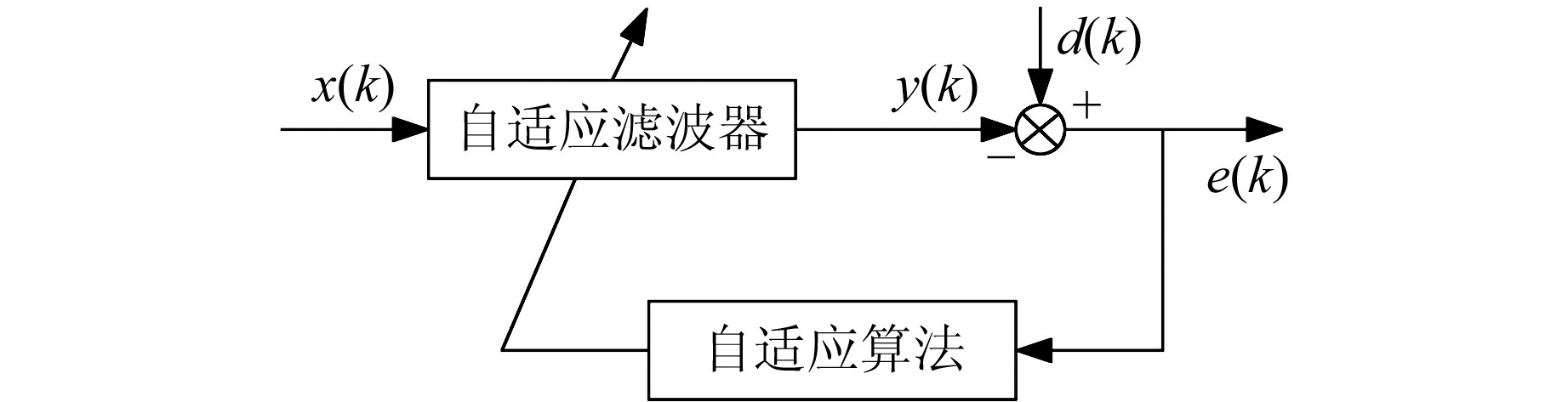
图 1 自适应滤波器结构 Fig. 1 Structure diagram of adaptive filter |
图 1中x为输入信号,d为期望信号,y为滤波器输出信号,e为期望信号d与输出信号y之差。自适应滤波器通过e和滤波器步长因子μ共同调节滤波器权系数,使得下一时刻输出信号更接近期望信号值,k表示当前时间。
针对无法获取参考噪声的难题,本文在标准双通道LMS算法研究基础上,利用被检测信号的相关性及其噪声的非相关性,构造一个单通道LMS自适应滤波器,其参考输入为被检测信号时域延时量,其滤波器结构如图 2所示。
|
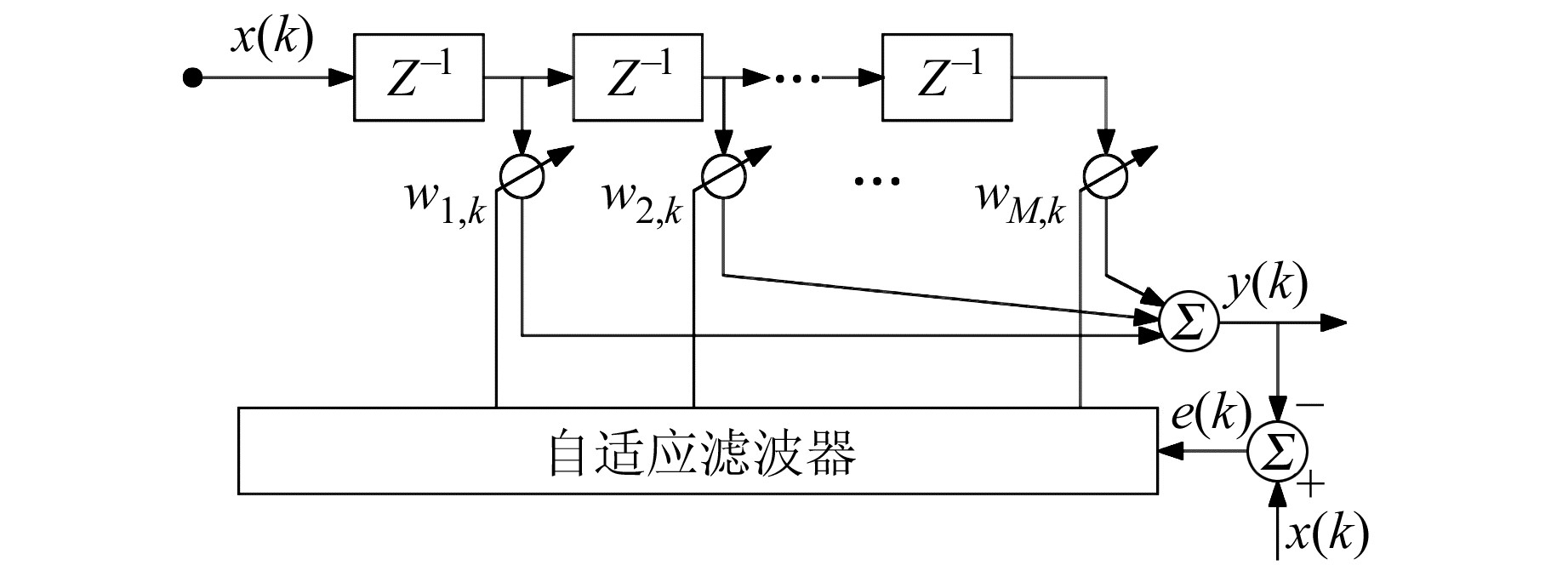
图 2 单通道LMS自适应滤波器结构 Fig. 2 Structure of single-channel LMS adaptive filter |
图 2利用延时去除噪声的相关性,并保留被检测信号的相关性。期望输入x为被检测含噪声信号,参考输入为x延时后的信号。单通道LMS实现原理是利用被检测信号的短时相关性预测当前数据,并根据预测误差e自适应调整预测滤波器的权系数。
1.2 改进的变步长LMS自适应滤波算法传统固定步长LMS自适应滤波器无法同时兼顾稳态误差和收敛速度两项性能指标,即步长越小,稳态误差也越小,但是收敛速度相对较慢。覃景繁等[11]提出一种基于Sigmoid函数的变步长LMS自适应滤波算法,滤波过程中步长因子μ是预测误差e的Sigmoid函数,即
| $ \mu \left( k \right) = \beta \left[ {\frac{1}{{1 + \exp \left( { - a\left| {e\left( k \right)} \right|} \right)}} - 0.5} \right] $ | (1) |
式中,α控制Sigmoid函数的形状,其取值决定函数曲线的上升速度,β控制Sigmoid函数的取值范围。由于μ(k)随着e(k)的减小而减小,当e(k)为0时,μ(k)也减小为0。由此可见,该算法满足步长自适应变化需求,但是在曲线收敛过程中,当误差接近0时步长变化较大,使得算法稳定性差,对滤波性能有影响。为此,本文对Sigmoid函数进行改进,使其在误差较大时采用较大的步长,以加快收敛速度;当误差比较小时采用较小的步长,以提高整个算法的性能。改进的Sigmoid函数如式(2)所示。α=1,β=2时,改进的Sigmoid函数和Sigmoid函数对比曲线如图 3所示。
| $ \mu \left( k \right) = \beta \left[ {\frac{1}{{1 + \exp {{\left( { - a\left| {e\left( k \right)} \right|} \right)}^3}}} - 0.5} \right] $ | (2) |
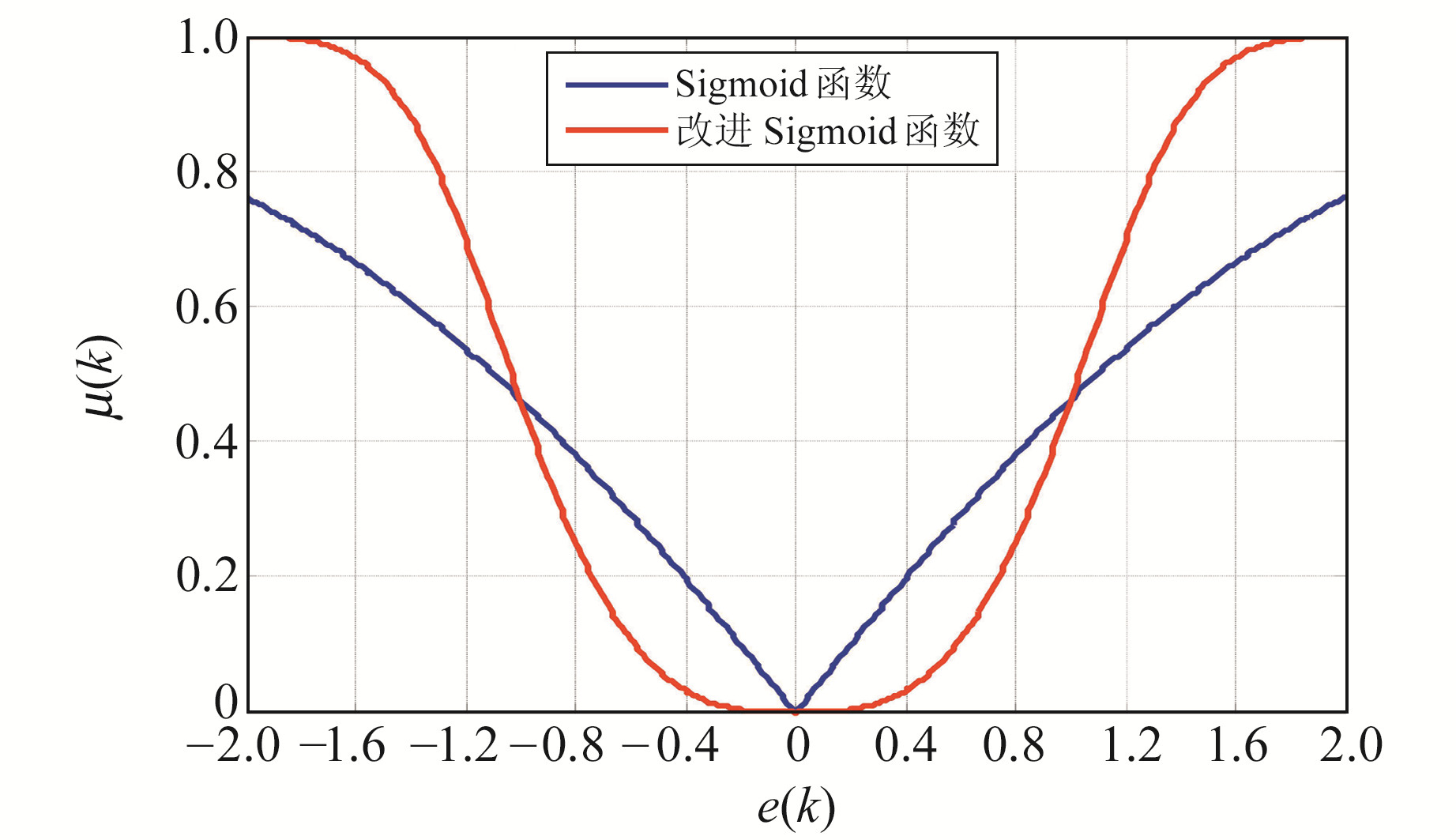
由图 3可以看出,当误差为2时,Sigmoid函数与改进的Sigmoid函数曲线都已经达到或者接近步长因子的最大值,说明此时滤波算法的收敛速度较快,有利于滤波输出结果快速向误差减小的方向变化;当系统接近收敛时,改进的Sigmoid函数步长因子变化更为缓慢,引起的振荡较小,因此系统稳定性能更好。
|
图 3 改进的Sigmoid函数和Sigmoid函数对比曲线 Fig. 3 Contrast curve of improved Sigmoid function and Sigmoid function |
GNSS接收机实时输出伪距和载波相位观测值,电离层延时对码和载波相位测距的影响具有大小相等、符号相反的特点,即
| $ \rho \left( k \right) = {\rho _{{\rm{IF}}}}\left( k \right) + I\left( k \right) + {\varepsilon _\rho }\left( k \right) $ | (3) |
| $ \varphi \left( k \right) = {\rho _{{\rm{IF}}}}\left( k \right) - I\left( k \right) + \lambda N + {\varepsilon _\varphi }\left( k \right) $ | (4) |
| $ {\rho _{{\rm{IF}}}}\left( k \right) = r\left( k \right) + c\left[ {\delta {t_u}\left( k \right) - \delta {t_s}\left( k \right)} \right] + T\left( k \right) $ | (5) |
式中,ρ(k)和φ(k)分别为伪距和载波相位观测值,ρIF(k)为k时刻无电离层延时影响时伪距测量值,r(k)为k时刻卫星与接收机之间的几何距离,c为光在真空中的传播速度,δtu(k)和δts(k)分别为k时刻接收机和卫星钟差,I(k)和T(k)分别为k时刻电离层和对流层延时误差,λ和N分别为载波波长和整周模糊度,ερ(k)和εφ(k)分别为k时刻接收机伪距和载波相位测量误差。
对码减载波(CMC)进行差分是一种常用的评估电离层梯度大小方法,CMC计算为[12]:
| $ \begin{array}{l} {\rm{CMC}}\left( k \right) = \rho \left( k \right) - \varphi \left( k \right) = \\ 2I\left( k \right) + {\varepsilon _\rho }\left( k \right) - {\varepsilon _\varphi }\left( k \right) - \lambda N \end{array} $ | (6) |
假设一段时间内,接收机处于锁定状态,无失锁和失周现象,因而N值大小不变;同时令δε(k)=ερ(k)- εφ(k),则有:
| $ \begin{array}{*{20}{l}} {{\rm{d}}z\left( k \right) = \frac{1}{{2{T_S}{k_0}}}\left( {{\rm{CMC}}\left( k \right) - {\rm{CMC}}\left( {k - {k_0}} \right)} \right) = }\\ {\frac{{I\left( k \right) - I\left( {k - {k_0}} \right)}}{{{T_S}{k_0}}} + \frac{1}{{2{T_S}{k_0}}}\left( {\delta \varepsilon \left( k \right) - \delta \varepsilon \left( {k - {k_0}} \right)} \right) = }\\ {\dot I\left( k \right) + \frac{1}{{2{T_S}{k_0}}}\left( {\delta \varepsilon \left( k \right) - \delta \varepsilon \left( {k - {k_0}} \right)} \right)} \end{array} $ | (7) |
式中,dz(k)为CMC差分值,也称为卫星信号CCD;İ(k)为电离层延时速率;TS为相邻两个历元的间隔时间;k0为平滑窗口时间长度,根据数据预处理需求,其取值通常在20~80。
由于伪距观测噪声、多路径误差等属于高频信号,通过低通滤波后,CCD高频噪声将被抑制,进而可以得到电离层延时速率İ(k)。Xie[4]和Simili等[9]分别利用一阶和二阶LTI低通滤波器抑制高频噪声。为了兼顾滤波器估计精度和响应时间两项指标,本文提出采用最小LMS自适应滤波器抑制CCD高频噪声,采用的滤波器结构如图 2所示,由图 2可以得到LMS自适应滤波算法递推形式如下。
初始化:
| $ \boldsymbol{W}{\rm{ }}(M) = 0 $ | (8) |
计算输出值:
| $ y(k) = {\rm{ }}{\boldsymbol{W}^{\rm{T}}}(k){\rm{ }}\boldsymbol{X}(k),k = M + 1,M + 2, \cdot \cdot \cdot $ | (9) |
计算估计误差:
| $ e(k) = dz(k) - y(k) $ | (10) |
步长因子调整:
| $ \mu (k) = \beta \left[ {\frac{1}{{1 + \exp {{\left( { - a{{\left| {e\left( k \right)} \right|}^3}} \right)}^{}}}} - 0.5} \right] $ | (11) |
权重更新:
| $ \boldsymbol{W}\left( {k + 1} \right) =\boldsymbol{W}\left( k \right) + 2\mu (k)e(k)\boldsymbol{X}(k) $ | (12) |
式中,W(k)=[w1,k, w2,k, …, wM, k]T,M为窗口长度,X(k)=[dz(k-1), dz(k-2), …, dz(k-M)]T,α、β为μ(k)的调整参数。
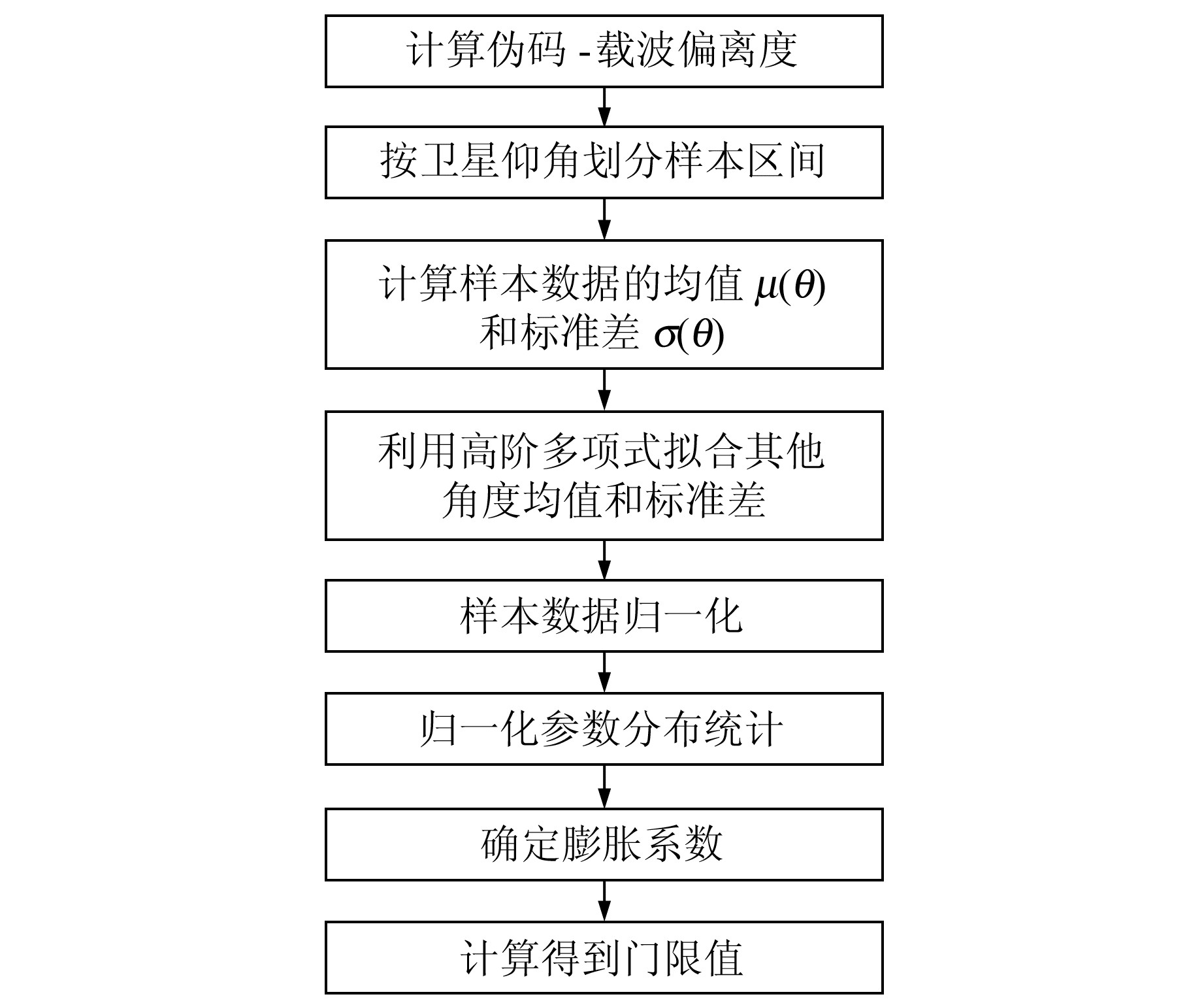
为了判断被检测信号是否异常,需要确定适合的检测门限值,可以根据一段时间内无异常的卫星信号CCD的均值以及标准差确定检测门限值。同时为了减小完好性虚警率,对样本数据进行膨胀,以确定最佳膨胀系数,计算过程如图 4所示。
|
图 4 检测门限值计算流程 Fig. 4 Calculation process of detection threshold |
由图 4可以看出,确定好膨胀系数后,根据实时卫星仰角可以得到对应仰角下的CCD均值和标准差,由式(13)可以得到异常检测门限值:
| $ {\rm{Threshold}}\left( \theta \right) = \mu (\theta ) \pm {K_{{\rm{ffd}}}} \cdot f \cdot \sigma (\theta ) $ | (13) |
式中,μ(θ)、σ(θ)分别为样本数据CCD在卫星仰角θ时的均值和标准差;Kffd为乘数因子,为满足Ⅰ类精密进近导航完好性需求,这里取值为6;f表示为了覆盖检验统计量重尾分布的膨胀系数,由于航空电子设备相关误差特性可以假设服从高斯分布,因此利用高斯膨胀法确定膨胀系数值,具体实现过程可以参考文献[4]。
对样本数据进行高斯膨胀后其分布特性满足χ~N(μ, f2σ2),当采用式(13)作为电离层异常检测门限值时,可以计算得电离层异常检测误警概率小于P(∣x-μ∣≥6fσ)=2Q(6)=1.973×10-9,满足飞机CAT Ⅰ类精密进近与着陆导航完好性风险需求。
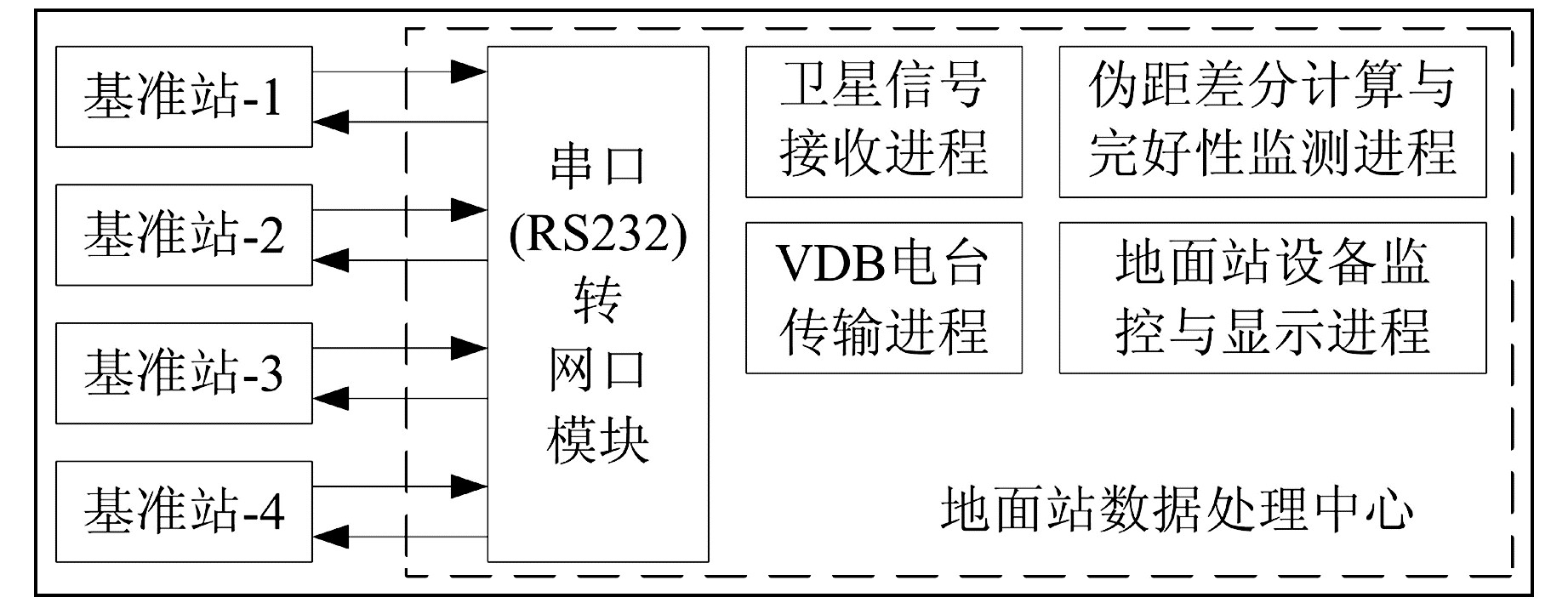
3 验证实验 3.1 实验环境实验室于2017年初研制了GBAS原型样机,可实时监测GPS卫星状态,为本文提出算法的验证提供了大量数据。GBAS地面站包括4个基准站、数据处理中心、多载体导航信号模拟器、VDB电台以及卫星天线。软件部分即地面站数据处理中心模块,由卫星信号接收进程、伪距差分计算与完好性监测进程、地面站设备监控与显示进程以及VDB电台传输进程组成,如图 5所示。
|
图 5 地面站数据处理中心模块 Fig. 5 Module of data processing center of ground facility |
大气层中电离层异常概率大约在10-7~10-8量级[13],因此以一组2018-03-21观测数据为基础,在其中14#卫星伪距和载波相位观测值上注入一段电离层异常数据,所采用的电离层斜坡模型由斯坦福大学提出,如图 6所示[4]。

|
图 6 电离层延时梯度模型 Fig. 6 Ionospheric delay gradient model |
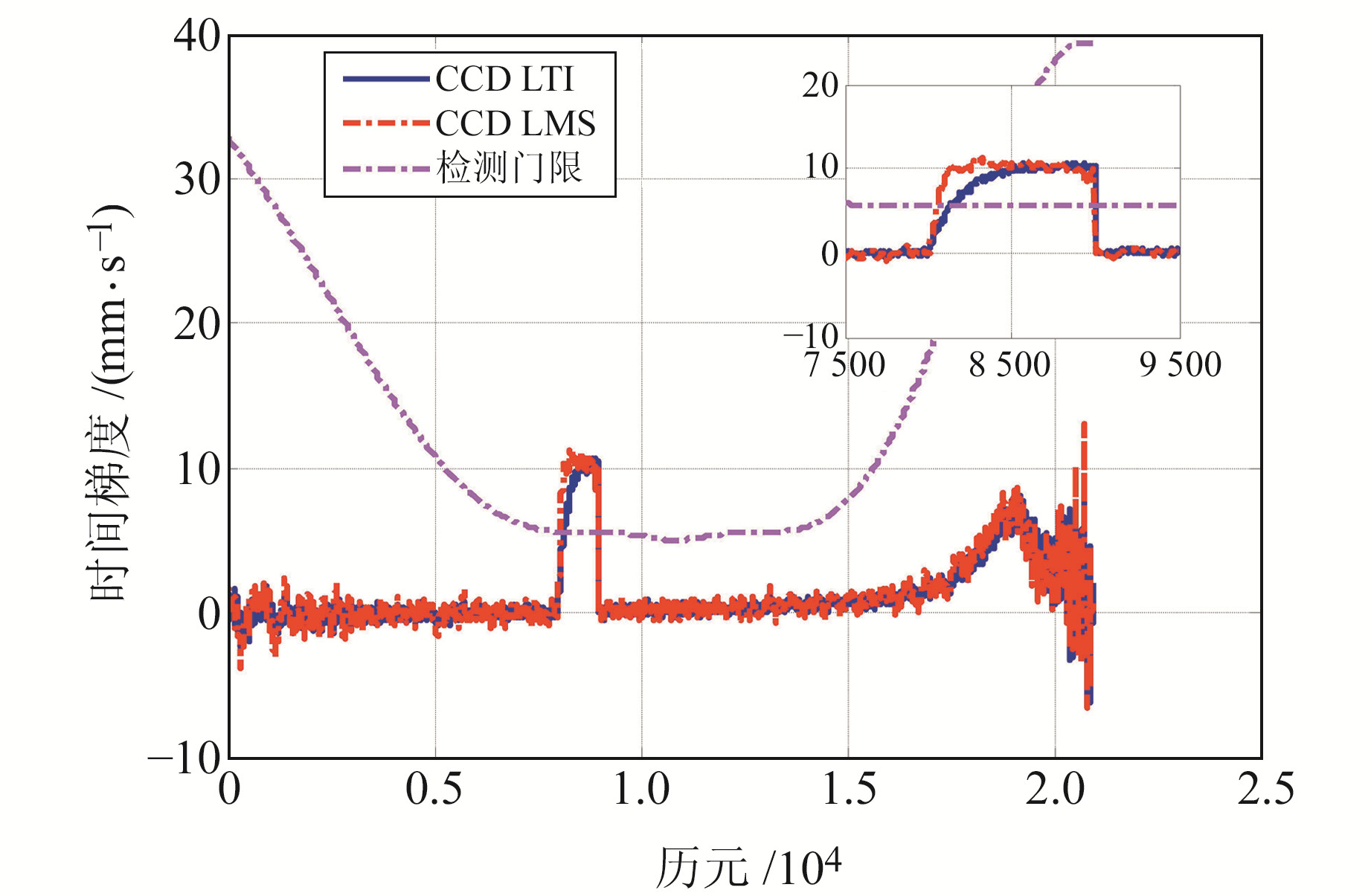
由图 6可以看出,该模型有4个参数表征,分别为斜坡梯度、宽度、前锋速度以及前锋前进方向与飞机接近方向的夹角。Huang等[14]研究指出,极端情况下的电离层时间和空间梯度分别为6 mm/s和12.5 mm/km。电离层时间梯度和空间梯度具有非独立性,电离层空间梯度变化最终反映在时间梯度上[15]。因此,本文在模拟电离层异常时统一用时间梯度表示电离层的异常。在卫星仰角20°~80°区间分别模拟10 mm/s的电离层异常,比较二阶LTI低通滤波与LMS自适应滤波所需的异常检测时间,如表 1所示。图 7为历元8 000~9 000之间对应卫星仰角60°~70°时两种滤波方法检测时间对比曲线。
|
|
表 1 不同卫星仰角两种方法检测时间对比 Tab. 1 Comparison of detection time of two methods with different satellite elevations |
|
图 7 卫星仰角60°~70°时两种方法检测时间对比 Fig. 7 Comparison of detection time of two methods for satellite elevation in the range of 60° to 70° |
由表 1可以看出,卫星仰角大小相同的情况下,采用本文所提出的LMS自适应滤波方法时,电离层异常检测灵敏度要优于二阶LTI低通滤波器。由图 7可以看出,当卫星仰角在60°~70°区间时,电离层异常检测时间由117 s缩短为48 s,检测效率得到提高。
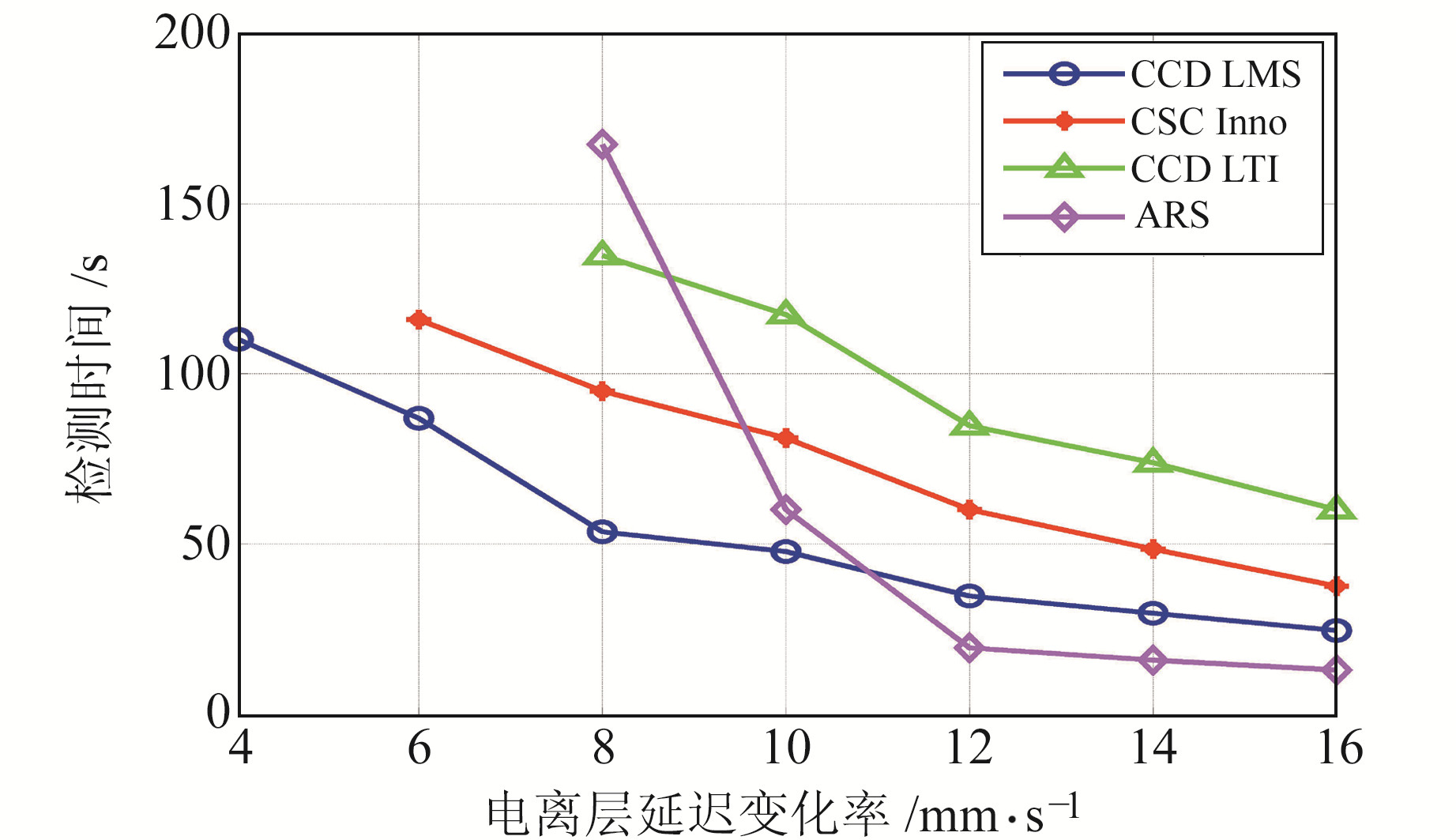
为进一步验证本文所提出自适应滤波方法的有效性,在14#卫星观测时段历元8 000~9 000之间模拟不同大小的电离层时间梯度值,电离层时间梯度分别设置为4 mm/s、6 mm/s、8 mm/s、10 mm/s、12 mm/s、14 mm/s以及16 mm/s,然后利用已有算法(CCD LTI、CSC Inno、ARS)以及本文所提出方法进行异常检测,检测响应时间如图 8所示。
|
图 8 不同方法检测响应时间 Fig. 8 Response time of different detection methods |
由图 8可以看出,相比其他方法,本文方法检测灵敏度高且响应时间快。同时可以看出,当电离层延时变化率较大时,ARS检测效果更优,因此实际应用时可以组合使用这两种异常检测方法。
4 结语本文在对标准双通道LMS算法和现有的变步长因子确定方法进行分析的基础上,提出一种新的单通道基于改进的Sigmoid函数的变步长LMS自适应滤波算法,该算法能够同时兼顾滤波收敛速度和稳态误差两项指标,具有更优的滤波性能。将该方法应用于GBAS电离层异常检测中,实验结果表明,其具有更好的高频噪声抑制效果,对电离层慢增长故障检测性能最优,具有工程应用价值。
| [1] |
Khanafseh S, Pullen S, Warburton J. Carrier Phase Ionospheric Gradient Ground Monitor for GBAS with Experimental Validation[J]. Journal of the Institute of Navigation, 2012, 59(1): 51-60
(  0) 0) |
| [2] |
Pullen S, Luo M, Gleason S, et al. GBAS Validation Methodology and Test Results from the Stanford LAAS Integrity Monitor Testbed[C]. ION GPS, Salt Lake City, 2000
(  0) 0) |
| [3] |
Jiang Y P, Milner C, Macabiau C. Code Carrier Divergence Monitoring for Dual-Frequency GBAS[J]. GPS Solutions, 2016, 21(2): 1-13
(  0) 0) |
| [4] |
Xie G. Optimal On-Airport Monitoring of the Integrity of GPS-Based Landing System[D]. Palo Alto: Stanford University, 2004
(  0) 0) |
| [5] |
Kim E, Walter T, Powell J D. Adaptive Carrier Smoothing Using Code and Carrier Divergence[C]. ION NTW, San Diego, 2007 https://www.researchgate.net/publication/241090240_Adaptive_Carrier_Smoothing_Using_Code_and_Carrier_Divergence
(  0) 0) |
| [6] |
Ouzeau C, Macabiau C, Roturier B, et al. Ionospheric Delay Estimation in a Single Frequency Mode for Civil Aviation[C]. ION GNSS, Savannah, 2008 https://www.researchgate.net/publication/200052789_Ionospheric_Code_Delay_Estimation_in_a_Single_Frequency_Case_for_Civil_Aviation
(  0) 0) |
| [7] |
Zhang B C, Ou J K, Yuan Y B, et al. Extraction of Line-of-Sight Ionospheric Observables from GPS Data Using Precise Point Positioning[J]. Science China Earth Sciences, 2012, 55(11): 1919-1928 DOI:10.1007/s11430-012-4454-8
(  0) 0) |
| [8] |
Lou Y D, Zheng F, Gu S F, et al. The Impact of Non-Nominal Yaw Attitudes of GPS Satellites on Kinematic PPP Solutions and Their Mitigation Strategies[J]. Journal of Navigation, 2015, 68(4): 718-734 DOI:10.1017/S0373463315000041
(  0) 0) |
| [9] |
Simili D V, Pervan B. Code-Carrier Divergence Monitoring for the GPS Local Area Augmentation System[C]. PLANS, IEEE/ION, San Diego, 2006 https://www.researchgate.net/publication/261151376_Code-Carrier_Divergence_Monitoring_for_the_GPS_Local_Area_Augmentation_System
(  0) 0) |
| [10] |
王立辉, 孙枫, 季强, 等. LMS自适应滤波算法在FOG数据处理中的应用[J]. 系统工程与电子技术, 2010, 32(5): 1047-1050 (Wang Lihui, Sun Feng, Ji Qiang, et al. Application of LMS Adaptive Filtering Algorithm in FOG Data Processing[J]. Systems Engineering and Electronics, 2010, 32(5): 1047-1050 DOI:10.3969/j.issn.1001-506X.2010.05.036)
(  0) 0) |
| [11] |
覃景繁, 欧阳景正. 一种新的变步长LMS自适应滤波算法[J]. 数据采集与处理, 1997, 12(3): 171-174 (Qin Jingfan, Ouyang Jingzheng. A Novel Variable Step Size LMS Adaptive Filtering Algorithm Based on Sigmoid Function[J]. Journal of Data Acquisition and Processing, 1997, 12(3): 171-174)
(  0) 0) |
| [12] |
Rife J, Sen S. Design of a Single-Frequency Filter That Minimizes Ionosphere Divergence Error[C]. ION GNSS, Salt Lake City, 2007 https://www.researchgate.net/publication/289953576_Design_of_a_single-frequency_filter_that_minimizes_ionosphere_divergence_error
(  0) 0) |
| [13] |
Shively C A, Braff R. An Overbound Concept for Pseudorange Error from the LAAS Ground Facility[C]. ION, San Diego, 2000 https://www.researchgate.net/publication/237823240_An_Overbound_Concept_for_Pseudorange_Error_from_the_LAAS_Ground_Facility
(  0) 0) |
| [14] |
Huang Z G, Huang Z G, Zhu Y B. A New Optimal Hatch Filter to Minimize the Effects of Ionosphere Gradients for GBAS[J]. Chinese Journal of Aeronautics, 2008, 21(6): 526-532 DOI:10.1016/S1000-9361(08)60170-3
(  0) 0) |
| [15] |
王志鹏, 张军, 朱衍波, 等. 一种抑制电离层异常的优化Hatch滤波方法[J]. 华中科技大学学报:自然科学版, 2013, 41(10): 11-15 (Wang Zhipeng, Zhang Jun, Zhu Yanbo, et al. An Optimized Hatch Filter Method to Inhibit Ionospheric Anomaly[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2013, 41(10): 11-15)
(  0) 0) |
2. State Key Laboratory of Air Traffic Management System and Technology, 1 Yongzhi Road, Nanjing 210014, China
 2020, Vol. 40
2020, Vol. 40

