2. 国家自然资源部大地测量数据处理中心,西安市友谊东路334号,710054
地球自转参数(ERP)是实现天球坐标框架与地球坐标框架相互转换的必要参数,对高精度航天器定轨具有重要意义[1]。ERP通常需要利用全球观测数据进行联合处理解算,因此产品具有一定的时延。低轨卫星精密轨道预报通常依赖于ERP,在不能实时上注ERP数据的情况下,需要通过预报来提供较高精度的ERP,因此ERP预报误差将会对低轨卫星自主定轨产生影响。本文借助珞珈一号卫星的轨道数据,分析ERP预报误差对其精密轨道预报的影响,探讨预报时长与定轨误差的关系。
1 ERP对卫星轨道预报的影响低轨卫星轨道预报计算依赖动力学积分方法,因此必须使用惯性系(如GCRS)进行轨道积分计算。为便于使用,低轨卫星轨道产品通常在地固系(如ITRS)下进行表达。轨道预报需要将ITRS系的轨道转换到GCRS系进行积分,再转回ITRS系。IERS 2010协议中已定义GCRS和ITRS之间的转换模型,计算公式如下[2-3]:
| $ [{\rm{GCRS}}] = {\rm{ }}\boldsymbol{Q}{\rm{ }}(t){\rm{ }}\boldsymbol{R}{\rm{ }}(t){\rm{ }}\boldsymbol{W}{\rm{ }}(t)[{\rm{ITRS}}]{\rm{ }} $ | (1) |
式中,Q(t)与R(t)分别为岁差-章动矩阵和地球自转矩阵,W(t)为极移矩阵。
地球自转和极移运动不规律,需要定期计算并发布ERP产品。式(1)中t为观测时刻至参考时刻J2000.0间的儒略世纪数,计算公式如下:
| $ t = ({\rm{TT — JD2 451 545}}.{\rm{0TT}}){\rm{/36 525}} $ | (2) |
式中,TT为地球时。
岁差-章动矩阵Q(t)计算模型如下:
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \boldsymbol{Q}(t) = }\\ {\left[ {\begin{array}{*{20}{c}} {1 - a{X^2}}&{ - aXY}&X\\ { - aXY}&{1 - a{Y^2}}&Y\\ { - X}&{ - Y}&{1 - a\left( {{X^2} + {Y^2}} \right)} \end{array}} \right]{\boldsymbol{R}_3}\left( s \right)} \end{array} $ | (3) |
式中,X和Y为CIP在GCRS系中球面坐标的两个分量,s为参考历元和指定时刻t之间天球历书原点CEO的累积位移。
地球自转矩阵R(t)的计算模型如下:
| $ {\rm{ }}\boldsymbol{R}{\rm{ }}(t) = {\rm{ }}{\boldsymbol{R}_3}( - \rm{ERA}) $ | (4) |
式中,ERA为地球自转角,即在天球中间极CIP的赤道上指向天球中间原点CIO和地球中间原点TIO之间的旋转角度。
极移矩阵W(t)的计算模型如下:
| $ \boldsymbol{W}{\rm{ }}(t) = {\rm{ }}{\boldsymbol{R}_3}( - s'){\boldsymbol{R}_2}\left( {{x_p}} \right){\boldsymbol{R}_1}\left( {{y_p}} \right) $ | (5) |
式中,xp、yp为天球中间极CIP在国际地球参考系ITRS中的坐标,该坐标需要对由IERS直接提供的极移坐标进行潮汐变化项改正和章动项改正,计算公式如下:
| $ \begin{array}{l} ({x_p},{y_p}) = {({x_p},{y_p})_{{\rm{IERS}}}} + {(\Delta {x_p},\Delta {y_p})_{{\rm{tidal}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {(\Delta {x_p},\Delta {y_p})_{{\rm{nutation}}}} \end{array} $ | (6) |
式中,(Δxp, Δyp)tidal、(Δxp, Δyp)nutation计算公式可参考IERS Conventions 2010[4]。
2 ERP预报方法ERP预报方法主要分为线性预报方法和非线性预报方法[5-8]。目前常用的ERP预报方法为LS+AR方法,该方法利用最小二乘(LS)对线性和周期项进行拟合并外推,采用自回归(AR)模型对拟合残差进行预报,拟合外推值加上残差预报值即为ERP预报值[2]。
ERP数据拟合模型可表示为[2]:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} X(t) = {a_0} + {a_1}t + \\ \sum\limits_{i = 1}^k {({b_i}\cos (\frac{{2\pi t}}{{{p_i}}})} + {c_i}\sin (\frac{{2\pi t}}{{{p_i}}})) \end{array} $ | (7) |
式中,a0为常数项,a1为趋势项系数,bi、ci均为周期项拟合系数,pi为周期项,k为周期项个数。通过对长期的ERP序列进行频谱分析,根据分析结果,对极移序列取k =2,对UT1-UTC序列取k =5。极移序列的两个主要周期项分别为钱德勒摆动项(431.16 d)和周年项(364.09 d),UT1-UTC序列周期项分别为8 692 d、5 461.33 d、4 096 d、364.09 d和182.04 d。
利用最小二乘算法求出上式中各个系数,表达式为:
| $ \boldsymbol{X} = [{a_0},{a_1},{b_1},{c_1},{b_2},{c_2}...] $ | (8) |
| $ \boldsymbol{X} = {({\boldsymbol{B}^{\rm{T}}}\boldsymbol{B})^{ - 1}}{\boldsymbol{B}^{\rm{T}}}\boldsymbol{L} $ | (9) |
式中,L为ERP数据观测值矩阵。
利用AR模型进行拟合残差预报。AR模型表示平稳随机序列Zt(t=1, 2, …, N)在t时刻之前的规律性变化与t时刻的白噪声的关系,其数学模型表达式如下:
| $ {Z_t} = \sum\limits_{i = 1}^p {({\varphi _i}{Z_{t - i}} + {a_t})} $ | (10) |
式中,φi为模型参数,at为t时刻的白噪声,p为AR模型阶数。
AR模型预报的精度主要由阶数p确定,可采用AIC准则来确定阶数[5]。
3 ERP预报误差对珞珈一号卫星轨道预报的影响为研究ERP预报误差对低轨卫星轨道预报的影响,在珞珈一号卫星研究基础上[9-10],结合珞珈一号卫星的轨道数据进行数值计算。本次实验选取珞珈一号2018-11-01~11-30的轨道数据。为进一步探讨预报时长与定轨误差的关系,采用2015年IERS EOP08C04序列作为地球自转参数的拟合数据,预报2018-11-01~11-30的ERP,并将每天的ERP预报数据生成单独文件。利用Bernese软件分别计算由精密ERP产品和预报ERP产品得到的珞珈一号轨道结果。将精密ERP产品对应的轨道结果作为参考值,计算由ERP预报误差引起的轨道误差,分析ERP预报误差变化对珞珈一号轨道的影响。由于极移和日长变化对轨道的影响不同,为对比分析两者预报误差对低轨卫星轨道定轨误差的影响,设计以下方案:
方案1,使用预报的极移产品和精密的UT1-UTC产品,分析极移预报误差对轨道的影响。
方案2,使用预报的极移与UT1-UTC产品,分析ERP预报误差对轨道的影响,结合方案1对比分析UT1-UTC预报误差对轨道的影响。
ERP预报根据预报时长可分为超短期、短期和长期3种,通常将1~10 d预报称为超短期预报,将30 d预报称为短期预报,1 a及以上时长预报称为中长期预报[11]。本文主要分析ERP超短期和短期预报对低轨卫星轨道的影响。
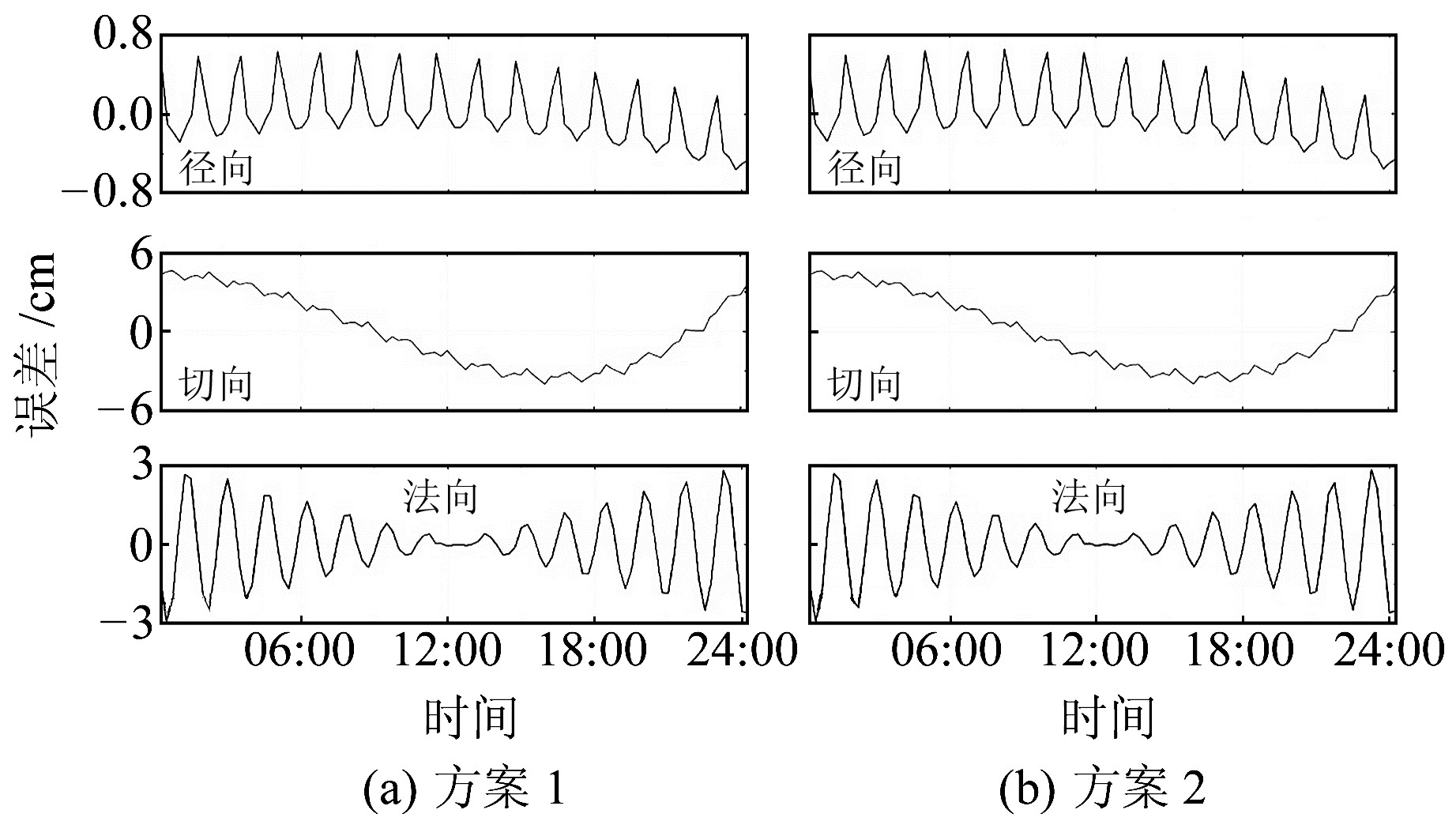
3.1 超短期ERP预报误差对低轨卫星定轨的影响图 1为单天预报数据对轨道的影响,由图可见,方案1和方案2对轨道产生的误差趋势和误差大小几乎相同,切向和法向的最大误差达到cm级;径向误差较小,保持在mm级。低轨卫星绕地周期较短,因此单天的解算结果各方向误差都存在周期性波动(表 1)。
|
图 1 单天预报ERP误差对低轨卫星轨道的影响 Fig. 1 Impact of single-day prediction ERP error on LEO orbit |
|
|
表 1 单天极移预报误差和低轨卫星轨道误差 Tab. 1 Prediction error of single-day polar motion and LEO orbit error |
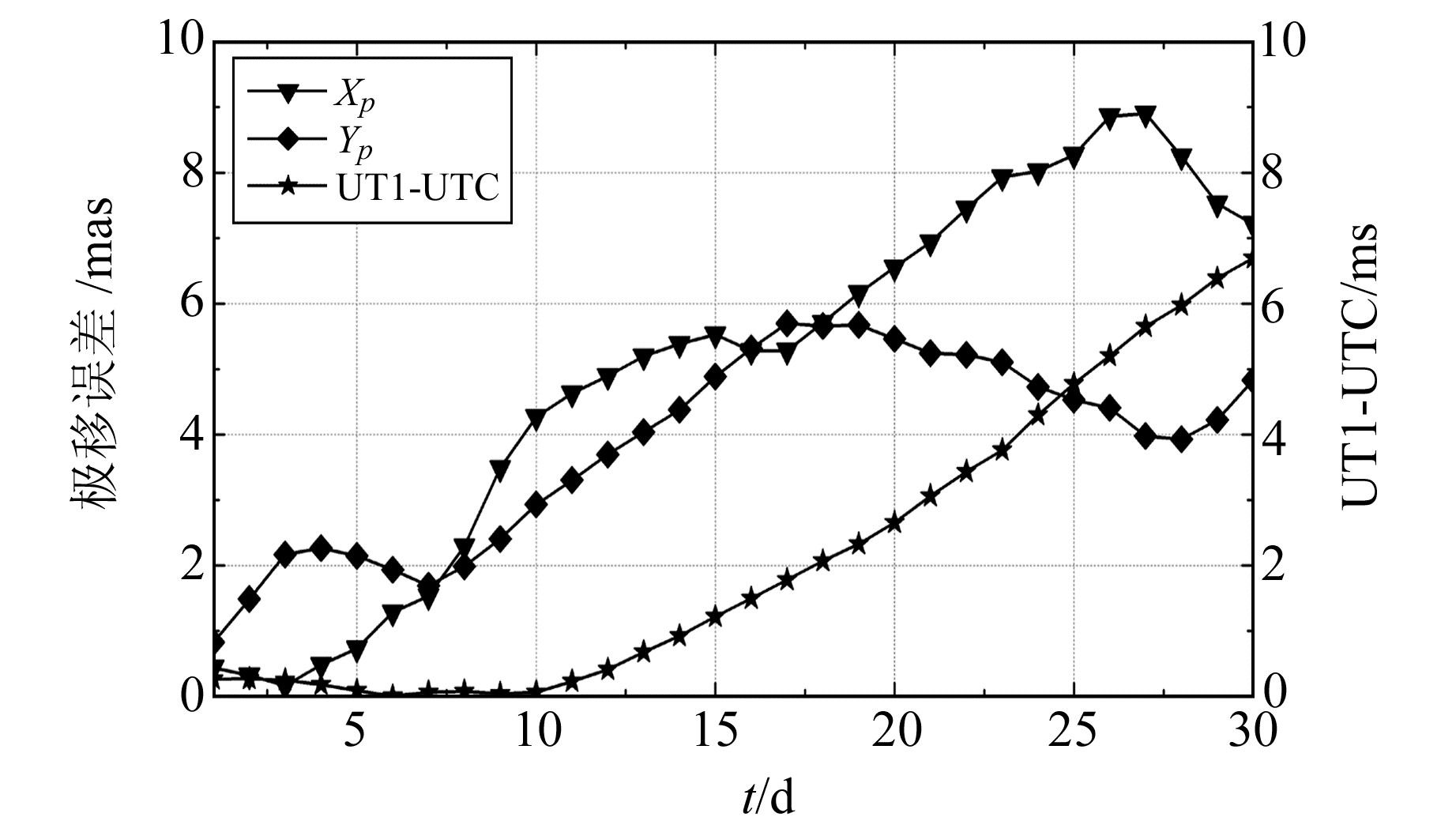
利用LS+AR模型对ERP进行预报,图 2为30 d预报误差趋势。由图可见,Xp和Yp预报误差随时间增大而显著增大;UT1-UTC预报误差在10 d内变化很小,之后显著增大。
|
图 2 预报30 d ERP误差 Fig. 2 ERP error of 30-day prediction |
图 3为30 d预报误差对低轨卫星轨道的影响,由图可见,各方向轨道误差存在规律性波动,且波动幅度随时间增长而增大,预报30 d时径向误差最大约为0.05 m,切向误差最大约为0.5 m,法向误差最大约为0.2 m(表 2)。

|
图 3 预报30 d ERP误差对低轨卫星轨道的影响 Fig. 3 Impact of 30-day prediction ERP error on LEO orbit |
|
|
表 2 短期极移预报误差和低轨卫星轨道误差 Tab. 2 Short-term polar motion prediction error and LEO orbit error |
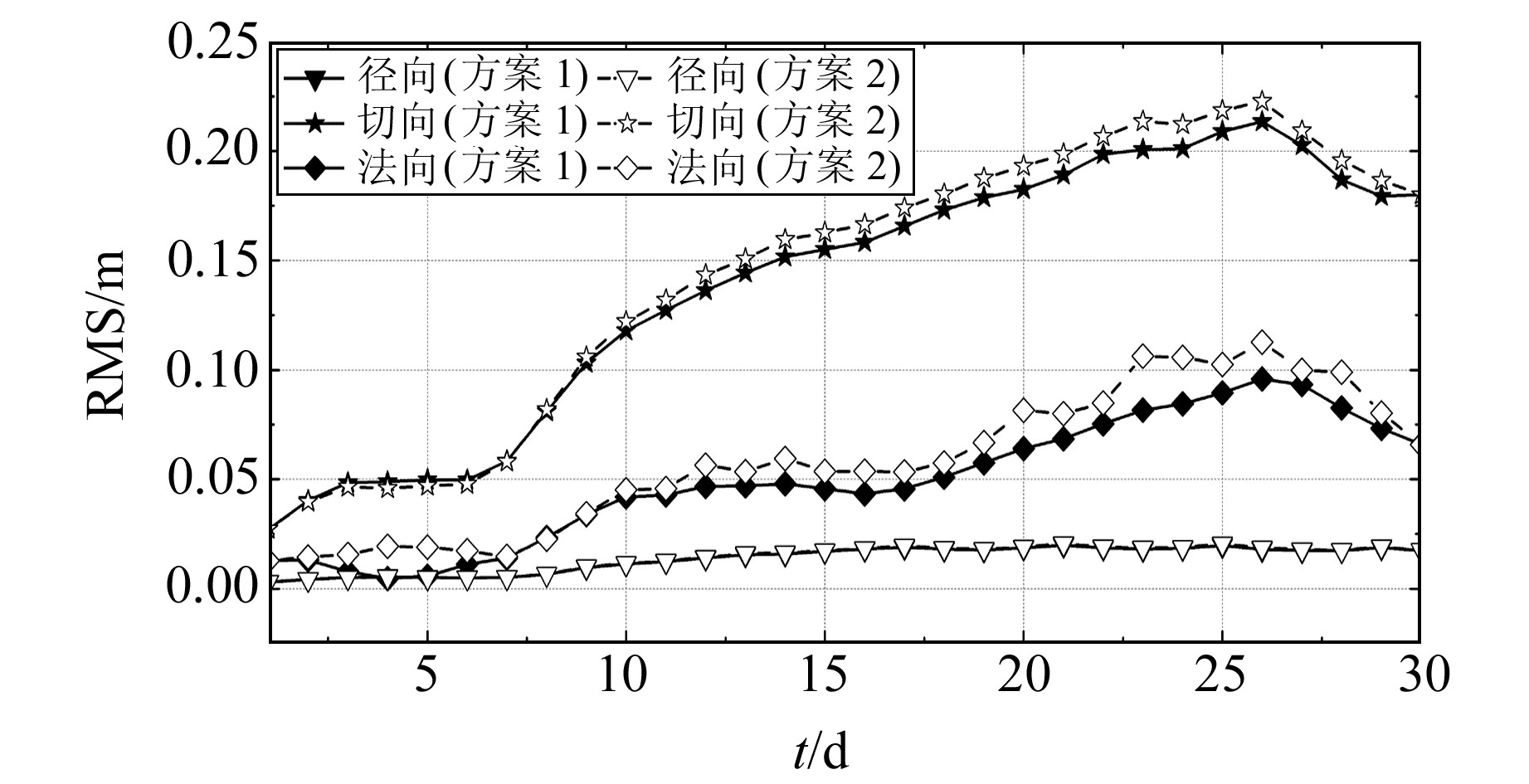
图 4为方案1和方案2对低轨卫星轨道影响的对比分析,从图中可以看出,引入UT1-UTC的预报误差对珞珈一号卫星定轨结果影响较小。UT1-UTC的预报误差在径向上影响非常小,在切向和法向上在一定程度上降低了低轨卫星的轨道精度。珞珈一号卫星的定轨结果受ERP预报误差的影响,在3个不同方向上的轨道误差均随时间的增加而增大。切向方向受影响最大,其次为法向,径向误差最小,因此应该重点考虑ERP预报误差对珞珈一号卫星切向和法向的影响。在预报时长为10 d时,切向误差为dm级,这对cm级定轨影响较大。
|
图 4 方案1和方案2对低轨卫星轨道影响的对比分析 Fig. 4 Comparison analysis of the impact of scenario 1 and scenario 2 on LEO orbit |
由表 3可知,只改变极移数据时,预报10 d的切向误差为0.118 0 m,而引入UT1-UTC预报误差时,切向误差为0.122 1 m。对于珞珈一号卫星,ERP预报10 d的误差对其自主定轨的影响达到dm级,ERP预报30 d的误差对轨道切向方向影响最大可达到0.18 m。
|
|
表 3 不同预报时长ERP中轨道各方向RMSE Tab. 3 RMSE of different orbit directions of ERP with different prediction duration |
本文主要研究ERP预报误差对低轨卫星自主定轨的影响。结果表明,ERP预报误差主要对低轨卫星轨道的切向和法向影响较大,对径向影响较小,低轨卫星的切向误差最为明显。由于低轨卫星绕地运行周期短,单天预报的轨道误差具有周期性。随着预报时间的增加,轨道各方向误差均呈现波动性增大,预报30 d时径向误差最大约为0.05 m,切向误差最大约为0.5 m,法向误差最大约为0.2 m。只引入极移预报误差与引入极移和UT1-UTC预报误差的对比分析表明,UT1-UTC预报误差对低轨卫星定轨影响较小,且主要影响切向和法向的精度。ERP预报10 d时,低轨卫星自主定轨的切向误差达到dm级;ERP预报30 d时,预报误差对轨道切向影响最大,误差可达到0.18 m,这对cm级定位有较大影响。
| [1] |
柳文明, 李峥嵘, 刘文祥, 等. EOP预报误差对导航卫星轨道预报的影响分析[J]. 全球定位系统, 2009, 34(6): 17-22 (Liu Wenming, Li Zhengrong, Liu Wenxiang, et al. Influence of EOP Prediction Errors on Orbit of Navigation Satellites[J]. GNSS World of China, 2009, 34(6): 17-22 DOI:10.3969/j.issn.1008-9268.2009.06.004)
(  0) 0) |
| [2] |
许雪晴.地球定向参数高精度预报方法研究[D].上海: 中国科学院上海天文台, 2012 (Xu Xueqing. Researches on High Accuracy Prediction Methods of Earth Orientation Parameters[D]. Shanghai: Shanghai Astronomical Observatory, CAS, 2012) http://d.wanfangdata.com.cn/Thesis/Y2382305
(  0) 0) |
| [3] |
张卫星, 刘万科, 龚晓颖. EOP预报误差对自主定轨结果影响分析[J]. 大地测量与地球动力学, 2011, 31(5): 106-110 (Zhang Weixing, Liu Wanke, Gong Xiaoying. Analysis of Influence of EOP Prediction Error on Autonomous Orbit Determination[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 106-110)
(  0) 0) |
| [4] |
Petit G, Luzum B. IERS Conventions (2010)[C]. IERS Technical Note, Frankfurt, 2010 https://link.springer.com/content/pdf/10.1007%2Fs40328-015-0139-z.pdf
(  0) 0) |
| [5] |
XU X Q, Zhou Y H. EOP Prediction Using Least Square Fitting and Autoregressive Filter Over Optimized Data Intervals[J]. Advances in Space Research, 2015, 56(10): 2248-2253 DOI:10.1016/j.asr.2015.08.007
(  0) 0) |
| [6] |
王志文, 王潜心, 何义磊, 等. 一种考虑PMX与PMY之间相关性的极移预报新方法[J]. 大地测量与地球动力学, 2017, 37(11): 1178-1182 (Wang Zhiwen, Wang Qianxin, He Yilei. A New Method to Predict Pole Shift Based on the Correlation between PMX and PMY[J]. Journal of Geodesy and Geodynamics, 2017, 37(11): 1178-1182)
(  0) 0) |
| [7] |
Niedzielski T, Kosek W. Prediction Analysis of UT1-UTC Time Series by Combination of the Least-Squares and Multivariate Autoregressive Method[M]. Berlin: Springer-Verlag Berlin Heidelberg, 2012
(  0) 0) |
| [8] |
Liao D C, Wang Q J, Zhou Y H, et al. Long-Term Prediction of the Earth Orientation Parameters by the Artificial Neural Network Technique[J]. Journal of Geodynamics, 2012, 62: 87-92 DOI:10.1016/j.jog.2011.12.004
(  0) 0) |
| [9] |
Wang L, Chen R Z, Li D R, et al. Initial Assessment of the LEO Based Navigation Signal Augmentation System from Luojia-1A Satellite[J]. Sensors, 2018, 18(11): 3919 DOI:10.3390/s18113919
(  0) 0) |
| [10] |
王磊, 陈锐志, 李德仁, 等. 珞珈一号低轨卫星导航增强系统信号质量评估[J]. 武汉大学学报:信息科学版, 2018, 43(12): 2191-2196 (Wang Lei, Chen Ruizhi, Li Deren, et al. Quality Assessment of the LEO Navigation Augmentation Signals from Luojia-1A Satellite[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2191-2196)
(  0) 0) |
| [11] |
Kalarus M, Schuh H, Kosek W, et al. Achievements of the Earth Orientation Parameters Prediction Comparison Campaign[J]. Journal of Geodesy, 2010, 84(10): 587-596 DOI:10.1007/s00190-010-0387-1
(  0) 0) |
2. Geodetic Data Processing Centre of Ministry of Natural Resources, 334 East-Youyi Road, Xi'an 710054, China
 2020, Vol. 40
2020, Vol. 40

