全国海洋观测网在中国大陆沿岸及岛屿的长期海洋环境监测站(海洋站)上建立了50余个与验潮站并址的GNSS连续运行基准站,为研究中国沿海验潮站的地壳垂直形变和验潮站绝对海平面变化提供了极其重要的基础数据。在这些研究中,准确判定基准站时间序列的噪声特性,进而估计测站的速度信息是研究工作的基础。
随着GNSS坐标时间序列资料的不断积累,GNSS基准站时间序列中所包含的噪声性质及其定量估计问题也逐渐引起重视。国外学者Bock等[1-2]指出,GPS连续观测站的坐标时间序列噪声不具备纯白噪声的特性。国内学者黄立人等[3-5]对中国境内GPS基准站和IGS站的研究表明,GPS连续观测资料所包含的噪声不仅仅含白噪声,同时包含闪烁噪声,少数测站也包含随机漫步噪声。
事实上,不同地区的GNSS观测数据中普遍存在各类噪声。验潮站均布设在大陆和岛屿的海边,有些直接布设在海上平台,验潮站GNSS相对内陆GNSS观测具有更复杂的观测环境,时间序列中的噪声也更为复杂。国内研究对象多是IGS基准站、陆太网基准站或沿海城市的CORS基准站,而建设于海边与验潮站并址的GNSS基准站的连续观测资料的噪声特性目前少有学者进行专门的研究分析。本文选用中国沿海22个与验潮站并址的GNSS基准站的连续观测站资料,利用CATS[6]软件,采用最大似然估计法,对坐标时间序列采用不同噪声模型组合的方式定量估计各站的噪声含量,针对各个地区的特点逐个测站分析其最优噪声模型;然后利用最优噪声模型确定各站的速率,并将速度值与GAMIT/GLOBK计算的速度结果进行对比,分析不同噪声模型对测站速度估计的影响,并在此基础上对验潮站的GNSS资料处理提出若干建议。
1 GNSS时间序列噪声分析方法 1.1 中国沿海验潮站GNSS数据处理对全国海洋观测网的GNSS数据处理采用以下步骤:首先,利用GAMIT软件采用同一策略联合海洋观测网的GNSS站和IGS基准站进行解算,获取基线解向量;然后,选取全球IGS站在ITRF2014框架的坐标和速度值作为约束,利用GLOBK软件平差处理单日松弛解;最后,利用GLOBK进行时间序列分析,并采用相邻两个观测值之差[7]和人工判读方法对粗差进行剔除后,进行多次迭代平差得到最后的时间序列。采用上述方法对近9 a的验潮站GNSS数据进行处理,统计得到坐标时间序列水平分量的重复性优于5mm,垂直分量的重复性优于10mm。
GNSS时间序列中包含地壳的各种信息,包括线性速度、不同原因造成的偏移、周期性变化以及其他噪声。本文采用文献[8]的坐标时间序列模型,运用时间序列分析软件GAMIT/GLOBK和CATS拟合模型中的系数,对测站每个坐标分量时间序列求出模型参数后得到观测噪声时间序列,进行噪声特性分析。
1.2 噪声分析频谱分析法和最大似然估计法是两种常用的噪声分析方法。对于GNSS时间序列扣除拟合值后的噪声时间序列,可以利用噪声功率谱密度与之对应的噪声频率之间存在的幂律关系获取其噪声类型,本文采用文献[9]模型分析噪声的谱指数。
最大似然估计(maximum likelihood estimation, MLE)是一种非线性的最小二乘法,通过调整协方差矩阵使得似然函数取得最大值,即可得到与该时间序列最相近的噪声模型。假设观测值服从高斯正态分布,最大似然函数可表示为[10]:
| $ l(\mathit{\boldsymbol{\hat v}},\mathit{\boldsymbol{C}}) = \frac{1}{{2{\pi ^{N/2}}{{( {\rm{det}} \mathit{\boldsymbol{C}})}^{1/2}}}} {\rm{exp}} ( - 0.5{\mathit{\boldsymbol{\hat v}}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}\mathit{\boldsymbol{\hat v}}) $ |
协方差矩阵C可以表达白噪声模型与有色噪声模型,以及它们之间的不同组合,如白噪声模型包括简单白噪声模型(white noise, WH)和可变白噪声模型(variable white noise, VMN),有色噪声模型包括闪烁噪声模型(flicker noise, FN)、随机漫步噪声模型(random walk noise, RWN)、一阶马尔科夫噪声模型(first order Gauss Markov noise, FOGM)、幂律噪声模型(power law noise, PL)以及带通噪声模型(band pass noise, BP)等[11]。
2 验潮站GNSS噪声特征 2.1 谱指数分析本文假设GNSS具有WH+PL噪声,采用最大似然估计法(MLE)计算22个验潮站GNSS坐标时间序列的谱指数(见表 1,1~7为北海区站点,8~15为东海区站点,16~22为南海区站点)。根据各站谱指数可知,大部分站的水平分量谱指数介于-2~-1之间,垂向分量谱指数多数介于-1~0之间,这说明,各站坐标分量噪声均不具有纯白噪声特性,验潮站GNSS水平分量以白噪声+闪烁噪声+随机漫步噪声为主,垂向分量以白噪声+闪烁噪声为主。同一测站不同坐标分量的噪声特性也不完全一致,因此各站的不同坐标分量也不宜采用同一噪声模型进行分析。
|
|
表 1 沿海验潮站GNSS时间序列谱指数 Tab. 1 Spectral index of tide GNSS stations coordinates time series |
为了进一步确定各测站不同坐标分量的噪声特性,根据谱指数分析结果并考虑测站变化的周期项和有色噪声的确定性,本文假设时间序列除包含WH外,有可能存在FN、RWN、FOGMN、PLN,因此选取WH、WH+FN、WH+RWN、WH+FN+RWN、WH+FOGM、WH+FOGM+RWN、WH+PL共7种噪声模型,根据最大似然估计原理计算不同噪声模型下的MLE值。通常根据MLE值的大小判断模型的可靠性,即MLE越大结果越可靠。以塘沽站为例,首先利用最大似然估计法计算各模型的MLE值;然后利用与文献[12]相同的判断准则确定最佳噪声模型,并计算WH模型与其他6种模型MLE的差值(图 1),结果显示,塘沽站东坐标WH+FN、WH+FN+RWN、WH+FOGM、WH+FOGM+RWN和WH+PL模型MLE差值小于3.0,北坐标WH+FN、WH+FN+RWN和WH+PL模型MLE差值小于3.0。北坐标WH+GM和WH+GM+RW模型MLE差值小于3.0,垂向分量WH+FN+RWN、WH+FOGM+RWN和WH+PL模型MLE差值小于3.0,可区分度均较低。塘沽站东坐标和北坐标MLE值最大的模型均为WH+GM和WH+FOGM+RW,垂向分量MLE值最大的模型为WH+FOGM+RWN。
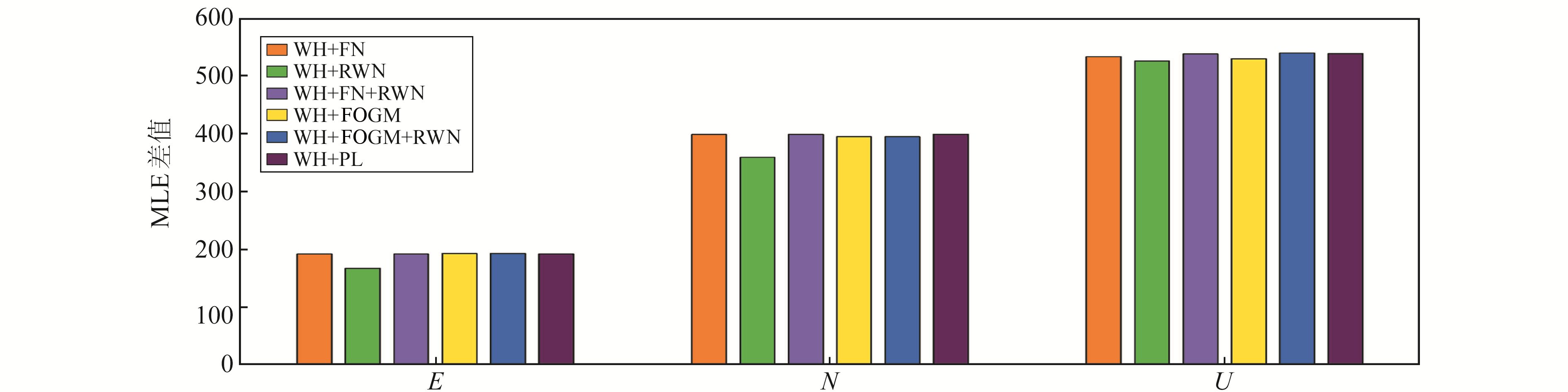
|
图 1 塘沽(TGU)站WH模型与其他模型的MLE差值 Fig. 1 MLE error between WH and other noise model ofTGUstation |
然而,随着噪声模型中包含的参数越多,MLE值越大,因此不能简单地通过MLE值来判断最优噪声模型。为确保结果的可靠性,本文进一步采用Langbein[13]等提出的保守估计准则判断选出各站最优噪声模型。以塘沽站高程分量为例,首先分别计算WH+FN和WH+RWN模型的MLE值,并选取MLE值较大的模型作为零假设。塘沽站垂向分量WH+FN组合模型的MLE值更大,作为零假设;然后将WH+PL和WH+FN+RWN模型的MLE值分别与零假设比较,如果MLE差值大于2.6则拒绝零假设,认为该模型更优,否则认为所选的模型无效。塘沽站垂向分量WH+PL和WH+FN+RWN模型MLE值与零假设MLE差值均大于2.6,因此选择MLE值更大的WH+PL模型作为最优模型;最后将WH+FOGM和WH+FOGM+RWN模型的MLE值与最优模型的MLE比较。本文将WH+FOGM+RWN模型和WH+FOGM模型的阈值设为5.2[14]。塘沽站垂向分量WH+FOGM和WH+FOGM+RWN模型与WH+PL模型的MLE差值均小于5.2,因此最终确定最优噪声模型为WH+PL模型。
3 验潮站GNSS噪声分布 3.1 噪声大小与分布采用与塘沽站相同的方法对其他测站的时间序列坐标分量逐一进行分析,得到各站最优噪声模型及其各模型噪声大小统计结果(表 2,单位mm),各海区白噪声和闪烁噪声统计结果如图 2所示。根据表 2、图 2可得出,沿海验潮站GNSS观测噪声具有以下特点:
|
|
表 2 各站坐标分量时间序列的最优噪声模型及噪声分量 Tab. 2 Optimum noise model and noise factor of each station coordinates time series |
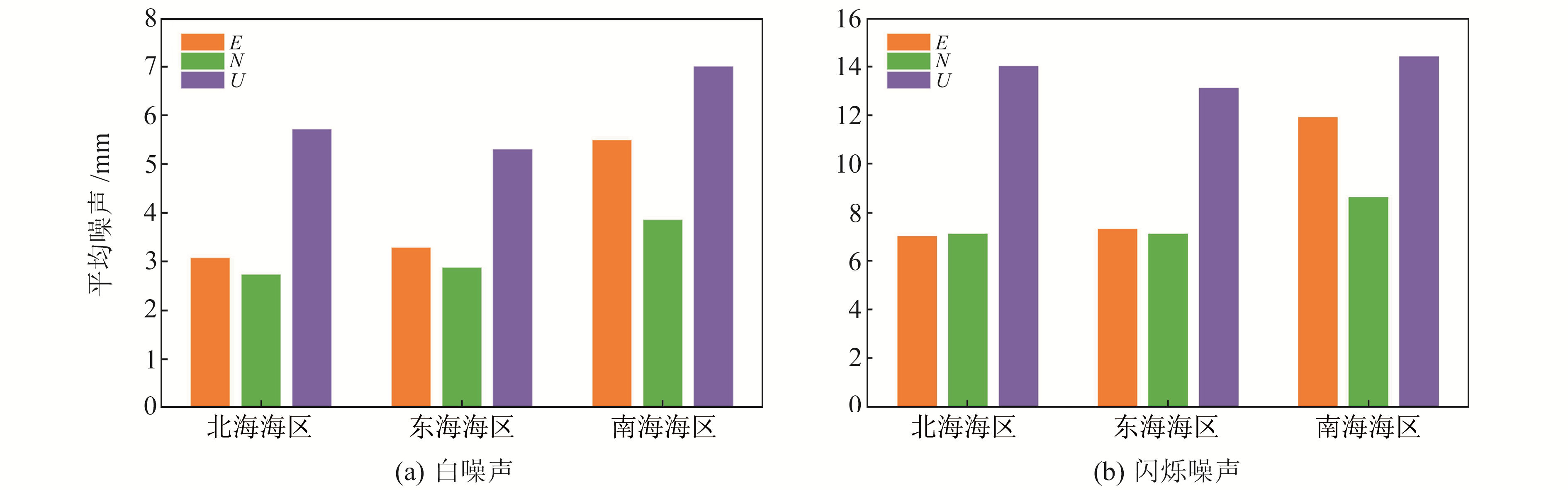
|
图 2 各海区坐标分量白噪声和闪烁噪声平均值 Fig. 2 Average Noise factor of each sea area |
1)沿海验潮站GNSS噪声存在多样性,E分量最佳噪声模型WH+FN占72.7%,WH+PL占18.2%,其余9.1%为WH+FN+RWN;N分量最佳噪声模型以WH+FN和WH+FOGM+RWN为主,各占36.4%和27.3%,WH+FOGM占18.2%,其余少数为WH+PL和WH+FN+RWN;U分量最佳噪声模型WH+FN占72.7%,WH+PL占13.6%,其余少数为WH+FOGM、WH+FOGM+RWN以及WH+FN+RWN。
2)沿海验潮站GNSS的N、E、U分量在地域分布上具有一定的特点。①北海区多数站E分量除具有白噪声和闪烁噪声外,也存在一定程度的随机漫步噪声和幂律噪声;东海区和南海区E分量除汕头站(STO)含有幂律噪声外,其余均为白噪声+闪烁噪声。②全国沿海N分量多数站点除具有白噪声外,北海区多数站还存在一定的闪烁噪声;东海区和南海区除具有白噪声外,近60%站也存在一阶马尔科夫噪声;全国沿海有近50%站存在随机漫步噪声,且呈不规律分布。③3个海区U分量均主要存在白噪声和闪烁噪声。④共有超过80%站的U分量噪声大小大于N和E分量的噪声大小。
3)从北到南,3个海区N和E分量的白噪声和闪烁噪声基本呈现越往南噪声越大的规律;东海区U分量白噪声和闪烁噪声比北海区和南海区都小,南海区U分量噪声最大。这种现象与我国上空电离层的稳定性有关,说明电离层扰动对闪烁噪声具有较大的贡献值。同时,这也验证了白噪声和闪烁噪声存在一定的纬度依赖性。南海区的NSA和XSA站均位于北纬17°以南,且远离大陆,相对于大陆其他沿岸站具有明显更大的白噪声和闪烁噪声。
3.2 顾及最优噪声模型的速率估计本文对22个验潮站GNSS时间序列采用最优噪声模型,利用最大似然估计法计算出各分量的速度及误差。并将各站最优噪声模型结果与采用白噪声模型计算的速度值和采用GAMIT/GLOBK获得的速度值进行对比分析(表 3)得出:
|
|
表 3 不同噪声模型下各站的速度及不确定度 Tab. 3 The speed and uncertainty of each station under different noise model |
1)仅考虑白噪声时速度的中误差(N、E、U方向平均值分别为0.06mm/a、0.08mm/a、0.18mm/a)明显小于顾及有色噪声的中误差(N、E、U方向平均值分别为0.43mm/a、0.54mm/a、0.94mm/a),与GLOBK的速度中误差(N、E、U方向平均值分别为0.04mm/a、0.05mm/a、0.16mm/a)基本相当。顾及有色噪声的速度中误差是仅考虑白噪声的中误差的5~10倍,这种差异比内陆观测站要大(田云峰[9],3~6倍;蒋志浩[15],2~6倍;张彦芬[16],4~7倍)。反映出验潮站GNSS观测站的闪烁噪声要大于内陆测站。
2)采用最优噪声模型获取的各站水平分量速度与只采用白噪声模型获取的速度差异很小(N、E分量速度差平均值分别为0.1mm/a和0.2mm/a),垂向分量速度差略大于水平分量(U分量速度差平均值为0.3mm/a);采用最优噪声模型与GLOBK获取的水平分量速度差异很小(N、E分量速度差平均值分别为0.2mm/a和0.2mm/a),垂向分量速度差略大于水平分量(U分量速度差平均值为0.3mm/a);采用白噪声模型与GLOBK获取的速度基本相同。
当测站序列存在有色噪声的情况下,若直接采用白噪声模型或直接使用GLOBK进行时间序列分析获取的速度误差估计的可靠性并不乐观。为获取正确的速度值,应当顾及有色噪声的影响。
4 结语通过对验潮站GNSS连续运行观测站时间序列的分析,得到以下结论:
1)沿海验潮站GNSS时间序列均含有有色噪声,其中,E方向以白噪声+闪烁噪声的组合噪声特性为主,N分量以白噪声+闪烁噪声和白噪声+一阶马尔科夫噪声+随机漫步噪声的组合噪声特性为主,U分量以白噪声+闪烁噪声的组合噪声特性为主。
2)白噪声和闪烁噪声存在一定的纬度依赖性,从北到南,3个海区N和E分量的白噪声和闪烁噪声基本呈现越往南噪声越大的规律;东海区U分量白噪声和闪烁噪声比北海区和南海区都小,南海区U分量噪声最大。且超过80%测站的U分量噪声大小大于N和E分量的噪声大小,反映了U分量的精度要低于N分量和E分量的精度。
3)仅考虑白噪声时速度估计的中误差明显小于估计有色噪声的最优模型的速度中误差,但与直接采用GLOBK获取速度的中误差基本相当;验潮站GNSS时间序列估计有色噪声的速度中误差估计值是仅考虑白噪声和采用GLOBK获取的速度中误差估计值的5~10倍,这种差异比内陆观测站的要大。
4)在对验潮站GNSS时间序列进行速度分析时,由于序列中存在有色噪声,因此直接采用白噪声模型或直接使用GLOBK进行时间序列分析获取的速度误差估计的可靠性并不乐观,为获取正确的速度值,应该先准确判断噪声的类型,再顾及有色噪声的影响估计测站速度。
| [1] |
Nikolaidis R. Observation of Geodectic and Seismic Deformation with the Global Positioning Sys-tem[J]. Cancer Research, 2002, 71(8): 714
(  0) 0) |
| [2] |
Bock Y.Environmental Issues and Monumentation[C].IGS workshop, Bern March1, 2004
(  0) 0) |
| [3] |
黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33 (Huang Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31-33)
(  0) 0) |
| [4] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Carto-graphica sinica, 2012, 41(4): 496-503)
(  0) 0) |
| [5] |
贺小星. GPS坐标序列噪声模型估计方法研究[J]. 测绘学报, 2017, 46(3): 398 (He Xiaoxing. Study on the Noise Model of GPS Coordinates Time Series[J]. Acta Geodaetica et Cartographica sini-ca, 2017, 46(3): 398)
(  0) 0) |
| [6] |
Williams SD P. CATS:GPS Coordinate Time Series Analysis Software[J]. GPS Solutions, 2008(12): 147-153
(  0) 0) |
| [7] |
黄立人, 韩月萍, 高艳龙, 等. GNSS连续站坐标的高程分量时间序列在地壳垂直运动研究中应用的若干问题[J]. 大地测量与地球动力学, 2012, 32(4): 10-13 (Huang Liren, Han Yueping, Gao Longyan, et al. Several Issues in Application of Elevation Component Time Series of GNSS CORS in Vertical Crustal Movement Studying[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 10-13)
(  0) 0) |
| [8] |
武曙光, 聂桂根, 李海洋, 等. 基于CATS软件的连续运行参考站噪声分析[J]. 测绘地理信息, 2018, 43(6): 48-51 (Wu Shuguang, Nie Guigen, Li Haiyang, et al. Noise Analysis of Continuously Op-erating Reference Stations Based on CATS[J]. Journal of Geomatics, 2018, 43(6): 48-51)
(  0) 0) |
| [9] |
田云锋, 沈正康, 李鹏. 连续GPS观测中的相关噪声分析[J]. 地震学报, 2010, 32(6): 696-704 (Tian Yunfeng, Shen Zhengkang, Li Peng. Analysis on Correlated Noise in Continuous GPS Observa-tions[J]. Acta Seismologica sinica, 2010, 32(6): 696-704)
(  0) 0) |
| [10] |
Langbein J. Noise in Two-Color Electronic Distance Meter Measurements Revisited[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B4): 1-16
(  0) 0) |
| [11] |
曹奇, 张迎燕, 岳东杰, 等. 城市CORS坐标时间序列噪声模型建立与分析[J]. 大地测量与地球动力学, 2015, 35(6): 1001-1006 (Cao Qi, Zhang Yingyan, Yue Dongjie, et al. Noise Model Establishment and Analysis of CORS Sites Coordinates Time Series[J]. Journal of Geodesy and Geodynam-ics, 2015, 35(6): 1001-1006)
(  0) 0) |
| [12] |
袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1372-1384 (Yuan Linguo, Ding Xiaoli, Chen Wu, et al. Charateristics of Daily Position Time Series from the Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5): 1372-1384 DOI:10.3321/j.issn:0001-5733.2008.05.011)
(  0) 0) |
| [13] |
Langbein J, Svarc J L. Evaluation of Temporally Correlated Noise in Global Navigation Satellite System Time Series: Geodetic Monument Performance[J]. Journal of Geophysical Research:Solid Earth, 2019, 124(1): 925-942 DOI:10.1029/2018JB016783
(  0) 0) |
| [14] |
Langbein J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research:Solid Earth, 2008, 113(B5): 1-12
(  0) 0) |
| [15] |
蒋志浩, 张鹏, 秘金钟, 等. 顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J]. 测绘学报, 2010, 39(4): 355-362 (Jiang Zhihao, Zhang Peng, Bei Jinzhong, et al. Velocity Estimation on the Colored Noise Properties of CORS Network in China Based on the CGCS2000 Frame[J]. Acta Geodaetica et Cartographica sinica, 2010, 39(4): 355-362)
(  0) 0) |
| [16] |
张彦芬, 毕刚, 陈华, 等. 山西CORS坐标时间序列噪声特性分析[J]. 大地测量与地球动力学, 2012, 32(4): 61-66 (Zhang Yanfen, Bi Gang, Chen Hua, et al. Research on Noise Characteristics of Time Series of CORS Sites Coordinates in Shanxi Region[J]. Journal of Geodesy and Geodynam-ics, 2012, 32(4): 61-66)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

