整周模糊度快速、准确地固定是GNSS领域多年来的一个难点。在众多模糊度解算方法中，以模糊度协方差矩阵降相关和球形离散搜索思想为基础的LAMBDA方法实际应用最为广泛^[1-3]。Liu等^[4]通过上下三角过程构造的联合去相关方法可有效地降低模糊度之间的相关性水平；Chang等^[5]利用对称旋转排序和贪心选择算法对降相关过程进行优化，提高降相关效率；Hassibi等^[6]首次将LLL格基规约方法用于降相关，并指出多维高斯整数降相关方法与LLL格基规约方法的原理相同；Xu^[7]首次提出逆整数Cholesky分解方法，并比较了多维高斯整数降相关、逆整数Cholesky分解及LLL格基规约3种方法的性能，指出采用逆整数Cholesky分解的浮点解协方差矩阵条件数最小，但在高维情况下3种方法产生的协方差矩阵条件数都较大。另外，有学者从格基规约的理论角度分析LLL算法的降相关性能^[8-10]，并针对LLL算法规约效率不高的问题作出相应改进，有效地提高了LLL算法的运行速度^[11-12]。Xu^[13]提出一种并行的基于Cholesky分解的降相关算法，但该方法只是将自然升序法、对称旋转法及扰动升序法笼统地进行并行计算，以牺牲运行时间来获得较好的降相关结果，并未对3种算法各自的性能分别进行分析，因此无法确定在并行计算过程中究竟是哪种算法起主导作用。

为研究排序算法对降相关性能的影响，本文利用模拟数据和实测数据，从降相关时间、搜索时间、整体耗时、Bootstrapping成功率^[14]及条件数^[13]等5个方面对自然升序法、对称旋转法和扰动升序法3种排序算法开展研究。

1 基于L^TDL分解的整数高斯变换数学模型 1.1 基本原理

根据模糊度整数最小二乘估计原理^[1]，已知模糊度浮点解â和浮点解协方差矩阵Q_ââ，则模糊度求解问题可转化为整数最小值的问题，即

$ \min {(a - \hat a)^{\rm{T}}}\boldsymbol{Q}_{\hat a\hat a}^{ - 1}(a - \hat a),a \in \boldsymbol{Z}{^n} $

(1)

由于模糊度a是整数，因此式(1)可采用离散搜索方法进行求解，但直接对式(1)进行搜索效率低下。针对这种情况，采用整数高斯变换对模糊度协方差矩阵进行降相关，可减少冗余的搜索候选节点数，进而提高模糊度的搜索效率^[2]。

为将式(1)进行搜索空间转换，整数高斯变换通过构建单模矩阵Z对浮点解â和相应的协方差矩阵Q_ââ进行变换：

$ z = \mathit{\boldsymbol{Z}}a,\hat z = \mathit{\boldsymbol{Z}}\hat a,{\mathit{\boldsymbol{Q}}_{\hat z\hat z}} = \mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Q}}_{\hat a\hat a}}{\mathit{\boldsymbol{Z}}^{\rm{T}}} $

(2)

其中det(Z)=1。将式(2)代入式(1)，得到新的整数最小二乘问题：

$ \min {(z - \hat z)^{\rm{T}}}\mathit{\boldsymbol{Q}}_{\hat z\hat z}^{ - 1}(z - \hat z),z \in {\mathit{\boldsymbol{Z}}^n} $

(3)

对Q_ââ进行下三角Cholesky分解，得到一个近似对角化的正定矩阵Q_ẑẑ：

$ {\mathit{\boldsymbol{Q}}_{\hat a\hat a}} = \mathit{\boldsymbol{LD}}{\mathit{\boldsymbol{L}}^{\rm{T}}},{\mathit{\boldsymbol{Q}}_{\hat z\hat z}} = \mathit{\boldsymbol{ZLD}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{Z}}^{\rm{T}}} = \mathit{\boldsymbol{\tilde LD}}{\mathit{\boldsymbol{\tilde L}}^{\rm{T}}} $

(4)

式中，L和$\mathit{\boldsymbol{\tilde L}}$为单位下三角矩阵，D为对角矩阵，D中对角线元素d_i为浮点解â的条件方差。

1.2 矩阵Z的构建

整数高斯变换矩阵Z是一个单模矩阵，其构造方式为：

$ \mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{I}} - [{l_{ij}}]{\mathit{\boldsymbol{e}}_i}\mathit{\boldsymbol{e}}_j^{\rm{T}} $

(5)

式中，I为n维单位矩阵，[·]为四舍五入取整，e_i和e_j为单位坐标向量。

对L进行整数变换，此时下三角矩阵元素需要进行更新：

$ {\tilde l_{ik}} = {l_{ik}} - [{l_{ij}}]{l_{jk}},i > j > k $

(6)

L经过多次整数变换，构成$\mathit{\boldsymbol{\tilde L}}$：

$ \mathit{\boldsymbol{\tilde L}} = \left[ {\begin{array}{*{20}{c}} 1&{}&{}&{}\\ {{{\tilde l}_{21}}}&1&{}&{}\\ \vdots & \vdots & \ddots &{}\\ {{{\tilde l}_{n1}}}&{{{\tilde l}_{n2}}}& \cdots &1 \end{array}} \right] $

(7)

$\mathit{\boldsymbol{\tilde L}}$中所有的${\tilde l_{ij}}$应满足：

$ {\left| {{{\tilde l}_{ij}}} \right|_{i > j}} \le 0.5 $

(8)

2 三种排序算法 2.1 自然升序法

自然升序法(natural ascending sorting, ASCE)是Xu^[13]提出的基于Cholesky分解的并行算法之一，其关键在于每次对浮点解的协方差矩阵Q_ââ进行LDL ^T分解之前，先对Q_ââ对角线元素进行升序排列。降相关后的协方差矩阵Q_ẑẑ对角线元素应满足：

$ {q_{11}} \le {q_{22}} \le \cdots \le {q_{nn}} $

(9)

具体算法为：

1) 利用置换矩阵P对Q_ââ的对角线元素进行升序排列：

$ {\mathit{\boldsymbol{Q}}_1}{\rm{ = }}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{Q}}_{\hat a\hat a}}{\mathit{\boldsymbol{P}}^{\rm{T}}} $

(10)

2) 对Q₁进行LDL^T分解：

$ {\mathit{\boldsymbol{Q}}_1} = \mathit{\boldsymbol{LD}}{\mathit{\boldsymbol{L}}^{\rm{T}}} $

(11)

3) 对L进行整数高斯变换：

$ \mathit{\boldsymbol{\tilde L}} = \mathit{\boldsymbol{L}} - u{\mathit{\boldsymbol{e}}_i}\mathit{\boldsymbol{e}}_j^{\rm{T}}\mathit{\boldsymbol{L}} $

(12)

4) 重新构建矩阵$\mathit{\boldsymbol{Q}}{{\rm{'}}_{\hat a\hat a}} = \mathit{\boldsymbol{\tilde LD}}{\mathit{\boldsymbol{\tilde L}}^{\rm{T}}}$，返回步骤1)进行循环，直到重构后的矩阵Q'_ââ对角线元素满足升序排列时停止，得到协方差矩阵Q_ẑẑ和变换矩阵Z，其中矩阵Z通过式(5)构造。

2.2 对称旋转法

对称旋转法是基于排序QR分解(sorted QR decomposition, SEQR)构建，该方法最初是由Xu等^[3]基于Cholesky分解提出，用于多维整数高斯降相关，后Chang等^[5]将其应用于MLAMBDA方法中。

假设协方差矩阵Q_ââ∈ R ^n×n为对称正定矩阵，对Q_ââ进行分解：

$ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Q}}_{\hat a\hat a}} = \left[ {\begin{array}{*{20}{c}} {{q_{11}}}&\mathit{\boldsymbol{q}}\\ {{\mathit{\boldsymbol{q}}^{\rm{T}}}}&{{{\mathit{\boldsymbol{\tilde Q}}}_{\hat a\hat a}}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} 1&{}\\ l&{\mathit{\boldsymbol{\tilde L}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{d_1}}&{}\\ {}&{\mathit{\boldsymbol{\tilde D}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&{{\mathit{\boldsymbol{l}}^{\rm{T}}}}\\ {}&{{{\mathit{\boldsymbol{\tilde L}}}^{\rm{T}}}} \end{array}} \right]} \end{array} $

(13)

由式(13)可得，${d_1} = {q_{11}},\mathit{\boldsymbol{q}} = {d_1}{\mathit{\boldsymbol{l}}^{\rm{T}}},{\mathit{\boldsymbol{\tilde Q}}_{\hat a\hat a}} - \mathit{\boldsymbol{l}}{d_1}{\mathit{\boldsymbol{l}}^{\rm{T}}} = \mathit{\boldsymbol{\tilde L\tilde D}}{\mathit{\boldsymbol{\tilde L}}^{\rm{T}}}$，其中d为条件方差。

首先利用对称旋转法将矩阵Q_ââ对角线中最小的元素排列到(1, 1)的位置，然后求解出d₁、l及${\mathit{\boldsymbol{\tilde Q}}_{\hat a\hat a}} - \mathit{\boldsymbol{l}}{d_1}{\mathit{\boldsymbol{l}}^{\rm{T}}}$，最后对排序后的矩阵${\mathit{\boldsymbol{\tilde Q}}_{\hat a\hat a}}$进行LDL ^T分解。假设第1个对称排序矩阵为P₁，则有：

$ {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{Q}}_{\hat a\hat a}}\mathit{\boldsymbol{P}}_1^{\rm{T}} = \left[ {\begin{array}{*{20}{c}} {{q_{11}}}&\mathit{\boldsymbol{q}}\\ {{\mathit{\boldsymbol{q}}^{\rm{T}}}}&{{{\mathit{\boldsymbol{\tilde Q}}}_{\hat a\hat a}}} \end{array}} \right] $

(14)

令d₁=q₁₁，$\mathit{\boldsymbol{l}} = \frac{{{\mathit{\boldsymbol{q}}^{\rm{T}}}}}{{{d_1}}}$, 对${\mathit{\boldsymbol{\tilde Q}}_{\hat a\hat a}} - \mathit{\boldsymbol{l}}{d_1}{\mathit{\boldsymbol{l}}^{\rm{T}}}$进行对称旋转排序，并进行LDL^T分解：

$ \mathit{\boldsymbol{\tilde P}}({\mathit{\boldsymbol{\tilde Q}}_{\hat a\hat a}} - \mathit{\boldsymbol{l}}{d_1}{\mathit{\boldsymbol{l}}^{\rm{T}}}){\mathit{\boldsymbol{\tilde P}}^{\rm{T}}} = \mathit{\boldsymbol{\tilde L\tilde D}}{\mathit{\boldsymbol{\tilde L}}^{\rm{T}}} $

(15)

式中，$\mathit{\boldsymbol{\tilde P}}$为排序矩阵的乘积。根据式(15)进行排序，得到最终的排序后的协方差矩阵${\mathit{\boldsymbol{\bar Q}}_{\hat a\hat a}}$：

$ \begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\bar Q}}}_{\hat a\hat a}} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{Q}}_{\hat a\hat a}}{\mathit{\boldsymbol{P}}^{\rm{T}}} = \mathit{\boldsymbol{LD}}{\mathit{\boldsymbol{L}}^{\rm{T}}},\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{P}}_1}\left[ {\begin{array}{*{20}{c}} 1&{}\\ {}&{\mathit{\boldsymbol{\tilde P}}} \end{array}} \right],}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} 1&{}\\ {l{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}}&{\mathit{\boldsymbol{\tilde L}}} \end{array}} \right],\mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{d_1}}&{}\\ {}&{\mathit{\boldsymbol{\tilde D}}} \end{array}} \right]} \end{array} $

(16)

对L中的元素按式(6)进行更新，当所有元素满足式(8)时，输出更新后的矩阵L，此时得到降相关后的协方差矩阵${\mathit{\boldsymbol{\bar Q}}_{\hat z\hat z}} = \mathit{\boldsymbol{\bar LD}}{\mathit{\boldsymbol{\bar L}}^{\rm{T}}}$。

2.3 扰动升序法

扰动升序法(perturbed ascending sorting strategy, PERT)源自Xu^[13]提出的基于Cholesky分解的并行算法，主要以自然升序法为基础，在迭代计算的第2步和第3步中使用对称旋转法加入扰动因素，最终完成协方差矩阵Q_ââ的降相关。

3 实验分析

由于时间效率和成功率是对一个算法性能优劣最直观的反映，本文分别采用模拟数据和实测数据对3种排序算法的降相关时间、搜索时间、总体耗时及Bootstrapping成功率进行对比分析，其中Bootstrapping成功率是模糊度采用序贯取整法正确解算的概率，可作为整数最小二乘模糊度估计成功率的下限^[14]。P_B的计算过程为：

$ {P_{\rm{B}}} = \prod\limits_{i = 1}^n {[2\Phi (\frac{1}{{2\sqrt {{d_i}} }}) - 1]} $

(17)

式中，d_i为${\mathit{\boldsymbol{Q}}_{\hat z\hat z}}$经过LDL^T分解后D的主对角线元素，Φ(x)为标准正态分布函数:

$ \Phi (x) = \int_{ - \infty }^x {\frac{1}{{\sqrt {2\pi } }}} \exp ( - \frac{1}{2}{z^2}){\rm{d}}z $

(18)

本文搜索算法均采用基于LDL^T分解的SE-VB算法^[15]。实验使用的计算机配置为i5-4210M处理器、8G内存、Windows 10系统，所有实验均在Matlab R2017b软件上完成。

3.1 模拟实验

本文模拟实验数据参考文献[5]提出的模拟方法，浮点解的构造为：

$ \hat a = 100 \times {\rm{rand}}\left( {n(n,1)} \right) $

(19)

式中，rand(n)为MATLAB内部函数，表示随机生成n个服从标准正态分布的元素。

协方差矩阵Q_ââ由下三角Cholesky分解构建，即

$ {\mathit{\boldsymbol{Q}}_{\hat a\hat a}} = \mathit{\boldsymbol{LD}}{\mathit{\boldsymbol{L}}^{\rm{T}}} $

(20)

式中，L为单位下三角矩阵，l_ij(i>j)服从标准正态分布，D为对角矩阵，主对角线元素为(10, 10, 10, 0.1, 0.1, …, 0.1)。

为尽可能模拟卫星在实际运行时产生的模糊度情况，本文采用15维和30维两组数据进行实验，分别模拟单系统和双系统两种情况，每组数据构建200个协方差矩阵，模拟200个历元情况。为避免偶然误差的影响，每个历元运行100次取平均计算结果，15维计算结果见表 1，30维计算结果见表 2。

从表 1和表 2可以看出，两组模拟实验情况下，采用SEQR排序方法模糊度平均解算结果的各项时间效率及Bootstrapping成功率最好，ASCE比PERT在降相关上耗时要少，但搜索时间较长，在解算较高维模糊度时，搜索耗时较长的劣势将被放大，进而导致整体耗时要比PERT的长。

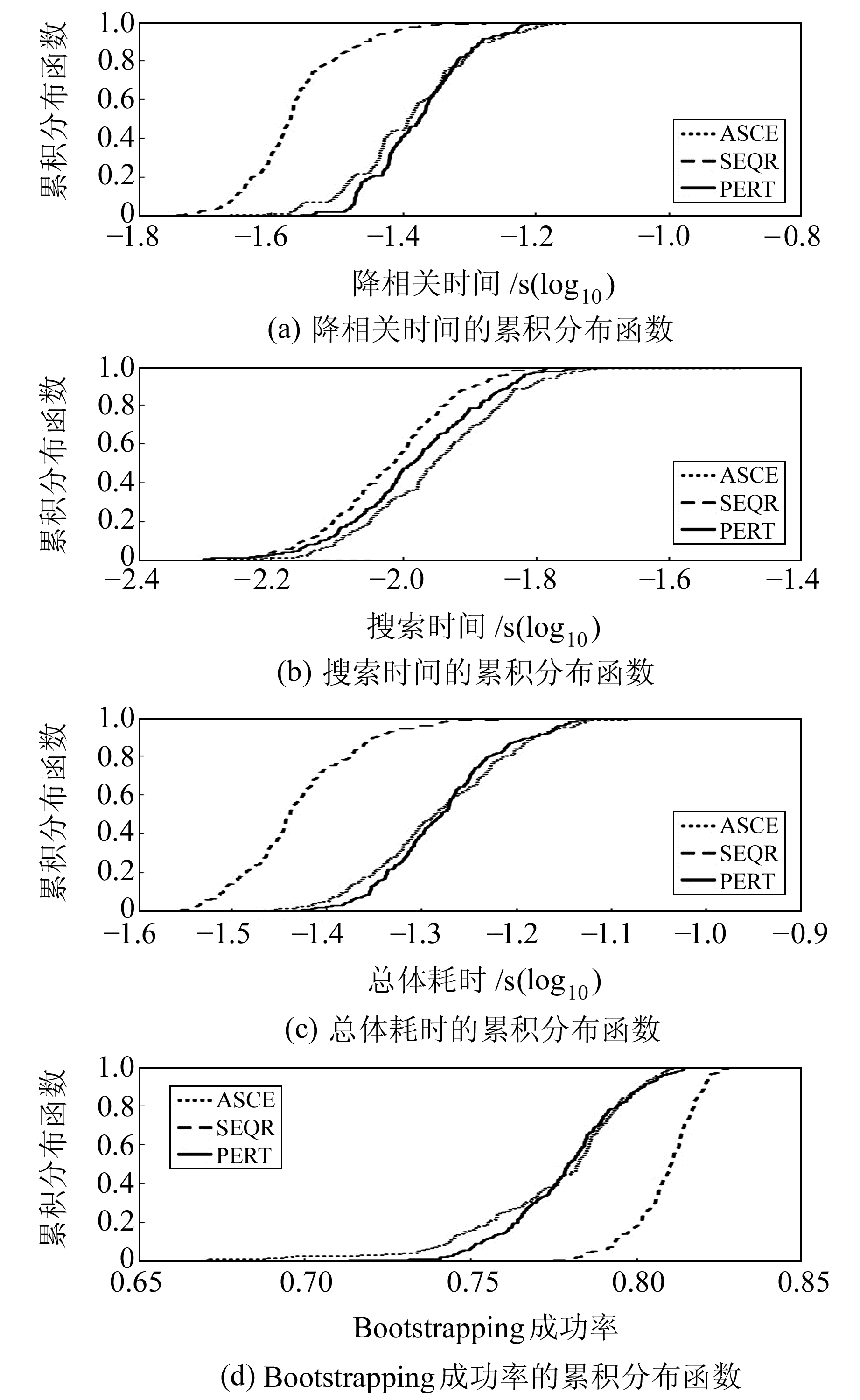
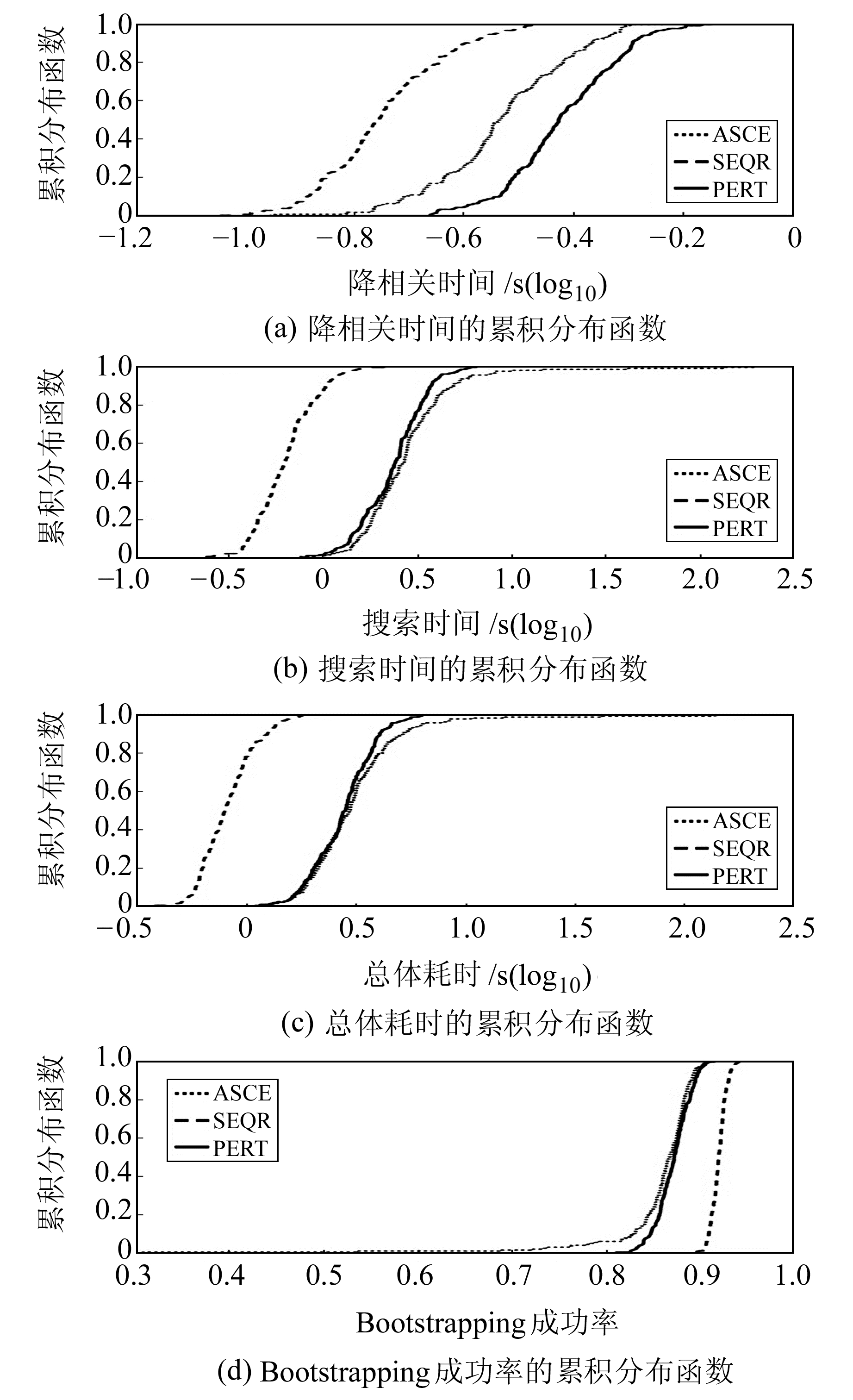
从图 1和图 2(图中log₁₀表示坐标轴取对数)可以看出，SEQR算法的降相关耗时、搜索耗时及整体耗时最少，且累积分布函数最为稳定，此外SEQR算法的Bootstrapping成功率也是3种算法中最优的。PERT算法在整体时间效率和成功率上与ASCE算法差异不大，但在分布的稳定性上要明显高于ASCE算法。此外，PERT算法的降相关效率要低于ASCE算法，但搜索效率更高，造成这种情况的原因在于，采用ASCE算法降相关后的协方差矩阵Q_ẑẑ和矩阵Z结构性能较差，在搜索过程中产生了异常节点，造成搜索时间过长，在高维情况下这种异常被放大，导致结果差异明显。

为探究3种排序方法各自的降相关程度与算法性能的关系，在15维和30维两种情况下，分别随机模拟了10 000组仿真数据来计算降相关后协方差矩阵条件数的累积分布函数，其中条件数是通过描述降相关后形成的搜索椭球区域的扁平程度来评价降相关的程度^[7]。条件数κ_β的计算方法为：

$ {\kappa _\beta }{\rm{ = }}{\lambda _{\max }}/{\lambda _{\min }} $

(21)

式中，λ_max为降相关后的协方差矩阵${\mathit{\boldsymbol{Q}}_{\hat z\hat z}}$的最大特征值，λ_min为${\mathit{\boldsymbol{Q}}_{\hat z\hat z}}$的最小特征值。

从图 3可以看出，条件数的大小排列依次为PERT < ASCE < SEQR。结果表明，尽管PERT算法的降相关程度最高，但其算法的解算速度和成功率较差，且过高的降相关程度反而增加其降相关耗时；而SEQR算法的降相关程度尽管在3种算法中最差，但算法整体效率和成功率是最高的。

3.2 实测实验

为进一步对比3种算法的性能，实验采用一组由NovAtel OEM628板卡采集的静态观测数据，基线长为3.6 km，采样间隔为1 s，实验数据采用前200个历元的GPS+BDS单历元处理结果。

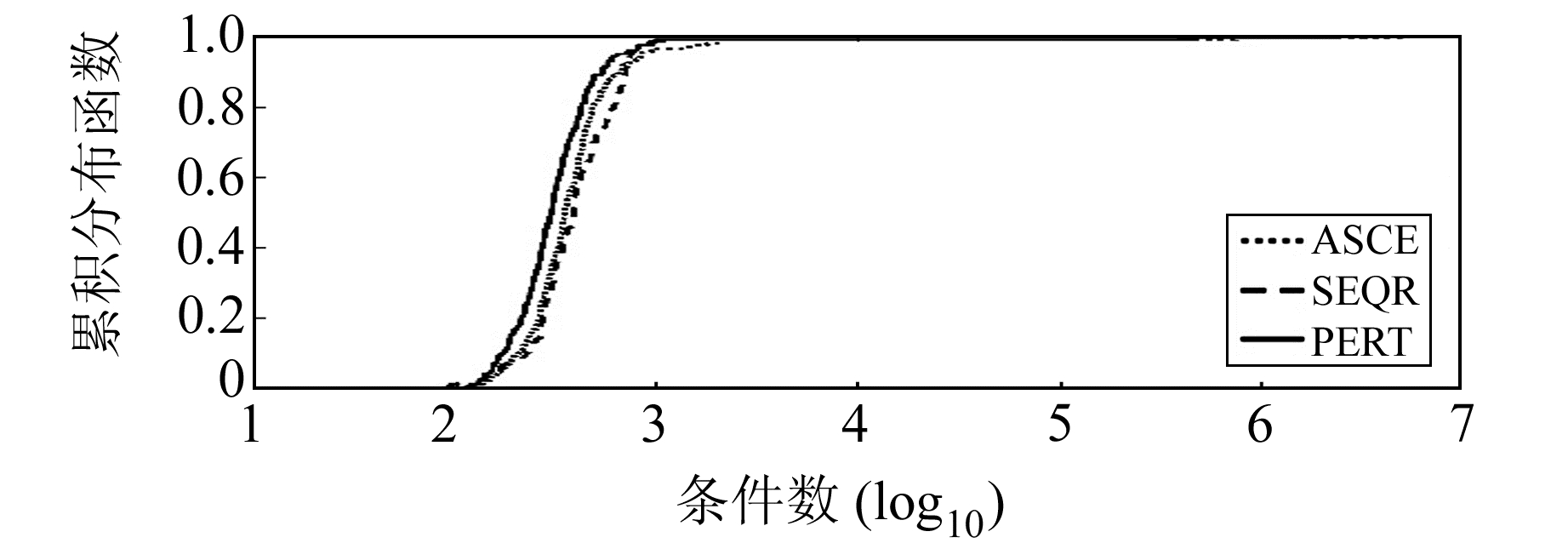
表 3为该组实测数据前200个历元的平均解算结果，图 4为前200个历元实测数据的累积分布函数，图 5为前200个历元实测数据浮点解协方差矩阵降相关后条件数的累积分布函数。从图表可以看出，SEQR算法的总体性能最好，但降相关程度最差；ASCE算法的降相关效率要高于PERT算法，但降相关程度不及PERT算法；PERT算法的搜索效率要高于ASCE算法。由于实测数据的浮点解精度较高，3种方法的搜索时间和Bootstrapping成功率差异不明显，此时Bootstrapping成功率无法体现3种算法的性能。由于搜索算法的时间差异不明显，而PERT算法的降相关耗时明显高于ASCE算法，所以PERT算法的总体耗时较长。

3.3 结果分析

通过分析模拟实验和实测实验的结果可知，3种排序算法对降相关性能的影响主要体现在两个方面：1)降相关效率的差异；2)对搜索效率的影响。

降相关效率存在差异的主要原因首先在于3种算法本身的复杂度不同，其中SEQR算法的执行效率最高，而PERT算法因为结合了前两种算法，使得算法的复杂度增加，导致其效率最低；其次是3种算法的降相关程度不同，从条件数和降相关耗时的结果看，条件数越小(表明压缩椭球程度越高)降相关耗时越大。

通过对3种排序算法的原理和实验结果进行分析发现，影响搜索效率的主要原因在于是否对条件方差按一定方向排序。ASCE算法只是对协方差矩阵Q_ââ的对角线元素q_ii进行升序排序，并没有对条件方差进行排序，因此其搜索效率最低；SEQR算法在执行过程中不仅对q_ii进行了升序排序，而且对条件方差d_i按升序方式进行排序，故搜索效率最高；PERT算法在第2次和第3次迭代过程中，运用SEQR算法对条件方差进行排序，故搜索效率介于ASCE算法和SEQR算法之间。

4 结语

本文从理论上系统分析自然升序法、对称旋转法和扰动升序法3种排序算法，通过模拟实验和实测实验分别从降相关时间、搜索时间、整体时间、Bootstrapping成功率和条件数5个方面分析不同排序算法对模糊度降相关性能的影响，得出以下结论：

1) 通过对条件数和降相关时间进行理论分析可知，条件数可以衡量搜索椭球的压缩程度，进而表示降相关程度；降相关时间可以表示降相关算法本身的效率。比较3种排序算法的解算结果发现，降相关时间与条件数呈负相关关系，即降相关效率与搜索椭球压缩程度呈负相关关系，搜索椭球压缩程度越高，降相关效率越低。

2) 对条件数和搜索时间进行分析发现，SEQR算法的条件数最大(即搜索椭球压缩程度最低)，但搜索效率却最高，而PERT算法的条件数最小(即搜索椭球压缩程度最高)，而搜索效率却不及SEQR算法。分析结果表明，条件数与搜索时间并没有明显的相关关系，即单一的增强搜索椭球压缩程度并不能有效地提高搜索效率。

3) 通过分析3种排序算法的原理发现，提高搜索效率的关键在于对条件方差按一定方向进行排序。SEQR算法对条件方差按升序方式进行排列，使其搜索效率最高；PERT算法通过两次扰动对条件方差进行部分升序排列，故其搜索效率要略高于ASCE算法；而ASCE算法完全没有对条件方差进行排序，所以搜索效率最低。该结果为进一步改进降相关算法和研究其评价指标提供了方向。